安徽省安庆市2008~2009学年度第一学期教学质量监测高三数学试题(理科)
- 格式:doc
- 大小:1.02 MB
- 文档页数:10



2008年普通高等学校招生全国统一考试(安徽卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至 第4页。
全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2.答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮控干净后,再选涂其他答案标号。
3.答第Ⅰ卷时,必须使用0.5毫米的黑色笔迹签字笔在答题卡上书写,要求字体工事、笔迹清晰。
作图题可先铅笔在答题卡规定的位臵绘出,确认后再用0.5毫米的黑色笔迹字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、早稿纸上答题无效。
4.考试结束,务必将试题和答题卡一并上交。
参考公式:如果事件A 、B 互斥,那么()()()P A B P A P B +=+ 如果事件A 、B 相互独立,那么()()()P A B P A P B = 如果随机变量~(,)B n p ξ,那么(1-)D np p ξ= 球的表面积公式2S =4R π ;球的体积公式34V =3R π,其中R 表示球的半径第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数()231i i += 【 】 (A)2 (B)-2 (C)2i (D )-2i (2)集合{}{}|lg ,1,2,1,1,2A y R y x x B =∈=>=--,则下列结论中正确的是 【 】 (A){}2,1A B =-- (B)()(),0R A B =-∞ ð (C)()0,A B =+∞ (D)(){}2,1R A B =-- ð(3)在平行四边形ABCD 中,AC 为一条对角线,若A B =(2,4),A C =(1,3) ,B D= 【 】(A)(-2,-4) (B)(-3,-5) (C)(3,5) (D)(2,4)(4)已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是 【 】 (A)若,m n αα∥∥,则m n ∥ (B)若,αγβγ⊥⊥,则αβ∥ (C)若,m n ββ∥∥,则αβ∥ (B)若,m n αα⊥⊥,则m n ∥(5)将函数y=sin 23x π⎛⎫+⎪⎝⎭的图象按向量a 平移后所得的图象关于点,012π⎛⎫-⎪⎝⎭中心对称,则向量a 的坐标可能为 【 】 (A),012π⎛⎫-⎪⎝⎭ (B),06π⎛⎫- ⎪⎝⎭ (C),012π⎛⎫⎪⎝⎭(D),06π⎛⎫ ⎪⎝⎭ (6)设()880181...x a a x a x +=+++,则018,,...,a a a 中奇数的个数为 【 】 (A)2 (B)3 (C)4 (D)5(7)0a <是方程2210ax x ++=至少有一个负数根的 【 】 (A)必要不充分条件 (B)充分不必要条件(C)充分必要条件 (D)既不充分也不必要条件(8)若过点()4,0A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为 【 】(A)⎡⎣(B)((C),33⎡-⎢⎣⎦ (D)33⎛⎫- ⎪ ⎪⎝⎭ (9)在同一平面直角坐标系中,函数()y g x =的图象与x y e =的图象关于直线y x =对称,而函数()y fx =的图象与()y g x =的图象关于y 轴对称,若()1f m =-,则m 的值为 【 】 (A)-e (B )-1e(C)e (D)1e(10)设两个正态分布N(μ1, σ21)(σ 1 >0)和N(μ2, σ22)(σ2>0)的密度函数图象如图所示,则有 【 】(A) 1212,μμσσ<< (B) 1212,μμσσ<> (C) 1212,μμσσ>< (D) 1212,μμσσ>> (11)若函数()(),f x g x 分别为R上的奇函数、偶函数,且满足()()xfx g x e -=,则有【 】 (A)()()()230f f g << (B)()()()032g f f << (C)()()()203f g f << (B)()()()023g f f <<(12)12名同学合影,站成了前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是 【 】 (A)2283C A (B)2686C A (C)2286C A (D)2285C A2008年普通高等学校招生全国统一考试(安徽卷)数 学(理 科)第Ⅱ卷 (非选择题 共90分)考生注意事项:请用0.5毫米黑色签字笔在答题卡上.....作答,在试题卷上答题无效.........。
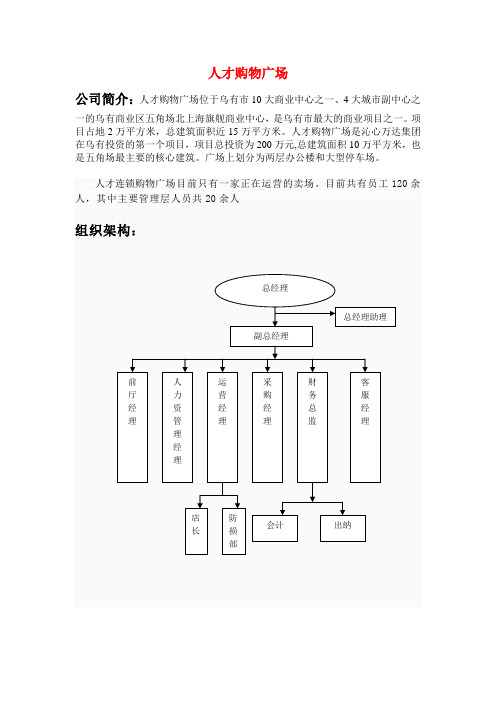
人才购物广场
公司简介:人才购物广场位于乌有市10大商业中心之一、4大城市副中心之
一的乌有商业区五角场北上海旗舰商业中心,是乌有市最大的商业项目之一。
项目占地2万平方米,总建筑面积近15万平方米。
人才购物广场是沁心万达集团在乌有投资的第一个项目,项目总投资为200万元,总建筑面积10万平方米,也是五角场最主要的核心建筑。
广场上划分为两层办公楼和大型停车场。
岗位职务:
总经理:公司最高领导
总经理助理:协助总经理处理好各项事务
副总经理:主要负责财务事物,监管采购和客户服务
前厅经理:主要负责客户接待和通知事项工作
人力资源管理经理:主要负责职工的考勤,岗位调动,培训开发,绩效考核以及薪酬管理的事物
运营经理:主管公司的日常运营和防损工作
采购经理:主要负责月初的采购货物和月末的盘点监管货物的质量检查
财务总监:主要负责公司的资金周转和运营状况
客服经理:主要负责客户的投诉,意见和建议反馈并及时做以回答和处理
店长:主要负责卖场的供货情况和安全防损工作
防损部:防损部员工主要负责公司安全工作和产品的保护
会计出纳:做好公司的每一笔账款记录并及时分析和汇报上级领导。

2009年高考安徽数学(理科)试题及参考答案本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷1至2页。
第II 卷3 至4页。
全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名,座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2.答第I 卷时、每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮檫干净后,在选涂其他答案标号。
3.答第II 卷时,必须用直径0.5毫米黑色黑水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后在用0.5毫米的黑色墨色签字笔清楚。
必须在标号所指示的答题区域作答,超出答题卡区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.考试结束,务必将试题卷和答题卡一并上交。
参考公式:S 表示底面积,h 表示底面的高如果事件A 、B 互斥,那么 棱柱体积 V S h = P(A+B)=P(A)+P (B) 棱锥体积 13V S h =第I 卷(选择题 共50分)一.选择题:本大题10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)i 是虚数单位,若17(,)2i a bi a b R i+=+∈-,则乘积a b 的值是(B )(A )-15 (B )-3 (C )3 (D )15 (2)若集合{}21|21|3,0,3x A x x B xx ⎧+⎫=-<=<⎨⎬-⎩⎭则A ∩B 是(D ) (A ) 11232x x x ⎧⎫-<<-<<⎨⎬⎩⎭或 (B) {}23x x <<(C) 122x x ⎧⎫-<<⎨⎬⎩⎭ (D) 112x x ⎧⎫-<<-⎨⎬⎩⎭(32(B )(A )22124xy-= (B )22142xy-= (C )22146x y -= (D )221410x y -=(4)下列选项中,p 是q 的必要不充分条件的是(A )(A )p:a c +>b+d , q:a >b 且c >d(B )p:a >1,b>1 q:()(10)xf x a b a =-≠>的图像不过第二象限(C )p: x=1, q:2x x =(D )p:a >1, q: ()log (10)a f x x a =≠>在(0,)+∞上为增函数(5)已知{}n a 为等差数列,1a +3a +5a =105,246a a a ++=99,以n S 表示{}n a 的前n 项和,则使得n S 达到最大值的n 是(B )(A )21 (B )20 (C )19 (D ) 18 (6)设a <b,函数2()()y x a x b =--的图像可能是(C )(7)若不等式组03434x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域被直线43y kx =+分为面积相等的两部分,则k 的值是(A ) (A )73(B )37(C )43(D ) 34(8)已知函数()cos (0)f x x x ωωω=+>,()y f x =的图像与直线2y =的两个相邻交点的距离等于π,则()f x 的单调区间是(C ) (A )5[,],1212k k k Zππππ-+∈ (B )511[,],1212k k k Z ππππ++∈(C )[,],36k k k Zππππ-+∈ (D )2[,],63k k k Zππππ++∈(9)已知函数()f x 在R 上满足2()2(2)88f x f x x x =--+-,则曲线()y f x =在点(1,(1))f 处的切线方程是(A ) (A )21y x =- (B )y x = (C )32y x =- (D )23y x =-+(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于(D ) (A )175(B ) 275(C )375(D )475二.填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。

2009年普通高等学校招生全国统一考试(安徽卷)数学(理科)第I 卷(选择题共50分)一、选择题:本大题共10个小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)i 是虚数单位,若1+7i2-ia bi =+(a 、b ∈R ),则乘积ab 的值是 (A )-15 (B )-3 (C )3 (D )15 (2)若集合A={x |︱2x-1︱<3},B={x |2x+13-x<0},则A ∩B 是 (A ){x |-1<x <1-2或2<x <3} (B ){x |2<x <3} (C ){x |1-2<x <2} (D ){x |-1<x <1-2}(3)下列曲线中离心率为26的是 (A )14222=-y x (B )12422=-y x (C )16422=-y x (D )110422=-y x (4)下列选项中,p 是q 的必要不充分条件的是 (A )d b c a p +>+:, d c b a q >>且:(B )11:>>b a p ,, :q )1,0()(≠>-=a a b a x f x且的图像不过第二象限 (C )1:=x p , x x q =2:(D )1:>a p , )1,0(log )(:≠>=a a x x f q a 且在),0(+∞上为增函数 (5)已知{}n a 为等差数列,105531=++a a a ,99642=++a a a 。
以n S 表示{}n a 的前n 项和,则使得n S 达到最大值的n 是(A )21 (B )20 (C )19 (D )18 (6)设b a <,函数)()(2b x a x y --=的图像可能是0≥x(7)若不等式组 43≥+y x 所表示的平面区域被直线34+=kx y 分为面积相等的两43≤+y x 部分,则k 的值是 (A )37 (B )73 (C )34 (D )43 (8)已知函数)0(cos sin 3)(>+=ωωωx x x f ,)(x f y =的图像与直线2=y 的两个相邻交点的距离等于π,则)(x f 的单调递增区间是 (A )Z k k k ∈⎥⎦⎤⎢⎣⎡+-,,12512ππππ (B )Z k k k ∈⎥⎦⎤⎢⎣⎡++,,1211125ππππ (C )Z ∈⎥⎦⎤⎢⎣⎡+-k ,6k 3k ππππ, (D )Z k 326k ∈⎥⎦⎤⎢⎣⎡++,,ππππk (9)已知函数)(x f 在R 上满足88)2(2)(2-+--=x x x f x f ,则曲线)(x f y =在点))1(,1(f 处的切线方程是(A )12-=x y (B )x y = (C )23-=x y (D )32+-=x y (10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于 (A )751 (B )752 (C )753 (D )754(在此卷上答题无效)2009年普通高等学校招生全国统一考试(安徽卷)数 学(理科)第Ⅱ卷(非选择题 共100分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上.....作答,在试题卷上答题无效.......... 二. 填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置. (11)若随机变量X~N (μ,σ2),则P (X ≤μ)= . (12)以直角坐标系的原点为极点,x 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线的 极坐标方程为)(4R ∈=ρπθ,它与曲线αcos 21+=x(α为参数)相交于两点A 和B ,则 αsin 22+=y|AB|= .(13)程序框图(即算法流程图)如图所示,其输出结果是 .(14)给定两个长度为1的平面向量OA 和OB ,它们的夹角为120°.如图所示,点C 在以O 为圆心的圆弧AB 上变动.若OB y OA x OC +=,其中R y x ∈,,则x+y 的最大值是 .(15)对于四面体ABCD ,下列命题正确的是 (写出所有正确命题的编号). ①相对棱AB 与CD 所在的直线异面;②由顶点A 作四面体的高,其垂足是△BCD 三条高线的交点;③若分别作△ABC 和△ABD 的边AB 上的高,则这两条高所在的直线异面;④分别作三组相对棱中点的连线,所得的三条线段相交于一点; ⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.三、解答题:本大题共6小题,共75分。
安徽省安庆市2009年高三模拟考试(二模)09.3.26数 学 试 题(理科)本试卷分第Ⅰ卷(选择题)和(第Ⅱ卷)(非选择题)两部分,全卷满分150分,考试时间120分钟。
一、 选择题(本大题共12小题,每小题5分。
在每小题给出的四个选项中,只有一项是符合题目要求的) 1、 复数z 满足()1z i i i -=+,则复数z 的模为 A 、2 B 、1 CD2、下面框图表示的程序所输出的结果是 A 、2021 B 、1920 C 、 4121D 、39203、一个几何体的三视图如上图所示,则该几何体外接球的表面积为 A 、3πB 、43πC 、83πD 、163π4、极坐标方程2cos21ρθ=表示的曲线为A 、两条直线B 、椭圆C 、双曲线D 、抛物线5、已知等差数列{}n a 的前n 项和为n S ,且2510,55S S ==,则过点P(n ,)n a 和2(2,)n Q n a ++()n N *∈的直线的一个方向向量的坐标是A 、(2,1)2B 、1(,2)2--C 、1(,1)2-- D (1,1)-- 6、已知直线L 经过点(2,1)2,其横截距与纵截距分别为,a b (,a b 均为正数),则使a b c +≥恒成立的c 的取值范围(第2题图) 2 2 2 22 2 侧视图俯视图第3题图A 、9(,]2-∞ B 、(0,1] C 、(,9)-∞ D 、(,8]-∞7、设()lg(101)xf x ax =++是偶函数,4()2x xbg x -=是奇函数,那么a b +为A 、2B 、1C 、12D 、0 8、在锐角三角形ABC 中,设(1sin )(1sin ),(1cos )(1cos )x A B y A B =++=++,则x 、y 大小关系为 A 、x>y B 、x y ≥ C 、x<y D 、x y ≤9、已知命题p :不等式|x|+|x-1|>m 的解集为R ,命题q :命题()(52)x f x m =-- 是减函数,则p 是q 的A 、充分但不必要条件B 、必要但不充分条件C 、充要条件D 、即不充分也不必要条件 10、已知定义在R 上的函数()y f x =满足()(2)f x f x -=-+,当x>1 时,()f x 单调递减,若122x x +<且12(1)(1)0x x --<,则12()()f x f x +的值为A 、恒小于0B 、恒大于0C 、可能等于0D 、可正可负11、已知椭圆C 的方程为2214x y +=,双曲线D 与椭圆有相同的焦点12,,F F P 为它们的一个交点,若120PF PF =,则双曲线的离心率e 为 ABC 、D12、某同学在自己房间的墙上挂了一块边长为3的正方形木板, 上面画有振幅为1的正弦曲线半个周期的图案用于练习投镖, 如图所示。
2008年普通高等学校招生全国统一考试(安徽卷)数 学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第2页,第Ⅱ卷第3至第4页.全卷满分150分,考试时间120分钟.考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的座位号、姓名,并认真核对答题卡上所粘贴的条形码中“座位号、姓名、科类”与本人座位号、姓名、科类是否一致.2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.3. 答第Ⅱ卷时,必须用0.5毫米黑色墨水签字笔在答题卡上书写.在试题卷上作答无效. 4. 考试结束,监考员将试题卷和答题卡一并收回. 参考公式:如果事件A B ,互斥,那么球的表面积公式 24πS R = ()()()P A B P A P B +=+其中R 表示球的半径 如果事件A B ,相互独立,那么()()()P A B P A P B =球的体积公式 34π3V R =如果随机变量(,),B n p ξ那么 其中R 表示球的半径(1)D np p ξ=-第I 卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1).复数 32(1)i i +=( )A .2B .-2C .2i D . 2i -(2).集合{}|lg ,1A y R y x x =∈=>,}{2,1,1,2B =--则下列结论正确的是( )A .}{2,1AB =--B . ()(,0)RC A B =-∞C .(0,)AB =+∞D . }{()2,1R C A B =--(3).在平行四边形ABCD 中,AC 为一条对角线,若(2,4)AB =,(1,3)AC =,则AB =( )A . (-2,-4)B .(-3,-5)C .(3,5)D .(2,4)(4).已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( )A .,,m n m n αα若则‖‖‖B .,,αγβγαβ⊥⊥若则‖C .,,m m αβαβ若则‖‖‖D .,,m n m n αα⊥⊥若则‖(5).将函数sin(2)3y x π=+的图象按向量α平移后所得的图象关于点(,0)12π-中心对称,则向量α的坐标可能为( )A .(,0)12π-B .(,0)6π-C .(,0)12πD .(,0)6π(6).设88018(1),x a a x a x +=+++则0,18,,a a a 中奇数的个数为( )A .2B .3C .4D .5(7).0a <是方程2210ax x ++=至少有一个负数根的( )A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件(8).若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( )A .[B .(C .[33-D .(33-(9).在同一平面直角坐标系中,函数()y g x =的图象与x y e =的图象关于直线y x =对称。
2009年普通高等学校招生全国统一考试(安徽卷)数学(理科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分,第I 卷1至2页。
第II 卷3 至4页。
全卷满分150分,考试时间120分钟。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名,座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2.答第I 卷时、每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮檫干净后,在选涂其他答案标号。
3.答第II 卷时,必须用直径0.5毫米黑色黑水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后在用0.5毫米的黑色墨色签字笔清楚。
必须在标号所指示的答题区域作答,超出答题卡区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.考试结束,务必将试题卷和答题卡一并上交。
参考公式:S 表示底面积,h 表示底面的高如果事件A 、B 互斥,那么 棱柱体积 V S h = P(A+B)=P(A)+P (B) 棱锥体积 13V S h =第I 卷(选择题 共50分)一.选择题:本大题10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)i 是虚数单位,若17(,)2ia bi ab R i+=+∈-,则乘积ab 的值是(B ) (A )-15 (B )-3 (C )3 (D )15 (2)若集合{}21|21|3,0,3x A x x B xx ⎧+⎫=-<=<⎨⎬-⎩⎭则A ∩B 是(D )(A ) 11232x x x ⎧⎫-<<-<<⎨⎬⎩⎭或 (B) {}23x x <<(C) 122x x ⎧⎫-<<⎨⎬⎩⎭ (D) 112x x ⎧⎫-<<-⎨⎬⎩⎭(3(B )(A )22124x y -= (B )22142x y -= (C )22146x y -= (D )221410x y -=(4)下列选项中,p 是q 的必要不充分条件的是(A )(A )p:a c +>b+d , q:a >b 且c >d(B )p:a >1,b>1 q:()(10)xf x a b a =-≠>的图像不过第二象限(C )p: x=1, q:2x x =(D )p:a >1, q: ()log (10)a f x x a =≠>在(0,)+∞上为增函数 (5)已知{}n a 为等差数列,1a +3a +5a =105,246a a a ++=99,以n S 表示{}n a 的前n 项和,则使得n S 达到最大值的n 是(B )(A )21 (B )20 (C )19 (D ) 18 (6)设a <b,函数2()()y x a x b =--的图像可能是(C )(7)若不等式组03434x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域被直线43y kx =+分为面积相等的两部分,则k 的值是(A ) (A )73 (B ) 37 (C )43 (D ) 34(8)已知函数()cos (0)f x x x ωωω=+>,()y f x =的图像与直线2y =的两个相邻交点的距离等于π,则()f x 的单调区间是(C )(A )5[,],1212k k k Z ππππ-+∈ (B )511[,],1212k k k Z ππππ++∈(C )[,],36k k k Z ππππ-+∈ (D )2[,],63k k k Z ππππ++∈(9)已知函数()f x 在R 上满足2()2(2)88f x f x x x =--+-,则曲线()y f x =在点(1,(1))f 处的切线方程是(A )(A )21y x =- (B )y x = (C )32y x =- (D )23y x =-+(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于(D ) (A )175 (B ) 275 (C )375 (D )475二.填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
安徽省安庆市2008~2009学年度第一学期教学质量监测高三数学试题(理科)一、 选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项的序号填写在答题卷相应的表格内) 1、集合{1,0,1},{|cos ,}A B y y x x A =-==∈,则AB = ( ).A {0} .{1}B .{0,1}C .{1,0,1}D - 2、若110a b<<,则下列结论不正确的是 ( ) 22.A a b < 2.B ab b < .2a bC b a+> .||||||D a b a b +>+3、设A 、B 两点的坐标分别为(1,0),(0,1)-,条件甲:0AC BC ∙>;条件乙:点C 的坐标是方程221(0)43x y y +=≠的解,则甲是乙的 ( ) .A 充分不必要条件 .B 必要不充分条件.C 充要条件 .D 既不是充分条件也不是必要条件4、根据表格中的数据,可以判定方程20xe x --=的一个根所在的区间为 ( ).(1,0)A - .(0,1)B .(1,2)C .(2,3)D5、已知△ABC 的三边,,a b c 满足222a b c +-=,则△ABC 是 ( ) .A 锐角三角形 .B 直角三角形.C 最大角等于0135钝角三角形 .D 最大角等于0120钝角三角形6、公差不为0的等差数列{}n a 中,23711220a a a -+=,数列{}n b 是等比数列,且77b a =,则68b b = ( ).A 2 .B 4 .C 8 .D 167、设,a b 是非零向量,若函数()()()f x xa b a xb =+∙-的图像是一条直线,则必有( ).A a b ⊥ .//B a b .||||C a b = .||||D a b ≠8、如图,一个空间几何体的主视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为 ( ).1A 1.2B 1.3C 1.6D9、已知(1,0)A -、(1,0)B ,以AB 为一腰作090DAB ∠=的直角 梯形ABCD ,且||3||,AD BC CD =中点的纵坐标为1,若椭圆以A 、B 为焦点且经过点D ,则此椭圆的方程为( )22.132x y A += 22.134x y B += 22.143x y C += 22.154x y D +=10、若关于x 的方程|21|x m -=有两个不相等的实数根,则实数m 的取值范围是 ( ).(0,)A +∞ .(0,1)B .(1,)C +∞ .[0,1]D11、如图所示,四边形ABCD 中,00//,,45,90AD BC AD AB BCD BAD =∠=∠=,将△ABD 沿BD 折起,使平面ABD ⊥平面BCD ,构成三棱锥A BCD -,则在三棱锥A BCD -中,下列命题正确的是.A 平面ABD ⊥平面ABC .B 平面ADC ⊥平面BDC .C 平面ABC ⊥平面BDC .D 平面ADC ⊥平面ABC12、已知函数()log (01)a f x x a a =>≠且满足23()()f f a a> 则1(1)1f x->的解是 ( ).A 10x a <<.B 101x a <<- .C 11x a << .D 111x a<<-二、填空题(本大题共4个小题,每小题4分,共16分)13、以221124y x -=的焦点为顶点,顶点为焦点的椭圆方程为____________. 14、为了了解高三学生的身体状况,抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为12,则抽取的男生人数是___________.15、右上图给出一个程序框图,其运行结果是________.16、甲、乙两人玩数字游戏,先由甲心中任想一个数字为a ,再由乙猜甲刚好想的数字,把乙想的数字记为b ,且,{1,2,3,4,5,6}a b ∈,若||1a b -≤,则称“甲乙心有灵犀”,现任意找出两个人玩这个游戏,得出他们“心有灵犀”的概率为_________.三、解答题:(本大题共6个小题,分值分别为12分、12分、12分、12分、13分、13份、共74分。
解答应写出文字说明,证明过程或演算步骤)17、(本题满分12分)在△ABC 中,角,,A B C 的对边分别为,,a b c 向量2(2s i n ,3),(2c o s 2.2c o s 1)2B m B n B =-=-,且//m n (1)求锐角B 的大小;(2)如果2b =,求△ABC 的面积ABC S #的最大值18、(本题满分12分)函数22()log 1xf x x -=-的定义域为集合A ,关于x 的不等式2212()()2ax a x a R +<∈的解集为B ,求使A B B =的实数a 的取值范围19、(本题满分12分)已知数列{}n a 的前n 项和为n S ,且对任意n N *∈,有,,n n n a S 成等差数列 (1)求数列{}n a 的通项公式; (2)求数列{}n na 的前n 项和n T20、(本题满分12分)如图,直三棱住111ABC A B C -090,1,ABC CB ∠==CA =1AA =M 为侧棱1CC 上一点,1AM BA ⊥。
(1)求证:AM ⊥平面1A BC ; (2)求二面角B AM C --的大小; (3)求点C 到平面ABM 的距离。
21、(本题满分13分)设直线:1l y x =+与椭圆22221(a b 0)x y a b+=>>相交于A 、B 两个不同的点,与x 轴相交于点F 。
(1)证明:221a b +>; (2)若F 是椭圆的一个焦点,且2AF FB =,求椭圆的方程。
22、(本题满分13分)设12()(,2x x af x a b b+-+=+为常数)。
(1)当1a b ==时,证明:()f x 不是奇函数; (2)设()f x 是奇函数,求a 与b 的值;(3)当()f x 是奇函数时,研究是否存在这样的实数集的子集D ,对任何属于D 的x 、c ,都有2()33f x c c <-+成立?若存在试找出所有这样的D ;若不存在,请说明理由。
安徽省安庆市2008-2009学年度第一学期教学质量监测高三数学试题参考答案及评分标准(理科)一、选择题(本大题共12小题,每小题5分,共60分)二、填空题:(本大题共 4个小题,每小题 4 分,共 16 分 )13. 221164y x += 14. 48 15.30 16. 94三、解答题17. (本题满分12分)解:(Ⅰ)n m// B B B 2cos 3)12cos 2(sin 22-=-∴ B B 2cos 32sin -=∴ 即 32t a n -=B ……………2分又B 为锐角 ()π,02∈∴B ……………………………4分322π=∴B 3π=∴B ……………………………………6分 (Ⅱ)得,由余弦定理acb c a B b B 2cos 2,3222-+===π0422=--+ac c a又ac c a 222≥+ 代入上式得:4≤ac (当且仅当 2==c a 时等号成立)…9分343sin 21≤==∆ac B ac S ABC (当且仅当 2==c a 时等号成立) 3的最大值为ABC S ∆∴……………………………………………………12分18.(本题满分12分) 解:A B B A B =∴⊂由 20 {|12}1xA x x x ->⇒=<<- 由 2212() 222axa x ax a x +<⇒<-- 即 2(1)a x a +<-………………4分若 10a +< 即 1a <-则 212(1)2(1)3a ax A B a a a >-⊂∴-≤⇒≤-++ ∴1a <- 若 10a += 即 1a =- 则x R ∈ 满足 1A B a ⊂∴=-适合若 10a +> 即 1a >- 则 422(1)2(1)5aa x A B a a a <-⊂∴-≥⇒≤-++ 415a ⇒-<≤- 综上,4(,]5a ∈-∞- ……………………12分 19.(本题满分12分)解:(Ⅰ)依题意知:n a S n n -=2 )1(211+-=++n a S n n12122111+=⇒--=⇒+++n n n n n a a a a a ……………………2分)1(211+=+⇒+n n a a ……………………………………………4分又由11112 1 1S a a a ==-⇒=故{1}n a +是首项为2,公比为2的等比数列, 12 21n n n n a a ∴+=⇒=-…6分(Ⅱ)12(121)(222)(2)n n T n n =⨯-+⨯-++⨯-2(12222)(12)n n n =⨯+⨯++⨯-+++ ………………………………8分由错位相减法得:2112222(1)22n n n n +⨯+⨯++⨯=-+ ………………10分又(1)122n n n ++++=所以:2)1(22)1(1+-+-=+n n n T n n ………12分 20.(本题满分12分)证明:(Ⅰ)在直三棱柱ABC -A 1B 1C 1中,易知面ACC 1A 1⊥面ABC ,∵∠ACB=90°,∴BC ⊥面ACC 1A 1, ………2分 ∵AM ⊂面ACC 1A 1,∴BC ⊥AM ∵1AM BA ⊥,且1BCBA B =,∴ AM ⊥平面1A BC ……4分解:(Ⅱ)设AM 与A 1C 的交点为O ,连结BO ,由(1)可知AM ⊥ OB ,且AM ⊥ OC ,所以∠BOC 为二面角B -AM -C 的平面角,……6分在Rt △ACM 和Rt △A 1AC 中,∠OAC+∠ACO=90°,∴∠AA 1C=∠MAC∴Rt △ACM ∽Rt △A 1AC ,∴21AC MC AA =⋅∴MC =∴在Rt △ACM中,AM = ∵1122AC MC AM CO ⋅=⋅,∴1CO = ∴在Rt △BCO 中,tan 1==∠COBCBOC ∴45BOC ∠=︒,故所求二面角的大小为45° …… 8分 (Ⅲ)设点C 到平面ABM 的距离为h,易知BO =,可得1132222ABM S AM BO ∆=⋅⋅=⋅ ……9分 ∵C ABM M ABC V V --= ∴1133ABM ABC hS MC S ∆∆⋅=⋅⋅,∴22322ABCABMMC S h S ∆∆⋅=== ∴点C 到平面ABM的距离为2……12分 解法二:(1)同解法一 ……………4分(Ⅱ)如图以C 为原点,CA ,CB , CC 1所在直线分别 为x 轴,y 轴,z 轴,建立空间直角坐标系,则1(0,1,0)A A B ,设1(0,0,)M z∵1AM BA ⊥,∴10AM BA ⋅=即1300-++=,故1z =,所以M ……6分 设向量(,,)m x y z =为平面AMB 的法向量,则,m AM m AB ⊥⊥,则0m AM m AB ⎧⋅=⎪⎨⋅=⎪⎩ 即00y ⎧=⎪⎨⎪+=⎩, 令x =1,则平面AMB 的一个法向量为)(1,23,m =,显然向量CB 是平面AMC 的一个法向量, 2cos ,||||m CB m CB m CB ⋅<>==⋅ 易知,m 与CB 所夹的角等于二面角B -AM -C 的大小,故所求二面角的大小为45°.……8分(Ⅲ)向量CB 在法向量m 上的投影的长||||m CB m⋅即为所求距离, ∵||32||mCB m ⋅== ∴点C 到平面ABM ……12分 21(本小题满分13分)(Ⅰ)证明:将112222=++=by a x x y 代入,消去x ,得0)1(2)(222222=-+-+a b y b y b a ① ……………………3分由直线l 与椭圆相交于两个不同的点,得0)1(4)1)((44222222224>-+=-+-=∆b a b a a b a b b所以 122>+b a …………………5分 (Ⅱ)解:设),(),(2211y x B y x A ,由①,得 22222122221)1(2b a a b y y b a b y y +-=+=+, ………………7分因为 2122y y FB AF -==,得所以, 222222212222212)1(2y ba ab y y y b a b y y -=+-=-=+=+,消去2y ,得 22222222)2(2)1(ba b b a a b +-=+- 化简,得22228)1)((b a b a =-+ ……………………10分 因F 是椭圆的一个焦点,故1,122-==a b c 代入上式,解得 272922==b a , ………………12分 所以,椭圆的方程为 1729222=+y x ………………13分 22.(本小题满分13分)(Ⅰ)举出反例即可.1212)(1++-=+x xx f ,511212)1(2-=++-=f ,412121)1(=+-=-f ,所以)1()1(f f -≠-,)(x f 不是奇函数;……………4分 (Ⅱ))(x f 是奇函数时,)()(x f x f -=-,即bab a x x x x ++--=++-++--112222对定义域内任意实数x 成立.化简整理得0)2(2)42(2)2(2=-+⋅-+⋅-b a ab b a x x,这是关于x 的恒等式,所以⎩⎨⎧=-=-042,02ab b a 所以⎩⎨⎧-=-=21b a 或⎩⎨⎧==21b a . 经检验都符合题意.……………8分(Ⅲ)(1)当⎩⎨⎧==21b a 时,121212212)(1++-=++-=+x x x x f ,因为02>x,所以112>+x ,11210<+<x ,从而21)(21<<-x f ;而4343)23(3322≥+-=+-c c c 对任何实数c 成立;所以可取D =R ,对任何x 、c 属于D ,都有33)(2+-<c c x f 成立.……10分(2)当⎩⎨⎧-=-=21b a 时,)0211212212)(1≠-+-=---=+x x f xx x (, 所以当0>x 时,21)(-<x f ;当0<x 时,21)(->x f ;1)因此取),0(+∞=D ,对任何x 、c 属于D ,都有33)(2+-<c c x f 成立.2)当0<c 时,3332>+-c c ,解不等式321121≤-+-x 得:75log 2≤x . 所以取]75log ,(2-∞=D ,对任何属于D 的x 、c ,都有33)(2+-<c c x f 成立.………13分。