连“点”成“线”

九点连线问题知识的表征方式九点连线问题是一种求解数形结合题目中，从一个点到另一个点的连线。

当两个以上的点连在一起，当相邻两个以上的点连在一起时可以求解。

也就是一组九个小圆圈可以被分解成九个九点小圆。

从表1可以看出求解九点连线问题的关键在于需要将每个点或圆中的任意两点连线起来，并且将每一点与小圆中另一个点或圆的连接长度乘以3就可以得到结果。

从表2可以看出九点连线问题的本质就是：一个点可以连得更多。

具体到这个九点连线问题的表征方式就是：以点为起点画一个直线到两个圆圈之间的所有点（即起点）或者两个圆圈之间的所有点为终点时所出现的问题。

因为九点连线问题是两个以上相邻数量点发生连接而引起这两个以上数形结合题目中：一个连线有一个方向就有另外一个方向的连线的问题；一个连线是多点还是单点都是由连不起来而起的问题。

一、两种方法最早的九点连线问题出现在高中数学教学实践中。

当时我们所讲的数形结合题型很大一部分属于几何应用题。

其中比较典型的题型为：以一组十个左右的小圆圈作为一个基本载体，分别画出每个小圆圈都有的一点与其相连接来求解这个九点连线问题。

其中的方法如图2所示：第一个方法就是在每个小圆中画出一个长为1的点（或圆）到一个点（或圆）之间的所有点（即起点）或者是所有点（或圆）之间的所有点（或圆）。

从表3中可以看出第三个方法是通过最短连接的距离乘以1而求解出九点连线问题；而第三种方法最终结果是三个点连成一条直线通过了该点连接距离乘以1得到了答案。

因此只要想求解这个九点连线问题，我们首先要解决的是两个方法：第一种方法是把两个半径相等的相同点通过画圆的方法进行连接获得了答案；第二种方法是以点为起点画一个直线到两个圆圈之间所有点（或圆）。

因为这个九点连线问题已经从数学角度考虑了它本身具有很多性质，因此只要根据题目中所要求的条件进行计算就可以得出答案。

二、计算分析现在我们开始计算，我们知道计算所需要的公式。

为了便于我们理解，我们先算出一个长度为3的方块体积，再乘以3得到最后的结果：其中: n×3=(3×1+3×3)/3,我们得3=9×9 (9×3)+9×9)=15×15),我们就知道了结果是9×9=16 (9×10)/16=17^12;又知道了每条直线被分解成9个扇形区域也就是10×9=10*10 (9×10)=20个扇形区域。

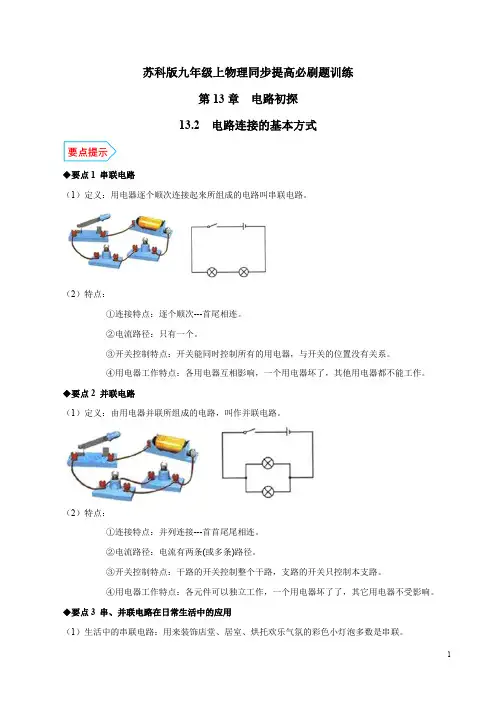
苏科版九年级上物理同步提高必刷题训练第13章电路初探13.2电路连接的基本方式◆要点1 串联电路（1）定义：用电器逐个顺次连接起来所组成的电路叫串联电路。

（2）特点：①连接特点：逐个顺次---首尾相连。

②电流路径：只有一个。

③开关控制特点：开关能同时控制所有的用电器，与开关的位置没有关系。

④用电器工作特点：各用电器互相影响，一个用电器坏了，其他用电器都不能工作。

◆要点2 并联电路（1）定义：由用电器并联所组成的电路，叫作并联电路。

（2）特点：①连接特点：并列连接---首首尾尾相连。

②电流路径：电流有两条(或多条)路径。

③开关控制特点：干路的开关控制整个干路，支路的开关只控制本支路。

④用电器工作特点：各元件可以独立工作，一个用电器坏了了，其它用电器不受影响。

◆要点3 串、并联电路在日常生活中的应用（1）生活中的串联电路：用来装饰店堂、居室、烘托欢乐气氛的彩色小灯泡多数是串联。

（2）生活中的并联电路：装点天安门等高大建筑物上的成千上万只灯泡是并联的，家庭中各用电器都是并联的，街道两旁的路灯是并联的，竞赛时的抢答器的电路是并联的，电冰箱中的灯泡和发动机之间是并联的。

（3）生活中串并联电路的识别：①串联电路：各个用电器互相影响，通则都通，断则都断。

②并联电路：各个支路用电器独立工作，互不影响，某一支路断路时，其他支路仍为通路。

③判断方法：电流流向法、隔离用电器法、节点法、结构观察法。

◆要点4 电路图与实物图的对应画法（1）根据电路图连接实物图：对照电路图，从电源正极出发，逐个顺次地将实物图中的各元件连接起来即可。

①在电路图中任选一条单一的回路，并对照这个回路在实物图中将相应的元件连接好。

②对照电路图，把所选回路以外的元件分别补连到实物图的相应位置，在连入回路以外的元件时，要找出电路中电流的分流点和会合点，将回路以外的元件连接在两点之间（2）根据实物图连接电路图：要用规定的电路符号代替实物，按照实物的连接方式画出规范的电路图。

五、拓展阶段
请同学们，想一想，为了我们能在年级坐立行比赛中夺得冠军，我们如何精彩的布置编排我们的方阵呢？
六、板书设计彩线连彩点
线、 点、 组合
（设计意图：将重点知识板书，有利于学生重点知识的掌握，一目了然。）
学生学习效果评价
本课学生学习美术的兴趣较浓厚，本课的结构安排上环环相扣，教学方法比较适合学生的心理发展特点，学生对重点知识的掌握较好，能用点和线美术元素进行创作，并能说出自己创作的感想。对点和线的初步认识，在课堂上我多次让学生从生活中找一找，看一看，再到画一画环节，调动学生的积极性，从而使学生掌握了点线的组合方式，创造出更美的画面。学生创作的进步不一样，有的学生很快画完了，能画2-3幅，有个别学生只画了一幅，所以，要区别对待，没画完的到课下时间再接着画。鼓励下次专注一些，提高绘画速度。
小结：今天同学们大胆的用点和线画出了美丽的画面，希望以后同学们，牵着彩线跳跳舞，拉着彩点转个圈，成为快乐的好朋友！
（设计意图：多种评价方式，在评价时多引导学生学会如何评价）
五、拓展阶段
同学们，在年级坐立行比赛的准备过程中，我们设计了“最美瞬间展示”和“彩点牵着彩线舞蹈”的设计我们每一个同学就是一个班集体中闪光的点，我们牵着彩线后，我们就变成了一股强大的力量，相信我们团结一心，一定能夺得冠军，加油，同学们！
（设计意图：教师通过承接上一节课的问题引入课题。激发学生的兴趣）
二、发展阶段
1.带着彩线和彩点动起来
师:要想动起来，我们首先要考虑哪些问题？生：线的姿态，点的分布。是的，不用的彩点和彩线带给我们的不同感受。
板书：线、点
师：那我们先按照第一名同学说的，同学们穿上彩色的上衣在方阵中随着音乐节拍，跳舞，动作统一，这样的布局会很美。你发现这种方法我们在编排上要注意什么问题？

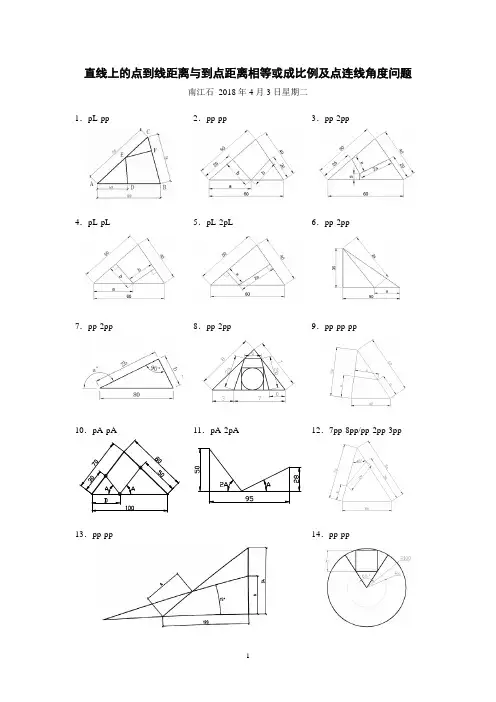
直线上的点到线距离与到点距离相等或成比例及点连线角度问题南江石 2018年4月3日星期二1．pL-pp 2．pp-pp 3．pp-2pp4．pL-pL 5．pL-2pL 6．pp-2pp7．pp-2pp 8．pp-2pp 9．pp-pp-pp10．pA-pA 11．pA-2pA 12．7pp-8pp/pp-2pp-3pp14．pp-pp13．pp-pp15．pp-pp 16．pp-pp17．pp-pp 18．pp-pp（1）点线距离与点到点的距离相等pL-pp题目1【解法1】相似三角形法【解法1】相似三角形法几何原理：相似三角形对应边比例相同CAD 操作：定点偏侧复制（通过点偏移，o-t ），参照缩放，sc-r ，对齐缩放，aL【解法2】三点圆法几何原理：圆半径相等以圆心到直线距离为半径作圆，直线与该圆相切，并垂直于切点处的半径 切点与定点在所求点为圆心的同一圆周上 圆弧垂直于直径半径CAD 操作：三点圆，交点-切点-垂足（c-3p-end-tan-per ） 操作步骤：命令: c CIRCLE 指定圆的圆心或 [三点(3P)/两点(2P)/切点、切点、半径(T)]: 3p 指定圆上的第一个点:指定圆上的第二个点: tan 到 指定圆上的第三个点: per 到【解法2】三点圆法题解【解法3】镜像三点圆法 几何原理：同题解2过圆心的直线为直径线圆相对于任何直径线半径线对称，对称图形的几何关系对称 相对于直径线对称的两半圆弧与其他对称图形的关系对称CAD 操作：镜像，三点圆，端点-端点-切点（c-3p–end–end–tan ）镜像，三点圆，切点-切点-交点（c-3p–tan–tan–int ）【解法3】镜像三点圆法，端点-端点-切点【解法3】镜像三点圆法，切点-切点-交点（2）点到一点的距离与点到另一点的距离相等pp-pp题目2题目14【解法4】垂直平分线法几何原理：线段的垂直平分线到线段两端点的距离相等 CAD 操作：中的穴点旋转复制【解法4】垂直平分线法题目2题解【解法1】相似三角形法题目14题解题目13【解法1】相似三角形法，解2题目13题解题目15【解法1】相似三角形法，题解1【解法1】相似三角形法，题解2 【解法1】相似三角形法，题解3题目16 【解法1】相似三角形法，解1【解法1】相似三角形法，解2 题目16题解题目9 1解2，题目9题解题目17 【解法1】相似三角形法，解1解2，题目17题解【解法5】椭圆法几何原理：以椭圆短轴为直径作同心圆，则与椭圆长轴平行的直线被椭圆、圆和短轴所截的线段成定比例，且比例为椭圆的长短轴之比CAD操作：椭圆【解法6】图块法CAD技巧：AutoCAD插入图块时，X轴、Y轴、Z轴方向可以采用不同的插入比例CAD操作：制作图块B，插入图块I，爆破X题目18 【解法5】椭圆法，题解【解法6】图块法，题解（3）点到一点的距离与点到另一点的距离成比例pp-2pp，pp-3pp等题目3 题目6 题目7题目8 题目12【解法7】阿波罗尼斯圆法几何原理：到两定点的距离为定比的动点的轨迹，是以两定点的内外定比分点连线为直径的圆，到两定点的距离为定比的点在阿波罗尼斯圆上。

学员编号：年级：课时数：学员姓名：辅导科目：物理学科教师：授课时间教学目标1. 知道串联电路和并联电路连接的特点; 2．会动手连接串联电路和并联电路; 3．会画简单的串联、并联的电路图;重点难点通过探究发现串并联电路的特点;目录Contents上节课回顾:作业检查+知识点复习一、导入二、知识梳理+经典例题三、随堂检测四、归纳总结五、课后作业上节课回顾：一、作业检查情况完成未完成二、知识点回顾~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~知识讲解课堂流程···§串联和并联···想想做做用一个电源、两个灯泡、一个开关和一些导线组成电路,要想让两个小灯泡都发光,可以有几种接法猜想……提出问题：在连接电路之前,思考连接电路时需注意哪些问题温馨提示1．开关要断开.2．绝不允许把电源的正负极直接用导线连接起来.3．连接电路后,需检查电路连接无误,然后方可闭合开关.接法1：接法2：你能根据连接的实物电路画出电路图吗一、串联和并联1．用电器依次相连的电路叫做串联电路;1特点：只有一条回路；2接画法：从电源正极出发,沿电流方向把元件依次相连;2．用电器并列相连的电路叫做并联电路;1特点:有多条回路,有干路和支路;有分流点和汇合点；2接画法：从电源正极出发,沿电流方向把每条回路的元件依次相连;二、连接串联电路和并联电路实验1:在串联电路中,开关的位置改变了,它的控制作用是否改变呢结论一：1在串联电路中,开关控制所有用电器;开关位置的改变不影响它对用电器的控制作用;2在串联电路中,各个用电器相互影响;实验2：在并联电路中,干路开关和支路开关对各用电器的控制作用有什么不同呢连接好电路检查无误后,按如下操作观察开关对两只灯泡的控制情况;1.开关S、S1、S2都闭合,灯泡L1___,L2____;填亮或不亮;2.开关S和S1闭合,S2断开,灯泡L1___, L2___;填亮或不亮;开关S和S2闭合,S1断开,灯泡L1___ ,L2___;填亮或不亮;3. S断开, S1和S2闭合, 灯泡L1___, L2___;填亮或不亮;4. S闭合, S1和S2断开, 灯泡L1___, L2___;填亮或不亮;结论二：1在并联电路中,干路开关控制所有用电器;2在并联电路中,支路开关只能控制所在支路的用电器;3在并联电路中,各个用电器独立工作,互不影响;点拨归纳1、串联电路：一处断路整路断,只有一条回路;2、并联电路：一支路断路另支路通,有两条以上回路;3、判断串并联方法：1断路法：断开任意用电器,另一用电器不能工作的是串联,能工作的是并联;2回路法：只有一条电流回路的是串联,有两条或两条以上的是并联;三生活中的电路1．家庭中的电灯、电扇、电冰箱、电视机、电脑等用电器是怎样连接的2. 街旁的路灯排成一列,路灯是串联还是并联3．教室里的各盞灯及插座是怎样连接的4．一个开关控制两个小灯泡,一定串联吗例1下列说法正确的是A、在连接电路的过程中,开关应该断开;B、用一只开关控制两盏灯,这两盏灯一定是并联的;C、一般电路中,开关应最靠近电源正极;D、我们教室内的电灯之间是并联的,和邻班的电灯是串联的;例2如图所示,下列四个电路图中与右边实物图对应的是A．B．C．D．例3一般家庭的卫生间都要安装照明灯和换气扇,使用时,有时需要各自独立工作,有时需要同时工作,你认为符合上述要求的是例4根据实物电路画电路图;例5根据电路图连接实物电路;例6根据实物电路画电路图;识别串并联电路的方法：电流路径法：电路中只有一条电流路径,中途不分流,则为串联;电路中电流从正极流出在某一点分流,经过用电器后又在某点汇合,最终回到负极,则为并联;拆除法：去掉任意一个用电器：若其他用电器不能正常工作,则为串联；若其他用电器能正常工作,则为并联;定义法：用电器依次相连相互影响的是串联；用电器并列相连,且各自独立工作互不影响是并联;1．如图所示的四个电路图中,开关闭合时,三盏灯属于并联关系的是节点法：在电路中,无论导线多长,只要中间没有电源、用电器等,则导线可以视为一个点;若用电器连接在同一个点上,则为并联；若连接在不同点上则为串联;2. 如图要用两个开关分别控制两个灯泡,应该怎样连接电路请在图中画出接线;3. 按照图甲的电路图,用笔画线表示导线,把图乙中所示的实物连接起来,并用箭头在电路图中标出干路和两个支路在开关闭合时的电流方向;4. 请分别根据图所示的两个实物电路画出它们的电路图;5. 如图所示,学校有前、后两个门,在前、后门各装一个按钮开关,学校传达室有甲、乙两盏灯和电池组;要求：前门来人按下开关时甲灯亮,后门来人按下开关时乙灯亮;请设计电路图并在实物图中连线;···§电流的测量···想一想你认为电力机车和工作时的电流有什么不同一、电流的强弱1．电流I：表示电流强弱的物理量;2．单位：安培,简称安,符号是A;电流的常用单位：毫安mA 1 mA=10-3 A微安mA 1 mA =10-6 A小资料二、电流的测量1. 电流表：测量电路中电流的仪器;认识电流表的结构：单位、指针、刻度盘、调零螺母、负接线柱、正接线柱、量程、分度值;电流表的电路符号：2. 电流表的连接：1电流表必须和被测的用电器串联;2电流必须从红正接线柱流入,从黑负接线柱流出;3必须正确选择电流表量程试触法;4不允许把电流表直接连到电源的两极注意：电流表内部电阻很小,相当于一根导线;注意：使用前,应指针归零调零;例1以下电路中,电流表连接方法正确的是3. 电流表的读数：1明确所选电流表的量程；2确定电流表的分度值；3由指针位置读出示数;先大格后小格;量程：分度值：示数为：例2请读出下列电流表的示数;思考：改变电流表在电路中的位置,影响测量结果吗,请举例子说明4. 实验过程中的电流表故障1若指针偏向左侧刻度线以外2若指针偏角太小3若指针偏向右侧刻度线以外4若电流表与用电器并联,则该用电器,电流表,可能烧坏电流表；例3连接实物图,要求两灯并联,开关控制两盏灯,电流表测灯L2的电流约A,并画出电路图;例4根据所给电路图连接实物图;例5开关控制,电流表A1测的电流,电流表A2测的电流;再画出电路图;试触法：为避免电流过大损坏电流表,在不能事先估算电流的情况下,先选择大量程后,可以先闭合开关然后迅速断开叫做“试触”,看看在开关闭合的瞬间指针的偏转是否在最大测量值之内;若在小量程范围内,则改用小量程,因为小量程分度值小更精确;1. 流过某手电筒小灯泡的电流大约是A,等于多少毫安某半导体收音机电池的供电电流最大可达120 mA,等于多少安2. 画线连接下面的实物图图,使小灯泡能够发光并且电流表能够测出流过小灯泡的电流估计为~ A3. 某同学在使用电流表测量通过某一灯泡的电流的实验,闭合开关后,发现电流表的指针偏转到如图所示的位置,于是他立即断开开关.则：1测量时产生这种现象的原因是；2该同学为了完成实验,下一步应该采取的措施是;3改正错误后,该同学再闭合开关,发现指针的读数是,请你在图中画出指针的位置;4.在图甲所示的电路中,A1的示数为,A2的示数如图乙所示．下列判断正确的是A ．通过L l的电流为B．通过L l的电流为C．通过L2的电流为D．通过L2的电流为5. 在图中,能正确测量通过灯L1电流的电路是~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~归纳总结一、串联和并联1.串联电路：把电路元件逐个顺次连接起来特点：①电流只有一条路径②各用电器相互影响③开关控制所有用电器,开关位置的改变不影响它对用电器的控制作用2.并联电路：把电路元件并联连接起来特点：①电流有两条或两条以上路径②用电器互不影响③干路的开关控制所有用电器,支路的开关只控制所在支路的用电器二、生活中的电路：家庭电路、路灯、、、、、、三、串联电路和并联电路的特点：~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~串并联1. 教室里有4盏电灯,去掉其中任意一盏灯泡,另外三盏电灯都能继续发光,则这4盏灯A．一定是串联; B．一定是并联;C．可能是串联,也可能是并联; D．无法判断;2. 一个开关,能同时控制三个灯泡,则这三个灯泡的连接方式为A．一定是串联; B．一定是并联;C．串联或并联都可以; D．以上都不对;3.在组成串联电路和并联电路的实验中,连接电路前,先要________________,电路的连接要按照________进行,连接电路时,开关要跟所控制的用电器________,且开关应该是________的,为防止因电路连错而损坏实验器材,要经________后再闭合开关进行观察．4. 在如图所示的电路中,灯泡L1和L2的连接方式依次是连接方式串联电路并联电路连接特点逐个顺次连接并列连接在两点之间电流路径电流的路径只有一条电流的路径两条或两条以上开关作用开关控制整个电路,开关位置对它的控制作用没有影响干路开关控制所有用电器支路开关只控制本支路用电器用电器间是否相互干扰各用电器相互干扰,若其中一个断开,其它无法工作用电器互不影响 ,若其中一个断开,其它照常工作家庭作业A．并联、并联、并联、串联; B．串联、串联、并联、串联;C．并联、串联、并联、串联; D．串联、并联、并联、串联;5. 如图所示的电路中,3个灯泡始终完好;当开关S断开时,3个灯泡都发光；当开关S闭合时A． L1、L2、L3都不亮 B ．L1、L2、L3都亮C．L2不亮,L1、L3亮 D ．L1、L2不亮,L3亮6. 如图所示电路,开关可以使L1、L2同时发光和熄灭的是A、甲、丙B、乙、丁C、甲、丁D、丙、丁7. 如图所示电路中,灯、电动机和电铃都并联的电路图是．8. 如下图所示的各电路中,三盏灯并联的是A B C D9. 如图所示,L1、L2、L3三个灯泡的连接方式是A．三个串联 B．三个并联C．L1与L3串联后再与L2并联 D．L1与L3并联后再与L2串联10. 学了电路的串并联知识后,小文问“家中的电视机、电灯、电风扇等用电器之间是什么方式连接的”“当然是并联”小玲回答说;哪些现象能说明它们是并联的举一例3.画好电路图一定顺序串联断开检查连接无误达标练习 10. 各用电器都能独立工作；断开电灯不影响电视机工作 ; 例如电灯烧了,不影响其他用电器工作等等;11. 马路上的路灯应该是并联的电流的测量1. 在“探究并联电路电流的特点”实验中,实验电路如图甲所示,闭合开关S后,电流表A1、A2示数分别如图乙、丙所示,则通过灯泡L1、L2电流大小的判断正确的是A．L1的电流大于L2的电流 B．L1的电流等于L2的电流C．L1的电流小于L2的电流 D．无法比较L1、L2的电流大小2.①实验用的小灯泡的电流约为 ,等于mA．②半导体收音机电源的电流约为50 mA,等于A．③家用电冰箱的电流约1 A,等于μA．3.如图是测量通过小灯泡的四个电路图,其中接法正确的是4. 在使用电源时绝对不允许用导线把电源的正、负两极直接连接起来,这是因为A．电流太大,会损坏电源B．电流太大,会损坏用电器C．电流太小,用电器不能工作D．电流太大,会损坏电源和用电器5.一位同学在使用电流表测较小电流时,应该使用“—”和“”两个接线柱,但错误地使用了“—”和“3”两个接线柱接入了电路,其他操作正确,这样会出现：A．指针不动B．指针反向偏转C．指针摆动偏小D．指针摆动太大,电流表可能被烧坏6. 如图所示是小刚同学在探究电流特点的实验中曾经接过的电路,其中正确的电路是7. 如图所示是小明连接电流表时存在的问题,请在下面横线上分别写出造成其现象的原因．甲图的问题：_____________________；乙图的问题：____________________________．8. 请你帮助林铃用铅笔线代替导线,将图中的两灯连成串联电路,用电流表测量电路中的电流,在虚线框中画出对应的电路图;9.张华同学连接了如图所示的电路来测量电路中的电流．仔细观察一下他连接的电路是否正确___________________________,用文字描述原因．若不正确,要求只改动一根导线改成正确电路．10. 王刚在做一电学实验时,闭合开关后,发现电流表的指针偏转如图所示,产生这一现象的原因及纠正方法是 ;3. A 6.错误!200 错误!0. 05 错误!10611.1电流表的正、负接线柱接反了 2电流表的量程接大了 12.略 13.不正确,原因是电流表不经用电器直接接在电源两极修改电路如图所示~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~老师填写：上次讲义复习效果本次课堂重难点学员课堂表现随堂练习效果本次家庭作业老师建议：家长填写：讲义作业完成情况具体完成时间是否复习讲义家长建议或意见家长回馈并签字。

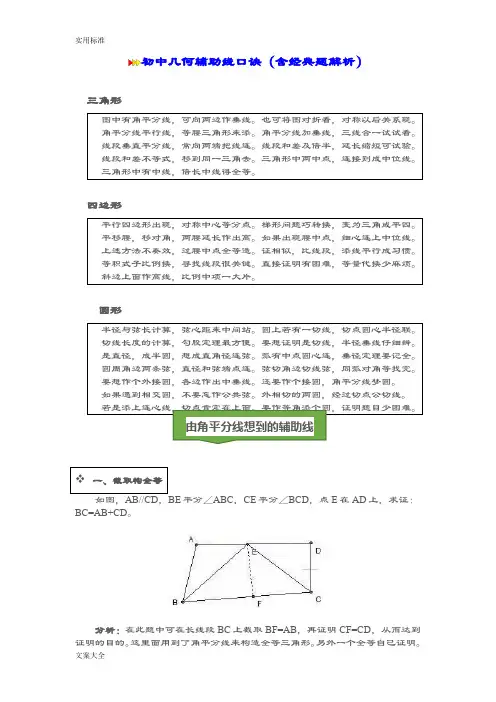
初中几何辅助线口诀（含经典题解析）BC=AB+CD。

如图，已知AB>AD, ∠BAC=∠FAC,CD=BC。

求证：∠ADC+∠B=180
如图，AB=AC，∠BAC=90 ，AD为∠ABC的平分线，CE⊥BE.求证：BD=2CE。

AC平分∠BAD，CE⊥AB，且∠B+∠D=180°，求证：AE=AD+BE。

中线。

已知ΔABC的面积为2，求：ΔCDF的面积。

分析：利用中线分等底和同高得面积关系。

CD的延长线分别交EF的延长线G、H。

求证：∠BGE=∠CHE。

如图，已知梯形ABCD中，AB//DC，AC⊥BC，AD⊥BD，求证：AC=BD。

分析：取AB中点得RTΔ斜边中线得到等量关系。

已知，如图△ABC中，AB=5，AC=3，则中线AD的取值围是。

∠C=180
由全等三角形想到的辅助线
如图，在△ABC的边上取两点D、E，且BD=CE，求证：AB+AC>AD+AE 的度数
BC＝17. 求CD的长。

分别是AD、BC的中点，连接EF，求EF的长。

的面积。

在梯形ABCD中，AD为上底，AB>CD，求证：BD>AC。

证：EF//AD
（2）在梯形ABCD中，AD∥BC，∠BAD=90°，E是DC上的中点，连接AE和BE，求∠AEB=2∠CBE。

分析：在梯形中出现一腰上的中点时，过这点构造出两个全等的三角形达到解题的目的。

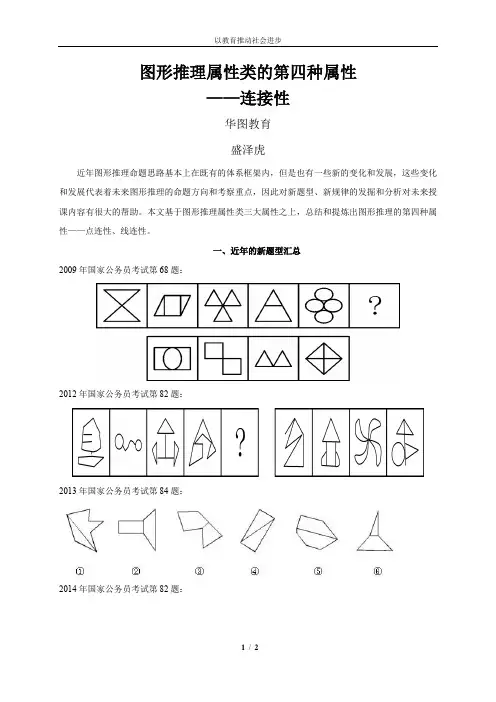
图形推理属性类的第四种属性——连接性华图教育盛泽虎近年图形推理命题思路基本上在既有的体系框架内，但是也有一些新的变化和发展，这些变化和发展代表着未来图形推理的命题方向和考察重点，因此对新题型、新规律的发掘和分析对未来授课内容有很大的帮助。

本文基于图形推理属性类三大属性之上，总结和提炼出图形推理的第四种属性——点连性、线连性。

一、近年的新题型汇总2009年国家公务员考试第68题：2012年国家公务员考试第82题：2013年国家公务员考试第84题：2014年国家公务员考试第82题：2014年天津公务员考试第71题：二、解题方法分析这些题除了2013年的84题外，都是考察点连接还是线连接这样的一个属性，将复合图形是通过一个点连接的称为点连接，将复合图形通过线连接的称为线连接。

而84题是考察线连接中的最长线连接这样的规律。

这些图形符合属性类的规律特点即图形极其简单或者极其复杂。

通过观察，发现这些图形有这样的一些特点：1、都是一个复合的图形。

所谓的复合图形指的是由两个以上图形组成的图形，而仅仅由一个图形组成的就是单图形。

2、复合图形的每个组成部分都是封闭图形。

3、复合图形是一个整体，没有独立的元素。

其实在复合图形中有一种性质叫做稳定性，就是按照图形的重合部分的多少来判断整个图形的稳定性，也就是不易分散成若干个部分的属性。

按照这种说法2013年的84题就可以认为每个图形通过长线连接的稳定性最好。

但是这样的一个后果就是不易分清图形的稳定性和物理的稳定性，以及这样的名词不够直观。

因此，本文还是采取点连性还是线连性这种说法，认为是除对称性、曲直性、封闭性外的第四种属性。

4\分为四类:点连接\线连接\连接线的长短\部分链接或者完全链接,可涵盖全部考题.。

因不染色的线段至多3条，所以至多去掉3个顶点，则还剩下6个顶点，其两两连线都染上了红色或蓝色．即得到k6（6阶完全图）图的2-染色．
熟知，存在同色三角形．
其次，存在一个9顶点32条边的图，把图的边2－染色，可使图中无同色三角形．如图所示，将9个点分成5组A＝{V1，V2}、B＝{V3，V4}、C＝{V5，V6}、D＝{V7，V8}、E＝{V9}，两组间连一条红线表示从这两组中任取一点都连有红线；两组间连一条蓝线表示从这两组中任取一点都连有蓝线；每一组内部的点之间不连线．该图构成有9个顶点，有C －4＝32条边，且不存在2－染色的同色三角形．
注意到di在上述和式中出现了di次，而G中共有m条边，故k≥ ( d －mn)．
由于 di＝2m，故n d ≥( di)2＝4m2 d ≥ ．∴k≥ ( －mn)＝ (m－ )．
例7．十个学生参加一次考试，试题共有十道，已知没有两个学生做对的题目完全相同，证明：这十道题中可以找到一道题，把这道题取消后，每两个学生所做对的题目仍不会全同．(假定每个题，都只有做对与做错这两种情况，没有部分对的情况发生)
设n＝k(k≥4)时，命题成立．当n＝k＋1时，由于统计各点连出线段数的和＝2 ＋2．则连线数最少的点A，则点A的连线数≤ ．
当k＝2t时， ＝t(t＋1)． ＝ (2t2＋2t＋2)＝t＋ ．即该点连线段数≤t．此时，去掉点A及所连之线段，则余下k个点，且余下线段数≥t2+1＝ +1．
当k＝2t－1时， ＝t2． ＝ (2t2＋2)＝t＋ ．即该点连线段数≤t．此时，去掉点A及所连之线段，则余下k个点，且余下线段数≥t2－t＋1＝ ＋1＝ ＋1．
⑷把数1，2，3，4，5任意分成两组，试证明：在这两组数中，总有一组数中存在两个数，它们的差(的绝对值)也在这一组中．

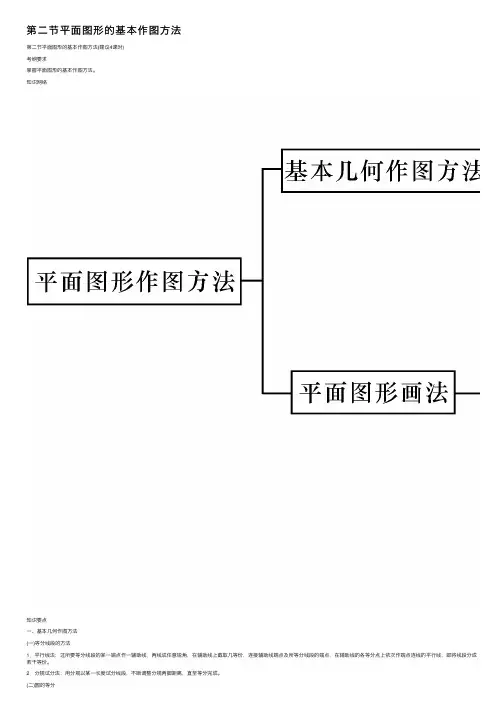
第⼆节平⾯图形的基本作图⽅法第⼆节平⾯图形的基本作图⽅法(建议4课时)考纲要求掌握平⾯图形的基本作图⽅法。

知识⽹络知识要点⼀、基本⼏何作图⽅法(⼀)等分线段的⽅法1．平⾏线法：过所要等分线段的某⼀端点作⼀辅助线，两线成任意锐⾓，在辅助线上截取⼏等份，连接辅助线端点及所等分线段的端点，在辅助线的各等分点上依次作端点连线的平⾏线，即将线段分成若⼲等份。

2．分规试分法：⽤分规以某⼀长度试分线段，不断调整分规两脚距离，直⾄等分完成。

(⼆)圆的等分1．尺规作图法：运⽤直尺、圆规，运⽤⼏何规律来等分。

要求能对圆周进⾏三、四、五、六等分的作图。

2．查表计算法：按公式a＝k·D(D为圆直径，k为等分系数)计算出正多边形每边长度，然后依次在圆周上截取，即得。

这种⽅法适合于任意等分圆周。

(三)椭圆的画法1．同⼼圆法(理论画法)：先求出曲线上⼀定数量的点，再⽤光滑的曲线将各点连接起来。

2．四⼼法(近似画法)：求出画椭圆的四个圆⼼和半径，⽤四段圆弧近似地代替椭圆。

(四)斜度与锥度画法1．斜度：⼀直线(或平⾯)对另⼀直线(或平⾯)的倾斜程度。

表⽰符号：∠或>，符号的⽅向应与斜度的⽅向⼀致。

2．锥度：指正圆锥体底圆直径与锥⾼之⽐。

表⽰符号?或?，符号所⽰⽅向应与圆锥⽅向⼀致。

3．斜度与锥度的⽐值均要写成1∶n的形式，如∠1∶n或?1∶n。

4．标注锥度时，锥度符号配置在基准线上，表⽰圆锥的图形符号和锥度应靠近轮廓标注，基准线应通过指引线与圆锥的轮廓素线相连。

基准线应与圆锥的轴线平⾏，图形符号的⽅向与圆锥⽅向⼀致。

当所标注的锥度是标准圆锥系列之⼀时，可⽤标准系列号和相应的标记表⽰。

(五)圆弧连接1．圆弧连接的实质，就是要使连接圆弧与相邻线段相切，以达到圆弧连接处光滑过渡的要求，切点即为连接点。

2．圆弧连接的基本作图步骤：(1)求作连接圆弧圆⼼；(2)找切点；(3)画连接圆弧。

作图时第(2)步找切点不要忽视，因为切点是连接圆弧的起点和终点，必须要找出。

连接和连结的区别
1、连接与连结都是指用线将两个点连起来，但“连接”两点的线可以是线段，也可以是曲线，而“连结”两点的线却只能是线段。

显然，联接两点有无数种方法，但连结两点却只有一种途径，特指连成线段；
2、连结两点是联接两点的一种特殊情形。

并且，在联结两点的线中，线段最短。

连接连结不同的是，连接是用一个点将两条线接起来，其关键在“接”，而连结则是用线将两个点连起来，其关键在“连”；
3、连接的“接”并非简单的接，而是要实现线与线间的平滑过渡。

连接主要有两种类型，一是线段与圆弧的连接，必须满足两个条件即线段所在直线与圆弧所在圆相切和线段与圆弧必须在圆心与切点所在直线的两侧；另一种是圆弧与圆弧的连接，也必须满足两个条件即圆弧所在圆必须相切和两段圆弧必须在连心线的两侧。

这种情况又分内连接和外连接，可见，线段与圆弧，圆弧与圆弧在连接处相切。

局面描写之宇文皓月创作（一）局面描写：1、用点连成线：总结：一个点，连一片，跟着点点连线线，连成一个大局面。

2、到底什么是局面描写呢？总结起来就是一句话：特定时间、特定地点、许多人物、一起活动。

连一连1：下面的局面会在什么特定时间和特定地点进行？连连线吧。

A玩“老鹰抓小鸡” 1.每逢初三或集市B赛龙舟 2.六一儿童节、运动场C挤车 3.课间、操场D人来人往买商品 4.端午节、西湖E赛跑5.春节后，火车站总结：发现了吗？原来这些都是“局面”：活动局面、考试局面、角逐局面、年节局面、赶集局面、观景局面、送别局面、挤车局面。

那这些局面会在什么作文题目中出现呢？你能对号入座吗？A活动局面 1.《记一次拔河角逐》B角逐局面 2.《记一次难忘的大扫除》C劳动局面 3.《上车记》D挤车局面 4.《怎一个“乐”字了得》3.说一说：你想写什么局面，起一个什么样的作文题目呢？比方：我想写考试局面，作文题目是《记一次紧张的考试》我想写（）局面，作文题目是《》3.怎样进行局面描写呢？回顾一下“局面描写”：我们回忆一下开我们画的图案，是用点连成面。

那么在局面描写中什么是点？什么是面呢？比方拔河局面：乍一看：一大片热闹景象，这就是“面”——“面”是局面给人的整体感受；仔细一看：看到一个个人，这就是“点”——点是局部给人的个体感受。

我们写的时候记住两句口诀：面点点面挨着写，写成一个大局面。

（二）实战演习：找面点：1句________ 2句_________ 3句___________1.“嘟——”哨声吹响了，激烈的拔河角逐在一片欢呼声中开始了，同学们拼命抓住绳子，用力拉起来。

2.有的眼睛瞪得圆圆的，两排牙齿咬得紧紧的；有的双眼紧闭，边使劲边大喊：“嘿——嘿——”；有的竭尽全力把绳子向后拉，身子拼命向后躺，几乎快要贴到地面上了。

3.大家一个个脸憋得通红，都使出了吃奶的力气。

总结：发现了吗？从面到点，从点又写到面。

而中间的点又分成了好多小点，一点一点又一点，这就叫“面点点面挨着写，写成一个大局面”。

常见的网络拓扑结构有哪些？并说明其优缺点。

计算机网络的拓扑结构是指网络中各个站点相互连接的形式，在局域网中明确一点讲就是文件服务器、工作站和电缆等的连接形式。

现在最主要的拓扑结构有总线型拓扑、星型拓扑、环型拓扑以及它们的混合型。

顾名思义，总线型其实就是将文件服务器和工作站都连在称为总线的一条公共电缆上，且总线两端必须有终结器；星型拓扑则是以一台设备作为中央连接点，各工作站都与它直接相连形成星型；而环型拓扑就是将所有站点彼此串行连接，像链子一样构成一个环形回路；把这三种最基本的拓扑结构混合起来运用自然就是混合型了。

计算机网络的拓扑结构是引用拓扑学中研究与大小，形状无关的点，线关系的方法。

把网络中的计算机和通信设备抽象为一个点，把传输介质抽象为一条线，由点和线组成的几何图形就是计算机网络的拓扑结构。

网络的拓扑结构反映出网中个实体的结构关系，是建设计算机网络的第一步，是实现各种网络协议的基础，它对网络的性能，系统的可靠性与通信费用都有重大影响。

最基本的网络拓扑结构有：环形拓扑、星形拓扑、总线拓扑三个。

1. 总线拓扑结构是将网络中的所有设备通过相应的硬件接口直接连接到公共总线上，结点之间按广播方式通信，一个结点发出的信息，总线上的其它结点均可“收听”到。

优点：结构简单、布线容易、可靠性较高，易于扩充，是局域网常采用的拓扑结构。

缺点：所有的数据都需经过总线传送，总线成为整个网络的瓶颈；出现故障诊断较为困难。

最著名的总线拓扑结构是以太网（Ethernet）。

2. 星型拓扑结构每个结点都由一条单独的通信线路与中心结点连结。

优点：结构简单、容易实现、便于管理，连接点的故障容易监测和排除。

缺点：中心结点是全网络的可靠瓶颈，中心结点出现故障会导致网络的瘫痪。

3. 环形拓扑结构各结点通过通信线路组成闭合回路，环中数据只能单向传输。

优点：结构简单，适合使用光纤，传输距离远，传输延迟确定。

缺点：环网中的每个结点均成为网络可靠性的瓶颈，任意结点出现故障都会造成网络瘫痪，另外故障诊断也较困难。

彩线连彩点教案彩线连彩点教案1教学目标：１、引导同学运用不同的点与线，自由表达自己想象中的画面，体验绘画与制造的乐趣。

２、引导同学把生活中常见的建筑、人物、字母及各种自然物体，用点、线、面概括成的形态进行重新组合，绘制成非具象的画面效果，产生丰富的想象空间。

教材简析：本课是让同学初步感受点、线、面的关系，但不要讲定义，只引导同学具有用点线面造型的意识，边画边说，引导同学感受点和线能组合成不同的图形。

教学重、难点：如何引导同学在实践中运用点线面作画。

教学预备:(1)师生课上要使用的：蜡笔、水笔、颜色纸。

(2)供同学欣赏的相关计算机图像、中国画资料。

《康定斯基作品选》。

教学活动过程:（１）引导阶段：１、欣赏《康定斯基作品选》、计算机图像资料和中国画资料中各种由点、线组成的画面。

引导同学打破常规的具象描写思维模式，用点线自由表现自己对事物的感受、从中感受到绘画与创作的乐趣。

２、通过欣赏引导同学用比一比、说一说等方法了解线的粗细、点的大小、颜色的`变化、画面的节奏以及其协调性。

３、出示各种常见的线材料，请同学说一说他们的名字、比一比他们的相同点和不同点（相同点：形状瘦长。

不同点：材料不同、有的直、有的弯、有粗有细、颜色不同。

）４、线材料变成点材料：老师把纸条揉成团、把纸条、绒线和绳子剪成小段或碎片。

引导同学观看他们的形状都发生了什么变化。

引申：再将点材料拼摆成线材料。

（２）进展阶段：１、体验用不同的笔画成不同的点和线；２、接受单线、涂色及剪贴等形式来表现自己对事物的感受。

３、鼓舞同学选择各种点线面组成新的画面。

利用手中的各种工具试着绘制一至两张与众不同的画面。

课后拓展：尝试在同一内容中用单线、涂色及剪贴各种不同形式表现物体形象、体会不同的画面效果。

教学评价：１、能否用点线大胆组合成一张完整的画面。

２、能否用其中一种形式自由表现自己的所见所闻。

３、能否与同学沟通自己画面所表达的意图。

彩线连彩点教案2教学目标：１、引导同学运用不同的点与线，自由表达自己想象中的画面，体验绘画与制造的乐趣。

【导语】这是⼀节学习具体造型知识的美术课。

点和线是体的造型语⾔，这节课中只是初步对点和线的形态进⾏了解，并运⽤它组织出⼀幅具有抽象美感的画⾯。

⽆忧考准备了以下内容，供⼤家参考!篇⼀ 教学⽬标： 1、⽤点、线⼤胆组合成⼀张完整的画⾯。

2、运⽤不同的点线，⾃由表达⾃⼰想象中的画⾯。

3、引导学⽣把⽣活中常见的建筑、⼈物以及各种⾃然物体、⽤点、线、⾯概括成完整的画⾯。

教学重、难点：能否⽤点、线、⾯组合成⼀张完整的画⾯。

教具学具：绘画⼯具 教学过程： ⼀、导⼊ 1、教师出⽰多种⼯具描绘出的各种点、线、⾯。

A、你觉得这些点、线、⾯有趣吗？ B、你在什么地⽅见过他们呢？ 2、揭⽰课题：彩线连彩点 师：你觉得彩线和彩点连在⼀起会是怎样的呢？ ⼆、欣赏作品 1、教师展⽰⼤师康定斯基的作品： 师：你从画中看到了那些东西？他们是怎样组合排列在⼀起的？ 2、展⽰⼉童有关于“彩线连彩点”的绘画作品和⼿⼯作品。

三、造型和表现 1、请学⽣思考： A、你想⽤点、线、⾯来表现画⾯吗？ B、想⼀想，你准备⽤他们来表现哪些东西？ 2、分⼩组尝试运⽤点、线、⾯来表现⾃⼰想表现的画⾯。

采⽤单线、涂⾊及剪贴等各种形式来表现⾃⼰对事物的感受。

进⼀步了解线的组细、点的⼤⼩、⾊彩的变化、画⾯的构图…… 3、组织⼩组之间相互学习，并对创作的难点重点“画⾯要完整”进⾏进⼀步讲解。

4、教师出⽰相关的作品帮助学⽣理解。

四、练习和评价 1、提出本节课练习的要求。

学⽣练习，利⽤⼿中的⼯具和喜欢的形式表现彩线连彩点的形象。

2、组织学⽣进⾏⾃评、互评。

3、教师适当评价，对课堂表现好的同学进⾏表扬和⿎励。

4、组织学⽣作好课堂结束的收拾和整 五、收拾整理篇⼆ (⼀课时) 教学⽬标：能⽤⾃⼰喜欢的颜⾊，⼤胆地涂绕。

1、能按⾃⼰意愿涂绕出不同的形象，培养学⽣的发散性思维。

2、在涂绕中感受到绘画的乐趣，增强学⽣的⾃信⼼。

教学重点：能按⾃⼰意愿，⼤胆地涂绕出不同的形象。

5.在邻居王阿姨关切的目光中接过了那碗热腾腾的面， 此时，我的内心——（感慨）
（1）对事件过程进行合理的取舍安排， 确定详写的部分；
（2）聚焦详写的部分，通过细节描写 的叠加来写好重点场景当中的一个个镜 头，反过来，一个个镜头也构成了一个 个丰富多彩的场景；
（3）在记叙过程中尝试运用心理与环 境描写来尝试议论与抒情。
详写or略写
略写 略写 略写 详写 详写 略写
三到六年级叙事文写作重点虽有 不同，但又互相关联，是一种递进的 关系，我们要清楚每个年级指导的重 点，把力气花在刀刃上。
二、连点成线
有些叙事文我们中段写，高段也在写， 那么，在习作指导的时候该如何加以区别， 既体现一个学段的特点，又体现习作指导的 递进性呢？
细节决定成败
1.抓点，突出特写镜头。
鸭子:“最后一只小鸭子，一直战战兢兢，不 敢上前，它一个劲地嘎嘎乱叫，摇头晃脑， 生怕路上的车子开来。呀，看，这小家伙， 连脚都似乎在抖了，叫声越来越急促了，真 是太糟糕了。
鸭妈妈:鸭妈妈昂着头，挺着胸，大步带领小 鸭子走过大街，一边走，一边还似乎在说:孩 子们，跟紧了，别怕! 勇敢向前，现在我们最 大！”
2.叙述过程加 环境描写心理描写 入议论抒情
《一颗螺丝钉》
场景 1.溜冰场溜冰，心情愉快 2.发现冰鞋掉螺丝，心情沮丧 3.大叔了解沮丧原因 4.大叔帮忙寻找螺丝 5.找到螺丝，大叔帮忙组装 6.和大叔告别，内心充满感激
《一颗螺丝钉》
场景
1.溜冰场溜冰，心情愉快 2.发现冰鞋掉螺丝，心情沮丧 3.大叔了解沮丧原因 4.大叔帮忙寻找螺丝 5.找到螺丝，大叔帮忙组装 6.和大叔告别，内心充满感激
总之，到了六年级，叙事文写 作就是一个聚焦再聚焦的过程，将 前面所学的写作方法，综合运用， 最终连线成面。

13.4 课题学习最短路径问题基础知识if車技能f 厂一.▲—亠 r ----------- ■—nr-^rr — --------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------I】I f J rz jr I s j F i j r JI t? x j j V f；1 .最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题，只要连接这两点，与直线的交点即为所求.如图所示，点A，B分别是直线I异侧的两个点，在I上找一个点C,使CA + CB最短，这时点C是直线I与AB的交点.(2)求直线同侧的两点与直线上一点所连线段的和最小的问题，只要找到其中一个点关于这条直线的对称点，连接对称点与另一个点，则与该直线的交点即为所求.如图所示，点A, B分别是直线I同侧的两个点，在I上找一个点C,使CA + CB最短，这时先作点B关于直线I的对称点B'贝山点C是直线I 与AB '的交点.B r为了证明点C的位置即为所求，我们不妨在直线上另外任取一点C',连接AC',BC',B'C‘，证明AC+ CB V AC’t’B•如下：证明：由作图可知，点B和B'关于直线对称，所以直线I是线段BB'的垂直平分线.因为点C与C'在直线上，所以BC= B'C, BC'=BC在△ABC '中,AB 'iAC'+C',所以AC+ B 'C<AC ' + C ',所以AC+ BC v AC ' -C B.【例1 ］在图中直线I上找到一点M ,使它到A, B两点的距离和最小.分析：先确定其中一个点关于直线I的对称点，然后连接对称点和另一个点，与直线I的交点M即为所求的点.解：如图所示：(1)作点B关于直线I的对称点B ';(2)连接AB '交直线于点M .(3)则点M即为所求的点.点拨：运用轴对称变换及性质将不在一条直线上的两条线段转化到一条直线上，然后用“两点之间线段最短”解决问题.基本方法塘本fig力^£JJ J fl K iM F A N f« F A J Hf K A X l< N ifJ JJ2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长，是解决距离之和最小问题的基本思路，不论题目如何变化，运用时要抓住直线同旁有两点，这两点到直线上某点的距离和最小这个核心，所有作法都相同.警误区利用轴对称解决最值问题应注意题目要求根据轴对称的性质、利用三角形的三边关系，通过比较来说明最值问题是常用的一种方法.解决这类最值问题时，要认真审题，不要只注意图形而忽略题意要求，审题不清导致答非所问.3.利用平移确定最短路径选址选址问题的关键是把各条线段转化到一条线段上.如果两点在一条直线的同侧时，过两点的直线与原直线的交点处构成线段的差最大，如果两点在一条直线的异侧时，过两点的直线与原直线的交点处构成的线段的和最小，都可以用三角形三边关系来推理说明，通常根据最大值或最小值的情况取其中一个点的对称点来解决.解决连接河两岸的两个点的最短路径问题时，可以通过平移河岸的方法使河的宽度变为零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.在解决最短路径问题时，我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上，从而作出最短路径的方法来解决问题.【例2］如图，小河边有两个村庄A, B,要在河边建一自来水厂向A 村与B村供水.A.E F(1)若要使厂部到A, B村的距离相等，贝S应选择在哪建厂？(2)若要使厂部到A, B两村的水管最短，应建在什么地方？分析：(1)到A, B两点距离相等，可联想到“线段垂直平分线上的点到线段两端点的距离相等”，又要在河边，所以作AB的垂直平分线，与EF的交点即为符合条件的点.(2)要使厂部到A村、B村的距离之和最短，可联想到“两点之间线段最短”，作A(或B)点关于EF的对称点，连接对称点与B点，与EF的交点即为所求.解：(1)如图1，取线段AB的中点G,过中点G画AB的垂线，交EF 于P,贝S P到A, B的距离相等.也可分别以A、B为圆心,以大于2AB为半径画弧，两弧交于两点，过这两点作直线，与EF的交点P即为所求.⑵如图2,画出点A关于河岸EF的对称点A'，连接A'B交EF于P，则P到A, B的距离和最短.【例3】如图，从A地到B地经过一条小河（河岸平行），今欲在河上建一座与两岸垂直的桥，应如何选择桥的位置才能使从A地到B地的路程最短?思路导引：从A到B要走的路线是A—M —N —B,如图所示，而MN是定值，于是要使路程最短，只要AM + BN最短即可.此时两线段应在同一平行方向上，平移MN到AC,从C到B应是余下的路程，连接BC的线段即为最短的，此时不难说明点N即为建桥位置，MN 即为所建的桥.解：（1）如图2，过点A作AC垂直于河岸，且使AC等于河宽.⑵连接BC与河岸的一边交于点N.（3）过点N作河岸的垂线交另一条河岸于点M •则MN为所建的桥的位置.■思维拓展0/新应川fV 石Bi F说i 彳石:i fj-.'A ivc x7前亍俑*; yriSr;4 .生活中的距离最短问题由两点之间线段最短（或三角形两边之和大于第三边）可知，求距离之和最小问题，就是运用等量代换的方式，把几条线段的和想办法转化在一条线段上，从而解决这个问题，运用轴对称性质，能将两条线段通过类似于镜面反射的方式转化成一条线段，如图，AO + BO = AC的长.所以作已知点关于某直线的对称点是解决这类问题的基本方法.【例4】（实际应用题）茅坪民族中学八⑵班举行文艺晚会，桌子摆成如图a所示两直排（图中的AO, BO）, A0桌面上摆满了橘子, 0B桌面上摆满了糖果，站在C处的学生小明先拿橘子再拿糖果，然后到D处座位上，请你帮助他设计一条行走路线，使其所走的总路程最短?A --------- 0irB图a解：如图b.(1)作C点关于OA的对称点C i，作D点关于OB的对称点D i, ⑵连接C iD i，分别交OA, OB于P, Q,那么小明沿C-P-Q-D 的路线行走，所走的总路程最短.5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键.先做出其中一点关于对称轴的对称点，然后连接对称点和另一个点，所得直线与对称轴的交点，即为所求.根据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值.破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方法.【例5］如图所示，A, B两点在直线I的两侧，在I上找一点C,使点C到点A、B的距离之差最大.ClB分析：此题的突破点是作点A（或B）关于直线I的对称点A'（或B）, 作直线A 'B（AB'）与直线I交于点C,把问题转化为三角形任意两边之差小于第三边来解决.解：如图所示，以直线I为对称轴，作点A关于直线I的对称点A',AB的连线交I于点C,则点C即为所求.理由：在直线I上任找一点C（异于点C），连接CA, CA, CA',CB.因为点A, A'关于直线I对称，所以I为线段AA '的垂直平分线，则有CA= CA',所以CA—CB=CA ' -CB= A B.又因为点C'在上，所以C 'A = C 'A '•在8 ' BC '中,C 'A—C B= C A' -C B v A B,所以C 'A ' -C B v CA —CB.点拨：根据轴对称的性质、利用三角形的三边关系，通过比较来说明最值问题是常用的一种方法.。