国防科技大学离散数学1997真题

一、填空题（每小题3分，共15分）1.谓词公式⌝(∀xF(x，y)∨∃yG(x，y))的前束范式为∃x∀y(⌝F(x，u)∧⌝G(v，y))．2.设A={1，2，3，4，5}，〈P(A)，⊕〉构成群，其中⊕为集合的对称差．令B={1，4，5}，则由B生成的循环子群〈B〉={∅，B}．3.模加群G=〈Z6, ⊕〉的所有生成元为1，5 ．4.n阶无向简单图G的∆=δ=n-1，则G为K n．5.设〈G，＊〉为群，a∈G且|a|=m，则|a-1|= m ．二、选择题（每小题3分，共15分）1.命题公式¬(p→q)∧q∧r的类型是【D】A．重言式．B．非重言式的可满足式．C．简单合取式．D．矛盾式．2.5阶无向完全图的非同构的自补图有【B】A．1个．B．2个．C．3个．D．4个．3.设〈A，*〉是独异点，e是其单位元，若∀a∈A，有a*a=e，则〈A，*〉【B】A．是群但不是Abel群．B．是Abel群．C．不是群．D．不是代数系统．4.树T中有3个3度顶点，2个2度顶点,其余顶点都是树叶，则T中树叶片数为【C】A．1 B．4C．5 D．65.对完全二部图K r，s，当【A】时，K r，s为哈密尔顿图．A．r=s．B．r≠s．C．r<s．D．r>s．三、计算与简答题（每小题10分，共40分）1.利用等值演算法求公式⌝(r→p)∨(q∧(p∨r))的主析取范式，并给出其成真赋值．⌝(r→p)∨(q∧(p∨r))⇔⌝(⌝r∨p)∨(q∧p)∨(q∧r)⇔(⌝p∧r)∨(p∧q)∨(q∧r)⇔((⌝p∧r)∧(⌝q∨q))∨((p∧q)∧(⌝r∨r))∨((q∧r)∧(⌝p∨p))⇔(⌝p∧⌝q∧r)∨(⌝p∧q∧r)∨(p∧q∧⌝r)∨(p∧q∧r)⇔m1∨m3∨m6∨m7此为公式的主析取范式．公式的成真赋值为001、011、110和111．2.设S45表示45的全体正因子（包括1和45）组成的集合，在S45上定义整除关系≤：m≤n⇔m|n．（１）画出偏序集〈S45，≤〉的哈斯图．哈尔滨工程大学试卷考试科目：离散数学C（051121，051131-32）1 / 3（２） 求出〈S 45，≤〉中最大元、最小元和所有可逆元的逆元． （３） 〈S 45，≤〉是否构成格？简要说明理由． （1）S 45={1，3，5，9，15，45}．（2）〈S 45，≤〉中最大元、最小元分别为1和45；元素1和45互为逆元，5和9互为逆元，元素3和15无逆元． （3）〈S 45，≤〉构成格，因为S 45中任意两个元素均有最小上界和最大下界．3. 求模15加群G =〈Z 15，⊕〉的所有生成元与所有子群．G =〈Z 15，⊕〉的所有生成元为与15互质的整数有：1，2，4，7，8，11，13，14，它们就是群的生成元．15的所有正因子为1，3，5，15，因此Z 15=〈1〉有4个循环子群, 分别为〈115/1〉=〈115〉=〈15〉=〈0〉={0}， 〈115/3〉=〈15〉=〈5〉={0，5，10}，〈115/5〉=〈13〉=〈3〉={0，3，6，9，12}， 〈115/15〉=〈1〉=G ．4. 设集合Ａ={a ，b ，c ，d }上的二元关系R={〈a ，b 〉，〈b ，a 〉，〈b ，c 〉，〈c ，b 〉}，求R 的自反闭包r (R )和对称闭包s (R )．r (R )=I A ⋃R ={〈a ，a 〉，〈a ，b 〉，〈b ，a 〉，〈b ，b 〉，〈b ，c 〉，〈c ，b 〉，〈c ，c 〉，〈d ，d 〉}．s (R )=R ⋃R -1=R ={〈a ，b 〉，〈b ，a 〉，〈b ，c 〉，〈c ，b 〉}．5. 设有向图D 如图，求D 中长度为3的通路数， 并指出其中的回路数．有向图D 的邻接矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=0011100001010111A ，由于 ⎪⎪⎪⎪⎪⎭⎫⎝⎛=02120011*********A ，⎪⎪⎪⎪⎪⎭⎫⎝⎛=23230212122323343A 因此，D 中长度为3的通路数为矩阵A 3中所有元素之和，为12+8+5+10=35；其中回路数为4+2+2+2=10．四、 证明题（每小题10分，共20分）1. 在一阶逻辑中构造下面推理的证明：前提：∀x (H (x )∧D (x )→⌝S (x ))，∀x (H (x )→(S (x )∨F (x )))，∃x (H (x )∧⌝F (x )) 结论：∃x (H (x )∧⌝D (x ))．(1) ∃x (H (x )∧⌝F (x )) 前提引入159 353(2)H(a)∧⌝F(a))EI规则(3)H(a)(2)化简(4)⌝F(a) (2)化简(5)∀x(H(x)→(S(x)∨F(x))) 前提引入(6)H(a)→(S(a)∨F(a))，UI规则(7)S(a)∨F(a)(3)(6)假言推理(8)S(a)(4)(7)析取三段论(9)∀x(H(x)∧D(x)→⌝S(x)) 前提引入(10)H(a)∧D(a)→⌝S(a) UI规则(11)⌝(H(a)∧D(a)) (8)(10)拒取式(12)⌝H(a)∨⌝D(a) (11)置换(13)⌝D(a) (3)(12) 析取三段论(14)H(a)∧⌝D(a) (3)(13)合取(15)∃x(H(x)∧⌝D(x)) EG规则2.设〈G，＊〉是一个群，令C={a∈G|∀x∈G，a＊x=x＊a}证明：〈C，＊〉是〈G，＊〉的子群．对∀x∈G，e＊x=x＊e故e∈C，即C非空．∀a，b∈C，(a＊b-1)＊x=a＊(b-1＊x)=a＊(x-1＊b)-1=a＊(b＊x-1)-1=a＊(x＊b-1)=(a＊x)＊b-1=(x＊a)＊b-1 =x＊(a＊b-1)．故a＊b-1∈C，由子群判断定理知〈C，＊〉是〈G，＊〉的子群．五、应用题（10分）今有20人参加一个小型会议．这20人中每人至少与其中10人（不包括自己）认识，能否将这20人安排在一个圆桌上，使得每个人都和他身边的人认识，为什么？请说明理由．将每个人看作是一个图的顶点，如果两个人认识，则将这两个顶点连接起来，从而构成一个有20个顶点的简单连通图．由于每人至少与其中10人认识，这样，每个顶点的度数至少是10．因此，任意不相邻顶点的度数之和至少是20．根据哈密尔顿图的充分条件，该图是一个哈密尔顿图，从而有哈密尔顿图回路．按照该回路上顶点的排列顺序安排这20个人即可．3 / 3。

离散数学单项选择题习题(有答案)集(共13页)单项选择题第一章第二章1. 下列表达式正确的有( )A. Q Q P ⇒ → ⌝ ) (B.P Q P ⇒∨ C .P Q P Q P ⇔⌝∧∨∧)()( D.T Q P P ⇔→→)(2. 下列推理步骤错在( )①))()((x G x F x →∀P ②)()(y G y F →US① ③)(x xF ∃P ④)(y FES③ ⑤)(y GT②④I ⑥)(x xG ∃EG⑤ A.② B.④ C.⑤ D.⑥3. 设P ：2×2=5，Q ：雪是黑的，R ：2×4=8，S ：太阳从东方升起，下列( )命题的真值为真。

A.R Q P ∧→B.S P R ∧→C.R Q S ∧→D.)()(S Q R P ∧∨∧4. 下列公式中哪些是永真式？( )A.(┐P ∧Q)→(Q→⌝R) →(Q→Q) C.(P ∧Q)→P →(P ∧Q)5. 下列等价关系正确的是( )A.)()())()((x xQ x xP x Q x P x ∀∨∀⇔∨∀B .)()())()((x xQ x xP x Q x P x ∃∨∃⇔∨∃ C.Q x xP Q x P x →∀⇔→∀)())((D.Q x xP Q x P x →∃⇔→∃)())((6. 下列推导错在( )①)(y x y x >∃∀P ②)(y z y >∃US① ③z z >ES② ④)(x x x >∀UG③ A.② B. ④ C . ③ D.无 7. 若公式)()(R P Q P ∧⌝∨∧的主析取范式为111110011001m m m m ∨∨∨则它的主合取范式为( )A.111110011001m m m m ∧∧∧B.101100010000M M M M ∧∧∧ ；C.111110011001M M M M ∧∧∧D.101100010000m m m m ∧∧∧ 。

离散数学期末试卷一、选择题（共10题，每题2分，共20分）1.下列哪个是真值？–[ ] A. $P \\vee \\sim P$–[ ] B. $P \\wedge \\sim P$–[ ] C. $P \\rightarrow \\sim P$–[ ] D. $P \\leftrightarrow \\sim P$2.下列哪个式子是永真式？–[ ] A. $(P \\rightarrow Q) \\wedge (Q \\rightarrow P)$–[ ] B. $(P \\rightarrow Q) \\vee (Q\\rightarrow P)$–[ ] C. $(P \\wedge \\sim P) \\vee (Q \\wedge \\sim Q)$–[ ] D. $(P \\rightarrow Q) \\rightarrow (Q \\rightarrow P)$3.下列集合中的哪个是无穷集合？–[ ] A. $\\{1, 2, 3\\}$–[ ] B. $\\{1, 2, 3, ...\\}$–[ ] C. $\\{\\emptyset\\}$–[ ] D. $\\{\\emptyset, \\{1\\}, \\{2\\}\\}$4.对于集合$A = \\{1, 2, 3\\}$和$B = \\{3, 4, 5\\}$，下面哪个选项是$A \\cap B$？–[ ] A. $\\{1, 2\\}$–[ ] B. $\\{2, 4\\}$–[ ] C. $\\{3\\}$–[ ] D. $\\{1, 3\\}$5.对于集合$A = \\{1, 2, 3\\}$和$B = \\{3, 4, 5\\}$，下面哪个选项是$A \\cup B$？–[ ] A. $\\{1, 2, 4, 5\\}$–[ ] B. $\\{\\emptyset\\}$–[ ] C. $\\{1, 2, 3, 4, 5\\}$–[ ] D. $\\{1, 3\\}$6.哪个选项是集合$A = \\{2, 4, 6, 8, 10\\}$的幂集？–[ ] A. $\\{2, 4, 6, 8, 10\\}$–[ ] B. $\\{2, 4, 6, 8, 10, \\{\\}\\}$–[ ] C. $\\{\\{2\\}, \\{4\\}, \\{6\\}, \\{8\\},\\{10\\}, \\{2, 4\\}, \\{2, 6\\}, \\{2, 8\\}, \\{2, 10\\}, \\{4, 6\\}, \\{4, 8\\}, \\{4, 10\\}, \\{6, 8\\}, \\{6,10\\}, \\{8, 10\\}, \\{2, 4, 6\\}, \\{2, 4, 8\\}, \\{2, 4, 10\\}, \\{2, 6, 8\\}, \\{2, 6, 10\\}, \\{2, 8, 10\\}, \\{4, 6, 8\\}, \\{4, 6, 10\\}, \\{4, 8, 10\\}, \\{6, 8, 10\\},\\{2, 4, 6, 8\\}, \\{2, 4, 6, 10\\}, \\{2, 4, 8, 10\\}, \\{2, 6, 8, 10\\}, \\{4, 6, 8, 10\\}, \\{2, 4, 6, 8, 10\\}\\}$–[ ] D. $\\{\\{\\}, \\{2\\}, \\{4\\}, \\{6\\},\\{8\\}, \\{10\\}, \\{2, 4\\}, \\{2, 6\\}, \\{2, 8\\},\\{2, 10\\}, \\{4, 6\\}, \\{4, 8\\}, \\{4, 10\\}, \\{6,8\\}, \\{6, 10\\}, \\{8, 10\\}, \\{2, 4, 6\\}, \\{2, 4,8\\}, \\{2, 4, 10\\}, \\{2, 6, 8\\}, \\{2, 6, 10\\}, \\{2, 8, 10\\}, \\{4, 6, 8\\}, \\{4, 6, 10\\}, \\{4, 8, 10\\},\\{6, 8, 10\\}, \\{2, 4, 6, 8\\}, \\{2, 4, 6, 10\\}, \\{2, 4, 8, 10\\}, \\{2, 6, 8, 10\\}, \\{4, 6, 8, 10\\}, \\{2, 4, 6, 8, 10\\}\\}$7.下列哪个命题是正确的？–[ ] A. 如果x>10，则x>5–[ ] B. 如果x>5，则x>10–[ ] C. 如果x>10，则x<5–[ ] D. 如果x<5，则x>108.哪个选项是命题$P: (P \\rightarrow Q) \\wedgeP$的否定？–[ ] A. $\\sim P \\rightarrow (\\sim Q \\vee \\sim P)$–[ ] B. $(P \\rightarrow \\sim Q) \\vee P$–[ ] C. $(P \\rightarrow Q) \\wedge \\sim P$–[ ] D. $Q \\rightarrow P$9.对于命题$P: (x > 5) \\wedge (y < 10)$，下列哪个选项是x与$Q: (x < 2) \\vee (y > 8)$的合取式？–[ ] A. $(x > 5) \\wedge (y < 10) \\vee (x < 2) \\vee (y > 8)$–[ ] B. $(x > 5) \\vee (y < 10) \\wedge (x < 2) \\vee (y > 8)$–[ ] C. $(x > 5) \\vee (y < 10) \\vee (x < 2) \\wedge (y > 8)$–[ ] D. $(x > 5) \\vee (x < 2) \\vee (y < 10) \\vee (y > 8)$10.下列哪个命题是等价的？–[ ] A. $P \\rightarrow Q$–[ ] B. $\\sim P \\vee Q$–[ ] C. $\\sim Q \\rightarrow \\sim P$–[ ] D. $P \\wedge \\sim Q$二、填空题（共5题，每题4分，共20分）1.集合$\\{x | x > 0\\}$的基数是\\\\\\。

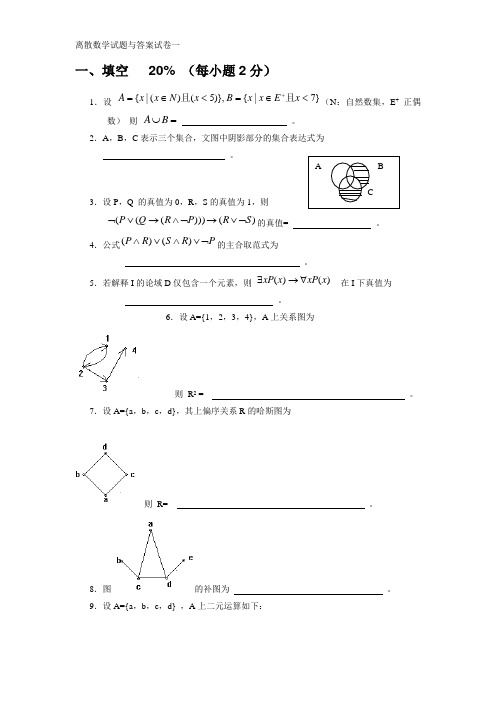
离散数学试题与答案试卷一一、填空 20% （每小题2分）1．设 }7|{)},5()(|{<∈=<∈=+x E x x B x N x x A 且且（N ：自然数集，E + 正偶数） 则 =⋃B A 。

2．A ，B ，C 表示三个集合，文图中阴影部分的集合表达式为 。

3．设P ，Q 的真值为0，R ，S 的真值为1，则)()))(((S R P R Q P ⌝∨→⌝∧→∨⌝的真值= 。

4．公式P R S R P ⌝∨∧∨∧)()(的主合取范式为 。

5．若解释I 的论域D 仅包含一个元素，则 )()(x xP x xP ∀→∃ 在I 下真值为 。

6．设A={1，2，3，4}，A 上关系图为则 R 2 = 。

7．设A={a ，b ，c ，d}，其上偏序关系R 的哈斯图为则 R= 。

8．图的补图为 。

9．设A={a ，b ，c ，d} ，A 上二元运算如下：那么代数系统<A ，*>的幺元是 ，有逆元的元素为 ，它们的逆元分别为 。

10．下图所示的偏序集中，是格的为 。

二、选择 20% （每小题 2分）1、下列是真命题的有（ ） A ． }}{{}{a a ⊆；B ．}}{,{}}{{ΦΦ∈Φ；C ． }},{{ΦΦ∈Φ；D ． }}{{}{Φ∈Φ。

2、下列集合中相等的有（ ）A ．{4，3}Φ⋃；B ．{Φ，3，4}；C ．{4，Φ，3，3}；D ． {3，4}。

3、设A={1，2，3}，则A 上的二元关系有（ ）个。

A ． 23 ； B ． 32 ； C ． 332⨯； D ． 223⨯。

4、设R ，S 是集合A 上的关系，则下列说法正确的是（） A ．若R ，S 是自反的， 则S R 是自反的； B ．若R ，S 是反自反的， 则S R 是反自反的； C ．若R ，S 是对称的， 则S R 是对称的； D ．若R ，S 是传递的， 则S R 是传递的。

5、设A={1，2，3，4}，P （A ）（A 的幂集）上规定二元系如下|}||(|)(,|,{t s A p t s t s R =∧∈><=则P （A ）/ R=（ ）A．A ；B．P(A) ；C．{{{1}}，{{1，2}}，{{1，2，3}}，{{1，2，3，4}}}；D．{{Φ}，{2}，{2，3}，{{2，3，4}}，{A}}6、设A={Φ，{1}，{1，3}，{1，2，3}}则A上包含关系“⊆”的哈斯图为（）7、下列函数是双射的为（）A．f : I→E , f (x) = 2x ；B．f : N→N⨯N, f (n) = <n , n+1> ；C．f : R→I , f (x) = [x] ；D．f :I→N, f (x) = | x | 。

第 1 页 共 1 页国防科技大学研究生院1998年硕士生入学考试
软件基础试题(离散数学部分)
注：1. 不用抄题 ，答案必须写在统一配发的答题纸上
2．单独考生做一、1,2,3,5 ; 二、1,2,3,4,5,6,8；三、,,,,o 1o 3o 4o 5o 6
3．统考生做一、1,2,3,4 ; 二、1,2,3,4,5,6,7；三、,,,,o 1o 2o 4o 5o
6
三、离散数学部分(30分)(8分) (统考生做，单独考生不做) 设集合o 2i ) 证明R 为A 上的一个等价关系; (4分)
(8分)(统考生不做，单独考生做) 设Z ，D 为集合，f 和g 都是从Z 到D 的函数且
o 3
(7分)试判断下列合式公式是否为可满足的，并证明你的结论：
o 4
其中P 为二元谓词，Q 为一元谓词。

(5分) 试求叶的权分别为2，3，5，7，11，13，17，19的最优叶加权二叉树，及其叶加权路径长度。

o 5(6分)设<G ， >为交换群。

若H = { a G| a 的周期是有限的},证明H 是<G ， >的不变子群。

o 6。

《离散数学》题库与答案一、选择或填空（数理逻辑部分）1、下列哪些公式为永真蕴含式？( A )(1)⌝Q=>Q→P (2)⌝Q=>P→Q (3)P=>P→Q (4)⌝P∧(P∨Q)=>⌝P答：在第三章里面有公式（1）是附加律，（4）可以由第二章的蕴含等值式求出（注意与吸收律区别）2、下列公式中哪些是永真式？( )(1)(┐P∧Q)→(Q→⌝R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答：（2），（3），（4）可用蕴含等值式证明3、设有下列公式，请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ⌝(P→Q)=>P (6) ⌝P∧(P∨Q)=>⌝P答：（2）是第三章的化简律，（3）类似附加律，（4）是假言推理，（3），（5），（6）都可以用蕴含等值式来证明出是永真蕴含式4、公式∀x((A(x)→B(y，x))∧∃z C(y，z))→D(x)中，自由变元是( )，约束变元是( )。

答：x,y, x,z（考察定义在公式∀x A和∃x A中，称x为指导变元，A为量词的辖域。

在∀x A和∃x A的辖域中，x的所有出现都称为约束出现，即称x为约束变元，A中不是约束出现的其他变项则称为自由变元。

于是A(x)、B(y，x)和∃z C(y，z)中y为自由变元，x和z为约束变元，在D(x)中x为自由变元）5、判断下列语句是不是命题。

若是，给出命题的真值。

( )(1)北京是中华人民共和国的首都。

(2) 陕西师大是一座工厂。

(3) 你喜欢唱歌吗？ (4) 若7+8＞18，则三角形有4条边。

(5) 前进！ (6) 给我一杯水吧！答：（1）是，T （2）是，F （3）不是（4）是，T （5）不是（6）不是（命题必须满足是陈述句，不能是疑问句或者祈使句。

）6、命题“存在一些人是大学生”的否定是( )，而命题“所有的人都是要死的”的否定是( )。

国防科技大学研究生院2002年硕士生入学考试428- 离散数学 试题 题单号：40628 （可不抄题）考生注意：1、答案必须写在统一配发的答题纸上；2、统考生做第一、二、三、四、五、六、七、八、九题；3、单独考生做第一、二、三、四、五、六、七、十、十一题。

一、（每小题6分，共12分）设集合A={1，2，3，4}上的二元关系R ₁和R ₂定义如下：i)试分别指出R ₁和R ₂所具有的性质（即是否具有自反性，反 自反性，对称性，反对称性和传递性这五种性质）。

ii )).()(,2121R tsr R t R R 和二、（8分）求合式公式))(())((R Q P R Q P ⌝∧⌝→⌝∧∧→的主合取范式和主析取范式。

三、（10分）设二元关系R ⊆A 2 是自反的。

证明R 为等价关系的充要条件是：若〈a,b 〉，〈a,c 〉∈ R, 则<b,c>∈ R. 2四、（每小题5分，共15分）在1到2000这2000个正整数中，试求出：I ） 能被3、5或7整除的正整数的个数；II ） 仅能被3、5或7这三数中的两者整除的正整数的个数；III ） 能被3整除，但不能被5整除，也不能被7整除的正整数的个数。

五、（10分）设A ，B 为非空集合且A ⋂B=∅. 证明：存在函数h:A →A ⋃B 和k:B →A ⋃B ，使得对任意集合D 及任意函数f :A →D 和g:B →D ，都存在唯一的函数ϕ:A ⋃B →D 使.k g h f ϕϕ==且六、（10分）证明：若n 阶简单无向图G 的任意两个结点的度数之和大于等于n-1，则G 是连通的。

七、（10分）设A 为非空集合，Π={π|π为A 的划分}。

若令R={<π,π'>|π,π'∈∏且对每个u ∈π皆有v ∈π'使u ⊆v }试证明R 为II 上的半序。

八、（10分）任给52个整数，证明其中必有两数之和能被100整除或两数之差能被100整除。

离散数学试题与答案【篇一：离散数学试题及答案】一、填空题1 设集合a,b，其中a＝{1,2,3}, b= {1,2}, 则a - b＝____________________;＝ __________________________ .3. 设集合a = {a, b}, b = {1, 2}, 则从a到b的所有映射是__________________________ _____________, 其中双射的是__________________________.4. 已知命题公式g＝?(p?q)∧r，则g的主析取范式是_____________________________________________________________________________________ ____.5.设g是完全二叉树，g有7个点，其中4个叶点，则g的总度数为__________，分枝点数为________________.7. 设r是集合a上的等价关系，则r所具有的关系的三个特性是______________________, ________________________,_______________________________.8. 设命题公式g＝?(p?(q?r))，则使公式g为真的解释有__________________________，_____________________________,__________________________.9. 设集合a＝{1,2,3,4}, a上的关系r1 = {(1,4),(2,3),(3,2)}, r1 = {(2,1),(3,2),(4,3)}, 则 r1?r2 = ________________________,r2?r1 =____________________________,=________________________.10. 设有限集a, b，|a| = m, |b| = n, 则| |?(a?b)| =_____________________________.11 设a,b,r是三个集合，其中r是实数集，a = {x | -1≤x≤1, x?r}, b = {x | 0≤x 2, x?r},则a-b = __________________________ , b-a = __________________________ , a∩b =__________________________ , .13. 设集合a＝{2, 3, 4, 5, 6}，r是a上的整除，则r以集合形式(列举法)记为_________________________________________________________________ _.14. 设一阶逻辑公式g = ?xp(x)??xq(x)，则g的前束范式是__________________________ _____.15.设g是具有8个顶点的树，则g中增加_________条边才能把g 变成完全图。

国防科技大学研究生院2001年硕士生入学考试试题考试科目：操作系统考生注意：1．答案必须写在我校统一配发的专用答题纸上2．统考生做 一、二、三、四、五；3．单独考生做一、二、三、六、七；一．（58分）回答如下问题1．（6分）假定有一个支持实时、分时和批处理的操作系统，对该系统应如何设计进程调度策略？2．（5分）什么叫线程？为什么要引进线程？3．（6分）某计算机系统设计成只有一级中断(该级中有多个中断)的中断系统，简述当中断发生时，是如何进入该中断处理程序的？4．（5分）在文件系统中为什么要引进“Open”系统调用？操作系统是如何处理的？5．(5分)假定存储器空闲块有如下结构：请你构造一串内存请求序列，对该请求序列首次满足分配算法能满足，而最佳满足分配法则不能。

6．(6分)为什么要在设备管理中引入缓冲技术？操作系统如何实现缓冲技术？7．(6分)用什么办法可以破坏死锁的循环等待条件？为什么？8．(6分)进程的状态主要有哪些？当发生状态转换时，操作系统完成哪些工作？9．(6分)在文件系统中，为什么要设立“当前目录”？操作系统如何实现改变“当前目录”？10．(7分)举例说明P、V操作为什么要用原语实现？操作系统如何实现这种原语操作？ 二．(12分)设有四个进程P1，P2，P3，P4，它们到达就绪队列的时刻，运行时间及优先级如下表所示：进程 到达就绪队列时间运行时间(基本时间单位)优先级(基本时间单位)P1 0 9 1P2 1 4 2P3 2 8 3P4 3 10 4问：(1)若采用可剥夺的优先级调度算法，给出各进程的调度次序以及每个进程的等待时间。

(2)若采用时间片轮转调度算法，且时间片为2个基本时间单位，试给出各进程的调度次序及平均周围时间。

三．(8分)假设系统由相同类型的m个资源组成，有 n 个进程，每个进程至少请求一个资源。

证明：当n个进程最多需要的资源数之和小于m+n时，该系统无死锁。

四．(12分)在页式虚存系统中，一程序的页面走向(访问串)为 1，2，3，4，1，2，5，1，2，3，4，5 ，设分配给该程序的驻留集为m，试分别计算m=3和m=4时，FIFO和LRU五．(10分)对于下述优先图，用Parbegin/Parend语句及操作系统提供的同步/互斥工具，写出并发程序。