圆的切线判定定理及性质定理讲义

【变式1】 如图所示，在梯形ABCD中，AD∥BC，∠C＝90°，且 AD＋BC＝AB，AB为⊙O的直径． 求证：⊙O与CD相切．
证明 过 O 作 OE⊥CD，垂足为 E. 因为 AD∥BC，∠C＝90°，所以 AD∥OE∥BC. 因为 O 为 AB 的中点，所以 E 为 CD 的中点． 所以 OE＝12(AD＋BC)． 又因为 AD＋BC＝AB， 所以 OE＝12AB， 且等于⊙O 的半径． 所以⊙O 与 CD 相切．
⊙O的割线，与⊙O交于B、C两点，圆心O在∠PAC的内部， 点M是BC的中点．
(1)证明：A、P、O、M四点共圆； (2)求∠OAM＋∠APM的大小．
(1)证明 连接OP，OM，
因为AP与⊙O相切于点P，所以OP⊥AP. 因为M是⊙O的弦BC的中点，所以OM⊥BC. 于是∠OPA＋∠OMA＝180°， 由圆心O在∠PAC的内部， 可知四边形APOM的对角互补， 所以A，P，O，M四点共圆．
又∠P 为公共角，∴△PAB∽△PCA. ∴CABA＝PPAC＝1200＝12. ∵BC 为⊙O 的直径，∴∠CAB＝90°. ∴AC2＋AB2＝BC2＝225.∴AC＝6 5，AB＝3 5. 又∠ABC＝∠E，∠CAE＝∠EAB， ∴△ACE∽△ADB，∴AABE＝AADC. ∴AD·AE＝AB·AC＝3 5×6 5＝90.
自学导引
1．圆的切线的性质定理及推论 (1)定理：圆的切线垂直于经过切点的 半径 ． (2)推论1：经过圆心且垂直于切线的直线必经过 切点 ． (3)推论2：经过切点且垂直于切线的直线必经过 圆心 ．
斟酌引申：(1)本定理及其两个推 论可以用一个定理叙述出来，即： 如果圆的一条直线满足以下三个 条件中的任意两条，那么就一定 满足第三条．它们是：①垂直于切线；②过切点；③过圆心． (2)本定理题设为：一条直线既过圆心又过切点，结论为：这条直 线与圆的切线垂直．如图所示，若直线l切⊙O于A，直线l′经过点 O、A，则直线l′⊥l.

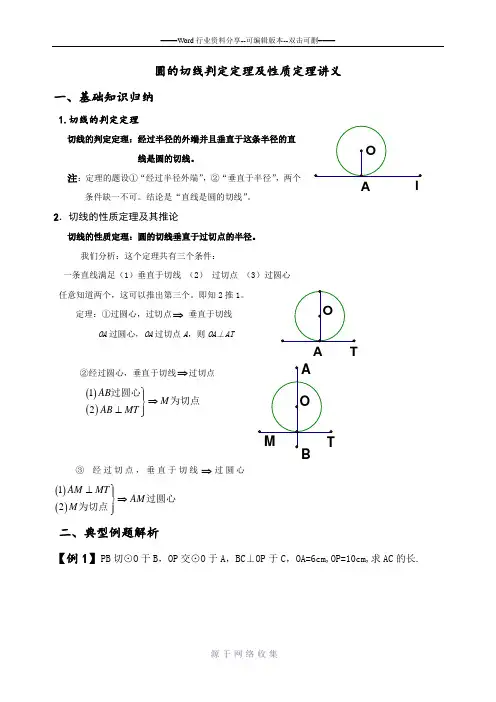
AT圆的切线判定定理及性质定理讲义一、基础知识归纳1.切线的判定定理切线的判定定理：经过半径的外端并且垂直于这条半径的直 线是圆的切线。

注：定理的题设①“经过半径外端”，②“垂直于半径”，两个 条件缺一不可。

结论是“直线是圆的切线”。

2．切线的性质定理及其推论切线的性质定理：圆的切线垂直于过切点的半径。

我们分析：这个定理共有三个条件：一条直线满足（1）垂直于切线 （2） 过切点 （3）过圆心 任意知道两个，这可以推出第三个。

即知2推1。

定理：①过圆心，过切点⇒ 垂直于切线 OA 过圆心，OA 过切点A ，则OA ⊥AT②经过圆心，垂直于切线⇒过切点()()12AB M AB MT ⎫⎪⇒⎬⊥⎪⎭过圆心为切点③ 经过切点，垂直于切线⇒过圆心()()12AM MT AM M ⊥⎫⎪⇒⎬⎪⎭过圆心为切点二、典型例题解析【例1】PB 切⊙O 于B ，OP 交⊙O 于A ，BC ⊥OP 于C ，OA=6cm,OP=10cm,求AC 的长.AAOBPCM【例2】如图，⊙O 的直径AB =6cm ，点P 是AB 延长线上的动点，过点P 作⊙O 的切线，切点为C ，连结AC ．若CPA 的平分线交AC 于点M ，你认为∠CMP 的大 小是否发生变化？若变化，请说明理由；若不变，求出∠CMP 的度数【例3】如图,若⊙的直径AB 与弦AC 的夹角为30°,切线CD 与AB 的延长线交于点D,且⊙O 的半径为2,则CD 的长是多少？【例4】如图，AB 为半圆O 的直径，CB 是半圆O 的切线，B 是切点，AC•交半圆O 于点D ，已知CD=1，AD=3，那么cos ∠CAB=________．【例5】设直线ι到⊙O 的圆心的距离为d ，半径为R ，并使x 2－2d x ＋R=0，BDC试由关于x 的一元二次方程根的情况讨论ι与⊙O 的位置关系．【例6】在Rt ABC △中，90ACB ∠=°，D 是AB 边上一点，以BD 为直径的O ⊙与边AC 相切于点E ，连结DE 并延长，与BC 的延长线交于点F ． （1）求证：BD BF =；（2）若64BC AD ==，，求O ⊙的面积．。

证明:连接OD. ∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
C
∴OD//AC.
又∵∠DEC=90º ∴∠ODE=90º 又∵D在圆周上,
∴DE是⊙O是切线..
E D
B
A
O
例2 如图. AB为⊙O的直径,C为⊙O上一点,AD和 过C点的切线互相垂直,垂足为D.
求证:AC平分∠DAB.
证明:连接OC, ∵CD是⊙O的切线,
C
2.已知:OA和OB是⊙O的半径,并且OA⊥OB,P是OA 上任意一点,BP的延长线交⊙O于Q.过Q作⊙O的切 线交OA的延长线于R,.
求证:RP=RQ
B
PA
O
R
Q
∠AQO= ∠APQ
3.AB是⊙O的直径,BC是⊙O的切线,切点为B,OC 平行于弦AD. 求证:DC是⊙O的切线.
C
D
3
1
42
A
∴OC⊥CD.
又∵AD⊥CD, ∴OC//AD.由此得 ∠ACO=∠CAD. ∵OC=OA. ∴ ∠CAO=∠ACO.
D C
A
O
B
∴ ∠CAD=∠CAO. 故AC平分∠DAB.
习题2.3
1.如图,△ABC为等腰三角形,O是底边BC的中点, ⊙O与腰AB相切于点D.
求证:AC与⊙O相切.
A
E D
B
O
推论2: 经过切点且垂直于切线的直线必经过圆心.
思考: 切线的性质定理逆命题是否成立?
切线的判定定理: 经过半径的外端并且垂直于这条半径的直线是圆的切线.
在直线上任取异于A的点B.
l
A
B
连OB.
则在Rt△ABO中
OB>OA=r

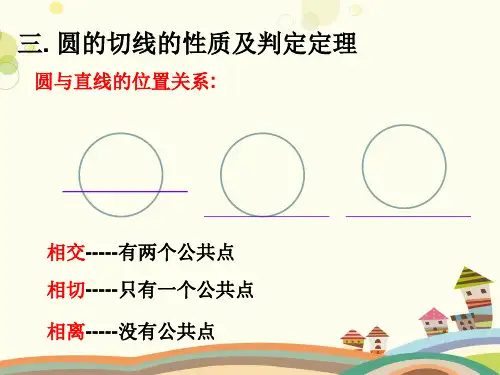
圆的切线和切线定理圆是几何中常见的形状之一，有很多有趣的性质和定理。

其中一个重要的定理就是圆的切线定理，它描述了切线与圆的关系以及相应的性质。

接下来，我们将详细介绍这个定理。

一、切线的定义在介绍切线定理之前，先给出切线的定义。

对于一个圆，如果从圆外的一点引一条直线，该直线与圆仅有一个交点，那么这个交点与圆的弧上的点之间的线段就是切线。

切线与圆相切于一个点，与该点处的切点重合。

二、切线定理的规定切线定理是关于切线和切线外一点与圆的关系的重要定理。

根据切线定理，以下规定成立：规定1：切线与半径的垂直性。

切线与半径的相交点处的半径垂直于切线。

规定2：切线与切线之间的垂直性。

如果两条切线分别与两个圆相切于同一点，那么这两条切线互相垂直。

规定3：切线长度的规律性。

如果从圆的外一点引两条切线，那么这两条切线的长度相等。

三、切线定理的证明以下是对切线定理的证明：首先，证明规定1。

设圆的半径为r，交点为A。

连接A与圆心的线段，记为OA。

根据垂直定理，如果OA与切线AD垂直，那么OA与圆上任意一点（如点B）处的切线BC也是垂直的。

因此，切线与半径的垂直性得证。

接下来，证明规定2。

设圆的两个切点分别为A和B，切线分别为AD和BC。

连接OA和OB，并延长这两条线段相交于点C。

根据垂直定理，如果AD与BC垂直，那么OA与OB也垂直。

根据垂直线的性质，切线AD与切线BC的垂直性得证。

最后，证明规定3。

设从点P引两条切线分别与圆交于点A和点B，切线长度分别为AD和BE。

连接圆心O与点A、点B，并连接OA和OB。

由于圆心到切点的距离相等，即OA = OB。

通过几何推理，可以得出三角形OAD和三角形OBE是全等的，因此AD = BE。

切线长度的规律性得证。

四、切线定理的应用切线定理在几何问题中的应用十分广泛。

它可以帮助我们解决一些与圆相关的问题，例如求解切线的长度、判断两条切线是否相互垂直等。

总结：切线定理是关于切线和切线外一点与圆的关系的重要定理。

【典例训练】
1.在Rt△ABC中，∠C=90°，AC=3 cB的关系为( )
(A)相切
(B)相离
(C)相交
(D)无法判断
2.如图所示，CB为⊙O的直径，P是CB的延
长线上一点，且OB=BP，∠AOC=120°，
则PA与⊙O的位置关系是_____.
圆的切线的性质
圆的切线的性质 (1)已知一条直线是圆的切线时,常作出过切点的半径,则该半 径垂直于切线,从而出现了直角. (2)从圆外一点引圆的两条切线,这点与圆心的连线平分这两条 切线的夹角,这点到切点的切线长相等. (3)连接圆的两条平行切线的切点的线段是圆的直径.
【典例训练】 1.如图所示，DB，DC是⊙O的两条切线，A是圆上一点，已知 ∠D=46°，则∠A=_____.
DO AD
AD
2.如图，已知EB是半圆O的直径，A是BE延长线上的一点，AC是 半圆O的切线，D为切点，BC⊥AC于C，若BC=6，AC=8，则 AE=_______.
【解析】1.如图所示，连接OB，OC，
则OB⊥BD，OC⊥CD，
则∠DBO+∠DCO=90°+90°=180°，
则四边形OBDC内接于一个圆，
则有∠BOC=180°-∠D=180°-46°=134°，
【解析】连接OC，∵OA=OB,AC=CB,OC=OC, ∴△OAC≌△OBC, ∴∠OCA=∠OCB=90°, ∴直线AB与⊙O相切. 答案：相切
1.圆的切线的其他相关性质 (1)切线和圆只有一个公共点; (2)切线和圆心的距离等于圆的半径; (3)过圆心且过切点的直线与过该点的切线垂直.
2.切线的判定定理 在切线的判定定理中要分清定理的题设和结论，“经过半径外 端”和“垂直于这条半径”这两个条件缺一不可，否则就不是 圆的切线，如图①②中的例子就不同时满足这两个条件，所以 都不是圆的切线.

圆的切线的定义和判定定理圆的切线可以通过以下两种方式进行定义和判定定理的解释：
定义：
1. 切线的几何定义，对于圆上的任意一点，通过该点且与圆相切的直线称为圆的切线。

2. 切线的代数定义，如果直线的方程和圆的方程联立成方程组有且只有一个解，且该解恰好是圆上的一点，则该直线即为圆的切线。

判定定理：
1. 切线判定定理一，直线与圆相切的充分必要条件是直线与圆的切点处的切线垂直于半径。

2. 切线判定定理二，直线与圆相切的充分必要条件是直线与圆的切点处的切线的斜率等于圆的半径的斜率的负倒数。

通过这些定义和判定定理，我们可以清晰地理解圆的切线的概念及其性质。

希望这些解释对你有所帮助。

一、切线的性质及判定1．切线的性质2．切线的判定3． 切线长和切线长定理切线的性质及判定（）定理：圆的切线垂直于过切点的半径．推论：经过圆心且垂直于切线的直线必经过切点．推论：经过切点且垂直于切线的直线必经过圆心．（）注意：这个定理共有三个条件，即一条直线满足：①垂直于切线②过切点③过圆心过圆心，过切点垂直于切线．过圆心，过切点，则．②过圆心，垂直于切线过切点．过圆心，，则过切点．③过切点，垂直于切线过圆心．，过切点，则过圆心．（）定义法：和圆只有一个公共点的直线是圆的切线；（）距离法：和圆心距离等于半径的直线是圆的切线；（）定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．注意：定理的题设是①“经过半径外端”，②“垂直于半径”，两个条件缺一不可；定理的结论是“直线是圆的切线”．因此，证明一条直线是圆的切线有两个思路：①连接半径，证直线与此半径垂直；②作垂直，证垂直在圆上．（）切线长：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长．（）切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．（）证明圆切线辅助线的方法：①若给出直线与圆有公共点：连半径、证垂直；②若没给直线与圆的交点：做垂直、证半径；（）圆中证明角相等的方法：①同角（或等角）余角相等；爱智康2018/06/121122⇒AB AB M AB ⊥l ⇒AB AB ⊥l AB M ⇒AB ⊥l AB M AB 1231212②圆周角定理；③半径相等出等腰三角形；④平行线出同位角或内错角相等；⑤全等或相似三角形中的对应角相等；⑥在同圆或等圆中，等弧或等弦所对的圆周角相等（常见于弧的等分点）。

（）给出圆的切线，作辅助线，连接过切点的半径，则半径垂直于切线．爱智康 2018/06/123。

切线的判定：
1、直线与圆交点的个数：只有一个交点。 2、圆心到直线的距离与半径的大小关系，即d=r。 3、经过半径外端且垂直于这条半径的直线是圆的切线。
切线的判定： 1、直线与圆交点的个数：只有一个交点。 2、圆心到直线的距离与半径的大小关系，即d=r。 3、经过半径外端且垂直于这条半径的直线是圆的切线。
。
变式一：在△ABC中，AB=2，AC= ，以A为圆心，1为
半径的圆与边BC相切 ，则BC的长为
。
变式二：如图，点A是圆O外一点，OA=4，AB与圆相切于点
B，且AB=2 ，弦BC∥OA，则BC的长为
。
A
B
D CB
A C
O A
C
B
7、如图,AB为⊙O的直径，C为⊙O上一点，AD和过C点的切 线互相垂直，垂足为D，求证：AC平分∠DAB。
A
L
线L就要与圆相交，而这与直线
O
L是圆O的切线相矛盾。
因此，OA与直线L垂直。
MA
L
性质3：圆的切线垂直于过切点的半径。
证明或 ∵ 直线L是圆O的切线 解答： ∴ OA ⊥ L
练习与巩固：
1、如图，A、B是⊙O上的两点，AC是⊙O的切线，∠B=70°， 则∠BAC等于（ ） A. 70° B. 35° C. 20° D. 10°
A
C
C
O
P
A
O
BP
B （4）
（5）
5、如图，⊙O的直径AB与弦AC的夹角为30°，过C点的切线 PC与AB的延长线交于P，PC=5，则⊙O的半径为（ ）
A. 5 3
3
B.
53 6
C. 10
D. 5
辅助线的作法：作过切点的半径

提示：连接AO，DO，作 OE⊥AC 于点E．
E
总结：看到切线，就要连接切点和圆心，利用切线性质．
AB 是 ⊙O 的直径，AE 平分∠BAC 交 ⊙O 于点E，过点 E 作⊙O 的切线交AC 于点D，试判断△AED 的形状，并说明理 由提．示：连接OE．
答案：△AED是直角三角形． 总结：看到切线，就要连接切点和圆心，利用切线性质．
判断一条直线是圆的切线，你现在会有多少种方法? 有以下三种方法： 1．定义法：和圆有且只有一个公共点的直线是圆的切线． 2．数量法（d=r）：圆心到直线的距离等于半径的直线是圆 的切线． 3．判定定理：经过半径外端且垂直于这条半径的直线是圆的 切线．
生活中的切线
1．当你在下雨天快速转
2．砂轮打磨零件时
知识回顾 直线和圆的位置关系
相交
图形
公共点个数 公共点名称 直线名称 距离d与半径r的关系
2个 交点 割线 d＜r
相切
相离
1个 切点 切线 d=r
0个 —— —— d＞r
思考
如图，在 ⊙O 中，经过半径 OA 的外端点 A 作直线 l⊥OA， 则圆心 O 到直线 l 的距离是多少？直线 l 和 ⊙O 有什么位置关 系？
圆的切线垂直于过切点的半径．
切线的性质定理 圆的切线垂直于过切点的半径．
几何表述： ∵ l 与 ⊙O 相切于点 A ∴ OA⊥l
切线的性质定理的证明
证明切线性质定理需要用到反证法：
假设OA与 l 不垂直，
过点O 作OM⊥l，垂足为M．
M
根据垂线段最短的性质，有OM＜OA，
这说明圆心 O 到直线l的距离小于半径OA．
提示：连接OD，证明三角形全等.
补充题

证明：连接OQ. ∵QR是⊙O的切线， ∴OQ⊥QR. ∵OB＝OQ， ∴∠B＝∠OQB. ∵BO⊥OA， ∴∠BPO＝90°－∠B＝∠RPQ， ∠PQR＝90°－∠OQP， ∴∠RPQ＝∠PQR， ∴RP＝RQ
1．分析圆的切线的性质定理及两个推论的条件和结论间 的关系，可以得出如下结论：如果一条直线具备下列三个条件 中的任意两个，就可以推出第三个：①垂直于切线；②过切点； ③过圆心．于是，在利用切线性质时，通常作的辅助线是过切 点的半径．
PA=AO=OB=1. (1)求∠P的度数. (2)求DE的长. 解析：(1)如图，连接OC. ∵点C为切点， ∴OC⊥PC，△POC为直角三角形. ∵OC=OA=1,PO=PA+AO=2, ∴sin∠ p OC 1 ,
PO 2
∴∠P=30°
(2)∵BD⊥PD, ∴在Rt△PBD中，由∠P=30°， PB=PA+AO+OB=3,得BD= 3 .
A．∠1＝∠2＝∠3 B．AM·CN＝CM·BN C．CM＝CD＝CN D．△ACM∽△ABC∽△CBN
5．如图所示，⊙O是正△ABC的内切圆，切点分别为E、 F、G，P是 EG 上任意一点，则∠EPF的度数等于( C )
A．120° B．90° C．60° D．30°
6．如图所示，⊙O为△ABC的内切圆，∠C＝90°， AO的延长线交BC于点D，AC＝4，CD＝1，则⊙O的半径等 于( A )
解析：连接 OA.∵AP 为⊙O 的切线， ∴OA⊥AP. 又∠ABC＝30°，∴∠AOC＝60°. ∴在 Rt△AOP 中，OA＝1，PA＝OA·tan 60°＝ 3. 答案： 3
9．PA、PB切⊙O于点A、B，PA＝5，在劣弧 AB上取一点 C，过C作⊙O的切线， 分别交PA、PB于D、E两点，则△PDE

t3=17÷2=8.5（秒）
y
A
· · C2 O C3
B x
第16页/共19页
大显身手
③设当C运动到C4时圆与直线AB相切于Q点， 连C4 Q，则C4 Q⊥AB ∠C4 BQ=30° ∴ B C4 =2 C4 Q=14 ∴ CC4 =10+12+14=36 ∴ t4=36÷2=18（秒）
y
A
· O C3 B
C4
x
Q
第17页/共19页
心得体会
1、判定切线的方法有哪些？ 与圆有唯一公共点
是圆的切线
直线l与圆心的距离等于圆的半径
是圆的切线
经过半径外端且垂直这条半径
是圆的切线
2、常用的添辅助线方法？ （1）直线与圆的公共点已知时，作出过公共点的半径，再证半径垂直 于该直线。（连半径，证垂直） （2）直线与圆的公共点不确定时，过圆心作直线的垂线段，再证明这 条垂线段为圆的半径。（作垂直，证半径）
.O
➢1、 P l 与圆有唯一公共点的直线是圆的切线。
rO
➢2、 d
l 当d=r时直线是圆的切线。
O
➢3、 P
l 经过半径的外端并且垂直于这条半径的 直线是圆的切线。
第2页/共19页
小试牛刀
例1：直线l和⊙O的公共点的个数为m，且m满足方程 m2+2m- 3=0, 试判断直线l和⊙ O的位置关系，并 说明理由.
3、圆的切线性质定理：圆的切线垂直于经过切点的半径。 辅助线作法：连接圆心与切点可得半径与切线垂直。 即“连半径，得垂直”。
第18页/共19页
感谢您的观看！
第19页/共19页
y A
·· C C1 O
B x
第11页/共19页

[解题过程] (1)证明：依据题意，得 a＋b＝c＋4，ab＝4(c＋2)， 则 a2＋b2＝(a＋b)2－2ab ＝(c＋4)2－2×4(c＋2)＝c2， 所以△ABC 是直角三角形．
(2)∵∠C＝90°，tan A＝ab＝34， ∴不妨设 a＝3k，b＝4k，则 c＝5k(k>0)， 代入 a＋b＝c＋4，得 k＝2. ∴a＝6，b＝8，c＝10. 连接 OE，得 BC∥OE. ∴OBCE＝AAOB，即O6E＝10－10OE.解得 OE＝145. 在 Rt△AOE 中，tan A＝OAEE＝34，∴AE＝5.
[规律方法] 用切线的性质定理求解线段的长度时，应注 意哪些问题？
(1)如果已知三边的一元二次方程，可利用韦达定理建立起 三角形的三边之间的关系；
(2)在应用切线的性质定理及其推论进行几何证明和求解 时，如果已知切点，则连接圆心和切点构成垂直是一种常用的 方法．
(江苏高考)AB是圆O的直径，D为圆O上一点， 过D作圆O的切线交AB延长线于点C，若DA＝DC，求证：AB
[思路点拨]
[解题过程] 如图所示，连接OA、OB、OC．
∵PA和PB分别切⊙O于点A和B， ∴∠PAO＝∠PBO＝90°. ∴∠AOB＋∠APB＝180°. ∴∠AOB＝180°－∠APB＝140°. ∵DC切⊙O于点C，∴∠OCD＝90°.
又∵∠PAO＝90°， 在 Rt△CDO 与 Rt△ADO 中， 有 OD＝DO，CO＝AO， ∴△CDO≌△ADO.
∴∠COD＝∠AOD＝12∠COA． 同理可证，∠COE＝∠BOE＝12∠COB．
∴∠DOE＝12(∠COA＋∠COB)＝12×140°＝70°.
[规律方法] (1)如何利用切线性质定理及推论求解有关角 的问题？

证明:连接OD. ∵BD=CD,OA=OB,
∴OD是△ABC的中位线,
C
∴OD//AC.
E
又∵∠DEC=90º
∴∠ODE=90º
又∵D在圆周上,OD是半径 A ∴DE是⊙O的切线..
D
B O
【例题解析】
例2 如图. AB为⊙O的直径,C为⊙O上一点,AD和 过 C点的切线互相垂直,垂足为 D,求证:AC平分∠DAB.
证明:连接OC, ∵CD是⊙O的切线,
∴OC⊥CD. 又∵AD⊥CD,
∴OC//AD. 由此得 ∠ACO=∠CAD.
D C
∵OC=OA. ∴ ∠CAO=∠ACO. ∴ ∠CAD=∠CAO. 故AC平分∠DAB.
A
O
B
【例题解析】
例3 作经过一定点C的圆的切线．
(1)点C在圆上．
(２)点C在圆外．
A
【切线的性质定理 切线的】性质定理: 圆的切线垂直于经过切点的半径
因为经过一点只有一条直线与已知直线垂直， 所以，经过圆心垂直于切线的直线一定过切点 ；反之,过切点且垂直于切线的直线也一定过圆
心.由此得到： l A M
推论１： 经过 圆心且垂直于 切线的直线必 经过切点．
推论２:经过切
点且垂直于切
即圆心到直线的距离小于半径. 推论１： 经过圆心且垂直于切线的直线必经过切点．
∴OD是△ABC的中位线,
反之,过切点且垂直于切线的直线也一定过圆心.
∴ ∠CAD=∠CAO. ∴∠ABO=180°－(∠AOB+∠A)
这与“直线l是圆O的切线”矛盾.
切线的性质定理: 圆的切线垂直于经过切点的半径
故直线l与圆O一定垂直.
能否仿照上节研究圆内接四边形的判 定定理的方法来得出一个圆的切线的判定 定理呢？

所以PF1＋PF2＝PQ1＋PQ2＝Q1Q2. 由正圆锥的对称性，知Q1Q2的长度等于两圆S1，S2所在平 行平面间的母线段的长度，而与P的位置无关，由此我们可知 在β>α时，平面π与圆锥的交线为一个椭圆．
平面与圆柱面的截线
[例2] 如图，在圆柱O1O2内嵌入双球，使它们 与圆柱面相切，切线分别为⊙O1和⊙O2，并且和圆柱 的斜截面相切，切点分别为F1，F2.
求证：斜截面与圆柱面的截线是以F1，F2为焦点 的椭圆．
[思路点拨] 证明曲线的形状是椭圆，利用椭圆的定义 (平面上到两个定点的距离之和等于定长的点的轨迹)来证明．
[证明] 如图，设点P为曲线上任一点，连接 PF1，PF2，则PF1，PF2分别是两个球面的切线，切点 为F1，F2，过P作母线，与两球面分别相交于K1， K2，则PK1，PK2分别是两球面的切线，切点为K1，K2.
根据切线长定理的空间推广 ， 知PF1＝PK1，PF2＝PK2， 所以PF1＋PF2＝PK1＋PK2＝K1K2. 由于K1K2为定值，故点P的轨迹是以F1，F2为焦点的椭圆．
平面与圆锥面的截线
[例3] 证明：定理2的结论(1)，即β>α时，平面π与圆锥的交 线为椭圆．
[思路点拨] 本题直接证明，难度较大，故可仿照定理1的 方法证明，即Dandelin双球法．
[证明] 如图，在圆锥内部嵌入Dandelin双球，一个位于 平面π的上方，一个位于平面π的下方，并且与平面π及圆锥均 相切．
做这个图形的平行射影．
3．正射影与平行射影的联系与区别 正射影与平行射影的投影光线与投影方向都是平行的．因 此，正射影也是平行射影，不同的是正射影的光线与投影面垂 直．而平行射影的投影光线与投影面斜交．平面图形的正射影 与原投影面积大小相等．而一般平行射影的面积要小于原投影 图形的面积．

∴∠1＝∠3，∴OD∥AE.
∵DE⊥AE，∴DE⊥OD， 即 DE 是⊙O 的切线．
(2)过 D 作 DG⊥AB， ∵∠1＝∠2，∴DG＝DE＝3. 在 Rt△ODG 中，OG＝ 52－32＝4， ∴AG＝4＋5＝9.
∵DG⊥AB，FB⊥AB，∴DG∥FB.
∴△ADG∽△AFB，∴DBFG＝AAGB. ∴B3F＝190，∴BF＝130.
【自主解答】 (1)如图所示，连接 BC. ∵CD 为⊙O 的切线， ∴OC⊥CD. 又 AD⊥CD，
∴OC∥AD.
(2)∵AC 平分∠DAB， ∴∠DAC＝∠CAB. ∵AB 为⊙O 的直径，∴∠ACB＝90°. 又 AD⊥CD，∴∠ADC＝90°， ∴△ADC∽△ACB. ∴AADC＝AACB，∴AC2＝AD·AB. ∵AD＝2，AC＝ 5，∴AB＝52.
1．“以圆的两条平行切线的切点为端点的线段是圆的 直径”这句话对吗？为什么？
【提示】 正确．如图 AB、CD 分别切⊙O 于 E、F， 连接 EO 并延长交 CD 于 F′，∵AB 是⊙O 的切线，∴OE
⊥AB.∵AB∥CD，∴OF′⊥CD，∴F′为切点，∴F′与 F
重合，即 EF 是⊙O 的直径．
圆的切线的性质及判定定理
1．切线的性质定理及推论
(1)性质定理：圆的切线垂直于经过 切点的半径．
如图 2－3－1，已知 AB 切⊙O 于点 A，则 OA⊥AB.
(2)推论 1：经过圆心且 垂直于切线的直线 必经过切点． (3)推论 2：经过切点且 垂直于切线的直线 必经过圆心．
图 2－3－1
2．切线的判定定理 经过半径的 外端 并且 垂直于 这条半径的直线是圆的 切线．
如图 2－3－2 所示，已知
AB 是⊙O 的直径，直线 CD 与⊙O 相切 于点 C，AC 平分∠DAB，AD⊥CD.

三圆的切线的性质及判定定理[对应学生用书P25]1．切线的性质(1)性质定理：圆的切线垂直于经过切点的半径． 如图，已知AB 切⊙O 于A 点，则OA ⊥AB .(2)推论1：经过圆心且垂直于切线的直线必经过切点． (3)推论2：经过切点且垂直于切线的直线必经过圆心． 2．圆的切线的判定方法(1)定义：和圆只有一个公共点的直线是圆的切线． (2)数量关系：到圆心距离等于半径的直线是圆的切线． (3)定理：过半径外端点且与这条半径垂直的直线是圆的切线．其中(2)和(3)是由(1)推出的，(2)是用数量关系来判定，而(3)是用位置关系加以判定的．[说明] 在切线的判定定理中要分清定理的题设和结论，“经过半径的外端”和“垂直于这条半径”这两个条件缺一不可，否则该直线就不是圆的切线．[对应学生用书P25]圆的切线的性质[例1] 如图，已知∠C ＝90°，点O 在AC 上，CD 为⊙O 的直径，⊙O 切AB于E ，若BC ＝5，AC ＝12.求⊙O 的半径．[思路点拨] ⊙O 切AB 于点E ，由圆的切线的性质，易联想到连接OE 构造Rt △OAE ，再利用相似三角形的性质，求出⊙O 的半径．[解] 连接OE ，∵AB 与⊙O 切于点E ， ∴OE ⊥AB ，即∠OEA ＝90°. ∵∠C ＝90°，∠A ＝∠A ， ∴Rt △ACB ∽Rt △AEO ， ∴OE BC ＝AOAB. ∵BC ＝5，AC ＝12，∴AB ＝13， ∴OE 5＝12－OE 13，∴OE ＝103.即⊙O 的半径为103.利用圆的切线的性质来证明或进行有关的计算有时需添加辅助线，其中连接圆心和切点的半径是常用辅助线，从而可以构造直角三角形，利用直角三角形边角关系求解，或利用勾股定理求解，或利用三角形相似求解等．1．如图，AB 切⊙O 于点B ，延长AO 交⊙O 于点C ，连接BC .若∠A ＝40°，则∠C ＝( )A ．20°B ．25°C ．40°D ．50°解析：连接OB ，因为AB 切⊙O 于点B ，所以OB ⊥AB ，即∠ABO ＝90°，所以∠AOB ＝50°.又因为点C 在AO 的延长线上，且在⊙O 上， 所以∠C ＝12∠AOB ＝25°.答案：B2.如图，已知P AB 是⊙O 的割线，AB 为⊙O 的直径．PC 为⊙O 的切线，C 为切点，BD ⊥PC 于点D ，交⊙O 于点E ，P A ＝AO ＝OB ＝1.(1)求∠P 的度数； (2)求DE 的长． 解：(1)连接OC .∵C 为切点，∴OC ⊥PC ，△POC 为直角三角形． ∵OC ＝OA ＝1，PO ＝P A ＋AO ＝2， ∴sin ∠P ＝OC PO ＝12.∴∠P ＝30°.(2)∵BD ⊥PD ，∴在Rt △PBD 中， 由∠P ＝30°，PB ＝P A ＋AO ＋OB ＝3， 得BD ＝32.连接AE .则∠AEB ＝90°，∴AE ∥PD . ∴∠EAB ＝∠P ＝30°，∴BE ＝AB sin 30°＝1，∴DE ＝BD －BE ＝12.圆的切线的判定[例2] 已知D 是△ABC ADB ＝60°，求证：AB 是△BCD 的外接圆的切线．[思路点拨]连接OB ，OC ，OD →∠BOD ＝90°→ ∠OBC ＝∠OCB ＝30°→∠ABO ＝90°→结论. [证明] 如图，连接OB ，OC ，OD ，OD 交BC 于E . ∵∠DCB 是BD 所对的圆周角， ∠BOD 是BD 所对的圆心角，∠BCD ＝45°， ∴∠BOD ＝90°.∵∠ADB 是△BCD 的一个外角， ∴∠DBC ＝∠ADB －∠ACB ＝60°－45°＝15°， ∴∠DOC ＝2∠DBC ＝30°， 从而∠BOC ＝120°，∵OB ＝OC ，∴∠OBC ＝∠OCB ＝30°. 在△OEC 中，因为∠EOC ＝∠ECO ＝30°， ∴OE ＝EC ，在△BOE 中，因为∠BOE ＝90°，∠EBO ＝30°. ∴BE ＝2OE ＝2EC ， ∴CE BE ＝CD DA ＝12， ∴AB ∥OD ，∴∠ABO ＝90°， 故AB 是△BCD 的外接圆的切线．要证明某直线是圆的切线，主要是运用切线的判定定理，除此以外，还有圆心到直线的距离等于半径等判定方法，但有时需添加辅助线构造判定条件，其中过圆心作直线的垂线是常用辅助线．3．本例中，若将已知改为“∠ABD ＝∠C ”，怎样证明：AB 是△BCD 的外接圆的切线． 证明：作直径BE ，连接DE ， ∵BE 是⊙O 的直径，∴∠BDE ＝90°， ∴∠E ＋∠DBE ＝90°. ∵∠C ＝∠E ，∠ABD ＝∠C ， ∴∠ABD ＋∠DBE ＝90°. 即∠ABE ＝90°.∴AB 是△BCD 的外接圆的切线．4.如图，△ABC 内接于⊙O ，点D 在OC 的延长线上，sin B ＝12，∠D ＝30°.(1)求证：AD 是⊙O 的切线． (2)若AC ＝6，求AD 的长． 解：(1)证明：如图，连接OA ， ∵sin B ＝12，∴∠B ＝30°，∵∠AOC ＝2∠B ，∴∠AOC ＝60°， ∵∠D ＝30°，∴∠OAD ＝180°－∠D －∠AOC ＝90°， ∴AD 是⊙O 的切线． (2)∵OA ＝OC ，∠AOC ＝60°，∴△AOC 是等边三角形，∴OA ＝AC ＝6， ∵∠OAD ＝90°，∠D ＝30°， ∴AD ＝3AO ＝6 3.圆的切线的性质和判定的综合考查[例3] 如图，AB 为⊙O 的直径，D 是BC 的中点，DE ⊥AC 交AC 的延长线于E ，⊙O 的切线BF 交AD 的延长线于点F .(1)求证：DE 是⊙O 的切线；(2)若DE ＝3，⊙O 的半径为5，求BF 的长． [思路点拨] (1)连接OD ，证明OD ⊥DE ； (2)作DG ⊥AB . [证明] (1)连接OD ， ∵D 是BC 中点，∴∠1＝∠2. ∵OA ＝OD ，∴∠2＝∠3. ∴∠1＝∠3. ∴OD ∥AE .∵DE ⊥AE ，∴DE ⊥OD ，即DE 是⊙O 的切线． (2)过D 作DG ⊥AB ， ∵∠1＝∠2，∴DG ＝DE ＝3. 在Rt △ODG 中，OG ＝52－32＝4， ∴AG ＝4＋5＝9.∵DG ⊥AB ，FB ⊥AB ，∴DG ∥FB . ∴△ADG ∽△AFB . ∴DG BF ＝AG AB. ∴3BF ＝910.∴BF ＝103.对圆的切线的性质与判定的综合考查往往是热点，其解答思路常常是先证明某直线是圆的切线，再利用切线的性质来求解相关结果．5.如图，已知两个同心圆O ，大圆的直径AB 交小圆于C 、D ，大圆的弦EF 切小圆于C ，ED 交小圆于G ，若小圆的半径为2，EF ＝43，试求EG 的长．解：连接GC ，则GC ⊥ED . ∵EF 和小圆切于C ， ∴EF ⊥CD ，EC ＝12EF ＝2 3.又CD ＝4，∴在Rt △ECD 中， 有ED ＝EC 2＋CD 2 ＝(23)2＋42＝27.由射影定理可知EC 2＝EG ·ED ， ∴EG ＝EC 2ED ＝(23)227＝677.6．如图，以Rt △ABC 直角边AC 上一点O 为圆心，OC 为半径的⊙O 与AC 的另一个交点为E ，D 为斜边AB 上一点且在⊙O 上，AD 2＝AE ·AC .(1)证明：AB 是⊙O 的切线； (2)若DE ·OB ＝8，求⊙O 的半径． 解：(1)证明：连接OD ，CD ，∵AD 2＝AE ·AC ， ∴AD AE ＝ACAD.又∵∠DAE ＝∠DAC ， ∴△DAE ∽△CAD ，∴∠ADE ＝∠ACD . ∵OD ＝OC ，∴∠ACD ＝∠ODC ， 又∵CE 是⊙O 的直径，∴∠ODE ＋∠CDO ＝90°，∴∠ODA ＝90°， ∴AB 是⊙O 的切线． (2)∵AB ，BC 是⊙O 的切线，∴OB ⊥DC ，∴DE ∥OB ，∴∠CED ＝∠COB ， ∵∠EDC ＝∠OCB ，∴△CDE ∽△BCO ， ∴DE CO ＝CEBO，DE ·OB ＝2R 2＝8， ∴⊙O 的半径为2.[对应学生用书P27]一、选择题1．下列说法：①与圆有公共点的直线是圆的切线；②垂直于圆的半径的直线是圆的切线；③与圆心的距离等于半径的直线是圆的切线；④过直径的端点，垂直于此直径的直线是圆的切线．其中正确的有( )A ．①②B ．②③C ．③④D ．①④答案：C2．如图，AB 是⊙O 的直径，BC 是⊙O 的切线，AC 交⊙O 于D .AB ＝6，BC ＝8，则BD 等于( )A ．4B ．4.8C ．5.2D ．6解析：∵AB 是⊙O 的直径，∴BD ⊥AC . ∵BC 是⊙O 的切线，∴AB ⊥BC . ∵AB ＝6，BC ＝8，∴AC ＝10. ∴BD ＝AB ·BCAC ＝4.8.答案：B3.如图，CD 切⊙O 于B ，CO 的延长线交⊙O 于A ，若∠C ＝36°，则∠ABD 的度数是( )A ．72°B ．63°C ．54°D ．36°解析：连接OB .∵CD 为⊙O 的切线，∴∠OBC ＝90°. ∵∠C ＝36°，∴∠BOC ＝54°. 又∵∠BOC ＝2∠A ，∴∠A ＝27°， ∴∠ABD ＝∠A ＋∠C ＝27°＋36°＝63°. 答案：B4．如图，在⊙O 中，AB 为直径，AD 为弦，过B 点的切线与AD 的延长线交于C ，若AD ＝DC ，则sin ∠ACO 等于( )A.1010 B.210 C.55D.24 解析：连接BD ，则BD ⊥AC .∵AD ＝DC ，∴BA ＝BC ， ∴∠BCA ＝45°.∵BC 是⊙O 的切线，切点为B ， ∴∠OBC ＝90°.∴sin ∠BCO ＝OB OC ＝OB 5OB ＝55，cos ∠BCO ＝BC OC ＝2OB 5OB ＝255.∴sin ∠ACO ＝sin(45°－∠BCO ) ＝sin 45°cos ∠BCO －cos 45°sin ∠BCO ＝22×255－22×55＝1010. 答案：A 二、填空题5．如图，已知∠AOB ＝30°，M 为OB 边上一点，以M 为圆心、2为半径作⊙M .若点M 在OB 边上运动，则当OM ＝________时，⊙M 与OA 相切．解析：若⊙M 与OA 相切，则圆心M 到直线OA 的距离等于圆的半径2.过M作MN⊥OA于点N，则MN＝2.在Rt△MON中，∵∠MON＝30°，∴OM＝2MN＝2×2＝4.答案：46．已知P A是圆O的切线，切点为A，P A＝2，AC是圆O的直径，PC与圆O交于B点，PB＝1.则圆O 的半径R＝________.解析：AB＝AP2－PB2＝ 3.由AB2＝PB·BC，∴BC＝3，Rt△ABC中，AC＝AB2＋BC2＝2 3.∴R＝ 3.答案： 37．圆O的直径AB＝6，C为圆周上一点，BC＝3，过C作圆的切线l，过A作l的垂线AD，AD分别与直线l、圆交于点D、E，则∠DAC＝________，DC＝________.解析：连接OC，∵OC＝OB，∴∠OCB＝∠OBC.又∠DCA＋∠ACO＝90°，∠ACO＋∠OCB＝90°，∴∠DCA＝∠OCB，∵OC＝3，BC＝3，∴△OCB是正三角形．∴∠OBC＝60°，即∠DCA＝60°.∴∠DAC＝30°.在Rt△ACB中，AC＝AB2－BC2＝33，DC＝AC sin 30°＝32 3.答案：30°33 2三、解答题8.如图所示，D是⊙O的直径AB的延长线上一点，PD是⊙O的切线，P是切点，∠D＝30 °.求证：P A＝PD.证明：如图，连接OP，∵PD是⊙O的切线，P为切点．∴PO⊥PD.∵∠D＝30°，∴∠POD＝60°.又∵OA＝OP，∴∠A＝∠APO＝30°.∴∠A＝∠D.∴P A＝PD.9.如图，已知在△ABC中，AB＝AC，以AB为直径的⊙O交BC于D，过D点作⊙O的切线交AC于E.求证：(1)DE⊥AC；(2)BD2＝CE·CA.证明：(1)连接OD，AD.∵DE是⊙O的切线，D为切点，∴OD⊥DE.∵AB是⊙O的直径，∴AD⊥BC.又AB＝AC，∴BD＝DC.∴OD∥AC.∴DE⊥AC.(2)∵AD⊥BC，DE⊥AC，∴△CDE∽△CAD.∴CDCA＝CECD.∴CD2＝CE·CA.∴BD＝DC.∴BD2＝CE·CA.10.如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE.(1)求证：AE是⊙O的切线；(2)若∠DBC＝30°，DE＝1 cm，求BD的长．解：(1)证明：连接OA.∵DA平分∠BDE，∴∠BDA＝∠EDA.∵OA＝OD，∴∠ODA＝∠OAD.∴∠OAD＝∠EDA.∴OA∥CE.∵AE⊥DE，∴∠AED＝90°，∴∠OAE＝∠DEA＝90°.∴AE⊥OA.∴AE是⊙O的切线．(2)∵BD是直径，∴∠BCD＝∠BAD＝90°.∵∠DBC＝30°，∴∠BDC＝60°.∴∠BDE＝120°.∵DA平分∠BDE，∴∠BDA＝∠EDA＝60°.∴∠ABD＝∠EAD＝30°.在Rt△AED中，∠AED＝90°，∠EAD＝30°，∴AD＝2DE.在Rt△ABD中，∠BAD＝90°，∠ABD＝30°，∴BD＝2AD＝4DE.∵DE的长是1 cm，∴BD的长是4 cm.。

A T
2.3圆的切线判定定理及性质定理讲义
1：切线的判定定理与切线的性质定理及其推论。

2：掌握切线的性质定理。

1.认真研读教材20-22页并温习重要概念，然后认真限时完成导学案。

切线的性质定理及其推论与切线的判定定理
课前预习
一：知识链接
1.切线的判定定理
切线的判定定理：
注：定理的题设①“经过半径外端”，②“垂直于半径”，两个 条件缺一不可。

结论是“直线是圆的切线”。

2．切线的性质定理及其推论
切线的性质定理：。

我们分析：这个定理共有三个条件：
一条直线满足（1）垂直于切线 （2） 过切点 （3）过圆心 任意知道两个，这可以推出第三个。

即知2推1。

定理：①过圆心，过切点⇒ 垂直于切线
OA 过圆心，OA 过切点A ，则OA ⊥AT
②经过圆心，垂直于切线⇒过切点 ()
()12AB M AB MT ⎫⎪⇒⎬⊥⎪⎭过圆心为切点
A
③经过切点，垂直于切线⇒过圆心()
()
1
2
AM MT
AM
M
⊥⎫⎪
⇒
⎬
⎪⎭
过圆心为切点
二：试一试。