全等三角形探究题各种题型非常全

全等三角形证明经典50题（含答案）1.已知：AB=4 , AC=2 , D 是BC 中点，AD 是整数，求 AD延长AD 至U E,使DE=AD, 则三角形ADC 全等于三角形EBD即 BE=AC=2 在三角形 ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数，则AD=512.已知：D 是 AB 中点，/ ACB=90 °，求证： CD - AB2为BC=ED,CF=DF, / BCF= / EDF 。

所以 三角形BCF 全等于三角形 EDF （边角边）。

所以BF=EF, / CBF= / DEF 。

连接 BE 。

在三角形 BEF 中,BF=EF 。

所以 / EBF= / BEF 。

/ ABE= / AEB 。

所以 AB=AE 。

在三角形 ABF 和 / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF 。

所以/ C= / D , F 是 CD 中点，求证：/ 1 = / 2证明：连接BF 和EF 。

因又因为 / ABC= / AED 。

所以 三角形 AEF 中， AB=AE,BF=EF, 三角形ABF 和三角形AEF 全等。

所以 / BAF= / EAF （ / 仁/ 2）。

A3因为 EB = EF ,CE = CE ， 所以△ CEBCEF 所以/ B = / CFE 因为/ B +/ D = 180° / CFE + / CFA = 180° 所以/ D = / CFA 因为 AC 平分/ BAD 所以/ DAC = / FAC 又因为 AC = AC 所以△ ADC 也厶AFC ( SAS ) 所以AD = AF 所以AE = AF + FE = AD + BE12.如图，四边形 ABCD 中，AB // DC ，BE 、CE 分别平分/ ABC 、/ BCD ，且点 E 在AD 上。

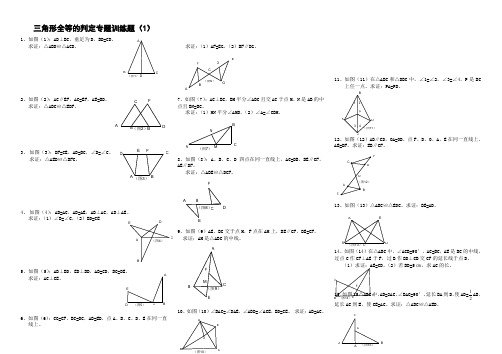
三角形全等的判定专题训练题（1）1、如图（1）：AD ⊥BC ，垂足为D ，BD=CD 。

求证：△ABD ≌△ACD 。

2、如图（2）：AC ∥EF ，AC=EF ，AE=BD 。

求证：△ABC ≌△EDF 。

3、 如图（3）：DF=CE ，AD=BC ，∠D=∠C 。

求证：△AED ≌△BFC 。

4、 如图（4）：AB=AC ，AD=AE ，AB ⊥AC ，AD ⊥AE 。

求证：（1）∠B=∠C ，（2）BD=CE5、如图（5）：AB ⊥BD ，ED ⊥BD ，AB=CD ，BC=DE 。

求证：AC ⊥CE 。

6、如图（6）：CG=CF ，BC=DC ，AB=ED ，点A 、B 、C 、D 、E 在同一直线上。

求证：（1）AF=EG ，（2）BF ∥DG 。

7、如图（7）：AC ⊥BC ，BM 平分∠ABC 且交AC 于点M 、N 是AB 的中点且BN=BC 。

求证：（1）MN 平分∠AMB ，（2）∠A=∠CBM 。

8、如图（8）：A 、B 、C 、D 四点在同一直线上，AC=DB ，BE ∥CF ，AE ∥DF 。

求证：△ABE ≌△DCF 。

9、如图（9）AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

10、如图（10）∠BAC=∠DAE ，∠ABD=∠ACE ，BD=CE 。

求证：AB=AC 。

11、如图（11）在△ABC 和△DBC 中，∠1=∠2，∠3=∠4，P 是BC上任一点。

求证：PA=PD 。

12、如图（12）AB ∥CD ，OA=OD ，点F 、D 、O 、A 、E 在同一直线上，AE=DF 。

求证：EB ∥CF 。

13、如图（13）△ABC ≌△EDC 。

求证：BE=AD 。

14、如图（14）在△ABC 中，∠ACB=90°，AC=BC ，AE 是BC 的中线，过点C 作CF ⊥AE 于F ，过B 作BD ⊥CB 交CF 的延长线于点D 。

全等三角形证明经典50题（含答案）1. 已知：AB=4,AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD ，则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE 〈AB+BE 即：10—2〈2AD 〈10+2 4〈AD 〈6 又AD 是整数，则AD=52. 已知:D 是AB 中点，∠ACB=90°,求证:12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED ，CF=DF,∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE.在三角形BEF 中，BF=EF.所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB.所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF ，∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2）。

ADBC4. 已知:∠1=∠2，CD=DE,EF//AB ，求证：EF=AC 证明：过E 点,作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE(AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD,求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证:AE=AD+BE证明： 在AE 上取F,使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°,∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC(SAS) 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图,四边形ABCD 中，AB ∥DC,BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

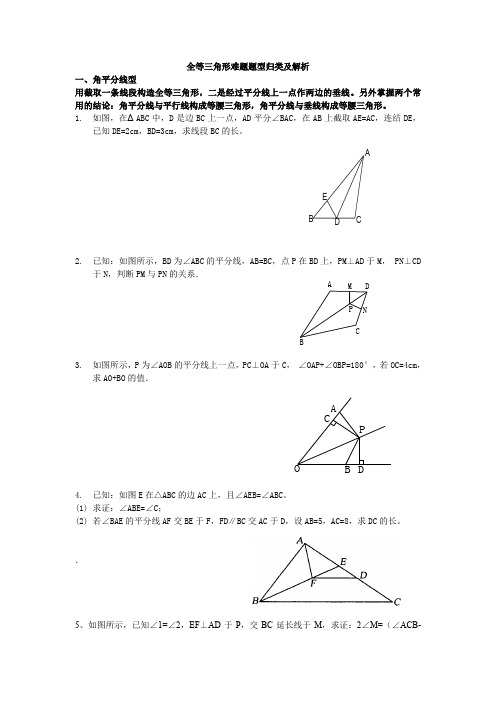
全等三角形难题题型归类及解析一、角平分线型用截取一条线段构造全等三角形，二是经过平分线上一点作两边的垂线。

另外掌握两个常用的结论：角平分线与平行线构成等腰三角形，角平分线与垂线构成等腰三角形。

1. 如图，在ΔABC 中，D 是边BC 上一点，AD 平分∠BAC ，在AB 上截取AE=AC ，连结DE ，已知DE=2cm ，BD=3cm ，求线段BC 的长。

2. 已知：如图所示，BD 为∠ABC 的平分线，AB=BC ，点P 在BD 上，PM ⊥AD 于M ，•PN ⊥CD于N ，判断PM 与PN 的关系．3. 如图所示，P 为∠AOB 的平分线上一点，PC ⊥OA 于C ，•∠OAP+∠OBP=180°，若OC=4cm ，求AO+BO 的值．4. 已知：如图E 在△ABC 的边AC 上，且∠AEB=∠ABC 。

(1) 求证：∠ABE=∠C ；(2) 若∠BAE 的平分线AF 交BE 于F ，FD ∥BC 交AC 于D ，设AB=5，AC=8，求DC 的长。

．5、如图所示，已知∠1=∠2，EF ⊥AD 于P ，交BC 延长线于M ，求证：2∠M=（∠ACB-A B C DE P D A CB M N P DAC BO∠B ）21PFMDBA CE6、如图，已知在△ABC 中，∠BAC 为直角，AB=AC ，D 为AC 上一点，CE ⊥BD 于E ．（1） 若BD 平分∠ABC ，求证CE=12BD ；（2） 若D 为AC 上一动点，∠AED 如何变化，若变化，求它的变化范围；若不变，求出它的度数，并说明理由。

7、如图：四边形ABCD 中，AD ∥BC ，AB=AD+BC ，E 是CD 的中点，求证：AE ⊥BE 。

8、如图，在△ABC 中，∠ABC=60°，AD 、CE 分别平分∠BAC 、∠ACB ， 求证：AC=AE+CD ．1 已知：如图，四边形ABCD 中，AC 平分∠BAD ，CE ⊥AB 于E ，且∠B+∠D=180︒，求证：E D CB A A DBCEAE=AD+BEABDCE 12二、中点型由中点应产生以下联想： 1、想到中线，倍长中线2、利用中心对称图形构造8字型全等三角形3、在直角三角形中联想直角三角形斜边上的中线4、三角形的中位线已知：如图2，在∆A B C 中，A B A C >，AD 是BC 边的中线。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E ，使DE=AD ，则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中，AB —BE<AE 〈AB+BE 即：10—2〈2AD<10+2 4<AD 〈6 又AD 是整数，则AD=52. 已知:D 是AB 中点,∠ACB=90°，求证:12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED ，CF=DF,∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF ，∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中，BF=EF.所以 ∠EBF=∠BEF.又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF （∠1=∠2）.ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点,作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE(AAS)∴EG=AC ∵EF//AB ∴∠DF E=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证:∠B=2∠C证明：在AC 上截取AE=AB,连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB,AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BD AC=AE+CE ∴CE=DE ∴∠C=∠EDC ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD,CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB ＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC,BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

最新全等三角形经典题型50题(含答案)连接CF，BD。

因为AC平分∠BAD，所以∠CAE=∠CAD。

又∠CEB=90°，所以∠BEC=∠BAE。

因为EF＝EB，所以∠XXX∠XXX。

所以∠XXX∠BAE+∠XXX∠CAE+∠BEF=∠CAF。

所以三角形BCF和三角形CAF全等。

所以CF=AC。

又因为∠B+∠D=180°，所以∠XXX∠BAC。

所以三角形BDC和三角形BAC相似。

所以XXX。

又∠CAE=∠CAD，所以三角形CAE和三角形CAD相似。

所以XXX。

因为CE⊥AB，所以CE＝BD。

所以AE/AD=BD/CD。

所以AE/AD=AB+BD/CD。

所以AE/AD=AB/CD+BD/CD。

所以AE/AD=AB/AC+BD/AC。

所以AE/AD=AB+BD/AC。

所以AE=AD+BE。

AF=AB又因为，∠ABE=2∠C，∠XXX∠BAC-∠CAE=3∠C-90，∠ABF=180-∠ABE-∠BAF=5∠C-90所以，∠XXX-∠ABF=2∠C-90，∠BEF=180-∠ABE-∠FBE=3∠C因此，△XXX和△ABC相似所以，BE/AB=EF/BC，即BE=(AB×EF)/BC又因为，AC=AB+BC，所以AC-AB=BC所以，AC-AB=BC=(AB×EF)/BE=2BE所以，PC-PB<AC-AB成立。

AB=AF。

BF=2BE。

∠XXX∠ABC-∠ABE=3∠C-2∠C=∠CBF=CFAC-AB=AC-AF=CF=BF=2BE已知AB为线段，其中E为中点，AF=BD=5，AC=7，求DC。

作AG∥BD，交DE延长线于G。

因为AGE全等于BDE，所以AG=BD=5.又因为AGF∽CDF，所以AF=AG=5.所以DC=CF=2BE=2A。

在△ABC中，BD=DC，∠1=∠2，求证：AD⊥BC。

延长AD至H交BC于H，BD=DC。

所以∠XXX∠DCB，∠1=∠2.DBC+∠1=∠DCB+∠2，∠XXX∠XXX。

三角形全等的判定方法(5种)例题+练习(全面)本文讲述了全等三角形的判定方法，重点是边角边和角边角。

边角边指两边及其夹角分别相等的两个三角形全等，可以简写成“SAS”。

需要注意的是，必须是两边及其夹角，不能是两边和其中一边的对角。

例如，在图中的△ABC和△ABD中，虽然有一个角和两边相等，但是这两个三角形不全等。

但是在例1中，如果AC=AD，且∠CAB=∠DAB，则可以证明△ACB≌△ADB。

在例2中，如果AD∥BC，且∠ABC=∠DCB，AB=DC，AE=DF，则可以证明BF=CE。

角边角是指两角及其夹边分别相等的两个三角形全等，可以简写成“ASA”。

例如，在例2中，如果AD平分∠BAC，且∠ABD=∠ACD，则可以直接判定△ABD≌△ACD。

在例3中，如果在Rt△ABC中，BC=2cm，CD⊥AB，且EC=BC，EF=5cm，则可以求出AE的长度。

除了边角边和角边角外，还有三种判定全等三角形的条件。

在例5中，如果在△ABC和△DEF中，AB=DE，BC=EF，且有一个角相等，则可以证明△ABC≌△DEF。

在例6中，如果AB∥DE，AB=DE，BF=CE，则可以证明△ABC≌△DEF。

在例7和例8中，分别是通过角平分线和垂线的判定方法来证明两个三角形全等。

总之，掌握全等三角形的判定方法对于解决几何问题非常重要。

1.如图所示，在三角形ABC中，已知AB=DC，∠ABC=∠DCB。

根据角角边相等可知，∠ACB=∠DCB。

又因为AB=DC，所以BC=AC。

因此，根据SSS（边边边）相等可知，△ABC≌△DCB。

同时，∠ACB=∠DCB，AC=BC=DC。

2.如图所示，在三角形ABD和ABF中，已知AD=AE，∠1=∠2，BD=CE。

根据角角边相等可知，∠ABD=∠BCE。

又因为AD=CE，所以BD=BE。

因此，根据SAS（边角边）相等可知，△ABD≌△BCE。

同时，∠ABD=∠BCE，AD=CE=BE。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB-BE<AE<AB+BE 即:10-2<2AD<10+2 4<AD<6 又AD 是整数,则AD=52. 已知：D 是AB 中点，∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点，求证：∠1=∠2证明：连接BF 和EF 。

因为 BC=ED,CF=DF,∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边)。

所以 BF=EF,∠CBF=∠DEF 。

连接BE 。

在三角形BEF 中,BF=EF 。

所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED 。

所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2)。

ADBC4. 已知：∠1=∠2，CD=DE ，EF//AB ，求证：EF=AC 证明：过E 点，作EG//AC ，交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC ，AC=AB+BD ，求证：∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB ，AD=AD ∴⊿AED ≌⊿ABD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证：AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°，∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC （SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12. 如图，四边形ABCD 中，AB ∥DC ，BE 、CE 分别平分∠ABC 、∠BCD ，且点E 在AD 上。

专题01 全等三角形（35题12种题型）一、全等图形的识别（共2小题）1．（2022秋·河南驻马店·八年级校考期中）下列各组中的两个图形属于全等图形的是（ ）A．B．C．D．【答案】B【分析】根据全等图形的定义，逐一判断选项，即可．【详解】解：A、两个图形不能完全重合，不属于全等图形，故此选项不符合题意；B、两个图形能完全重合，属于全等图形，故此选项符合题意；C、两个图形不能完全重合，不属于全等图形，故此选项不符合题意；D、两个图形不能完全重合，不属于全等图形，故此选项不符合题意．故选：B．【点睛】本题主要考查全等图形的定义，熟练掌握“能完全重合的两个图形，是全等图形”是解题的关键．2．（2022秋·广西南宁·八年级广西大学附属中学校考期末）下列四个图形中，属于全等图形的是（ ）A．①和②B．②和③C．①和③D．③和④【答案】A【分析】根据全等形的概念：能够完全重合的两个图形叫做全等形可得答案．【详解】解：①、②和④都可以完全重合，因此全等的图形是①和②．故选：A．【点睛】此题主要考查了全等图形，关键是掌握能够完全重合的两个图形叫做全等形．二、利用全等三角形求正方形网格中的角度之和（共2小题）3．（2022秋·江苏宿迁·八年级统考期中）如图所示的网格是由9个相同的小正方形拼成的，图形的各个顶点∠-∠-∠的度数为（）．均为格点，则123A．30°B．45°C．55°D．60°【答案】B【分析】根据网格特点，可得出190∠=o ，24∠∠=，3445∠+∠=o ，进而可求解．【详解】解：如图，则190∠=o ，24∠∠=，3445∠+∠=o ，∴123∠-∠-∠904545=-=o o o ，故选：B ．【点睛】本题考查网格中的全等图形、三角形的外角性质，会利用全等图形求正方形网格中角度之和是解答的关键．4．（2022秋·山东菏泽·八年级统考期末）如图为6个边长相等的正方形的组合图形，则∠1+∠3-∠2=（ ）A ．30°B ．45°C ．60°D ．135°【答案】B 【分析】首先利用SAS 定理判定△ABC ≌△DBE ，根据全等三角形的性质可得∠3=∠ACB ，再由∠ACB+∠1=∠1+∠3=90°，可得∠1+∠3-∠2．【详解】∵在△ABC 和△DBE 中AB BD A D AC ED ìï∠∠íïî＝＝＝，∴△ABC ≌△DBE （SAS ），∴∠3=∠ACB ，∵∠ACB+∠1=90°，∴∠1+∠3=90°，∵∠2=45°∴∠1+∠3-∠2=90°-45°=45°，故选B ．【点睛】此题主要考查了全等图形，关键是掌握全等三角形的判定，以及全等三角形对应角相等．三、全等三角形的识别（共2小题）5．（2022秋·四川乐山·八年级统考期中）已知ABC DEF ≌△△，且A ∠与D ∠是对应角，B ∠和E ∠是对应角，则下列说法中正确的是（ ）A ．AC 与DF 是对应边B ．AC 与DE 是对应边C ．AC 与EF 是对应边D ．不能确定AC 的对应边【答案】A【分析】根据全等三角形的概念即可得到答案．【详解】解：A Q ∠与D ∠是对应角，B ∠和E ∠是对应角，C \∠和F ∠是对应角，AC \与DF 是对应边，故选A ．【点睛】本题考查了全等三角形，理解全等三角形的概念，准确找出对应边是解题关键．6．（2022秋·河南开封·八年级统考期末）下列说法中，正确的有（ ）①形状相同的两个图形是全等形 ②面积相等的两个图形是全等形 ③全等三角形的周长相等，面积相等 ④若ABC DEF ≌△△，则A D ∠=∠，AB EF=A ．1个B ．2个C ．3个D ．4个【答案】A【分析】根据全等的定义和性质判断即可．【详解】①形状大小都相同的两个图形是全等形，故①错误；②面积相等的两个图形不一定是全等形，故②错误；③全等三角形的周长相等，面积相等，是对的，故③正确；④若ABC DEF ≌△△，则A D ∠=∠，AB DE =，故④错误；故正确的有1个．故选：A【点睛】此题考查全等三角形的定义和性质，解题关键是掌握全等三角形的定义．四、全等三角形的性质（共3小题）7．（2022秋·湖北荆门·八年级统考期中）如图，在ABC V 中，D ，E 分别是边AC ，BC 上的点，若ADB EDB EDC V V V ≌≌，则C ∠的度数为（ ）A ．15°B ．20°C ．25°D ．30°【答案】D 【分析】根据EDB EDC V V ≌，推出90,DEB DEC DBE DCE ∠=∠=°∠=∠，再由ADB EDB V V ≌，得到90,DAB DEB DBA DBE ∠=∠=°∠=∠，利用直角三角形中两个锐角互余即可得出.【详解】∵EDB EDC V V ≌，∠DEB +∠DEC =180°，∴90,DEB DEC DBE DCE ∠=∠=°∠=∠，又∵ADB EDB V V ≌，∴90,DAB DEB DBA DBE∠=∠=°∠=∠∴90DBA DBE DCE ∠+∠+∠=°，即30DBA DBE DCE ∠=∠=∠=°故选：D ．【点睛】本题考查了全等三角形的性质，直角三角形两个锐角和等于90°，掌握全等的性质是解题的关键.8．（2022秋·河北石家庄·八年级统考期末）如图，若ABC ADE △△≌则下列结论中不成立的是（ ）A ．BAD CAE ∠=∠B ．BAD CDE ∠=∠C ．DA 平分BDE ∠D ．AC DE=【答案】D 【分析】根据全等三角形的性质得出∠B ＝∠ADE ，∠BAC ＝∠DAE ，AB ＝AD ，∠E ＝∠C ，再逐个判断即可．【详解】解：A ．∵△ABC ≌△ADE ，∴∠BAC ＝∠DAE ，∴∠BAC −∠DAC ＝∠DAE −∠DAC ，∴∠BAD ＝∠CAE ，故本选项不符合题意；B ．如图，∵△ABC ≌△ADE ，∴∠C ＝∠E ，∵∠AOE ＝∠DOC ，∠E ＋∠CAE ＋∠AOE ＝180°，∠C ＋∠COD ＋∠CDE ＝180°，∴∠CAE ＝∠CDE ，∵∠BAD ＝∠CAE ，∴∠BAD ＝∠CDE ，故本选项不符合题意；C ．∵△ABC ≌△ADE ，∴∠B ＝∠ADE ，AB ＝AD ，∴∠B ＝∠BDA ，∴∠BDA ＝∠ADE ，∴AD 平分∠BDE ，故本选项不符合题意；D ．∵△ABC ≌△ADE ，∴BC ＝DE ，故本选项符合题意；故选：D ．【点睛】本题考查了全等三角形的性质，等腰三角形的性质和三角形内角和定理，能熟记全等三角形的性质是解此题的关键，注意：全等三角形的对应角相等，对应边相等．9．（2022秋·河南信阳·八年级统考期末）三个全等三角形按如图的形式摆放，则123∠+∠+∠的度数是（ ）A ．90oB ．120oC ．135oD ．180o【答案】D 【分析】根据全等三角形的性质和三角形的内角和定理和三角形的外角可得123456360,578180°°∠+∠+∠+∠+∠+∠=∠+∠+∠=，即123360180°°∠+∠+∠=-．【详解】解：如图所示：∵图中是三个全等三角形，∴48,67∠=∠∠=∠,又∵三角形ABC 的外角和123456360°=∠+∠+∠+∠+∠+∠=，又578180°∠+∠+∠=，即564180∠+∠+∠=°，∴123360180018°°∠+∠+=∠=-°，故选：D ．【点睛】本题主要考查了全等三角形性质以及三角形的内角和定理， 解题关键点：熟记全等三角形的性质．五、利用“SSS”证明两个三角形全等（共4小题）10．（2022秋·福建龙岩·八年级校考期中）工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在AOB ∠的两边OA 、OB 上分别在取OC OD =，移动角尺，使角尺两边相同的刻度分别与点C 、D 重合，这时过角尺顶点M 的射线OM 就是AOB ∠的平分线．这里构造全等三角形的依据是（ ）A ．SASB ．ASAC ．AASD ．SSS【答案】D 【分析】根据全等三角形的判定条件判断即可．【详解】解：由题意可知,OC OD MC MD==在OCM ODM △和△中OC OD OM OMMC MD =ìï=íï=î∴OCM ODM @△△(SSS )∴COM DOM∠=∠∴OM 就是AOB ∠的平分线故选：D【点睛】本题考查全等三角形的判定及性质、角平分线的判定、熟练掌握全等三角形的判定是关键．11．（2023秋·河北张家口·八年级统考期末）如图，通过尺规作图得到A O B AOB '''∠=∠的依据是（ ）A．SSS B．SAS C．ASA 【答案】A△△【分析】根据作图过程利用SSS可以证明OCD≌【详解】解：根据作图过程可知，14．（2022秋·福建龙岩·八年级统考期中）如图，已知AB AD =，BC DE =，且10CAD ∠=°，25B D ∠=∠=°，120EAB ∠=°，则EGF ∠的度数为（ ）A．120°B．135A．60°B．【答案】B【分析】先证△BAE ≌△CAD ，得出∠B=∠C，再证∠CFB=∠BAC=90°即可．【详解】解：∵AB ⊥AC ，AD ⊥AE ，∴∠BAC=∠DAE=90°,∴∠BAE=∠CAD ，在△BAE 和△CAD 中，BA CA BAE CAD AE AD =ìï∠=∠íï=î,∴△BAE ≌△CAD ，∴∠B=∠C ，∵∠BGA=∠CGF ，∴∠CFB=∠BAC=90°,∴∠BFD =90°,故选：B ．【点睛】本题考查了全等三角形的判定与性质，解题关键是确定全等三角形并通过8字型导角求出度数．16．（2022秋·四川凉山·八年级统考期末）如图，△ABC 中，AB ＝AC ，BD ＝CE ，BE ＝CF ，若∠A ＝50°，则∠DEF 的度数是（ ）A ．60°B ．65°C ．70°D ．75°【答案】B 【分析】首先证明△DBE ≌△ECF ，进而得到∠EFC ＝∠DEB ，再根据三角形内角和计算出∠CFE ＋∠FEC 的度数，进而得到∠DEB ＋∠FEC 的度数，然后可算出∠DEF 的度数．【详解】解：∵AB ＝AC ，∴∠B ＝∠C ，在△DBE 和△ECF 中，BD CE B C BE CF =ìï∠=∠íï=î，∴△DBE ≌△ECF （SAS ），∴∠EFC ＝∠DEB ，∵∠A ＝50°，∴∠C ＝（180°−50°）÷2＝65°，∴∠CFE ＋∠FEC ＝180°−65°＝115°，∴∠DEB ＋∠FEC ＝115°，∴∠DEF ＝180°−115°＝65°，故选：B ．【点睛】本题考查了全等三角形的性质和判定，三角形内角和定理，关键是掌握三角形内角和是180°．17．（2022秋·河南漯河·八年级校考期末）如图，已知C D ∠=∠，AC AD =，增加下列条件：①AB AE =；②BC ED =；③12∠=∠；④B E ∠∠=．其中能使ABC V ≌AED △的条件有（ ）A ．4个B ．3个C ．2个D ．1个【答案】B 【分析】根据全等三角形的判定方法，逐一判断即可解答．【详解】解：①C D ∠∠=Q ，AC AD =，AB AE =，ABC \V 和AED △不一定全等，故①不符合题意；②C D ∠∠=Q ，AC AD =，BC DE =，ABC \V ≌()SAS AED V ，故②符合题意；③12∠∠=Q ，12EAB EAB ∠∠∠∠\+=+，CAB DAE ∠∠\=，C D ∠∠=Q ，AC AD =，ABC \V ≌()ASA AED V ，故③符合题意；④B E ∠∠=Q ，C D ∠=∠，AC AD =，ABC \V ≌()D AAS AE V ，故④符合题意；所以，增加上列条件，其中能使ABC V ≌AED △的条件有3个，故选：B ．【点睛】本题考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解题的关键．七、利用“SSS”证明两个三角形全等（共3小题）A ．3cm 2B ．4cm 【答案】C 【分析】证△ABP ≌△EBP ，推出12S PBC S ABC D =D ，代入求出即可．∵BP 平分∠ABC ，∴∠ABP ＝∠EBP ，∵AP ⊥BP ，∴∠APB ＝∠EPB ＝90°，在△ABP 和△EBP 中，∠ABP ＝∠EBPA ．SSSB ．SASC ．ASAD ．AAA【答案】C 【分析】根据垂直的定义和全等三角形的判定和性质定理即可得到结论．【详解】解：士兵的视线通过帽檐正好落在碉堡的底部点B ；然后转过身保持刚才的姿势，这时视线落在了我军阵地的点E 上；得∠A =∠D ，∵AC =DF ，∴∠ACB =∠DFE =90°，∴判定△ABC ≌△DFE 的理由是ASA ．故选：C ．【点睛】本题考查了全等三角形的应用，分析题意找到相等的角和边判定三角形的全等是解题的关键．21．（2021秋·吉林长春·八年级统考期中）如图，在ABC V 中，过点A 作ABC ∠的平分线的垂线AD 交ABC V 内部于点P ，交边BC 于点D ，连结CP ，若ABP V ，CDP △的面积分别为4、2，则ABC V 的面积是（ ）A ．24B ．12C ．8D ．6【答案】B 【分析】根据ASA 可证ABP DBP @V V ，由全等的性质可得，AP DP =，即P 是AD 中点，由等底同高可得，DBP ABP S S =V V ，APC DPC S S =V V ，从而计算ABC ABP DBP APC DPC S S S S S =+++V V V V V ，故得出答案．【详解】由题可得：ABP DBP ∠=∠，BP AD ^，90BPA BPD \∠=∠=°，在ABP V 与DBP V 中，ABP DBP BP BPBPA BPD ∠=∠ìï=íï∠=∠î，()ABP DBP ASA \@V V ，AP DP \=，4DBP ABP S S \==V V ，2APC DPC S S ==V V ，442212ABC ABP DBP APC DPC S S S S S \=+++=+++=V V V V V ．故选：B ．【点睛】本题考查全等三角形的判定与性质，求等底同高的面积，掌握全等三角形的判定方法是解题的关键．八、利用“AAS”证明两个三角形全等（共小题）A ．50B ．62【答案】A 【分析】由AE AB ^，EF FH ^，BG ^以证明EFA ABG @V V ，所以AF BG =，A ．30B ．32【答案】B 【分析】根据角的和差关系可得∠AEF =∠BAG ，利用可证明△CDH ≌△BCG ，可得CH =BG ，CG =DH 形EFHD -2S △ABC ，利用梯形和三角形面积公式即可得答案．24．（2022秋·河北保定·八年级统考期末）如图，在ABC V 中，AB AC =，AD 是高，能直接判断ABD ACD @△△的依据是（ ）A ．SSSB ．SASC ．HLD ．ASA【答案】C【分析】根据直角三角形的全等证明即可判断．【详解】证明：∵AD ⊥BC∴ABD △和ACD V 是直角三角形，∵AB AC =，AD =AD （公共边），所以ABD △≌ACD V （HL ）故选C【点睛】本题主要考查直角三角形的全等证明，掌握直角三角形的全等证明方法是解题的关键．25．（2023春·河北张家口·八年级统考期中）已知：如图，在△ABC 中，点D 在边BC 上，DB ＝DC ，DE AB ^，DF AC ^，垂足分别为E ，F ，DE ＝DF ．求证：Rt Rt DEB DFC ≌△△．以下是排乱的证明过程：①∴∠BED ＝∠CFD ＝90°，②∴()Rt Rt DEB DFC HL ≌△△．③∵DE ⊥AB ，DF ⊥AC ，④∵在Rt DEB △和Rt DFC △中，DB DC DE DF =ìí=î，证明步骤正确的顺序是（ ）A ．③→②→①→④B ．③→①→④→②C ．①→②→④→③D ．①→④→③→②【答案】B【分析】根据垂直定义得出∠BED =∠CFD =90°，再根据全等三角形的判定定理推出即可．【详解】证明：∵DE ⊥AB ，DF ⊥AC ，∴∠BED =∠CFD =90°，在Rt △DEB 和Rt △DFC 中，BD CD DE DF =ìí=î，∴Rt △DEB ≌Rt △DFC （HL ），即选项B 正确；选项A 、选项C 、选项D 都错误；故选：B ．【点睛】本题考查了垂直定义和全等三角形的判定，注意：全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ，两直角三角形全等还有HL ．26．（2022·辽宁葫芦岛·八年级校考期中）如图，CA ⊥AB ，垂足为点A ，AB ＝12米，AC ＝6米，射线BM ⊥AB ，垂足为点B ，动点E 从A 点出发以2米/秒沿射线AN 运动，点D 为射线BM 上一动点，随着E 点运动而运动，且始终保持ED ＝CB ，当点E 经过t 秒时，由点D 、E 、B 组成的三角形与△BCA 全等．请问t有几种情况？（ ）A．1种B．2种C．3种D．4种【答案】D【分析】首先分两种情况：当E在线段AB上和当E在BN上，然后再分成两种情况：AC＝BE和AB＝EB，分别进行计算，即可得出结果．【详解】解：①当E在线段AB上，AC＝BE时，△ACB≌△BED，∵AC＝6，∴BE＝6，∴AE＝12﹣6＝6，∴点E的运动时间为6÷2＝3（秒）；②当E在BN上，AC＝BE时，△ACB≌△BED，∵AC＝6，∴BE＝6，∴AE＝12+6＝18，∴点E的运动时间为18÷2＝9（秒）；③当E在线段AB上，AB＝EB时，△ACB≌△BDE，这时E在A点未动，因此时间为0秒；④当E在BN上，AB＝EB时，△ACB≌△BDE，∵AB＝12，∴BE＝12，∴AE＝12+12＝24，∴点E的运动时间为24÷2＝12（秒），综上所述t的值为：0，3，9，12．共4种情况．故选D．【点睛】本题考查了全等三角形的综合问题，解本题的关键在于找到所有符合题意的情况．27．（2021秋·河北沧州·八年级统考期末）如图所示，有两个长度相同的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯水平方向DF的长度相等，则（1）AB=DE；（2）∠ABC+∠DFE=90°；（3）∠ABC=∠DEF．其中正确的有（）A ．0个B ．1个C ．2个D ．3个【答案】D 【分析】由已知条件判断两个直角三角形全等，根据全等三角形的性质逐一分析即可.【详解】解：由题意知90BAC EDF ∠=∠=o在Rt BAC V 和Rt EDF V 中：∵BC EF AC DF=ìí=î∴Rt BAC Rt EDF @△△(HL )∴AB DE =，ABC DEF∠=∠∴（1）、（3）正确∵+90DEF DFE ∠∠=o ，ABC DEF∠=∠∴+90ABC DFE ∠∠=o∴（2）正确故选：D【点睛】本题考查两个直角三角形全等的判定和性质，牢记相关的定理和性质内容是解题的关键．十、添加一个条件使两个三角形全等（共小题）28．（2023春·湖南衡阳·八年级校考期末）如图，点B ，F ，C ，E 共线，∠B =∠E ，BF =EC ，添加一个条件，不能判断△ABC ≌△DEF 的是（ ）A ．AB =DEB ．∠A =∠DC ．AC =DFD ．AC ∥FD【答案】C 【分析】根据全等三角形的判定与性质逐一分析即可解题．【详解】解：Q BF =EC ，BC EF\=A. 添加一个条件AB =DE ，又,BC EF B E=∠=∠Q ()ABC DEF SAS ∴△≌△故A 不符合题意；B. 添加一个条件∠A =∠D又,BC EF B E=∠=∠Q ()ABC DEF AAS \V V ≌故B 不符合题意；C. 添加一个条件AC =DF ，不能判断△ABC ≌△DEF ，故C 符合题意；D. 添加一个条件AC ∥FDACB EFD\∠=∠又,BC EF B E=∠=∠Q ()ABC DEF ASA \V V ≌故D 不符合题意，故选：C ．【点睛】本题考查添加条件使得三角形全等即全等三角形的判定，是重要考点，难度较易，掌握相关知识是解题关键．29．（2022秋·安徽合肥·八年级统考期末）如图，点B 、E 在线段CD 上，若A DEF ∠=∠，则添加下列条件，不一定能使ABC EFD V V ≌的是（ ）A ．C D ∠=∠，AC DE=B ．BC DF =，AC DE =C ．ABC DFE ∠=∠，AC DE=D ．AC DE =，AB EF=【答案】B 【分析】利用三角形全等的判定方法进行分析即可．【详解】解：A ．添加∠C =∠D ，AC =DE 可利用ASA 判定△ABC ≌△EFD ，故此选项不合题意；B ．添加BC =FD ，AC =ED 不能判定△ABC ≌△EFD ，故此选项符合题意；C ．添加∠ABC =∠DFE ，AC =DE 可利用AAS 判定△ABC ≌△EFD ，故此选项不合题意；D ．添加AC =DE ，AB =EF 可利用SAS 判定△ABC ≌△EFD ，故此选项不合题意；故选：B ．【点睛】本题重点考查了三角形全等的判定定理，普通两个三角形全等共有四个定理，即AAS 、ASA 、SAS 、SSS，直角三角形可用HL定理，注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．十一、尺规作图与三角形全等（共3小题）故答案为：④．【点睛】本题考查了利用SSS 定理判定三角形全等，熟练掌握三角形全等的判定方法是解题关键．31．（2021秋·浙江宁波·八年级统考期末）已知：两边及其夹角，线段a ，c ，a ∠．求作：ABC V ，使BC a =，AB c =，（用尺规作图，保留作图痕迹，不写作法）．请你根据所学的知识，说明尺规作图作出ABC a ∠=∠，用到的是三角形全等判定定理中的______，作出的ABC V 是唯一的，依据是三角形全等判定定理中的______．【答案】作图见解析；SSS ，SAS ．【分析】（1）首先根据一个角等于已知角的方法作∠B=∠α，再在角的两边分别截取BC=a ，AB=c ，再连接AC ；（2）根据三角形全等的判定定理可得．【详解】解：（1）如图所示：（2）尺规作图作出∠ABC=∠α，用到的是三角形全等判定定理中的SSS ，作出的△ABC 是唯一的，依据是三角形全等判定定理中的SAS ．【点睛】本题主要考查用尺规作三角形，全等三角形的判定定理，关键是掌握作一个角等于已知角的方法以及全等三角形的判定方法．32．（2021秋·重庆梁平·八年级校联考期中）用尺规作图的方法，画出与下面△ABC 全等的△DEF （保留作图痕迹）．【答案】见解析【分析】分析根据SSS 画一个△DEF 与△ABC 全等即可．【详解】作法：作射线EM，在EM上截取线段EF，使EF=BC；分别以E点和F点为圆心，以BA、CA长为半径画弧，两弧相交于D点；连接ED，FD．则△DE F即为所求作的三角形．【点睛】本题主要考查了利用尺规作图法作全等三角形．可以根据全等三角形的判定方法SSS，SAS，ASA 选择一种方法即可．熟练掌握基本的尺规作图是解题的关键．十二、证明两个三角形全等（共3小题）33．（2022秋·贵州铜仁·八年级统考期中）如图，点B、E、C、F四点在一条直线上，∠A=∠D，AB//DE，老师说：再添加一个条件就可以使△ABC≌△DEF．下面是课堂上三个同学的发言，甲说：添加AB=DE；乙说：添加AC//DF；丙说：添加BE=CF．（1）甲、乙、丙三个同学说法正确的是________；（2）请你从正确的说法中选择一种，给出你的证明．【答案】（1）甲、丙；（2）见详解【分析】（1）根据平行线的性质，由AB∥DE可得∠B＝∠DEC，再加上条件∠A=∠D，只需要添加一个能得出对应边相等的条件，即可证明两个三角形全等，添加AC//DF不能证明△ABC≌△DEF；（2）添加AB=DE，再由条件AB∥DE可得∠B＝∠DEC，然后再利用ASA判定△ABC≌△DEF即可．【详解】（1）解：∵AB//DE，∴∠B＝∠DEC，又∵∠A=∠D，∴添加AB=DE，可得△ABC≌△DEF（ASA）；添加BE=CF，可得BC=EF，可得△ABC≌△DEF（AAS）∴说法正确的是：甲、丙，故答案为：甲、丙；（2）选“甲”，理由如下：证明：∵AB ∥DE ，∴∠B ＝∠DEC ，在△ABC 和△DEF 中A DB DEF AB DE ∠∠ìï∠∠íïî＝＝＝ ∴△ABC ≌△DEF （ASA ）．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．34．（2021秋·江西抚州·八年级统考期中）如图，从①AB AC =；②AD AE =；③BD CE =；④ADB E ∠=∠；⑤BAC DAE ∠=∠五个条件中，选出三个条件，利用全等三角形的判定定理，可使ABD ACE ≌△△，你能想出几种方法，罗列出来，并挑选其中一种方法写出你的证明过程．【答案】可选①②③或①②⑤或①④⑤或②③④或③④⑤或②④⑤ ，证明见解析【分析】根据全等三角形的判定定理，即可求解．【详解】解：可选①②③或①②⑤或①④⑤或②③④或③④⑤或②④⑤选①②③，证明：在ABD △与ACE △中，∵AB AC =，AD AE =，BD CE = ，∴()ABD ACE SSS V V ≌；选①②⑤，证明：∵BAC DAE ∠=∠，∴BAD CAE ∠=∠，在ABD △与ACE △中，∵AB AC =，BAD CAE ∠=∠，AD AE =，∴()ABD ACE SAS △≌△；选①④⑤，证明：∵BAC DAE ∠=∠，∴BAD CAE ∠=∠，在ABD △与ACE △中，∵ADB E ∠=∠，BAD CAE ∠=∠，AB AC =，（1）求证：FC AD =；（2）若4AE =，4BE =【答案】（1）见解析；（2【分析】（1）利用ASA 证明（2）根据题意，ABCD S 四边形。

全等三角形证明经典50题（含答案）1. 已知：AB=4，AC=2，D 是BC 中点，AD 是整数，求AD延长AD 到E,使DE=AD,则三角形ADC 全等于三角形EBD即BE=AC=2 在三角形ABE 中,AB —BE 〈AE<AB+BE 即：10-2<2AD<10+2 4〈AD 〈6 又AD 是整数，则AD=52. 已知：D 是AB 中点,∠ACB=90°，求证：12CD AB3. 已知：BC=DE ，∠B=∠E ，∠C=∠D ，F 是CD 中点,求证:∠1=∠2证明：连接BF 和EF 。

因为 BC=ED ，CF=DF ，∠BCF=∠EDF 。

所以 三角形BCF 全等于三角形EDF(边角边）.所以 BF=EF,∠CBF=∠DEF 。

连接BE.在三角形BEF 中，BF=EF.所以 ∠EBF=∠BEF 。

又因为 ∠ABC=∠AED.所以 ∠ABE=∠AEB 。

所以 AB=AE 。

在三角形ABF 和三角形AEF 中，AB=AE ，BF=EF ，∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF 。

所以 三角形ABF 和三角形AEF 全等。

所以 ∠BAF=∠EAF (∠1=∠2）。

ADBC4. 已知:∠1=∠2，CD=DE ，EF//AB ，求证:EF=AC 证明：过E 点，作EG//AC,交AD 延长线于G 则∠DEG=∠DCA ，∠DGE=∠2又∵CD=DE ∴⊿ADC ≌⊿GDE （AAS ）∴EG=AC ∵EF//AB ∴∠DFE=∠1∵∠1=∠2∴∠DFE=∠DGE ∴EF=EG ∴EF=AC5. 已知：AD 平分∠BAC,AC=AB+BD ，求证:∠B=2∠C证明：在AC 上截取AE=AB ，连接ED ∵AD 平分∠BAC ∴∠EAD=∠BAD 又∵AE=AB,AD=AD ∴⊿AED ≌⊿A BD （SAS ）∴∠AED=∠B ，DE=DB ∵AC=AB+BDAC=AE+CE ∴CE=DE ∴∠C=∠ED C ∵∠AED=∠C+∠EDC=2∠C ∴∠B=2∠C6. 已知：AC 平分∠BAD ，CE ⊥AB ，∠B+∠D=180°，求证:AE=AD+BE证明： 在AE 上取F ，使EF ＝EB ，连接CF 因为CE ⊥AB 所以∠CEB＝∠CEF ＝90° 因为EB ＝EF ，CE ＝CE ， 所以△CEB ≌△CEF 所以∠B ＝∠CFE 因为∠B ＋∠D ＝180°,∠CFE ＋∠CFA ＝180° 所以∠D ＝∠CFA 因为AC 平分∠BAD 所以∠DAC ＝∠FAC 又因为AC ＝AC 所以△ADC ≌△AFC(SAS ） 所以AD ＝AF 所以AE ＝AF ＋FE ＝AD ＋BE12。