3-1 逻辑运算、基本定理、基本规则
- 格式:ppt
- 大小:1.14 MB
- 文档页数:12



逻辑运算法则逻辑运算一直是人类思维中重要的组成部分,对于逻辑运算法则的研究则进一步拓展了人们对于逻辑思维的认识。
本文将从逻辑运算法则的基本概念出发,深入探讨其在不同情景下的应用,并探讨其对于日常生活和决策制定的重要性。
逻辑运算法则的基本概念逻辑运算法则是指在逻辑思维中使用的一系列规则和原则,旨在确保推理和论证的准确性和有效性。
其基本概念包括三大部分:命题逻辑、联结词和推理规则。
命题逻辑命题逻辑是逻辑运算法则的基础,它涉及命题的真假和逻辑关系的推断。
在命题逻辑中,命题可以是真可以是假,用符号P、Q、R等表示。
通过逻辑运算法则可以对命题之间的关系进行推理和推断,帮助我们更好地理清思路。
联结词联结词是连接命题的逻辑符号,包括“与”、“或”、“非”等。
它们用于表达不同的逻辑关系,帮助我们更准确地描述信息之间的关系。
推理规则推理规则是逻辑运算法则的重要组成部分,包括假言推断、析取三段论、假言三段论等。
通过这些推理规则,我们可以从已知的命题中得出新的结论,进行更深入的推理和论证。
逻辑运算法则在实际生活中的应用逻辑运算法则不仅仅是一种抽象的概念和原则,它还广泛应用于我们的日常生活中。
决策制定在面对日常生活中的选择和决策时,逻辑运算法则可以帮助我们分析各种因素的优劣,做出明智的决策。
通过逻辑运算法则,我们可以更好地评估风险和机会,提高决策的准确性和效率。
辩论和讨论在辩论和讨论中,逻辑运算法则可以帮助我们更好地组织自己的观点,避免逻辑混乱和谬误。
通过合理运用推理规则和联结词,我们可以更有说服力地表达自己的观点,并有效地驳倒对方的论证。
问题解决在解决问题和处理矛盾时,逻辑运算法则可以帮助我们快速定位问题的关键点,并找出解决问题的方法。
通过正确应用逻辑运算法则,我们可以更系统地分析问题,找出最佳解决方案。
总结逻辑运算法则作为人类思维中重要的一部分,对于我们的日常生活和决策制定具有重要意义。
通过深入理解逻辑运算法则的基本概念和应用,我们可以提高自己的逻辑思维能力,更好地应对各种挑战和问题。

《数字电子技术基础》读书笔记02 逻辑代数基础2.1从布尔代数到逻辑代数1849年英国数学家乔治布尔(George Boole)提出布尔代数,使用数学方法进行逻辑运算。
把布尔代数应用到二值逻辑电路中,即为逻辑代数。
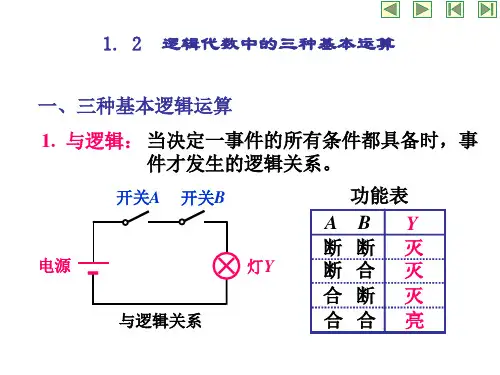
2.2逻辑代数中的运算(想想初等代数中的加减乘除)2.2.1三种基本运算与(AND):逻辑乘,Y=A B或(OR):逻辑加,Y=A+B非(NOT):逻辑求反,Y=Aˊ简单逻辑运算(与、或、非)的两套图形符号,均为IEEE(国际电气与电子工程师协会)和IEC(国际电工协会)认定。
上排为国外教材和EDA软件中普遍使用的特定外形符号;下排为矩形符号。
2.2.2复合逻辑运算(都可以表示为与、或、非的组合)与非(NAND):先与后非,与的反运算,Y=(A B)ˊ或非(NOR):先或后非,非的反运算,Y=(A+B)ˊ与或非(AND-NOR):先与再或再非,Y=(A B+C D)ˊ异或(Exclusive OR):Y=A⊕B=A Bˊ+AˊB A和B不同,Y为1;A和B相同,Y为0。
当A与B相反时,A Bˊ和AˊB,肯定有一个结果为1,则Y为1。
同或(Exclusive NOR):Y=A⊙B=A B+AˊBˊA和B相同,Y为1;A和B不同,Y为0。
当A与B相同时,A B和AˊBˊ,肯定有一个结果为1,则Y为1。
同或与同或互为反运算,即两组运算,只要输入相同,一定结果相反。
A⊕B=(A⊙B)ˊA⊙B=(A⊕B)ˊ复合逻辑运算的图像符号和运算符号。
2.3逻辑代数的基本公式和常用公式2.3.1基本公式(见对偶定理)2.3.2若干常用公式(见逻辑函数化简方法之公式化简法)2.4逻辑代数的基本定理2.4.1代入定理(相当于初等代数中的换元)任何一个包含逻辑变量A的逻辑等式中,若以另外一个逻辑式代入式中所有A的位置,则等式依然成立。
2.4.2反演定理对于任意一个逻辑式Y,若将其中所有的""换成"+","+"换成"","0"换成"1","1"换成"0",原变量换成反变量,反变量换成原变量,则得到的结果就是Yˊ。

For personal use only in study and research; notfor commercial use蚇3.3逻辑运算定理羇 3.3.1逻辑函数相等有两个逻辑函数F和G,如果对于F和G的每一种取值组合,对应的输出都相同,我们说这两个逻辑函数相等,记作F=G。
由逻辑函数相等的概念,可以得到下面的推论:如果F=G,则F和G对应的真值表完全相同;反过来,如果两个逻辑函数的真值表完全相同,则F=G.例3.3.1证明A+AB=A+B解:根据题意,列出真值表如表3.3.1所示。
膁表3.3.1 例3.3.1的真值表膃由表,对于A+AB和A+B两个逻辑函数的每一种取值组合,它们的输出完全相同。
所以,A+AB=A+B逻辑函数相等的概念是逻辑函数运算、化简和变换的基础。
我们介绍的定理、公式都可以利用逻辑函数相等的概念加以证明。
3.3.2逻辑运算公理常用的逻辑运算公理如表薁表3.3.2 常用逻辑运算公理莆3.3.3逻辑运算定理常用的逻辑运算定理如表蚆表3.3.3 常用逻辑运算定理3.3.4常用公式逻辑运算的公式有许多,在表,实际上,只要经过证明的等式都可以在以后的变换和化简时使用。
表3.3.4 常用公式注:公式1、2为吸收律和分配律的应用,公式3为多余因子定律,公式4为多余项定律,公式5为与或和或与转换定律。
3.3.5逻辑代数的三个基本规则1.代入规则若两个逻辑函数相等,即F=G,且F和G中都存在变量A,如果将所有出现变量A 的地方都用一个逻辑函数L代替,则等式仍然成立。
这个规则称为代入规则。
因为任何一个逻辑函数,它和一个逻辑变量一样,只有两种可能的取值(0和1),所以代入规则是正确的。
有了代入规则,就可以将基本等式(定理、常用公式)中的变量用某一逻辑函数来代替,从而扩大了它们的应用范围。
例3.3.2已知等式A(B+E)=AB+AE,将所有出现E的地方代之以(C+D),试证明等式成立。
解: 原式左边=A[B+(C+D)]=AB+A(C+D)=AB+AC+AD原式右边=AB+A(C+D)=AB+AC+AD所以等式A[B+(C+D)]=AB+A(C+D)成立。





逻辑代数的基本定律及规则文章来源:互联网作者:佚名发布时间:2012年05月26日浏览次数: 1 次评论:[已关闭] 功能:打印本文一、逻辑代数相等:假定F、G都具有n个相同变量的逻辑函数,对于这n个变量中的任意一组输入,如F和G都有相同的输出值,则称这两个函数相等。
在实际中,可以通过列真值表来判断。
二、逻辑代数的基本定律:在逻辑代数中,三个基本运算符的运算优先级别依次为:非、与、或。
由此推出10个基本定律如下:1.交换律A+B=B+A;A·B=B·A2.结合律A+(B+C)=(A+B)+C;A·(BC)=(AB)·C3.分配律A·(B+C)=AB+AC;A+BC=(A+B)·(A+C)4.0-1律A+0=A;A·1=AA+1=1 ;A·0=05.互补律A+=1 ;A·=06.重叠律A·A=A;A+A=A7.对合律=A8.吸收律A+AB=A;A·(A+B)=AA+B=A+B;A·(+B)=ABAB+B=B;(A+B)·(+B)=B9.反演律=·;=+10.多余项律AB+C+BC=AB+C;(A+B)·(+C)·(B+C)=(A+B)·(+C)上述的定律都可用真值表加以证明,它们都可以用在后面的代数化简中。
三、逻辑代数的基本规则:逻辑代数中有三个基本规则:代入规则、反演规则和对偶规则。
1.代入规则:在任何逻辑代数等式中,如果等式两边所有出现某一变量(如A)的位置都代以一个逻辑函数(如F),则等式仍成立。
利用代入规则可以扩大定理的应用范围。
例:=+,若用F=AC代替A,可得=++2.反演规则:已知函数F,欲求其反函数时,只要将F式中所有的“·”换成“+”,“+”换成“·”;“0”换成“1”,“1”换成“0”时,原变量变成反变量,反变量变成原变量,便得到。
一.逻辑运算当二进制代码表示不同的逻辑状态时,可以按照一定的规则进行推理运算1.三种基本的逻辑关系①与②或③非④几种常用的复合逻辑运算2.逻辑代数的基本公式和常用公式①基本公式①基本公式3.逻辑代数的基本定理①代入定理:在任何一个包含A的逻辑式中,若以另外一个逻辑式代入式子中A的位置,则等式依然成立②反演定理:如果一个表达式想要取反,那么就在这个表达式中将原变量变为反变量,将反变量变为原变量即可。
4.逻辑函数及其表示方法如果以逻辑变量为输入,运算结果为输出,则输入变量的值确定以后,输出的取值也会随之而定。
输入输出之间是一种函数关系注:在二值逻辑中,输入输出都只有两种取值可能,非零即一。
1.逻辑函数的两种标准表达形式①最小项之和:最小项M,其中M是乘积项,它包含N个因子,N个变量均以原变量和反变量的形式在M中出现一次最小项的编号:最小项的性质:在输入变量任意一个取值下,有且仅有一个最小项的值为1.全体最小项之和为1.任何两个最小项之积为0两个相邻的最小项之和可以合并,消掉一对因子,只留下一个公共因子。
注:相邻指的仅一个变量不同的两项。
②最大项之积最大项:M是相加项,它包含了N个因子,N个变量均以原变量或者反变量的形式在M中出现一次。
其实最小项与最大项是可以相互进行转变的,转变的方式就是摩根定理。
5.逻辑函数的化简逻辑函数的最简形式:最简与或包含的乘积项已经最少,每个乘积项的因子也最少称为最简的与或逻辑式。
①卡诺图化简法:实质:将逻辑函数的最小项之和以图形的方式表达出来以2的N次方分别代表N变量的所有最小项,并且将他们排列成矩阵,而且使得几何位置相邻的两个最小项在逻辑上也是相邻的(只有一个变量不同),这样就得到表示N变量全部最小项的卡诺图。
用卡诺图化简函数:依据:具有相邻的最小项可以合并,消去不同的因子,并且在卡诺图中,最小项的相邻可以直观的从图中反映出来。
合并最小项的原则:两个相邻的最小项可以合并成一项,消去一对因子;四个排成矩形的相邻最小项可以合并成一项,消去两对因子;八个相邻的最小项可以合并为一项,消去三对因子;。
2454.2 逻辑运算的基本定理教学要求本节要求学生熟悉逻辑运算的基本法则,能熟练运用真值表证明复合命题不同表达式的相等,能准确领会实际问题中命题所表达的实际意义.知识点1. 集合运算的基本法则2. 逻辑运算的基本法则3. 命题的蕴含4. 命题的等价5. 解析逻辑性问题4.2.1. 集合运算的基本法则集合的并、交、补运算满足下列定理给出的一些基本运算法则. 定理4.2.1. 设A ,B ,C 为任意三个集合,Ω与«分别表示全集和空集,则下面的运算法则成立: (1)交换律:A ∪B =B ∪A ,A ∩B =B ∩A ;(2)结合律:(A ∪B )∪C =A ∪(B ∪C )=A ∪B ∪C , (A ∩B )∩C =A ∩(B ∩C )=A ∩B ∩C ; (3)分配律: (A ∩B )∪C =(A ∪C )∩(B ∪C ) , (A ∪B )∩C =(A ∩C )∪(B ∩C ); (4)摩根(Morgan)律: B A B A I U =,B A B A U I =; (5)等幂律: A ∪A =A ,A ∩A =A ;(6)吸收律: (A ∩B )∪A =A ,(A ∪B )∩A =A ;(7)0―1律: A ∪«=A ,A ∩Ω=A , A ∪Ω=Ω,A ∩«=«; (8)互补律: =A A U Ω , =A A I «;(9)重叠律: B A B A A U I U =)( , B A B A A I I =∪)( .证. 我们借助文氏(Venn)图绘出分配律第一式及摩根律第一式的证明,余者由读者模仿完成.图4.12246图4.13例4.2.1 试证明等式 C C A C B C B A =)()())((I U I U I I . 证. )()())((C A C B C B A I U I U I I结合律)()()(C A C B C B A I U I U I I )(摩根律)()()(C A C B C B A I U I U I U 分配律)(()(C A B C B A I U U I U ) 交换律)(()(C B A C B A I U U I U ) 分配律C B A B A I U U U )(()=Ω∩C =C .对偶. 定理4.2.1的九条定律中每一条都包含两个或四个公式,只要将其中一个公式中的∪换成∩,同时把∩换成∪,把«换成Ω,同时把Ω换成«,这样就得到了另一个公式,这种有趣的规则称为对偶原理. 例如,摩根定律B A B A I U =中的∪换成∩,∩换成∪,就得到了另一个摩根公式B A B A U I = . 例4.2.2)(C B A U I 的对偶为)(C B A I U ;)()(C A B A I U I 的对偶为)()(C A B A U I U ;C B A U U 的对偶式是C B A I I .4.2.2. 逻辑运算的基本法则在逻辑代数中,三种基本的逻辑运算:∨,∧,┓与集合的三种基本运算:∪,∩,完全相仿,因此有类似的定理.定理4.2.2. 设P ,Q ,R 为三个任意命题,则下面的运算法则成立: (1)交换律: P ∨Q =Q ∨P ,P ∧Q =Q ∧P ;(2)结合律: (P ∨Q )∨R =P ∨(Q ∨R )=P ∨Q ∨R ,(P ∧Q )∧R =P ∧(Q ∧R )=P ∧Q ∧R ; (3)分配律: (P ∧Q )∨R =(P ∨R )∧(Q ∨R ),(P ∨Q )∧R =(P ∧R )∨(Q ∧R ); (4)摩根(Morgan)律: ┓(P ∨Q )= ┓P ∧┓Q ,┓(P ∧Q )= ┓P ∨┓Q ; (5)等幂律: P ∨P =P , P ∧P =P ;(6)吸收律: (P ∧Q )∨P =P ,(P ∨Q )∧P =P ;(7) 0―1律: P ∨0=P ,P ∧1=P , P ∨1=1,P ∧0=0;(8)互补律:P∨(┓P)=1 , P∧(┓P)= 0;(9)重叠律:P∨(┓P∧Q )= P∨Q,P∧(┓P∨Q )= P∧Q.证. 我们可以借助命题真值表来证明逻辑等式.如果两复合命题的真值相同,则说这两个形式上不同的命题实质是同一命题,它们是相等的.下面给出分配律第一式与摩根律第二式的证明.余者请读者由真值表自行模仿完成证明.P Q R P∧Q(P∧Q)∨R P∨R Q∨R(P∨R)∧(Q∨R)111 1 1 1 1 1111 1 0 1 1 1111 0 1 0 1 11 0 0 0 0 1110 1 1 0 1 110 1 0 0 0 010 0 1 0 1 110 0 0 0 0 0由此看出,复合命题(P∧Q)∨R,(P∨R)∧(Q∨R)的真值完全相同,所以有(P∧Q)∨R= (P∨R)∧(Q∨R)再由真值表P Q P∧Q┓(P∧Q) ┓P┓Q┓P∨┓Q1 1 1 0 011 0 0 1 0110 1 0 1 1110 0 0 1 1看出复合命题┓(P∧Q)和┓P∨┓Q有相同的真值,因此它们是相等的命题.即┓(P∧Q)= ┓P∨┓Q .在逻辑代数中,对偶法则仍然成立.只是要将集合Ω与«的对偶改成恒真命题1与恒假命题0的对偶.例4.2.3试证明:(A∨B)∧(A∨┓B)=A .证一.(A∨B)∧(A∨┓B)=A∨(B∧┓B)=A∨0=A .证二. 运用真值表,命题(A∨B)∧(A∨┓B)的真值表是A B┓B A∨B A∨┓B(A∨B)∧(A∨┓B)1 1 0 1 1 11 0 1 1 1 10 1 0 1 0 00 0 1 0 1 0(A∨B)∧(A∨┓B) 与A给出同样的真值.因此(A∨B)∧(A∨┓B) = A .例4.2.4试证明┓A∨┓(A∧B)∨┓(A∨B) = ┓A∨┓B .证.┓A∨┓(A∧B)∨┓(A∨B)=┓A∨(┓A∨┓B)∨(┓A∧┓B)=(┓A∨┓A)∨┓B∨(┓A∧┓B)=(┓A∨┓B)∨(┓A∧┓B) = ┓A∨┓B .4.2.3.命题的蕴含设A,B, C为平面上的三条直线,考虑它们之间是否垂直与平行,令命题:P:A⊥B与B⊥C247Q:A∥C那么可能出现四种情况:(1) P为真命题,Q为真命题.(2) P为真命题,Q为假命题.(3) P为假命题,Q为真命题.(4) P为假命题,Q为假命题.(1) (2) (3)图4.13由(1)我们说“P蕴含Q”显然是真的(见图4.13中(1)).由(2)我们说“P蕴含Q”显然是假的,因为这种情况不可能发生(见图4.13中(1)).由(3)或(4),前提P是假的,结果Q是真是假都有可能发生,对这两种情况我们仍可以说“P蕴含Q”,即“P蕴含Q”是真的(见图4.13中(2)或(3)).注. 这里所说的“真”是指其中的蕴含关系是真,并不是指命题Q为真.现在,对一般的两个命题P和Q组成的复合命题“命题P蕴含命题Q”作如下定义:定义.设P,Q为两个命题,通过联接词“若…则…”联接P与Q的复合命题“若P则Q”称为“P蕴含Q”,记为:P→Q.其真值由下表给出.逻辑蕴含的真值表P Q P→Q1 1 11 0 00 1 10 0 1即当且仅当P真Q假时,P→Q为假,其余情况,P→Q均为真.例4.2.5 下列蕴含命题为真命题:(2是偶数) → (3是奇数)(2是奇数) → (3是奇数)(2是奇数) → (3是偶数)它们分别对应真值表的一,三,四行.命题:(2是偶数) → (3是偶数)是假命题,它对应真值表的第二行.例4.2.6 设命题P:函数f(x)在区间(a,b)内可微.Q:函数f(x)在区间(a,b)内连续.则有P→Q:若f(x) 在区间(a,b)内可微的,则它在区间(a,b)内连续.证.当P,Q均为真命题时,由P推得Q是正确的,即P→Q是真命题.当P=1,Q=0,即f(x)可微,由f(x)的可微性推得它是不连续的,显然这是错的,即P→Q是假命题.最后,当P=0,即f(x)不可微时,此时f(x)或者连续,或者不连续,两种情况均存在,因此P→Q是真命题.248249例4.2.7 试证明 : P → Q = ┓P ∨Q . 证. 借助真值表PQ┓PP → Q ┓P ∨Q 1 1 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0 111得知,对任一组P 、Q 的真值,由P ,Q 复合而成的命题P → Q 和┓P ∨Q ,具有相同的真值,因此它们表达的是相等的命题,即P → Q = ┓P ∨Q . 例4.2.8 试证明:P → (Q ∨R )= (P → Q )∨(P → R ). 证. 通过命题的逻辑运算P → (Q ∨R ) = ┓P ∨(Q ∨R ) = ┓P ∨Q ∨R= (┓P ∨Q )∨(┓P ∨R )= (P → Q )∨(P → R ) 得知,等式P → (Q ∨R )= (P → Q )∨(P → R )成立.4.2.4. 逻辑的等价设A ,B 为平面上的两条直线,命题 P : A ⊥B Q : B ⊥A当P 为真命题,即A ⊥B 时,Q 也为真命题,即B ⊥A;这时P →Q , Q →P 均为真命题. 当P 为假命题时,即A 不垂直于B ,Q 也为假命题,B 不垂直于A; 这时P → Q , Q →P 均为假命题.图4.14当P 为真命题,Q 为假命题时,即A ⊥B ,而 B 不垂直于A,这是不可能的,即 P → Q 为假命题.同样当P 为假命题,Q 为真命题,即A 不垂直于B ,,此时B ⊥A 也是不可能的.综上所述,将命题A ⊥B ↔B ⊥A 叙述为:当A ⊥B ,B ⊥A 同时为真命题或同时为假命题时,它是真命题.其余情况下均为假命题.定义. 设P ,Q 为两个命题,称P ,Q 是等价的,并记为P ↔Q :当P 、Q 同时为真命题或同时为假命题时,命题P ↔Q 为真命题,而在其它情况下,P ↔Q 为假命题.即有下列逻辑等价的真值表:P Q P ↔Q 1 1 0 01 0 1 01 0 0 1例4.2.9 试证明: P ↔Q =(P →Q )∧(Q →P ). 证.借助真值表P Q P →Q Q →PP ↔Q(P →Q )∧(Q →P ) 1 1 11 111 0 0 01111111得知,对任一组P,Q的真值,命题P↔Q,(P→Q)∧(Q→P)具有相同的真值,因而它们是相等的命题,即P↔Q = (P→Q)∧(Q→P).因此,有时也把P,Q的等价说成同时有P→Q,Q→P.即所谓的P当且仅当Q.注. 两个命题的等价与两个命题的相等是两个不同的概念,前者是两个命题间的蕴含关系,而后者是指由几个相同的简单命题复合成真值表完全相同的两个复合命题.例4.2.10试证明:P↔Q = (┓P∧┓Q)∨(P∧Q).证. P↔Q = (P→Q)∧(Q→P)=(┓P∨Q)∧(┓Q∨P)= (┓P∧(┓Q∨P))∨(Q∧(┓Q∨P))=(┓P∧┓Q)∨(┓P∧P)∨(Q∧┓Q)∨(Q∧P)=(┓P∧┓Q)∨(P∧Q).例4.2.11设E为任一集合,证明:«⊂E .证.由⊂(包含)的定义知«⊂E↔ (x∈«→x∈E)而对任x,“x∈«”是假命题.因此,x∈«→x∈E是真命题.于是,由等价↔的定义,知«⊂E是真命题.至此,我们有了五种逻辑联接词:或,与,非,若…则…,当且仅当.也可把它们看成是五种逻辑运算:∨,∧,┓,→,↔.有时它们在同一逻辑式中出现,关于它们的运算先后顺序,除了加括号外,规定按下列优先级别进行:↔,→,∧,∨,┓即其中左边的比右边的作用范围大,也即右边的运算优先于左边的运算.例如逻辑式P∧Q∨R→Q∧┓S∨R就意味着((P∧(Q∨R)) → (Q∧((┓S)∨R)))规定最外层括号与┓S的括号可省略,于是上述逻辑式实际上就是(P∧(Q∨R)) → (Q∧(┓S∨R))例4.2.12设P:这是盗窃案.Q:有脏物.观察真值表P Q P→Q┓Q P∧┓Q ┓(P∧┓Q)1 1 0 0 11111111111可知P→Q = ┓(P∧┓Q) . 由P→Q说明,既是盗窃案,就应该有赃物; 而由┓(P∧┓Q)说明,这是盗窃案而没有赃物,这是不可能的.这两句话具有相同的意义,它们代表相等的命题.由例4.2.7及4.2.10可以看出,命题的蕴含与等价这两种运算可以由基本逻辑运算加,乘,非来实现.由有限个命题通过有限次基本逻辑运算产生的复合命题称为逻辑函数,其中的命题都是250251逻辑变量. 例如F =P ∨Q ∧R →┓S ∨R就是一个逻辑函数,其中含有P ,Q ,R ,S 四个逻辑变量.逻辑函数是逻辑代数的重要研究对象.逻辑代数与普通代数的区别:(1)普通代数中变量的取值根据实际问题的需要,可以取各种各样的数,甚至可以取任意的实数或复数.但逻辑变量,即命题只取0或1两个值,而这0与1之间不分大小,只是两个不同的抽象符号.(2)运算方法上的差别:逻辑代数中只有三种基本运算:逻辑加∨,逻辑乘∧与逻辑非┓.而普通代数中有加,减,乘,除,还有乘方,开方.(3)基本运算律的差异:两者都有交换律,结合律,分配律,但逻辑代数中多一个加对乘的分配律:(P ∧Q )∨R =(P ∨R )∧(Q ∨R ),这不同于普通代数.此外,逻辑代数中还有些特殊的定律,如摩根律,重叠律,吸收律等.4.2.5. 解析逻辑性问题在这一段里我们通过几个有趣的实例,向读者介绍逻辑运算的实际应用.在逻辑代数中, 我们把含有未知量的等式称为逻辑方程. 利用逻辑代数中关于命题的演算规律, 可以对逻辑方程求解. 在解决与命题有关的逻辑问题时,往往引入命题的记号, 把问题转化为解逻辑方程, 这就是所谓解析逻辑性问题. 例4.2.13 如何排课程表?在给某班排课程表时, 数学、物理与语文老师都提出了各自的要求: 数学必须排在第一或第二节, 物理要排在第二或第三节,语文则要求排在第一或第三节.试问应该如何排那一天的课程表(假定那天只排三节课)才能满足三位老师的所有要求,有几种方案可供选择. 解一. 我们先用排列的方法处理.第一节 第二节 第三节 第一方案 数学 物理 语文 第二方案 语文 数学 物理 说明: (1) 按题意, 第一节只能排数学或语文.(2) 第一节排数学后, 第二节只能排物理, 而语文不能排在第二节, 只能排在第三节.(3) 第一节排语文后, 第二节可排物理或数学, 但数学不能排在第三节, 故应把数学排在第二节, 最后物理排在第三节. 于是可得上述两种方案 .解二. 为理解逻辑方程的应用方法, 现令命题. 3 2, ,1====i i Y i W i S i i i 节”“语文课排在第节”“物理课排在第节”“数学课排在第 于是根据题意, 建立逻辑方程组:==∧=∧=∧=∨=∨=∨.3 .2 ,1 ,031 132 121 1313221因一节只能排一门课节节或第语文要排在第节节或第物理要排在第节节或第数学要排在第i W Y Y S W S Y Y W W S S i i i i i i 现在求解上述逻辑方程组.252将前三个方程做逻辑乘:(S 1∨S 2)∧(W 2∨W 3)∧(Y 1∨Y 3)=1, 再对上述方程中前两个逻辑加用分配律:( ( S 1∧W 2 )∨(S 1∧W 3)∨(S 2∧W 2)∨(S 2∧W 3))∧(Y 1∨Y 3 ) = 1022=∧⇔W S 分配律(S 1∧W 2∧Y 1)∨(S 1∧W 2∧Y 3)∨(S 1∧W 3∧Y 1)∨(S 1∧W 3∧Y 3)∨(S 2∧W 3∧Y 1)∨(S 2∧W 3∧Y 3) =13311=∧=∧⇔Y W Y S (S 1∧W 2∧Y 3)∨(S 2∧W 3∧Y 1) = 1 .由此得=∧∧=∧∧01323211Y W S Y W S 或 =∧∧=∧∧10323211Y W S Y W S 或 =∧∧=∧∧11323211Y W S Y W S ,其中第三组显然无解.由此得课程表的两种排法,即前述两种方案.例4.2.14 由父亲(A),母亲(B)与三个子女(C, D, E)组成的某五口之家买了一台彩电.当天晚上打开电视,关于他们五人看电视的情况有下列五种正确的描述:1) A 看电视时B 也在看;2) D 和E :或是两人都看了,或他们之中的一个看了; 3) B 和C 只有一个看了;4) C 和D :或是两人都看了,或是两人都没有看; 5) 若E 看了,则A 和D 也都看了.试问:那天晚上,这个家庭中哪几个人确实看了电视? 解. 令命题 : A =“父亲(A) 看了电视”,B =“母亲(B) 看了电视”, C =“子女C 看了电视”, D =“子女D 看了电视”, E =“子女E 看了电视”. 根据题意, 建立逻辑方程组: 1) A → B = 1 (1)(注意命题“A 看电视时B 也在看”与命题“A 与B 都在看”的差别) 2) D ∨E = 1 (2)3) ( B ∧┓C )∨(┓B ∧C ) = 1 …… (3) 4) (C ∧D )∨(┓C ∧┓D ) = 1 …… (4) 5) E →A ∧D = 1 …… (5) 下面求解.(1) ⇔ ┓A ∨B = 1 (6)(5) ⇔ ┓E ∨(A ∧D ) = 1 (7)现将 (2), (3), (4), (6), (7)五个式子作逻辑乘:(┓A ∨B )∧(D ∨E )∧((B ∧┓C )∨(┓B ∧C ))∧((C ∧D )∨(┓C ∧┓D ))∧(┓E ∨(A ∧D ))= 1 ,对上式作逻辑非得( A ∧┓B )∨(┓D ∧┓E )∨((┓B ∨C )∧(B ∨┓C ))∨((┓C ∨┓D )∧(C ∨D ))∨ (E ∧(┓A ∨┓D ))= 0分配律⇔(A ∧┓B )∨(┓D ∧┓E )∨(┓B ∧┓C )∨(C ∧B )∨(┓C ∧D )∨(┓D ∧C )∨(E ∧┓A )∨(E ∧┓D )=0⇔(A∧┓B)∨(┓B∧┓C)∨(C∧B)∨(┓C∧D)∨(┓D∧C)∨(┓A∧E)∨(┓D∧(┓E∨E)) = 0⇔ (A∧┓B)∨(┓B∧┓C)∨(B∧C)∨(┓C∧D)∨(C∧┓D)∨(┓A∧E)∨┓D = 0⇒┓D = 0⇔D = 1,代入上式得(A∧┓B)∨(┓B∧┓C)∨(B∧C)∨┓C∨(┓A∧E) = 0⇒┓C = 0⇔C = 1,再代入上式得(A∧┓B)∨B∨(┓A∧E) = 0⇒B = 0⇔┓B = 1,再代入上式得A∨(┓A∧E) = 0⇒A = 0⇔┓A = 1,再代入上式得E = 0综上所述,我们可以断定:父亲, 母亲与子女E未看电视,而子女C与D看了电视.例4.2.15 现有A, B, C三位女同学在舞台上分别扮演维吾尔、藏与苗族姑娘,化妆以后就不能辨认.有人判断说:“A扮维吾尔族,B不扮维吾尔族,C没有扮苗族”.事实上,他的三个判断中有一个对两个错.试问: A, B, C三位女同学究竟各扮演了哪个民族的姑娘?解.令命题:A w:A扮演维吾尔族姑娘; A z:A扮演藏族姑娘; A m:A扮演苗族姑娘.其他命题记号与之相仿.某人的判断是:A w∧┓B w∧┓C m,据题设知,命题A w , ┓B w , ┓C m中有一真两假.下面分三种情况讨论:(1) 设A w= 1,┓B w = 0,┓C m = 0 .则A w= 1, B w = 1, C m = 1.但A与B不能同时扮演维吾尔族姑娘.因此导致矛盾,这种情况被排除.(2) 设┓B w = 1,A w= 0,┓C m = 0 .则┓A w = 1,C m = 1, 此时A与B均不扮演维吾尔族姑娘,她们只能一个扮藏族,一个扮苗族,这与C已扮演苗族发生冲突.因此这种情况也被排除.(3) 设┓C m = 1,A w= 0,┓B w = 0,则由┓B w = 0 ⇔B w = 1 知B扮演维吾尔族姑娘;由┓C m= 1 知C不扮演苗族,她可扮演维吾尔族或藏族,但维吾尔族已由B扮演,因此C必然扮演藏族姑娘;由A w= 0及B w = 1、C z = 1知,A 必扮演苗族姑娘.因此A, B, C三人分别扮演了苗族, 维吾尔族, 藏族姑娘.例4.2.16某地有九个顽劣少年,一天他们躲在屋顶平台向下面行人掷石子,恶作剧的结果是:其中一人恰好把一块石子打中某行人的眼睛,造成眼球破碎致残的严重后果.经公安人员对他们审问,九人作了如下交代:朱:这是卢某干的;韦:不, 这不是事实;汪:这块石子是我抛的;余:这要么是汪某干的,要么是黄某干的;卢:韦某说的是谎话;袁:这是汪某干的;王:不对,汪某没干这事;黄:无论是我还是汪某都没干这事;江:黄某讲的是对的,但也没有卢某的事.经反复调查核实,上述九人的交代中只有三人说的是真话.试问肇事者是谁?解.从九人的交代可以看出,肇事者涉及到卢某、汪某与黄某.故令命题L = “卢某是肇事者”.253W = “汪某是肇事者”.H = “黄某是肇事者”.于是九人的交代分别是: (1) L;(2) ┓L;(3) W;(4) (W∨H )∧┓(W∧H );(5) ┓┓L;(6) W;(7) ┓W; (8) ┓H∧┓W;(9) ┓H∧┓W∧┓L.首先我们分析一下,有没有可能卢某、汪某与黄某都没有干,而是哪个另外的第四者干的?若是这样,则┓H∧┓W∧┓L = 1,即┓H = 1, ┓W = 1, ┓L = 1均为真,由此推出(2), (7), (8), (9)均为真,但题设只有三个命题为真,因此这不可能.这说明肇事者确实在卢某、汪某与黄某中间.现有(5) ┓┓L = L.设L = 1,则┓H = 1, ┓W = 1 均为真,由此推出(1), (5), (7), (8)均为真,这与三个为真的事实矛盾,因此我们断定L = 0.再假定W = 1,那么┓L = 1,┓H = 1为真,由此推出(2), (3), (4), (6)均为真.这又导致矛盾,故W = 0.最后,只有H = 1.事实上,此时┓L = 1,┓W = 1 均为真,于是(2), (4), (7)为真, 且(1), (3),(5), (6), (8), (9)均为假,与实际相符.于是此案告破, 肇事者是黄某.习题4.2.1 用逻辑推理的方法证明定理4.2.1中的(2)与(9),并用文氏图加以说明.4.2.2 用真值表证明定理4.2.2中未被证明的各定律.4.2.3 写出下列各逻辑函数的对偶式:(1) (P ∨Q)∧(┐P∨R)∧((R∨(S∧T))∨P);(2)┐(┐(P∧┐Q)∧(R∧┐S)∧T∧┐(P∧Q));(3)P∧(┐Q∨(R∧┐S∨┐T∧Q)∧R); (4)P∧┐Q∨Q∧┐R∨R∧(┐P∨S) .4.2.4 设命题P和Q的真值为1, 命题R和S的真值为0.求下列逻辑式的真值:(1)(P∧(Q→R))→S;(2)((P→Q)∧P∧┐Q)∧(R→S);(3)(P∧(Q∧R))∨┐((P∨Q)∧(R∨S));(4)(P∨(Q→(R∧┐P)))↔(Q∨┐S);4.2.5 运用真值表证明下列各等式:(1) (P∧┐Q) ∨(┐P∧Q)=( ┐P∨┐Q) ∧(P∨Q) ;(2)P→(Q∧R)=(P→Q)∧(P→R) ; (3)P→(Q→P)= ┐P →(P→Q) .4.2.6 运用逻辑运算法则证明下列各等式:(1)(┐P∧(┐Q∧R))∨(Q∧R) ∨(P∧R)=R ; (2) (P→Q)∧(R→Q)=(P∨R)→Q;(3) P∧(P∨Q)∧(┐P∨S)∧(┐Q∨S)∧(P∨R∨T∨W)=P∧S ; (4)┐((┐Q∧R)∨R)= ┐R ;(5) ┐P∨┐((P∧Q)∨┐Q)= ┐P; (6) P→((P→Q)∧┐(┐Q∨┐P))= ┐P∨Q .4.2.7 设A,B,C,D四个足球队举行比赛,有三位球迷传来如下消息:球迷甲说:C队第一名,B队第二名;球迷乙说:C队第二名,D队第三名;球迷丙说:A队第二名,D队第四名.他们每人说的都是一句正确,一句错误.试问这四个足球队的名次如何?4.2.8 四名同学A,B,C,D报名无偿献血,结果其中两名同学被批准.关于谁献血,有下列四种正确判断:(1)A与B只有一人被批准;(2)若C被批准,则D也必参加;(3)B与D不会同时被批准;(4)D不被批准时A就不参加.试问哪两人参加无偿献血?4.2.9 某集体宿舍里发生了一起盗窃收录机的案件,经保卫人员现场勘察,初步确定为内盗;且作案者为同宿舍A,B,C,D四人中的一个,在对这四人审查时,A说:收录机肯定是B偷的;B说:收录机是D偷的;C说:反正我不会干这种坏事;D说:我也决不会干这种坏事.254保卫人员反复调查、核实,断定他们中只有一人说了真话,那么究竟是谁偷了收录机?思 考 题4.2.10 命题的蕴含P →Q为什么要定义为“P →Q为假命题当且仅当P 真Q假” ?4.2.11 写出给定逻辑函数(复合命题)的对偶式时, 应注意什么?4.2.12 命题的等价与命题的相等这两个概念有什么差别?4.2.13 逻辑蕴含→与逻辑推理⇒之间有何区别?255。
逻辑代数的公式与基本定理逻辑代数是一门研究命题和命题逻辑关系的数学分支。
它通过符号表示和操作来研究命题的逻辑结构。
在逻辑代数中,有一些重要的公式和基本定理,它们对于理解和应用逻辑代数具有重要的意义。
一、公式1. 吸收律(Absorption Law):a∨(a∧b)=aa∧(a∨b)=a这个定律表明,当两个命题中一个包含另一个时,可以通过去除其中一个命题来简化表达式。
2. 结合律(Associative Law):(a∨b)∨c=a∨(b∨c)(a∧b)∧c=a∧(b∧c)这个定律表明,当有多个命题连接在一起时,可以改变它们的组合方式而不改变逻辑等价关系。
3. 分配律(Distributive Law):a∨(b∧c)=(a∨b)∧(a∨c)a∧(b∨c)=(a∧b)∨(a∧c)这个定律表明,当一个命题与两个命题的逻辑运算混合时,可以通过改变运算的顺序来简化表达式。
4. 归纳法则(Inductive Law):a∨¬a=1a∧¬a=0这个定律表明,任何命题与其否定的逻辑运算结果为真或假。
二、基本定理1. 双重否定定理(Double Negation Theorem):¬(¬a)=a这个定理表明,一个命题的否定再次否定后与原命题等价。
2. 德·摩根定理(De Morgan's Theorem):¬(a∨b)=¬a∧¬b¬(a∧b)=¬a∨¬b这个定理表明,一个命题的合取或析取的否定可以分别表示为各个命题的否定的合取或析取。
3.等幂律(Law of Identity):a∧1=aa∨0=a这个定理表明,一个命题与恒等元素进行合取或析取运算后仍等于原命题。
4. 否定消除律(Law of Noncontradiction):a∨¬a=1a∧¬a=0这个定理表明,一个命题与其否定进行合取或析取运算后结果为真或假。