25对应分析

对应分析方法与对应图解读方法——七种分析角度对应分析是一种多元统计分析技术，主要分析定性数据Category Data方法，也是强有力的数据图示化技术，当然也是强有力的市场研究分析技术。

这里主要介绍大家了解对应分析的基本方法，如何帮助探索数据，分析列联表和卡方的独立性检验，如何解释对应图，当然大家也可以看到如何用SPSS操作对应分析和对数据格式的要求！对应分析是一种数据分析技术，它能够帮助我们研究由定性变量构成的交互汇总表来揭示变量间的联系。

交互表的信息以图形的方式展示。

主要适用于有多个类别的定类变量，可以揭示同一个变量的各个类别之间的差异，以及不同变量各个类别之间的对应关系。

适用于两个或多个定类变量。

主要应用领域：概念发展（Concept Development)新产品开发 (New Product Development)市场细分 (Market Segmentation)竞争分析 (Competitive Analysis)广告研究 (Advertisement Research)主要回答以下问题：谁是我的用户？还有谁是我的用户？谁是我竞争对手的用户？相对于我的竞争对手的产品，我的产品的定位如何？与竞争对手有何差异？我还应该开发哪些新产品？对于我的新产品，我应该将目标指向哪些消费者？数据的格式要求对应分析数据的典型格式是列联表或交叉频数表。

常表示不同背景的消费者对若干产品或产品的属性的选择频率。

背景变量或属性变量可以并列使用或单独使用。

两个变量间——简单对应分析。

多个变量间——多元对应分析。

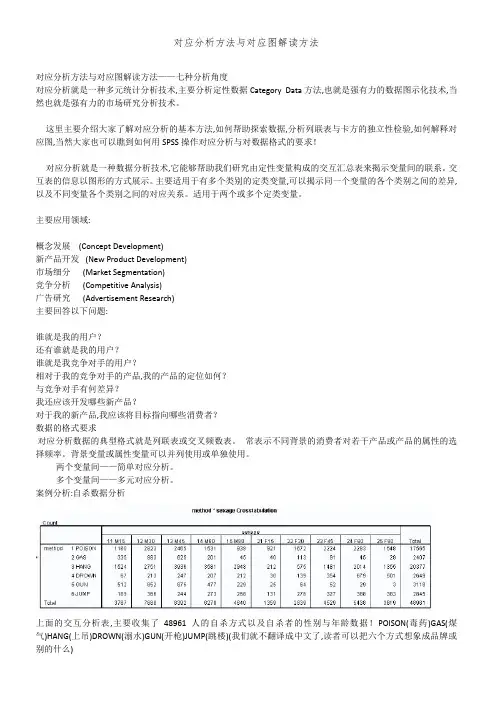
案例分析：自杀数据分析上面的交互分析表，主要收集了48961人的自杀方式以及自杀者的性别和年龄数据！POISON（毒药）GAS（煤气）HANG（上吊）DROWN（溺水）GUN（开枪）JUMP（跳楼）（我们就不翻译成中文了，读者可以把六个方式想象成品牌或别的什么）当然，我们拿到的最初原始数据可能是SPSS数据格式记录表，其中，性别取值1-male 2-female，年龄取值1-5，分别表示不同年龄段。

对应分析方法与对应图解读方法——七种分析角度对应分析就是一种多元统计分析技术,主要分析定性数据Category Data方法,也就是强有力的数据图示化技术,当然也就是强有力的市场研究分析技术。

这里主要介绍大家了解对应分析的基本方法,如何帮助探索数据,分析列联表与卡方的独立性检验,如何解释对应图,当然大家也可以瞧到如何用SPSS操作对应分析与对数据格式的要求！对应分析就是一种数据分析技术,它能够帮助我们研究由定性变量构成的交互汇总表来揭示变量间的联系。

交互表的信息以图形的方式展示。

主要适用于有多个类别的定类变量,可以揭示同一个变量的各个类别之间的差异,以及不同变量各个类别之间的对应关系。

适用于两个或多个定类变量。

主要应用领域:概念发展(Concept Development)新产品开发(New Product Development)市场细分(Market Segmentation)竞争分析(Competitive Analysis)广告研究(Advertisement Research)主要回答以下问题:谁就是我的用户？还有谁就是我的用户？谁就是我竞争对手的用户？相对于我的竞争对手的产品,我的产品的定位如何？与竞争对手有何差异？我还应该开发哪些新产品？对于我的新产品,我应该将目标指向哪些消费者？数据的格式要求对应分析数据的典型格式就是列联表或交叉频数表。

常表示不同背景的消费者对若干产品或产品的属性的选择频率。

背景变量或属性变量可以并列使用或单独使用。

两个变量间——简单对应分析。

多个变量间——多元对应分析。

案例分析:自杀数据分析上面的交互分析表,主要收集了48961人的自杀方式以及自杀者的性别与年龄数据！POISON(毒药)GAS(煤气)HANG(上吊)DROWN(溺水)GUN(开枪)JUMP(跳楼)(我们就不翻译成中文了,读者可以把六个方式想象成品牌或别的什么)当然,我们拿到的最初原始数据可能就是SPSS数据格式记录表,其中,性别取值1-male 2-female,年龄取值1-5,分别表示不同年龄段。

对应分析法一、简介对应分析(Correspondence analysis)也称关联分析、R-Q型因子分析，是近年新发展起来的一种多元相依变量统计分析技术，是一种多元统计分析技术，主要分析定性数据的方法，也是强有力的数据图示化技术。

对应分析是一种数据分析技术，它能够帮助我们研究由定性变量构成的交互汇总表来揭示变量间的联系。

交互表的信息以图形的方式展示。

主要适用于有多个类别的定类变量，可以揭示同一个变量的各个类别之间的差异，以及不同变量各个类别之间的对应关系，适用于两个或多个定类变量。

对应分析是由法国人Benzenci于1970年提出的，起初在法国和日本最为流行，然后引入到美国。

对应分析法是在R型和Q型因子分析的基础上发展起来的一种多元统计分析方法，因此对应分析又称为R－Q型因子分析。

在因子分析中，如果研究的对象是样品，则需采用Q型因子分析；如果研究的对象是变量，则需采用R型因子分析。

但是，这两种分析方法往往是相互对立的，必须分别对样品和变量进行处理。

因此，因子分析对于分析样品的属性和样品之间的内在联系，就比较困难，因为样品的属性是变值，而样品却是固定的。

于是就产生了对应分析法。

对应分析就克服了上述缺点，它综合了R型和Q型因子分析的优点，并将它们统一起来使得由R型的分析结果很容易得到Q型的分析结果，这就克服了Q 型分析计算量大的困难；更重要的是可以把变量和样品的载荷反映在相同的公因子轴上，这样就把变量和样品联系起来便于解释和推断。

对应分析数据的典型格式是列联表或交叉频数表。

常表示不同背景的消费者对若干产品或产品的属性的选择频率。

背景变量或属性变量可以并列使用或单独使用。

两个变量间——简单对应分析；多个变量间——多元对应分析。

对应分析的基本思想是将一个联列表的行和列中各元素的比例结构以点的形式在较低维的空间中表示出来。

它最大特点是能把众多的样品和众多的变量同时作到同一张图解上，将样品的大类及其属性在图上直观而又明了地表示出来，具有直观性。

对应分析对应分析的基本思想对应分析( Correspondence Analysis )又称为相应分析，是由法国统计学家于1970提出的，是在R型和Q型因子分析基础上，发展起来的一种多元相依的变量统计分析技术。

它通过分析由定性变量构成的交互汇总表来揭示变量间的关系。

当以变量的一系列类别以及这些类别的分布图来描述变量之间的联系时，使用这一分析技术可以揭示同一变量的各个类别之间的差异以及不同变量各个类别之间的对应关系。

对应分析方法是通过对交互表的频数分析来确定变量及其类别之间的关系。

例如，在分析顾客对不同品牌商品的偏好时，可以将商品与顾客的性别、收入水平、职业等进行交叉汇总，汇总表中的每一项数字都代表着某一类顾客喜欢某一品牌的人数，这一人数也就是这类顾客与这一品牌的“对应”点，代表着不同特点的顾客与品牌之间的联系。

通过对应分析，可以把品牌、顾客特点以及它们之间的联系同时反映在一个二维或三维的分布图上，顾客认为比较相似的品牌在图上的分布就会彼此靠近在一起。

根据顾客特点与每一品牌之间的距离，就可以判断它们之间关系的密切程度。

在对应分析中，每个变量的类别差异是通过直观图上的分值距离来表示。

这个距离并不是我们通常所说的距离，而是经过加权的距离，在加权的过程中，以卡方值的差异表现出来。

因此，对应分析的基础是将卡方值转变为可度量的距离。

卡方值是由累计交叉汇总表中每一交互组的实际频数与期望频数的差值计算得出。

如果卡方值是负值，就说明这一单元中实际发生频数低于期望频数。

每一单元格(每个行变量类别与列变量类别在表中的交叉点)频数的期望值取决于它在行分布中所占比例和列分布中所占比例。

如果某一单元格的卡方值是正值，而且数值很大，就说明这一单元格对应的行变量与列变量有很强的对应关系，这两个类别在图上的距离就会很近。

反之，若为负值，则在图上的距离就会远。

总之，对应分析是通过对定性变量构成的交互表进行分析，将定性变量的数据转变成可度量的分值，减少维度并做出分值分布图。

对应分析（Correspondence Analysis）在进行数据分析时，经常要研究两个定性变量（品质变量）之间的相关关系。

我们曾经介绍过使用列联表和卡方检验来检验两个品质变量之间相关性的方法，但是该方法存在一定的局限性。

卡方检验只能对两个变量之间是否存在相关性进行检验，而无法衡量两个品质型变量各水平之间的内在联系。

例如，汽车按产品类型可以分豪华型、商务型、节能型、耐用型，按销售区域可分为华北区、华南区、华中区、华东区、西南区、西北区、东北区。

利用卡方检验，只能检验销售地区与对型的偏好之间是否相关，但无法知道不同地区的消费者到底比较偏好哪种车型。

对应分析方法（Correspondence Analysis）又称相应分析、关联分析，是一种多元相依变量统计分析技术，是对两个定性变量（因素）的多种水平之间的对应性进行研究，通过分析由定性变量构成的交互汇总数据来解释变量之间的内在联系。

同时，使用这种分析技术还可以揭示同一变量的各个类别之间的差异以及不同变量各个类别之间的对应关系。

特别是当分类变量的层级数比较大时，对应分析可以将列联表中众多的行和列的关系在低维的空间中表示出来。

而且，变量划分的类别越多，这种方法的优势就越明显。

对应分析以两变量的交叉列联表为研究对象，利用“降维”的方法，通过图形的方式，直观揭示变量不同类别之间的联系，特别适合于多分类定性变量的研究。

对应分析的基本思想是将一个联列表的行和列中各元素的比例结构以点的形式在较低维的空间中表示出来。

它最大特点是能把众多的样品和众多的变量同时作到同一张图上，将样品的大类及其属性在图上直观而又明了地表示出来，具有直观性。

另外，它还省去了因子选择和因子轴旋转等复杂的数学运算及中间过程，可以从因子载荷图上对样品进行直观的分类，而且能够指示分类的主要参数（主因子）以及分类的依据，是一种直观、简单、方便的多元统计方法。

该统计研究技术在市场细分、产品定位、品牌形象以及满意度研究等领域得到了广泛的运用。

25的倍数的特征1. 引言在数学中，25是一个有特殊性质的数字。

它是5的平方，也是5的倍数。

因此，25的倍数有一些独特的特征和性质。

本文将探讨25的倍数的一些特征和其背后的数学原理。

2. 能被25整除的数字25的倍数是指能够被25整除的数字。

例如，25、50、75、100等都是25的倍数。

在每个25的倍数中，其末尾两位数字都是00、25、50或75，因为25乘以一个整数仍然是一个以00、25、50或75结尾的数字。

3. 数字的末尾两位的特征25的倍数的特征之一是，其末尾两位数字非常有规律。

每个25的倍数末尾两位数字的变化循环为：00、25、50、75。

例如，25的倍数序列为：25、50、75、00、25、50、75、00，以此类推。

4. 按位展开的特征以25为基础的倍数在按位展开时，也有一些规律。

以100为例，100可以表示为4位数，每个位上的数字都是25的倍数。

例如，个位数为25，十位数为50，百位数为75，千位数为00。

这一规律适用于大于100的所有25的倍数。

5. 与其他数字的关系25的倍数与其他数字之间还有一些有趣的关系。

例如，25的倍数乘以0.25等于其倍数除以4。

特别地，25的倍数乘以4等于其倍数乘以100乘以0.01。

这些关系有时在实际问题中可以起到一些便利的作用。

6. 应用举例25的倍数的特征在实际生活中有一些应用。

例如，考虑一个时钟上的指针，每小时移动30度。

在指针移动的整个周期中，共有12个25的倍数。

这一特征可以帮助我们在时间问题中更快地计算出指针所在的位置。

另一个例子是在计算货币兑换时。

如果知道一个单位货币兑换为25的倍数的话，我们可以利用25的倍数的特征来简化计算。

7. 总结25的倍数具有一些独特的特征和性质。

它们能够被25整除，其末尾两位数字有规律，可以按位展开，与其他数字有一些特殊的关系。

在实际生活中，这些特征可以在一些问题的计算中提供便利。

了解和利用25的倍数的特征，可以帮助我们更好地理解数字的性质和数学规律。

对应分析方法与对应图解读方法——七种分析角度对应分析是一种多元统计分析技术，主要分析定性数据Category Data方法，也是强有力的数据图示化技术，当然也是强有力的市场研究分析技术。

这里主要介绍大家了解对应分析的基本方法，如何帮助探索数据，分析列联表和卡方的独立性检验，如何解释对应图，当然大家也可以看到如何用SPSS操作对应分析和对数据格式的要求！对应分析是一种数据分析技术，它能够帮助我们研究由定性变量构成的交互汇总表来揭示变量间的联系。

交互表的信息以图形的方式展示。

主要适用于有多个类别的定类变量，可以揭示同一个变量的各个类别之间的差异，以及不同变量各个类别之间的对应关系。

适用于两个或多个定类变量。

主要应用领域：概念发展（Concept Development)新产品开发(New Product Development)市场细分(Market Segmentation)竞争分析(Competitive Analysis)广告研究(Advertisement Research)主要回答以下问题：谁是我的用户还有谁是我的用户谁是我竞争对手的用户相对于我的竞争对手的产品，我的产品的定位如何与竞争对手有何差异我还应该开发哪些新产品对于我的新产品，我应该将目标指向哪些消费者数据的格式要求对应分析数据的典型格式是列联表或交叉频数表。

常表示不同背景的消费者对若干产品或产品的属性的选择频率。

背景变量或属性变量可以并列使用或单独使用。

两个变量间——简单对应分析。

多个变量间——多元对应分析。

案例分析：自杀数据分析上面的交互分析表，主要收集了48961人的自杀方式以及自杀者的性别和年龄数据！POISON（毒药）GAS（煤气）HANG（上吊）DROWN（溺水）GUN （开枪）JUMP（跳楼）（我们就不翻译成中文了，读者可以把六个方式想象成品牌或别的什么）当然，我们拿到的最初原始数据可能是SPSS数据格式记录表，其中，性别取值1-male 2-female，年龄取值1-5，分别表示不同年龄段。

数字25的秘密解析它的数学背后的意义数字25的秘密解析：它的数学背后的意义数字在我们生活中非常常见，每一个数字都有其独特的含义和象征。

在数学中，数字25也有其特殊的含义和背后的意义。

在本文中，我们将深入解析数字25的秘密，探索其数学背后的意义。

一、数字25的起源和特点数字25的起源可追溯到古代，它来自于拉丁文中的"viginti quinque"（意为二十五）。

在罗马数字系统中，数字25用"XXV"表示。

它是由拉丁文中的两个数字字母组成，其中"X"表示10，"V"表示5。

因此，将这两个数字字母相加，得到了数字25。

在阿拉伯数字系统中，数字25直接以阿拉伯数字"25"表示。

数字25有以下几个特点：首先，它是奇数和平方数的结合。

其次，25是5的平方，也是较小的平方数之一。

此外，数字25处于数字序列的中间位置，介于20和30之间，具有一定的特殊性。

二、数字25在数学中的意义1. 数字25在代数中的意义在代数中，数字25与方程求解和变量运算等方面有关。

例如，方程x^2 - 25 = 0表示一个关于未知数x的二次方程，解该方程将得到两个解：x = 5和x = -5。

这说明数字25在代数中与解方程和数值运算等相关。

2. 数字25在几何中的意义在几何中，数字25与图形的面积和长度等概念有关。

例如，一个边长为5单位的正方形的面积等于25单位平方。

此外，数字25也与圆的面积有关，当半径为5单位时，圆的面积也等于25π单位平方。

这展示了数字25在几何学中的重要性与面积和长度概念相关。

3. 数字25在概率和统计中的意义在概率和统计学中，数字25与概率计算和统计分析有关。

例如，当抛掷一个均匀的6面骰子时，数字25代表着第二个最大数出现的概率。

此外，数字25也在某些统计方法中充当阈值或截断点，例如，当使用t分布表时，25可能是自由度和显著性水平的组合。

对应分析数据一、背景介绍对应分析数据是一种统计分析方法，用于研究两个或多个变量之间的关系。

通过对这些变量之间的相关性进行分析，可以帮助我们了解它们之间的相互关系，并从中得出有价值的结论。

本文将以某公司销售数据为例，对应分析数据进行详细解析。

二、数据收集为了进行对应分析，我们首先需要收集相关的数据。

在这个例子中，我们收集了某公司过去一年的销售数据，包括产品销售额、广告投入、促销活动次数以及客户满意度等信息。

这些数据将用于分析销售额与其他变量之间的关系。

三、数据准备在进行对应分析之前，我们需要对数据进行准备。

首先，我们需要对数据进行清洗，删除缺失值或异常值。

然后，我们需要将数据进行标准化处理，以消除不同变量之间的量纲差异。

最后，我们需要将数据进行整理，以便于对应分析的进行。

四、对应分析方法对应分析是一种多元统计分析方法，可以用于研究多个变量之间的相关性。

在本例中，我们将使用主成分分析（Principal Component Analysis，PCA）作为对应分析的方法。

主成分分析可以将多个相关变量转换为少数几个无关变量，从而简化数据分析。

五、对应分析结果通过对销售数据进行对应分析，我们得到了以下结果：1. 主成分分析结果：- 第一主成分（PC1）解释了销售额的60%的方差，主要与广告投入和促销活动次数相关。

- 第二主成分（PC2）解释了销售额的25%的方差，主要与客户满意度相关。

- 其他主成分的解释方差较小，可以忽略不计。

2. 对应分析图：我们绘制了对应分析的图表，展示了销售额与其他变量之间的关系。

在图表中，不同变量之间的距离越近，表示它们之间的相关性越高。

通过观察图表，我们可以发现广告投入和促销活动次数与销售额之间存在较强的正相关关系，而客户满意度与销售额之间存在较弱的正相关关系。

六、结论与建议基于对应分析的结果，我们可以得出以下结论和建议：1. 广告投入和促销活动次数对销售额的影响较大，增加广告投入和促销活动次数可能会提高销售额。