对应分析方法与对应图解读方法
- 格式:doc
- 大小:567.50 KB
- 文档页数:11

对应分析当A 与B 的取值较少时,把所得的数据放在一张列联表中,就可以很直观的对A 与B 之间及它们的各种取值之间的相关性作出判断,当ij P 较大时,则说明属性变量A 的第i 状态与B 的第j 状态之间有较强的依赖关系.但是,当A 或者B 的取值比较多时,就很难正确的作出判断,此时就需要利用降维的思想简化列联表的结构.几个基本定义:我们此处讨论因素A 有n 个水平,因素B 有p 个水平。
行剖面:当变量A 的取值固定为i 时(i=1,2,…,n ),变量B 的各个状态相对出现的概率情况,即:可以方便的把第i 行表示成在p 维欧氏空间中的一个点,其坐标为:),,,(..2.1i ip i i i i rip p p p p p p = ,i=1,2,… , n ,实际上,该坐标可以看成p 维超平面121=+++p x x x 上的点。
记n 个行剖面的集合为n(r)。
由于列联表行与列的地位是对等的,由上面行剖面的定义方法,可以很容易的定义列剖面。
列剖面:),,,(..2.1j njj j j j cjp p p p p p p = ,j=1,2,… , p,实际上,该坐标可以看成n 维超平面121=+++n x x x 上的点。
记p 个列剖面的集合为p(c)。
定义了行剖面和列剖面之后,我们看到属性变量A 的各个取值情况可以用p 维空间的n 个点来表示,而B 的不同取值情况可以用n 维空间上的p 个点来表示。
而对应分析就是利用降维思想,把A 的各个状态表现在一张二维图上,又把B 的各个状态表现在一张二维图上,且通过后面的分析可以看到,这两张二维图的坐标有着相同的含义,即可以把A 的各个取值与B 的各个取值同时在一张二维图上表示出来。
距离:通过行剖面与列剖面的定义,A 的不同取值可以利用P 维空间中的不同点表示,各个点的坐标分别为ri P (i=1,2,…,n )。
而B的不同取值可以用n 维空间中的不同点表示,各个点的坐标分别为cj P (j=1,2,…,p )。


对应分析方法与对应图解读方法——七种分析角度对应分析是一种多元统计分析技术,主要分析定性数据Category Data方法,也是强有力的数据图示化技术,当然也是强有力的市场研究分析技术。
这里主要介绍大家了解对应分析的基本方法,如何帮助探索数据,分析列联表和卡方的独立性检验,如何解释对应图,当然大家也可以看到如何用SPSS操作对应分析和对数据格式的要求!对应分析是一种数据分析技术,它能够帮助我们研究由定性变量构成的交互汇总表来揭示变量间的联系。
交互表的信息以图形的方式展示。
主要适用于有多个类别的定类变量,可以揭示同一个变量的各个类别之间的差异,以及不同变量各个类别之间的对应关系。
适用于两个或多个定类变量。
主要应用领域:概念发展(Concept Development)新产品开发 (New Product Development)市场细分 (Market Segmentation)竞争分析 (Competitive Analysis)广告研究 (Advertisement Research)主要回答以下问题:谁是我的用户?还有谁是我的用户?谁是我竞争对手的用户?相对于我的竞争对手的产品,我的产品的定位如何?与竞争对手有何差异?我还应该开发哪些新产品?对于我的新产品,我应该将目标指向哪些消费者?数据的格式要求对应分析数据的典型格式是列联表或交叉频数表。
常表示不同背景的消费者对若干产品或产品的属性的选择频率。
背景变量或属性变量可以并列使用或单独使用。
两个变量间——简单对应分析。
多个变量间——多元对应分析。
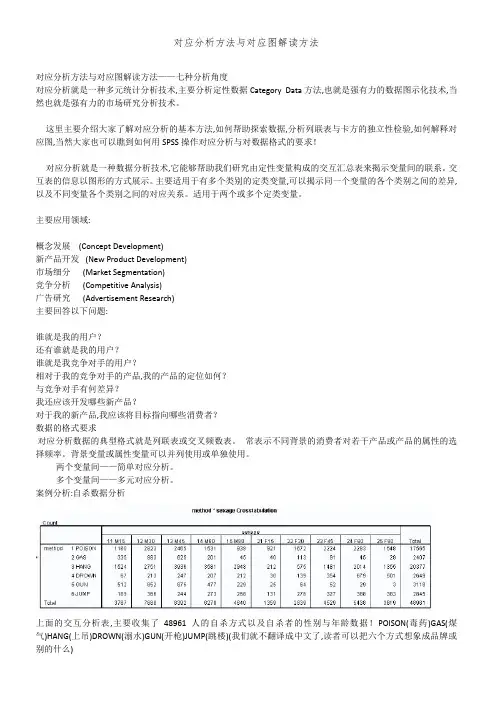
案例分析:自杀数据分析上面的交互分析表,主要收集了48961人的自杀方式以及自杀者的性别和年龄数据!POISON(毒药)GAS(煤气)HANG(上吊)DROWN(溺水)GUN(开枪)JUMP(跳楼)(我们就不翻译成中文了,读者可以把六个方式想象成品牌或别的什么)当然,我们拿到的最初原始数据可能是SPSS数据格式记录表,其中,性别取值1-male 2-female,年龄取值1-5,分别表示不同年龄段。


对应分析数据一、概述对应分析数据是一种数据分析方法,用于研究两个或者多个变量之间的关系。
通过对数据进行对应分析,可以揭示变量之间的相关性,并匡助我们理解数据暗地里的模式和趋势。
本文将介绍对应分析数据的基本概念、步骤和应用场景。
二、基本概念1. 对应分析对应分析是一种多元数据分析方法,它通过将多个变量映射到一个低维空间中,从而揭示变量之间的关系。
对应分析可以匡助我们发现数据中的结构和模式,进而进行更深入的分析。
2. 对应图对应图是对应分析结果的可视化表示。
对应图通常是一个二维平面图,其中每一个数据点表示一个观测值,不同的颜色或者符号表示不同的组别或者类别。
通过观察对应图,我们可以看到数据点之间的关系和趋势。
三、步骤对应分析数据的步骤如下:1. 数据准备首先,需要准备要进行对应分析的数据。
数据可以是任何类型的,可以是定量数据(如数值)或者定性数据(如类别)。
确保数据的质量和完整性非常重要。
2. 数据标准化对应分析需要对数据进行标准化,以消除不同变量之间的量纲差异。
常用的标准化方法包括Z-score标准化和归一化等。
3. 计算对应分析利用对应分析的算法,对标准化后的数据进行计算,得到对应分析的结果。
对应分析的算法有多种,常用的包括主成份分析(PCA)和多维尺度分析(MDS)等。
4. 绘制对应图将对应分析的结果绘制成对应图,以便更直观地观察数据之间的关系和趋势。
对应图可以通过各种数据可视化工具来实现,如散点图、气泡图等。
5. 解读对应图通过观察对应图,我们可以解读数据之间的关系和趋势。
可以观察数据点的分布情况、类别之间的距离和相对位置等。
根据对应图的结果,可以进一步进行数据分析和决策。
四、应用场景对应分析数据在各个领域都有广泛的应用,以下列举几个常见的应用场景:1. 市场调研对应分析数据可以匡助市场调研人员了解不同产品或者品牌之间的关系和竞争状况。
通过对应分析,可以发现市场中的潜在细分市场和目标客户群体。
对应分析方法与对应图解读方法——七种分析角度对应分析就是一种多元统计分析技术,主要分析定性数据Category Data方法,也就是强有力的数据图示化技术,当然也就是强有力的市场研究分析技术。
这里主要介绍大家了解对应分析的基本方法,如何帮助探索数据,分析列联表与卡方的独立性检验,如何解释对应图,当然大家也可以瞧到如何用SPSS操作对应分析与对数据格式的要求!对应分析就是一种数据分析技术,它能够帮助我们研究由定性变量构成的交互汇总表来揭示变量间的联系。
交互表的信息以图形的方式展示。
主要适用于有多个类别的定类变量,可以揭示同一个变量的各个类别之间的差异,以及不同变量各个类别之间的对应关系。
适用于两个或多个定类变量。
主要应用领域:概念发展(Concept Development)新产品开发(New Product Development)市场细分(Market Segmentation)竞争分析(Competitive Analysis)广告研究(Advertisement Research)主要回答以下问题:谁就是我的用户?还有谁就是我的用户?谁就是我竞争对手的用户?相对于我的竞争对手的产品,我的产品的定位如何?与竞争对手有何差异?我还应该开发哪些新产品?对于我的新产品,我应该将目标指向哪些消费者?数据的格式要求对应分析数据的典型格式就是列联表或交叉频数表。
常表示不同背景的消费者对若干产品或产品的属性的选择频率。
背景变量或属性变量可以并列使用或单独使用。
两个变量间——简单对应分析。
多个变量间——多元对应分析。
案例分析:自杀数据分析上面的交互分析表,主要收集了48961人的自杀方式以及自杀者的性别与年龄数据!POISON(毒药)GAS(煤气)HANG(上吊)DROWN(溺水)GUN(开枪)JUMP(跳楼)(我们就不翻译成中文了,读者可以把六个方式想象成品牌或别的什么)当然,我们拿到的最初原始数据可能就是SPSS数据格式记录表,其中,性别取值1-male 2-female,年龄取值1-5,分别表示不同年龄段。




应用多元统计分析第九章对应分析对应分析又称相应分析,于1970年由法国统计学家J.P.Beozecri提出的.它是在R型和Q型因子分析基础上发展起来的多元统计分析方法,故也称为R-Q型因子分析.因子分析方法是用少数几个公共因子去提取研究对象的绝大部分信息,既减少了因子的数目,又把握住了研究对象的相互关系.在因子分析中根据研究对象的不同,分为R型和Q型,如果研究变量间的相互关系时采用R型因子分析;如果研究样品间相互关系时采用Q型因子分析.无论是R型或Q型都未能很好地揭示变量和样品间的双重关系.另方面在处理实际问题中,样本的大小经常是比变量个数多得多.当样品个数n很大(如n>100),进行Q型因子分析时,计算n阶方阵的特征值和特征向量对于微型计算机的容量和速度都是难以胜任的.还有进行数据处理时,为了将数量级相差很大的变量进行比较,常常先对变量作标准化处理,然而这种标准化处理对于变量和样品是非对等的,这给寻找R型和Q型之间的联系带来一定的困难.第九章什么是对应分析对应分析方法是在因子分析的基础上发展起来的,它对原始数据采用适当的标度方法.把R型和Q型分析结合起来,同时得到两方面的结果---在同一因子平面上对变量和样品一块进行分类,从而揭示所研究的样品和变量间的内在联系.对应分析由R 型因子分析的结果,可以很容易地得到Q 型因子分析的结果,这不仅克服样品量大时作Q 型因子分析所带来计算上的困难,且把R 型和Q 型因子分析统一起来,把样品点和变量点同时反映到相同的因子轴上,这就便于我们对研究的对象进行解释和推断. 第九章 对应分析的基本思想由于R 型因子分析和Q 型分析都是反映一个整体的不同侧面,因而它们之间一定存在内在的联系. 对应分析就是通过一个变换后的过渡矩阵Z 将二者有机地结合起来.具体地说,首先给出变量间的协差阵R S =Z'Z 和样品间的协差阵Q S =ZZ' ,由于Z'Z 和ZZ'有相同的非零特征根,记为12...m λλλ≥≥≥,如果R S 的特征根i λ对应的特征向量为i v ,则Q S 的特征根i λ对应的特征向量i u Zv =由此可以很方便地由R 型因子分析而得到Q 型因子分析的结果.对应分析的基本思想由A 的特征根和特征向量即可写出R 型因子分析的因子载荷阵(记为R A )和Q 型因子分析的因子载荷阵(记为Q A ).§9.1 什么是对应分析基本思想由于A和B具有相同的非零特征根,而这些特征根又正是各个公共因子的方差,因此可以用相同的因子轴同时表示变量点和样品点,即把变量点和样品点同时反映在具有相同坐标轴的因子平面上,以便对变量点和样品点一起考虑进行分类.第十章典型相关分析相关分析是研究多个变量与多个变量之间的相关关系.如研究两个随机变量之间的相关关系可用简单相关系数表示;研究一个随机变量与多个随机变量之间的相关关系可用全相关系数表示.1936年Hotelling首先将相关分析推广到研究多个随机变量与多个随机变量之间的相关关系,故而产生了典型相关分析,广义相关系数等一些有用的方法.第十章什么是典型相关分析在实际问题中,经常遇到要研究一部分变量和另一部分变量之间的相关关系,例如:在工业中,考察原料的主要质量指标(1,.....,p X X ) 与产品的主要质量指标(1,.....,p Y Y )间的相关性;在经济学中,研究主要肉类的价格与销售量之间的相关性; 在地质学中,为研究岩石形成的成因关系,考察岩石的化学成份与其周围围岩化学成份的相关性;在气象学中为分析预报24小时后天气的可靠程度,研究当天和前一天气象因子间的相关关系;第十章 什么是典型相关分析在教育学中,研究学生在高考的各科成绩与高二年级各主科成绩间的相关关系;在婚姻的研究中,考察小伙子对追求姑娘的主要指标与姑娘想往的小伙子的主要尺度之间的相关关系;在医学中,研究患某种疾病病人的各种症状程度与用科学方法检查的一些结果之间的相关关系;在体育学中,研究运动员的体力测试指标与运动能力指标之间的相关关系等.第十章 什么是典型相关分析一般地,假设有一组变量1,.....,p X X 与另一组变量1,.....,p Y Y (也可以记为1,....,p p q X X ++),我们要研究这两组变量的相关关系,如何给两组变量之间的相关性以数量的描述,这就是本章研究的典型相关分析.当p=q=1时,就是研究两个变量X 与Y 之间的相关关系.简单相关系数是最常见的度量.其定义为第十章 什么是典型相关分析当p ≥ 1 ,q=1时(或 q ≥ 1 , p =1) 设 则称为Y 与(X1,…,Xp) 的全相关系数.其实Y 对X 的回归为1(|)()()Y YX XX X E Y X x def x μμϕ-=+∑∑-且 并称R 为全相关系数 .第十章 什么是典型相关分析当p,q>1时,利用主成分分析的思想,可以把多个变量与多个变量之间的相关化为两个新变量之间的相关.也就是求α=(α1,…, αp ) '和β =(β1,…, βq ) ' , 使得新变量:V = α1X 1+…+αp X p = α 'X1~(,),0XX XY p YX YY X N Y μσ+∑∑⎛⎫⎛⎫∑∑=> ⎪ ⎪∑⎝⎭⎝⎭1/21YX XX XY YY R σ-⎛⎫∑∑∑= ⎪⎝⎭(,())Y x Rρϕ=W = β1Y 1+…+ βq Y q = β 'Y 之间有最大可能的相关,基于这个思想就产生了典型相关分析(Canonical correlatinal analysis).第十章 总体典型相关设X=(X1,...,Xp )及Y=(Y1,...,Yq)为随机向量(不妨设p ≤q),记随机向量Z 的协差阵为 其中Σ11是X 的协差阵,Σ22是Y 的协差阵,Σ12=Σ’21是X,Y 的协差阵. 第十章 总体典型相关我们用X 和Y 的线性组合V=a X 和W=b Y 之间的相关来研究X 和Y 之间的相关.我们希望找到a 和b,使ρ(V,W) 最大.由相关系数的定义:又已知⎪⎭⎫ ⎝⎛∑∑∑∑=∑22211211第十章总体典型相关故有对任给常数c1,c2,d1,d2,显然有ρ(c1V+d1, c2W+d2)=ρ(V,W)即使得相关系数最大的V=a'X和W=b'X并不唯一.故加附加约束条件 Var(V)=a'Σ11a=1,Var(W)=b'Σ22b=1.问题化为在约束条件Var(V)= 1,Var(W)=1下,求a和b,使得ρ(V,W)= a'Σ12b达最大 .第十章样本典型相关设总体Z=(X1,...,X p,Y1,…,Y q )’.在实际问题中,总体的均值E(Z)= 和协差阵D(Z)= 通常是未知的,因而无法求得总体的典型相关变量和典型相关系数.首先需要根据观测到的样本资料阵对其进行估计.已知总体Z的n个样品:第十章 样本典型相关样本资料阵为若假定Z ~N(μ,∑),则协差阵 的最大似然估 计为第十章 样本典型相关我们从协差阵 的最大似然估计S*(或样本协差阵S)出发,按上节的方法可以导出样本典型相关变量和样本典型相关系数.还可以证明样本典型相关变量和样本典型相关系数是总体典型相关变量和样本典型相关系数的极大似然估计.也可以从样本相关阵R 出发来导出样本典型相关变量和样本典型相关系数.第十章 样本典型相关典型相关系数的显著性检验:总体Z 的两组变量X=(X 1,...,X p )’和Y =(Y 1, …,Y q )’如果不相()()()()1(1,2,...,)t t t p q X Z t n Y +⨯⎛⎫== ⎪⎝⎭'()()11()()nt t t Z Z Z Z def Sn ∧=∑=--∑关,即COV(X,Y )=∑12=0,以上有关两组变量典型相关的讨论就毫无意义.故在讨论两组变量间相关关系之前,应首先对以下假设H 0作统计检验.(1) 检验H 0 : ∑12=0 (即λ1=0)设总体Z ~N p+q (μ,∑).用似然比方法可导出检验H 0的似然比统计量为(A ,A 11,A 22为离差阵)第十章 样本典型相关典型相关系数的显著性检验 (2)检验H 0(i): λi =0 (i =2,...,p )当否定H 0时,表明X,Y 相关,进而可得出至少第一个典型相关系数λ1≠ 0.相应的第一对典型相关变量V 1,W 1可能已经提取了两组变量相关关系的绝大部分信息.在实际问题中,经常迂到需要研究两组多重相关变量间的相互依赖关系,并研究用一组变量(常称为自变量或预测变量)去预测另一组变量(常称为因变量或响应变量),除了最小二乘准则下的经典多元线性回归分析(MLR),提取自变量组主成分的主成分回归分析(PCR)等方11221122||||||A S A A S S Λ==⨯⨯法外,还有近年发展起来的偏最小二乘(PLS)回归方法.第十一章什么是偏最小二乘回归偏最小二乘回归提供一种多对多线性回归建模的方法,特别当两组变量的个数很多,且都存在多重相关性,而观测数据的数量(样本量)又较少时,用偏最小二乘回归建立的模型具有传统的经典回归分析等方法所没有的优点。
1. 稀释性曲线(Rarefaction Curve)采用对测序序列进行随机抽样的方法,以抽到的序列数与它们所能代表OTU的数目构建曲线,即稀释性曲线。
当曲线趋于平坦时,说明测序数据量合理,更多的数据量对发现新OTU的边际贡献很小;反之则表明继续测序还可能产生较多新的OTU。
横轴:从某个样品中随机抽取的测序条数;"Label 0.03" 表示该分析是基于OTU 序列差异水平在0.03,即相似度为97% 的水平上进行运算的,客户可以选取其他不同的相似度水平。
纵轴:基于该测序条数能构建的OTU数量。
曲线解读:Ø 图1中每条曲线代表一个样品,用不同颜色标记;Ø 随测序深度增加,被发现OTU 的数量增加。
当曲线趋于平缓时表示此时的测序数据量较为合理。
2. Shannon-Wiener 曲线反映样品中微生物多样性的指数,利用各样品的测序量在不同测序深度时的微生物多样性指数构建曲线,以此反映各样本在不同测序数量时的微生物多样性。
当曲线趋向平坦时,说明测序数据量足够大,可以反映样品中绝大多数的微生物物种信息。
横轴:从某个样品中随机抽取的测序条数。
纵轴:Shannon-Wiener 指数,用来估算群落多样性的高低。
Shannon 指数计算公式:其中,S obs= 实际测量出的OTU数目;n i= 含有i 条序列的OTU数目;N = 所有的序列数。
曲线解读:Ø 图2每条曲线代表一个样品,用不同颜色标记,末端数字为实际测序条数;Ø 起初曲线直线上升,是由于测序条数远不足覆盖样品导致;Ø 数值升高直至平滑说明测序条数足以覆盖样品中的大部分微生物。
3.Rank-Abundance 曲线用于同时解释样品多样性的两个方面,即样品所含物种的丰富程度和均匀程度。
物种的丰富程度由曲线在横轴上的长度来反映,曲线越宽,表示物种的组成越丰富;物种组成的均匀程度由曲线的形状来反映,曲线越平坦,表示物种组成的均匀程度越高。
学生实验报告学院:统计学院课程名称:多元统计分析专业班级:统计123班姓名:叶常青学号: 0124253学生实验报告一、实验目的及要求:目的熟悉和掌握对应分析的原理和上机操作方法内容及要求本次操作就父母与孩子的受教育程度的关系进行对应分析,分别对父亲与孩子和母亲与孩子的受教育程度做对应分析,最后再对输出结果进行详细的分析。
三、实验方法与步骤:打开GSS93 subset .sav数据,对变量Degree与变量padeg和madeg进行对应分析,依次选择分析→降维…进入对应分析对话框,进行进行如下设置,便可输出想要的数据的:四、实验结果与数据处理:按照上述方法和步骤得出以下输出结果.对父亲受教育程度与孩子受教育程度的关系进行分析如下:表2,第二部分摘要给出了惯量,卡方值以及每一维度所解释的总惯量的百分比信息。
总惯量为0.189,卡方值为228.193 ,有关系式228.193=0.189*1205,由此可以清楚的看到总惯量和卡方的关系。
Sig.是假设卡方值为0成立的概率,它的值几乎为0说明列联表之间有较强的相关性。
表注表明的自由度为(5-1)*(5-1)=16。
惯量部分是四个公共因子分别解释总惯量的百分比。
表5第三部分的结果是在对应分析中点击Statistics按钮,进入Statistics对话框,选中Row profiles和Column profiles 交友程序运行所得到的。
表6表7概述列点aR's Highest Degree 质量维中的得分惯量贡献1 2 点对维惯量维对点惯量1 2 1 2 总计Lessthan HS.160 -.998 .652 .075 .399 .416 .851 .149 1.000Highschool.524 -.165 -.305 .014 .036 .298 .417 .582 .998 Juniorcollege.062 .127 -.512 .003 .003 .100 .127 .845 .972Bachelor .171 .976 .321 .069 .406 .108 .948 .042 .990 Graduate .082 .874 .395 .029 .157 .078 .875 .073 .949 有效总计 1.000 .189 1.000 1.000a. 对称标准化第四部分是概述行点和概述列点,是对列联表行与列各状态有关信息的概括. 其中质量是行与列的边缘概率,也就是PI与PJ。
对应分析方法与对应图解读方法——七种分析角度
对应分析是一种多元统计分析技术,主要分析定性数据Category Data方法,也是强有力的数据图示化技术,当然也是强有力的市场研究分析技术。
这里主要介绍大家了解对应分析的基本方法,如何帮助探索数据,分析列联表和卡方的独立性检验,如何解释对应图,当然大家也可以看到如何用SPSS操作对应分析和对数据格式的要求!
对应分析是一种数据分析技术,它能够帮助我们研究由定性变量构成的交互汇总表来揭示变量间的联系。
交互表的信息以图形的方式展示。
主要适用于有多个类别的定类变量,可以揭示同一个变量的各个类别之间的差异,以及不同变量各个类别之间的对应关系。
适用于两个或多个定类变量。
主要应用领域:
概念发展(Concept Development)
新产品开发(New Product Development)
市场细分(Market Segmentation)
竞争分析(Competitive Analysis)
广告研究(Advertisement Research)
主要回答以下问题:
谁是我的用户?
还有谁是我的用户?
谁是我竞争对手的用户?
相对于我的竞争对手的产品,我的产品的定位如何?
与竞争对手有何差异?
我还应该开发哪些新产品?
对于我的新产品,我应该将目标指向哪些消费者?
数据的格式要求
对应分析数据的典型格式是列联表或交叉频数表。
常表示不同背景的消费者对若干产品或产品的属性的选择频率。
背景变量或属性变量可以并列使用或单独使用。
两个变量间——简单对应分析。
多个变量间——多元对应分析。
案例分析:自杀数据分析
上面的交互分析表,主要收集了48961人的自杀方式以及自杀者的性别和年龄数据!POISON(毒药)GAS(煤气)HANG(上吊)DROWN(溺水)GUN(开枪)JUMP(跳楼)(我们就不翻译成中文了,读者可以把六个方式想象成品牌或别的什么)
当然,我们拿到的最初原始数据可能是SPSS数据格式记录表,
其中,性别取值1-male 2-female,年龄取值1-5,分别表示不同年龄段。
要回答的问题是:
1-不同性别的人在选择自杀方式上有什么差别?
2-不同年龄的人在选择自杀方式上有什么差别?
3-不同性别年龄的人在选择自杀方式上有什么差别?
我们首先,把性别字段乘上10加上年龄字段生成新字段sexage,取值是11-15,21-25,然后分别用M/F和年龄组中值代表Sexage字段的变量值标,这样我们就可以进行简单对应分析了!
现在问大家,如果你看到上面的6×10的矩阵-列联表,你能看出什么差异?
现在我们采用SPSS软件进行对应分析!
(我现在用的是SPSS17.0多语言版本,前两天听博易智讯的人说,现在SPSS已经有18.0版本了,不过从对应分析方法角度我还是希望用11.5版本,因为可以自己拆分重新组合修改图形,现在的版本是图片了,不能随心所欲的修改,不爽!)
分别定义好行列变量以及它们的取值范围!
对应分析中,6×10的列联表(交互表)可以得到行列维度最小值减1的维度,我们看到第一维度Dim1解释了列联表的60.4%,第二维度Dim2解释了列联表的33.0%,说明在两个维度上已经能够说明数据的93.4%,这是比较理想的,当然我们也可以看卡方检验等!
下面我们主要解释如何解读对应图(小蚊子的博客中也有非常相似的解释,我非常欣赏他的博客)
首先对SPSS分析得到的对应图进行修饰和编辑,在零点增加两条中线!
解读方法:
1-总体观察:
我们从图上左右可以看出,左边全部是M*,男性,右边F*全部是女性,说明男女有显著差异;同时看横轴中线上方都是年龄大的,下面都是年龄小的,说明年龄有差异;这样就一目了然看出和回答了前两个问题;
2-观察邻近区域
我们从图上可以看出,老的男性比较喜欢HANG,GAS和GUN是年轻男性的偏好;老的女性比较喜欢DAWN,年轻的女性比较偏好POISON;
3-向量分析——偏好排序
我们可以从中心向任意点连线-向量,例如从中心向GUN做向量,然后让所有的人往这条向量及延长线上作垂线,垂点越靠近向量正向的表示越偏好这种方法。
记住:是垂点到GUN正向排名,从图中我们可以看出,希望GUN方法的人依次是M15、M30、M45、M60、M80、F15等等;依次类推,我们还可以从中心向任意一种方法作垂线,都可以排出每种方法选择人群的偏好次序;当然,你也可以从中心往所有的人作向量,得到每一类人在选择六种方法上的偏好排名!
你是否可以看出,F15年轻的女性对六个“品牌”的偏好吗?
4-向量的夹角——余弦定理
接着,我们可以从向量夹角的角度看不同方法或不同人之间的相似情况,从余弦定理的角度看相似性!
从图上我们可以看出,当我们从中心向任意两个点(相同类别)做向量的时候,夹角是锐角的话表示两个方法具有相似性,锐角越小越相似;也就是说,GUN和GAS是相似品牌,当如也是竞争品牌,也具有替代性,如果这次开枪没有自杀成功,下次他一定选择毒气啦;我们也看出F15和F30的人比较相似,但F15与M80就有非常大的差异了,因为如果作向量他们是钝角,几乎是平角了!
5-从距离中的位置看:
越靠近中心,越没有特征,越远离中心,说明特征越明显
从这张对应图中我们看到,有些点远离中心,有些点靠近中心,这说明什么呢?从几何空间的角度,如果我对每一人都一样的好,在规范图上我就应该站在大家的重心,也就是中心;这说明越靠近中心的点,越没有差异,(记住:没有差异并不代表不重要,只是没有差异,因为统计的技术是研究差异的技术,差异越大往往重要性就大!),越远离中心特征越明显,也就是说,如果听到一个M80的人自杀了,估计你就会想到是不是HANG 啦!
心的品牌,消费者不易识别,也说明你的品牌定位没有显著可识别的特征,没有差异认知!
6-坐标轴定义和象限分析
我们还没有定义坐标轴呢?从第一点的分析,其实我们很快就可以定义坐标轴的含义了!(当然有时候对应图的座位是非常难定义的)
因此,落在第四象限的是年轻的女性所喜欢的品牌!
7-产品定位:理想点与反理想点模型
我们可以在图上以POISON为定位点,以POISON为圆心,以它的利益为半径画圆,那么我们可以得出这样的结论:越先圈进来的人就是最喜欢这个品牌的消费群,越先圈进来的品牌越可能是竞争品牌;当然,你也可以以某类人作为圆心,同意解读;如果POISON是市场不存在的,在调查中可以设定为理想点,这样我们就可以得到理想点模型,同理也可以得到反理想点模型分析!
8-市场细分和定位
最后,研究人员可以根据前面的分析和自身市场状况,进行市场细分,找到目标消费群,然后定位进行分析!最终选择不同的目标市场制定有针对性的营销策略和市场投放!
我们也可以尝试采用多元对应分析,但不如简单对应分析有意义!
.
简单对应分析的优点:
定性变量划分的类别越多,这种方法的优势越明显,揭示行变量类别间与列变量类别间的联系,将类别联系直观地表现在二维图形中(对应图),可以将名义变量或次序变量转变为间距变量。
简单对应分析的缺点:不能用于相关关系的假设检验,维度要由研究者决定,有时候对应图解释比较困难,对极端值比较敏感。
如有侵权请联系告知删除,感谢你们的配合!
精品。