偏心受压构件计算方法

矩形截面偏心受压构件正截面的承载力计算一、矩形截面大偏心受压构件正截面的受压承载力计算公式 （一）大偏心受压构件正截面受压承载力计算（1）计算公式由力的平衡条件及各力对受拉钢筋合力点取矩的力矩平衡条件，可以得到下面两个基本计算公式：s y s y c A f A f bx f N -+=''1α （7-23）()'0''012a h A f x h bx f Ne s y c -+⎪⎭⎫ ⎝⎛-=α （7-24）式中： N —轴向力设计值；α1 —混凝土强度调整系数；e —轴向力作用点至受拉钢筋A S 合力点之间的距离；a he e i -+=2η （7-25） a i e e e +=0 （7-26）η—考虑二阶弯矩影响的轴向力偏心距增大系数，按式（7-22）计算；e i —初始偏心距；e 0 —轴向力对截面重心的偏心距，e 0 =M/N ；e a —附加偏心距，其值取偏心方向截面尺寸的1/30和20㎜中的较大者； x —受压区计算高度。

（2）适用条件1) 为了保证构件破坏时受拉区钢筋应力先达到屈服强度，要求b x x ≤ (7-27)式中 x b — 界限破坏时，受压区计算高度，o b b h x ξ= ，ξb 的计算见与受弯构件相同。

2) 为了保证构件破坏时，受压钢筋应力能达到屈服强度，和双筋受弯构件相同，要求满足：'2a x ≥ (7-28) 式中 a ′ — 纵向受压钢筋合力点至受压区边缘的距离。

（二）小偏心受压构件正截面受压承载力计算（1）计算公式根据力的平衡条件及力矩平衡条件可得s s s y c A A f bx f N σα-+=''1 （7-29）⎪⎭⎫ ⎝⎛'-+⎪⎭⎫ ⎝⎛-=s s y c a h A f x h bx f Ne 0''012α （7-30） ()'0''1'2s s s s c a h A a x bx f Ne -+⎪⎭⎫⎝⎛-=σα （7-31）式中 x — 受压区计算高度，当x ＞h ，在计算时，取x ＝h ；σs — 钢筋As 的应力值，可根据截面应变保持平面的假定计算，亦可近似取：y b s f 11βξβξσ--=(7-32)要求满足：y s y f f ≤≤σ'x b — 界限破坏时受压区计算高度，0h x b b ξ=；b ξξ、 — 分别为相对受压区计算高度 x/h 0和相对界限受压区计算高度x b /h 0 ；'e e 、′— 分别为轴向力作用点至受拉钢筋A s 合力点和受压钢筋A s ′合力点之间的距离 a he e i -+=2η (7-33) ''2a e he i --=η (7-34) （2）对于小偏心受压构件当bh f N c >时，除按上述式（7-30）和式（7-31）或式（7-32）计算外，还应满足下列条件：()()s s y c a a h A f h h bh f e e a h N -+⎪⎭⎫⎝⎛-≤⎥⎦⎤⎢⎣⎡---'0''00'22 (7-35 )式中 '0h — 钢筋's A 合力点至离纵向较远一侧边缘的距离，即s a h h -='0。

第8章 偏心受压构件正截面承载力知 识 点 回 顾•破坏形式及特点 •大小偏心划分 •大偏心算法第8章 偏心受压构件正截面承载力8.1.4 矩形截面偏心受压构件正截面承载力 1. 大偏心受压x £ xb 正截面破坏åN =0g 0 N £ N u = a1 f c bx + f y¢ As¢ - f y Asxö æ ¢ g 0 Ne £ N u e = a1 f c bx ç h0 - ÷ + f y¢ As¢ ( h0 - as ) 2ø èå M As = 0适用条件： x £ xb ¢ x ³ 2 as As 配筋率： r= ³ r min = max ( 0.45 ft fy, 0.2% ) bh第8章 偏心受压构件正截面承载力¢ 当 x < 2as 时，受压钢筋（此时不屈服）计算， 有两种处理方式： （1）规范算法设混凝土合力中心与 As¢ 形心重合。

åM¢ As=0¢ Ne¢ £ N u e¢ = f y As ( h0 - as )（2）平截面假定算法¢ s s¢ = Ese cu (1 - b1 as x )第8章 偏心受压构件正截面承载力2. 小偏心受压构件 （1）基本计算公式 x > xb矩形截面小偏心受压构件承载力计算简图第8章 偏心受压构件正截面承载力小偏心受压构件计算公式：åN =0åMAsg 0 N £ N u = a1 f c bx + f y¢ As¢ - s s Asxö æ ¢ g 0 Ne £ N u e = a1 f c bx ç h0 - ÷ + f y¢ As¢ ( h0 - as ) 2ø è=0依据平截面假定（ b1 = 0.8 ）：æ b1hoi ö s si = Ese cu ç - 1÷ è x ø公路桥规：æ b1 - x ö s si = ç ÷ fy è b1 - xb øxb < x £ 2 b1 - xb第8章 偏心受压构件正截面承载力依据平截面假定:公路桥规：第8章 偏心受压构件正截面承载力（2） “反向破坏”的计算公式 偏心距很小，且远离轴向压力一侧的钢筋配置得 不够多，偏心压力有可能位于换算截面形心轴和 截面几何中心之间。

4.2轴心受压构件承载力计算一、偏心受压构件破坏特征偏心受压构件在承受轴向力N和弯矩M的共同作用时，等效于承受一个偏心距为的偏心力N的作用，当弯矩M相对较小时，气就很小，构件接近于轴心受压，相反当N相对较小时，气就很大，构件接近于受弯，因此，随着气的改变，偏心受压构件的受力性能和破坏形态介于轴心受压和受弯之间。

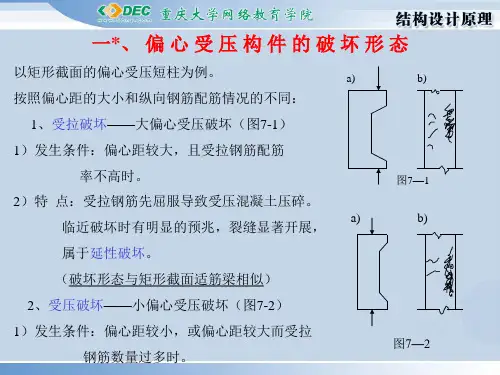
按照轴向力的偏心距和配筋情况的不同，偏心受压构件的破坏可分为受拉破坏和受压破坏两种情况。

1.受拉破坏当轴向压力偏心距分较大，且受拉钢筋配置不太多时，构件发生受拉破坏。

在这种情况下，构件受轴向压力N后，离N较远一侧的截面受拉，另一侧截面受压。

当N增加到一定程度，首先在受拉区出现横向裂缝，随着荷载的增加，裂缝不断发展和加宽，裂缝截面处的拉力全部由钢筋承担。

荷载继续加大，受拉钢筋首先达到屈服，并形成一条明显的主裂缝，随后主裂缝明显加宽并向受压一侧延伸，受压区高度迅速减小。

最后，受压区边缘出现纵向裂缝，受压区混凝土被压碎而导致构件破坏（图4.3.1）。

此时，受压钢筋一般也能屈服。

由于受拉破坏通常在轴向压力偏心距分较大发生，故习惯上也称为大偏心受压破坏。

受拉破坏有明显预兆，属于延性破坏。

2.受压破坏当构件的轴向压力的偏心距分较小，或偏心距分虽然较大但配置的受拉钢筋过多时，就发生这种类型的破坏。

加荷后整个截面全部受压或大部份受压，靠近轴向压力M 一侧的混凝土压应力较高，远离轴向压力一侧压应力较小甚至受拉。

随着荷载逐渐增加，靠近轴一侧混凝土出现纵向裂缝，进而混凝土达到极限应变先被压碎,受压钢筋的应力也达到远离一侧的钢筋可能受压，也可能受拉，但因本身截面应力太小，或因配筋过多，都达不到屈服强度（图4.3.2）。

由于受压破坏通常在轴向压力偏心距％较小时发生，故习惯上也称为小偏心受压破坏。

受压破坏无明显预兆，属脆性破坏。

3.受拉破坏与受压破坏的界限综上可知，受拉破坏和受压破坏都属于“材料破坏”。

其相同之处是，截面的最终破坏都是受压区边缘混凝土达到极限压应变而被压碎。

非对称配筋矩形截面偏心受压构件正截面承载力设计与复核1、大小偏心的判别当i e ≤0h 时，属于小偏心受压。

i e >0h 时，可暂先按大偏心受压计算，若b ξξ>，再改用小偏心受压计算。

2、大偏心受压正截面承载力设计1）．求s A 和/s A ，令）级，；级，52.040055.0335(,===b b b HRB HRB ξξξξ )()5.01(0201a h f bh f Ne A y b b c s '-'--='ξξα( 混规，RE γsy y y b c s A f f f Nbh f A ''+-=ξα01 适用条件： bh A s /≥min ρ，且不小于y t f f /；bh A s //≥minρ'。

2). 求s A321s s s s A A A A -+=如果x </2a ，)()2/(/0/a h f a h e N A y i s -+-= 适用条件：bh A s /≥min ρ，且不小于y t f f /；bh A s //≥minρ'。

3、 小偏心受压正截面承载力设计b cy ξβξ-=12（0）若b ξξ≤ 按照大偏心（1）若cy b ξξξ<<b ξβ-=12)()2/1(0201a h f bh f Ne A y c s '-'--='ξξα如果,0πs σbh A s min ρ'=，再重新求ξ,再计算sA ' （2）若≥≥ξ0/h h cy ξ，取y s f '-=σ，bh a h f h h bh f e N A y c s /min 001)()2(ρα≥-''-'-'= 然后计算ξ和sA '。

（3）若0/h h >ξ,取h x =，y s f '-=σ。

)()2/()2/(0/1/0a h f a h bh f a e e h N A y c a s '-'---+-=α /1y s y c s f A f bh f N A '--='α情况（2）和（3）验算反向破坏。

偏心受压构件计算偏心受压构件是指受到压力作用的构件，该压力作用点与构件的几何中心不重合。

由于受力点与几何中心的偏心距，使得构件不仅承受压力，还承受弯矩和剪力，因此其计算相对复杂。

下面将就偏心受压构件的计算进行详细介绍。

首先来看压力的计算。

偏心受压构件所受到的压力大小可以通过材料的抗压强度和偏心距来确定。

偏心距越大，结构所受到压力越大。

压力的大小可以通过下式来计算：P=N+M/e其中，P表示构件所受到的压力大小，N表示构件的轴力大小，M表示构件所受到的弯矩大小，e表示偏心距。

在计算压力的时候，需要注意到材料的屈服强度和抗压强度。

屈服强度是指材料开始发生塑性变形的临界点，而抗压强度是指材料能够抵抗压力的极限。

因此，在计算压力的时候，需要判断压力是否超过了材料的抗压强度，以确保结构的安全。

接下来是弯矩和剪力的计算。

偏心受压构件所受到的弯矩和剪力可以通过材料的弹性模量和截面形状来确定。

弯矩的计算可以有两种方法，一种是通过偏心受压构件的截面形状和压力大小来计算，另一种是通过构件所受到的轴力大小和偏心距来计算。

弯矩的计算可以使用以下公式：M=P*e其中M表示弯矩大小，P表示构件所受到的压力大小，e表示偏心距。

剪力的计算可以使用以下公式：V=N其中V表示剪力大小，N表示构件的轴力大小。

在计算弯矩和剪力的时候，需要根据结构的受力状态来判断构件所受到的压力和剪力的方向。

如果构件上部受到压力，下部受到拉力，则弯矩的方向为正，剪力的方向为竖向；如果构件上部受到拉力，下部受到压力，则弯矩的方向为负，剪力的方向为竖向。

综上所述，偏心受压构件的计算主要包括压力的计算，弯矩的计算和剪力的计算。

在进行计算的时候，需要确定构件所受到的压力大小，以及构件的受力状态和偏心距，以确保结构的安全。

偏心受压构件计算步骤嘿，咱今儿就来说说这偏心受压构件计算步骤。

你说这偏心受压构件啊，就像是一个有点挑剔的家伙，得好好琢磨它才行呢！第一步，那可得先搞清楚这构件的基本情况呀。

就好比你要了解一个人的脾气性格一样，得知道它是啥样的材料做的，尺寸大小是多少。

这要是不清楚，后面可就容易糊涂啦！第二步，计算它的内力。

这就好像给这个构件来一次全面的“体检”，看看它里面的力是怎么分布的，有多大的压力和拉力。

这可不是随随便便就能算好的，得细心再细心呐！第三步，判断偏心受压的类型。

这就像是给它分个类，看看它是大偏心还是小偏心。

这可重要啦，不同类型那计算方法可不一样哦，要是弄错了，那可就全乱套啦！第四步，根据类型来选择合适的计算公式。

这就像是给它量身定制一套计算方法，得找对了才行。

不然就像给大人穿小孩衣服，或者给小孩穿大人衣服，那能合适吗？第五步，代入数据进行计算。

这时候就得小心啦，一个数字错了都不行，就跟走钢丝似的，得稳稳当当的。

第六步，得出结果后还得检查检查。

这就像考试完了要检查一遍试卷一样，看看有没有算错的地方。

要是不检查，万一有个小错误没发现，那后果可能很严重哦！你想想看，要是建房子的时候，这偏心受压构件没算好，那房子还能结实吗？会不会摇摇晃晃的呀？那多吓人呐！所以说，这计算步骤可千万不能马虎呀！咱再回过头来想想，这计算偏心受压构件是不是就跟我们做一件重要的事情一样？得一步一步来，每一步都要做好，不能有丝毫的马虎。

这就跟我们走路一样，一步一个脚印，稳稳当当的才能走到目的地。

总之呢，这偏心受压构件计算步骤可真是个细致活儿，需要我们认真对待，不能有半点马虎。

只有这样，我们才能保证计算结果的准确性，才能让我们的建筑更加牢固可靠。

大家说是不是这个理儿呀？。