必修1 第三章 函数的概念与性质 第3.2节(1)

必修1→4→5→2→3普通高中课程标准实验教科书数学必修1第一章集合与函数概念1．1 集合1．2 函数及其表示1．3 函数的基本性质第二章基本初等函数（Ⅰ）2．1 指数函数2．2 对数函数2．3 幂函数第三章函数的应用3．1 函数与方程3．2 函数模型及其应用普通高中课程标准实验教科书数学必修2第一章空间几何体1．1 空间几何体的结构1．2 空间几何体的三视图和直观图1．3 空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2．1 空间点、直线、平面之间的位置关系2．2 直线、平面平行的判定及其性质2．3 直线、平面垂直的判定及其性质第三章直线与方程3．1 直线的倾斜角与斜率3．2 直线的方程3．3 直线的交点坐标与距离公式第四章圆与方程4．1 圆的方程4．2 直线、圆的位置关系4．3 空间直角坐标系普通高中课程标准实验教科书数学必修3第一章算法初步1．1 算法与程序框图1．2 基本算法语句1．3 算法案例阅读与思考割圆术第二章统计2．1 随机抽样阅读与思考一个著名的案例阅读与思考广告中数据的可靠性阅读与思考如何得到敏感性问题的诚实反应2．2 用样本估计总体阅读与思考生产过程中的质量控制图2．3 变量间的相关关系阅读与思考相关关系的强与弱第三章概率3．1 随机事件的概率阅读与思考天气变化的认识过程3．2 古典概型3．3 几何概型阅读与思考概率与密码普通高中课程标准实验教科书数学必修4第一章三角函数1．1 任意角和弧度制1．2 任意角的三角函数1．3 三角函数的诱导公式1．4 三角函数的图象与性质1．5 函数y=Asin（ωx+ψ）1．6 三角函数模型的简单应用第二章平面向量2．1 平面向量的实际背景及基本概念2．2 平面向量的线性运算2．3 平面向量的基本定理及坐标表示2．4 平面向量的数量积2．5 平面向量应用举例第三章三角恒等变换3．1 两角和与差的正弦、余弦和正切公式3．2 简单的三角恒等变换普通高中课程标准实验教科书数学必修5第一章解三角形1．1 正弦定理和余弦定理探究与发现解三角形的进一步讨论1．2 应用举例阅读与思考海伦和秦九韶1．3 实习作业第二章数列2．1 数列的概念与简单表示法阅读与思考斐波那契数列阅读与思考估计根号下2的值2．2 等差数列2．3 等差数列的前n项和2．4 等比数列2．5 等比数列前n项和阅读与思考九连环探究与发现购房中的数学第三章不等式3．1 不等关系与不等式3．2 一元二次不等式及其解法3．3 二元一次不等式（组）与简单的线性规划问题阅读与思考错在哪儿信息技术应用用Excel解线性规划问题举例3．4 基本不等式普通高中课程标准实验教科书数学选修1-1第一章常用逻辑用语1．1 命题及其关系1．2 充分条件与必要条件1．3 简单的逻辑联结词1．4 全称量词与存在量词第二章圆锥曲线与方程2．1 椭圆探究与发现为什么截口曲线是椭圆信息技术应用用《几何画板》探究点的轨迹：椭圆2．2 双曲线2．3 抛物线阅读与思考圆锥曲线的光学性质及其应用第三章导数及其应用3．1 变化率与导数3．2 导数的计算探究与发现牛顿法──用导数方法求方程的近似解3．3 导数在研究函数中的应用信息技术应用图形技术与函数性质3．4 生活中的优化问题举例实习作业走进微积分普通高中课程标准实验教科书数学选修1-2第一章统计案例1．1 回归分析的基本思想及其初步应用1．2 独立性检验的基本思想及其初步应用第二章推理与证明2．1 合情推理与演绎证明阅读与思考科学发现中的推理2．2 直接证明与间接证明第三章数系的扩充与复数的引入3．1 数系的扩充和复数的概念3．2 复数代数形式的四则运算第四章框图4．1 流程图4．2结构图信息技术应用用Word2002绘制流程图选修2 系列2由3个模块组成选修2-1常用逻辑用语圆锥曲线空间中的向量与立体几何选修2-2导数及其应用推理与证明数系的扩充与复数的引入选修2-3计数原理统计案例概率选修3 系列3由6个模块组成选修3-1 数学史选讲选修3-2 信息安全与密码选修3-3球面上的几何选修3-4对称与群选修3-5欧拉公式与闭曲面分类选修3-6三等分角与数域扩充选修4 系列4由10专题组成选修4-1几何证明选讲选修4-2矩阵与变换选修4-3数列与差分选修4-4坐标系与参数方程选修4-5不等式选讲第一章不等式的基本性质和证明的基本方法第一节不等式的基本性质和一元二次不等式的解法第二节基本不等式第三节绝对值不等式的解法第四节绝对值的三角不等式第五节不等式证明的基本方法第二章柯西不等式与排序不等式及其应用第一节柯西不等式第二节排序不等式第三节平均值不等式（选学）第四节最大值与最小值问题，优化的数学模型第三章数学归纳法与贝努利不等式第一节数学归纳法原理第二节用数学归纳法证明不等式，贝努利不等式选修4-6初等数论初步选修4-7优选法与试验设计初步选修4-8统筹法与图论初步选修4-9风险与决策选修4-10开关电路与布尔代数。

第三章 函数的概念与性质1函数的概念：一般地，设B A ,是非空的实数集，如果对于集合A 中的 x ，按照某种 f ，在集合B 中都有 y 与它对应，那么就称B A f →:为从集合A 到集合B 的一个函数，记作A x x f y ∈=),(，其中，x 叫做 ，x 的取值范围A 叫做函数的 ，与x 的值相对应的y 值叫做 ，函数值的集合}|)({A x x f ∈叫做函数的 ，值域是集合B 的子集．2函数的三要素： 、 、 ． 求函数定义域的原则：(1)若()f x 为整式，则其定义域是 ；(2)若()f x 为分式，则其定义域是 ；(3)若()f x 是二次根式(偶次根式)，则其定义域是 ；(4)若()0f x x =，则其定义域是 ；(5)若()()0,1x f x a a a =>≠，则其定义域是 ；(6)若()()log 0,1a f x x a a =>≠，则其定义域是 ；(7)若f (x )=sinx,g (x )=cosx ，则其定义域是 ；(8)若x x f tan )(=，则其定义域是 ；求函数值域的方法：配方法，换元法，图象法，单调性法等；求函数的解析式的方法：待定系数法，换元法，配凑法，方程组法等；3函数的表示方法：解析法(用函数表达式表示两个变量之间的对应关系)、图象法(用图象表达两个变量之间的对应关系)、列表法(列出表格表示两个变量之间的对应关系)．4分段函数：在定义域内，对于自变量x 的不同取值区间，有不同对应关系的函数．6函数的单调性：(1)单调递增：设任意 ，当 时，有 .特别的，当函数在它的定义域上单调递增时，该函数称为增函数；(2)单调递减：设任意 ，当 时，有 特别的，当函数在它的定义域上单调递增时，该函数称为减函数．7单调区间：如果函数在区间上单调递增或单调递减，那么就说函数在这一区间有(严格的)单调性，区间就叫做函数的单调区间，单调区间分为单调增区间和单调减区间．8复合函数的单调性：同增异减．9函数的最大值、最小值：一般地，设函数)(x f y =的定义域为I ，如果存在实数M 满足: ,都有 ； 使得 ，那么称M 是函数的最大(小)值．10函数的奇偶性：偶函数：一般地，设函数)(x f y =的定义域为I ，如果 ，都有 ，且 ，那么函数叫做 ；偶函数的图象关于 对称；奇函数：一般地，设函数)(x f y =的定义域为I ，如果 ，都有 ，且 ，那么函数叫做 ；奇函数的图象关于 对称；若奇函数)(x f y =的定义域中有零，则其函数图象必过原点，即(0)0f =.11幂函数：一般地，函数 叫做幂函数，其中 是自变量， 是常数． 12幂函数()f x x α=的性质：①所有的幂函数在 都有定义，并且图象都通过点 ； ①如果0α>，则幂函数的图象过原点，并且在区间[)0,+∞上是 ； ①如果0α<，则幂函数的图象在区间()0,+∞上是 ，①幂函数图象不出现于第四象限．。

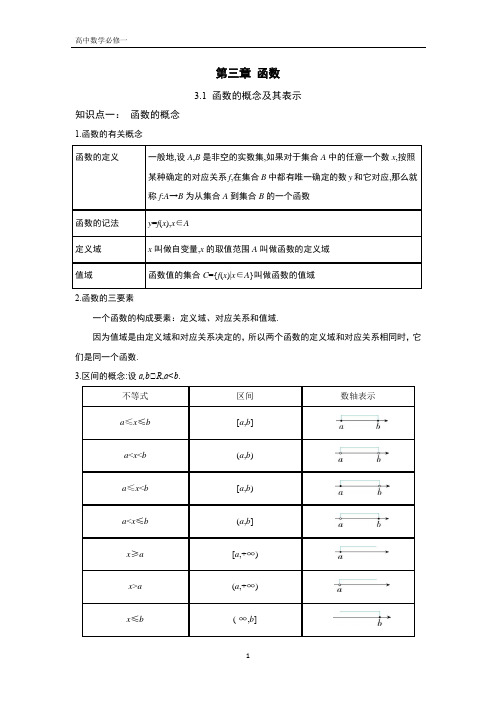
第三章函数3.1 函数的概念及其表示知识点一：函数的概念1.函数的有关概念2.函数的三要素一个函数的构成要素：定义域、对应关系和值域.因为值域是由定义域和对应关系决定的，所以两个函数的定义域和对应关系相同时，它们是同一个函数.3.区间的概念:设a,b∈R,a<b.实数集R可以用区间表示为(-∞,+∞).知识点二：函数的表示法1.函数的三种表示法2.分段函数已知函数y=f(x)，x∈A，如果自变量x在不同的取值范围内，函数有着不同的对应关系，那么我们称这样的函数为分段函数.【思考】1.函数的定义域和值域是否一定是无限集?2.区间是数集的另一种表示方法,是否任何数集都能用区间表示?3.根据函数的定义,任何一个自变量x是否都有唯一的函数值y与之对应?任何一个函数值y 是否都有唯一的自变量x与之对应?4.如何确定分段函数的定义域和值域?【解析】1.不一定.函数的定义域和值域也可能是有限集,如f(x)=1，x∈{1,2,3}.2.不是.如集合{0,1}就不能用区间表示.3.任何一个自变量x都有唯一的函数值y与之对应，但是函数值y不一定有唯一的自变量x 与之对应。

如f(x)=x2中，函数值4有两个自变量2、-2与之对应。

函数中x，y的对应关系是“一对一”或“多对一”,不能“一对多”.4.分段函数的定义域是每一段自变量取值范围的并集,值域也是每一段函数值取值范围的并集.3.1.1 函数的概念基础练一函数的概念1.（多选题）下面选项中,变量y是变量x的函数的是()A.x表示某一天中的时刻,y表示对应的某地区的气温B.x表示年份,y表示对应的某地区的GDP(国内生产总值)C.x表示某地区学生的某次数学考试成绩,y表示该地区学生对应的考试号D.x表示某人的月收入,y表示对应的个税2.下列四组函数中,表示同一个函数的是()3A.y=|x|与y=√x3B.y=√x2与s=(√t)2C.y=2t+1与y=2u+1D.y=1与y=x03.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面的4个图形中,能表示以集合M为定义域,集合N为值域的函数关系的有()A.①②③④B.①②③C.②③D.②④二函数的定义域4.函数f(x)=√x−1的定义域为() x−2A.[1,+∞)B.[1,2)C.[1,2)∪(2,+∞)D.(1,2)∪(2,+∞)5.已知某矩形的周长为定值a,若该矩形的面积S是这个矩形的一边长x的函数,则这个函数的定义域是.6.已知函数y=f(x)的定义域为[-2,3],则函数y=f(2x+1)的定义域为.x+1三函数值及函数的值域7.已知集合P={x|y=√x−1},集合Q={y|y=√x−1},则()A.P=QB.P⫋QC.Q⫋PD.P∩Q=⌀8.函数y=√x2−2x+3的值域为.,则f(x)的值域为.9.已知函数f(x)=1x2−2x10.已知函数f(x)的定义域是[0,1],值域是[1,2],则这样的函数可以是f(x)=.11.已知函数f(x)=x2+x-1.);(1)求f(2), f(1x(2)若f(x)=5,求x的值.3.1.2 函数的表示法基础练一 函数的表示法及其应用 1.函数y =x x+1的图象大致是 ( )A B C D2.某同学从家里到学校,为了不迟到,先匀速跑一段时间,跑累了再匀速走余下的路,设在途中花费的时间为t ,离开家的距离为d ,则下面图象中,能正确表示d 与t 的关系的是( )A B C D3.已知函数y =f (x )的对应关系如表,函数y =g (x )的图象为如图所示的曲线ABC ,则g (f (3))的值为 .二 函数解析式的求法5.已知函数f (x +2)=x 2+6x +8,则函数f (x )的解析式为( ) A.f (x )=x 2+2x B.f (x )=x 2+6x +8 C.f (x )=x 2+4x D.f (x )=x 2+8x +66.函数f (x )满足f (1-2x )=-1x ,则f (2)=( )A.2B.-2C.12 D.-12 7.已知函数f (2x -1)=3x -5,若f (x 0)=4,则x 0= .8.已知f (x )是一次函数,2f (2)-3f (1)=5,2f (0)-f (-1)=1,则f (x )= .9.(1)已知函数g (√x +1)=2x +1,求g (x )的解析式;(2)已知f (x )为二次函数,且f (0)=2, f (2)=f (-1)=0,求f (x )的解析式.三 分段函数问题10.已知函数f (x )={√x,x >0,|x +1|,x ≤0,则f (f (-3))=( )A.√3B.1C.2D.√2 11.已知f (x )={x +2,x ≤−1,x 2,−1<x <2,2x,x ≥2,若f (x )=3,则x 的值是( )A.1B.1或32C.1,32或±√3 D.√312.函数f (x )=x +|x |x 的图象是( )A B C D13.(2022山西大同期中)已知函数f (x )={x 2,x ≤0,4−2x,x >0.(1)画出函数f (x )的图象;(2)当f (x )≥2时,求实数x 的取值范围.。

数学必修一第三章知识点总结第三章是关于函数的知识点总结。

1. 函数的概念：函数是一个特殊的关系，将一个数集的每个元素与另一个数集的元素对应起来。

函数可以用一个公式、图像或者表格来表示。

2. 定义域和值域：函数的定义域是指能够使函数有意义的所有输入值的集合，值域是所有函数可能的输出值的集合。

3. 函数的图像：函数的图像是将函数的输入和输出对应起来的一种形象表示。

在平面直角坐标系中，函数的图像是一条曲线或者直线。

4. 函数的性质：函数可以是奇函数、偶函数或者普通函数。

奇函数满足 f(-x) = -f(x)；偶函数满足 f(-x) = f(x)；普通函数不满足奇偶性质。

5. 函数的性质：函数可以是单调递增函数、单调递减函数、增函数或者减函数。

单调递增函数满足 f(x1) < f(x2) 当且仅当 x1 < x2；单调递减函数满足 f(x1) > f(x2) 当且仅当 x1 < x2；增函数在定义域上满足 f(x1) < f(x2) 当且仅当 x1 < x2；减函数在定义域上满足 f(x1) > f(x2) 当且仅当 x1 < x2。

6. 反函数：函数的反函数将函数的输入和输出颠倒过来，即输入变为输出，输出变为输入。

反函数的定义域和值域与原函数相反。

7. 复合函数：复合函数是两个或多个函数的组合。

复合函数的定义域是能够使复合函数有意义的所有值的集合。

8. 基本初等函数：基本初等函数包括常函数、一次函数、幂函数、指数函数、对数函数和三角函数等。

这些函数具有特定的性质和图像特征。

9. 函数的运算：函数之间可以进行加减乘除和求导等运算。

函数的运算结果仍然是一个函数，具有相应的性质和图像特征。

以上是第三章关于函数的知识点总结。

在学习函数时，需要理解函数的概念和性质，掌握常见的函数类型和图像特征，以及函数的运算和组合等操作。

同时，还需要通过练习题和实例来巩固和应用所学知识。

四、教学过程
教学
环节
教学内容设计意图
情境引入
课堂探究通过观察生活中熟悉的事物，引入本节新课。

提高学生概括、推理的能力。

通过思考，观察函数的图象，从特殊到一般，归纳总结最值的定义，提高学生的解决问题、分析问题的能力。

得出定义
类比定义类比得出最小值定义
函数最值的几何意义
常见题型
通过实际问题让学生明白怎样求二次函数在整个定义域上的最值以及利用函数的单调性求函数的最值，提高学生解决问题的能力，进一步掌握单调性与最值的关系。

课堂
小结
通过总结，
让学生进
一步巩固
本节所学
内容，提高
概括能力,
板书设计
课后练习
、
课后提高学生的数学运算能力和逻辑推理能力。

通过练习。

第三章 函数的概念与性质3.1函数的概念与表示【知识要点】1.函数的概念：函数的定义 设A,B 是非空的数集,如果按照某种确定的对应关系f ,使对于集合A 中的任意一个数x,在集合B 中都有唯一确定的数)(x f 和它对应,那么就称B A f →:为从集合A 集合B 的一个函数.函数的记法 A x x f y ∈=),( 定义域 x 叫做自变量,x 的取值范围叫做函数的定义域 值域 函数值的集合{}A x x f ∈|)(叫做函数的值域函数相等如果函数的定义域相同,并且对应关系完全一致,我们就称这两个函数相等.2.区间的概念及表示：设a,b 是两个实数,而且a<b.1.一般区间的表示定义名称 符号数轴表示}{b x a x ≤≤| 闭区间 []b a ,}{b x a x <≤| 半开半闭区间 [)b a ,}{b x a x ≤<| 半开半闭区间 (]b a ,}{b x a x <<|开区间()b a ,2.特殊区间的表示定义 R}{a x x ≥| }{a x x >| }{a x x ≤| }{a x x <| 符号()+∞∞-,[)+∞,a (]+∞,a (]a ,∞- ()a ,∞-3.函数的表示方法：表示法 定义解析法 用数学表达式表示两个变量之间的对应关系图像法 用图象表示两个变量之间的对应关系 列表法列表格来表示两个变量之间的对应关系4.分段函数：对于自变量x 的不同的取值范围有不同的解析式的函数。

它是一个函数,而不是几个函数；分段函数的定义域是各段函数定义域的并集,值域也是各段函数值域的并集。

5.映射：两个非空集合A 与B 间存在着对应关系f ,而且对于A 中的每一个元素a,B 中总有唯一的一个元素b 与它对应,就这种对应为从A 到B 的映射,记作f ：A →B 。

考点一:函数的概念1.判断正误.(1)已知定义域和对应关系就可以确定一个函数. ( ) (2)区间不可能是空集. ( ) (3)集合A=｛x|x 为正方形｝可以作为某个函数的定义域. ( )(6)在函数的定义中,集合B 是函数的值域. ( )2.下列说法正确的是( )A.函数值域中每一个数在定义域中一定只有一个数与之对应.B.函数的定义域和值域可以是空集.C.函数的定义域和值域一定是数集.D.函数的定义域和值域确定后,函数的对应关系也就确定了.3.设集合{}20|≤≤=x x M ,{}20|≤≤=y y N .下列四个图象中能表示从集合M 到集合N 的函数关系的有( )A.3个B.2个C.1个D.0个4.设{}20|≤≤=x x M ,{}21|≤≤=y y N ,如下图所示,其中能表示从集合M 到集合N 的函数关系的有( )个A.1个B.2个C.3个D.4个考点二:函数的定义域1.函数2123)(-+-=x x x f 的定义域为( ) A.⎭⎬⎫⎩⎨⎧≠>232|x x x 且 B.⎭⎬⎫⎩⎨⎧><232|x x x 且 C.⎭⎬⎫⎩⎨⎧≤≤232|x x D.⎭⎬⎫⎩⎨⎧≠≥232|x x x 且 2.函数xx x f 11)(++=的定义域是( )A.[)+∞-,1B.[)0,1-C.[)()+∞-,00,1D.()()+∞∞-,00, 3.下列各组函数是同一个函数的是( )A.123++=x x x y 与y=xB.2)1(-=x y 与y=x-1 C.x x y 2=与y=x D.xx y =与y=14.下列各组函数中,两个函数是同一函数的有( ) A.x x f =)(和2)(x x g =B.1)(+=x x f 和1)(2-=xx gC.x xx f =)(和⎩⎨⎧<->=0,10,1)(x x x g D.1)(2-=x x f 和11)(-+=x x x g5.已知函数()2-x f 的定义域为()+∞,0,则函数()x f 的定义域为________.6.已知函数()x f y =的定义域为[]3,2-,则函数()112++=x x f y 的定义域为_______.7.已知函数()x f 的定义域为()2,0,则函数()4)3(--=x x f x g 的定义域为( )A.()+∞,3B.{}4,2C.)5,4(D.{}3,2-8.已知函数()2+x f 的定义域为(-3,4),则函数()13)(-=x x f x g 的定义域为( )A.⎪⎭⎫ ⎝⎛4,31 B.⎪⎭⎫ ⎝⎛2,31 C.⎪⎭⎫ ⎝⎛6,31 D.⎪⎭⎫ ⎝⎛1,31 9.若()x x x f 232+=,()()22-+f f 的值为_______. 10.若()x x x f 32-=,()()21-+f f 的值为_______.考点三:函数值及函数的值域1.函数()x x x f 422+--=的值域是_______.2.函数)50(62≤≤+-=x x x y 的值域是_______.3.函数())(112R x xx f ∈+=的值域是_______. 4.函数()524+-=x x x f 在[]1,2--上的值域是_______. 5.已知函数222+-=x x y 的值域是[]2,1,则其定义域可能是_______.6.已知函数()x f 的定义域为R,对于任意实数x,y 满足())()(y f x f y x f =+,且()21=f ,则)2023()2024()3()4()1()2(f f f f f f ⋅⋅⋅++=__________.7.已知函数213)(+++=x x x f . (1)求()x f 的定义域和()3-f 的值； (2)当a>0时,求()a f ,()1-a f 的值.8.已知函数21612)(xx x f -++=的定义域为集合A,集合{}122|-≤≤-=m x m x B .(1)若m=3,求B A ；(2)若B B A = ,求m 的取值范围.考点四:函数的表示法1.在函数[]1,1|,|-∈=x x y 的图象上有一点|)|,(t t P ,此函数与x 轴、直线x=-1及x=t 围成图形如图阴影部分的面积为S,则S 与t 的函数关系图可表示为( )A. B. C. D.2.若函数()x f y =的定义域为{}5,83|≠≤≤-x x x ,值域为{}0,21|≠≤≤-y y y ,则()x f y =的图象可能是( )A. B. C. D.3.若函数()x f 的定义域为[]2,0,值域为[]2,0,则()x f 的图象可能为( )A. B. C. D.4.设已知函数())(,x g x f 如下表所示：则不等式()()())(x f g x g f >的解集为( ) A.{}3,1 B.{}3,5 C.{}4,3,2 D.{}55.已知函数()x f y =的部分x 与y 的对应关系如下表：则()[]=4f f ( ) A.-1 B.-2 C.-3 D.36.已知函数()x g y =的对应关系如表所示,函数()x f y =的图象是如图所示,则[])1(f g 的值为( ) A.-1 B.0 C.3 D.4考点五:函数解析式的求法1.如图中的图象所表示的函数的解析式为( )A.)20(123≤≤-=x x y B.)20(12323≤≤--=x x y C.)20(123≤≤--=x x y D.)20(11≤≤--=x x y2.已知函数()1142+=-x x f ,则函数()x f y =的解析式是( )A.()0,222≥++=x x x x fB.()1,222-≥++=x x x x fC.()0,222≥+-=x x x x fD.()1,222-≥+-=x x x x f 3.若函数5)1(2-=+x x f ,则=)(x f ( )A.622-+x xB.422-+x xC.622--x xD.422--x x 6.已知函数()x f 满足()3412++=+x x x f ,则()x f 解析式是( )A.()x x x f 22+=B.()22+=x x fC.()x x x f 22-=D.()22-=x x f7.已知函数()x f 满足()()bx x f x af =-+,其中1±≠a ,求函数()x f 的解析式..8.某企业生产某种产品时的能耗y 与产品件数x 之间的关系式为xbax y +=,其中,当x=2时,y=100；当x=7,y=35,且次产品生产件数不超过20.求函数y 关于x 的解析式.考点六:分段函数1.已知函数()⎩⎨⎧<≥-=0),(0,52x x f x x x f ,则()=+-)2(3f f ( )A.1-B.1C.7D.52.函数()⎩⎨⎧≥-<=0,20,12x x x x x f 则()=-)2018(f f ( )A.1B.-1C.2018D.-20183.已知()⎩⎨⎧<≥+=0,20,12x x x x x f ,若()10=a f ,则a=_________.4.已知函数()⎪⎩⎪⎨⎧<≥-=0,1,1x xx x x f 那么⎪⎭⎫ ⎝⎛)31(f f 的值是_________. 5.已知函数⎪⎪⎩⎪⎪⎨⎧->+--≤-=1,111,4)(x xx x xx x f ,1)(2-=x x g .(1)求())2(,2g f 的值； (2)若()97)2(-=g f ,求实数a 的值.6.已知函数()⎪⎩⎪⎨⎧>≤≤--<-=1,211,21,2x x x x x x f(1)求⎪⎭⎫ ⎝⎛-23f ,⎪⎭⎫ ⎝⎛21f ,⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛21f f ； (2)若()6=a f ,求a 的值.7.如图所示,函数()x f 的图象是折线图ABC,其中A,B,C 的坐标分别是(0,4),(2,0),(6,4). (1)求()[]0f f 的值.(2)求函数()x f 的解析式.8.已知函数()⎪⎪⎩⎪⎪⎨⎧>-≤≤-<=2,32120,0,2x x x x x x x f (1）求()()()1,0f f f ；(2)若()1-=m f ,求m 的值；(3)在给定的坐标系中,作出函数()x f 的图象.考点七：映射1.下列对应是A 到B 上的映射的是（ ）A.3:,,-→==**x x f N B N AB.{}()1:,2,1,1,-→--==*x f B N AC.xx f Z B Z A 3:,,→== D.x x f R B N A →==*:,,的平方根2.映射B A f →:，在f 的作用下A 中元素（x,y ）与B 中元素（x-1,3-y ）对应，则与B 中元素（0，1）对应的A 中元元素是（ ）A.（-1，2）B.（0，3）C.（1，2）D.（-1,3）。

3．2.2 奇偶性第1课时 函数奇偶性的概念教材要点要点1．偶函数的概念一般地，设函数f (x )的定义域为I ，如果∀x ∈I ，都有－x ∈I ，且f (－x )＝f (x )，那么函数f (x )就叫做偶函数．2．奇函数的概念一般地，设函数f (x )的定义域为I ，如果∀x ∈I ，都有－x ∈I ，且f (－x )＝－f (x )，那么函数f (x )就叫做奇函数．3．奇、偶函数的图象特征(1)奇函数的图象关于________成中心对称图形；反之，如果一个函数的图象是以坐标原点为对称中心的中心对称图形，则这个函数是奇函数．(2)偶函数的图象关于________对称；反之，如果一个函数的图象关于y 轴对称，则这个函数是偶函数．状元随笔 奇偶函数的定义域关于原点对称，反之，若定义域不关于原点对称，则这个函数一定不具有奇偶性．基础自测1.思考辨析(正确的画“√”，错误的画“×”)(1)已知f (x )是定义在R 上的函数．若f (－1)＝f (1)，则f (x )一定是偶函数．( ) (2)奇函数的图象一定过原点．( )(3)偶函数的图象与x 轴交点的个数一定是偶数．( ) (4)f (x )是定义在R 上的奇函数，则f (0)＝0.( ) 2．下列函数为奇函数的是( ) A ．y ＝|x | B ．y ＝3－xC ．y ＝1x 3 D ．y ＝－x 2＋143．若函数y ＝f (x )，x∈[－2，a ]是偶函数，则a 的值为( ) A ．－2 B ．2C ．0D ．不能确定4．下列图象表示的函数是奇函数的是________，是偶函数的是________．(填序号)题型1 函数奇偶性的判断 例1 判断下列函数的奇偶性 (1)f (x )＝√1−x 2+√x 2−1； (2)f (x )＝2x 2+xx+1；(3)f (x )＝x 2−1|x|；(4)f (x )＝{x (1−x )，x ＜0x (1+x )，x ＞0.方法归纳判断函数奇偶性的方法(1)定义法：根据函数奇偶性的定义进行判断．步骤如下：①判断函数f (x )的定义域是否关于原点对称．若不对称，则函数f (x )为非奇偶函数，若对称，则进行下一步．②验证．f (－x )＝－f (x )或f (－x )＝f (x )． ③下结论．若f (－x )＝－f (x )，则f (x )为奇函数； 若f (－x )＝f (x )，且f (x )为偶函数；若f (－x )≠－f (x )，且f (－x )≠f (x )，则f (x )为非奇非偶函数．(2)图象法：f (x )是奇(偶)函数的等价条件是f (x )的图象关于原点(y 轴)对称． 跟踪训练1 (1)(多选)下列函数中，是偶函数的是( )A ．y ＝√1+x 2B ．y ＝x ＋1x C ．y ＝x 2＋1x 2 D ．y ＝x ＋x 2 (2)函数f (x )＝{12x 2+1，x ＞0，−12x 2−1，x ＜0是()A ．奇函数B ．偶函数C ．既是奇函数又是偶函数D ．既不是奇函数也不是偶函数 题型2 函数奇偶性的图象特征例2 已知函数y ＝f (x )是定义在R 上的偶函数，且当x ≤0时，f (x )＝x 2＋2x .现已知画出函数f (x )在y 轴左侧的图象，如图所示．(1)请补出完整函数y ＝f (x )的图象．(2)根据图象写出函数y ＝f (x )的递增区间．(3)根据图象写出使y ＝f (x )＜0的x 的取值范围．方法归纳1．巧用奇偶性作函数图象的步骤 (1)确定函数的奇偶性．(2)作出函数在[0，＋∞)(或(－∞，0])上对应的图象．(3)根据奇(偶)函数关于原点(y 轴)对称得出在(－∞，0](或[0，＋∞))上对应的函数图象． 2．奇偶函数图象的应用类型及处理策略(1)类型：利用奇偶函数的图象可以解决求值、比较大小及解不等式问题．(2)策略：利用函数的奇偶性作出相应函数的图象，根据图象直接观察．跟踪训练2 设奇函数f (x )的定义域为[－5，5]，若当x ∈[0，5]时，f (x )的图象如图，则不等式f (x )＜0的解集是________．题型3 利用函数奇偶性求值 角度1 利用函数的奇偶性求参数例3 (1)已知函数f (x )＝x 2－(2－m )x ＋3为偶函数，则m 的值是( ) A ．1 B ．2 C ．3 D ．4(2)函数f (x )＝x+2a+3x 2+8为奇函数，则实数a ＝( )A ．－1B ．1C ．－32D ．32角度2 利用函数的奇偶性求函数值例4 (1)已知函数f (x )，g (x )分别是定义在R 上的偶函数和奇函数，且f (x )－g (x )＝x 3＋x 2＋2，则f (1)＋g (1)＝( )A ．－2B ．－1C ．1D ．2(2)已知函数f (x )＝ax 3＋bx ＋3，且f (－2)＝10，则函数f (2)的值是________．方法归纳1．已知函数的奇偶性求参数值的三种思路(1)若表示定义域的区间含有参数，则可利用对称性列出关于参数的方程．(2)一般化策略：对x 取定义域内的任一个值，利用f (－x )与f (x )的关系式恒成立来确定参数的值．(3)特殊化策略：根据定义域内关于原点对称的特殊自变量值对应的函数值的关系列方程求解，不过，这种方法求出的参数值要代入解析式检验，看是否满足条件，不满足的要舍去．2．利用函数的奇偶性求函数值的方法已知函数的某一个值，求对应的函数值时，常利用函数的奇偶性或部分函数的奇偶性求值．跟踪训练3 (1)设函数f (x )＝(x+1)(x+a )x为奇函数，则a ＝________．(2)若函数f (x )＝ax 2＋bx ＋3a ＋b 是偶函数，定义域为[a －2，2a ]，则a ＝________，b ＝________．(3)已知f (x )＝x 5＋ax 3＋bx －8，且f (－2)＝10，则f (2)＝________． 易错辨析 忽视函数的定义域致误例5 关于函数f (x )＝√x 2−4+√4−x 2与h (x )＝√x −4+√4−x 的奇偶性，下列说法正确的是( )A ．两函数均为偶函数B ．两函数都既是奇函数又是偶函数C ．函数f (x )是偶函数，h (x )是非奇非偶函数D ．函数f (x )既是奇函数又是偶函数，h (x )是非奇非偶函数解析：函数f (x )＝√x 2−4+√4−x 2的定义域满足{x 2−4≥0，4−x 2≥0，即x 2＝4，因此函数f (x )的定义域为{－2，2}，关于原点对称，此时f (x )＝0，满足f (－x )＝－f (x )，f (－x )＝f (x )，所以函数f (x )既是奇函数又是偶函数，而函数h (x )＝√x −4+√4−x 的定义域为{4}，不关于原点对称，因此函数h (x )是非奇非偶函数．故选D.答案：D课堂十分钟1．(多选)下列函数是奇函数的有( )A ．y ＝x 3＋√x 3B ．y ＝1x (x ＞0)C ．y ＝x 3＋1D ．y ＝x 2+1x2．函数f (x )＝√1−x 2|x+3|−3的奇偶性是( ) A ．奇函数 B ．偶函数C．既不是奇函数也不是偶函数D．既是奇函数又是偶函数3．函数y＝4xx2+1的图象大致为()4．已知函数f(x)＝{−x2+x，x＞0，ax2+x，x＜0是奇函数，则a＝________．5．已知奇函数f(x)的定义域为[－5，5]，且在区间[0，5]上的图象如图所示．(1)画出在区间[－5，0]上的图象；(2)写出使f(x)＜0的x的取值集合．3．2.2 奇偶性第1课时 函数奇偶性的概念 新知初探·课前预习要点3．原点 y 轴[基础自测]1．答案：(1)× (2)× (3)× (4)√ 2．答案：C 3．答案：B4．答案：(2)(4) (1)(3)题型探究·课堂解透例1 解析：(1)函数f (x )＝√1−x 2+√x 2−1的定义域为{－1，1}，关于原点对称，此时f (x )＝0，所以函数f (x )＝√1−x 2+√x 2−1既是奇函数又是偶函数．(2)函数f (x )的定义域是(－∞，－1)∪(−1，+∞)，不关于原点对称，∴f (x )是非奇非偶函数．(3)函数f (x )＝x 2−1|x|的定义域为(－∞，0)∪(0，+∞)，关于原点对称．又f (－x )＝(−x )2−1|−x|＝x 2−1x ＝f (x )，所以函数f (x )＝x 2−1|x |是偶函数．(4)方法一：∵函数f (x )的定义域是(－∞，0)∪(0，+∞)，关于原点对称． 当x ＞0时，－x ＜0，∴f (－x )＝(－x )[1－(－x )]＝－x (1＋x )＝－f (x )． 当x ＜0时，－x ＞0， ∴f (－x )＝－x (1－x )＝－f (x )． ∴函数f (x )为奇函数．方法二：作出函数的图象，如图所示的实线部分：由图可知，该函数为奇函数．跟踪训练1 解析：(1)由偶函数的定义可知AC 是偶函数．故选AC.(2)函数的定义域为(－∞，0)∪(0，+∞)，关于原点对称．当x ＞0时，－x ＜0，f (－x )＝－12(－x )2－1＝－(12x 2＋1)＝－f (x )；当x ＜0时，－x ＞0，f (－x )＝12(－x )2＋1＝12x 2＋1＝－(－12x 2－1)＝－f (x )． 综上可知，函数f (x )＝{12x 2+1，x ＞0，−12x 2−1，x ＜0是奇函数．故选A. 答案：(1)AC (2)A例2 解析：(1)由题意作出函数图象如图：(2)据图可知，单调递增区间为(－1，0)，(1，＋∞).(3)据图可知，使f (x )＜0的x 的取值范围为(－2，0)∪(0，2)．跟踪训练2 解析：由奇函数的性质知，其图象关于原点对称，则f (x )在定义域[－5，5]上的图象如图，由图可知不等式f (x )<0的解集为{x |－2<x <0或2<x ≤5}．答案：{x |－2<x <0或2<x ≤5}例3 解析：(1)f (－x )＝(－x )2－(2－m )(－x )＋3＝x 2＋(2－m )x ＋3，由函数y ＝f (x )为偶函数，知f (－x )＝f (x )，即x 2＋(2－m )x ＋3＝x 2－(2－m )x ＋3，∴2－m ＝－(2－m )，∴m ＝2.故选B.(2)由题意f (x )为奇函数，则f (0)＝0，即0＋2a ＋3＝0，∴a ＝－32.此时f (x )＝xx 2+8为奇函数．故选C.答案：(1)B (2)C例4 解析：(1)∵f (x )－g (x )＝x 3＋x 2＋2， 由－x 代入x 得：f (－x )－g (－x )＝－x 3＋x 2＋2 由题意知f (－x )＝f (x )，g (－x )＝－g (x )， ∴f (x )＋g (x )＝－x 3＋x 2＋2，所以f (1)＋g (1)＝－1＋1＋2＝2.故选D. (2)令g (x )＝ax 3＋bx∵g (－x )＝a (－x 3)＋b (－x )＝－ax 3－bx ＝－(ax 3＋bx )＝－g (x )， ∴g (x )为奇函数．∴f (－x )＝g (－x )＋3＝－g (x )＋3， ∴g (2)＝－7，∴f (2)＝g (2)＋3＝－7＋3＝－4. 答案：(1)D (2)－4跟踪训练3 解析：(1)方法一(定义法) 由已知f (－x )＝－f (x )， 即(−x+1)(−x+a )−x＝－(x+1)(x+a )x.显然x ≠0得，x 2－(a ＋1)x ＋a ＝x 2＋(a ＋1)x ＋a ， 故a ＋1＝0，得a ＝－1.(经检验满足题意) 方法二(特值法) 由f (x )为奇函数得 f (－1)＝－f (1)， 即(−1+1)(−1+a )−1＝－(1+1)(1+a )1，整理得a ＝－1.解析：(2)由f (x )为偶函数知，其定义域关于原点对称， 故有a －2＋2a ＝0，解得a ＝23.又f (x )为偶函数，所以其图象关于y 轴对称， 即－b2a ＝0，解得b ＝0. (3)令g (x )＝x 5＋ax 3＋bx ， 则g (x )是定义在R 上的奇函数． 从而g (－2)＝－g (2)．又f (x )＝g (x )－8，∴f (－2)＝g (－2)－8＝10. ∴g (－2)＝18，∴g (2)＝－g (－2)＝－18. ∴f (2)＝g (2)－8＝－18－8＝－26. 答案：(1)－1 (2)23 0 (3)－26[课堂十分钟]1．答案：AD 2．答案：A 3．答案：A 4．答案：15．解析：(1)如图，在[0，5]上的图象上选取5个关键点O ，A ，B ，C ，D .分别描出它们关于原点的对称点O ′，A ′，B ′，C ′，D ′， 再用光滑曲线连接即得．(2)由(1)图可知，当且仅当x ∈(－2，0)∪(2，5)时，f (x )<0. ∴使f (x )<0的x 的取值集合为(－2，0)∪(2，5)．。