图解法分析火车转弯中的侧向压力和正压力

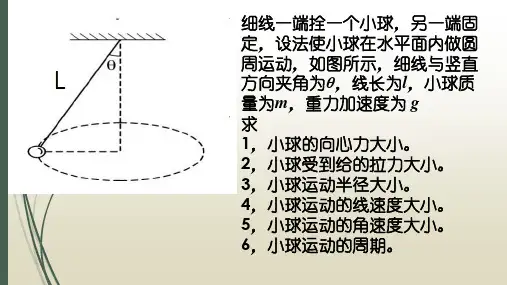
图解法分析火车转弯问题中的侧向压力和正压力第一部分 问题的提出 基本概念火车转弯时如果速度合适，铁轨就不会受到轮缘的侧向压力。

如果速度低于所要求的速度，内侧铁轨就会受到侧向挤压；如果速度高于所要求的速度，外侧铁轨就会受到侧向挤压。

这个结论需要高中生掌握，但这个结论的得出，我们不得不承认在一定程度上是凭的直觉。

本文试图用图解法来讨论这个问题。

在本文中，我们约定平行于铁轨所在平面的压力称为侧向压力；垂直于铁轨所在平面的压力称为正压力。

第二部分 定性分析我们所要讨论的问题中轨道圆在水平面内，因此合力（向心力）的方向总是水平的。

另一方面，重力的大小和方向也总是不变的。

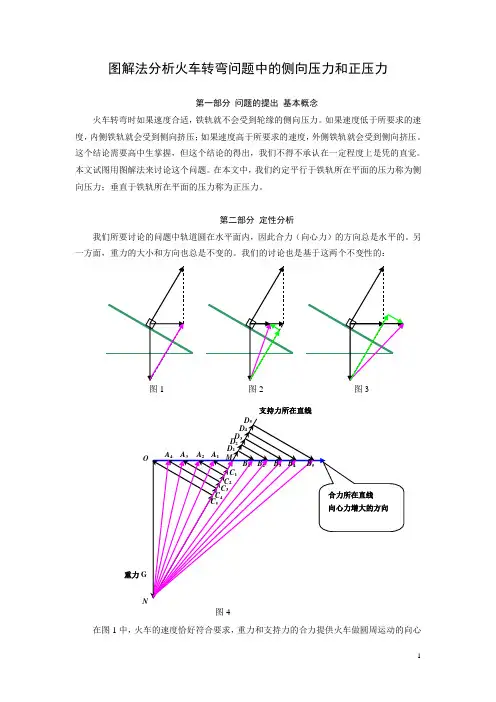
我们的讨论也是基于这两个不变性的：在图1中，火车的速度恰好符合要求，重力和支持力的合力提供火车做圆周运动的向心支持力所在直线重力图1 图2图3图4力。

若火车的速度减小，根据向心力的表达式Rv m F 2=知向心力将减小。

然而重力是不变的，因此其他力的合力将变成图2中粉红色的有向线段所表示的力。

我们进一步分析这个力的分力：一是轨道对火车的垂直于轨道所在平面的力（正压力）；一是轨道对火车的平行于轨道所在平面的力（侧向压力）。

我们把这个粉红色的线段所表示的力分解到它的两个分力所在的方向，就得到了表示侧向压力的线段和正压力的线段（图2中鲜绿色线段）。

从图中可以看出，这时火车将受到一个沿轨道平面向上的侧向压力，并且它将随着速度的减小而增大（图4）。

另一方面，表示垂直于斜面的支持力（正压力）的线段比原来短了，表明支持力减小了，并且我们会看到，随着速度的减小，支持力将逐渐减小。

当火车的速度增大时（大于所要求的数值），用同样的方法（图3）可以得到：火车将受到一个沿轨道所在平面向下的侧向压力，并且随着速度的增大而增大（图4）。

另一方面，支持力将大于原来的支持力（图3），并且随着速度的增大而增大（图4）。

第三部分 定量计算侧向压力的计算：首先我们先看速度较小时的情景，如图2所示，设轨道所在平面的倾角为θ，火车驶过转弯处没有侧向压力时的速度为0v 。

火车拐弯的知识点总结一、火车拐弯的原理1.1 轨道几何火车在铁路线上进行拐弯时，首先需要了解轨道的几何形状。

铁路线上的弯道通常是按照一定的曲线半径来设计的，这个曲线半径决定了列车在进行转弯时所需要施加的侧向力。

1.2 车辆动力学火车在行驶中会受到多种力的作用，包括牵引力、阻力、侧向力等。

当火车进入弯道时，需要施加一定的侧向力来使列车保持在曲线轨道上行驶，这就需要进行合理的车辆动力学设计。

1.3 车辆稳定性火车在拐弯时需要保持稳定，以避免出现脱轨等情况。

车辆的稳定性设计是通过合理的结构设计和调整来保证的，包括车辆的重心、转向架的设计等方面。

1.4 铁路工程技术铁路线的设计和建设需要考虑到列车在拐弯时所产生的侧向力和动态影响，因此需要进行合理的工程技术设计，确保铁路线的弯道段能够满足列车的安全行驶。

二、影响火车拐弯的因素2.1 轨道条件铁路线的轨道条件对列车进行拐弯有着重要的影响。

包括轨道的曲线半径、轨道的超高等因素都会直接影响列车在拐弯时所需要施加的侧向力和车辆的稳定性。

2.2 车辆结构火车的车辆结构对拐弯也有着重要的影响。

包括车辆的转向架设计、车辆的长宽高等尺寸参数都会对列车的拐弯性能产生影响。

2.3 速度列车在进行拐弯时的速度也是一个重要的因素。

速度越快，列车所需要施加的侧向力就越大，对于车辆稳定性的要求也越高。

2.4 牵引力牵引力是火车行驶时所受到的牵引和推动力，它对列车的加速度和速度有着直接的影响，进而影响列车在拐弯时的侧向力和稳定性。

2.5 负载情况列车的负载情况也会对拐弯产生影响。

负载越重，对列车稳定性的要求就越高，因此需要进行合理的负载计算和分布设计。

2.6 铁路线路设计铁路线路的设计包括曲线半径、超高等参数，都需要考虑到列车在拐弯时的需要，以保证列车的行驶安全和舒适性。

三、火车拐弯的技术控制3.1 制动系统制动系统是火车进行拐弯时的重要控制手段。

合理的制动系统设计可以使列车在拐弯时减小速度和惯性，有效提高列车的稳定性。

火车拐弯问题知识点总结火车在行驶过程中，经常会遇到拐弯的情况。

在火车拐弯时，会出现一系列的物理和工程问题，这些问题涉及到火车的结构、动力系统、制动系统和轨道系统等多个方面。

本文将对火车拐弯问题涉及的知识点进行总结，包括火车的拐弯原理、拐弯时的力学原理、拐弯对轨道的影响以及解决火车拐弯问题的方法等方面。

一、火车的拐弯原理1. 车轮与铁轨的接触火车的拐弯原理首先涉及到车轮与铁轨的接触。

火车的车轮是通过与铁轨接触来提供支撑力和传递动力的，因此车轮与铁轨的接触是火车行驶的基础。

在火车拐弯时，车轮必须能够顺利地在铁轨上进行转向，以确保车辆在拐弯时不会脱轨。

2. 列车的车型和结构拐弯时，火车的车型和结构也对拐弯性能有着直接的影响。

不同类型的列车在拐弯时会有不同的性能表现，例如高速列车和货运列车在拐弯时的要求是不相同的。

同时，车辆的车体结构、重心位置和转向架等部件的设计也会影响火车的拐弯性能。

3. 转向架的设计火车的转向架是用来支撑车轮并使其能够转向的机械结构。

转向架的设计直接影响着火车在拐弯时的稳定性和可靠性。

不同类型的转向架会对车轮与铁轨的接触、车轮的转向过程以及车辆的侧向力等方面产生不同的影响。

二、拐弯时的力学原理火车在拐弯时会受到一系列力的影响，这些力来自于车辆自身的惯性和外部环境的影响。

了解拐弯时的力学原理对于理解车辆行驶过程有着重要的意义。

1. 离心力在火车拐弯时，车辆会受到离心力的影响。

离心力是由于车辆的速度和质量导致的一种惯性力，它会使车辆向拐弯的外侧产生向外的力。

这种力会对车辆的稳定性和安全性产生一定的影响。

2. 摩擦力火车的拐弯还会受到铁轨与车轮之间的摩擦力的影响。

摩擦力是支撑火车行驶的核心力量，它不仅影响着车辆的加速和制动能力，还会对车辆的转向过程产生影响。

在拐弯时，摩擦力会受到车辆侧向力和离心力的影响，从而影响着车轮与铁轨之间的摩擦力。

3. 侧向力侧向力是由于车辆拐弯时车轮受到的侧向推力而产生的力。

火车拐弯知识点总结火车拐弯是火车在铁路上运行的一个重要环节，也是一个涉及到多方面知识的复杂过程。

在火车拐弯过程中，需要考虑到列车速度、转向架设计、轨道曲率和铁路线路等多个因素。

不合适的拐弯设计或者不当的操作都可能会造成列车脱轨或者发生其他安全事故。

本文将从列车拐弯原理、拐弯过程中的安全技术、铁路线路设计和维护等方面进行总结，以帮助读者更好地了解火车拐弯的知识点。

一、列车拐弯原理1.1 轨道曲率列车在铁路上行驶时，需要沿着轨道进行运行。

轨道曲率是指铁路线路在平面上的曲率半径，它决定了列车在拐弯时需要施加多大的侧向力来保持稳定。

一般来说，铁路线路的曲率半径越小，列车在拐弯时所受到的侧向力越大。

因此，在铁路线路设计中，需要合理设置曲率半径，以适应列车的运行速度和性能。

1.2 车辆转向架设计列车的转向架是用来支撑车轮并使之能够转向的机构，它在列车拐弯时发挥着重要的作用。

转向架的设计需要考虑到列车的运行速度、轨道曲率和其他因素，以确保列车在拐弯时能够保持稳定。

不同类型的车辆可能采用不同的转向架设计，比如传统的钢轮车辆和现代的磁浮列车可能会采用不同的转向架结构。

1.3 侧向力和摩擦力列车在拐弯时需要施加侧向力来克服惯性力和轨道曲率对列车的影响，以使列车保持在轨道上。

侧向力的大小取决于列车的速度、轨道曲率和车辆质量等因素。

同时，列车在拐弯时需要克服摩擦力对车轮的影响，确保列车能够稳定地行驶。

因此，在列车拐弯时需要根据实际情况调整侧向力和摩擦力的大小，以保证列车的安全运行。

二、拐弯过程中的安全技术2.1 速度控制列车在拐弯时需要根据轨道曲率和车辆性能来确定合适的速度，以确保列车能够安全地通过拐弯段。

一般来说，列车在拐弯时需要降低速度，以减小侧向力和减轻对轨道的影响。

铁路管理部门会根据轨道条件和列车性能设定拐弯段的最高速度限制，列车驾驶员需要遵守这些限速要求，以确保列车的安全运行。

2.2 列车悬挂系统列车的悬挂系统是用来支撑车厢并吸收震动的重要部件，它在列车拐弯时发挥着重要的作用。

火车转弯（圆周运动）问题圆周运动专题二题号一二总分得分一、单选题（本大题共9小题，共分）1.高速公路的拐弯处,通常路面是外高内低,如图所示,在某路段车向左转弯,司机左侧的路面比右侧路面低一些车的运动可看作是做半径为R的圆周运动内外路面高度差为h,路基的水平宽度为已知重力加速为g,要使车轮与路面之间的横向摩擦力即垂直于前进方向的摩擦力等于零,则汽车转弯时的车速应等于()A. B. C. D.【答案】D【解析】解：路面的斜角为,作出车的受力图由数学知识得：如图,支持力与重力的合力提供向心力,由牛顿第二定律得：联立得故选：D由题意知汽车转弯时所需的心力完全由重力和支持力的合力提供,根据受分析计算即可得出结论．类似于火车拐弯问题,知道按条件转弯时,向心力由重力和支持力的合力提供．2.如图所示的圆周运动,下列说法不正确的是()A. 如图a,汽车通过拱桥的最高点处于失重状态置B. 如图b,火车转弯超过规定速度行驶时,外轨对外侧车轮的轮缘会有挤压作用C. 如图c,钢球在水平面做圆周运动,钢球距悬点的距离为则圆锥摆的周期D. 如图d,在水平公路上行驶的汽车,车轮与路面之间的静摩擦力提供转弯所需的向心力【答案】C【解析】【分析】根据加速度的方向确定汽车在最高点处于超重还是失重；根据合力提供向心力得出角速度的表达式,从而进行判断；抓住重力不变,结合平行四边形定则比较支持力和向心力,结合半径不同分析角速度的关系；当火车转弯的速度超过规定速度,支持力和重力的合力不够提供向心力,会挤压外轨。

此题考查圆周运动常见的模型,每一种模型都要注意受力分析找到向心力,从而根据公式判定运动情况,如果能记住相应的规律,做选择题可以直接应用,从而大大的提高做题的速度,所以要求同学们要加强相关知识的记忆。

【解答】A.汽车在最高点知,故处于失重状态,故A正确；B.火车转弯超过规定速度行驶时,外轨对内轮缘会有挤压作用,故B正确；C.圆锥摆,重力和拉力的合力,,则圆锥摆的周期,故C错误；D.在水平公路上行驶的汽车,车轮与路面之间的静摩擦力提供转弯所需的向心力,故D正确。

火车转弯问题考点规律分析甲乙(1)弯道的特点：在实际的火车转弯处，外轨高于内轨，若火车转弯所需的向心力完全由重力和支持力的合力提供，如图所示，即mgtanO=mR则v0=冷丽而，其中R为弯道半径，0为轨道平面与水平面间的夹角,v0为转弯处的规定速度。

(2)速度与轨道压力的关系①当火车行驶速度v等于规定速度v0时，所需向心力仅由重力和弹力的合力提供，此时火车对内外轨无挤压作用。

②当火车行驶速度v>v0时，火车对外轨有挤压作用。

③当火车行驶速度v<v0时，火车对内轨有挤压作用。

(3)注意事项①合外力的方向：因为火车转弯的圆周平面是水平面，不是斜面，所以火车的向心力即合外力应沿水平面指向圆心，而不是沿轨道斜面向下。

②规定速度的唯一性：火车轨道转弯处的规定速率一旦确定则是唯一的，火车只有按规定的速率转弯，内外轨才不受火车的挤压作用。

速率过大时，由重力、支持力及外轨对轮缘的挤压力的合力提供向心力；速率过小时，由重力、支持力及内轨对轮缘的挤压力的合力提供向心力。

典型例题例有一列质量为100t的火车，以72km/h的速率匀速通过一个内外轨一样高的弯道，轨道半径为400m。

(g取10m/s2)(1)试计算铁轨受到的侧压力大小；(2)若要使火车以此速率通过弯道，且使铁轨受到的侧压力为零，我们可以适当倾斜路基，试计算路基倾斜角度0的正切值。

［规范解答］(1)m=100t=1X105kg,v=72km/h=20m/s,夕卜轨对轮缘的侧内侧）、外侧压力提供火车转弯所需要的向心力厮以有林二m 牛二气晋N =1X 105N 。

由牛顿第三定律可知铁轨受到的侧压力大小为1X 105N 。

⑵火车过弯道,重力和铁轨对火车的支持力的合力正好提供向心力,如图所示，则mg tan 0二m 竺，由此可得tan 0=—=0.1。

［完美答案］（1）1X 105N （2）0.1一［规评点崗火车转弯（或赛道上赛车转弯）的圆轨道是水平轨道，所以合力的方向水平指向圆心。

铁路弯道中的力学知识在修筑铁路时，常常因地理环境和工程造价等因素的影响，在线路中设置铁路弯道，但弯道设置中，需要应用力学知识对弯道的几何参数进行分析，如果设计不当，会对形车安全产生影响，甚至带来严重的后果。

一、车辆通过弯道时车辆自身的离心力机车车辆在曲线上行驶时，由于惯性离心力作用，将机车车辆推向外股钢轨，加大了外轨钢轨的压力，使旅客产生不适，货物移位等。

列车以速度v沿半径R的圆曲线运行时，产生离心力F：F=mv2/R=Gv2/gR （公式1）式中G—车辆重力（KN）；v—行车速度（m/s）；R—曲线半径（m）；g—重力加速度，g=9.8m/s2；由公式1可知，列车通过曲线时，离心力的大小由三大因素影响：①车辆自重；②车辆行车速度；③铁路曲线半径。

二、对曲线行驶中的离心力应对措施1、铁路曲线半径为了保证列车的行驶安全，在铁路的设计和建造时，国家《修规》对不同速度等级的铁路规定了车辆可以安全通过的圆曲线的最小半径，高速铁路和平原地区干线铁路一般比较平直，用较大的曲线半径；山区铁路、工厂支线、车辆段道岔的咽喉区、编组站、城市地铁等受地形的制约较大的地段，只能使用较小的曲线半径，列车必须限速通过。

2、曲线超高与限速结合为了平衡列车曲线行驶中所产生的离心力，需要把曲线外轨适当抬高，使机车车辆的自身重力产生一个向心的水平分力，以抵消离心惯性力，达到内外两股钢轨受力均匀和垂直磨耗均匀等，满足旅客舒适感，提高线路的稳定性和安全性。

外轨超高是指曲线外轨顶面与内轨顶面水平高度之差。

在设置外轨超高时，主要有外轨提高法和线路中心高度不变法两种方法。

外轨提高法是保持内轨标高不变而只抬高外轨的方法。

线路中心高度不变法是内外轨分别各降低和抬高超高值一半而保证线路中心标高不变的方法。

曲线超高的大小由列车通过时离心力的大小确定。

由于离心力与行车速度的平方成正比，与曲线半径大小成反比，因此曲线半径越小，行车速度越高，则离心力越大，所需设置的超高就越大。

图解法分析火车转弯问题中的侧向压力和正压力第一部分问题的提出基本概念火车转弯时如果速度合适，铁轨就不会受到轮缘的侧向压力。

如果速度低于所要求的速度，内侧铁轨就会受到侧向挤压；如果速度高于所要求的速度，外侧铁轨就会受到侧向挤压。

这个结论需要高中生掌握，但这个结论的得出，我们不得不承认在一定程度上是凭的直觉。

本文试图用图解法来讨论这个问题。

在本文中，我们约定平行于铁轨所在平面的压力称为侧向压力；垂直于铁轨所在平面的压力称为正压力。

第二部分定性分析我们所要讨论的问题中轨道圆在水平面内，因此合力（向心力）的方向总是水平的。

另一方面，重力的大小和方向也总是不变的。

我们的讨论也是基于这两个不变性的：在图1中，火车的速度恰好符合要求，重力和支持力的合力提供火车做圆周运动的向心力。

若火车的速度减小，根据向心力的表达式Rv m F 2知向心力将减小。

然而重力是不变支持力所在直线重力图1 图2图3图4的，因此其他力的合力将变成图2中粉红色的有向线段所表示的力。

我们进一步分析这个力的分力：一是轨道对火车的垂直于轨道所在平面的力（正压力）；一是轨道对火车的平行于轨道所在平面的力（侧向压力）。

我们把这个粉红色的线段所表示的力分解到它的两个分力所在的方向，就得到了表示侧向压力的线段和正压力的线段（图2中鲜绿色线段）。

从图中可以看出，这时火车将受到一个沿轨道平面向上的侧向压力，并且它将随着速度的减小而增大（图4）。

另一方面，表示垂直于斜面的支持力（正压力）的线段比原来短了，表明支持力减小了，并且我们会看到，随着速度的减小，支持力将逐渐减小。

当火车的速度增大时（大于所要求的数值），用同样的方法（图3）可以得到：火车将受到一个沿轨道所在平面向下的侧向压力，并且随着速度的增大而增大（图4）。

另一方面，支持力将大于原来的支持力（图3），并且随着速度的增大而增大（图4）。

第三部分定量计算侧向压力的计算：首先我们先看速度较小时的情景，如图2所示，设轨道所在平面的倾角为θ，火车驶过转弯处没有侧向压力时的速度为0v 。