传热学第二章-导热理论基础-2

格式：ppt
大小：862.50 KB
文档页数：29

下载文档原格式

传热学(第二章)

(2-32)
热阻
R=
1 1 1 ( 4πλ r r2 1
(2-33)
由球坐标系一般形式的导热微分方程
1 T 1 T 1 T T (λr2 + 2 2 (λ ) + 2 (λ sin θ ) + Φ = ρcp r2 r r) r sin θ r sin θ θ θ τ
2 1
λ1
第二章
导热基本定律及稳态导热
2-3 通过平壁,圆筒壁,球壳和其他变截面物体的导热通过平壁,圆筒壁,
1 T 1 T T T (λr + 2 (λ ) + (λ ) + Φ = ρcp τ r r r) r z z d dt 简化变为 dr (r dr ) = 0 (2-25)
⒉ 通过圆筒壁的导热由导热微分方程式(2—12)
⒉ 通过圆筒壁的导热根据热阻的定义,通过整个圆筒壁的导热热阻为 (2-29) 29) 与分析多层平壁—样,运用串联热阻叠加的原则,可得通过图2-9所示的多层圆筒壁的导热热流量 2πl(t1 t4 ) Φ= (2-30) ln( d2 / d1) / λ1 + ln( d3 / d2 ) / λ2 + ln( d4 / d3) / λ3 ⒊ 通过球壳的导热导热系数为常数,无内热源的空心球壁.内,外半径为r1,r2,其内外表面均匀恒定温度为t1,t2,球壁内的温度仅沿半径变化,等温面是同心球面. 由傅立叶定律得: dt 各同心球面上的热流率q不相等,而热流量Φ相等. Φ = 4πr2λ dr dr Φ 2 = 4πλdt r
的热传导微分方程:
T(r,τ ) τ ρc 当 λ = const 时, 2T(r,τ ) + Φ = p T(r,τ ) λ λ τ [λT(r,τ )] + g(r,τ ) = ρcp

传热学第二章第二节导热微分方程式

∂t ∂z
)
+
qv
第二节导热微分方程式
若物性参数 λ、c 和 ρ 均为常数：
∂t ∂τ
=
a(
∂2t ∂x2
+ ∂2t ∂y2
+
∂2t ∂z2
)
+
qv ; ρc
or
∂t = a∇2t + qv
∂τ
ρc
a = λ — 热扩散率（导温系数） [m2 s] ρc （Thermal diffusivity）
dxdydz ⋅ dτ
[J]
第二节导热微分方程式
[导入与导出净热量]:
[1] = [dQ x − dQ x+ dx ] + [dQ y − dQ y + dy ] + [dQ z − dQ z + dz ]
[1] = − ( ∂ q x + ∂ q y + ∂ q z ) d x d y d z d τ
qw
=
−
λ
(
∂t ∂n
)n
−
(
∂t ∂n
)
n
=
qw λ
第二类边界条件相当于已知任何时刻物体边界面法向的温度梯度值
稳态导热： qw = const (恒热流边界条件）
非稳态导热： q w = f (τ )
第二节导热微分方程式特例：绝热边界面：绝热边界条件
qw
=
−λ
⎛ ⎜⎝
∂t ∂n
⎞ ⎟⎠w
=
对特定的导热过程：需要得到满足该过程的补充说明条件的唯一解
单值性条件：确定唯一解的附加补充说明条件
完整数学描述：导热微分方程 + 单值性条件单值性条件包括四项：几何、物理、时间、边界

第2章-导热理论基础以及稳态导热

第二章导热基本定律及稳态导热1、重点内容：① 傅立叶定律及其应用；② 导热系数及其影响因素； ③ 导热问题的数学模型。

2、掌握内容：一维稳态导热问题的分析解法3、了解内容：多维导热问题第一章介绍传热学中热量传递的三种基本方式：导热、对流、热辐射。

根据这三个基本方式，以后各章节深入讨论其热量传递的规律，理解研究其物理过程机理，从而达到以下工程应用上目的：基本概念、基本定律:傅立叶定律,牛顿冷却定律,斯忒藩—玻耳兹曼定律。

① 能准确的计算研究传热问题中传递的热流量 ② 能准确的预测研究系统中的温度分布导热是一种比较简单的热量传递方式,对传热学的深入学习必须从导热开始，着重讨论稳态导热。

首先，引出导热的基本定律，导热问题的数学模型，导热微分方程；其次，介绍工程中常见的三种典型（所有导热物体温度变化均满足）几何形状物体的热流量及物体内温度分布的计算方法。

最后，对多维导热及有内热源的导热进行讨论。

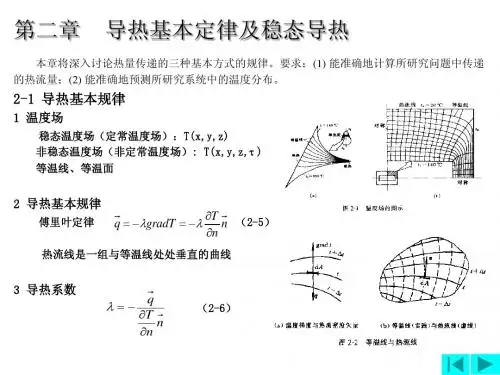
§2—1 导热基本定律一、温度场1、概念温度场是指在各个时刻物体内各点温度分布的总称。

由傅立叶定律知：物体导热热流量与温度变化率有关，所以研究物体导热必涉及到物体的温度分布。

一般地，物体的温度分布是坐标和时间的函数。

即：),,,(τz y x f t =其中z y x ,,为空间坐标，τ为时间坐标。

2、温度场分类1）稳态温度场（定常温度场）：是指在稳态条件下物体各点的温度分布不随时间的改变而变化的温度场称稳态温度场，其表达式),,,(z y x f t =。

2）稳态温度场（非定常温度场）：是指在变动工作条件下，物体中各点的温度分布随时间而变化的温度场称非稳态温度场，其表达式),,,(τz y x f t =。

若物体温度仅一个方向有变化，这种情况下的温度场称一维温度场。

3、等温面及等温线1）等温面：对于三维温度场中同一瞬间同温度各点连成的面称为等温面。

2）等温线（1）定义：在任何一个二维的截面上等温面表现为等温线。

传热学第二章导热问题数学描述

由Fourier定律：
qn

t
n
w
t nw
h

twtf
当: h , twtf 转化为第一类边界条件
当: h0,nt w0qw0
（绝热）转化为第二类边界条件
导热微分方程＋定解条件求解温度场热流场
补充：其他坐标下的导热微分方程
对于圆柱坐标系
grt aL dim n i j k
n 0 n n x y z
梯度的性质：
1．方向导数等于梯度在该方向上的投影；
2．每点梯度都垂直于该点等温面，并指向温度增大的方向
（法线方向）。
4）傅里叶定律一般形式：

A
t
n
n
傅里叶定律的文字表述为:在导热现象中,单位时间内通过给定截面的热流量,正比于该截面法线方向的温度变化率和截面面积,热量传递的方向与温度升高的方向相反.
热扩散率a 只对非稳态过程才有意义, 因为稳态过程温度不
随时间变化，热容大小对导热过程没有影响。
常见材料热扩散率：木材：a=1.510-7;钢：a=1.2510-5；银：a=210-4。木材比钢材的导温系数小100倍，所以木材一端着火而另一端不烫手。
2）定解条件
导热微分方程是描写物体的温度随时间和空间变化的一般关系，没有涉及具体、特定的导热过程，是通用表达式。
b.第二类边界条件:已知物体边界上任何时刻的热流
密度或温度变化率，
q s
qw或 n t s
qw
最简单的形式：恒热流， qw const
恒热流的特例是绝热边界条件：
t 0 n s
c.第三类边界条件:已知物体边界与周围流体间的表

《传热学》(第五版)

第一章导热理论基础2已知：10.62()W m K λ=∙、20.65()W m K λ=∙、30.024()W m K λ=∙、40.016()W m K λ=∙求：'R λ、''R λ 解：2'3124124224259210 1.1460.620.650.016m K R W λσσσλλλ-⨯⨯⨯⨯⎛⎫∙=++=++⨯= ⎪⎝⎭'"232232560.265/0.650.024R m k W λσσλλ⨯⎛⎫=+=+=⋅ ⎪⎝⎭由计算可知，双Low-e 膜双真空玻璃的导热热阻高于中空玻璃，也就是说双Low-e 膜双真空玻璃的保温性能要优于中空玻璃。

5．6．已知：50mm σ=、2t a bx =+、200a =℃、2000b =-℃/m 2、45()Wm K λ=∙求：（1）0x q =、6x q = （2）v q解：（1）00020x x x dtq bx dx λλ====-=-= 3322452(2000)5010910x x x dtW q bx m dx σσσλλ-====-=-=-⨯⨯-⨯⨯=⨯（2）由220vq d t dx λ+=2332245(2000)218010v d t W q b m dxλλ=-=-=-⨯-⨯=⨯9．取如图所示球坐标，其为无内热源一维非稳态导热故有：22t a t r r r r τ∂∂∂⎛⎫= ⎪∂∂∂⎝⎭00,t t τ==0,0tr r∂==∂ ,()f tr R h t t rλ∂=-=-∂ 10．解：建立如图坐标，在x=x 位置取dx 长度微元体，根据能量守恒有：x dx x Q Q Q ε++= （1）x dt Q dx λ=-+()x dx d dtQ t dx dx dxλ+=-++∙ 4()b b Q EA E A T Udx εεεσ===代入式（1），合并整理得：2420b fU d t T dx εσλ-= 该问题数学描写为：2420b f U d t T dx εσλ-= 00,x t T == ,0()x ldtx l dx ===假设的 4()b e x ldtfT f dx λεσ=-=真实的第二章稳态导热3.解：（1）温度分布为 121w w w t t t t x δ-=-(设12w w t t >)其与平壁的材料无关的根本原因在 coust λ=（即常物性假设），否则t 与平壁的材料有关（2）由 dtq dxλ=- 知，q 与平壁的材料即物性有关5.解： 2111222()0,(),w w ww d dt r dr drr r t t t t r r t t===>==设有：12124()11w w Q t t r r πλ=-- 21214F r r R r r λπλ-=7.已知：4,3,0.25l m h m δ=== 115w t =℃, 25w t =-℃, 0.7/()W m k λ=⋅ 求：Q解： ,l h δ ，可认为该墙为无限大平壁15(5)0.7(43)6720.25tQ FW λδ∆--∴==⨯⨯⨯= 8.已知：2220,0.14,15w F m m t δ===-℃，31.28/(), 5.510W m k Q W λ=⋅=⨯ 求：1w t解：由 tQ Fλδ∆= 得一无限平壁的稳态导热312 5.510150.141520 1.28w w Q t t F δλ⨯=+=-+⨯=⨯℃ 9.已知：12240,20mm mmδδ==，120.7/(),0.58/()W m k W m k λλ=⋅=⋅3210.06/(),0.2W m k q q λ=⋅=求：3δ解：设两种情况下的内外面墙壁温度12w w t t 和保持不变，且12w w t t >221313由题意知：1211212w w t t q δδλλ-=+122312123w w t t q δδδλλλ-=++再由： 210.2q q =，有121231212121230.2w w w w t t t t δδδδδλλλλλ--=+++得：123312240204()40.06()90.60.70.58mm δδδλλλ=+=⨯⨯+= 10.已知：1450w t =℃，20.0940.000125,50w t t λ=+=℃，2340/q W m ≤ 求：δ 解： 412,0.094 1.25102w w t t tq m m λλδ+∆==+⨯⨯41212[0.094 1.2510]2w w w w t t t t tmq qδλ+-∆==+⨯⋅ 44505045050[0.094 1.2510]0.14742340m +-=+⨯⨯⨯= 即有 2340/147.4q W m m mδ≤≥时有 11.已知：11120,0.8/()mm W m k δλ==⋅，2250,0.12/()mm W m k δλ==⋅33250,0.6/()mm W m k δλ==⋅求：'3?δ=解： '2121'3123112313,w w w w t t t t q q δδδδδλλλλλ--==+++由题意知：'q q =212tw 1tw 2q 11λ12λ23λ322即有：2121'3123112313w w w wt t t t δδδδδλλλλλ--=+++'33322λδδδλ=+ 0.6250505000.12mm =+⨯= 12.已知：1600w t =℃，2480w t =℃，3200w t =℃，460w t =℃ 求：123,,R R R R R R λλλλλλ解：由题意知其为多层平壁的稳态导热故有： 14122334123w w w w w w w w t t t t t t t t q R R R R λλλλ----====∴112146004800.2260060w w w w R t t R t t λλ--===-- 223144802000.5260060w w w w R t t R t t λλ--===--33414200600.2660060w w w w R t t R t t λλ--===-- 14.已知：1）11012,40/(),3,250f mm W m k mm t δλδ==⋅==℃，60f t =℃ 220112,75/(),50/()h W m k h W m k λλ==⋅=⋅ 2）223,320/()mm W m k δλ==⋅ 3）2'23030,,70/()h W m k δδλλ===⋅求：123123,,,,,q q q k k k ∆∆∆ 解：未变前的122030102250605687.2/1113101754050f f t t q W m h h δλ---===⨯++++tw 1tw 4tw 2tw 3R 1R2R3R =R 1+R 2R3+t αt f221）21311121129.96/()1112101754050k W m k h h δλ-===⋅⨯++++ 21129.96(25060)5692.4/q k t W m =∆=⨯-= 21105692.45687.2 5.2/q q q W m ∆=-=-= 2）22321221129.99/()11131017532050k W m k h h δλ-===⋅⨯++++ 22229.99(25060)5698.4/q k t W m =∆=⨯-= 22205698.45687.211.2/q q q W m ∆=-=-= 3) 22330'101136.11/()131********k W m k h h δλ-===⋅⨯++++ 23336.11(25060)6860.7/q k t W m =∆=⨯-= 23306860.75687.21173.5/q q q W m ∆=-=-= 321q q q ∴∆∆>∆ ，第三种方案的强化换热效果最好 15.已知：35,130A C B mm mm δδδ===，其余尺寸如下图所示，1.53/(),0.742/()A C B W m k W m k λλλ==⋅=⋅求：R λ解：该空斗墙由对称性可取虚线部分，成为三个并联的部分R 1R 1R 1R2R3R 2R 2R3R311113222,A B C A B C R R R R RR R R R =++==++ 3321111311135101301020.1307()/1.53 1.53C A B A B C R R m k W δδδλλλ--⨯⨯∴=++=⨯+==⋅332322222335101301020.221()/1.530.742C A B A B C R m k W δδδλλλ--⨯⨯=++=⨯+=⋅2212115.0410()/1111220.13070.221R m k W R R λ-∴===⨯⋅⨯+⨯+16.已知：121160,170,58/()d mm d mm W m k λ===⋅，2230,0.093/()mm W m k δλ==⋅33140,0.17/(),300w mm W m k t δλ==⋅=℃，450w t =℃求：1）123,,R R R λλλ; 2) l q : 3) 23,w w t t . 解：1）4211111170lnln 1.66410()/2258160d R m k W d λπλπ-===⨯⋅⨯2222221117060lnln 0.517()/220.093170d R m k W d λδπλπ++===⋅⨯ 223332222111706080lnln 0.279()/2220.1717060d R m k W d λδδπλδπ++++===⋅+⨯+tw 1112323tw 4132R R R λλλ∴< 2) 2330050314.1/0.5170.279l i t t q W m R R R λλλ∆∆-====++∑ 3）由 121w w l t t q R λ-=得 4211300314.1 1.66410299.95w w l t t q R λ-=-=-⨯⨯=℃ 同理：34350314.10.279137.63w w l t t q R λ=+=+⨯=℃ 17.已知：1221211,,22m m d d δδλλ=== 求：'ll q q 解：忽略管壁热阻010121020122211ln ln 222d d R d d λδδδπλπλδ+++=++ '010122010122211ln ln 222d d R d d λδδδπλπλδ+++=++ '',l l t tq q R R λλ∆∆== （管内外壁温13,w w t t 不变）01012'20101'010*******22211lnln 22222211ln ln 222l l d d q R d d d d q R d d λλδδδπλπλδδδδπλπλδ+++++∴==+++++01010010101001241lnln 22241ln ln 22d d d d d d d d δδδδδδ++++=++++由题意知： 1001011[(2)]2m d d d d δδ=++=+ 2112011[(2)]32mm m d d d d δδ=++=+ 即：21010101232()m m d d d d d δδδ=⇒+=+⇒= （代入上式）3''15ln 3ln23 1.277ln 3ln 23l l q R q R λλ+∴===+ 即： '0.783l l q q ='21.7%l llq q q -∆==即热损失比原来减小21.7%。

传热学课件第二章导热基础理论

也称导温系数,
单位为m2/s。
其大小反映物体被瞬态加热或冷却时温度变化的快慢。
导热微分方程式的简化
(1) 物体无内热源：V = 0 t a2t
(2) 稳态导热： t 0 a2t V 0 c
(3)稳态导热、无内热源：
2t 2t 2t 2t = 0，即 x2 y2 z2 0
（4）热流密度
q d
dA
nt dA
热流密度的大小和方向可以用热流密度矢量q 表示
q
d
q d n
dA
热流密度矢量的方向指向温度降低的方向。
在直角坐标系中，热流密度矢量可表示为
q qxi qy j qzk
qx、qy、qz分别表示q在三个坐标方向的分量的大小。
2. 2 导热的基本定律—傅里叶定律
第二章导热基础理论
例内重基题容点本赏精难要析粹点求
基本要求
1．理解温度场、等温面（线）、温度梯度、热流密度等概念。
2．掌握傅立叶定律及其应用。 3. 掌握热导率和热扩散率的定义、意
义、影响因素和确定方法。 4．能写出典型简单几何形状物体导热问
题的数学描述表达式。
重点与难点
重点： 1. 傅里叶定律与热导率。 2. 导热微分方程及单值性条件。难点： 1. 傅里叶定律的矢量表达式。 2. 导热微分方程及单值性条件。
标量形式的付里叶定律表达式为
q t
n
对于各向同性材料, 各方向上的导热系数相等,
q qxi qy j qzk
gradt t i t j t k x y z
q

t x

传热学--导热理论基础--ppt课件精选全文

此时表观热导率最小。最佳密度一般由实验确定。
第二章导热理论基础
第三节热导率
3、隔热层必须采取防潮措施
（1）湿材料干材料或水
因多孔材料很容易吸收水分，吸水后，由于热导率较大的水
代替了热导率较小的介质，加之在温度梯度的推动下引起水分
迁移，使多孔材料的表观热导率增加很多。
0.35
0.599
第二章导热理论基础
※导热是在温度差作用下依靠物质微粒（分子、原子和自由电子等）的运动（移动、振动和转动）进行的能量传递。因此，导热与物体内的温度分布密切相关。 ※本章将从温度场、温度梯度等基本概念出发阐述导热过程的基本规律讨论描述物体导热的导热微分方程和定解条件
第二章导热理论基础
第一节温度场和温度梯度一、温度场（P13）
第二章导热理论基础
第三节热导率
4、几点说明
（1）保温材料的λ值界定值随时间和行业的不同有所变化。保温材料热导率的界定值大小反映了一个国家保温材料的生
产及节能的水平。
20世纪50年代我国沿用前苏联标准为0.23W/(m·K)； 20世纪80年代，GB4272-84规定为0.14W/(m·K)， GB4272-92《设备及管道保温技术通则》中则降低到（0.122）W对/(于m各·K向) 异性材料，其热导率还与方向有关。
1、等温面：同一瞬间，温度场中温度相同的点所连成的面。 2、等温线：等温面与其他任一平面的交线。
3、立体的等温面常用等温线的平面图来表示。
为了在平面内清晰地表示一组等温面，常用这些等温面与一平面垂直相交所得的一簇等温线来表示。图2-1是用等温线表示的内燃机活塞和水冷燃气轮机叶片的温度场
第二章导热理论基础
三、温度梯度（P13-14）

传热学-第2章-导热的理论基础

温度是标量，因而温度场是标量场
4
2.1 基本概念和导热基本定律
2.1.1 温度场
从不同的角度对温度场进行分类：按温度场是否随时间变化，可分为:
稳定(Steady-state)温度场：物体内各点温度不随时间变化——稳态导热
t f (x, y, z)
稳态温度场、定常温度场
5
2.1 基本概念和导热基本定律
提出的，傅里叶是导热理论的奠基人，他通过实验，分析和总结了物体内的导热规律，建立了傅立叶导热定律。
19
2.1 基本概念和导热基本定律
2.1.3 导热的基本定律
Fourier定律的表述：在任意时刻，各向同性连续介质内任意位置处的热
流密度在数值上与该点的温度梯度成正比，但方向相反
q gradt t n
❖ 实验表明，除了甘油和0～120℃范围内的水以外，其他液体的导热系数值随温度升高而减小
❖ 压力变化对液体导热系数的影响很小，通常可以忽略
43
2.2 物质的导热特性
液体中液态金属和电解液是一类特殊的液体 ——依靠原子的运动和自由电子的迁移来传递热量，导热
系数要比一般非金属液体大10～1000倍
44
q gradt t n
n
❖ 热流密度是一个矢量与温度梯度位于等温线同一的法线上方向相反，永远指向温度降低的方向
❖ 在直角坐标系下，热流密度矢量可表示为
q qxi qyj qzk 22
2.1 基本概念和导热基本定律
2.1.3 导热的基本定律
温度梯度和热流密度矢量、等温线和热流线间的关系
湿量等 ❖ 有些材料，如木材、结构体、胶合板等还与方向有关
（各向异性材料）有关
30
2.2 物质的导热特性

传热学第二章--稳态导热精选全文

t
无内热源，λ为常数，并已知平 t1
壁的壁厚为，两个表面温度分别维持均匀而恒定的温度t1和t2
t2
c t ( t ) Φ x x
d 2t dx2
0
o
x 0,
x ,
t t
t1 t2
x
直接积分，得：
dt dx
c1
t c1x c2
2024/11/6
35
带入边界条件：
c1
t2
t1
c t
1 r2
r 2
r
t r
1
r 2 sin
sin
t
r2
1
sin 2
t
Φ
2024/11/6
26
6 定解条件导热微分方程式的理论基础：傅里叶定律+能量守恒。它描写物体的温度随时间和空间变化的关系；没有涉及具体、特定的导热过程。通用表达式。
完整数学描述：导热微分方程 + 单值性条件
4
2 等温面与等温线
①定义
等温面：温度场中同一瞬间同温度各点连成的面。等温线：在二维情况下等温面为一等温曲线。
t+Δt t
t-Δt
2024/11/6
5
②特点
t+Δt t
t-Δt
a) 温度不同的等温面或等温线彼此不能相交
b)在连续的温度场中，等温面或等温线不会中
止，它们或者是物体中完全封闭的曲面（曲
它反映了物质微观粒子传递热量的特性。
不同物质的导热性能不同：
固体液体气体
金属非金属
金属 12~418 W (m C) 非金属 0.025 ~ 3W/(mC)
合金纯金属

高等传热学-2

已知圆柱坐标系与直角坐标系之间的函数关系
x = r cos j , y = r sin j , z = z
令 x1 = r , x2 = j , x3 = z 求出拉梅系数
H1 = Hr = 1 H2 = Hj = r H3 = Hz =1
圆柱坐标系的导热方程
H = H1H 2H3 = r
rc ¶T ¶t
高等传热学
张靖周
南京航空航天大学能源与动力学院
第二章导热的理论基础
2-1 导热基本定律
一、经典傅里叶(Fourier)定律 qv = - l Ñ T = - l gradT = - l ¶ T nv ¶n
Fourier定律作为导热的本构方程，描述了热流量和温度分布之间的关系。思考： Fourier定律的适定条件？
r n
方向
温度升高，即
( ¶T ¶n
)w
>
0
，故
-
l(
¶T ¶n
)w
<
0
(2)假设 Tf < Tw ，表面温度比内部温度低，则沿 nr方向
温度降低，即
( ¶T ¶n
)w
<
0
，故
-
l(
¶T ¶n
)w
>0
第二类和第三类边界条件的具体应用
热流密度导热
q0
=
-l
¶T (0,t ¶x
)
导热热流密度
-
l
¶T
C 是热传播速度 a 是导温系数
t0
=
a C2
t 0 是弛豫时间：温度场的重新建立滞后于热扰动改
变的时间，反映了系统趋于新的平衡状态的快慢程度
(1) 对于稳态导热过程，热流密度矢量场不随时间变化，传播项的影响消失

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

bt
dt dx
0
对于第一类换热边界，对上式积分求解后可得：
t
1 2
b
t
w1
1 2
b
2 b
tw1
tw2
t w1
tw2
x
此时，通过平壁的热流为：
q
dt dx
t w1
tw2
0
1
b 2
t w1
tw2
2）平壁边界为第三类边界条件，即
dt dx
x0
h1
t f1
t
x0
t f1
tf2
阻 R
B
A
C
E
D
如B、C、D的导热系数相差不大时，把A和E相应地划分三块，则其热阻的计算相当于复合电路电阻的计算。
等效热流路图：
A1
B
E1
t w1
A2
C
E2
tw2
A3
D
E3
1
1
1
1
Rt RA1 RB RE1 RA2 RC RE2 RA3 RD RE3
因实际中组成复合平壁的各向材料导热系数差别较大，其热阻值与真实热阻值可能会有较大出入，目前一般采用修正系数加以校正。
tf1 tf2
1
n
i
1
h1 A i1 i A h2 A
5）通过复合平壁的导热
一般而言，因各向材料的导热系数不同，复合平壁的温度场是二维或三维的，但当各向不同材料的导热系数相差不大时，仍可把复合平壁的导热问题近似地作一维处理，写成
Q t
R
求解复合平壁导热问题的关键仍是确定其各种形态下的总热
Rreal Rt
6）具有内热源时复合平壁的导热
条件：常物性；稳态；各向同性；一维导热
热扩散方程为：
d 2t dx2
qv
0
通解为：对于第一类边界条件
t
qv
2
x2
c1x
c2
t x
t w.1
t x
t w.2
则最后可得其温度分布为：
tx
qv 2
1
x
2
tw1
tw2 2
x
q dt q dx dt
dx
两边积分后有
q
dx
tw2 dt q
t w1 t w2
0
tw1
这种直接积分法特别适合于求解变截面一维稳态导热问题
如果构成平壁的材料的导热系数随温度发生变化，即
0 1 bt
则可改写其导热方程为： d dt 0
dx dx
d dx
0 1
dt dx
x
h2
t f 2 t x
t w1
这里，h
1 , h2
,t
f1,t
f
，
2
已知
h1
tw2
h2
对于常物性，当稳态情况下可得：
q
tf1 tf2
1 1
k tf1 tf2
h1 h2
其中， 1 1 1 又根据傅里叶定律 q dt
k h1 h2
dx
则得dt dxq来自1tf1 tf2
Q
q
A
tw1 tw(n1)
n i
i1 i A
4）多层平壁导热，第三类边界条件
t f1
tf2
相当于多电阻串联电路
t f1
1
1
h1
1
Rt
1 h1
n i 1
i i
1 h2
对于面积为A的平壁，其热流量Q为：
h1
h2
1
2 3
tf2
2
3
1
2
3
h2
q t t f 1 t f 2
Rt Rt
Q qA
通解为：
t c1x c2
，无内热源，一维导热
1）平壁边界为第一类边界条件，即
t x0 t w1 t x t w2
代入可得：
t
t w1
t w1
tw2
x
通过平壁的热流通量（密度）q为：
q dt tw1 tw2 tw1 tw2
dx
当然，对于一维稳态导热，由于 q=const
由
热扩散方程为：
T h
初始条件
1 a
t
2t x 2
qv
tx,0 T0
qv
T0
x
边界条件
t
0,
T0
t x
xL
h
tL, t f
例2：一锅炉炉墙采用密度为300kg/m3的水泥珍珠岩制
作，壁厚 = 100 mm，已知内壁温度t1=500℃，外壁温度 t2=50℃，求炉墙单位面积、单位时间的热损失。
(500
50)
423
W/m2
若是多层壁，t2、t3的温度未知：
可先假定它们的温度，从而计算出平均温度并查出导热系
数值，再计算热流密度及t2、t3的值。
若计算值与假设值相差较大，需要用计算结果修正假设值，
逐步逼近，这就是迭代法。
例3：一双层玻璃窗，高2m，宽1m，玻璃厚0.3mm，玻璃
的导热系数为1.05 W/(mK)，双层玻璃间的空气夹层厚度
tw1
tw2 2
例1：一矩形截面长铜排，宽度w》厚度L，铜排下表面与冰浴
接触，因此开始时整个铜排的温度大致等于冰的温度T。，突然对铜排通以电流，同时一股温度为T∞的气流吹过上表面，此时铜排下表面继续维持T。，试列出扩散方程以及求解该铜排温度分布的初始条件和边值条件。
分析：因W》L，导热可以认为是x方向上的一维传热
1 1
h1 h2
dt q dx 温度分布微分方程式
t f1
t w1
tw2
tf2
1
1
h1
h2
3）多层平壁导热，第一类边界条件
t w1
tw4
相当于多电阻串联电路
1
2 3
t w1
tw2
1
2
tw3
3
tw4
1
2
3
Rt
n i 1
i i
q t tw1 tw4
Rt Rt
对于n层平壁，其热流量Q为：
为5mm，夹层中的空气完全静止，空气的导热系数为
0.025W/(mK)。如果测得冬季室内外玻璃表面温度分别为 15℃和5℃，试求玻璃窗的散热损失，并比较玻璃与空气
夹层的导热热阻。
分析：这是一个三层平壁的稳态导热问题。散热损失
为：
Q
tw1 tw4 δ1 δ2 δ3
tw1 tw4
Rλ1 Rλ2 Rλ3
2-3 通过平壁与圆筒壁的稳态导热
本节研究内容： 1. 平壁的一维稳态导热
2. 圆管壁的一维稳态导热
回顾：
稳态导热特征： t 0
热扩散方程：
2t x 2
2t y 2
2t z 2
qv
0
无内热源时
2t x 2
2t y 2
2t z 2
0
2-3-1 通过平壁的导热
条件：平壁厚度，导热系数
导热方程为： d 2t 0 dx2
解：材料的平均温度为：
t = (t1 + t2)/2 = (500 + 50)/2 = 275 ℃
由p318附录4查得：
{}W/(mk) 0.0651 0.000105 {t}C
得：
0.0651 0.000105 275
0.0940 W/(m k)
则：
q
(t1
t2
)
0.0940 0.1
Aλ1 Aλ2 Aλ3
0.003
15 5 0.005
0.003 94.3W
2 0.5 2 0.025 2 0.5
可见，单层玻璃的导热热阻为0.003 K/W，而空气夹层的导热热阻为0.1 K/W，是玻璃的33.3倍。
如果采用单层玻璃窗，则散热损失为

传热学第二章-导热理论基础-2

合集下载