当前位置：文档之家 › 传热学-第二章k4

传热学-第二章k4

  • 格式：ppt
  • 大小：1.90 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

传热学(第二章)

传热学(第二章)

(2-32)
热阻
R=
1 1 1 ( 4πλ r r2 1
(2-33)
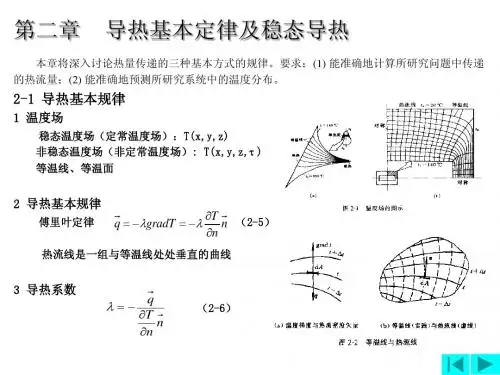
由球坐标系一般形式的导热微分方程
1 T 1 T 1 T T (λr2 + 2 2 (λ ) + 2 (λ sin θ ) + Φ = ρcp r2 r r) r sin θ r sin θ θ θ τ
2 1
λ1
第二章
导热基本定律及稳态导热
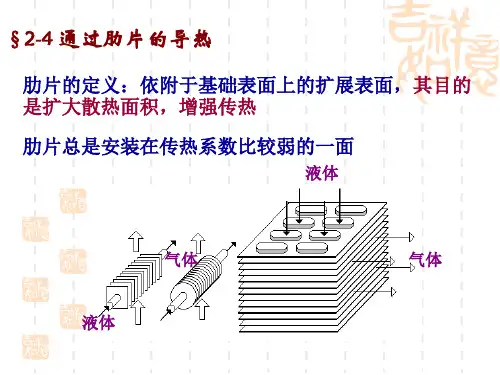
2-3 通过平壁,圆筒壁,球壳和其他变截面物体的导热 通过平壁,圆筒壁,
1 T 1 T T T (λr + 2 (λ ) + (λ ) + Φ = ρcp τ r r r) r z z d dt 简化变为 dr (r dr ) = 0 (2-25)
⒉ 通过圆筒壁的导热 由导热微分方程式(2—12)
⒉ 通过圆筒壁的导热 根据热阻的定义,通过整个圆筒壁的导热热阻为 (2-29) 29) 与分析多层平壁—样,运用串联热阻叠加的原则,可得通过图2-9所示的多层圆筒壁的 导热热流量 2πl(t1 t4 ) Φ= (2-30) ln( d2 / d1) / λ1 + ln( d3 / d2 ) / λ2 + ln( d4 / d3) / λ3 ⒊ 通过球壳的导热 导热系数为常数,无内热源的空心球壁.内,外半径为r1,r2,其内外表面均匀 恒定温度为t1,t2,球壁内的温度仅沿半径变化,等温面是同心球面. 由傅立叶定律得: dt 各同心球面上的热流率q不相等,而热流量Φ相等. Φ = 4πr2λ dr dr Φ 2 = 4πλdt r
的热传导微分方程:
T(r,τ ) τ ρc 当 λ = const 时, 2T(r,τ ) + Φ = p T(r,τ ) λ λ τ [λT(r,τ )] + g(r,τ ) = ρcp

传热学第二章课件PPT教案

传热学第二章课件PPT教案

第16页/共73页
沿x 轴方向导入与导出微元体净热量
Φx
Φxdx
x
t x
dxdydz
同理可得：
沿 y 轴方向导入与导出微元体净热量
Φy
Φydy
y
t y
dxdydz
沿 z 轴方向导入与导出微元体净热量
Φz
Φzdz
z
t z
dxdydz
传热学 Heat Transfer
第17页/共73页
t f (x, y, z, )
二维温度场 三维温度场
t f (x, y)
t f (x, y, )
t f (x, y, z)
t f (x, y, z, )
第2页/共73页
2、温度分布的图示法
传热学 Heat Transfer
第3页/共73页
2、温度分布的图示法
等温线
传热学 Heat Transfer
第6页/共73页
3、意义
已知物体内部的温度分布后，则由该定律求得各 点的热流密度或热流量。
例1：已知右图平板中的温度分布可以表示成如下 的形式：
t c1x2 c2
其中C1、C2 和平板的导热系数为
常数，计算在通过x 0 截面处的
热流密度为多少？
x 0
传热学 Heat Transfer
第7页/共73页
3. 一块厚度为 的平板，平板内有均匀的内热源，
热源强度为 ，平板一侧绝热，平板另一侧与温
度为tf 的流体对流换热，且表面传热系数为h。
传热学 Heat Transfer
第26页/共73页
4. 已知一单层圆筒壁的内、外半径分别为 r1、r2 ，导热系数为常量，无内热源，内、外壁面维持 均匀恒定的温度tw1，tw2 。

传热学第2章

传热学第2章

根据第一类边界条件时的结果:
dt tw1 tw2 1
（此时壁温tw1和tw2为未知）
dr
ln r1 r
r2
与以上两个边界条件共三式变形后
相加,可消去tw1和tw2，得：
单层圆筒壁的单位管长热流量：
ql
tf1 tf2 1 1 ln r2 1
tf1 tf 2
1 1 ln d 2 1
h1 2r1 2 r1 h2 2r2 h1d1 2 d1 h2d 2
x h2 t x t f 2
根据第一类边界条件时的结果: （此时壁温tw1和tw2为未知）
q dt tw1 tw2 dx
与以上两个边界条件共三式变形后 相加,可消去tw1和tw2，得：
单层平壁的热流密度：
q
tf1 tf2
1 1
k tf1 tf2
h1 h2
多层平壁的热流密度：
接触热阻的定义：
Rc
tc
接触热阻的影响因素： 粗糙度
挤压压力 硬度匹配情形 空隙中介质的性质
减小接触热阻的措施： 表面尽量平整 增加挤压压力
两表面一软一硬 涂导热姆
第七节 二维稳态导热
应用领域：房间墙角，地下埋管，矩形保温层，短肋片
二维稳态导热微分方程：
2t x2
2t y 2
0
解析法
二维稳态导热问题的研究手段：
几种导热过程的形状因子
第二章重点：
1.各种稳态导热问题的数学模型 和求解方法
2.临界热绝缘直径问题
3.肋片性能分析
请同学们思考一个问题:
肋高越大，肋的散热面积越大，因而采用 增加肋高的方法可以增加肋的散热量。这 种方法在实际换热器设计中是否可行？若 可行，是否会有某些局限性？

传热学-第二章

传热学-第二章

金属 非金属; 固相 液相 气相
不同物质热导率的差异：构造差别、导热机理不同
1、气体的热导率
气体 0.006~0.6W (m C)
0 C : 空气 0.0244W (m C) ; 20 C : 空气 0.026W (m C)
气体的导热：由于分子的热运动和相互碰撞时发生的能量传递
dt dx
表示t只与x有关，是一维导热；
t x
表示t只与x有关，是一维导热，且在Δ x内dt/dx保持不变。
§2-2 导热微分方程式（Heat Diffusion Equation） 傅里叶定律： q -grad t [ W m2 ]
确定热流密度的大小，应知道物体内的温度场: t f ( x, y, z, ) 确定导热体内的温度分布是导热理论的首要任务 一、导热微分方程式 理论基础：傅里叶定律 + 热力学第一定律 假设：(1) 所研究的物体是各向同性的连续介质 (2) 热导率、比热容和密度均为已知 (3) 物体内具有内热源；强度 qv [W/m3]; 内热源均匀分布；qv 表示单位体积的导热 体在单位时间内放出的热量
T
大多数建筑材料和绝热材料具有多孔或纤维结构 多孔材料的热导率与密度和湿度有关
、湿度
保温材料：国家标准规定，温度低于350度时热导率小于 0.12W/(mK) 的材料（绝热材料）
t dt t 问题： 、 、 有何区别？ x dx x
t 表示t除与x有关还与其他因素有关，如y、z、时间等； x
t t t q x ; q y ; q z x y z
注：傅里叶定律只适用于各向同性材料 各向同性材料：热导率在各个方向是相同的
有些天然和人造材料，如：石英、木材、叠层塑料板、叠层 金属板，其导热系数随方向而变化 —— 各向异性材料

传热学课件第2章

传热学课件第2章

（1）定义： 各时刻空间所有各点温度分布的总称。 温度场是时间和空间的函数 t f ( x，y，z， ) （2）分类：
稳态温度场（Steady-state conduction）
t 0
t 0
t f ( x，y，z)
t f ( x，y，z， )
非稳态温度场（Transient conduction）
t [3] c dzc d ) [J]
由 [1]+ [2]= [3]：
导热微分方程式
t t t t c ＝ ＋ ＋ ＋ x x y y z z
: 热导率（导热系数） （Thermal conductivity）
2.1 导热基本定律
图2-2 等温线与热流线
2.1 导热基本定律
四、导热系数
q t — 物质的重要热物性参数 n n 导热系数的数值：就是物体中单位温度梯度、单位 时间、通过单位面积的导热量，W/(m.K)。
导热系数的数值表征物质导热能力大小。实验测定。 影响导热系数的因素：物质的种类、材料成分、 温度、湿度、压力、密度等。 1 bt
第二类边界条件相当于已知任何时刻物体边界 面法向的温度梯度值
q s qw f2 τ qw const 非稳态导热： 稳态导热： t t 0 0 特例：绝热边界面： qw n w n w
2.2 导热问题的数学描写
三、傅里叶定律及导热微分方程的适用范围
傅里叶定律的假定: 热扰动的传递速度是无限大的。 热流密度不是很高 过程的作用时间足够长 过程发生的尺度范围足够大 非傅里叶导热: 温度效应:极低温度(接近于0K)时的导热问题 时间效应:当过程的作用时间极短,与材料本身固有 的时间尺度相接近时 尺度效应:当过程发生的空间尺度极小,与微观粒子 的平均自由行程相接近时

传热学第二章 稳态导热

传热学第二章 稳态导热

金属非金属
金 属 12~418W (mC ) 非金 0 属 .02~5 3W/C (m )
合金
纯金属
2019/11/12
13
温 度 低 于 350 度 时 热 导 率 小 于 0.12W/(mK) 的材料称为保温 材料（绝热材料）
同一种物质的导热系数也会因 其状态参数的不同而改变。
第二章 稳态导热
§2-1 基本概念 §2-2 一维稳态导热
2019/11/12
1
分析传热问题基本上是遵循经典力学的研究 方法，即针对物理现象建立物理模型，而后 从基本定律导出其数学描述(常以微分方程的 形式表达，故称数学模型)，接下来考虑求解 的理论分析方法。
导热问题是传热学中最易于采用此方法处理 的传热方式。
根据付里叶定律
dΦx qxdyd zxt dydz
dΦy qydxdzytdxdz dΦz qzdxd yztdxdy
2019/11/12
18
qxdxqx
qx x
dx
z
dΦxd
xqxd
xdydzqxd
ydzqx x
d
xd
yd
z
d
x
dΦx
2019/11/12
22
在同样加热条件下，物体的热扩散率越大，物 体内部各处的温度差别越小。
a 木 材 1 .5 1 0 7 m 2s ， a 铝 9 .4 5 1 0 5 m 2s
a木材 a铝1600
2019/11/12
23
c t x( x t) y( y t) z( z t)
2019/11/12
11
根据一维稳态平壁导热模型，可

《传热学》第2章_稳态热传导

《传热学》第2章_稳态热传导

三三
三三三三三三三三三 三三
三三 三三
三三三三三三三
三三
三三三三三三三三
三三
三三三三三三三三三三三
18
第2章 稳态热传导
2.1 典型一维稳态导热问题的分析解
2.3.1 通过平壁的导热：
一维、稳态、常物性、无内热源情况，考察平板的导热情况。
c t


x
t x
t x
n
中，gradt表示空间某点的温度梯度，
n表示通过该点的等温线上的法向单位矢量，温度升高的方向。
利用等温线和热流线来定量且形 象地表述一个导热过程： 等温线表示热流梯度，而热流线 是与等温线处处垂直的一组曲线， 通过平面上任一点的热流线与该 点的热流密度相切。 相邻两条热流线之间所传递的热 流量处处相等，相当于构成了一 个热流通道。 该方法用于现代工程软件应用。
2.类似于非导电固体;(倾向于此观点)
2
第2章 稳态热传导
等温场(temperature field)：
温度场：物体中存在温度的场。 温度分布：各时刻物体中各点温度所组成的集合
分类：
稳态温度场：物体中各点温度不随时间而变。 t f x, y, z 瞬态温度场：物体中各点温度随时间变化。 t f x, y, z,
几何条件： 说明导热体的几何形状(平壁或圆筒壁)和大小(厚度、直径等)
物理条件:
说明导热体的物理特征如：物性参数λ、c 和 r 的数值，是否 随温度变化；有无内热源、大小和分布；是否各向同性 初始(时间)条件: 说明在时间上导热过程进行的特点 稳态导热过程不需要时间条件 — 与时间无关 对非稳态导热过程应给出过程开始时刻导热体内的温度分布
疏密可直观反映出不同区域温度热流密度的相对大小。

[工学]传热学-第二章_4节

[工学]传热学-第二章_4节

边界：肋根：第一类；肋端：绝热；四周：对流换热
求解：这个问题可以从两个方面入手：
a ) 导热微分方程，
b) 能量守恒＋Fourier law
1）采用b)，取整个肋片为控 制体，求温度分布
能量守恒：
Φx Φxdx Φd
Fourier 定律dt dx
（2）
Φxdx
Φx
m hP
Ac
mH hP H h2L H 2h H 3 2
Ac
L
H
L P 2L
H AL 肋片的纵截面积
1
mH
2h H 3 2
2
h

2
H
3 2
H
AL
可见，与参量

h
1

2
H
3 2
有关，其关系曲线如图2－19所
AL
＝0＝t0
t
x

H
时，
d
dx

0
方程的通解为： c1emx c2emx
应用边界条件可得：
c1

0
emH emH emH
c2
0
emH emH emH
最后可得等截面肋片内的温度分布：

0
em(H x) emH
em(H x) emH
(2)上述分析近似认为肋片温度场为一维。
当Bi=h/ 0.05 时，误差小于1%。对于短而厚
的肋片，二维温度场，上述算式不适用；实际上， 肋片表面上表面传热系数h不是均匀一致的 — 数值计算
3 肋片效率
由于肋片中存在导热热阻，因此肋片的散热量 随肋高的增加而减小。

最新-传热学第二章 稳态导热-PPT文档资料

最新-传热学第二章 稳态导热-PPT文档资料
2019/4/19 8
4 付里叶定律(Fourier’s Law) 第一章中给出了稳态条件下的付里叶定律，这 里可推广为更一般情况。 n dt dn t q grad t n t1 t t+dt x 热流密度在x, y, z 方向 的投影的大小分别为：
0
t2
δ
x
t t t q ;q ;q x y z x y z
第二章 稳态导热
§2-1 基本概念 §2-2 一维稳态导热
2019/4/19
1
分析传热问题基本上是遵循经典力学的研究 方法，即针对物理现象建立物理模型，而后 从基本定律导出其数学描述(常以微分方程的 形式表达，故称数学模型)，接下来考虑求解 的理论分析方法。 导热问题是传热学中最易于采用此方法处理 的传热方式。
2019/4/19 7
系统中某一点所在的等温面与相邻等温面 之间的温差与其法线间的距离之比的极限 为该点的温度梯度，记为gradt。
t t t t t gradt Lim n i j k n 0 n n x y z
注：温度梯度是向量；正向朝着温度增加 的方向
2019/4/19 16
假设：(1) 所研究物体是各向同性的连续介质； (2) 热导率、比热容和密度均为已知 (3) 物体内具有内热源；强度 [W/m3]; 表示单位体积的导热体在单位时间内放出 的热量
z
dz+dz dy
dx
导入微元体的总热流量 +内热源的生成热 =导出微元体的总热流量 +内能的增量
2019/4/19
dy+dy dz
dx+dx
x
17

传热学-讲稿第二章

传热学-讲稿第二章

k0 A b 2 [(T2 T1 ) (T2 T12 )] x 2
(2-2)
dT kA dx


0
T2 dT dx kA dx Ak 0 (1 bT )dT T1 T1 dx 1 ( 0) Ak0 (T bT 2 ) |T12 T 2 Ak0 b 2 [(T2 T1 ) (T2 T12 )] x 2 T2
1 1 Rth RA 1 1 1 RE 1 1 RB RC RD RF RG
2-3 INSULATION AND R VALUES
In Chap. 1 we noted that the thermal conductivities for a number of insulating materials are given in Appendix A. In classifying the of insulation, it is a common practice in the building industry to use a term called the R value, which is defined as
(2-1)
when the thermal conductivity is considered constant. The wall thickness is x, and T1 and T2 are the wall-face temperatures. If the thermal conductivity varies with temperature according to some linear relation k = k0(1 + bT), the resultant equation for the heat flow is

传热学-第二章k4

传热学-第二章k4

x
一维、稳态、物性参数为常数、无内热源的导热问题
1、肋片导热微分方程及其求解
针对该模型，取一微元 体，在稳态下其能量平 衡方程可以表达为：
H
净导入微元体的导热热流量(沿着肋片高度方向)=散 失于环境中的对流换热热流量（从肋片四周表面）
由傅里叶定律，导入微元体的热流量为
dt Qx Ac dx
导出微元体的热流量 :
Qx dx
H
Qx dt d dt Qx dx Ac Ac dx x dx dx dx
净导入微元体的热流量为 :
Q Qx Qx+dx
d dt Ac dx dx dx
12 32.16 10 0.025 1. 12 0.0025 1 80
424.75W
未安装肋片时，光管的散热量：
0 hF t0 tf
10 0.025 80 62.88W
424.75 6.76 0 62.83
hP 140 4.71102 故：m 44.9m－1 A 40 8.16 105
管壁
t∞ t0
mH 44.9 0.06 2.7
蒸汽 查附录可得： tf，h
l
ch mH ch 2.7 7.47
d1 tH
1 H 0 ch mH
mH
2h

H
对于圆形截面的直肋片（针形肋片）:
hP mH H Ac
P d Ac d 2 4
4h mH H d
0
x
工程上采用的肋片几何形状是十分复杂的。
y
r

传热学-第二章

传热学-第二章

方程的通解为：
x x c1e m c 2e m
应用边界条件可得： c1 0
e mH e
mH
e
mH
c2 0
e mH e mH e mH
最后可得等截面内的温度分布：
0
e m (H x ) e m (H x ) e mH e mH
可见，f 与参量
这样，矩形直肋的散热量可以不用(2-42)计算，而直接用图 2-19查出f，然后计算散热量 Φ f h ( PH ) (t0 t )
h 2 有关，其关系曲线如图2-19所示。 A H L
1 2
3
影响肋片效率的因素：肋片材料的热导率 、肋片表面与 周围介质之间的表面传热系数 h、肋片的几何形状和尺寸（P 、A、H）
在工程技术中有许多有内热源的导热问题。如：电器及线
圈中有电流通过的发热，化工中的放热，吸热反应引起的热传
递；核能装置中燃料元件的放射反应等。以平壁中具有均匀内 热源为例。
已知：平壁具有均匀内热源，其两侧
与温度为tf 的流体发生对流换 热，表面传热系数为h。 求： 平壁中任意一点x处的温度及通 过该截面处的热流密度qx。 0
稳态时，套筒得到的热流=筒身的导热+套筒的辐射换热 ∴ 套筒的壁面温度<压缩空气的温度 即：温度计的读数不能准确地代表被测地点处的空气温度。 (2) 把套管看成是一个截面积为d的直肋，测量误差就等于套 管顶端的过余温度，即
H=tH－tf
根据肋端过余温度的计算公式
H
t 0 tf ch(mH)
t 1 t 1 t t c ( r ) 2 ( ) ( ) Φ r r r r z z

最新传热学第二章 稳态热传导PPT课件

最新传热学第二章 稳态热传导PPT课件

实用计算中，大多数材料的导热 系数都可以用线性近似关系，即 λ= λ0（a+bt），式中，t为温度， a,b为常量， λ0是直线段的延长线 在纵坐标轴上的截距。
3 、保温材料（隔热、绝热材料）
把导热系数小的材料称保温材料。我国规
t 定： ≤ 350 ℃ 时， ≤ 0.12w/mk 保温材
料导热系数界定值的大小反映了一个国家保 温材料的生产及节能的水平。 越小，生产及 节能的水平越高。
传热学第二章 稳态热传导
1.重点内容：
① 傅立叶定律及其应用； ② 导热系数及其影响因素； ③ 导热问题的数学模型。
2.掌握内容：一维稳态导热问题的分析解法 3.了解内容：多维导热问题
导热特点
1)物体之间不发生宏观相对位移。
2)依靠微观粒子（分子、原子、电子等）的无规 则热运动。
3)是物质的固有本质。
微元体的导热热平衡分析
① 通过 x=x 、 y=y 、 z=z ，三个微元表面而导 入微元体的热流量：фx 、фy 、фz 的计算。 根 据傅立叶定律得
x
t x
dydz
y
t y
dxdz
(a) 通过 x=x+dx 、 y=y+dy 、 z=z+dz 三个微元 表面而导出微元体的热流量ф x+dx 、ф y+dy 、ф z+dz 的计算。根据傅立叶定律得：
物体的温度场通常用等温面或等温线表示。
等温线图的物理意义： 若每条等温线间的温度间隔相等时，等
温线的疏密可反映出不同区域导热热流 密度的大小。
三 、导热基本定律
1 、导热基本定律（傅立叶定律） 1 ）定义：在导热现象中，单位时间内通过给 定截面所传递的热量，正比例于垂直于该截 面方向上的温度变化率，而热量传递的方 向与温度升高的方向相反，即 ~ t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
t0=2000C
t0=2000C
h=17W/（m2.K） tf=380C
12.5mm
30cm
解：
th mH hP0 H 1/2 Ac0mth mH hP Ac0 th mH mH
例 蒸汽管道上装有如图所示的测温套管。套管长 l= 6cm，直径为1.5cm，壁厚为2mm，套管的导热 系数为40W/m.K，水银温度计的读数为1800C,管道 壁温t0=1000C,蒸汽与套管壁的表面传热系数为 140W/m2.K,如果仅考虑套管中的导热，则蒸汽真实 的温度是多少？ 管壁 分析：温度计套管可以看成一个等 截面的空心的环肋。 套管的截面积：
一、通过等截面直肋的导热
从肋基处开始导热 x
肋片表面和空气间的复合 换热量为 h
t0 t
h
x
H
dx
Ac

t0
x dx
l=1
h t
假定：
1、肋片在垂直于纸面方向很长，不考虑温度 沿该方向上的变化（取单位长度l=1） 2、导热系数和表面传热系数皆为常数 y 3、沿着肋片高度H方向，截面积Ac不变 4、表面换热热阻远大于导热热阻，所以截面 上温度可以认为是均匀的 5、肋片顶端可以看成绝热 6、无内热源
对于等截面的直肋，方程变为：
H
t∞ t∞
d 2t hP (t t ) 0 2 dx Ac
引入过余温度 =t t
d 2 2 m 0 2 dx
dt x 0, t t0 ; x H , 0 dx
hP m Ac
1 m
m：一为正的常数，其倒数具有 长度量纲，表征肋片导热性能、 换热性能及几何结构之间的相 d x 0, t0 t 0 ; x H , 0 对关系。 dx
导出微元体的热流量 :
Qx dx
H
Qx dt d dt Qx dx Ac Ac dx x dx dx dx
净导入微元体的热流量为 :
Q Qx Qx+dx
d dt Ac dx dx dx
§2-4 通过肋片的导热 肋片的定义：依附于基础表面上的扩展表面，其目的 是扩大散热面积，增强传热
肋片总是安装在传热系数比较弱的一面
液体
气体
气体
液体
工程上常用的肋片
肋片分析的主要任务是确定肋片沿高度方向的温度分布 情况以及肋片的散热量
Hale Waihona Puke 工程应用背景： （1）换热器翅片 （2）燃气轮机叶片 （3) 室内暖气片 （4) 温度计套管 生物应用背景：
d 2 2 m 0 2 dx
此公式是一个二阶线性齐 次常微分方程，其通解形 式为 :
H
t∞ t∞
c1e c2e
mx
mx
边界条件：肋基温度已知，肋端绝热，即： d x H, 0 x 0, 0； dx x H 带入定解条件，得到肋片的温度分布为：
＝ 0
3) 肋片问题为一维的假定
当 Bi h 0.05 时，这种近似分析的误差

不超过1％
肋片温度为二维温度场的模型，采用数值解法求解
例 如图所示长为30cm，直径为12.5mm的铜杆，导热 系数为386W/（m.K）,两端分别连接在温度为2000C的墙 上。温度为380C的空气横向掠过铜杆，表面传热系数为 17W/（m2.K）,求杆散失给空气的热量是多少？
ch m x H ch mH
= 0
ch m x H ch mH
H
等截面直肋片中的温度变化为双 曲线余弦函数关系逐渐下降
肋端（x=H）处的温度
H
ch mH
0
H tH t
0 t0 t
由肋片散入外界的全部热流量都要通过x=0处的肋基
科学家有争论说：恐龙是温血的动物， 其身上的肋片加强了过多运动带来的 热量散失。
肋片的伸展方向有对流换热和辐射传热
由于肋片的作用是为了增大传热，故肋片材料的导热性能都比 较好，而环境的换热都比较差，且从节省材料的角度出发，肋 片的厚度通常远小于它的高度。 因而垂直于肋面方向上的导热热阻会远小于它与环境的换热 热阻。于是我们可以把通过肋片的导热问题视为沿肋片方向 上的一维导热问题。
x
一维、稳态、物性参数为常数、无内热源的导热问题
1、肋片导热微分方程及其求解
针对该模型，取一微元 体，在稳态下其能量平 衡方程可以表达为：
H
净导入微元体的导热热流量(沿着肋片高度方向)=散 失于环境中的对流换热热流量（从肋片四周表面）
由傅里叶定律，导入微元体的热流量为
dt Qx Ac dx
按照牛顿冷却公式，微元体散失 于环境中的对流换热热流量为 :
Qh h t t Pdx
P为肋片的截面周长
H
一般形式的肋片导热的微分方程式 :
d dt Ac hP(t t ) 0 dx dx
d dt Ac hP(t t ) 0 dx dx
表面，故肋片总的散热量也可由傅里叶定律得出 ：
d = Ac dx
= 0
d dx
x 0
Ac0mth mH hP Ac0 th mH
hP m Ac
ch m x H ch mH
m0 th mH
x 0
emH e mH emH e mH ch(mH ) ; th(mH ) mH 2 e e mH
几点考虑
1) 肋端散热的考虑 推导中忽略了肋端的散热（认为肋端绝热）。 对于一般工程计算，尤其高而薄的肋片，足够 精确。若必须考虑肋端散热，取：H’=H+ /2
H
2) 换热系数为常数的假定 为了推导和求解的方便，我们将h、均假定为常数。 但实际上换热系数h并不是常数，而是随肋高而变 化的。而在自然对流环境下换热系数还是温度的函 数。因此，我们在肋片散热计算中也应注意由此引 起的误差。
1 A d12 d 2 2 4