第一章 分数乘法(讲义)

40、人类法律，事、只有永远躺在泥坑里的人，才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭，生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍，就是一下子不要学很多。——洛克
分数乘法讲义完整版知识讲解
36、如果我们国家的法律中只有某种 神灵， 而不是 殚精竭 虑将神 灵揉进 宪法， 总体上 来说， 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日，便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持，法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例，它们 迅速累 聚，进 而变成 法律。 ——朱 尼厄斯

个性化教学辅导教案
初夏早上六点，清亮透明的月儿还躲藏在云朵里，不忍离去，校园内行人稀少，我骑着单车，晃晃悠悠的耷拉着星松的睡眼。

校园内景色如常，照样是绿意盈盈，枝繁叶茂，鸟儿歌唱。

经过西区公园，看那碧绿的草地，飞翔中的亭子，便想起十七那年，在这里寻找春天的日子。

本想就此停车再感受一遍，可惜心中记挂北区的荷塘。

回想起冬日清理完荷塘的枯枝败叶，一片萧条的景色：湖水变成墨绿色，没有鱼儿游动，四处不见了鸟儿的踪影，只有莲藕躺在湖底沉沉睡去。

清洁大叔撑着竹竿，乘一叶扁舟，把一片片黑色腐烂的枯叶残枝挑上船。

几个小孩用长长的铁钩把莲蓬勾上岸，取下里头成熟的莲子。

4.培养学生大胆猜测，勇于实践的思维品质。
教学内容
教学内容
教学内容
教学内容
第一课时分数乘整数
一、旧知铺垫
1、计算下列各题
+++++
过程要求：
(1)写出计算过程。
(2)说一说分数加法的计算方法。
2、想一想，能不能把++改写成乘法算式呢？
二、探索新知
1、例1
（1）根据题意列出解答算式：
++==
×3=
(2)探索分数乘整数的计算方法。
×＝
1发现分数乘分数的计算方法。
2引导学生观察算式和结果，看一看其中的联系。
×＝=
想一想：虚线框中，应该是怎样的一个计算过程呢？
×＝=
然后，联系以上的算式，让学生说一说计算方法。
分数乘分数，用分子相乘的积作分子，分母相乘的积作分母。
问题二：小时粉刷多少呢？（引导学生列出算式）
×＝=
总结分数乘分数的计算方法
（3）一辆汽车，每小时行驶全程的,4小时行驶全程的几分之几？
二、探索新知
1、教学例3。
问题一：小时粉刷这面墙的几分之几？怎样列式？
×
分数乘分数怎样计算？
×表示什么？使学生理解×，就是求的是多少,也就是说把平均分成4份，取其中一份是多少？
画示意图分析。
每小时粉刷这面墙的
这面墙的的
从图上可以看出，这面墙的的，是占整面墙的
1
×10×7==60(kg)
1
2、课本练习二第1、2题
四、课堂练习设计
1、填空：看图写算式
＋＋＝
++=
×( ) =
2、计算

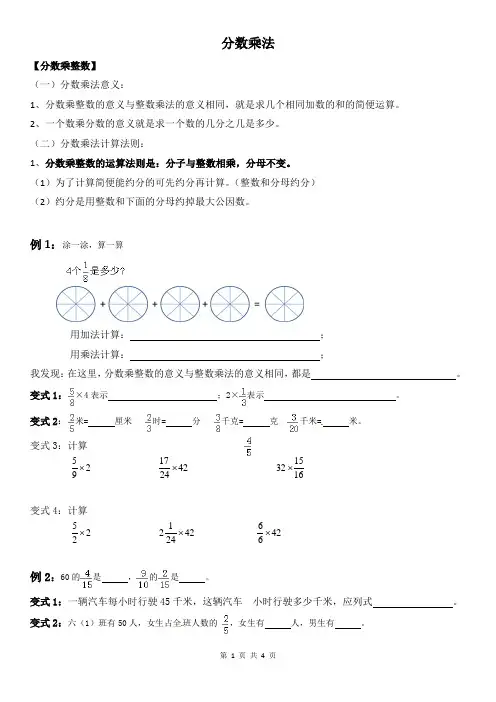
分数乘法【分数乘整数】（一）分数乘法意义：1、分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

2、一个数乘分数的意义就是求一个数的几分之几是多少。

（二）分数乘法计算法则：1、分数乘整数的运算法则是：分子与整数相乘，分母不变。

（1）为了计算简便能约分的可先约分再计算。

（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。

例1：涂一涂，算一算用加法计算： ；用乘法计算： ；我发现：在这里，分数乘整数的意义与整数乘法的意义相同，都是 。

变式1：×4表示 ；2×表示 。

变式2：米= 厘米 时= 分 千克= 克千米= 米。

变式3：计算295⨯ 422417⨯ 161532⨯变式4：计算225⨯ 422412⨯ 4266⨯例2：60的是 ，的是 。

变式1：一辆汽车每小时行驶45千米，这辆汽车 小时行驶多少千米，应列式 。

变式2：六（1）班有50人，女生占全班人数的 ，女生有 人，男生有 。

变式3：用5千克棉花的和1千克铁的相比较，结果是（ ）。

A.5千克棉花的重B.1千克铁的重C.一样重D.无法比较变式4：全世界有桦数40种，我国的桦树的种类占其中的，我国有多少种桦树？分数乘分数】1、分数乘分数的运算法则是：用分子相乘的积做分子，分母相乘的积做分母。

（分子乘分子，分母乘分母）（1）如果分数乘法算式中含有带分数，要先把带分数化成假分数再计算。

（2）分数化简的方法是：分子、分母同时除以它们的最大公因数。

（3）在乘的过程中约分，是把分子、分母中，两个可以约分的数先划去，再分别在它们的上、下方写出约分后的数。

（约分后分子和分母必须不再含有公因数，这样计算后的结果才是最简单分数）。

（4）分数的基本性质：分子、分母同时乘或者除以一个相同的数（0除外），分数的大小不变。

2、积与因数的关系：一个数（0除外）乘大于1的数，积大于这个数。

a ×b=c,当b >1时，c>a 。

第1讲分数乘法一，整数、小数乘分数【知识梳理】1.分数乘分数的计算方法：用分子相乘的积作分子，用分母相乘的积作分母。

用字母表示为：b d b da c a c⨯⨯=⨯()0,0a c≠≠【注意】计算分数乘分数时，为了简便，可以先约分，再计算。

2.分数乘整数：求几个相同加数和的运算；分数乘分数的计算方法同样适用于分数乘整数，即先把整数化为分母是1的分数，再计算。

3.小数乘分数的计算方法：（1）把小数化成分数计算；（2）如果所乘分数能化成有限小数，也可以把分数化成小数计算；（3）小数和分母能约分的，先约分再计算比较简便。

例1.计算：（1）7384⨯；（2）7489⨯；（3）3475⨯；（4）314×718；例2.计算：（1）126×213；（2）292314⨯；（3）211135⨯；（4）533174⨯.例3.计算：（1）71339⨯；（2）51012⨯. (3)133×9；（4）2897⨯.例4.计算：422417⨯ 321615⨯ 659⨯ 1430⨯例5：某食堂原有煤212吨，烧去了85，还剩几分之几？剩下多少吨？例6.一块冰，每小时失去其质量的一半，8小时后的质量为kg 165，一开始这块冰的质量是多少千克？ 例7. 1. 判断题．（1）小数乘分数，可以把小数化成分数计算，但不可以把分数化成小数计算 （ ） （2）小数乘分数的意义就是求这个小数的几分之几是多少 （ ）2.用三种方法计算2.4×433.计算下面各题：__________ ____________________ ____________________ __________试一试： 1、分数乘以整数112×11＝ 92×27＝ 6017×8＝ 509×8＝ 187×3＝ 9825×7＝52×2500＝ 3×97＝ 127×6＝ 174×5＝ 545×6＝ 5027×2＝2、分数乘以分数85×154＝ 209×215＝ 56×35＝ 257×1415＝ 113×21＝2811×338＝ 3920×1513＝ 187×143＝ 165×158＝ 3925×3013＝3. 分数乘以小数 （1）把小数画成分数0.6 1.8 0.45 0.125 2.5（2）把分数化成小数43 57 83 21 41 87 52（3）计算0.8×43 57×1.5 83×2.4 2.6×21 3.5×75 0.45×530.625×154 8.8×225 0.56×7552×0.15 87×0.24 2.6×1310达标检测一、计算(直接写出得数)73× 65 = 95 × 43 = 258 × 245 = 107 × 143=87 × 73= 2120 × 83 = 209 × 154 = 145 × 2521=二、填空1、看图列式计算（ ）×（ ）=（ ）（ ）×（ ）=（）2、先涂色表示计算结果，再填空。

分数乘除法讲义分数乘除法，听起来是不是就像数学课本里的“老顽固”？但其实，它可是咱们生活中的小能手，能帮咱们解决不少实际问题呢！想象一下，你要分蛋糕给朋友们吃，或者要算出打折后的价格，这时候，分数乘除法就像你的超级英雄，嗖嗖嗖地帮你搞定一切。

咱们先来说说分数乘法。

这就像是你有个大蛋糕，要分给几个小伙伴，但你又不想切得一块大一块小，这时候，分数乘法就能派上用场了。

比如说，你有个八分之五的蛋糕（别问我为啥是这个数，咱就假设是这样），你要分给两个小伙伴，那你就得把八分之五乘以二。

这时候，你可以想象成，你把那个八分之五的蛋糕，想象成两个一样的部分，然后再合起来，看看总共是多少。

嘿，算出来是五分之四，虽然不是整个蛋糕，但两个小伙伴都能分到一样多的蛋糕，多公平啊！分数除法呢，就像是你要算出打折后的价格。

比如说，你看中了一件衣服，原价是100块，但现在打五折。

这时候，你就得用分数除法来算了。

把原价100块当成一个整体，然后除以二分之一（因为五折就是一半嘛）。

这样一来，你就能算出打折后的价格了。

嘿，结果是50块，多划算啊！分数乘除法其实挺有意思的，它就像咱们生活中的小助手，能帮咱们解决很多麻烦。

而且，它还不止能帮咱们算数学题，还能帮咱们理解生活中的一些现象。

比如说，你知道为啥咱们吃蛋糕的时候，总是感觉吃得特别快吗？那就是因为，当你把蛋糕切成很多小块的时候，每一块都看起来很少，所以你就吃得特别快。

这其实就跟分数乘法有点像，你把一个大蛋糕分成很多小块，每一小块都是一个大蛋糕的一部分，所以你就感觉吃得特别快了。

分数除法也是一样，它就像咱们生活中的“减法”。

比如说，你有个大苹果，你要分给两个小朋友吃，那你就得把苹果切成两半。

这时候，你就相当于用了一个分数除法，把一个大苹果“减”成了两个小苹果。

虽然看起来是少了，但两个小朋友都能吃到苹果，多开心啊！所以你看，分数乘除法其实并不是那么可怕，它就像是咱们生活中的好朋友，能帮咱们解决很多实际问题。

06
课程总结与拓展延伸
关键知识点回顾
分数乘法的定义
01
分数乘法是将两个分数相乘的运算，其结果仍为分数。
分数乘法的计算方法
02
分数乘法计算时，将分子与分子相乘，分母与分母相乘，然后
化简得到最简分数。
分数乘法在实际问题中的应用03通过分数乘法可以解决生活中一些实际问题，如计算面积、体
积等。
拓展延伸内容引导
分数乘法中，分子与分子相乘 、分母与分母相乘，这与整数 乘法中的位数对齐原则相呼应 。
分数乘法中，最终结果需要化 为最简分数，这与整数乘法中 求得最终积的概念相同。
在后续数学知识中应用
分数乘法是后续学习分数除法的基础 ，掌握分数乘法有助于理解分数除法 的运算过程。
在解决一些实际问题时，如计算面积 、体积等，分数乘法也是不可或缺的 计算工具。
在计算过程中，要注意对结果进行约分，得到最简分数。
带分数的乘法
将带分数转化为假分数，然后进行分数乘法运算。
详细步骤和思路解析
复杂分数的乘法
对于复杂分数的乘法，需要仔细进行每一步的计算，确保结果的准确性。
与实际问题结合的分数乘法应用题
首先根据题意建立数学模型，将实际问题转化为分数乘法问题，然后进行计算。在计算过程中，要注 意单位的统一和结果的合理性。
针对不同难度层次练习题
高难度练习题 复杂分数的乘法，如：5/12 × 7/15
与实际问题结合的分数乘法应用题
详细步骤和思路解析
简单的分数乘法运算
直接按照分数乘法的规则进行计算， 即分子乘分子、分母乘分母。
涉及整数与分数的乘法
将整数视为分母为1的分数，然后进 行分数乘法运算。
详细步骤和思路解析

分数乘法（讲义）小学数学教案主题：分数乘法适用年级：四年级教学目标：1. 理解分数乘法的概念；2. 掌握分数乘法的运算方法；3. 能够运用分数乘法解决实际问题。

教学内容：1. 什么是分数乘法？分数乘法是指将两个或多个分数相乘的运算。

例如：⅔ × ½ = 1/32. 如何计算分数乘法？方法一：直接将分子相乘，分母相乘得到分数积即可。

例如：2/3 × 1/2 = (2 × 1) / (3 × 2) = 1/3方法二：将分数化为带分数，再进行乘法运算。

例如：2/3 × 1/2 = 2 ÷ 3 × 1 ÷ 2 = 4 ÷ 6 = 2/3方法三：将分数化为小数，再进行乘法运算。

例如：2/3 × 1/2 = 0.666… × 0.5 = 0.333…3. 几个实际的分数乘法例子①. 小明有5/6个苹果，小红有2/3个苹果，两人共有多少苹果？解：小明和小红共有的苹果数为：5/6 × 2/3 = (5 × 2) / (6 × 3) = 10/18 = 5/9答：两人共有5/9个苹果。

②. 三个人所分得的一块披萨面积分别为2/5、3/5和1/5，共分到多少面积?解：三个人分得的披萨面积之和为：2/5 + 3/5 + 1/5 = (2 + 3 + 1) / 5 = 6/5答：三个人共分到6/5面积的披萨。

③. 一种糖果每盒有3/4磅，共有10盒，求这种糖果的总重量。

解：一盒这种糖果的重量为：3/4磅十盒这种糖果的总重量为：3/4 × 10 = 30/4 = 7.5磅答：这种糖果的总重量为7.5磅。

教学步骤：1. 引入：玩海盗游戏，分数相乘。

2. 提出问题：如果有⅔的小朋友去绿地玩，而⅕的小朋友去了华山游玩，（⅔ × ⅕ = ？）会有几个小朋友既去了绿地，又去了华山？3. 让学生依次进行计算。

× ○ × ○ ×1○ ×0
4、一个平行四边形的高是 分米，它的底是高的 ，这个平行四边形的面积是多少？
【家庭作业】
1、在○里填上“＞”、“＜”或“＝”。
×10○ ×1○ ×0○
2、 + + + =( )×( )=( )
3、 + + +……+ =( )×( )=( )
100个
3、实验小学有一长方形花坛，花坛的宽是 米，长是宽的20倍，花坛的面积是多少平方米？
（5）一个长方形正好可以平均分割成六个边长是 米的正方形，求这个长方形的面积和周长。
【最新整理，下载后即可编辑】
个性化教学辅导教案
学科 数学 任课教师： 授课时间：2014 年 月 日( ) 部长审核签字：
姓名
年级
课题
分数乘整数及一个数乘分数
第_ _课
教学
目标
1、结合具体情境，借助示意图理解分数乘整数的意义，渗透数形结合思想，并借助转化的方法理解分数乘整数的算理，并能正确地进行计算，提高计算能力。
【例1】小明、小红和小芳是三个好朋友，一天小明过生日买了一个蛋糕，他们三人一起吃蛋糕，每人吃 个，3人一共吃多少个？
【小结】1、分数乘整数的意义与整数乘法的意义相同，都是求几个相同加数和的简便运算。
2、分数乘整数的计算方法：用分子乘整数的积作为分子，分母不变。能约分的，可以先约分，再计算。
【例2】计算
第二部分
【课堂练习】
练一、
1、 ×7表示；
2、 + + =( )×( )=( ) + + =( )×( )=( )
3、计算。
×6 ×8 12×
4、解答下列应用题。

课前检测：回顾整数乘法和小数乘法运算知识梳理：1、什么叫乘法多个相同加数求和的简便运算例：7+7+7+7+7=7×56+6+6+6+6=6×52、小数乘法和分数加法推导分数乘法一个物体每分钟移动0.6千米，5分钟移动多少千米？0.6×5=3（千米）分析：0.6千米=610千米=600米 600×5=3000米即：610×5=3（千米）另：610×5=610+610+610+610+610=6+6+6+6+610=5×610=3010=3（千米）总结：分数乘以整数，分母不变，分子和整数相乘。

3 8×6=3×63=94能约分的时候，要先约分，使计算简便3、分数乘以分数课本第10页，例3我每小时刷这面墙的15，14小时刷这面墙的几分之几？拿出一张纸，用它表示这面墙，涂出它的15涂出1的1是多少想：14小时刷这面墙的几分之几，就是求15的14是多少 列式：15×14=1×15×4=120 总结：分数乘以分数，应该分子和分子相乘，分母和分母相乘。

例4：蜂鸟是目前所发现的世界上最小的鸟，也是唯一能倒飞的鸟，蜂鸟每分钟可飞行310千米，23分钟能飞行多少千米？ 310×23=3×2510×3=15（千米） 注：分数和分数相乘，能约分的要先约分，使计算简便课外拓展：1、单位换算45千米=（ ）米 45×1000=800米 56小时=（ ）分 56×60=50分2、一个不为0的数乘以大于1的数，积比原数大乘以小于1的数，积比原数小。

在分数乘法中同样适用,即一个数乘以真分数，积小于这个数，一个数乘以大于1的假分数，积大于这个数。

3、分数乘整数的意义和整数（或分数）乘分数的意义比较：分数乘整数的意义表示几个相同的分数相加的和整数（或分数）乘分数的意义表示一个数的几分之几是多少4、分数后带单位和没带单位的问题34吨和34是不能进行比较的 一段绳子，用了34，还剩34米，问用去的和剩下的谁更长？（无法比较）分数乘法的简便运算乘法交换律：a ×b =b ×a乘法结合律：a ×(b ×c)=(a ×b)×c乘法交换律：a ×(b +c )=a ×b +a ×c。

分数乘法一、分数乘法（一）、分数乘法的计算法则：1、分数与整数相乘：分子与整数相乘的积做分子，分母不变。

（整数和分母约分）2、分数与分数相乘：用分子相乘的积做分子，分母相乘的积做分母。

3、为了计算简便，能约分的要先约分，再计算。

注意：当带分数进行乘法计算时，要先把带分数化成假分数再进行计算。

（二）、规律：（乘法中比较大小时）一个数（0除外）乘大于1的数，积大于这个数。

一个数（0除外）乘小于1的数（0除外），积小于这个数。

一个数（0除外）乘1，积等于这个数。

（三）、分数混合运算的运算顺序和整数的运算顺序相同。

（四）、整数乘法的交换律、结合律和分配律，对于分数乘法也同样适用。

乘法交换律： a xb = b >a乘法结合律：（a X ）>= a >b X）乘法分配律：（a + b ）>c = a c + b c a c + b c = （a + b）xc二、分数乘法的解决问题（已知单位“ 1的量（用乘法），求单位“ 1的几分之几是多少）1、找单位“1：”在分率句中分率的前面；或占”、是”、比”的后面2、求一个数的几倍：一个数 >几倍；求一个数的几分之几是多少：一个数x。

3、写数量关系式技巧：（1）的”相当于“x”占”、是”、比”相当于“=”（2）分率前是的”：单位“ 1的量X分率=分率对应量（3 ）分率前是多或少”的意思：单位“ 1的量x（1分率）=分率对应量三、倒数1、倒数的意义：乘积是1的两个数互为倒数。

强调：互为倒数，即倒数是两个数的关系，它们互相依存，倒数不能单独存在。

（要说清谁是谁的倒数）。

2、求倒数的方法：（1）、求分数的倒数：交换分子分母的位置。

（2）、求整数的倒数：把整数看做分母是1的分数，再交换分子分母的位置。

（3）、求带分数的倒数：把带分数化为假分数，再求倒数。

（4）、求小数的倒数：把小数化为分数，再求倒数。

3、1的倒数是1 ; 0没有倒数。

因为1 X1=1 ；0乘任何数都得0 ,（分母不能为0）4、对于任意数，它的倒数为；非零整数的倒数为；分数的倒数是;5、真分数的倒数大于1 ;假分数的倒数小于或等于1 ;带分数的倒数小于1。

分数乘法学习要求1. 掌握分数乘整数，用分数的分子和整数相乘的积做分子，分母不变。

分母与整数能约分时，可以先约分，再计算。

2. 掌握分数乘分数的计算，用分子相乘的积作分子，分母相乘的积做分母。

计算时，能约分的可以先约分再乘。

3. 知道分数的运算方法：分数混合运算的顺序和整数混合运算顺序相同，整数乘法的交换律、结合律和分配律，对于分数乘法也适用。

讲练互动口答：把什么看作单位“1”的量，谁是几分之几相对应的量？(1)一块布做衣服用去53。

(2)用去一部分钱后，还剩下52。

(3)一条路，已修了103。

(4)水结成冰，体积膨胀111。

(5)甲数比乙数少51 口头列式：（1）32的83是多少？ （2）120页的61是多少？ （3）绿化造林对可降低噪音，原来80分贝的汽笛噪音，经绿化隔离带后，降低了81，降低了多少分贝？（4）绿化造林对可降低噪音，原来80分贝的汽笛噪音，经绿化隔离带后只剩下原来的87，现在人听到的声音是多少分贝？例1 计算。

（1）41×28 65×15×2 （2）53×43 98×87×21 分析：分数乘整数，先将分数的分母与整数进行约分，再计算；分数乘分数，用分子相乘的积作分子，分母相乘的积做分母，能约分的先约分再乘，计算更简便。

解：（1）41×28=41×28 =7 65×15×2=65×15×2=25×5×2=25 1 7 2 5 1 11(2) 53×43=5433⨯⨯=209 98×87×21=98×87×21=219171⨯⨯⨯⨯=187 1即时练习1 计算。

76×28 13397⨯ 367×3×659313⨯ 32×23×43 432811⨯例2 （1）43×（94＋54＋154） （2）2517×3729＋2517×378 （3）100×9998 分析：可以运用乘法的分配律计算。

分数乘法的意义
分数乘法的意义
分数乘法是数学运算中的基本运算之 一，它可以帮助我们解决生活中的一 些实际问题。
分数乘法的实际应用
比如计算物体的面积、体积，计算商 品的折扣等等。
分数乘法在生活中的应用
分数乘法在生活中的应用
在日常生活中，我们经常会遇到需要使用分数乘法的情况 。比如计算商品的折扣、计算房屋的面积等等。
3
合并分子
对于已经通分的分数，将它们的分子进行合并， 得到最终的乘积。
分数乘法的简化计算方法
01
02
03
交叉相乘
将分子与另一个分数的分 母相乘，将分母与另一个 分数的分子相乘，得到的 结果作为最终的乘积。
分配律的应用
将分数与整数相乘时，可 以将整数分配到每个分数 上，再相乘得到最终的乘 积。
灵活运用运算律
×分子/分母。
例如，2 × 3/4 = 2 × 3/(4 × 1) = 6/4。
这种乘法规则的原理是将整数转 化为以1为分母的分数，然后按 照分子与分母的乘法规则进行计
算。
小数与分数的乘法规则
小数与分数的乘法规则是指小数与分数相乘时，小数要转化为以10或100为分母的 分数，然后按照分子与分母的乘法规则进行计算。
详细描述
在物理量计算中，我们经常需要处理具有分数单位的量。例如，速度、加速度等 物理量可能具有米/秒或米/秒^2等单位。在这种情况下，我们可以使用分数乘法 将这些量转换为具有更简单单位的量，从而更好地理解和解决实际问题。
化学量计算中的分数乘法
总结词
化学量计算中，分数乘法同样扮演着重要的角色。
详细描述
详细描述
在单位换算中，我们经常需要将一个物理量从一种单位转换为另一种单位。例如，将米转换为千米，将英里转换 为公里等。在这个过程中，分数乘法可以发挥重要作用。通过将单位转换因子表示为分数，我们可以轻松地使用 分数乘法进行单位换算。

第一单元：分数乘法一、分数乘法的概念分数乘法是指在乘法运算中，其中有一个或两个乘数是分数，通过乘法运算规则，计算出分数的乘积。

分数乘法涉及到分数的乘法运算法则，要求掌握分数相乘的方法和技巧。

二、分数乘法的基本原理1. 分数乘法的定义分数乘法是指两个分数相乘的运算。

示例：1/2 × 3/4 = 3/82. 分数乘法的规则分数相乘时，先将两个分数的分子和分母分别相乘，得到的结果即为分数的乘积。

示例：1/3 × 2/5 = (1×2) / (3×5) = 2/153. 分数乘法的方法分数相乘时，可以先化简分数，然后再进行乘法运算得到最简分数，也可以先进行分子相乘和分母相乘，再进行化简得到最简分数。

示例：4/6 × 5/3 = 20/18 = 10/9三、分数乘法的实际应用1. 分数乘法在日常生活中的运用分数乘法在日常生活中有着广泛的应用，比如在烹饪中需要按照食谱中的比例计算食材的用量，就需要进行分数乘法的运算来得到准确的结果。

示例：如果食谱中需要用1/2杯的面粉，而需要一倍的食谱，则需要1/2 × 1 = 1/2杯的面粉。

2. 分数乘法在数学问题中的应用在解决数学问题中，也会遇到分数相乘的情况，需要根据题目要求进行分数乘法的运算。

示例：假设一个长方形的长为2/3米，宽为1/4米，求其面积。

解：长方形的面积为长乘以宽，即(2/3) × (1/4) = 2/12 = 1/6平方米。

四、分数乘法中的注意事项1. 分数乘法的注意事项在进行分数乘法运算时，需要注意分子相乘、分母相乘的顺序，并且最终的结果需要进行化简，得到最简分数形式。

示例：5/6 × 2/3 = (5×2) / (6×3) = 10/18 = 5/92. 分数乘法中的常见错误在分数乘法中，常见的错误包括忽略化简、分子错乘、分母错乘等，需要学生在练习分数乘法时要注意避免这些错误。

分数乘法(约分)
课题：
分数乘法（约分）
教学
时间
9月6日
教
学
目
标
1.掌握分数乘法计算过程中的约分方法，能正确熟练进行分数乘法计算，提高学生计算的能力。
2.能解答生活中简单的分数乘法问题，了解分数乘法在现实生活中的作用。
教
学பைடு நூலகம்
重
难
点
1、掌握分数乘法计算过程中的约分方法。
2、熟练掌握约分方法，提高计算的能力。
无脊椎动物中游泳最快的是乌贼，它的速度是 千米/分。
2.解决问题一：李叔叔的游泳速度是乌贼的 。李叔叔每分钟游多少千米？
（1）阅读理解。
学生阅读题目，理解题意。
组织交流对题意的理解，得出：
①乌贼的速度是 千米/分。
②李叔叔的游泳速度是 千米/分的 。
（2）列式解答。
让学生根据已经掌握的计算方法独立解答，交流解答过程。师根据学生回答板书：
三、巩固练习
1.教材第5页“做一做”第1题。
这道题是分数乘法计算的练习，三个小题都可以在计算过程中进行约分的。先让学生独立练习，再组织学生交流汇报，汇报时重点交流约分的方法。
2.教材第5页“做一做”第2题。
问题1：先让学生阅读题目，理解题意，根据“速度×时间=路程”的数量关系列出算式： × ；再让学生独立计算，最后组织交流。通过交流，教师强调能约分的要先约分再乘。
问题2：让学生独立完成列式计算，并展示学生的计算过程和结果。引导学生注意分数和整数相乘可以怎样约分。
3.教材第5页“做一做”第3题。
阅读与理解：求这个人的身高是多少米，就是求28米的 是多少。
学生独立解答，组织交流订正。
四、总结
通过本课的学习，你有什么收获？还有哪些疑问？

第一讲：分数乘法（上）【知识点一】分数的基本性质1、分数乘整数的意义：求几个相同加数和的简便运算例：512×6，表示（ ），还可以表示（ ）。

注意： 求几个相同分数的和是多少 或 求一个分数的几倍是多少 就用 这个分数ד几”。

例：求3个112是多少，即可以列式（ ）。

练习：1、685⨯的意义是（ ），或（ ），得（ ）。

2、计算下列各题并说出计算方法。

9×718 = 347 ×28= 130×12 = 注意：分数的结果必须是最简分数。

2、分数乘分数的意义：是求一个数的几分之几是多少。

例如： 27 ×512 ，表示：27 的512是多少。

例 题：（说说计算方法及意义和图） 79×32= 32×23= 47×47= 3、（1）分数乘分数的计算方法也适用于小数乘分数，先把小数化成分数，再根据分数成分数的计算方法，然后计算。

例如：1417121715.0=⨯=⨯。

（2）分数乘分数，这里的分数也可以是带分数，计算时先把带分数化成假分数，再根据分数成分数的计算方法，然后计算。

例如：157513751312=⨯=⨯。

分数乘分数的简便算法也适用于分数连乘法。

例如281578315327158332=⨯⨯⨯⨯=⨯⨯。

例 题 34 ×815 ×310= 判断：12×14 和14×12的结果相同，意义也相同。

（ ） 4、单位换算。

412吨=（ ）千克 65小时=（ ）分 43分=（ ）秒 257平方米=（ ）平方分米 总结：5.常考填空题比20米多43是（ ）米 100米增加52是（ ）米 【知识点二】因数与积的大小关系1、比较大小，并说说你发现了什么规律 3231⨯○31 2152⨯○52 32×1○32 5×45○5 0×31○31总结：当一个因数大于1时，积大于另一个因数（0除外）；当一个因数小于1时，积小于另一个因数（0除外）；当一个因数小于1时，积就等于另一个因数。

分数乘法的注意事项
分数单位的确定
在计算分数乘法时，需要 明确每个分数所代表的单 位，以便正确理解结果的 含义。
结果的化简
在得到初步结果后，需要 对结果进行化简，以便更 好地理解其含义。
运算顺序
在计算过程中，需要遵循 运算顺序，先乘除后加减 ，以免出现错误的结果。
03
分数乘法的应用题
简单的分数乘法应用题
02
在化学中，分数乘法用 于计算化学反应中各物 质的比例。
03
在物理学中，分数乘法 用于计算物理量之间的 关系，如速度、加速度 等。
04
在经济学中，分数乘法 用于计算投资回报率、 成本效益等。
02
分数乘法的计算方法
分数乘法的基本步骤
01
02
03
确定分子
将两个分数相乘，将分子 相乘得到新的分子。
确定分母
总结词：基础入门
输标02入题
简单的分数乘法应用题是分数乘法学习的基础，通常 涉及到两个分数相乘的情况，如“一个苹果的1/2是 多少？”等。
01
03
解题方法通常包括将分数相乘，约分，化简等步骤。
04
这类题目主要考察学生对分数乘法基本概念的理解， 以及如何将实际问题转化为数学表达式的能力。
中等难度的分数乘法应用题
04
分数乘法的练习题
基础练习题
分数乘法的基本概念
包括分数乘法的定义、计算方法等。
简单的分数乘法计算
如1/2乘以1/2，2/3乘以1/3等。
分数乘法的几何意义
通过图形解释分数乘法的意义，帮助理解。
进阶练习题
1 2
分数乘法的约分
如2/3乘以3/4，需要先进行约分再进行计算。