圆的综合解答题复习过程

专题解析几何中与圆相关的综合问题专题概述纵观近三年的高考题，解析几何题目是每年必考题型，主要体现在解析几何知识内的综合及与其它知识之间的综合，圆不会单独出大题，一般是结合椭圆、抛物线一起考查，预计在高考中解答题仍会重点考查圆与椭圆、抛物线相结合的综合问题，同时可能与平面向量、导数相交汇，每个题一般设置了两个问，第（1）问一般考查曲线方程的求法，主要利用定义法与待定系数法求解，而第（2）问主要涉及最值问题、定值问题、对称问题、轨迹问题、探索性问题、参数范围问题等.这类问题综合性大，解题时需根据具体问题，灵活运用解析几何、平面几何、函数、不等式、三角知识，正确构造不等式，体现了解析几何与其他数学知识的密切联系.这体现了考试中心提出的“应更多地从知识网络的交汇点上设计题目，从学科的整体意义、思想含义上考虑问题”的思想.典型例题【例1】（2020•湖南模拟）已知圆22++=，点(2,0):(2)32C x yD，点P是圆C上任意一点，线段PD的垂直平分线交线段CP于点Q．（1）求点Q的轨迹方程．（2）设点(0,2)A，M，N是Q的轨迹上异于顶点的任意两点，以MN为直径的圆过点A．求证直线MN过定点，并求出该定点的坐标．【例2】（2020•南昌一模）已知圆2221:(1)(3)F x y r l r ++=，圆2222:(1)(4)F x y r -+=-． （Ⅰ）证明圆1F 与圆2F 有公共点，并求公共点的轨迹E 的方程；（Ⅰ）已知点(Q m ，0)(0)m <，过点E 斜率为(0)k k ≠的直线与()I 中轨迹E 相交于M ，N 两点，记直线QM 的斜率为1k ，直线QN 的斜率为2k ，是否存在实数m 使得12()k k k +为定值？若存在，求出m 的值，若不存在，说明理由．【例3】（2020•常熟市模拟）江南某湿地公园内有一个以O 为圆心，半径为20米的圆形湖心洲．该湖心洲的所对两岸近似两条平行线1l ，2l ，且两平行线之间的距离为70米．公园管理方拟修建一条木栈道，其路线为A B C --（如图，A 在B 右侧）．其中，BC 与圆O 相切于点Q ，1OA l ⊥，30OA =米．设CBP θ∠=，θ满足02πθ<<．（1）试将木栈道A B C --的总长表示成关于θ的函数()L θ，并指出其定义域； （2）求木栈道A B C --总长的最短长度．【变式训练】1.（2020•珠海一模）设P 为圆226x y +=上任意一点，过点P 作x 轴的垂线，垂足为Q ，点M 是线段PQ 上的一点，且满足3PQ MQ =． （1）求点M 的轨迹C 的方程；（2）过点(2,0)F 作直线l 与曲线C 相交于A ，B 两点，设O 为坐标原点，当OAB ∆的面积最大时，求直线l 的方程．2．（2020春•山西月考）已知直线1x my =+与圆22(1)(1)4x y -+-=相交于A ，B 两点，O 为坐标原点． （1）当1m =时，求||AB ；（2）是否存在实数m ，使得OA OB ⊥，若存在，求出m 的值；若不存在，请说明理由．专题15 解析几何中与圆相关的综合问题专题概述纵观近三年的高考题，解析几何题目是每年必考题型，主要体现在解析几何知识内的综合及与其它知识之间的综合，圆不会单独出大题，一般是结合椭圆、抛物线一起考查，预计在高考中解答题仍会重点考查圆与椭圆、抛物线相结合的综合问题，同时可能与平面向量、导数相交汇，每个题一般设置了两个问，第（1）问一般考查曲线方程的求法，主要利用定义法与待定系数法求解，而第（2）问主要涉及最值问题、定值问题、对称问题、轨迹问题、探索性问题、参数范围问题等.这类问题综合性大，解题时需根据具体问题，灵活运用解析几何、平面几何、函数、不等式、三角知识，正确构造不等式，体现了解析几何与其他数学知识的密切联系.这体现了考试中心提出的“应更多地从知识网络的交汇点上设计题目，从学科的整体意义、思想含义上考虑问题”的思想.典型例题【例1】（2020•湖南模拟）已知圆22:(2)32C x y ++=，点(2,0)D ，点P 是圆C 上任意一点，线段PD 的垂直平分线交线段CP 于点Q ． （1）求点Q 的轨迹方程．（2）设点(0,2)A ，M ，N 是Q 的轨迹上异于顶点的任意两点，以MN 为直径的圆过点A ．求证直线MN 过定点，并求出该定点的坐标．【分析】（1）根据椭圆的定义和性质，建立方程求出a ，b 即可．（2）当直线斜率存在时，代入椭圆方程，利用韦达定理及向量数量积的坐标运算，即可求得t 的值，则直线过直线MN 恒过点2(0,)3-．【解答】解：（1）点Q 在线段PD 的垂直平分线上，||||PQ PD ∴=．又||||||CP CQ QP =+=，||||||4CQ QD CD ∴+=>=．Q ∴的轨迹是以坐标原点为中心，(2,0)C -和(2,0)D 为焦点，长轴长为的椭圆．设曲线的方程为222211x y a b+==，(0)a b >>．2c =，a =，2844b ∴=-=．∴点Q 的轨迹的方程为22184x y +=；（2）当直线MN 的斜率不存在时，则8(3M ，2)3-，8(3N -，2)3-，直线MN 的方程为23y =-，当直线MN 斜率存在时，设:MN y kx t =+，1(M x ，1)y ，2(N x ，2)y ， 则2228y kx tx y =+⎧⎨+=⎩，整理得：222(12)4280k x ktx t +++-=， 122412ktx x k +=-+，21222812t x x k -=+， 由AM AN ⊥，则0AM AN =，即221212(1)(2)()(2)0k x x k t x x t ++-++-=，则22222284(1)(2)()(2)01212t ktk k t t k k-+⨯+--+-=++， 整理得：23440t t --=，解得：2t =（舍去）或23t =-，则直线MN 的方程23y kx =-，则直线MN 恒过点2(0,)3-， 当直线MN 的斜率不存在时，则8(3M ，2)3-，8(3N -，2)3-，直线MN 的方程为23y =-，综上可知：直线MN 过点2(0,)3-．【例2】（2020•南昌一模）已知圆2221:(1)(3)F x y r l r ++=，圆2222:(1)(4)F x y r -+=-． （Ⅰ）证明圆1F 与圆2F 有公共点，并求公共点的轨迹E 的方程；（Ⅰ）已知点(Q m ，0)(0)m <，过点E 斜率为(0)k k ≠的直线与()I 中轨迹E 相交于M ，N 两点，记直线QM 的斜率为1k ，直线QN 的斜率为2k ，是否存在实数m 使得12()k k k +为定值？若存在，求出m 的值，若不存在，说明理由．【分析】（Ⅰ）利用圆心距与两圆半径和与差的大小关系，即可判断圆1F 与圆2F 有公共点，再利用定义法得到P 点的轨迹E 是以1(1,0)F -，2(1,0)F 为焦点的椭圆，从而求出公共点P 的轨迹E 的方程；（Ⅰ）过2F 点且斜率为k 的直线方程为(1)y k x =-，与椭圆方程联立，利用韦达定理代入2121212212122(1)()2()()x x m x x m k k k k x x m x x m-++++=-++，整理得：212222(624)()4(1)312m k k k k m k m -+=-+-，所以当23120m -= 时，即2m =-时，12()1k k k +=-，为定值．【解答】解：（Ⅰ）因为1(1,0)F -，2(1,0)F ，所以12||2F F =， 因为圆1F 的半径为r ，圆2F 的半径为4r -，又因为13r ，所以|4|2r r --，即12|4||||4|r r F F r r ---+，所以圆1F 与圆2F 有公共点，设两圆公共点为点P ，所以12||||44PF PF r r +=+-=， 所以P 点的轨迹E 是以1(1,0)F -，2(1,0)F 为焦点的椭圆， 所以24a =，1c =，所以23b =，所以椭圆方程为22143x y +=；（Ⅰ）过2F 点且斜率为k 的直线方程为(1)y k x =-，设1(M x ，2)y ，2(N x ，2)y ， 联立方程22(1)143y k x x y =-⎧⎪⎨+=⎪⎩，消去y 得：2222(43)84120k x k x k +-+-=，∴2122843k x x k +=+，212241243k x x k -=+①，111y k x m =-，222y k x m=-， 22212121212211212122121212121212(1)(1)11(1)()(1)()2(1)()2()()()()()()()y y k x k x x x x x m x x m x x m x x m k k k k k k k k x m x m x m x m x m x m x m x m x x m x x m ------+---+++∴+=+=+=+==---------++， 将①式代入整理得：212222(624)()4(1)312m k k k k m k m -+=-+-0m <，∴当23120m -= 时，即2m =-时，12()1k k k +=-，为定值，故存在实数2m =-，使得12()k k k +为定值1-．【例3】（2020•常熟市模拟）江南某湿地公园内有一个以O 为圆心，半径为20米的圆形湖心洲．该湖心洲的所对两岸近似两条平行线1l ，2l ，且两平行线之间的距离为70米．公园管理方拟修建一条木栈道，其路线为A B C --（如图，A 在B 右侧）．其中，BC 与圆O 相切于点Q ，1OA l ⊥，30OA =米．设CBP θ∠=，θ满足02πθ<<．（1）试将木栈道A B C --的总长表示成关于θ的函数()L θ，并指出其定义域； （2）求木栈道A B C --总长的最短长度．【分析】（1）试将木栈道A B C --的总长表示成关于θ的函数()L θ，由0AB >且0BC >求三角不等式得函数定义域；（2）利用导数求木栈道A B C --总长的最短长度．【解答】解：（1）过Q 分别向AO 和1l 作垂线，垂足为H ，M ， 由题意可得，QOH θ∠=，20sin QH θ∴=，20cos OH θ=， 则3020cos AH MQ θ==-． 在直角三角形BMQ 中，3020cos tan tan QM BM θθθ-==． 3020cos 2030cos 20sin tan sin AB AM BM QH BM θθθθθ--∴=-=-=-=． 又70sin BC θ=，702030cos 9030cos (0)sin sin sin 2L BC AB θθπθθθθ--∴=+=+=<<． 0AB >且0BC >，∴2cos 3sin 0θθ⎧<⎪⎨⎪>⎩，令02cos 3θ=，则0(,)2πθθ∈．∴定义域为0(,)2πθ；（2）由9030cos ()sin L θθθ-=，得213cos ()30L sin θθθ-'=，0(,)2πθθ∈． 令()0L θ'=，得1cos 3θ=，1233<，∴当1cos 3θ=时，[()]min L θ= 故木栈道A B C --总长的最短长度为【变式训练】1.（2020•珠海一模）设P 为圆226x y +=上任意一点，过点P 作x 轴的垂线，垂足为Q ，点M 是线段PQ 上的一点，且满足3PQ MQ =． （1）求点M 的轨迹C 的方程；（2）过点(2,0)F 作直线l 与曲线C 相交于A ，B 两点，设O 为坐标原点，当OAB ∆的面积最大时，求直线l 的方程．【分析】（1）利用P 点轨迹以及3PQ MQ =，表示出M 的轨迹方程即可；（2）设出过(2,0)F 的直线的方程为：2x my =+，联立直线方程和椭圆方程，化为关于y 的一元二次方程，利用弦长公式求得||AB ，再由点到直线的距离公式求得O 到AB 所在直线的距离，代入三角形面积公式，利用换元法求得OAB ∆的面积最大时的m 值，则直线l 的方程可求 【解答】解：（1）设(,)P x y ，则(,0)Q x ，0(M x ，0)y 且0x x =又根据3PQ MQ =．可得(0，00)))y y y -=-=-，则0y =，所以2200)6x +=，整理可得M 的轨迹方程为2236x y +=； （2）设过(2,0)F 的直线的方程为：2x my =+， 联立整理得22(3)420m y my ++-=， 所以12243m y y m +=-+，1212223233y y y y m m ==-++，则2226||3m ABm ⨯==+，点O 到直线的距离d =，所以111||26222AOBS AB d ∆===⨯，212m+=时取“=”，此时1m=±，故直线方程为2x y=+或2x y=-+．2．（2020春•山西月考）已知直线1x my=+与圆22(1)(1)4x y-+-=相交于A，B两点，O为坐标原点．（1）当1m=时，求||AB；（2）是否存在实数m，使得OA OB⊥，若存在，求出m的值；若不存在，请说明理由．【分析】（1）利用垂径定理直接求解即可；（2）假设存在满足条件的实数m，根据已知条件建立关于m的方程，由方程解的情况即可得出结论．【解答】解：圆22(1)(1)4x y-+-=的圆心为(1,1)，半径为2，（1）当1m=时，直线1x y=+即为10x y--=，圆心(1,1)到直线10x y--=的距离为d==∴||AB=（2）设1(A x，1)y，2(B x，2)y，由221(1)(1)4x myx y=+⎧⎨-+-=⎩可得22(1)230m y y+--=，且△0>恒成立，12122223,11y y y ym m-+==++，∴212122221(1)(1)1m mx x my mym-++=++=+，若存在实数m，使得OA OB⊥，则1212OA OB x x y y=+=，即222221m mm-+-=+，亦即210m m-+=，无解，故不存在实数m，使得OA OB⊥．专题强化1．（2020•全国Ⅰ卷模拟）动圆P 过定点(2,0)A ，且在y 轴上截得的弦GH 的长为4． （1）若动圆圆心P 的轨迹为曲线C ，求曲线C 的方程；（2）在曲线C 的对称轴上是否存在点Q ，使过点Q 的直线l '与曲线C 的交点S 、T 满足2211||||QS QT +为定值？若存在，求出点Q 的坐标及定值；若不存在，请说明理由．【分析】（1）设(,)P x y ，过P 作PB GH ⊥，交GH 于点B ，则B 为GH 的中点，122GB GH ==，PG =PA ==24(0)y x x =≠；（2）假设存在(,0)Q a 满足题意，设1(S x ，1)y ，2(T x ，2)y ，设其方程为11(0)x t y a t =+≠，联立124x t y ay x =+⎧⎨=⎩，利用根与系数关系表示出2QS ，2QT ， 进而表示出2211||||QS QT +即可． 【解答】解：（1）设(,)P x y ，由题意知：PA PG =，当P 点不在y 轴上时，过P 作PB GH ⊥，交GH 于点B ，则B 为GH 的中点， 122GB GH ∴==，PG ∴=，又(PA =24(0)y x x =≠；当点P 在y 轴上时，易知P 点与O 点重合，(0,0)P 也满足24y x =，∴曲线C 的方程为24y x =，（2）假设存在(,0)Q a 满足题意，设1(S x ，1)y ，2(T x ，2)y ， 根据题意可知直线l '的斜率必不为0，设其方程为11(0)x t y a t =+≠， 联立124x t y a y x =+⎧⎨=⎩，整理可得21440y t y a --=，1214y y t ∴+=-，124y y a =-，222212112112121()24216x x t y y a t ax x y y a ∴+=++=+==， 222222111111()()4(42)QS x a y x a x x a x a =-+=-+=+-+，222222222222()()4(42)QT x a y x a x x a x a =-+=-+=+-+，222222221122121212(42)(42)()(42)()22QS QT x a x a x a x a x x a x x x x a ∴+=+-+++-+=++-+-+22212121211()(42)22(42)(44)x x x x a x x a t a t =+++--+=+++， 22222116(1)QS QT a t =+，则22212222221211||||2(1)t a QS QT QS QT QS QT a t +++==+， 当2a =时，上式14=与1t 无关为定值， 所以存在(2,0)Q 使过点Q 的直线与曲线交于点S 、T 满足2211||||QS QT +为定值14． 2．（2019秋•武汉期末）已知圆22:()(1)13()C x a y a R -+-=∈，点(3,3)P 在圆内，在过点P 所作的圆的所有弦中，弦长最小值为 （1）求实数a 的值；（2）若点M 为圆外的动点，过点M 向圆C 所作的两条切线始终互相垂直，求点M 的轨迹方程． 【分析】（1）直接利用点和圆的位置关系的应用求出a 的值． （2）利用圆的切线和圆的位置关系式的应用求出圆的方程． 【解答】解：（1）由圆22:()(1)13()C x ay a R -+-=∈， 得到圆心坐标为(,0)a ， 点(3,3)P 在圆内，解得06a <<，由圆的弦的性质可知，点P与圆心的连线与弦垂直， 即点P为弦的中点时，过点P 的弦长最短．在过点P 所作的圆的所有弦中，弦长最小值为 ， 解得2a =或4，（符合06)a <<．（2）由（1）可知，2a =或4a =时，因为过点M 向圆C 作的两条切线总互相垂直，所以，点M 的轨迹为(,1)a所以点M 的轨迹方程为22(2)(1)26x y -+-=或22(4)(1)26x y -+-=．3．（2019•全国）已知点1(2,0)A -，2(2,0)A ，动点P 满足1PA 与2PA 的斜率之积等于14-，记P 的轨迹为C ．（1）求C 的方程；（2）设过坐标原点的直线l 与C 交于M ，N 两点，且四边形12MA NA 的面积为l 的方程． 【分析】（1）设(,)P x y ，运用直线的斜率公式，化简运算可得所求轨迹方程；（2）设直线l 方程为y kx =，代入C 的方程，求得交点，再由四边形的面积公式，解方程可得斜率k ，进而得到所求方程．【解答】解：（1）设(,)P x y ，由题意可得121224PA PA y y k k x x ==-+-，化为221(2)4x y x +=≠±，可得C 的方程为221(2)4x y x +=≠±；（2）当直线l 的斜率不存在，即直线方程为0x =，可得四边形12MA NA 的面积为14242⨯⨯=，不符题意，舍去；设直线l 方程为y kx =，代入方程2214x y +=，可得22414x k=+，222414k y k =+， 由M ，N 关于原点对称，可得四边形12MA NA 的面积为2122114||||24222214M N k y y A A k -==+， 解得12k =±，即有直线l 的方程为12y x =±．4．（2019•新课标Ⅰ）已知点A ，B 关于坐标原点O 对称，||4AB =，M 过点A ，B 且与直线20x +=相切．（1）若A 在直线0x y +=上，求M 的半径；（2）是否存在定点P ，使得当A 运动时，||||MA MP -为定值？并说明理由．【分析】（1）由条件知点M 在线段AB 的中垂线0x y -=上，设圆的方程为M 的方程为222()()(0)x a y a R R -+-=>，然后根据圆与直线20x +=相切和圆心到直线0x y +=的距离，半弦长和半径的关系建立方程组即可；（2）设M 的坐标为(,)x y ，然后根据条件的到圆心M 的轨迹方程为24y x =，然后根据抛物线的定义即可得到定点． 【解答】解：M 过点A ，B 且A 在直线0x y +=上，∴点M 在线段AB 的中垂线0x y -=上，设M 的方程为：222()()(0)x a y a R R -+-=>，则 圆心(,)M a a 到直线0x y +=的距离d =又||4AB =，∴在Rt OMB ∆中， 2221(||)2d AB R +=，即224R +=①又M 与2x =-相切，|2|a R ∴+=② 由①②解得02a R =⎧⎨=⎩或46a R =⎧⎨=⎩，M ∴的半径为2或6；（2）线段AB 为M 的一条弦O 是弦AB 的中点，∴圆心M 在线段AB 的中垂线上， 设点M 的坐标为(,)x y ，则222||||||OM OA MA +=，M 与直线20x +=相切，|||2|MA x ∴=+， 22222|2|||||4x OM OA x y ∴+=+=++， 24y x ∴=，M ∴的轨迹是以(1,0)F 为焦点1x =-为准线的抛物线，|||||2|||MA MP x MP ∴-=+- |1|||1||||1x MP MF MP =+-+=-+，∴当||||MA MP -为定值时，则点P 与点F 重合，即P 的坐标为(1,0)，∴存在定点(1,0)P 使得当A 运动时，||||MA MP -为定值．5．（2020•4月份模拟）已知点P 在圆22:9O x y +=上运动，点P 在x 轴上的投影为Q ，动点M 满足432PQ MQ =．（1）求动点M 的轨迹E 的方程；（2）设(3,0)G -，(3,0)H ，过点(1,0)F 的动直线l 与曲线E 交于A 、B 两点．问：直线AG 与BH 的斜率之比是否为定值？若为定值，求出该定值；若不为定值，试说明理由． 【分析】（1）设(,)M x y ，0(P x ，0)y ，0(Q x ，0)，则由432PQ MQ =，得0x x =，0y y ，代入圆22:9O x y +=，可得动点M 的轨迹E 的方程；（2）设直线l 为1x my =+，1(A x ，1)y ，2(B x ，2)y ，联立直线方程与椭圆方程，利用根与系数的关系即可求得直线AG 与BH 的斜率之比为定值12． 【解答】解：（1）设(,)M x y ，0(P x ，0)y ，0(Q x ，0)， 则由432PQ MQ =，得4(0，00)y x x -=-，)y -， 0x x ∴=，0y y ， 代入圆22:9O x y +=，可得22198x y +=．∴动点M 的轨迹E 的方程为22198x y +=；（2）直线AG 与BH 的斜率之比为定值12． 证明如下：设直线l 为1x my =+，1(A x ，1)y ，2(B x ，2)y ． 联立221198x my x y =+⎧⎪⎨+=⎪⎩，得22(89)16640m y my ++-=．则1221689m y y m -+=+，1226489y y m -=+． 12124()my y y y ∴=+，则121212112121223(2)23(4)4AG BH k y x y my my y y k x y my y my y y ---===+++ 12112122124()22414()4482y y y y y y y y y y +-+===+++．6．（2020•东莞市模拟）在平面直角坐标系xOy 中，已知圆22:(1)1N x y -+=，圆心(1,0)N ，点E 在直线1x =-上，点P 满足//PE ON ，NP NE EP EN =，点P 的轨迹为曲线M ． （1）求曲线M 的方程．（2）过点N 的直线l 分别交M 和圆N 于点A 、B 、C 、D （自上而下），若||AC 、||CD 、||DB 成等差数列，求直线l 的方程．【分析】（1）设(,)p x y ，由//PE ON ，得(1,)E y -，求出向量的坐标代入NP NE EP EN =，化简得：24y x =，所以点P 的轨迹曲线M 的方程为：24y x =；（2）由||AC 、||CD 、||DB 成等差数列，得弦长||||||||6AB AC CD DB =++=，对直线l 的斜率分情况讨论，当斜率不存在时，||46AB =≠，不符合题意，当斜率存在时，1(A x ，1)y ，2(B x ，2)y ，设直线l 的方程为：(1)y k x =-，与椭圆方程联立，利用韦达定理结合抛物线的定义可求得k 的值，从而得到直线l 的方程．【解答】解：（1）设(,)p x y ，由//PE ON ，得(1,)E y -， 则(1,)NP x y =-，(2,)NE y =-，(1,0)EP x =+，(2,)EN y =-，由NP NE EP EN =，得(1x -，)(2y -，)(1y x =+，0)(2，)y -，即22222x y x -++=+， 化简得：24y x =，所以点P 的轨迹曲线M 的方程为：24y x =；（2）由||AC 、||CD 、||DB 成等差数列，得||||2||4AC DB CD +==， 所以弦长||||||||6AB AC CD DB =++=，①当斜率不存在时，直线l 的方程为：1x =，交点(1,2)A ，(1,2)B -，此时||46AB =≠，不符合题意， ②当斜率存在时，设直线l 的方程为：(1)y k x =-，1(A x ，1)y ，2(B x ，2)y ， 联立方程2(1)4y k x y x=-⎧⎨=⎩，消去y 得：2222(24)0k x k x k -++=，∴12242x x k +=+，121x x =，显然△216(1)0k =+>恒成立， 由抛物线的定义可知，12||26AB x x =++=，∴2446k +=，解得：k = ∴直线l的方程为1)y x =-．7．（2020•福建二模）已知(1,0)F ，点P 在第一象限，以PF 为直径的圆与y 轴相切，动点P 的轨迹为曲线C ． （1）求曲线C 的方程；（2）若曲线C 在点P 处的切线的斜率为1k ，直线PF 的斜率为2k ，求满足123k k +=的点P 的个数． 【分析】（1）设(,)P x y ，则PF 中点坐标为1(2x +，)2y ，由以PF 为直径的圆与y 轴相切得11||22x PF +=，化简即可得到曲线C 的方程； （2）由24(0)y x y =>，得y =y '=，利用导数的几何意义得到102k y =，022044y k y =-，由123k k +=，得：32000361280y y y --+=①，令32()36128f x x x x =--+，利用导数得到函数()f x 在(0,)+∞内有且只有两个零点，所以方程①有且只有两个不同的正根，即满足123k k +=的点P 的个数为2个． 【解答】解：（1）设(,)P x y ，0x >，0y >， 又(1,0)F ，则PF 中点坐标为1(2x +，)2y， 因为以PF 为直径的圆与y 轴相切，所以11||22x PF +=，即12x +， 整理得C 的方程为：24(0)y x y =>，（2）由24(0)y x y =>，得y =y '=，设20(4y P ，00)(0)y y >，则102k y ==，002220004414y y k y y -==--，由123k k +=，即02004234y y y +=-，得：32000361280y y y --+=①，令32()36128f x x x x =--+，由2()912120f x x x '=--=得，23x =-，或2x =，因为当(0,2)x ∈时，()0f x '<，当(2,)x ∈+∞时，()0f x '>，所以()f x在(0,2)上单调递减，在(2,)+∞上单调递增，又(0)80f=>，f（2）160=-<，f（4）560=>，()f x的图象连续不断，所以()f x在(0,)+∞内有且只有两个零点，所以方程①有且只有两个不同的正根，所以满足123k k+=的点P的个数为2个．。

一、圆的综合 真题与模拟题分类汇编（难题易错题）1．如图，AB 为O 的直径，弦//CD AB ，E 是AB 延长线上一点，CDB ADE ∠=∠． ()1DE 是O 的切线吗？请说明理由；()2求证：2AC CD BE =⋅．【答案】（1）结论：DE 是O 的切线，理由见解析；（2）证明见解析.【解析】【分析】 （1）连接OD ，只要证明OD DE ⊥即可；（2）只要证明：AC BD =，CDB DBE ∽即可解决问题.【详解】()1解：结论：DE 是O 的切线．理由：连接OD ．CDB ADE ∠=∠，ADC EDB ∴∠=∠，//CD AB ，CDA DAB ∴∠=∠，OA OD =，OAD ODA ∴∠=∠，ADO EDB ∴∠=∠， AB 是直径，90ADB ∴∠=，90ADB ODE ∴∠=∠=，DE OD ∴⊥，DE ∴是O 的切线．()2//CD AB，ADC DAB∴∠=∠，CDB DBE∠=∠，AC BD∴=，AC BD∴=，DCB DAB∠=∠，EDB DAB∠=∠，EDB DCB∴∠=∠，CDB∴∽DBE，CD DBBD BE∴=，2BD CD BE∴=⋅，2AC CD BE∴=⋅．【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识，解题的关键是学会添加常用辅助线，准确寻找相似三角形解决问题，属于中考常考题型.2．如图，已知AB是⊙O的直径，点C为圆上一点，点D在OC的延长线上，连接DA，交BC的延长线于点E，使得∠DAC=∠B．（1）求证：DA是⊙O切线；（2）求证：△CED∽△ACD；（3）若OA=1，sinD=13，求AE的长．【答案】（1）证明见解析；（22【解析】分析：（1）由圆周角定理和已知条件求出AD⊥AB即可证明DA是⊙O切线；（2）由∠DAC=∠DCE，∠D=∠D可知△DEC∽△DCA；（3）由题意可知AO=1，OD=3，DC=2，由勾股定理可知AD=2，故此可得到DC2=DE•AD，故此可求得DE的长，于是可求得AE的长．详解：（1）∵AB为⊙O的直径，∴∠ACB=90°，∴∠CAB+∠B=90°．∵∠DAC=∠B，∴∠CAB+∠DAC=90°，∴AD⊥AB．∵OA是⊙O半径，∴DA为⊙O的切线；（2）∵OB=OC，∴∠OCB=∠B．∵∠DCE=∠OCB，∴∠DCE=∠B．∵∠DAC=∠B，∴∠DAC=∠DCE．∵∠D=∠D，∴△CED∽△ACD；（3）在Rt△AOD中，OA=1，sin D=13，∴OD=OAsinD=3，∴CD=OD﹣OC=2．∵AD=22OD OA-=22．又∵△CED∽△ACD，∴AD CDCD DE=，∴DE=2CDAD=2，∴AE=AD﹣DE=22﹣2=2．点睛：本题主要考查的是切线的性质、圆周角定理、勾股定理的应用、相似三角形的性质和判定，证得△DEC∽△DCA是解题的关键．3．在平面直角坐标系xOy中，点M的坐标为（x1，y1），点N的坐标为（x2，y2），且x1≠x2，y1≠y2，以MN为边构造菱形，若该菱形的两条对角线分别平行于x轴，y轴，则称该菱形为边的“坐标菱形”．（1）已知点A（2，0），B（0，23），则以AB为边的“坐标菱形”的最小内角为；（2）若点C（1，2），点D在直线y=5上，以CD为边的“坐标菱形”为正方形，求直线CD 表达式；（3）⊙O的半径为2，点P的坐标为（3，m）．若在⊙O上存在一点Q，使得以QP为边的“坐标菱形”为正方形，求m的取值范围．【答案】（1）60°；（2）y=x+1或y=﹣x+3；（3）1≤m≤5或﹣5≤m≤﹣1【解析】分析：（1）根据定义建立以AB为边的“坐标菱形”，由勾股定理求边长AB=4，可得30度角，从而得最小内角为60°；（2）先确定直线CD与直线y=5的夹角是45°，得D（4，5）或（﹣2，5），易得直线CD的表达式为：y=x+1或y=﹣x+3；（3）分两种情况：①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3，根据等腰直角三角形的性质分别求P'B=BD=1，PB=5，写出对应P的坐标；②先作直线y=﹣x，再作圆的两条切线，且平行于直线y=﹣x，如图4，同理可得结论．详解：（1）∵点A（2，0），B（0，∴OA=2，OB．在Rt△AOB中，由勾股定理得：AB，∴∠ABO=30°．∵四边形ABCD是菱形，∴∠ABC=2∠ABO=60°．∵AB∥CD，∴∠DCB=180°﹣60°=120°，∴以AB为边的“坐标菱形”的最小内角为60°．故答案为：60°；（2）如图2．∵以CD为边的“坐标菱形”为正方形，∴直线CD与直线y=5的夹角是45°．过点C作CE⊥DE于E，∴D（4，5）或（﹣2，5），∴直线CD的表达式为：y=x+1或y=﹣x+3；（3）分两种情况：①先作直线y=x，再作圆的两条切线，且平行于直线y=x，如图3．∵⊙O，且△OQ'D是等腰直角三角形，∴OD OQ'=2，∴P'D=3﹣2=1．∵△P'DB是等腰直角三角形，∴P'B=BD=1，∴P'（0，1），同理可得：OA=2，∴AB=3+2=5．∵△ABP是等腰直角三角形，∴PB=5，∴P（0，5），∴当1≤m≤5时，以QP为边的“坐标菱形”为正方形；②先作直线y=﹣x，再作圆的两条切线，且平行于直线y=﹣x，如图4．∵⊙O，且△OQ'D是等腰直角三角形，∴OD'=2，∴BD=3﹣2=1．∵△P'DB是等腰直角三角形，∴P'B=BD=1，∴P'（0，﹣1），同理可得：OA=2，∴AB=3+2=5．∵△ABP是等腰直角三角形，∴PB=5，∴P（0，﹣5），∴当﹣5≤m≤﹣1时，以QP为边的“坐标菱形”为正方形；综上所述：m的取值范围是1≤m≤5或﹣5≤m≤﹣1．点睛：本题是一次函数和圆的综合题，考查了菱形的性质、正方形的性质、点P，Q的“坐标菱形”的定义等知识，解题的关键是理解题意，学会利用图象解决问题，学会用分类讨论的思想思考问题，注意一题多解，属于中考创新题目．4．某居民小区的一处圆柱形的输水管道破裂，维修人员为更换管道，需要确定管道圆形截面的半径．如图，若这个输水管道有水部分的水面宽AB=16cm，水最深的地方的高度为4cm，求这个圆形截面的半径．【答案】10cm【解析】分析：先过圆心O作半径CO⊥AB，交AB于点D设半径为r，得出AD、OD的长，在Rt△AOD中，根据勾股定理求出这个圆形截面的半径．详解：解：过点O作OC⊥AB于D，交⊙O于C，连接OB，∵OC⊥AB∴BD=12AB=12×16=8cm由题意可知，CD=4cm∴设半径为xcm，则OD=（x﹣4）cm在Rt△BOD中，由勾股定理得：OD2+BD2=OB2（x﹣4）2+82=x2解得：x=10．答：这个圆形截面的半径为10cm．点睛：此题考查了垂经定理和勾股定理，关键是根据题意画出图形，再根据勾股定理进行求解．5．如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA 的延长线相交于点E，G是AD的中点，连结CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．（1）求证：BF=EF：（2）求证：PA是⊙O的切线；（3）若FG=BF，且⊙O的半径长为32，求BD的长度.【答案】(1)证明见解析；(2) 证明见解析；（3）2【解析】分析：（1）利用平行线截三角形得相似三角形，得△BFC∽△DGC且△FEC∽△GAC，得到对应线段成比例，再结合已知条件可得BF=EF；（2）利用直角三角形斜边上的中线的性质和等边对等角，得到∠FAO=∠EBO，结合BE是圆的切线，得到PA⊥OA，从而得到PA是圆O的切线；（3）点F作FH⊥AD于点H，根据前两问的结论，利用三角形的相似性质即可以求出BD 的长度．详解：证明：(1)∵BC是圆O的直径，BE是圆O的切线，∴EB⊥BC.又∵AD⊥BC，∴AD∥BE.∴△BFC∽△DGC，△FEC∽△GAC，∴BFDG=CFCG，EFAG=CFCG，∴BFDG=EFAG，∵G是AD的中点，∴DG=AG，∴BF=EF；(2)连接AO，AB.∵BC是圆O的直径，∴∠BAC=90°，由(1)得：在Rt△BAE中，F是斜边BE的中点，∴AF=FB=EF，可得∠FBA=∠FAB，又∵OA=OB，∴∠ABO=∠BAO，∵BE是圆O的切线，∴∠EBO=90°，∴∠FBA+∠ABO=90°，∴∠FAB+∠BAO=90°，即∠FAO=90°，∴PA⊥OA，∴PA是圆O的切线；（3）过点F作FH⊥AD于点H，∵BD⊥AD，FH⊥AD，∴FH∥BC，由(2)，知∠FBA =∠BAF ，∴BF =AF .∵BF =FG ，∴AF =FG ，∴△AFG 是等腰三角形.∵FH ⊥AD ，∴AH =GH ，∵DG =AG ，∴DG =2HG . 即12HG DG =， ∵FH ∥BD ，BF ∥AD ，∠FBD =90°，∴四边形BDHF 是矩形，∴BD =FH ，∵FH ∥BC∴△HFG ∽△DCG ， ∴12FH HG CD DG ==， 即12BD CD =，∴ 2.15≈， ∵O 的半径长为，∴BC，∴BD =13BC ＝. 点睛：本题考查了切线的判定、勾股定理、圆周角定理、相似三角形的判定与性质.结合已知条件准确对图形进行分析并应用相应的图形性质是解题的关键.6．如图1，延长⊙O 的直径AB 至点C ，使得BC=12AB ，点P 是⊙O 上半部分的一个动点（点P 不与A 、B 重合），连结OP ，CP ．（1）∠C 的最大度数为 ；（2）当⊙O 的半径为3时，△OPC 的面积有没有最大值？若有，说明原因并求出最大值；若没有，请说明理由；（3）如图2，延长PO 交⊙O 于点D ，连结DB ，当CP=DB 时，求证：CP 是⊙O 的切线．【答案】（1）30°；（2）有最大值为9，理由见解析；（3）证明见解析.【解析】试题分析：（1）当PC与⊙O相切时，∠OCP的度数最大，根据切线的性质即可求得；（2）由△OPC的边OC是定值，得到当OC边上的高为最大值时，△OPC的面积最大，当PO⊥OC时，取得最大值，即此时OC边上的高最大，于是得到结论；（3）根据全等三角形的性质得到AP=DB，根据等腰三角形的性质得到∠A=∠C，得到CO=OB+OB=AB，推出△APB≌△CPO，根据全等三角形的性质得到∠CPO=∠APB，根据圆周角定理得到∠APB=90°，即可得到结论．试题解析：（1）当PC与⊙O相切时，∠OCP最大．如图1，所示：∵sin∠OCP=OPOC =24=12，∴∠OCP=30°∴∠OCP的最大度数为30°，故答案为：30°；（2）有最大值，理由：∵△OPC的边OC是定值，∴当OC边上的高为最大值时，△OPC的面积最大，而点P在⊙O上半圆上运动，当PO⊥OC时，取得最大值，即此时OC边上的高最大，也就是高为半径长，∴最大值S△OPC=12OC•OP=12×6×3=9；（3）连结AP，BP，如图2，在△OAP与△OBD中，OA ODAOP BODOP OB=⎧⎪∠=∠⎨⎪=⎩，∴△OAP≌△OBD，∴AP=DB，∵PC=DB，∴AP=PC，∵PA=PC，∴∠A=∠C，∵BC=12AB=OB，∴CO=OB+OB=AB，在△APB和△CPO中，AP CPA CAB CO=⎧⎪∠=∠⎨⎪=⎩，∴△APB≌△CPO，∴∠CPO=∠APB，∵AB为直径，∴∠APB=90°，∴∠CPO=90°，∴PC切⊙O于点P，即CP是⊙O的切线．7．已知P 是O 的直径BA 延长线上的一个动点，∠P 的另一边交O 于点C 、D ，两点位于AB 的上方，AB ＝6，OP=m ，1sin 3P ＝，如图所示．另一个半径为6的1O 经过点C 、D ，圆心距1OO n ＝．（1）当m=6时，求线段CD 的长；（2）设圆心O 1在直线AB 上方，试用n 的代数式表示m ；（3）△POO 1在点P 的运动过程中，是否能成为以OO 1为腰的等腰三角形，如果能，试求出此时n 的值；如果不能，请说明理由．【答案】(1)CD=2523812n n;(3) n 9559155 【解析】分析：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．解Rt △POH ，得到OH 的长．由勾股定理得CH 的长，再由垂径定理即可得到结论；（2）解Rt △POH ，得到Rt 3m OH OCH ＝．在和Rt △1O CH 中，由勾股定理即可得到结论；（3）△1POO 成为等腰三角形可分以下几种情况讨论：① 当圆心1O 、O 在弦CD 异侧时，分1OP OO ＝和11O P OO ＝．②当圆心1O 、O 在弦CD 同侧时，同理可得结论． 详解：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．在Rt △1sin 63POH P PO =中，＝，，∴2OH =．∵AB ＝6，∴3OC ＝．由勾股定理得： 5CH =∵OH ⊥DC ，∴225CD CH ==．（2）在Rt △1sin 3POH P PO m 中，＝，＝，∴3m OH ＝． 在Rt △OCH 中，2293m CH ⎛⎫- ⎪⎝⎭＝． 在Rt △1O CH 中，22363m CH n ⎛⎫-- ⎪⎝⎭＝． 可得： 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭＝，解得23812n m n -：＝． （3）△1POO 成为等腰三角形可分以下几种情况：① 当圆心1O 、O 在弦CD 异侧时i ）1OP OO ＝，即m n ＝，由23812n n n -＝，解得9n ：＝． 即圆心距等于O 、1O 的半径的和，就有O 、1O 外切不合题意舍去．ii ）11O P OO ＝22233m m n m -+-（）（） n ＝， 解得：23m n ＝，即23n 23812n n -＝，解得9155n ：＝ ②当圆心1O 、O 在弦CD 同侧时，同理可得： 28132n m n-＝． ∵1POO ∠是钝角，∴只能是m n =，即28132n n n -＝，解得955n ：＝ 综上所述：n 9559155点睛：本题是圆的综合题．考查了圆的有关性质和两圆的位置关系以及解直径三角形．解答（3）的关键是要分类讨论．8．如图，在Rt △ABC 中，90C ∠=︒，AD 平分∠BAC ，交BC 于点D ，点O 在AB 上，⊙O 经过A 、D 两点，交AC 于点E ，交AB 于点F ．（1）求证：BC 是⊙O 的切线；（2）若⊙O 的半径是2cm ，E 是弧AD 的中点，求阴影部分的面积（结果保留π和根号）【答案】（1）证明见解析 （2）233π- 【解析】【分析】 （1）连接OD ，只要证明OD ∥AC 即可解决问题；（2）连接OE ，OE 交AD 于K ．只要证明△AOE 是等边三角形即可解决问题．【详解】（1）连接OD ．∵OA =OD ，∴∠OAD =∠ODA ．∵∠OAD =∠DAC ，∴∠ODA =∠DAC ，∴OD ∥AC ，∴∠ODB =∠C =90°，∴OD ⊥BC ，∴BC 是⊙O 的切线．（2）连接OE ，OE 交AD 于K ．∵AE DE =，∴OE ⊥AD ．∵∠OAK =∠EAK ，AK =AK ，∠AKO =∠AKE =90°，∴△AKO ≌△AKE ，∴AO =AE =OE ，∴△AOE是等边三角形，∴∠AOE =60°，∴S 阴=S 扇形OAE ﹣S △AOE 26023360π⋅⋅=-⨯22233π=-． 【点睛】本题考查了切线的判定、扇形的面积、等边三角形的判定和性质、平行线的判定和性质、全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题，属于中考常考题型．9．如图，四边形为菱形，且，以为直径作，与交于点．请仅用无刻度的直尺按下列要求画图．(保留作图痕迹)(1)在如图中，过点作边上的高．(2)在如图中，过点作的切线，与交于点．【答案】(1)如图1所示．(答案不唯一),见解析；(2)如图2所示．(答案不唯一)，见解析.【解析】【分析】（1）连接AC交圆于一点F，连接PF交AB于点E,连接CE即为所求．（2）连接OF交BC于Q，连接PQ即为所求．【详解】(1)如图1所示．(答案不唯一)(2)如图2所示．(答案不唯一)【点睛】本题考查作图-复杂作图，菱形和圆的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．10．如图，已知AB是⊙O的直径，点C、D在⊙O上，∠D＝60°且AB＝6，过O点作OE⊥AC，垂足为E．（1）求OE的长；（2）若OE的延长线交⊙O于点F，求弦AF、AC和弧CF围成的图形（阴影部分）的面积．（结果保留 ）【答案】（1）OE的长为32；（2）阴影部分的面积为3 2π【解析】（1）OE=32（2）S=32π。

初三有关圆的解答题及答案初三数学教学中，圆是一个非常重要的内容，也是经常考察的一道题型。

下面，我们来探讨一些初三有关圆的解答题及其答案。

一、相切问题问题：两个圆相切，半径分别为$r_1$和$r_2$，求它们的公切线的长度$L$。

解析：根据勾股定理，可得：$(r_1 + r_2)^2 = L^2 + (r_1 - r_2)^2$化简得：$L = 2\sqrt{r_1r_2}$答案：$L = 2\sqrt{r_1r_2}$二、切线问题问题：已知一个圆心坐标$(a, b)$，与一直线$y=k$相切，求这个圆的方程。

解析：由于圆与直线相切，所以该直线的距离等于圆的半径。

直线$y=k$与圆的距离为$|b-k|$，因此圆的方程为：$(x-a)^2 + (y-b)^2 = (b-k)^2$答案：$(x-a)^2 + (y-b)^2 = (b-k)^2$三、垂直问题问题：已知直线$y=k$和圆$(x-a)^2+(y-b)^2=r^2$相交于点$P(x_0,y_0)$，求直线$OP$的斜率，其中$O(a,b)$为圆心。

解析：首先，求点$P$的坐标。

因为$P$是圆和直线的交点，所以可以列出以下方程组：$\begin{cases} y=k \\ (x-a)^2 + (y-b)^2 = r^2 \end{cases}$将$y=k$代入第二个方程，可得：$(x-a)^2 + (k-b)^2 = r^2$将$(x,y)$代入，得到：$(x_0-a)^2 + (k-b)^2 = r^2$整理可得：$x_0 = a\pm \sqrt{r^2-(k-b)^2}$由于直线$OP$与$x$轴垂直，所以直线$OP$的斜率为$-\frac{1}{\frac{y_0-b}{x_0-a}}$。

代入$x_0$和$y_0$，即可得到答案。

答案：$-\frac{1}{\frac{y_0-b}{x_0-a}}$四、分割问题问题：一个圆$O$被圆弧$AB$和直径$CD$所分割，分别为弧$AB$和弧$BCD$。

一、圆的综合真题与模拟题分类汇编（难题易错题）1．如图，⊙M交x轴于B、C两点，交y轴于A，点M的纵坐标为2．B（﹣33，O），C（3，O）．（1）求⊙M的半径；（2）若CE⊥AB于H，交y轴于F，求证：EH=FH．（3）在（2）的条件下求AF的长．【答案】（1）4；（2）见解析;（3）4．【解析】【分析】（1）过M作MT⊥BC于T连BM，由垂径定理可求出BT的长，再由勾股定理即可求出BM的长；（2）连接AE，由圆周角定理可得出∠AEC=∠ABC，再由AAS定理得出△AEH≌△AFH，进而可得出结论；（3）先由（1）中△BMT的边长确定出∠BMT的度数，再由直角三角形的性质可求出CG 的长，由平行四边形的判定定理判断出四边形AFCG为平行四边形，进而可求出答案．【详解】（1）如图（一），过M作MT⊥BC于T连BM，∵BC是⊙O的一条弦，MT是垂直于BC的直径，∴BT=TC=123∴124；（2）如图（二），连接AE，则∠AEC=∠ABC，∵CE⊥AB，∴∠HBC+∠BCH=90°在△COF中，∵∠OFC+∠OCF=90°，∴∠HBC=∠OFC=∠AFH，在△AEH和△AFH中，∵AFH AEHAHF AHE AH AH∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AEH≌△AFH（AAS），∴EH=FH；（3）由（1）易知，∠BMT=∠BAC=60°，作直径BG，连CG，则∠BGC=∠BAC=60°，∵⊙O的半径为4，∴CG=4，连AG，∵∠BCG=90°，∴CG⊥x轴，∴CG∥AF，∵∠BAG=90°，∴AG⊥AB，∵CE⊥AB，∴AG∥CE，∴四边形AFCG为平行四边形，∴AF=CG=4．【点睛】本题考查的是垂径定理、圆周角定理、直角三角形的性质及平行四边形的判定与性质，根据题意作出辅助线是解答此题的关键．2．如图所示，以Rt△ABC的直角边AB为直径作圆O，与斜边交于点D，E为BC边上的中点，连接DE．（1）求证：DE是⊙O的切线；（2）连接OE，AE，当∠CAB为何值时，四边形AOED是平行四边形？并在此条件下求sin∠CAE的值．【答案】(1)见解析;(2)1010. 【解析】 分析：（1）要证DE 是⊙O 的切线，必须证ED ⊥OD ，即∠EDB+∠ODB=90°（2）要证AOED 是平行四边形，则DE ∥AB ，D 为AC 中点，又BD ⊥AC ，所以△ABC 为等腰直角三角形，所以∠CAB=45°，再由正弦的概念求解即可．详解：（1）证明：连接O 、D 与B 、D 两点，∵△BDC 是Rt △，且E 为BC 中点，∴∠EDB=∠EBD ．（2分）又∵OD=OB 且∠EBD+∠DBO=90°，∴∠EDB+∠ODB=90°．∴DE 是⊙O 的切线．（2）解：∵∠EDO=∠B=90°，若要四边形AOED 是平行四边形，则DE ∥AB ，D 为AC 中点，又∵BD ⊥AC ，∴△ABC 为等腰直角三角形．∴∠C AB=45°．过E 作EH ⊥AC 于H ，设BC=2k ，则EH=22k ，AE=5k ， ∴sin ∠CAE=1010EH AE ．点睛：本题考查的是切线的判定，要证某线是圆的切线，已知此线过圆上某点，连接圆心和这点（即为半径），再证垂直即可．3．函数是描述客观世界运动变化的重要模型，理解函数的本质是重要的任务。

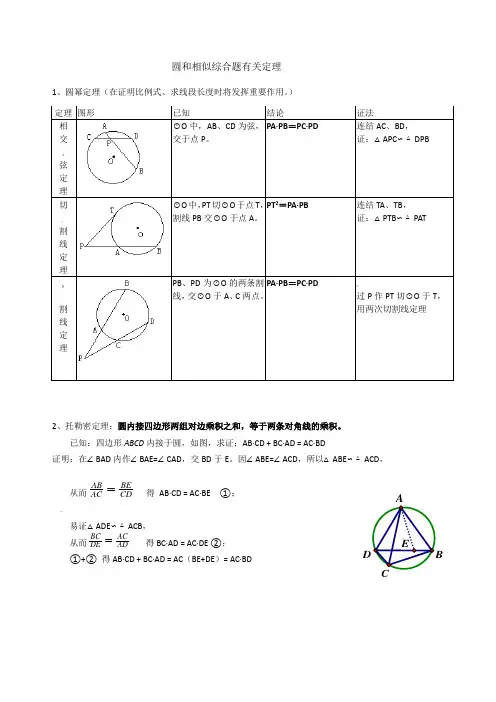
圆和相似综合题有关定理1、圆幂定理（在证明比例式、求线段长度时将发挥重要作用。

）2、托勒密定理：圆内接四边形两组对边乘积之和，等于两条对角线的乘积。

已知：四边形ABCD 内接于圆，如图，求证：AB·CD + BC·AD = AC·BD证明：在∠BAD 内作∠BAE=∠CAD ，交BD 于E 。

因∠ABE=∠ACD ，所以△ABE ∽△ACD ，从而AB BE ACCD =得 AB·CD = AC·BE ①； … 易证△ADE ∽△ACB ，从而BC AC DE AD = 得BC·AD = AC·DE ②； ①+② 得AB·CD + BC·AD = AC （BE+DE ）= AC·BD定理 图形已知 结论 证法 相交*弦定理⊙O 中，AB 、CD 为弦，交于点P 。

PA·PB ＝PC·PD 连结AC 、BD ， 证：△APC ∽△DPB 切 、割线定理 ⊙O 中，PT 切⊙O 于点T ，割线PB 交⊙O 于点A 。

PT 2＝PA·PB连结TA 、TB ， 证：△PTB ∽△PAT }割线定理PB 、PD 为⊙O 的两条割线，交⊙O 于A 、C 两点。

PA·PB ＝PC·PD ~ 过P 作PT 切⊙O 于T ，用两次切割线定理 C E3、弦切角定理：顶点在圆上，一边和圆相交，另一边和圆相切的角称为弦切角。

弦切角等于弦与切线所夹弧所对的圆周角。

}弦切角定理的证明：已知：AP切⊙O于P，PQ是弦，则∠APQ是弦切角，∠APQ夹的弧是弧PQ，弧PQ所对的圆周角记为∠PCQ证明：∠APQ=∠PCQ （弦切角的位置分以下三种情况）】1°圆心O在∠APQ外部过P作直径BP，联结BC则BP⊥AP，∠APB=90°，且∠BCP是直径BP所对的圆周角，∠BCP=90°#则有∠APB=∠BCP，即∠APQ+∠BPQ=∠BCQ+∠PCQ由于∠BPQ，∠BCQ都是弧BQ所对的圆周角，所以∠BPQ=∠BCQ所以∠APQ=∠PCQ2°圆心O在∠APQ的一边，PQ上此时PQ是直径，则PQ⊥AP，∠APQ=90°而且∠PCQ是直径PQ所对的圆周角，∠PCQ=90°所以∠APQ=∠PCQ3°圆心O在∠APQ内部过P作直径BP，联结BC则BP⊥AP，∠APB=90°，且∠BCP是直径BP所对的圆周角，∠BCP=90°则有∠APB=∠BCP由于∠BPQ，∠BCQ都是弧BQ所对的圆周角，所以∠BPQ=∠BCQ所以∠APB+∠BPQ=∠BCP+∠BCQ即∠APQ=∠PCQ。

圆的基本性质【命题趋势】圆的基本性质是中考考查的重点.常以选择题.填空题和解答题考查为主；其中选择题和填空题的难度不会太大.对应用、创新、开放探究型题目.会根据当前的政治形势、新闻背景和实际生活去命题.进一步体现数学来源于生活.又应用于生活。

【中考考查重点】一、运用垂径定理及其推论进行计算二、运用圆周角定理及其推论进行计算三、垂径定理雪与圆周角定理结合考点：圆的有关概念圆的定义：在一个平面内.线段OA绕它固定的一个端点O旋转一周.另一个端点A所形成的图形叫圆。

这个固定的端点O叫做圆心.线段OA叫做半径。

圆的表示方法：以O点为圆心的圆记作⊙O.读作圆O。

圆的特点：在一个平面内.所有到一个定点的距离等于定长的点组成的图形。

确定圆的条件：1）圆心；2）半径。

备注：圆心确定圆的位置.半径长度确定圆的大小。

【补充】1）圆心相同且半径相等的圆叫做同圆；2）圆心相同.半径不相等的两个圆叫做同心圆；3）半径相等的圆叫做等圆。

圆的对称性：1）圆是轴对称图形.经过圆心的每一条直线都是它的对称轴；2）圆是以圆心为对称中心的中心对称图形。

弦的概念：连结圆上任意两点的线段叫做弦(例如：右图中的AB)。

直径的概念：经过圆心的弦叫做直径（例如：右图中的CD）。

备注：1）直径是同一圆中最长的弦。

2）直径长度等于半径长度的2倍。

⏜.读弧的概念：圆上任意两点间的部分叫做圆弧.简称弧。

以A、B为端点的弧记作AB作圆弧AB或弧AB。

等弧的概念：在同圆或等圆中.能够互相重合的弧叫做等弧。

半圆的概念：圆的任意一条直径的两个端点把圆分成两条弧.每一条弧都叫做半圆。

优弧的概念：在一个圆中大于半圆的弧叫做优弧。

劣弧的概念：小于半圆的弧叫做劣弧。

弦心距概念：从圆心到弦的距离叫做弦心距。

1．（2021秋•顺义区期末）如图.在⊙O中.如果＝2.则下列关于弦AB与弦AC之间关系正确的是（）A．AB＝AC B．AB＝2AC C．AB＞2AC D．AB＜2AC【答案】D【解答】解：如图.取弧AB的中点D.连接AD.BD.则＝2＝2.∵＝2.∴＝＝.∴AD＝BD＝AC．在△ABD中.AD+BD＞AB.∴AC+AC＞AB.即AB＜2AC．故选：D．2．（2021秋•平原县期末）下列语句.错误的是（）A．直径是弦B．相等的圆心角所对的弧相等C．弦的垂直平分线一定经过圆心D．平分弧的半径垂直于弧所对的弦【答案】B【解答】解：直径是弦.A正确.不符合题意；在同圆或等圆中.相等的圆心角所对的弧相等.B错误.符合题意；弦的垂直平分线一定经过圆心.C正确.不符合题意；平分弧的半径垂直于弧所对的弦.D正确.不符合题意；故选：B．3．（2021秋•玉林期末）如图.从A地到B地有两条路可走.一条路是大半圆.另一条路是4个小半圆．有一天.一只猫和一只老鼠同时从A地到B地．老鼠见猫沿着大半圆行走.它不敢与猫同行（怕被猫吃掉）.就沿着4个小半圆行走．假设猫和老鼠行走的速度相同.那么下列结论正确的是（）A．猫先到达B地B．老鼠先到达B地C．猫和老鼠同时到达B地D．无法确定【答案】C【解答】解：以AB为直径的半圆的长是：π•AB；设四个小半圆的直径分别是a.b.c.d.则a+b+c+d＝AB．则老鼠行走的路径长是：a+πb+πc+πd＝π（a+b+c+d）＝π•AB．故猫和老鼠行走的路径长相同．故选：C．考点：垂径定理垂径定理：垂直于弦的直径平分这条弦.并且平分弦所对的两条弧。

2020-2021中考数学压轴题专题复习—圆的综合的综合附答案解析一、圆的综合1．如图，AB 是半圆的直径，过圆心O 作AB 的垂线，与弦AC 的延长线交于点D ，点E 在OD 上DCE B ∠=∠． （1）求证：CE 是半圆的切线； （2）若CD=10，2tan 3B =，求半圆的半径．【答案】（1）见解析；(2)413 【解析】分析: （1）连接CO ，由DCE B ∠=∠且OC=OB,得DCE OCB ∠=∠,利用同角的余角相等判断出∠BCO+∠BCE=90°，即可得出结论；（2）设AC=2x ，由根据题目条件用x 分别表示出OA 、AD 、AB ，通过证明△AOD ∽△ACB ，列出等式即可.详解：（1）证明：如图，连接CO .∵AB 是半圆的直径， ∴∠ACB =90°.∴∠DCB =180°-∠ACB =90°. ∴∠DCE+∠BCE=90°. ∵OC =OB , ∴∠OCB =∠B. ∵=DCE B ∠∠， ∴∠OCB =∠DCE . ∴∠OCE =∠DCB =90°. ∴OC ⊥CE . ∵OC 是半径， ∴CE 是半圆的切线. （2）解：设AC =2x ，∵在Rt △ACB 中，2tan 3AC B BC ==, ∴BC =3x .∴()()222313AB x x x =+=.∵OD ⊥AB , ∴∠AOD =∠A CB=90°. ∵∠A =∠A ， ∴△AOD ∽△ACB . ∴AC AOAB AD=. ∵1132OA AB x ==，AD =2x +10, ∴113221013xx x =+. 解得 x =8. ∴138413OA =⨯=. 则半圆的半径为413.点睛：本题考查了切线的判定与性质，圆周角定理，相似三角形.2．如图1O e ，的直径12AB P =，是弦BC 上一动点(与点B C ，不重合)30ABC o ，∠=，过点P 作PD OP ⊥交O e 于点D ．()1如图2，当//PD AB 时，求PD 的长；()2如图3，当»»DC AC=时，延长AB 至点E ，使12BE AB =，连接DE ． ①求证：DE 是O e 的切线；②求PC 的长．【答案】（1）262）333①见解析，②． 【解析】分析：()1根据题意首先得出半径长，再利用锐角三角函数关系得出OP PD ，的长；()2①首先得出OBD V 是等边三角形，进而得出ODE OFB 90∠∠==o ，求出答案即可；②首先求出CF 的长，进而利用直角三角形的性质得出PF 的长，进而得出答案．详解：()1如图2，连接OD ，//OP PD PD AB ⊥Q ，，90POB ∴∠=o ，O Q e 的直径12AB =，6OB OD ∴==，在Rt POB V 中，30ABC o ∠=，3tan30623OP OB ∴=⋅=⨯=o ， 在Rt POD V 中，22226(23)26PD OD OP =-=-=；()2①证明：如图3，连接OD ，交CB 于点F ，连接BD ，»»DC AC =Q ，30DBC ABC ∴∠=∠=o ， 60ABD o ∴∠=，OB OD =Q ， OBD ∴V 是等边三角形， OD FB ∴⊥，12BE AB =Q ，OB BE ∴=， //BF ED ∴，90ODE OFB o ∴∠=∠=，DE ∴是O e 的切线； ②由①知，OD BC ⊥，3cos30633CF FB OB ∴==⋅=⨯=o ， 在Rt POD V 中，OF DF =，13(2PF DO ∴==直角三角形斜边上的中线，等于斜边的一半)， 333CP CF PF ∴=-=-．点睛：此题主要考查了圆的综合以及直角三角形的性质和锐角三角函数关系，正确得出OBD V 是等边三角形是解题关键．3．矩形ABCD 中，点C （3，8），E 、F 为AB 、CD 边上的中点，如图1，点A 在原点处，点B 在y 轴正半轴上，点C 在第一象限，若点A 从原点出发，沿x 轴向右以每秒1个单位长度的速度运动，点B 随之沿y 轴下滑，并带动矩形ABCD 在平面内滑动，如图2，设运动时间表示为t 秒，当点B 到达原点时停止运动． （1）当t =0时，点F 的坐标为 ； （2）当t =4时，求OE 的长及点B 下滑的距离； （3）求运动过程中，点F 到点O 的最大距离；（4）当以点F 为圆心，FA 为半径的圆与坐标轴相切时，求t 的值．【答案】（1）F （3，4）；（2）8-33）7；（4）t 的值为245或325. 【解析】试题分析：（1）先确定出DF ，进而得出点F 的坐标； （2）利用直角三角形的性质得出∠ABO =30°，即可得出结论；（3）当O 、E 、F 三点共线时，点F 到点O 的距离最大，即可得出结论； （4）分两种情况，利用相似三角形的性质建立方程求解即可．试题解析：解：（1）当t =0时．∵AB =CD =8，F 为CD 中点，∴DF =4，∴F （3，4）； （2）当t =4时，OA =4．在Rt △ABO 中，AB =8，∠AOB =90°，∴∠ABO =30°，点E 是AB 的中点，OE =12AB =4，BO =43，∴点B 下滑的距离为843-．（3）当O 、E 、F 三点共线时，点F 到点O 的距离最大，∴FO=OE+EF=7．（4）在Rt △ADF 中，FD 2+AD 2=AF 2，∴AF =22FD AD +=5，①设AO =t 1时，⊙F 与x 轴相切，点A 为切点，∴FA ⊥OA ，∴∠OAB +∠FAB =90°．∵∠FAD +∠FAB =90°，∴∠BAO =∠FAD ．∵∠BOA =∠D =90°，∴Rt △FAE ∽Rt △ABO ，∴AB AO FA FE =，∴1853t=，∴t 1=245，②设AO =t 2时，⊙F 与y 轴相切，B 为切点，同理可得，t 2=325． 综上所述：当以点F 为圆心，FA 为半径的圆与坐标轴相切时，t 的值为245或325． 点睛：本题是圆的综合题，主要考查了矩形的性质，直角三角形的性质，中点的意义，勾股定理，相似三角形的判定和性质，切线的性质，解（2）的关键是得出∠ABO =30°，解（3）的关键是判断出当O 、E 、F 三点共线时，点F 到点O 的距离最大，解（4）的关键是判断出Rt △FAE ∽Rt △ABD ，是一道中等难度的中考常考题．4．如图．在△ABC 中，∠C =90°，AC =BC ，AB =30cm ，点P 在AB 上，AP =10cm ，点E 从点P 出发沿线段PA 以2c m/s 的速度向点A 运动，同时点F 从点P 出发沿线段PB 以1c m/s 的速度向点B 运动，点E 到达点A 后立刻以原速度沿线段AB 向点B 运动，在点E 、F 运动过程中，以EF 为边作正方形EFGH ，使它与△ABC 在线段AB 的同侧，设点E 、F 运动的时间为t （s ）（0＜t ＜20）．（1）当点H落在AC边上时，求t的值；（2）设正方形EFGH与△ABC重叠部分的面积为S．①试求S关于t的函数表达式；②以点C为圆心，12t为半径作⊙C，当⊙C与GH所在的直线相切时，求此时S的值．【答案】（1）t=2s或10s；（2）①S=22 2 9?(02)75050(210)240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩；②100cm2．【解析】试题分析：（1）如图1中，当0＜t≤5时，由题意AE=EH=EF，即10﹣2t=3t，t=2；如图2中，当5＜t＜20时，AE=HE，2t﹣10=10﹣（2t﹣10）+t，t=10；（2）分四种切线讨论a、如图3中，当0＜t≤2时，重叠部分是正方形EFGH，S=（3t）2=9t2．b、如图4中，当2＜t≤5时，重叠部分是五边形EFGMN．c、如图5中，当5＜t＜10时，重叠部分是五边形EFGMN．d、如图6中，当10＜t＜20时，重叠部分是正方形EFGH．分别计算即可；②分两种情形分别列出方程即可解决问题．试题解析：解：（1）如图1中，当0＜t≤5时，由题意得：AE=EH=EF，即10﹣2t=3t，t=2如图2中，当5＜t＜20时，AE=HE，2t﹣10=10﹣（2t﹣10）+t，t=10．综上所述：t=2s或10s时，点H落在AC边上．（2）①如图3中，当0＜t≤2时，重叠部分是正方形EFGH，S=（3t）2=9t2如图4中，当2＜t≤5时，重叠部分是五边形EFGMN，S=（3t）2﹣12（5t﹣10）2=﹣72t2+50t﹣50．如图5中，当5＜t＜10时，重叠部分是五边形EFGMN，S=（20﹣t）2﹣12（30﹣3t）2=﹣72t2+50t﹣50．如图6中，当10＜t＜20时，重叠部分是正方形EFGH，S=（20﹣t）2=t2﹣40t+400．综上所述：S=2229?(02)75050(210)240400?(1020)t tt t tt t t⎧<≤⎪⎪-+-<≤⎨⎪-+<<⎪⎩．②如图7中，当0＜t≤5时，12t+3t=15，解得：t=307，此时S=100cm2，当5＜t＜20时，12t+20﹣t=15，解得：t=10，此时S=100．综上所述：当⊙C与GH所在的直线相切时，求此时S的值为100cm2点睛：本题考查了圆综合题、正方形的性质、等腰直角三角形的性质、切线的性质等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，注意不能漏解，属于中考压轴题．5．如图，AB是圆O的直径，射线AM⊥AB，点D在AM上，连接OD交圆O于点E，过点D作DC=DA交圆O于点C（A、C不重合），连接O C、BC、CE．（1）求证：CD是⊙O的切线；（2）若圆O的直径等于2，填空：①当AD=时，四边形OADC是正方形；②当AD=时，四边形OECB是菱形．【答案】(1)见解析；（2）①1；②3．【解析】试题分析：（1）依据SSS证明△OAD≌△OCD，从而得到∠OCD=∠OAD=90°；（2）①依据正方形的四条边都相等可知AD=OA；②依据菱形的性质得到OE=CE，则△EOC为等边三角形，则∠CEO=60°，依据平行线的性质可知∠DOA=60°，利用特殊锐角三角函数可求得AD的长．试题解析：解：∵AM⊥AB，∴∠OAD=90°．∵OA=OC，OD=OD，AD=DC，∴△OAD≌△OCD，∴∠OCD=∠OAD=90°．∴OC⊥CD，∴CD是⊙O的切线．（2）①∵当四边形OADC是正方形，∴AO=AD=1．故答案为：1．②∵四边形OECB是菱形，∴OE=CE．又∵OC=OE，∴OC=OE=CE．∴∠CEO=60°．∵CE∥AB，∴∠AOD=60°．在Rt△OAD中，∠AOD=60°，AO=1，∴AD=．故答案为：．点睛：本题主要考查的是切线的性质和判定、全等三角形的性质和判定、菱形的性质、等边三角形的性质和判定，特殊锐角三角函数值的应用，熟练掌握相关知识是解题的关键．6．解决问题：()1如图①，半径为4的Oe上，则PA的最大值和e外有一点P，且7PO=，点A在O最小值分别是______和______．()2如图②，扇形AOB的半径为4，45∠=o，P为弧AB上一点，分别在OA边找AOBV周长的最小，请在图②中确定点E、F的位置并直点E，在OB边上找一点F，使得PEFV周长的最小值；接写出PEF拓展应用()3如图③，正方形ABCD 的边长为42；E 是CD 上一点(不与D 、C 重合)，CF BE ⊥于F ，P 在BE 上，且PF CF =，M 、N 分别是AB 、AC 上动点，求PMN V 周长的最小值．【答案】（1）11，3；（2）图见解析，PEF V 周长最小值为423）41042． 【解析】 【分析】()1根据圆外一点P 到这个圆上所有点的距离中，最远是和最近的点是过圆心和该点的直线与圆的交点，容易求出最大值与最小值分别为11和3；()2作点P 关于直线OA 的对称点1P ，作点P 关于直线OB 的对称点2P ，连接1P 、2P ，与OA 、OB 分别交于点E 、F ，点E 、F 即为所求，此时PEF V 周长最小，然后根据等腰直角三角形求解即可；()3类似()2题作对称点，PMN V 周长最小12PP =，然后由三角形相似和勾股定理求解．【详解】解：()1如图①，Q 圆外一点P 到这个圆上所有点的距离中，最大距离是和最小距离都在过圆心的直线OP 上，此直线与圆有两个交点，圆外一点与这两个交点的距离个分别最大距离和最小距离．PA ∴的最大值227411PA PO OA ==+=+=，PA 的最小值11743PA PO OA ==-=-=， 故答案为11和3；()2如图②，以O 为圆心，OA 为半径，画弧AB 和弧BD ，作点P 关于直线OA 的对称点1P ，作点P 关于直线OB 的对称点2P ，连接1P 、2P ，与OA 、OB 分别交于点E 、F ，点E 、F 即为所求．连接1OP 、2OP 、OP 、PE 、PF ，由对称知识可知，1AOP AOP ∠∠=，2BOP BOP ∠∠=，1PE PE =，2PF P F = ∴1245AOP BOP AOP BOP AOB ∠∠∠∠∠+=+==o ， 12454590POP o o o ∠=+=， 12POP ∴V 为等腰直角三角形，121PP ∴==PEF V 周长1212PE PF EF PE P F EF PP =++=++=，此时PEF V 周长最小．故答案为；()3作点P 关于直线AB 的对称1P ，连接1AP 、1BP ，作点P 关于直线AC 的对称2P ，连接1P 、2P ，与AB 、AC 分别交于点M 、N ．如图③ 由对称知识可知，1PM PM =，2PN P N =，PMN V 周长1212PM PN MN PM P N MN PP =++=++=，此时，PMN V 周长最小12PP =．由对称性可知，1BAP BAP ∠∠=，2EAP EAP ∠∠=，12APAP AP ==， ∴1245BAP EAP BAP EAP BAC o∠∠∠∠∠+=+== 12454590P AP ∠=+=o o o ，12P AP V ∴为等腰直角三角形，PMN ∴V 周长最小值12PP =，当AP 最短时，周长最小． 连接DF ．CF BE Q ⊥，且PF CF =，45PCF ∠∴=o ，PCCF=45ACD ∠=o Q ，PCF ACD ∠∠∴=，PCA FCD ∠∠=，又ACCD=， ∴在APC V 与DFC V 中，AC PCCD CF=，PCA FCD ∠∠=C AP ∴V ∽DFC V ，AP AC DF CD∴== ∴AP =90BFC ∠=o Q ，取AB 中点O ．∴点F 在以BC 为直径的圆上运动，当D 、F 、O 三点在同一直线上时，DF 最短．DF DO FO OC =-===AP ∴最小值为AP = ∴此时，PMN V 周长最小值12PP ====．【点睛】本题考查圆以及正方形的性质，运用圆的对称性和正方形的对称性是解答本题的关键．7．已知，ABC ∆内接于O e ，点P 是弧AB 的中点，连接PA 、PB ； （1）如图1，若AC BC =，求证：AB PC ⊥； （2）如图2，若PA 平分CPM ∠，求证：AB AC =； （3）在（2）的条件下，若24sin 25BPC ∠=，8AC =，求AP 的值．【答案】(1)见解析;(2)见解析5 【解析】 【分析】(1)由点P 是弧AB 的中点，可得出AP=BP , 通过证明APC BPC ∆≅∆ ,ACE BCE ∆≅∆可得出AEC BEC ∠=∠进而证明AB ⊥ PC.(2)由PA 是∠CPM 的角平分线，得到∠MPA=∠APC, 等量代换得到∠ABC=∠ACB, 根据等腰三角形的判定定理即可证得AB=AC.(3)过A 点作AD ⊥BC,有三线合一可知AD 平分BC,点O 在AD 上，连结OB ，则∠BOD ＝∠BAC ，根据圆周角定理可知∠BOD=∠BAC, ∠BPC=∠BAC ，由∠BOD=∠BPC 可得sin sin BDBOD BPC OB∠=∠=,设OB=25x ，根据勾股定理可算出OB 、BD 、OD 、AD 的长，再次利用勾股定理即可求得AP 的值. 【详解】解：（1）∵点P 是弧AB 的中点，如图1， ∴AP ＝BP ， 在△APC 和△BPC 中AP BP AC BC PC PC =⎧⎪=⎨⎪=⎩， ∴△APC ≌△BPC （SSS ）， ∴∠ACP ＝∠BCP ， 在△ACE 和△BCE 中AC BC ACP BCP CE CE =⎧⎪∠=∠⎨⎪=⎩， ∴△ACE ≌△BCE （SAS ）， ∴∠AEC ＝∠BEC ， ∵∠AEC +∠BEC ＝180°， ∴∠AEC ＝90°， ∴AB ⊥PC ；（2）∵PA 平分∠CPM ， ∴∠MPA ＝∠APC ，∵∠APC +∠BPC +∠ACB ＝180°，∠MPA +∠APC +∠BPC ＝180°， ∴∠ACB ＝∠MPA ＝∠APC ， ∵∠APC ＝∠ABC ， ∴∠ABC ＝∠ACB ， ∴AB ＝AC ；（3）过A 点作AD ⊥BC 交BC 于D ，连结OP 交AB 于E ，如图2，由（2）得出AB ＝AC ， ∴AD 平分BC ， ∴点O 在AD 上，连结OB ，则∠BOD ＝∠BAC ，∵∠BPC ＝∠BAC ， ∴sin sin BOD BPC ∠=∠=2425BDOB=， 设OB ＝25x ，则BD ＝24x ， ∴OD ＝22OB BD -＝7x ，在Rt ABD V 中，AD ＝25x +7x ＝32x ，BD ＝24x ， ∴AB ＝22AD BD +＝40x ，∵AC ＝8， ∴AB ＝40x ＝8， 解得：x ＝0.2，∴OB ＝5，BD ＝4.8，OD ＝1.4，AD ＝6.4， ∵点P 是¶AB 的中点， ∴OP 垂直平分AB ， ∴AE ＝12AB ＝4，∠AEP ＝∠AEO ＝90°， 在Rt AEO ∆中，OE ＝223AO AE -=，∴PE ＝OP ﹣OE ＝5﹣3＝2，在Rt APE ∆中，AP ＝22222425PE AE +=+=． 【点睛】本题是一道有关圆的综合题，考查了圆周角定理、勾股定理、等腰三角形的判定定理和三线合一，是初中数学的重点和难点，一般以压轴题形出现，难度较大.8．已知P 是O e 的直径BA 延长线上的一个动点，∠P 的另一边交O e 于点C 、D ，两点位于AB 的上方，AB ＝6，OP=m ，1sin 3P ＝，如图所示．另一个半径为6的1O e 经过点C 、D ，圆心距1OO n ＝． （1）当m=6时，求线段CD 的长；（2）设圆心O 1在直线AB 上方，试用n 的代数式表示m ；（3）△POO 1在点P 的运动过程中，是否能成为以OO 1为腰的等腰三角形，如果能，试求出此时n 的值；如果不能，请说明理由．【答案】(1)CD=25;(2)m=23812n n- ;(3) n 的值为955或9155 【解析】分析：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．解Rt △POH ，得到OH 的长．由勾股定理得CH 的长，再由垂径定理即可得到结论； （2）解Rt △POH ，得到Rt 3mOH OCH V ＝．在和Rt △1O CH 中，由勾股定理即可得到结论；（3）△1POO 成为等腰三角形可分以下几种情况讨论：① 当圆心1O 、O 在弦CD 异侧时，分1OP OO ＝和11O P OO ＝．②当圆心1O 、O 在弦CD 同侧时，同理可得结论． 详解：（1）过点O 作OH ⊥CD ，垂足为点H ，连接OC ．在Rt △1sin 63POH P PO =Q 中，＝，，∴2OH =． ∵AB ＝6，∴3OC ＝． 由勾股定理得： 5CH = ∵OH ⊥DC ，∴225CD CH ==．（2）在Rt △1sin 3POH P PO m Q 中，＝，＝，∴3m OH ＝． 在Rt △OCH 中，2293m CH ⎛⎫- ⎪⎝⎭＝． 在Rt △1O CH 中，22363m CH n ⎛⎫-- ⎪⎝⎭＝． 可得： 2236933m m n ⎛⎫⎛⎫--- ⎪ ⎪⎝⎭⎝⎭＝，解得23812n m n -：＝．（3）△1POO 成为等腰三角形可分以下几种情况： ① 当圆心1O 、O 在弦CD 异侧时i ）1OP OO ＝，即m n ＝，由23812n n n-＝，解得9n ：＝．即圆心距等于O e 、1O e 的半径的和，就有O e 、1O e 外切不合题意舍去．ii ）11O P OO ＝，由22233m m n m -+-（）（） n ＝， 解得：23m n ＝，即23n 23812n n-＝，解得9155n ：＝． ②当圆心1O 、O 在弦CD 同侧时，同理可得： 28132n m n-＝．∵1POO ∠是钝角，∴只能是m n =，即28132nn n-＝，解得955n ：＝． 综上所述：n 的值为955或9155． 点睛：本题是圆的综合题．考查了圆的有关性质和两圆的位置关系以及解直径三角形．解答（3）的关键是要分类讨论．9．定义：数学活动课上，李老师给出如下定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”.理解： ⑴如图，已知是⊙上两点，请在圆上找出满足条件的点，使为“智慧三角形”（画出点的位置，保留作图痕迹）；⑵如图，在正方形中，是的中点，是上一点，且，试判断是否为“智慧三角形”，并说明理由；运用：⑶如图，在平面直角坐标系中，⊙的半径为，点是直线上的一点，若在⊙上存在一点，使得为“智慧三角形”，当其面积取得最小值时，直接写出此时点的坐标.【答案】（1）详见解析；（2）详见解析；（3）P 的坐标（223-，13），（223，13）．【解析】试题分析：（1）连结AO并且延长交圆于C1，连结BO并且延长交圆于C2，即可求解；（2）设正方形的边长为4a，表示出DF=CF以及EC、BE的长，然后根据勾股定理列式表示出AF2、EF2、AE2，再根据勾股定理逆定理判定△AEF是直角三角形，由直角三角形的性质可得△AEF为“智慧三角形”；（3）根据“智慧三角形”的定义可得△OPQ为直角三角形，根据题意可得一条直角边为1，当斜边最短时，另一条直角边最短，则面积取得最小值，由垂线段最短可得斜边最短为3，根据勾股定理可求另一条直角边，再根据三角形面积可求斜边的高，即点P的横坐标，再根据勾股定理可求点P的纵坐标，从而求解．试题解析：（1）如图1所示：（2）△AEF是否为“智慧三角形”，理由如下：设正方形的边长为4a，∵E是DC的中点，∴DE=CE=2a，∵BC：FC=4：1，∴FC=a，BF=4a﹣a=3a，在Rt△ADE中，AE2=（4a）2+（2a）2=20a2，在Rt△ECF中，EF2=（2a）2+a2=5a2，在Rt△ABF中，AF2=（4a）2+（3a）2=25a2，∴AE2+EF2=AF2，∴△AEF是直角三角形，∵斜边AF上的中线等于AF的一半，∴△AEF为“智慧三角形”；（3）如图3所示：由“智慧三角形”的定义可得△OPQ为直角三角形，根据题意可得一条直角边为1，当斜边最短时，另一条直角边最短，则面积取得最小值，由垂线段最短可得斜边最短为3，由勾股定理可得PQ=，PM=1×2÷3=，由勾股定理可求得OM=，故点P的坐标（﹣，），（，）．考点：圆的综合题．10．如图，四边形为菱形，且，以为直径作，与交于点．请仅用无刻度的直尺按下列要求画图．(保留作图痕迹)(1)在如图中，过点作边上的高．(2)在如图中，过点作的切线，与交于点．【答案】(1)如图1所示．(答案不唯一),见解析；(2)如图2所示．(答案不唯一)，见解析.【解析】【分析】（1）连接AC交圆于一点F，连接PF交AB于点E,连接CE即为所求．（2）连接OF交BC于Q，连接PQ即为所求．【详解】(1)如图1所示．(答案不唯一)(2)如图2所示．(答案不唯一)【点睛】本题考查作图-复杂作图，菱形和圆的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．11．如图，△ABC中，AC＝BC＝10，cosC＝35，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长.【答案】（1）409R=;（2）25880320xy x xx=-++（3）505-【解析】【分析】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，即可求解；（2）首先证明PD∥BE，则EB BFPD PF=，即：2024588x yxxxy-+--=，即可求解；（3）证明四边形PDBE为平行四边形，则AG＝EP＝BD，即：AB＝DB+AD＝AG+AD＝45，即可求解．【详解】（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cosC＝35，则sinC＝45，sinC＝HPCP＝10RR-＝45，解得：R＝409；（2）在△ABC中，AC＝BC＝10，cosC＝35，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH＝ACsinC＝8，同理可得：CH＝6，HA＝4，AB＝5tan∠CAB＝2，BP228+(4)x-2880x x-+DA 25x，则BD＝525x，如下图所示，PA ＝PD ，∴∠PAD ＝∠CAB ＝∠CBA ＝β，tanβ＝2，则cosβ＝5，sinβ＝5， EB ＝BDcosβ＝（45﹣25x ）×5＝4﹣25x ， ∴PD ∥BE ， ∴EB BF PD PF =，即：2024588x y x xx y -+--=， 整理得：y ＝25x x 8x 803x 20-++； （3）以EP 为直径作圆Q 如下图所示，两个圆交于点G ，则PG ＝PQ ，即两个圆的半径相等，则两圆另外一个交点为D ， GD 为相交所得的公共弦，∵点Q 是弧GD 的中点，∴DG ⊥EP ，∵AG 是圆P 的直径，∴∠GDA ＝90°，∴EP ∥BD ，由（2）知，PD ∥BC ，∴四边形PDBE 为平行四边形，∴AG ＝EP ＝BD ，∴AB ＝DB+AD ＝AG+AD ＝5设圆的半径为r ，在△ADG 中，AD ＝2rcosβ＝5，DG ＝5，AG ＝2r ， 5+2r ＝45，解得：2r ＝51+， 则：DG ＝5＝50﹣105， 相交所得的公共弦的长为50﹣105．【点睛】本题考查的是圆知识的综合运用，涉及到解直角三角形、勾股定理等知识，其中（3），要关键是根据题意正确画图，此题用大量的解直角三角形的内容，综合难度很大．12．如图，四边形ABCD 是⊙O 的内接四边形，AC 为直径，»»BD AD =，DE ⊥BC ，垂足为E ．（1）判断直线ED 与⊙O 的位置关系，并说明理由；（2）若CE =1，AC =4，求阴影部分的面积．【答案】（1）ED 与O e 相切.理由见解析；（2）2=33S π-阴影 【解析】【分析】 （1）连结OD ，如图，根据圆周角定理，由»»BD AD =得到∠BAD =∠ACD ，再根据圆内接四边形的性质得∠DCE =∠BAD ，所以∠ACD =∠DCE ；利用内错角相等证明OD ∥BC ，而DE ⊥BC ，则OD ⊥DE ，于是根据切线的判定定理可得DE 为⊙O 的切线；（2）作OH ⊥BC 于H ，易得四边形ODEH 为矩形，所以OD =EH =2，则CH =HE ﹣CE =1，于是有∠HOC =30°，得到∠COD =60°，然后根据扇形面积公式、等边三角形的面积公式和阴影部分的面积=S 扇形OCD ﹣S △OCD 进行计算即可．【详解】（1）直线ED 与⊙O 相切．理由如下：连结OD ，如图，∵»»BD AD =，∴∠BAD =∠ACD ．∵∠DCE =∠BAD ，∴∠ACD =∠DCE ．∵OC =OD ，∴∠OCD =∠ODC ，而∠OCD =∠DCE ，∴∠DCE =∠ODC ，∴OD ∥BC ．∵DE ⊥BC ，∴OD ⊥DE ，∴DE 为⊙O 的切线；（2）作OH ⊥BC 于H ，则四边形ODEH 为矩形，∴OD =EH ．∵CE =1，AC =4，∴OC =OD =2，∴CH =HE ﹣CE =2﹣1=1．在Rt △OHC 中，∵OC =2，CH =1，∠OHC =90°，∠HOC =30°，∴∠COD =60°，∴阴影部分的面积=S 扇形OCD ﹣S △OCD26023360π⋅⋅=-•22 23=π3-．【点睛】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．也考查了扇形面积的计算．13．如图①，已知Rt ABC ∆中，90ACB ∠=o ，8AC =，10AB =，点D 是AC 边上一点（不与C 重合），以AD 为直径作O e ，过C 作CE 切O e 于E ，交AB 于F .（1）若O e 的半径为2，求线段CE 的长；（2）若AF BF =，求O e 的半径；（3）如图②，若CE CB =，点B 关于AC 的对称点为点G ，试求G 、E 两点之间的距离.【答案】(1)42CE =(2)O e 的半径为3；(3)G 、E 两点之间的距离为9.6.【解析】【分析】（1）根据切线的性质得出∠OEC=90°，然后根据勾股定理即可求得；（2）由勾股定理求得BC ，然后通过证得△OEC ∽△BCA ，得到OE BC =OC BA ，即r 8-r =610，解得即可； （3）证得D 和M 重合，E 和F 重合后，通过证得△GBE ∽△ABC ，GB GE AB AC=，即12108GE =，解得即可． 【详解】(1)如图，连结OE .∵CE 切O e 于E ，∴90OEC ∠=︒.∵8AC =，O e 半径为2，∴6OC =，2OE =.∴2242CE OC OE =-=；(2)设O e 半径为r .在Rt ABC ∆中，90ACB ∠=︒，10AB =，8AC =， ∴226BC AB AC -=. ∵AF BF =， ∴AF CF BF ==. ∴ACF CAF ∠=∠. ∵CE 切O e 于E ，∴90OEC ∠=︒.∴OEC ACB ∠=∠，∴OEC BCA ∆~∆.∴OE OC BC BA =， ∴8610r r -=， 解得3r =.∴O e 的半径为3；(3)连结EG 、OE ，设EG 交AC 于点M ，由对称性可知，CB CG =.又CE CB =，∴CE CG =.∴EGC GEC ∠=∠.∵CE 切O e 于E ，∴90GEC OEG ∠+∠=︒.又90EGC GMC ∠+∠=︒，∴OEG GMC ∠=∠.又GMC OME ∠=∠，∴OEG OME ∠=∠.∴OE OM =.∴点M 与点D 重合.∴G 、D 、E 三点在同一条直线上.连结AE 、BE ，∵AD 是直径，∴90AED ∠=︒，即90AEG ∠=︒.又CE CB CG ==，∴90BEG ∠=︒.∴180AEB AEG BEG ∠=∠+∠=︒，∴A 、E 、B 三点在同一条直线上.∴E 、F 两点重合.∵90GEB ACB ∠=∠=︒，B B ∠=∠，∴GBE ABC ∆~∆. ∴GB GE AB AC =，即12108GE =. ∴9.6GE =.故G 、E 两点之间的距离为9.6.【点睛】本题考查了切线的判定，轴的性质，勾股定理的应用以及三角形相似的判定和性质，证得G 、D 、E 三点共线以及A 、E 、B 三点在同一条直线上是解题的关键.14．如图，已知AB 是⊙O 的直径，点C 、D 在⊙O 上，∠D ＝60°且AB ＝6，过O 点作OE ⊥AC ，垂足为E ．（1）求OE 的长；（2）若OE的延长线交⊙O于点F，求弦AF、AC和弧CF围成的图形（阴影部分）的面积．（结果保留π）【答案】（1）OE的长为32；（2）阴影部分的面积为3 2π【解析】（1）OE=32（2）S=32π15．结果如此巧合!下面是小颖对一道题目的解答．题目：如图，Rt△ABC的内切圆与斜边AB相切于点D，AD=3，BD=4，求△ABC的面积．解：设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x．根据切线长定理，得AE=AD=3，BF=BD=4，CF=CE=x．根据勾股定理，得（x+3）2+（x+4）2=（3+4）2．整理，得x2+7x=12．所以S△ABC=12 AC•BC=12（x+3）（x+4）=12（x2+7x+12）=12×（12+12）=12．小颖发现12恰好就是3×4，即△ABC的面积等于AD与BD的积．这仅仅是巧合吗？请你帮她完成下面的探索．已知：△ABC的内切圆与AB相切于点D，AD=m，BD=n．可以一般化吗？（1）若∠C=90°，求证：△ABC的面积等于mn．倒过来思考呢？（2）若AC•BC=2mn，求证∠C=90°．改变一下条件……（3）若∠C=60°，用m、n表示△ABC的面积．【答案】（1）证明见解析；（2）证明见解析；（3）S△ABC=3mn；【解析】【分析】（1）设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，仿照例题利用勾股定理得（x＋m）2＋（x＋n）2＝（m＋n）2，再根据S△ABC＝AC×BC，即可证明S△ABC＝mn.（2）由AC•BC＝2mn，得x2＋（m＋n）x＝mn，因此AC2＋BC2＝（x＋m）2＋（x＋n）2＝AB2，利用勾股定理逆定理可得∠C＝90°.（3）过点A作AG⊥BC于点G，在Rt△ACG中，根据条件求出AG、CG，又根据BG＝BC－CG得到BG .在Rt△ABG中，根据勾股定理可得x2＋（m＋n）x＝3mn，由此S△ABC＝BC•AG＝mn.【详解】设△ABC的内切圆分别与AC、BC相切于点E、F，CE的长为x，根据切线长定理，得：AE＝AD＝m、BF＝BD＝n、CF＝CE＝x，（1）如图1，在Rt△ABC中，根据勾股定理，得：（x＋m）2＋（x＋n）2＝（m＋n）2，整理，得：x2＋（m＋n）x＝mn，所以S△ABC＝AC•BC＝（x＋m）（x＋n）＝[x2＋（m＋n）x＋mn]＝（mn＋mn）＝mn;（2）由AC•BC＝2mn，得：（x＋m）（x＋n）＝2mn，整理，得：x2＋（m＋n）x＝mn，∴AC2＋BC2＝（x＋m）2＋（x＋n）2＝2[x2＋（m＋n）x]＋m2＋n2＝2mn＋m2＋n2＝（m＋n）2＝AB2，根据勾股定理逆定理可得∠C＝90°；（3）如图2，过点A作AG⊥BC于点G，在Rt△ACG中，AG＝AC•sin60°＝（x＋m），CG＝AC•co s60°＝（x＋m），∴BG＝BC﹣CG＝（x＋n）﹣（x＋m），在Rt△ABG中，根据勾股定理可得：[（x＋m）]2＋[（x＋n）﹣（x＋m）]2＝（m＋n）2，整理，得：x2＋（m＋n）x＝3mn，∴S△ABC＝BC•AG＝×（x＋n）•（x＋m）＝3x2＋（m＋n）x＋mn]＝3（3mn＋mn）3．【点睛】本题考查了圆中的计算问题、与圆有关的位置关系以及直角三角形，注意掌握方程思想与数形结合思想的应用.。

2022-2023学年北师大版九年级数学下册《第3章圆》综合解答题优生辅导训练（附答案）1．已知点C是△ABD的边AB上一点，且，AC为⊙O的直径，BD切⊙O于点D，连接DO并延长交⊙O于点E，连接BE交⊙O于点M．（1）求证：∠BAD＝∠ABD；（2）若⊙O的半径为1，求线段EM的长．2．如图，已知∠MON＝90°，OT是∠MON的平分线，A是射线OM上一点，OA＝8cm．动点P从点A出发，以1cm/s的速度沿AO水平向左做匀速运动，与此同时，动点Q从点O出发，也以1cm/s的速度沿ON竖直向上做匀速运动．连接PQ，交OT于点B．经过O、P、Q三点作圆，交OT于点C，连接PC、QC．设运动时间为t（s），其中0＜t＜8．（1）求OP+OQ的值；（2）求四边形QPCQ的面积．3．如图，△ABC内接于⊙O，BC是⊙O的直径，E是上一点，弦BE交AC于点F，弦AD⊥BE于点G，连接CD、CG，且∠CBE＝∠ACG．（1）求证：∠CAG＝∠ABE；（2）求证：CG＝CD；（3）若AB＝4，BC＝2，求GF的长．4．如图，△ABC内接于⊙O，AB为⊙O的直径，AD＝16，CE＝6，连接OC，弦AD分别交OC，BC于点E，F，其中点E是AD的中点．（1）求证：∠CAD＝∠CBA．（2）求AB的长．5．如图，△ABC内接于⊙O，AE⊥BC于点E，BD⊥AC于点D，延长BD交⊙O于点G，连接AG．（1）求证：AF＝AG；（2）连接DE，若DE＝，∠F AG＝105°，求⊙O的半径．6．如图，四边形ABCD是⊙O的内接四边形，AC是⊙O直径，BE∥AD交DC延长线于点E，若BC平分∠ACE．（1）求证：BE是⊙O的切线；（2）若BE＝3，CD＝2，求⊙O的半径．7．如图，在等腰△ABC中，AB＝AC，以AB为直径的⊙O与BC交于点D，DE⊥AC，垂足为E，ED的延长线与AB的延长线交于点F．（1）求证：EF是⊙O的切线；（2）若⊙O的半径为，BD＝3，求CE的长．8．如图所示，已知A，B两点的坐标分别为（2，0），（0，2），点P是△AOB外接圆上一点，且∠AOP＝45°，OP与AB交于C点．（1）求∠BAO的度数；（2）求OC及AC的长；（3）求OP的长及点P的坐标．9．如图，△ABC内接于⊙O，AB＝AC，射线AD切⊙O于点A，过点B作BF∥AC，交⊙O 于点E，交AD于点F．（1）求证：四边形ACBF为平行四边形；（2）连接CE，延长BO交F A的延长线于点G，若BC＝6．CE＝3，求BG的长．10．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E，F，连接OF交AD于点G．（1）求证：BC是⊙O的切线；（2）若∠OF A＝60°，半径为4，在圆O上取点P，使∠PDE＝15°，求点P到直线DE 的距离．11．如图，⊙O是△ABC的外接圆，AE平分△ABC的外角∠DAC，OM⊥AB，ON⊥AC，垂足分别是点M、N，且OM＝ON．（1）求证：AE∥BC；（2）如图，延长ON交AE于E点，若OE＝7，ON＝1，求⊙O的半径长．12．在⊙O中，AB是⊙O的直径，P A，PC分别与⊙O相切于点A，C，连接AC，BC，点D是上一点，连接CD，OD，∠P＝48°．（Ⅰ）如图①，若CD⊥AB，求∠BOD的大小；（Ⅱ）如图②，若∠AOD＝70°，求∠ODC的大小．13．如图，AB是⊙O的直径，CD是⊙O的弦，AB⊥CD，垂足是点H，过点C作直线分别与AB，AD的延长线交于点E，F，且∠ECD＝2∠BAD．（1）求证：CF是⊙O的切线；（2）如果AB＝10，CD＝6，①求AE的长；②求△AEF的面积．14．如图，AB是⊙O的直径，AB＝13，C，D在圆上，且AC＝CD＝12，过点C的切线和DB的延长线交于点E．（1）求证：OC∥DE；（2）求DE的长．15．已知AB是⊙O直径，PC，PB分别切⊙O于点C，B．（Ⅰ）如图①，若∠A＝58°，求∠P的度数；（Ⅱ）如图②，延长OB到点D，使BD＝OB，连接PD，若∠DPC＝81°，求∠D的度数．16．已知P A，PB分别与⊙O相切于点A，B，C为⊙O上一点，连接AC，BC．（Ⅰ）如图①，若∠APB＝70°，求∠ACB的大小；（Ⅱ）如图②，AE为⊙O的直径交BC于点D，若四边形P ACB是平行四边形，求∠EAC 的大小．17．如图，△ABC内接于⊙O，AB为⊙O的直径，∠ACB的平分线交⊙O于D，过点D作DE∥AB交CA的延长线于E．（1）求证：DE是⊙O的切线；（2）当AC＝6，BC＝8时，求DE的长．18．如图，在矩形ABCD中，E为AD的中点，△EBC的外接圆⊙O分别交AB，CD于点M，N．（1）求证：AD与⊙O相切；（2）若DN＝1，AD＝4，求⊙O的半径r．19．如图，AB为⊙O的直径，C，D为⊙O上不同于A，B的两点，CD交AB于点G，∠ABD＝2∠BDG，M为AC上的点，过点M的弦DN⊥AB于点H．过点C的切线交DB 的延长线于点E，交AB的延长线于点F．（1）求证：DE⊥CF．（2）当BF＝5，BD＝3BE时，求MN的长．20．在△ABC中，∠C＝α，设BC＝a，AC＝b，AB＝c．⊙O是△ABC的内切圆，⊙P分别与CA的延长线、CB的延长线以及直线AB均只有一个公共点，⊙O的半径为m，⊙P 的半径为n．（1）当α＝90°时，b＝6，a＝8时，m＝，n＝．（2）如图①，α＝90°，则m＝，n＝.（用含有a、b、c的代数式表示）；并求出△ABC的面积（用含有m、n的代数式表示）（3）如图②，α＝60°，求出△ABC的面积（用含有m、n的代数式表示）．参考答案1．（1）证明：如图，连接CD，∵，AC为⊙O的直径，∴BC＝OC，∵BD切⊙O于点D，∴∠ODB＝90°，∴DC是Rt△OBD斜边上的中线，∴BC＝OC＝CD，∵OC＝OD，∴BC＝OC＝CD＝OD，∴△OCD是等边三角形，∴∠DOC＝∠OCD＝60°，∴∠CBD＝∠OAD＝30°，∴∠BAD＝∠ABD；（2）解：如图，连接DM，∵OD＝1，∴DE＝2，BD＝，∴BE＝＝，∵DE为⊙O的直径，∴∠DME＝90°，∴∠DMB＝90°，∵∠EDB＝90°，∴∠EDB＝∠DME，又∵∠DBM＝∠EBD，∴△BMD∽△BDE，∴＝，∴BM＝＝＝，∴EM＝BE﹣BM＝﹣＝．∴线段EM的长为．2．解：（1）由题意可得，OP＝（8﹣t）cm，OQ＝tcm，∴OP+OQ＝8﹣t+t＝8（cm）．（2）∵∠POQ＝90°，∴PQ是圆的直径，∴∠PCQ＝90°，∵OT是∠MON的平分线，∴∠QOC＝∠POC＝45°，∴∠PQC＝∠POC＝45°，∴△PCQ是等腰直角三角形，∴S△PCQ＝PC•QC＝×PQ•PQ＝PQ2，在Rt△POQ中，PQ2＝OP2+OQ2＝（8﹣t）2+t2，∴四边形OPCQ的面积S＝S△POQ+S△PCQ＝OP•OQ+PQ2＝t（8﹣t）+[（8﹣t）2+t2]＝4t﹣t2+t2﹣4t+16＝16．∴四边形OPCQ的面积为16cm2．3．（1）证明：∵BC是⊙O的直径，∴∠CAB＝90°，∴∠CAG+∠BAG＝90°，∵AD⊥BE，∴∠AGB＝90°，∴∠BAG+∠ABE＝90°，∴∠CAG＝∠ABE；（2）证明：∵∠CGD＝∠CAG+∠ACG，∠ABC＝∠ABE+∠CBE，由（1）知，∠CAG＝∠ABE，∵∠CBE＝∠ACG，∴∠CGD＝∠ABC，∵∠ABC＝∠D，∴∠DGC＝∠D，∴CG＝CD；（3）解：连接AE、CE，∵BC是直径，∴∠BEC＝90°，∴∠AGE＝∠BEC，∴AD∥CE，∵∠CAE＝∠EBC，∠ACG＝∠EBC，∴∠CAE＝∠ACG，∴AE∥CG，∴四边形AGCE是平行四边形，∴AF＝AC，∵AC2＝BC2﹣AB2，∴AC2＝﹣42，∴AC＝6，∴AF＝×6＝3，∵BF2＝AF2+AB2，∴BF2＝32+42，∴BF＝5，∵∠ABG＝∠ABF，∠AGB＝∠BAF，∴△BAG∽△BF A，∴BA：BF＝BG：BA，∴4：5＝BG：4，∴BG＝，∵FG＝BF﹣BG，∴FG＝5﹣＝．4．（1）证明：∵点E是AD的中点，∴AE＝DE，∵OC是半径，∴＝，∴∠CAD＝∠CBA；（2）解：∵AB是直径，∴∠ACB＝90°，∵AE＝DE＝AD＝8，，∴OC⊥AD，∴∠AEC＝90°，∵CE＝6，∴AC＝＝10，∵∠AEC＝∠ACB，∠CAD＝∠CBA，∴△AEC∽△BCA，∴＝，∴＝，∴AB＝．5．（1）证明：∵AE⊥BC于点E，BD⊥AC于点D，∴∠ACB+∠EFD＝180°，∵∠AFD+∠EFD＝180°，∴∠AFD＝∠ACB，∵∠AGD＝∠ACB，∴∠AFD＝∠AGD，∴AF＝AG；（2）解：延长AE交⊙O于M，连接BM，GM，GC，MC，MO，作直径GN，作MH⊥GN于H，∵AF＝AG，AC⊥FG，∴FD＝DG，同理，FE＝EM，∴MG＝2DE＝2（+），∵∠MAG+∠MCG＝180°，∴∠MCG＝180°﹣∠MAG＝180°﹣105°＝75°，∴∠MOG＝2∠MCG＝150°，∴∠MOH＝30°，设MH＝x，∴OM＝OG＝2x，OH＝x，∵MH2+GH2＝GM2，∴x2+（2+）2x2＝22（+）2，∴（8+4）x2＝4（8+4），∴x2＝4，∴x＝2，∴⊙O半径长为2x＝4．6．（1）证明：连接OB，∵OB＝OC，∴∠OBC＝∠OCB，∵∠BCE＝∠OCB，∴∠OBC＝∠BCE，∴OB∥DE，∵AC是⊙O直径，∴AD⊥DE，∵BE∥AD，∴BE⊥DE，∴OB⊥BE，∵OB是⊙O半径，∴BE是⊙O切线；（2）解：延长BO交AD于F，∵∠D＝∠DEB＝∠EBF＝90°，∴四边形BEDF是矩形，∴BF⊥AD，DF＝BE＝3，∴AD＝2DF＝6，∵AC2＝AD2+CD2，∴AC2＝62+22＝40，∴AC＝2，∴⊙O的半径为．7．（1）证明：连接OD，∵AB＝AC，∴∠ABC＝∠ACB，∵OB＝OD，∴∠ABC＝∠ODB，∴∠ACB＝∠ODB，∴OD∥AC，∵DE⊥AC，∴DE⊥OD即EF⊥OD，∵OD是⊙O的半径，∴EF是⊙O的切线；（2）解：连接AD，∵AB是⊙O直径，∴AD⊥BC，∵DE⊥AC，∴∠ADC＝∠DEC，∵∠C＝∠C，∴△CDE∽△CAD，∴CD：CA＝CE：CD，∵AB＝AC，∴DC＝DB＝3，∵AC＝AB＝7，∴3：7＝CE：3，∴CE＝．8．解：（1）∵A（2，0），B（0，2），∴OA＝2，OB＝2，∴∠BAO＝30°；（2）如图，过点C作CD⊥x轴于点D，∵∠AOP＝45°，∴∠OCD＝45°，∴DC＝DO，∴OC＝OD，由（1）知：∠BAO＝30°，∴AC＝2CD＝2OD，AD＝CD＝OD，∵AO＝OD+AD＝（+1）OD＝2，∴OD＝3﹣，∴OC＝（3﹣）＝3﹣，AC＝2（3﹣）＝6﹣2；∴OC及AC的长分别为3﹣，6﹣2；（3）作PH⊥x轴于H，连接P A、PB，如图，∵∠AOB＝90°，∴AB为△AOB外接圆的直径，∴∠BP A＝90°，∵A（2，0），B（0，2），∴OA＝2，OB＝2，∴AB＝＝4，∵∠AOP＝45°，∴∠PBA＝45°，∴△P AB和△POH都为等腰直角三角形，∴P A＝AB＝2，PH＝OH，设OH＝t，则PH＝t，AH＝2﹣t，在Rt△PHA中，∵PH2+AH2＝P A2，∴t2+（2﹣t）2＝（2）2，整理得t2﹣2t+2＝0，解得t1＝+1，t2＝﹣1（舍去），∴OH＝PH＝+1，∴OP＝OH＝+；∴P点坐标为（+1，+1）．9．（1）证明：如图，连接AO并延长交BC于点H，∵AB＝AC，∴弧AB＝弧AC，∵AH经过圆心O，∴AH⊥BC，∵AD切⊙O于点A，∴AO⊥AD，∴AD∥BC，∵BF∥AC，∴四边形ACBF为平行四边形；（2）解：∵BF∥AC，∴∠ABF＝∠BAC，∴弧AE＝弧BC，∴弧AB＝弧EC，∴EC＝AB＝3，∵BH＝BC＝3，∴AH＝9，设半径OA＝OB＝x，则OH＝9﹣x，在Rt△OBH中，根据勾股定理得，32+（9﹣x）2＝x2，∴x＝5，∴OH＝4，∵AG∥BH，∴△AOG∽△HOB，∴＝，∴＝，∴OG＝，∴BG＝OB+OG＝5+＝．10．（1）证明：连接OD，如图，∵AD平分∠BAC交BC于点D，∴∠OAD＝∠CAD．∵OA＝OD，∴∠ODA＝∠OAD，∴∠ODA＝∠CAD，∴OD∥AC，∴∠ODC+∠C＝180°．∵∠C＝90°，∴∠ODC＝90°，∴OD⊥BC，∵OD是⊙O的半径，∴BC是⊙O的切线；（2）解：①当点P在上时，PH的长为点P到直线DE的距离，连接OD，OP，过点O作OM⊥DE于点M，过点P作PN⊥OM于点N，如图，∵OA＝OF，∴∠OAF＝∠OF A＝60°，∵AD平分∠BAC，∴∠BAD＝∠DAC＝30°，∴∠EOD＝60°，∴△ODE是等边三角形，∴DE＝OE＝4．∵OM⊥DE，∴DM＝EM＝2，∠EOM＝∠EOD＝30°，∴OM＝2．∵∠PDE＝15°，∴∠POE＝30°，∴∠POM＝∠POE+∠EOM＝60°．∵PN⊥OM，∴ON＝OP•cos60°＝2，∴MN＝OM﹣ON＝2﹣2．∵PH⊥DE，OM⊥DE，PN⊥OM，∴四边形PHMN为矩形，∴PH＝MN＝2﹣2．∴点P到直线DE的距离为2﹣2；②当点P在上时，连接OP，交DE于点H，如图，∵∠EOP＝2∠PDE，∠PDE＝15°，∴∠EOP＝30°．由①知：∠EOD＝60°，∴∠EOP＝∠EOD，即OP为∠EOD的平分线，∴OH⊥DE，∴PH的长为点P到直线DE的距离，∵OH＝OD•cos30°＝2，∴PH＝OP﹣OH＝4﹣2．综上，若∠PDE＝15°，则点P到直线DE的距离为2﹣2或4﹣2．11．（1）证明：∵AE平分△ABC的外角∠DAC，∴∠DAC＝2∠DAE，∵OM⊥AB，ON⊥AC，且OM＝ON．∴AB＝AC，∴∠B＝∠C，∵∠DAC＝∠B+∠C＝2∠B，∴∠DAE＝∠B，∴AE∥BC；（2）解：延长AO交⊙O于F点，连接CF，由（1）知AE∥BC∴∠EAC＝∠ACB＝∠B，又∵∠B＝∠F，∴∠F＝∠EAC，∴∠EAC+∠CAO＝∠F+∠CAO＝90°＝∠ONA，∵∠AON＝∠EOA，∴△ONA∽△OAE，∴OA：ON＝OE：OA，∴OA2＝OE•ON＝7×1＝7，∴OA＝．12．（Ⅰ）解：如图，连接OC，∵P A，PC分别是OO的切线，∴P A⊥AB，PC⊥OC，∴∠P AB＝∠PCO＝90°，∴∠CAB+P AC＝∠OCA+∠PCA＝90°，∵OA＝OC，∴∠CAB＝∠OCA，∴∠P AC＝∠PCA，∴∠P＝48°，∴∠P AC＝∠PCA＝（180°﹣∠P）＝66°，∴∠CAB＝∠P AB﹣∠P AC＝90°﹣66°＝24°，∴∠OCA＝∠CAB＝24°，∵AB是⊙O的直径，CD⊥AB，∴∠OCD+∠BOC＝∠ODC+∠BOD＝90°，∵OC＝OD，∴∠OCD＝∠ODC，∴∠BOD＝∠BOC，∵∠BOC＝∠CAB+∠OCA＝48°，∴∠BOD＝48°；（Ⅱ）解：AB是⊙O的直径，∴∠ACB＝90°，∴∠CAB+∠CBA＝90°，由（1）知∠CAB+∠P AC＝90°，∠P AC＝66°，∴∠CBA＝∠P AC＝66°，∵∠AOD＝70°，∴∠BOD＝180°﹣∠AOD＝110°，∴∠BCD＝BOD＝55°，∵∠BOD+∠ODC＝∠BCD+∠CBA，∴∠ODC＝∠BCD+∠CBA﹣∠BOD＝55°+66°﹣110°＝11°．13．（1）证明：连接OC，如图，∵AB是⊙O的直径，AB⊥CD，∴，∴∠CAB＝∠DAB．∵∠COB＝2∠CAB，∴∠COB＝2∠BAD．∵∠ECD＝2∠BAD，∴∠ECD＝∠COB．∵AB⊥CD，∴∠COB+∠OCH＝90°，∴∠OCH+∠ECD＝90°，∴∠OCE＝90°．∴OC⊥CF．∵OC是⊙O的半径，∴CF是⊙O的切线；（2）解：①∵AB＝10，∴OA＝OB＝OC＝5，∵AB是⊙O的直径，AB⊥CD，∴CH＝DH＝CD＝3．∴OH＝＝4，∵OC⊥CF，CH⊥OE，∴△OCH∽△OEC，∴，∴，∴OE＝．∴AE＝OA+OE＝5+＝；②过点F作FG⊥AB，交AB的延长线于点G，如图，∵∠OCF＝∠FGE＝90°，∠CEO＝∠GEF，∴△OCE∽△FGE．∴，设FG＝4k，则FE＝5k，∴EG＝＝3k，∵DH⊥AB，FG⊥AB，∴DH∥FG．∴，∴，解得：k＝．∴FG＝4k＝5．∴△AEF的面积＝×AE•FG＝．14．（1）证明：∵∠EBC为圆内接四边形ACBD的外角，∴∠EBC＝∠CAD．∵AC＝DC，∴∠CAD＝∠CDA．∵∠CDA＝∠CBA，∴∠EBC＝∠CBA，∵OC＝OB，∴∠OCB＝∠CBA，∴∠OCB＝∠EBC，∴OC∥DE；（2）解：∵EC为⊙O的切线，∴∠ECO＝90°．∵OC∥DE，∴∠ECO+∠E＝180°，∴∠E＝90°．∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ACB＝∠E＝90°．∵∠EDC＝∠CAB，∴△EDC∽△CAB，∴＝，∵AB＝13，AC＝DC＝12，∴＝，∴DE＝．15．解：（Ⅰ）如图，连接OC，∵PC，PB分别切⊙O于点C，B，AB是直径，∴∠PCO＝∠PBO＝90°，∵OC＝OA，∴∠A＝∠ACO＝58°，∴∠BOC＝∠A+∠ACO＝116°，∴∠P＝360°﹣90°﹣90°﹣116°＝74°；（Ⅱ）如图，连接OP，∵PC，PB分别切⊙O于点C，B，AB是直径，∴∠CPO＝∠BPO，∠PBO＝90°，∵BD＝OB，∴PB是OD的垂直平分线，∴PO＝PD，∴∠OPB＝∠DPB，∴∠OPB＝∠DPB＝∠CPO，∵∠DPC＝81°，∴∠OPB＝∠DPB＝∠CPO＝81°＝27°，∴∠D＝90°﹣27°＝63°．16．解：（Ⅰ）如图①，连接OA、OB，∵P A，PB是⊙O的切线，∴P A⊥OA，PB⊥OB，∴∠OAP＝∠OBP＝90°，∵∠APB＝70°，∴∠AOB＝360°﹣90°﹣90°﹣70°＝110°，∴∠ACB＝∠AOB＝55°，∴∠ACB的大小为55°；（Ⅱ）连接CE，AB，OB，∵AE为⊙O的直径，∴∠ACE＝90°，∵四边形P ACB是平行四边形，∴∠ACB＝∠P，∴∠BCE＝90°﹣∠P，∴∠BAE＝∠BCE＝90°﹣∠P，∵∠AOB＝180°﹣∠P，∵OA＝OB，∴∠OAB＝∠ABO＝（180°﹣∠AOB）＝∠P，∴∠ACE＝∠ACB+∠BCE＝∠P+∠P＝90°，∴∠P＝60°，∴∠ACB＝60°，∠BAE＝∠BCE＝30°，∵AC∥PB，∴＝，∴∠EAC＝30°．17．（1）证明：连接OD，如图，∵AB为⊙O的直径，∴∠ACB＝90°．∵CD是∠ACB的平分线，∴∠BCD＝∠DCE＝∠ACB＝45°，∴∠BOD＝2∠BCD＝90°．∴OD⊥AB．∵DE∥AB，∴OD⊥DE，∵OD为圆的半径，∴DE是⊙O的切线；（2）解：过点A作AF⊥DE于点F，如图，∵AC＝6，BC＝8，∴AB＝＝10，∴OA＝OD＝5．∵OD⊥DE，OD⊥AB，AF⊥DE，∴四边形ODF A为矩形，∵OA＝OD，∴矩形ODF A为正方形．∴DF＝AF＝5．∵DE∥AB，∴∠BAC＝∠E．∵∠ACB＝∠AFE＝90°，∴△ABC∽△EAF．∴．∴，∴EF＝．∴DE＝DF+FE＝．18．（1）证明：连接EO并延长交BC于点F，连接OB、OC，∵四边形ABCD是矩形，∴AB＝CD，AD∥BC，∠A＝∠D＝90°，∵E为AD的中点，∴AE＝DE．∴△ABE≌△DCE（SAS），∴EB＝EC，∵OB＝OC，∴EF垂直平分BC，即∠EFC＝90°，∴∠DEF+∠EFC＝180°，∴∠DEF＝180°﹣∠EFC＝180°﹣90°＝90°，即EF⊥AD．∵点E在⊙O上，OE是⊙O的半径，∴AD与⊙O相切；（2）解：过点O作OH⊥CD，垂足为H，连接OE、ON，∵四边形ABCD是矩形，∴∠D＝90°．∵AD切⊙O于点E，∴∠OED＝90°．∵∠OHD＝90°，∴四边形OEDH是矩形，∴OH＝ED，DH＝OE＝r，∵E是AD的中点，∴OH＝ED＝AD＝2．在Rt△OHN中，由勾股定理得：OF2+NF2＝ON2，即22+（r﹣1）2＝r2．∴解得r＝2.5，故⊙O的半径r为2.5．19．（1）证明：如图，连接OC，∵∠BDG＝∠A，∠COB＝2∠A，∴∠COB＝2∠BDG．∵∠ABD＝2∠BDG，∴∠COB＝∠ABD．∴DE∥OC．∵FC是⊙O的切线，∴OC⊥FC．∴DE⊥CF．（2）解：连接AD，如图，∵AB为⊙O的直径，∴∠ADB＝90°．∵DE⊥CF，∴∠BEF＝90°．∴∠ADB＝∠BEF＝90°．∵∠ABD＝∠EBF，∴△ADB∽△FEB．∴．∵BF＝5，BD＝3BE，∴AB＝3BF＝15．∴OB＝OC＝7.5．∴OF＝OB+BF＝12.5．∵OC⊥CF，∴FC＝＝10，sin F＝．∵∠BAD＝∠F，∴sin∠BAD＝sin F＝．∴sin∠BAD＝．∴BD＝9．∴BE＝BD＝3．∴DE＝DB+BE＝12．∴AD＝＝12．∵DN⊥AB，∴sin∠BAD＝．∴DH＝．∵DN⊥AB，AB为⊙O的直径，∴NH＝DH＝．∵FE＝＝4，∴CE＝FC﹣FE＝6．∵DE⊥FC，∴tan∠CDE＝．∴tan∠CAB＝tan∠CDE＝．∵tan∠CAB＝，∴．∴HM＝AH＝＝＝．∴MN＝NH﹣MH＝＝．20．解：（1）∵α＝90°，b＝6，a＝8，∴c＝10，如图①，设点D，E，F分别是⊙O的切点，连接PD，PE，PF，连接OA，OB，OC，∵S△BCA＝S△ABO+S△ACO+S△BCO，∴×6×8＝×10m+×6m+×8m，∴m＝2，由已知，四边形DPEC为正方形，∴n＝PD＝（CD+CE），由切线长定理可知，AF＝AD，BF＝BE，∴n＝（CD+CE）＝（AD+AC+BE+BC）＝（AB+AC+BC）＝（10+6+8）＝12；故答案为：2，12；（2）如图①，由切线的性质可知：PD⊥CD，PE⊥BC，PF⊥AB，∵PD＝PE＝PF，设△ABC的面积为S△ABC，周长为C△ABC，同（1），根据面积法可知m＝＝＝，∵n＝（CD+CE）＝（AD+AC+BE+BC）＝（AB+AC+BC）＝C△ABC＝，∴S△ABC＝＝mn．故答案为：，；（3）如图②，连接CP，由切线长定理得：CD＝CE＝（CD+CE）＝（AD+AC+BE+BC）＝（AB+AC+BC）＝C△ABC，∵PD⊥CD，PE⊥BC，∴CP平分∠ACB，∴∠PCE＝30°，∴n＝PE＝＝＝，∵m＝，∴S△ABC＝＝mn．。

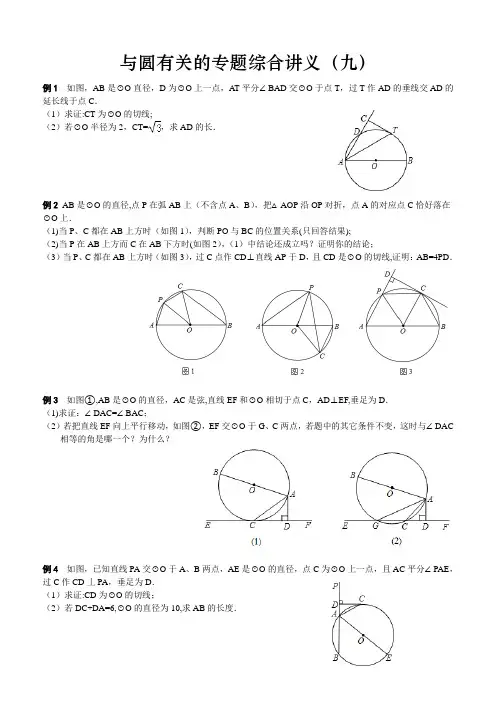
与圆有关的专题综合讲义（九）例1 如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．（1）求证:CT为⊙O的切线;（2）若⊙O半径为2，CT=，求AD的长．例2 AB是⊙O的直径,点P在弧AB上（不含点A、B），把△AOP沿OP对折，点A的对应点C恰好落在⊙O上．（1)当P、C都在AB上方时（如图1），判断PO与BC的位置关系(只回答结果);（2)当P在AB上方而C在AB下方时(如图2），（1）中结论还成立吗？证明你的结论；（3）当P、C都在AB上方时（如图3），过C点作CD⊥直线AP于D，且CD是⊙O的切线,证明：AB=4PD．例3 如图①,AB是⊙O的直径，AC是弦,直线EF和⊙O相切于点C，AD⊥EF,垂足为D．（1)求证：∠DAC=∠BAC；（2）若把直线EF向上平行移动，如图②，EF交⊙O于G、C两点，若题中的其它条件不变，这时与∠DAC 相等的角是哪一个？为什么？例4 如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD丄PA，垂足为D．（1）求证:CD为⊙O的切线；（2）若DC+DA=6,⊙O的直径为10,求AB的长度．例5 在△ABC中，AB=BC，点O是△ABC的外心，连接AO并延长交BC于D，交△ABC的外接圆于E，过点B作⊙O的切线交AO的延长线于Q，设OQ=,BQ=3．（1)求⊙O的半径;（2）若DE=,求四边形ACEB的周长．例6 如图，以△ABC的BC边上一点O为圆心的圆，经过A，B两点，且与BC边交于点E，D为BE的下半圆弧的中点,连接AD交BC于F，若AC=FC．（1）求证：AC是⊙O的切线：(2）若BF=8，DF=,求⊙O的半径r．例7 如图,AB为⊙O的直径，点C在⊙O上，延长BC至点D,使DC=CB，延长DA与⊙O的另一个交点为E，连接AC,CE．（1）求证：∠B=∠D;(2）若AB=4，BC﹣AC=2，求CE的长．例8 如图，△ABC内接与⊙O，AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E，交PC于点F，连接AF．（1）判断AF与⊙O的位置关系并说明理由;(2)若⊙O的半径为4,AF=3,求AC的长．例9 已知直线I与⊙O，AB是⊙O的直径，AD⊥I于点D．（Ⅰ）如图①，当直线I与⊙O相切于点C时，若∠DAC=30°,求∠BAC的大小；(Ⅱ）如图②，当直线I与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．例10 如图,AB是⊙O的直径，AM和BN是⊙O的两条切线，E是⊙O上一点，D是AM上一点，连接DE 并延长交BN于点C，且OD∥BE,OF∥BN．(1)求证:DE与⊙O相切；(2）求证：OF=CD．例11 平面直角坐标系中，⊙O的半径等于5，弦DH⊥x轴于K点，DH=8．（1）如图1,求点H的坐标；（2）如图2，点A为⊙O和x轴负半轴的交点,P为弧AH上任意一点，连接PK，PH，AM⊥PH交HP的延长线于点M,求的值；（3）如图3，⊙O与x轴正半轴交点为S，点E、F是线段OS上的动点(不与点S重合），连接并延长DE，DF交⊙O于点B、C，直线BC交x轴于点G，若△DEF是以EF为底的等腰三角形，当E、F两点在OS上运动时(不与点S重合），∠OGC+∠DOG的值是否发生变化？若不变,请求出其值；若变化，请求出其变化范围．例12 已知⊙O1与⊙O2相交于A、B两点，点O1在⊙O2上,C为⊙O2上一点（不与A，B,O1重合），直线CB与⊙O1交于另一点D．(1）如图(1），若AD是⊙O1的直径，AC是⊙O2的直径，求证：AC=CD；（2）如图（2），若C是⊙O1外一点，求证：O1C丄AD；（3）如图(3）,若C是⊙O1内的一点，判断（2)中的结论是否成立？例13 正方形ABCD的四个顶点都在⊙O上，E是⊙O上的一点．（1)如图①，若点E在上，F是DE上的一点，DF=BE．求证：△ADF≌△ABE;（2）在（1）的条件下，小明还发现线段DE、BE、AE之间满足等量关系：DE﹣BE=AE．请你说明理由；（3）如图②，若点E在上．写出线段DE、BE、AE之间的等量关系．例14 如图，AD是⊙O的切线，切点为A，AB是⊙O的弦．过B作BC∥AD,交⊙O于点C，连接AC，过点C作CD∥AB,交AD于点D．连接AO并延长交BC于点M，交过点C的直线于点P，且∠BCP=∠ACD．（1）判断直线PC与⊙O的位置关系，并说明理由;（2）若AB=9，BC=6．求PC的长．练习题1．如图，⊙O是Rt△ABC的外接圆，AB为直径，∠ABC=30°，CD是⊙O的切线,E为AC延长线上一点，ED⊥AB于F．（1)判断△DCE的形状；（2）设⊙O的半径为1，且OF=,求证：△DCE≌△OCB．2．如图,AB是⊙O的直径，C是⊙O上一点，过圆心O作OD⊥AC，D为垂足，E是BC上一点,G是DE的中点，OG的延长线交BC于F．（1）图中线段OD，BC所在直线有怎样的位置关系?写出你的结论,并给出证明过程；(2）猜想线段BE，EF，FC三者之间有怎样的数量关系？写出你的结论,并给出证明过程．3．已知:OA、OB是⊙O的半径，且OA⊥OB,P是射线OA上一点（点A除外），直线BP交⊙O于点Q,过Q 作⊙O的切线交直线OA于点E．(1）如图①,若点P在线段OA上,求证:∠OBP+∠AQE=45°；（2）若点P在线段OA的延长线上，其它条件不变，∠OBP与∠AQE之间是否存在某种确定的等量关系?请你完成图②，并写出结论（不需要证明）．4．在⊙O中,AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连结CD．（1）如图1，若点D与圆心O重合，AC=2，求⊙O的半径r；（2）如图2，若点D与圆心O不重合，∠BAC=25°,求∠DCA的度数．5．如图,在△ABC中,AB=AC，∠A=30°,以AB为直径的⊙O交BC于点D，交AC于点E,连接DE，过点B 作BP平行于DE，交⊙O于点P，连接EP、CP、OP．（1）BD=DC吗?说明理由；（2)求∠BOP的度数；（3）求证:CP是⊙O的切线;6．如图所示,MN是⊙O的切线，B为切点，BC是⊙O的弦且∠CBN=45°，过C的直线与⊙O,MN分别交于A，D两点，过C作CE⊥BD于点E．（1）求证：CE是⊙O的切线；（2）若∠D=30°，BD=2+2，求⊙O的半径r．1．(2013•安顺）如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T,过T作AD的垂线交AD的延长线于点C．(1）求证:CT为⊙O的切线；（2)若⊙O半径为2，CT=，求AD的长．考点：切线的判定与性质；勾股定理；圆周角定理．专题：压轴题．分析：（1）连接OT，根据角平分线的性质，以及直角三角形的两个锐角互余，证得CT⊥OT，CT为⊙O 的切线；(2）证明四边形OTCE为矩形,求得OE的长，在直角△OAE中,利用勾股定理即可求解．解答：（1）证明：连接OT，∵OA=OT，∴∠OA T=∠OTA，又∵AT平分∠BAD，∴∠DA T=∠OAT，∴∠DA T=∠OTA,∴OT∥AC，（3分）又∵CT⊥AC，∴CT⊥OT，∴CT为⊙O的切线；（5分）（2）解：过O作OE⊥AD于E，则E为AD中点,又∵CT⊥AC，∴OE∥CT，∴四边形OTCE为矩形，（7分）∵CT=，∴OE=，又∵OA=2,∴在Rt△OAE中，，∴AD=2AE=2．（10分）点评：本题主要考查了切线的判定以及性质,证明切线时可以利用切线的判定定理把问题转化为证明垂直的2．（2012•珠海）已知，AB是⊙O的直径，点P在弧AB上（不含点A、B）,把△AOP沿OP对折，点A 的对应点C恰好落在⊙O上．（1)当P、C都在AB上方时（如图1)，判断PO与BC的位置关系(只回答结果）;（2)当P在AB上方而C在AB下方时（如图2），(1）中结论还成立吗？证明你的结论；（3）当P、C都在AB上方时（如图3）,过C点作CD⊥直线AP于D，且CD是⊙O的切线，证明：AB=4PD．考点: 切线的性质；等边三角形的判定与性质；含30度角的直角三角形;圆心角、弧、弦的关系；圆周角定理．专题：几何综合题；压轴题．分析：（1）PO与BC的位置关系是平行；（2）(1）中的结论成立，理由为：由折叠可知三角形APO与三角形CPO全等，根据全等三角形的对应角相等可得出∠APO=∠CPO，再由OA=OP，利用等边对等角得到∠A=∠APO，等量代换可得出∠A=∠CPO，又根据同弧所对的圆周角相等得到∠A=∠PCB，再等量代换可得出∠COP=∠ACB,利用内错角相等两直线平行，可得出PO与BC平行；（3）由CD为圆O的切线,利用切线的性质得到OC垂直于CD，又AD垂直于CD,利用平面内垂直于同一条直线的两直线平行得到OC与AD平行，根据两直线平行内错角相等得到∠APO=∠COP,再利用折叠的性质得到∠AOP=∠COP,等量代换可得出∠APO=∠AOP，再由OA=OP，利用等边对等角可得出一对角相等,等量代换可得出三角形AOP三内角相等,确定出三角形AOP为等边三角形，根据等边三角形的内角为60°得到∠AOP为60°,由OP平行于BC,利用两直线平行同位角相等可得出∠OBC=∠AOP=60°，再由OB=OC，得到三角形OBC为等边三角形,可得出∠COB为60°，利用平角的定义得到∠POC也为60°，再加上OP=OC，可得出三角形POC为等边三角形，得到内角∠OCP为60°,可求出∠PCD为30°，在直角三角形PCD中，利用30°所对的直角边等于斜边的一半可得出PD 为PC的一半，而PC等于圆的半径OP等于直径AB的一半，可得出PD为AB的四分之一，即AB=4PD，得证．解答：解:（1）PO与BC的位置关系是PO∥BC;（2）(1）中的结论PO∥BC成立，理由为：由折叠可知：△APO≌△CPO，∴∠APO=∠CPO，又∵OA=OP，∴∠A=∠APO，∴∠A=∠CPO，又∵∠A与∠PCB都为所对的圆周角，∴∠CPO=∠PCB，∴PO∥BC;(3）∵CD为圆O的切线，∴OC⊥CD，又AD⊥CD,∴OC∥AD，∴∠APO=∠COP，由折叠可得:∠AOP=∠COP，∴∠APO=∠AOP,又OA=OP,∴∠A=∠APO，∴∠A=∠APO=∠AOP,∴△APO为等边三角形，∴∠AOP=60°，又∵OP∥BC，∴∠OBC=∠AOP=60°，又OC=OB，∴△BCO为等边三角形，∴∠COB=60°，∴∠POC=180°﹣（∠AOP+∠COB)=60°,又OP=OC,∴△POC也为等边三角形，∴∠PCO=60°，PC=OP=OC，又∵∠OCD=90°,∴∠PCD=30°，在Rt△PCD中，PD=PC，又∵PC=OP=AB,∴PD=AB，即AB=4PD．点评：此题考查了切线的性质,等边三角形的判定与性质,含30°直角三角形的性质，折叠的性质，圆周角定理，以及平行线的判定与性质，熟练掌握性质及判定是解本题的关键．3．(2011•昭通）如图①，AB是⊙O的直径，AC是弦,直线EF和⊙O相切于点C，AD⊥EF，垂足为D．（1）求证：∠DAC=∠BAC；(2）若把直线EF向上平行移动，如图②，EF交⊙O于G、C两点，若题中的其它条件不变，这时与∠DAC 相等的角是哪一个？为什么？考点：圆周角定理；切线的性质．专题：几何综合题;压轴题．（2）构造直径所对的圆周角，根据等弧所对的圆周角相等以及等角的余角相等，发现∠BAC=∠GAD，再根据等式的性质即可证明∠BAG=∠DAC．解答：（1)证明：连接OC；∵EF切⊙O于点C，∴OC⊥EF,∴∠1+∠4=90°;∵AD⊥EF，∴∠3+∠4=90°；又∵OA=OC，∴∠1=∠2，∴∠2=∠3，即∠DAC=∠BAC．（2）解：∠BAG=∠DAC，理由如下：连接BC;∵AB为⊙O的直径，∴∠BCA=90°，∠B+∠BAC=90°,∵∠AGD+∠GAD=90°，又∵∠B=∠AGD，∴∠BAC=∠GAD;即∠BAG+∠GAC=∠GAC+∠DAC，∴∠BAG=∠DAC．点评：此题运用了切线的性质定理、圆周角定理的推论．注意根据等角的余角相等是证明角相等的一种常用方法．4．（2011•芜湖）如图，已知直线PA交⊙O于A、B两点,AE是⊙O的直径，点C为⊙O上一点,且AC平分∠PAE，过C作CD丄PA,垂足为D．（1）求证：CD为⊙O的切线；（2)若DC+DA=6,⊙O的直径为10，求AB的长度．考点：切线的判定与性质；勾股定理；矩形的判定与性质；垂径定理．专题: 几何综合题；压轴题．分析： (1）连接OC，根据题意可证得∠CAD+∠DCA=90°，再根据角平分线的性质，得∠DCO=90°，则CD 为⊙O的切线；（2）过O作OF⊥AB，则OCD=∠CDA=∠OFD=90°,得四边形OCDF为矩形，设AD=x，在Rt△AOF 中,由勾股定理得（5﹣x）2+（6﹣x)2=25，从而求得x的值，由勾股定理得出AB的长．解答： (1）证明：连接OC∵OA=OC∴∠OCA=∠OAC∵AC平分∠PAE∴∠DAC=∠CAO∴∠DAC=∠OCA∴PB∥OC∵CD⊥PA∴CD⊥OC，CO为⊙O半径,∴CD为⊙O的切线；(2)解：过O作OF⊥AB，垂足为F，∴∠OCD=∠CDA=∠OFD=90°，∴四边形DCOF为矩形，∴OC=FD，OF=CD．∵DC+DA=6，设AD=x，则OF=CD=6﹣x，∵⊙O的直径为10，∴DF=OC=5，∴AF=5﹣x,在Rt△AOF中，由勾股定理得AF2+OF2=OA2．即（5﹣x）2+（6﹣x)2=25，化简得x2﹣11x+18=0，解得x1=2，x2=9．∵CD=6﹣x大于0，故x=9舍去，∴x=2，从而AD=2，AF=5﹣2=3，∵OF⊥AB，由垂径定理知,F为AB的中点,∴AB=2AF=6．点评：本题考查了切线的判定和性质、勾股定理、矩形的判定和性质以及垂径定理,是基础知识要熟练掌握．5．(2011•天水）在△ABC中，AB=BC，点O是△ABC的外心，连接AO并延长交BC于D，交△ABC的外接圆于E，过点B作⊙O的切线交AO的延长线于Q，设OQ=，BQ=3．（1）求⊙O的半径；(2）若DE=，求四边形ACEB的周长．考点：切线的性质;等腰三角形的性质;勾股定理；垂径定理．专题：几何综合题；压轴题．分析：（1）连接OB，根据BQ是圆的切线，则△OBQ是直角三角形，根据勾股定理即可求得半径OB的长；（2)根据AB=BC，O是△ABC的外心，可以得到：BC⊥AC,且AE是直径，BE=CE．易证△BOD∽△CED,根据相似三角形的对应边的比相等，即可求得CE的长,在Rt△ACE中根据勾股定理求得AC的长，在Rt△ABE中求得BE的长，据此即可求得四边形的周长．解答:解：（1）连接OB．∵BQ与⊙O相切，∴∠OBQ=90°∴OB===．故半径是：；(2)连接BO并延长交AC于点F，∵AB=BC则=，∴BF⊥AC，又∵AE是⊙O的直径，∴∠ACE=∠ABE=90°,∴BF∥CE，∴△BOD∽△CED，∴=，∴CE===1，∴在Rt△ACE中，AE=3，CE=1,则AC=2，又O是AE的中点，∴OF=CE=，则BF=2．∴在Rt△ABE中，BE=，∴四边形ACEB的周长是:1+2++．点评：本题主要考查了切线的性质定理,以及勾股定理，并多次运用了勾股定理，其中根据AB=AC和O是△ABC的内心，得到BF⊥AC，且AE是直径，是解决本题的关键．6．（2013•玉林）如图，以△ABC的BC边上一点O为圆心的圆，经过A,B两点，且与BC边交于点E，D 为BE的下半圆弧的中点，连接AD交BC于F，若AC=FC．(1）求证:AC是⊙O的切线:（2）若BF=8,DF=,求⊙O的半径r．考点: 切线的判定．分析：（1）连接OA、OD，求出∠D+∠OFD=90°，推出∠CAF=∠CFA,∠OAD=∠D,求出∠OAD+∠CAF=90°，根据切线的判定推出即可;（2）OD=r,OF=8﹣r，在Rt△DOF中根据勾股定理得出方程r2+（8﹣r）2=(）2，求出即可．解答:（1）证明：连接OA、OD，∵D为弧BE的中点，∴OD⊥BC，∠DOF=90°，∴∠D+∠OFD=90°，∵AC=AF，OA=OD,∴∠CAF=∠CFA,∠OAD=∠D，∵∠CFA=∠OFD，∴∠OAD+∠CAF=90°，∴OA⊥AC，∵OA为半径,∴AC是⊙O切线；（2）解：∵⊙O半径是r，当F在半径OE上时，∴OD=r，OF=8﹣r，在Rt△DOF中，r2+（8﹣r）2=（）2，r=6，r=2（舍）；当F在半径OB上时,∴OD=r，OF=r﹣8，在Rt△DOF中，r2+（r﹣8）2=(）2，解得:r=6或r=2（舍）；即⊙O的半径r为6．点评:本题考查了切线的判定,等腰三角形的性质和判定，勾股定理等知识点的应用，主要考查学生的推理和计算的能力．7．（2013•温州）如图,AB为⊙O的直径，点C在⊙O上,延长BC至点D，使DC=CB,延长DA与⊙O的另一个交点为E，连接AC，CE．(1）求证:∠B=∠D；（2）若AB=4,BC﹣AC=2,求CE的长．考点：圆周角定理；等腰三角形的判定与性质；勾股定理．分析： (1)由AB为⊙O的直径，易证得AC⊥BD,又由DC=CB，根据线段垂直平分线的性质,可证得AD=AB，即可得：∠B=∠D；（2）首先设BC=x,则AC=x﹣2，由在Rt△ABC中，AC2+BC2=AB2，可得方程：（x﹣2）2+x2=42,解此方程即可求得CB的长，继而求得CE的长．解答：（1）证明:∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,∵DC=CB，∴AD=AB，∴∠B=∠D；(2）解：设BC=x，则AC=x﹣2，在Rt△ABC中，AC2+BC2=AB2，∴（x﹣2）2+x2=42,解得：x1=1+,x2=1﹣（舍去），∵∠B=∠E，∠B=∠D，∴∠D=∠E，∴CD=CE，∵CD=CB,∴CE=CB=1+．点评：此题考查了圆周角定理、线段垂直平分线的性质、等腰三角形的判定与性质以及勾股定理等知识．此题难度适中，注意掌握方程思想与数形结合思想的应用．8．（2013•铁岭）如图，△ABC内接与⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于AC点E，交PC于点F，连接AF．(1）判断AF与⊙O的位置关系并说明理由；（2）若⊙O的半径为4，AF=3，求AC的长．考点: 切线的判定与性质．专题: 压轴题．分析:(1）AF为为圆O的切线,理由为：练级OC，由PC为圆O的切线，利用切线的性质得到CP垂直于OC，由OF与BC平行，利用两直线平行内错角相等，同位角相等，分别得到两对角相等，根据OB=OC,利用等边对等角得到一对角相等，等量代换得到一对角相等，再由OC=OA,OF为公共边，利用SAS 得出三角形AOF与三角形COF全等，由全等三角形的对应角相等及垂直定义得到AF垂直于OA，即可得证;(2）由AF垂直于OA，在直角三角形AOF中，由OA与AF的长，利用勾股定理求出OF的长，而OA=OC，OF为角平分线，利用三线合一得到E为AC中点，OE垂直于AC,利用面积法求出AE的长，即可确定出AC的长．解答：解：(1）AF为圆O的切线,理由为：连接OC,∵PC为圆O切线，∴CP⊥OC，∴∠OCP=90°，∵OF∥BC，∴∠AOF=∠B，∠COF=∠OCB，∵OC=OB，∴∠OCB=∠B，∴∠AOF=∠COF，∵在△AOF和△COF中，，∴△AOF≌△COF(SAS）,∴∠OAF=∠OCF=90°，则AF为圆O的切线;（2）∵△AOF≌△COF，∴∠AOF=∠COF,∵OA=OC，∴E为AC中点，即AE=CE=AC,OE⊥AC，∵OA⊥AF,∴在Rt△AOF中，OA=4,AF=3,根据勾股定理得：OF=5，∵S△AOF=•OA•AF=•OF•AE,∴AE=，则AC=2AE=．点评：此题考查了切线的判定与性质，涉及的知识有：全等三角形的判定与性质，平行线的性质,等腰三角形的性质，三角形的面积求法，熟练掌握切线的判定与性质是解本题的关键．9．（2013•天津）已知直线I与⊙O，AB是⊙O的直径，AD⊥I于点D．（Ⅰ）如图①，当直线I与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；（Ⅱ）如图②，当直线I与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．考点：切线的性质;圆周角定理；直线与圆的位置关系．分析： (Ⅰ)如图①,首先连接OC，根据当直线l与⊙O相切于点C，AD⊥l于点D．易证得OC∥AD，继而可求得∠BAC=∠DAC=30°；（Ⅱ）如图②，连接BF，由AB是⊙O的直径，根据直径所对的圆周角是直角,可得∠AFB=90°，由三角形外角的性质,可求得∠AEF的度数，又由圆的内接四边形的性质，求得∠B的度数，继而求得答案．解答:解：（Ⅰ)如图①，连接OC，∵直线l与⊙O相切于点C，∴OC⊥l，∵AD⊥l，∴OC∥AD，∴∠OCA=∠DAC,∵OA=OC,∴∠BAC=∠OCA，∴∠BAC=∠DAC=30°；（Ⅱ）如图②，连接BF，∵AB是⊙O的直径，∴∠AFB=90°，∴∠BAF=90°﹣∠B,∴∠AEF=∠ADE+∠DAE=90°+18°=108°，在⊙O中，四边形ABFE是圆的内接四边形，∴∠AEF+∠B=180°，∴∠B=180°﹣108°=72°，∴∠BAF=90°﹣∠B=90°﹣72°=18°．点评：此题考查了切线的性质、圆周角定理以及圆的内接四边形的性质．此题难度适中，注意掌握辅助线的作法,注意数形结合思想的应用．10．（2013•黄石）如图，AB是⊙O的直径，AM和BN是⊙O的两条切线，E是⊙O上一点,D是AM上一点，连接DE并延长交BN于点C，且OD∥BE,OF∥BN．（1）求证：DE与⊙O相切;（2）求证：OF=CD．考点: 切线的判定与性质；直角三角形斜边上的中线．分析：（1）连接OE，由AM与圆O相切，利用切线的性质得到OA与AM垂直，即∠OAD=90°,根据OD 与BE平行，利用两直线平行得到一对内错角相等,一对同位角相等，再由OB=OE,利用等边对等角得到一对角相等，等量代换得到一对角相等，再由OA=OE，OD为公共边,利用SAS得出三角形AOD 与三角形EOD全等，利用全等三角形的对应角相等得到∠OED=90°，即OE垂直于ED，即可得证；(2）连接OC，由CD与CB为圆的切线，利用切线的性质得到一对直角相等，由OB=OE，OC为公共边,利用HL得出两直角三角形全等,进而得到∠BOC=∠EOC,利用等量代换及平角定义得到∠COD=90°,即三角形COD为直角三角形,由OF与BN平行,AM与BN平行，得到三线平行，由O为AB的中的，利用平行线等分线段定理得到F为CD的中点，利用直角三角形斜边上的中线等于斜边的一半即可得证．解答：证明：（1）连接OE,∵AM与圆O相切，∴AM⊥OA，即∠OAD=90°,∵OD∥BE，∴∠AOD=∠ABE，∠EOD=∠OEB，∵OB=OE,∴∠ABE=∠OEB，∴∠AOD=∠OEB，∴∠AOD=∠EOD，在△AOD和△EOD中,，∴△AOD≌△EOD（SAS）,∴∠OED=∠OAD=90°，则DE为圆O的切线；（2）在Rt△BCO和Rt△ECO中,，∴Rt△BCO≌Rt△ECO，∴∠BOC=∠EOC，∵∠AOD=∠EOD，∴∠DOC=∠EOD+∠EOC=×180°=90°,∵AM、BN为圆O的切线，∴AM⊥AB，BN⊥AB，∴AM∥BN,∵OF∥BN，∴AM∥OF∥BN，又O为AB的中点，∴F为CD的中点,则OF=CD．点评：此题考查了切线的判定与性质,全等三角形的判定与性质，平行线的性质,以及等腰三角形的性质，熟练掌握切线的判定与性质是解本题的关键．11．平面直角坐标系中，⊙O的半径等于5，弦DH⊥x轴于K点，DH=8．（1）如图1,求点H的坐标；（2）如图2，点A为⊙O和x轴负半轴的交点，P为弧AH上任意一点，连接PK，PH，AM⊥PH交HP的延长线于点M，求的值；(3）如图3，⊙O与x轴正半轴交点为S，点E、F是线段OS上的动点(不与点S重合），连接并延长DE，DF交⊙O于点B、C，直线BC交x轴于点G，若△DEF是以EF为底的等腰三角形，当E、F两点在OS上运动时（不与点S重合),∠OGC+∠DOG的值是否发生变化？若不变，请求出其值;若变化，请求出其变化范围．考点：圆的综合题．分析：（1）连接OH，根据勾股定理求得OC=3,从而得出点H的坐标；（2）连接AD、AH，作AN⊥PD于N，由邻补角的定义,得∠APM=∠ADH=∠AHD=∠APN，可以证明△ADN≌△AHM，由垂径定理可得AD=AE,则△ADN≌△AHM,从而得出求的值；（3）当E、F两点在OS上运动时（不与点S重合），∠OGC+∠DOG的值不发生变化，由题意可得,弧DP=弧PN，则∠DOG=∠NOG，由△DEF是等腰三角形,得弧BN=弧CN,则∠OGC+∠NOG=90°，从而得出∠OGC+∠DOG=90°解答：解:（1）连接OH(如图1）,∵DH⊥x轴，∴DC=DH=DH=4，根据勾股定理OC2+HC2=OH2，∴OC=3，∴H（3,﹣4）;（2）连接AD、AH，作AN⊥PK于N，（如图2）∵∠APM+∠APH，=∠ADH+∠APH=180°，∴∠APM=∠ADH=∠AHD=∠APN,而AN⊥PD,AM⊥PH，∴AM=AN，又∵AP=AP，∵在Rt△APM和Rt△APN中，，∴△APM≌△APN（HL)，由垂径定理可得：，∴AD=AH，∵在Rt△ADN和Rt△AHM中，，∴△ADN≌△AHM（HL)，∴PM=PN，DN=HM，∴PD﹣PH=2PM，∴=2；（3）当E、F两点在OP上运动时（与点P不重合），∠OGC+∠DOG是定值．理由如下：过点D作DM⊥EF于M,并延长DM交⊙O于N，连接ON，交BC于T，（如图3）则弧DP=弧PN，∴∠DOG=∠NOG，∵△DEF为等腰三角形，DM⊥EF,∴DN平分∠BDC，∴弧BN=弧CN，∴OT⊥BC,∴∠OGC+∠NOG=90°，∴∠OGC+∠DOG=90°．点评：本题综合考查了勾股定理、全等三角形的判定、垂径定理和圆周角定理．解答这类题一些学生不会综合运用所学知识解答问题,不知从何处入手造成错解．12．（2011•黄石）已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上，C为⊙O2上一点（不与A，B，O1重合），直线CB与⊙O1交于另一点D．（1）如图(1），若AD是⊙O1的直径，AC是⊙O2的直径,求证：AC=CD;(2）如图（2)，若C是⊙O1外一点，求证：O1C丄AD；（3)如图（3），若C是⊙O1内的一点，判断（2)中的结论是否成立？考点：相交两圆的性质；圆周角定理．专题：几何综合题；压轴题．分析：（1）连接O1O2，连接C01，利用直径所对圆周角等于90度，以及垂直平分线的性质得出即可;（2）根据已知得出四边形AEDB内接于⊙O1，得出∠ABC=∠E，再利用=，得出∠E=∠AO1C，进而得出CO1∥ED即可求出;(3）根据已知得出∠B=∠EO1C，又∠E=∠B，即可得出∠EO1C=∠E，得出CO1∥ED,即可求出．解答:（1)证明：连接O1O2，连接C01∵AC为⊙O2直径∴∠AO1C=90°即CO1⊥AD,∵AO1=DO1∴DC=AC（垂直平分线的性质）;（2）证明:连接AO1，连接AB,延长AO1交⊙O1于点E，连接ED，∵四边形AEDB内接于⊙O1，∴∠E+∠ABD=180°，∵∠ABC+∠ABD=180°，∴∠ABC=∠E，又∵=,∴∠ABC=∠AO1C，∴∠E=∠AO1C，∴CO1∥ED，又AE为⊙O1的直径，∴ED⊥AD，∴O1C⊥AD，(3）(2）中的结论仍然成立．证明:连接AO1,连接AB，延长AO1交⊙O1于点E，连接ED,∵∠B+∠AO1C=180°，∠EO1C+∠AO1C═180°，∴∠B=∠EO1C，又∵∠E=∠B，∴∠EO1C=∠E，∴CO1∥ED，又ED⊥AD，∴CO1⊥AD．点评：此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质，根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键．13．（2010•三明）正方形ABCD的四个顶点都在⊙O上，E是⊙O上的一点．（1)如图①,若点E在上,F是DE上的一点，DF=BE．求证:△ADF≌△ABE;（2）在（1）的条件下，小明还发现线段DE、BE、AE之间满足等量关系：DE﹣BE=AE．请你说明理由; （3）如图②，若点E在上．写出线段DE、BE、AE之间的等量关系．（不必证明）考点：圆周角定理；全等三角形的判定；勾股定理；正方形的性质．专题：证明题;探究型．分析:(1）中易证AD=AB,EB=DF，所以只需证明∠ADF=∠ABE,利用同弧所对的圆周角相等不难得出,从而证明全等；（2）中易证△AEF是等腰直角三角形，所以EF=AE,所以只需证明DE﹣BE=EF即可，由BE=DF 不难证明此问题;（3）类比(2）不难得出（3）的结论．解答：解：（1）在正方形ABCD中，AB=AD（1分）∵∠1和∠2都对，∴∠1=∠2,（3分）在△ADF和△ABE中，，∴△ADF≌△ABE(SAS）；（4分)(2）由（1)有△ADF≌△ABE，∴AF=AE,∠3=∠4．(5分）在正方形ABCD中，∠BAD=90°．∴∠BAF+∠3=90°．∴∠BAF+∠4=90°．∴∠EAF=90°．（6分）∴△EAF是等腰直角三角形．∴EF2=AE2+AF2．∴EF2=2AE2．（7分）∴EF=AE．（8分)即DE﹣DF=AE．∴DE﹣BE=AE．(9分）（3）BE﹣DE=AE．理由如下：（12分）在BE上取点F，使BF=DE，连接AF．易证△ADE≌△ABF，∴AF=AE，∠DAE=∠BAF．(5分）在正方形ABCD中，∠BAD=90°．∴∠BAF+∠DAF=90°．∴∠DAE+∠DAF=90°．∴∠EAF=90°．（6分)∴△EAF是等腰直角三角形．∴EF2=AE2+AF2．∴EF2=2AE2．（7分）∴EF=AE．(8分)即BE﹣BF=AE．∴BE﹣DE=AE．（9分)点评：本题主要考查圆周角定理，全等三角形的判定及勾股定理，难度适中．14．（2013•南京）如图，AD是⊙O的切线，切点为A，AB是⊙O的弦．过点B作BC∥AD，交⊙O于点C,连接AC，过点C作CD∥AB，交AD于点D．连接AO并延长交BC于点M,交过点C的直线于点P，且∠BCP=∠ACD．（1)判断直线PC与⊙O的位置关系，并说明理由；(2）若AB=9,BC=6．求PC的长．考点：切线的判定与性质．分析： (1）过C点作直径CE，连接EB，由CE为直径得∠E+∠BCE=90°，由AB∥DC得∠ACD=∠BAC，而∠BAC=∠E，∠BCP=∠ACD，所以∠E=∠BCP，于是∠BCP+∠BCE=90°，然后根据切线的判断得到结论;（2）根据切线的性质得到OA⊥AD，而BC∥AD,则AM⊥BC，根据垂径定理有BM=CM=BC=3，根据等腰三角形性质有AC=AB=9，在Rt△AMC中根据勾股定理计算出AM=6；设⊙O的半径为r,则OC=r，OM=AM﹣r=6﹣r,在Rt△OCM中，根据勾股定理计算出r=，则CE=2r=，OM=6﹣=,利用中位线性质得BE=2OM=,然后判断Rt△PCM∽Rt△CEB，根据相似比可计算出PC．解答：解:（1）PC与圆O相切，理由为:过C点作直径CE，连接EB，如图，∵CE为直径,∴∠EBC=90°,即∠E+∠BCE=90°，∵AB∥DC,∴∠ACD=∠BAC,∵∠BAC=∠E,∠BCP=∠ACD．∴∠E=∠BCP,∴∠BCP+∠BCE=90°，即∠PCE=90°，∴CE⊥PC，∴PC与圆O相切;（2）∵AD是⊙O的切线，切点为A，∴OA⊥AD,∵BC∥AD，∴AM⊥BC，∴BM=CM=BC=3,∴AC=AB=9，在Rt△AMC中，AM==6,设⊙O的半径为r，则OC=r，OM=AM﹣r=6﹣r，在Rt△OCM中,OM2+CM2=OC2，即32+（6﹣r）2=r2，解得r=，∴CE=2r=,OM=6﹣=，∴BE=2OM=，∵∠E=∠MCP，∴Rt△PCM∽Rt△CEB,∴=，即=，∴PC=．点评：本题考查了切线的判定与性质：过半径的外端点与半径垂直的直线为圆的切线；圆的切线垂直于过切点的半径．也考查了勾股定理、圆周角定理的推论、三角形相似的判定与性质．练习题答案1．(2008•荆门）如图，⊙O是Rt△ABC的外接圆，AB为直径，∠ABC=30°,CD是⊙O的切线,E为AC延长线上一点，ED⊥AB于F．(1）判断△DCE的形状；（2）设⊙O的半径为1,且OF=,求证：△DCE≌△OCB．考点：切线的性质;全等三角形的判定;等腰三角形的判定．专题：几何综合题;压轴题．分析：（1）易得△AOC是正三角形，故有∠E=30°，由∠OCD=90°和平角的概念可得∠DCE=30°=∠E，所以DE=CD；进而可知此三角形为等腰三角形．（2）由勾股定理求得BC=，然后由直角三角形的性质，求得CE=,即可证得△DCE≌△OCB．解答：（1)解：∵∠ABC=30°，∴∠BAC=60°．又∵OA=OC,∴△AOC是正三角形．又∵CD是切线，∴∠OCD=90°．∴∠DCE=180°﹣60°﹣90°=30°．而ED⊥AB于F,∴∠CED=90°﹣∠BAC=30°．故△CDE为等腰三角形．（2）证明：∵CD是⊙O的切线,∴∠OCD=90°，∵∠BAC=60°，AO=CO，∴∠OCA=60°，∵∠DCE=30°．∴A，C,E三点同线在△ABC中,∵AB=2，AC=AO=1，∴BC==．∵OF=，∴AF=AO+OF=．又∵∠AEF=30°，∴AE=2AF=+1，∴CE=AE﹣AC==BC，而∠OCB=∠ACB﹣∠ACO=90°﹣60°=30°=∠ABC;故△CDE≌△COB．点评：本题利用了直径对的圆周角是直角，等边三角形的判定和性质，勾股定理，切线的性质，直角三角形的性质求解．2．（2007•益阳）如图，AB是⊙O的直径，C是⊙O上一点,过圆心O作OD⊥AC，D为垂足,E是BC上一点，G是DE的中点，OG的延长线交BC于F．（1）图中线段OD，BC所在直线有怎样的位置关系？写出你的结论，并给出证明过程；（2）猜想线段BE,EF，FC三者之间有怎样的数量关系？写出你的结论,并给出证明过程．考点：圆周角定理；平行线的判定;全等三角形的判定与性质；三角形中位线定理．专题：探究型．分析：（1）因为AB是直径，所以有∠ACB=90°，而OD⊥AC，又可得到∠ADO=90°，联合起来，可得∠ACB=∠ADO,因而OD∥BC；(2)由(1）知，OD∥BC，又O是AB中点，故D是AC中点,那么OD是△ABC的中位线，因而BC=2OD，还能得知△OGD≌△FGE（DG=EG），那么就有BC=2EF，而BC=BE+EF+CF，所以EF=BE+CF．解答:解：（1）结论:OD∥BC，证明:∵AB是⊙O直径,C是⊙O上一点，∴∠ACB=90°．即BC⊥AC．∵OD⊥AC，∴OD∥BC．（2）结论：EF=BE+FC，证明:∵OD⊥AC,∴AD=DC．∵O为AB的中点,∴OD是△ABC的中位线．∴BC=2OD．∵,∠ODG=∠FEG，DG=EG，∠GOD=∠GFE，∴△ODG≌△FEG．∴OD=EF．∴BE+EF+FC=BC=2OD=2EF．∴EF=BE+FC．点评：本题利用了平行线的判定(两同位角相等，两直线平行），以及三角形中位线定理、全等三角形的判定和性质、圆中直径所对的角是直角等知识．3．（2006•武汉）（人教版）已知:OA、OB是⊙O的半径，且OA⊥OB，P是射线OA上一点(点A除外）,直线BP交⊙O于点Q，过Q作⊙O的切线交直线OA于点E．（1）如图①，若点P在线段OA上,求证:∠OBP+∠AQE=45°；（2)若点P在线段OA的延长线上，其它条件不变，∠OBP与∠AQE之间是否存在某种确定的等量关系？请你完成图②，并写出结论（不需要证明）．考点：切线的性质．专题：几何综合题．分析：（1）连接OQ，则OQ⊥QE，根据等腰直角三角形两底角相等可得∠OBP=∠OQB，再根据∠BQA=45°,即可推出∠AQE+∠OBP=90°﹣∠OQA=45°;（2）连接OQ,可得△OBQ是等腰三角形,所以∠OBQ=∠OQB，由QE是⊙O的切线可得OQ⊥QE，根据圆周角定理可得∠AQB=135°,从而得到∠OQA=135°﹣∠OQB，然后整理即可得到∠OBP﹣∠AQE=45°．解答:（1）证明：如图①，连接OQ，∵OB=OQ,∴∠OBP=∠OQB，∵OA⊥OB，∴∠BQA=∠AOB=×90°=45°，∵EQ是切线，∴∠OQE=90°，∴∠OBP+∠AQE=∠OQB+∠AQE=90°﹣∠BQA=90°﹣45°=45°；（2）解：如图②，连接OQ,∵OB=OQ，∴∠OBQ=∠OQB,∵OA⊥OB,∴∠BQA=×（360°﹣90°）=135°，∴∠OQA=∠BQA﹣∠OQB=135°﹣∠OBQ,∵EQ是切线,∴∠OQE=90°，∴135°﹣∠OBQ+∠AQE=90°，整理得，∠OBQ﹣∠AQE=45°，即∠OBP﹣∠AQE=45°．点评：此题主要考查圆的切线的性质及同圆的半径相等等知识．此题(2）问为探索题，培养同学们的类比思想和探索问题的能力，此种问题一般都是继续利用前一问的求解思路进行求解．4．（2013•资阳）在⊙O中，AB为直径，点C为圆上一点，将劣弧沿弦AC翻折交AB于点D，连结CD．（1）如图1，若点D与圆心O重合，AC=2，求⊙O的半径r；(2）如图2，若点D与圆心O不重合，∠BAC=25°,请直接写出∠DCA的度数．考点：垂径定理；含30度角的直角三角形；圆周角定理；翻折变换（折叠问题）．分析:(1）过点O作OE⊥AC于E，根据垂径定理可得AE=AC，再根据翻折的性质可得OE=r，然后在Rt△AOE中，利用勾股定理列式计算即可得解；（2）连接BC,根据直径所对的圆周角是直角求出∠ACB,根据直角三角形两锐角互余求出∠B，再根据翻折的性质得到所对的圆周角,然后根据∠ACD等于所对的圆周角减去所对的圆周角，计算即可得解．解答：解：（1）如图，过点O作OE⊥AC于E，则AE=AC=×2=1，∵翻折后点D与圆心O重合,∴OE=r,在Rt△AOE中，AO2=AE2+OE2，即r2=12+(r）2,。