06柱锥台球的表面积1

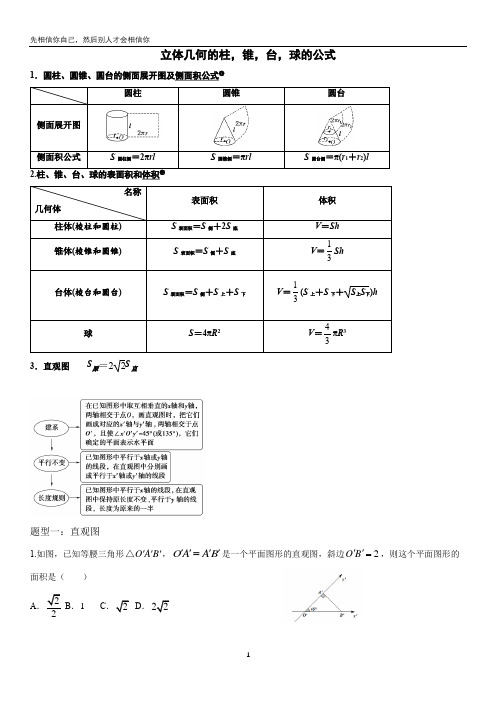
立体几何的柱，锥，台，球的公式1．圆柱、圆锥、圆台的侧面展开图及侧面积公式❶圆柱圆锥圆台侧面展开图侧面积公式S 圆柱侧＝2πrlS 圆锥侧＝πrlS 圆台侧＝π(r 1＋r 2)l2.柱、锥、台、球的表面积和体积❷名称几何体表面积 体积 柱体(棱柱和圆柱) S 表面积＝S 侧＋2S 底 V ＝Sh 锥体(棱锥和圆锥)S 表面积＝S 侧＋S 底V ＝13Sh 台体(棱台和圆台) S 表面积＝S 侧＋S 上＋S 下 V ＝13(S 上＋S 下＋S 上S 下)h 球S ＝4πR 2V ＝43πR 3 3．直观图 S 原＝22S 直题型一：直观图1.如图，已知等腰三角形O A B '''△，OA AB ''''=是一个平面图形的直观图，斜边2O B ''=，则这个平面图形的面积是（ ） A ．22B ．1C ．2D ．222.一个梯形的直观图是一个如图所示的等腰梯形，且1A B ''=，3O C ''=，2O A ''=，则原梯形的面积为( )A ．22B ．42C ．8D ．43．如图所示为水平放置的正方形ABCO ，在平面直角坐标系xOy 中点B 的坐标为(2,2)，用斜二测画法画出它的直观图A ′B ′C ′O ′，则四边形A ′B ′C ′O ′的面积为___________.4．如图所示，是三角形ABC 的直观图，则三角形ABC 的面积S △ABC =_______；（请用数字填写）5．如图，正方形O ′A ′B ′C ′的边长为1，它是一个水平放置的平面图形的直观图，则原图形的周长为（ ） A ．4 B ．6C ．8D ．222+6.正三角形ABC 的边长为2 cm ，如图，△A’B’C’为其水平放置的直观图，则△A’B’C’的周长为（ ） A .8 cmB .6 cmC .（2 +√6）cmD .（2 + 2√3）cm7.用斜二测画法画出水平放置的△ABC 的直观图如图所示，已知A’C’ = 3，B’C’ = 2，则△ABC 中AB 边上的中线长为_________.8.(多空题)在如图所示的直观图中，四边形O ′A ′B ′C ′为菱形且边长为2 cm ，则在平面直角坐标系中原四边形OABC 为________(填具体形状)，其面积为________ cm 2.9．已知用斜二测画法得到的某水平放置的平面图形的直观图是如图所示的等腰直角△O B C '''，其中1O B ''=，则原平面图形中最大边长为( ) A ．2B ．22C ．3D ．2310.如图，△A ′B ′C ′表示水平放置的△ABC 根据斜二测画法得到的直观图，A B ''在x '轴上，B ′C ′与x '轴垂直，且2B C ''=，则△ABC 的边AB 上的高为（ ）A ．2B ．22C ．4D ．4211.如图所示，△A ′B ′C ′表示水平放置的△ABC 在斜二测画法下的直观图，A ′B ′在x ′轴上，B ′C ′与x ′轴垂直，且B ′C ′＝3，则△ABC 的边AB 上的高为（ ） A ．6√2 B ．3√3 C ．3√2 D ．3题型二棱柱、棱锥、棱台的表面积和体积1.正三棱锥的所有棱长均为a ，则该三棱锥的表面积为（ ） A .33a 2B .23a 2C .3a 2D .4a 22.已知正四棱锥的底面边长是2，侧棱长是5，则该正四棱锥的表面积为（ ） A .3B .12C .8D .433.已知高为3的棱柱ABC -A 1B 1C 1的底面是边长为1的正三角形，如图，则三棱锥B -AB 1C 的体积为（ ） A .41 B .21 C .63 D .43 4.将一个棱长为a 的正方体，切成27个全等的小正方体，则表面积增加了（ ） A .26aB .212aC .218aD.224a5.将一个正方体截去四个角后得到一个正四面体，这个正四面体的体积是正方体体积的（ ）A .21 B .31 C .61 D .41 6.如图所示，在三棱台ABC - A 1B 1C 1中，A 1B 1：AB = 1：2，则三棱锥B - A 1B 1C 1与三棱锥A 1 - ABC 的体积比为（ ） A .1：2 B .1：3 C .1：2D .1：47.在底面半径为1的圆锥中，若该圆锥侧面展开图的面积是2π，则该圆锥的体积为（ ）A ．B ．C ．D ．8.已知球A 与球B 的体积之比为8：27，则球A 与球B 的半径之比为（ ） A ．：B ．4：9C ．2：3D ．3：29.球的一个截面面积为49πcm 2，球心到球截面距离为24cm ，则球的表面积是 ． 10.用一个平面截半径为25cm 的球，截面面积是49πcm 2，则球心到截面的距离是 ． 11.已知一个长方体的三个面的面积分别是2，3，6，则这个长方体的体积为_________。

第55课 柱、锥、台、球表面积和体积【复习目标】了解柱、锥、台、球的表面积和体积的计算公式（不要求记忆公式）；会求一些简单几何体的表面积和体积。

【重点难点】能运用柱、锥、台、球的表面积和体积的计算公式求一些简单几何体的表面积和体积，【自主学习】一、知识梳理1.空间几何体有关概念（1）棱柱：有两个面互相平行，其余每相邻两个面的交线互相平行，这样的多面体叫棱柱。

两个互相平行的面叫棱柱的底面(简称底)；其余各面叫棱柱的侧面；两侧面的公共边叫棱柱的侧棱；两底面所在平面的公垂线段叫棱柱的高(公垂线段长也简称高)直棱柱：正棱柱:(2) 棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，这样的多面体叫棱锥。

其中有公共顶点的三角形叫棱锥的侧面；多边形叫棱锥的底面或底；各侧面的公共顶点，叫棱锥的顶点，顶点到底面所在平面的垂线段，叫棱锥的高(垂线段的长也简称高)． 正棱锥：（3）棱台：棱锥被平行于底面的一个平面所截后，截面和底面之间的部分叫做棱台。

性质：各侧棱延长后（4）圆柱：由矩形绕着它的 所在直线旋转一周所形成的几何体。

圆锥：由直角三角形绕着它的一条 所在直线旋转一周所形成的几何体。

圆台：由直角梯形绕着它的 所在直线旋转一周所形成的几何体。

球：由半圆绕它的 所在直线旋转一周所形成的几何体。

2.正棱柱、正棱锥、正棱台及圆柱、锥、台的侧面积公式关系为：3.柱体、锥体、台体的体积公式有如下关系：sh V s s s s h V sh V s s s 31)(310＝＝＝锥台柱−−→−'+'+−−←=''=4.32344R V R S ππ＝，＝球球二、课前预习：1. 长方体ABCD-A 1B 1C 1D 1的AB=3，AD=2，CC 1=1，一条绳子从A 沿着表面拉到点C 1，绳子的最短长度是2. 若球的半径为R ，则这个球的内接正方体的全面积等于3. 边长为5cm 的正方形EFGH 是圆柱的轴截面, 则从E 点沿圆柱的侧面到相对顶点G 的最短距离是4. 球的大圆面积扩大为原大圆面积的4倍，则球的表面积扩大成原球面积的5. 正方体的全面积是a 2,它的顶点都在球面上，这个球的表面积是6. 已知正方体的棱长为a ，过有公共顶点的三条棱的中点的截面分别截去8个角，则剩余部分的体积是【共同探究】例1. 已知ABCD-A 1B 1C 1D 1是棱长为a 的正方体， E 、F 分别为棱AA 1与CC 1的中点，求四棱锥A 1-EBFD 1的体积．例2.如图，在四棱锥P-ABCD 中，PD ⊥平面ABCD ，四边形ABCD 是菱形，AC=6,BD=8,E 是PB 上任意一点，△AEC 面积的最小值是3。

柱,锥,台,球的表面积与体积【知识概述】空间几何体的表面积、体积是高考的必考知识点之一．题型既有选择题、填空题，又有解答题，难度为中、低档．客观题主要考查由三视图得出几何体的直观图，求其表面积、体积或由几何体的表面积、体积得出某些量；主观题考查比较全面，其中一步往往设置为表面积、体积问题，无论是何种题型都考查学生的空间想象能力．本节课通过知识的梳理和典型例题的讲解，使同学们理解和掌握空间几何体的表面积、体积的相关知识，并提高学生的空间想象能力、抽象概括能力、几何直观能力以及计算能力.1．柱、锥、台和球的侧面积和体积(1)棱柱、棱锥、棱台的表面积就是各面面积之和．(2)圆柱、圆锥、圆台的侧面展开图分别是矩形、扇形、扇环形；它们的表面积等于侧面积与底面面积之和．【学前诊断】1. [难度]易已知圆锥的底面半径为2cm，高为，则该圆锥的体积为 .2．[难度] 中若某空间几何体的三视图如图所示，则该几何体的体积是（）A.2B.1C.2 3D.1 33．[难度]中若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．等于( )AB．2C．D．6【经典例题】例1．将圆心角为2π3，面积为3π的扇形，作为圆锥的侧面，则圆锥的表面积等于______.例2．若某几何体的三视图（单位：cm）如下图所示，则此几何体的侧面积等于（）A. 212πcmB．215πcmC．224πcmD．230πcm例3．若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为________.例4．一个棱锥的三视图如图，则该棱锥的全面积(单位：cm2)为( )A. 48+B．48+C．36+D．36+例5．已知一个几何体的三视图如图所示，则此几何体的体积是________.例6．一个几何体的三视图如图所示，则这个几何体的体积等于（）A. 4B C ．6D ．2例 7．如图是一个几何体的三视图，若它的体积是a =___________.例 8．将边长为a 的正方形ABCD 沿对角线AC 折起，使BD =a ，则三棱锥D-ABC 的体积为（ ）A.36aB.312aC.312a D.312a 例 9．有一根长为3π cm 、底面半径为1 cm 的圆柱形铁管，用一段铁丝在铁管上缠绕2圈，并使铁丝的两个端点落在圆柱的同一母线的两端，则铁丝的最短长度为多少？ 【本课总结】1．面积、体积的计算中应注意的问题(1)柱、锥、台体的侧面积分别是某侧面展开图的面积，因此，弄清侧面展开图的形状及各线段的位置关系，是求侧面积及解决有关问题的关键．(2)计算柱、锥、台体的体积关键是找到相应的底面积和高．充分运用多面体的截面及旋转体的轴截面，将空间问题转化成平面问题．(3)球的有关问题，注意球半径与截面圆半径，球心到截面距离构成直角三角形． (4)有关几何体展开图与平面图形折成几何体问题，在解决的过程中注意按什么线作轴来展或折，还要坚持被展或被折的平面，变换前、后在该面内的大小关系与位置关系不变．在完成展或折后，要注意条件的转化对解题也很重要． 2．与球有关的组合体问题与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径．球与旋转体的组合，通常作它们的轴截面进行解题，球与多面体的组合，通过多面体的一条侧棱和球心，或“切点”、“接点”作出截面图． 【活学活用】1A CB1．[难度] 中若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（ ）A.3523cm 3B. 3203cm 3C. 2243cm 3D. 1603cm 32. [难度] 难如图，正方体1111ABCD-A B C D 的棱长为2，动点E 、F 在棱11A B 上.点Q 是CD 的中点动点P 在棱AD 上，若EF =1，DP=x ，1A E=y (x,y 大于零)，则三棱锥P-EFQ 的体积： A. 与x ，y 都有关； B. 与x ，y 都无关；C.与x 有关，与y 无关；D. 与y 有关，与x 无关； 3. [难度] 中一个几何体的三视图如图，该几何体的表面积为( ).A.280B. 292C. 360D. 372。

圆锥圆柱圆台球的表面积和体积公式圆锥、圆柱和圆台球是几何学中常见的三个立体图形，它们都具有特定的表面积和体积公式。

在本篇文章中，我将为您介绍这三个图形的定义、特点以及如何计算它们的表面积和体积。

一、圆锥圆锥是由一个圆和与圆上每一点相连的一条线段组成的立体图形。

圆锥有一个顶点和一个底面，底面是一个圆，而顶点则位于底面的正上方。

圆锥的表面积公式为：S = πr² + πrl其中，S表示圆锥的表面积，r表示底面圆的半径，l表示圆锥的斜高。

圆锥的体积公式为：V = (1/3)πr²h其中，V表示圆锥的体积，r表示底面圆的半径，h表示圆锥的高。

二、圆柱圆柱是由两个平行圆面和连接两个圆面的侧面组成的立体图形。

圆柱的底面是一个圆，而圆柱的高则是连接两个底面中心的线段。

圆柱的表面积公式为：S = 2πr² + 2πrh其中，S表示圆柱的表面积，r表示底面圆的半径，h表示圆柱的高。

圆柱的体积公式为：V = πr²h其中，V表示圆柱的体积，r表示底面圆的半径，h表示圆柱的高。

三、圆台球圆台球是由两个平行圆面和连接两个圆面的侧面组成的立体图形，其中一个圆面的半径较大，另一个圆面的半径较小。

圆台球的底面是一个圆，而圆台球的高则是连接两个底面中心的线段。

圆台球的表面积公式为：S = π(R+r)l + πR² + πr²其中，S表示圆台球的表面积，R表示底面较大圆的半径，r表示底面较小圆的半径，l表示圆台球的斜高。

圆台球的体积公式为：V = (1/3)πh(R²+r²+Rr)其中，V表示圆台球的体积，R表示底面较大圆的半径，r表示底面较小圆的半径，h表示圆台球的高。

通过以上公式，我们可以方便地计算出圆锥、圆柱和圆台球的表面积和体积。

这些公式的应用范围广泛，例如在建筑设计、工程测量以及日常生活中都有重要的应用。

在实际问题中，我们可以根据给定的数据，将公式中的参数代入，计算出具体的数值。

高中数学“圆柱、圆锥、圆台、球的表面积和体积”知识点详解一、引言在高中数学中，立体几何是一个非常重要的部分，它涉及到三维空间中图形的性质、度量以及变换等内容。

圆柱、圆锥、圆台和球是立体几何中最为常见的几何体，它们的表面积和体积计算是高中数学的重点和难点。

本文将详细介绍这些几何体的表面积和体积的计算方法，帮助同学们更好地掌握这一知识点。

二、圆柱的表面积和体积1.圆柱的表面积圆柱的表面积等于其侧面积与两个底面面积之和。

具体计算公式如下：表面积= 侧面积+ 2 ×底面面积= 2πrh + 2πr²= 2πr(h + r)其中，r为底面半径，h为高。

1.圆柱的体积圆柱的体积等于其底面面积与高的乘积。

具体计算公式如下：体积= 底面面积×高= πr²h三、圆锥的表面积和体积1.圆锥的表面积圆锥的表面积等于其侧面积与底面面积之和。

具体计算公式如下：表面积= 侧面积+ 底面面积= πrl + πr²= πr(l + r)其中，r为底面半径，l为母线长。

母线长l可以通过勾股定理求得：l = √(h² + r²)，其中h为高。

1.圆锥的体积圆锥的体积等于其底面面积与高的乘积的三分之一。

具体计算公式如下：体积= (1/3) ×底面面积×高= (1/3) × πr²h四、圆台的表面积和体积1.圆台的表面积圆台的表面积等于其侧面积与上、下底面面积之和。

具体计算公式如下：表面积= 侧面积+ 上底面面积+ 下底面面积= π(R + r)l + πR² + πr²= π(R + r)(l + R + r)其中，R为上底面半径，r为下底面半径，l为母线长。

母线长l可以通过勾股定理求得：l = √[(R - r)² + h²]，其中h为高。

1.圆台的体积圆台的体积可以使用以下公式计算：体积= (1/3) × (上底面面积+ 下底面面积+ √(上底面面积×下底面面积)) ×高= (1/3) × π(R² + r² + Rr) × h= (1/3) × π(R + r)(R² - Rr + r²)h / (R - r) （当R≠r时）= (1/3) × πh(R^2 + Rr + r^2) （当R=r时）五、球的表面积和体积1.球的表面积球的表面积等于其大圆的面积的4倍。

柱、锥、台表面积的求法求关于柱、锥、台体的表面积时，必须分清所求几何体的结构特征，即柱、锥、台体等的哪种几何体，或是由几个柱、锥、台等构成的几何体(组合体)，然后选用相应的面积公式求解.下面举例说明.一﹑求棱体的表面积棱柱的侧面展开图是平行四边形，上、下底面面积相等，因此只要计算出侧面积与一个底面的面积，其表面积可求；棱锥的侧面展开图是由若干个三角形拼成的，因此侧面积为各个三角形面积之和；棱台的侧面展开图为若干个梯形拼接而成，因此侧面积为各个梯形的面积之和.由此可知，求棱体的表面积主要分为两次运算，一次是计算侧面积，一次是计算底面积.例1六棱台的上、下底面均是正六边形，边长分别是8cm 和18cm ，侧面是全等的等腰梯形，侧棱长为13cm ，求它的表面积.解析：一个侧面如右图，易知a ＝18－82＝5，h ＝132－52＝12. 则S 侧面积＝6×18＋82×12＝936(cm 2)， S 上底＝12×8×(8×sin60︒)×6＝963(cm 2)，S 下底＝12×18×(18×sin60︒)×6＝4863(cm 2)，所以，表面积为936＋963＋4863＝936＋5823(cm 2).点评：本题在作图上比较麻烦，因此在解答时，根据所涉及的六棱台特殊性，可先通过解决一个侧面的面积，从而求侧面积，这是解答本题的一个关键.这种处理方法在求面积中用得较为广泛.二、求圆体的表面积圆柱的侧面展开图是矩形，上、下底面面积相等，因此只要计算出侧面积与一个底面的面积，其表面积就可求：设柱体的底面周长为c ，高为l ，则侧面积为S 侧面积＝cl ，故圆柱表面积公式为S 表面积＝S 侧面积＋S 底.圆锥的侧面展开图为扇形，利用扇形面积公式可求侧面积，故圆锥表面积公式为S 表面积＝S 侧面积＋S 底.圆台的侧面展开图为扇环，其侧面积可由大扇形的面积减去小扇形的面积而得到，所以它们的表面积公式为：S 表面积＝S 侧面积＋S 上底＋S 下底.例2一个立体几何圆台教具的上底半径是4cm ，下底半径为6cm ，母线长为12cm ，求此圆台的表面积.解析：如图，设圆台的侧面展开图的圆心角为∠B 'O B ＝θ，O A ＝x .又设圆台上下底面半径分别是r 、R ，则R ＝6cm ，r ＝4cm ，由相似三角形知识得x x ＋12＝23，解得x ＝24， 则圆心角θ＝2π×424＝π3， 所以S 扇形A 'OA ＝12×2π×4×24＝96π(cm 2)，S 扇形B OB ＝π(x ＋AB)2＝12×2π×6×(24＋12)＝216π(cm 2)， 所以圆台的表面积为216π－96π＝120π(cm 2).点评：（1）本题解答充分体现了立几问题平面化的一种重要思想方法，特别是在解决几何体表面上的相关问题时，作用尤为显著；（2）在解决与台休相关的问题时，一般都要用到三角的相似，建立方程，求得相关量；（3）求圆台的表面积（或侧面积）的一个关键就是确定侧面展开图所对就的圆心角.三﹑求三视图给出的几何体的表面积此类题没有直接给出或描述出所求几何体图形，而是通过给出一个几何体的三视图.因此求此类几何体的表面积时，要认真分析三视图，根据“长对正，宽相等，高平齐”的基本原则，明确三视图中数据对应于原几何体哪个量，一般根据一种或两种视图相结合可得出一个对应于原几何体中的一个量.例3右图所示的是一个三棱柱的三视图，此三棱柱的侧棱垂直底面，且底面为正三角形，求这个正三棱柱的表面积.解析：由三视图知三棱柱的侧棱长为2mm ，由左视图知正三棱柱的底面三角形的高23mm ，设底面边长为a ，则32a ＝23，∴a ＝4， ∴三棱柱的表面积为S ＝S 侧＋2S 底＝3×4×2＋2×12×4×23＝24＋83(mm 2). 点评：由于本题的原几何体是一个侧棱垂直底面，且底面为正三角形，因此在上面的解法中求出了三棱柱的侧棱长和底面边长就顺利作答了.一般地，由正视图和侧视图可以得到原几何体的高或底面的某些边的长，由俯视图可以得到原几何本的底面上的某些线段对应的量.四、求组合体的表面积求组合体的表面积的解答策略：(1)分解组合体：明确组合体的构成，即由几种基本几何体组成；(2)求各面面积：求出各个几何体为组合体表面的各个面的面积；(3)求各面面积和.例4如图，已知Rt △ABC 的斜边AB ＝13cm ，一条直角边AC ＝5cm ，以直线AB 为轴旋转一周得一个几何体．求这个几何体的表面积．解析：首先应了解这个几何体的形状是上下两个圆锥，共用一个底面，表面积即为两个圆锥的侧面积之和．根据公式S 侧＝πrl 可知，用第二个公式比较好求，但是得求出底面圆的半径，因为AB 垂直于底面圆，在Rt △ABC 中，由OC ·AB ＝BC ·AC 可求出r ，问题就解决了．在Rt △ABC 中，AB ＝13cm ，AC ＝5cm ，∴BC ＝12cm ．∵OC ·AB ＝BC ·AC ，∴r ＝OC ＝B C ·AC AB2＝5×1213＝6013． ∴S 表＝πr (BC ＋AC )＝π×6013×(12＋5)＝102013πcm 2． 点评：本题解答中必须注意组合体表面积为两个圆锥的侧面积之和．而不是两个圆锥的表面积之和，例5 右图中的几何体是一棱长为4厘米的正方体，若在它的各个面的中心位置上，各打一个直径为2厘米，深为1厘米的圆柱形的孔，求打孔后几何体的表面积是多少（π＝3.14）？解析：因为正方体的棱长为4厘米，而孔深只有1厘米，所以正方体没有被打透。

柱、锥、台表面积的求法求关于柱、锥、台体的表面积时，必须分清所求几何体的结构特征，即柱、锥、台体等的哪种几何体，或是由几个柱、锥、台等构成的几何体(组合体)，然后选用相应的面积公式求解.下面举例说明.一﹑求棱体的表面积棱柱的侧面展开图是平行四边形，上、下底面面积相等，因此只要计算出侧面积与一个底面的面积，其表面积可求；棱锥的侧面展开图是由若干个三角形拼成的，因此侧面积为各个三角形面积之和；棱台的侧面展开图为若干个梯形拼接而成，因此侧面积为各个梯形的面积之和.由此可知，求棱体的表面积主要分为两次运算，一次是计算侧面积，一次是计算底面积.例1六棱台的上、下底面均是正六边形，边长分别是8cm 和18cm ，侧面是全等的等腰梯形，侧棱长为13cm ，求它的表面积.解析：一个侧面如右图，易知a ＝18－82＝5，h ＝132－52＝12. 则S 侧面积＝6×18＋82×12＝936(cm 2)， S 上底＝12×8×(8×sin60︒)×6＝963(cm 2)，S 下底＝12×18×(18×sin60︒)×6＝4863(cm 2)，所以，表面积为936＋963＋4863＝936＋5823(cm 2).点评：本题在作图上比较麻烦，因此在解答时，根据所涉及的六棱台特殊性，可先通过解决一个侧面的面积，从而求侧面积，这是解答本题的一个关键.这种处理方法在求面积中用得较为广泛.二、求圆体的表面积圆柱的侧面展开图是矩形，上、下底面面积相等，因此只要计算出侧面积与一个底面的面积，其表面积就可求：设柱体的底面周长为c ，高为l ，则侧面积为S 侧面积＝cl ，故圆柱表面积公式为S 表面积＝S 侧面积＋S 底.圆锥的侧面展开图为扇形，利用扇形面积公式可求侧面积，故圆锥表面积公式为S 表面积＝S 侧面积＋S 底.圆台的侧面展开图为扇环，其侧面积可由大扇形的面积减去小扇形的面积而得到，所以它们的表面积公式为：S 表面积＝S 侧面积＋S 上底＋S 下底.例2一个立体几何圆台教具的上底半径是4cm ，下底半径为6cm ，母线长为12cm ，求此圆台的表面积.解析：如图，设圆台的侧面展开图的圆心角为∠B 'O B ＝θ，O A ＝x .又设圆台上下底面半径分别是r 、R ，则R ＝6cm ，r ＝4cm ，由相似三角形知识得x x ＋12＝23，解得x ＝24， 则圆心角θ＝2π×424＝π3， 所以S 扇形A 'OA ＝12×2π×4×24＝96π(cm 2)，S 扇形B OB ＝π(x ＋AB)2＝12×2π×6×(24＋12)＝216π(cm 2)， 所以圆台的表面积为216π－96π＝120π(cm 2).点评：（1）本题解答充分体现了立几问题平面化的一种重要思想方法，特别是在解决几何体表面上的相关问题时，作用尤为显著；（2）在解决与台休相关的问题时，一般都要用到三角的相似，建立方程，求得相关量；（3）求圆台的表面积（或侧面积）的一个关键就是确定侧面展开图所对就的圆心角.三﹑求三视图给出的几何体的表面积此类题没有直接给出或描述出所求几何体图形，而是通过给出一个几何体的三视图.因此求此类几何体的表面积时，要认真分析三视图，根据“长对正，宽相等，高平齐”的基本原则，明确三视图中数据对应于原几何体哪个量，一般根据一种或两种视图相结合可得出一个对应于原几何体中的一个量.例3右图所示的是一个三棱柱的三视图，此三棱柱的侧棱垂直底面，且底面为正三角形，求这个正三棱柱的表面积.解析：由三视图知三棱柱的侧棱长为2mm ，由左视图知正三棱柱的底面三角形的高23mm ，设底面边长为a ，则32a ＝23，∴a ＝4， ∴三棱柱的表面积为S ＝S 侧＋2S 底＝3×4×2＋2×12×4×23＝24＋83(mm 2). 点评：由于本题的原几何体是一个侧棱垂直底面，且底面为正三角形，因此在上面的解法中求出了三棱柱的侧棱长和底面边长就顺利作答了.一般地，由正视图和侧视图可以得到原几何体的高或底面的某些边的长，由俯视图可以得到原几何本的底面上的某些线段对应的量.四、求组合体的表面积求组合体的表面积的解答策略：(1)分解组合体：明确组合体的构成，即由几种基本几何体组成；(2)求各面面积：求出各个几何体为组合体表面的各个面的面积；(3)求各面面积和.例4如图，已知Rt △ABC 的斜边AB ＝13cm ，一条直角边AC ＝5cm ，以直线AB 为轴旋转一周得一个几何体．求这个几何体的表面积．解析：首先应了解这个几何体的形状是上下两个圆锥，共用一个底面，表面积即为两个圆锥的侧面积之和．根据公式S 侧＝πrl 可知，用第二个公式比较好求，但是得求出底面圆的半径，因为AB 垂直于底面圆，在Rt △ABC 中，由OC ·AB ＝BC ·AC 可求出r ，问题就解决了．在Rt △ABC 中，AB ＝13cm ，AC ＝5cm ，∴BC ＝12cm ．∵OC ·AB ＝BC ·AC ，∴r ＝OC ＝B C ·AC AB2＝5×1213＝6013． ∴S 表＝πr (BC ＋AC )＝π×6013×(12＋5)＝102013πcm 2． 点评：本题解答中必须注意组合体表面积为两个圆锥的侧面积之和．而不是两个圆锥的表面积之和，例5 右图中的几何体是一棱长为4厘米的正方体，若在它的各个面的中心位置上，各打一个直径为2厘米，深为1厘米的圆柱形的孔，求打孔后几何体的表面积是多少（π＝3.14）？解析：因为正方体的棱长为4厘米，而孔深只有1厘米，所以正方体没有被打透。

初数数学公式破解球台的表面积球台是体育运动中常见的器材之一，它的表面积是我们可以通过数学公式来计算的。

在初等数学中，有一些公式可以帮助我们准确地计算球台的表面积。

本文将介绍这些公式，并通过实例来演示如何破解球台的表面积计算。

一、球台的表面积公式球台的表面积可以通过以下公式来计算：1. 球台是圆柱面：球台的表面积公式为：S = 2πrh + 2πr²，其中S表示表面积，r表示底面半径，h表示高度。

2. 球台是圆锥面：球台的表面积公式为：S = πrl + πr²，其中S表示表面积，r表示底面半径，l表示母线的长度。

3. 球台是球面：球台的表面积公式为：S = 2πr²，其中S表示表面积，r表示球的半径。

二、计算实例下面通过实例来演示如何应用上述公式来计算球台的表面积。

以一个实际的球台为例，其底面半径为5米，高度为10米。

1. 圆柱面球台的表面积：根据公式S = 2πrh + 2πr²，代入r = 5，h = 10，我们可以计算得到球台的表面积：S = 2π(5)(10) + 2π(5)² = 100π + 50π = 150π（平方米）。

2. 圆锥面球台的表面积：根据公式S = πrl + πr²，代入r = 5，l需根据实际情况进行测量，假设为15米，我们可以计算得到球台的表面积：S = π(5)(15) + π(5)² = 75π + 25π = 100π（平方米）。

3. 球面球台的表面积：根据公式S = 2πr²，代入r = 5，我们可以计算得到球台的表面积：S = 2π(5)² = 50π（平方米）。

综上所示，针对不同类型的球台，我们可以利用对应的数学公式来计算其表面积。

三、应用场景球台的表面积计算在实际生活和工作中有着广泛的应用。

以下是一些常见的应用场景：1. 运动场地规划：在规划一个室内或室外球台场地时，需要准确计算其表面积，以确保场地的大小适合相关运动项目的要求。