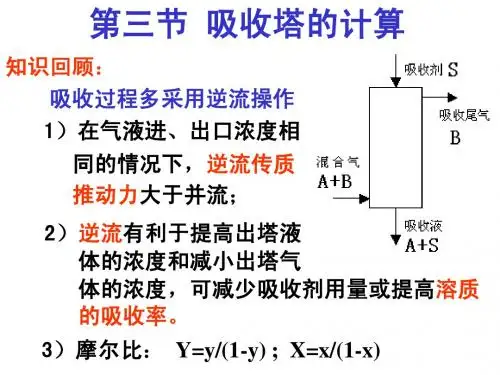
第4节吸收塔的计算吸收过程既可在板式塔内进行，也可在填料塔内进行。
在板式塔中气液逐级接触，而在填料塔中气液则呈连续接触。
本章对于吸收操作的分析和计算主要结合连续接触方式进行。
填料塔内充以某种特定形状的固体填料以构成填料层。
填料层是塔实现气、液接触的主要部位。
填料的主要作用是：①填料层内空隙体积所占比例很大，填料间隙形成不规则的弯曲通道，气体通过时可达到很高的湍动程度；②单位体积填料层内提供很大的固体表面，液体分布于填料表面呈膜状流下，增大了气、液之间的接触面积。
通常填料塔的工艺计算包括如下项目：（1）在选定吸收剂的基础上确定吸收剂的用量；（2）计算塔的主要工艺尺寸，包括塔径和塔的有效高度，对填料塔，有效高度是填料层高度，而对板式塔，则是实际板层数与板间距的乘积。
计算的基本依据是物料衡算，气、液平衡关系及速率关系。
下面的讨论限于如下假设条件：（1）吸收为低浓度等温物理吸收，总吸收系数为常数；（2）惰性组分B在溶剂中完全不溶解，溶剂在操作条件下完全不挥发，惰性气体和吸收剂在整个吸收塔中均为常量；（3）吸收塔中气、液两相逆流流动。
吸收塔的物料衡算与操作线方程式全塔物料衡算图2－12所示是一个定态操作逆流接触的吸收塔，图中各符号的意义如下：V －惰性气体的流量，kmol （B ）／s ；L —纯吸收剂的流量，kmol （S ）／S ；Y 1；、Y 2—分别为进出吸收塔气体中溶质物质量的比，kmol （A ）／kmol （B ）；X 1、X 2——分别为出塔及进塔液体中溶质物质量的比，kmol （A ）／kmol （S ）。
注意，本章中塔底截面一律以下标“l ”表示，塔顶截面一律以下标“2”表示。
在全塔范围内作溶质的物料衡算，得：VY 1＋LX 2＝VY 2＋LX 1或V （Y 1－Y 2）＝L （X 1－X 2） （2－38）一般情况下，进塔混合气体的流量和组成是吸收任务所规定的，若吸收剂的流量与组成已被确定，则V 、Y 、L 及X 2。
为已知数，再根据规定的溶质回收率，便可求得气体出塔时的溶质含量，即：Y 2＝Y l （1－фA ） （2－39）式中фA 为溶质的吸收率或回收率。
通过全塔物料衡算式2－38可以求得吸收液组成X 1。
于是，在吸收塔的底部与顶部两个截面上，气、液两相的组成Y 1、X l 与Y 2、X 2均成为已知数。
2．吸收塔的操作线方程式与操作线21图2-12 物料衡算示意图在定态逆流操作的吸收塔内，气体自下而上，其组成由Y 1逐渐降低至Y 2；液相自上而下，其组成由X 2逐渐增浓至X l ；而在塔内任意截面上的气、液组成 Y 与X 之间的对应夫系，可由塔内某一截面与塔的一个端面之间作溶质A 的物料衡算而得。
例如，在图2－12中的m －n 截面与塔底端面之间作组分A 的衡算： VY ＋LX 1＝VY 1＋LX或 Y ＝V L X ＋（Y 1－V LX 1） （2－40）式2－40称为逆流吸收塔的操作线方程式，它表明塔内任一横截面上的气相组成Y 与液相组成X 之间成直线关系。
直线的斜率为L ／V ，且此直线应通过B （X 1，Y 1）及T （X 2，Y 2）两点，如图2－13所示图中的直线BT 即为逆流吸收塔的操作线。
（1）上端点B 代表吸收塔底的情况，此处具有最大的气、液组成，故称为“浓端”；端点T 代表塔顶的情况，此处具有最小的气、液组成，故称之为“稀端”；操作线上任一点A ，代表着塔内相应截面上的液、气组成X 、Y 。
（2）当进行吸收操作时，在塔内任一截面上，溶质在气相中的实际组成总是高于与其接触的液相平衡组成，所以吸收操作线必位于平衡线上方。
反之，若操作线位于平衡线下方，则进行脱吸过程。
需要指出，操作线方程式及操作线都是由物料衡算得来的，与系统的平衡关系、操作温度和压强以及塔的结构类型都无任何牵连。
吸收剂用量的确定（1）液气比由图2－14a可知，在V、Y、Y1及X2已知的情况下，吸收操作线的一个端点T已经固定，另一个端点B则可在Y＝Y1的水平线上移动。
点B的横坐标将取决于操作线的斜率L／V。
操作线的斜率L／V称为“液气比”，是溶剂与惰性气体物质的量的比值。
它反映单位气体处理量的溶剂耗用量大小。
（2）由于V值已经确定，故若减少吸收剂用量L，操作线的斜率就要变小，点B 便沿水平线Y＝Y1向右移动，其结果是使出塔吸收液的组成加大，吸收推动力相应减小。
若吸收剂用量减小到恰使点B移至水平线Y＝Y1与平衡线的交点B*时，X1＝X1*：，意即塔底流出的吸收液与刚进塔的混合气达到平衡。
这是理论上吸收液所能达到的最高含量，但此时过程的推动力已变为零，因而需要无限大的相际传质面积。
这在实际上是办不到的，只能用来表示一种极限状况。
此种状况下吸收操作线（B*T）的斜率称为最小液气比，以（L／V）min表示，相应的吸收剂用量即为最小吸收剂用量，以Lmin 表示。
反之，若增大吸收剂用量，则点B 将沿水平线向左移动，使操作线远离平衡线，过程推动力增大；但超过一定限度后，效果便不明显，而溶剂的消耗、输送及回收等项操作费用急剧增大。
（3）最小液气比的求法最小液气比可用图解法求出。
如果平衡曲线符合图2－14a 所示的一般情况，则要找到水平线Y ＝Y 1与平衡线的交点B*，从而读出X*的数值，然后用下式计算最小液气比，即：2121min *X X Y Y V L --=⎪⎭⎫ ⎝⎛ （2－41） 或2121min *X X Y Y V L --= （2－14a ）如果平衡曲线呈现如图2－14b 中所示的形状，则应过点T 作平衡线的切线，找到水平线Y ＝Y 1与此切线的交点B ´，从而读出点B ´的横坐标X 1´的数值，用X 1´代替式2－41或式2－41a 中的X 1* ，便可求得最小液气比（L/V ）min 或最小吸收剂用量Lmin 。
若平衡关系符合亨利定律，可用 X*＝Y ／m 表示，则可直接用下式算出最小液气比，即：2121min X m Y Y Y V L --=⎪⎭⎫ ⎝⎛ （2－42） 2121min X m Y Y Y VL --= （2－42 a ）如果用纯溶剂吸收，则X 2＝0，式2－42及式2－42a 可表达为m V L A φ=⎪⎭⎫ ⎝⎛min （2－42b ）或 m V L A φ=min （2－42c ）由以上分析可见，吸收剂用量的大小，从设备费与操作费两方面影响到生产过程的经济效果，应权衡利弊，选择适宜的液气比，使两种费用之和最小。
根据生产实践经验，一般情况下取吸收剂用量为最小用量的～倍是比较适宜的，即：=⎪⎭⎫ ⎝⎛V L （～）m in ⎪⎭⎫ ⎝⎛V L （2－43）或 L ＝（～）Lmin （2－43a ）必须指出，为了保证填料表面能被液体充分润湿，还应考虑到单位塔截面积上单位时间内流下的液体量不得小于某一最低允许值。
如果按式2－43算出的吸收剂用量不能满足充分润湿填料的起码要求，则应采用更大的液气比。
［例2－2］用清水吸收混合气体中的可溶组分A 。
吸收塔内的操作压强为105．7 kPa ，温度为27℃，混合气体的处理量为1280 m 3／h 儿，其中A 物质的量的分数为0．03，要求A 的回收率为95％。
操作条件下的平衡关系可表示为：Y ＝。
若取溶剂用量为最小用量的倍，求每小时送人吸收塔顶的清水量L 及吸收液组成X 1。
解：（1）清水用量L平衡关系符合亨利定律，清水的最小用量可由式2－42a 计算，式中的有关参数为： V=)1(4.22100y P P T T V h -⨯⨯＝)03.01(33.1017.105272732734.221280-⨯+⨯＝h Y 1＝111y y -＝03.0103.0-＝Y 2＝Y 1（1－фA ）＝（1－）＝X 2＝0m ＝将有关参数代入式2－42a ，得到：2121min X m Y Y Y V L --=＝65.003093.0)00155.003093.0(62.52-＝h则L ＝＝h（2）吸收液组成X 1根据全塔的物料衡算可得：X 1＝X 2＋L Y Y V21-＝5.45)00155.003093.0(62.52-＝ 塔径的计算与精馏塔直径的计算原则相同，吸收塔的直径也可根据圆形管道内的流量公式计算，即：s V u D =24π则 u V D s π4=（2－44）式中 D ——塔径，m ；Vs ——操作条件下混合气体的体积流量，m 3／s ；u ——空塔气速，即按空塔截面积计算的混合气体线速度，m ／s 。
在吸收过程中，由于吸收质不断进人液相，故混合气体量由塔底至塔顶逐渐减小。
在计算塔径时，一般应以塔底的气量为依据。
计算塔径的关键在于确定适宜的空塔气速u 。
如何确定适宜的空塔气速，是属于气液传质设备内的流体力学问题，将在本册第3章中讨论。
填料层高度的计算填料层高度计算的基本思路是：根据吸收塔的传质负荷（单位时间内的传质量，kmol/s）与塔内的传质速率（单位时间内单位气液接触面积上的传质量，kmol ／（m2·s）计算完成规定任务所需的总传质面积；然后再由单位体积填料层所提供的气、液接触面积（有效比表面积）求得所需填料层的体积，该体积除以塔的横截面积便得到所需填料层的高度。
计算吸收塔的负荷要依据物料衡算关系，计算传质速率要依据吸收速率方程式，而吸收速率方程式中的推动力是实际组成与相应平衡组成的差额，因而要知道相平衡关系。
所以，填料层高度的计算将要涉及物料衡算、传质速率与相平衡这三种关系式的应用。
1．填料层高度的基本计算式在逆流操作的填料塔内，气、液相组成沿塔高不断变化，塔内各截面上的吸收速率各不相同。
在中介绍的所有吸收速率方程式，都只适用于吸收塔的任一横截面而不能直接用于全塔。
因此，为解决填料层高度的计算问题，需从分析填料吸收塔中某一微元填料层高度dZ的传质情况人手，如图2－15所示。
在微元填料层中，单位时间内从气相转人液相的溶质A的物质量为：dG A＝VdY＝LdX （2－45）在微元填料层中，因气、液组成变化很小，故可认为吸收速率N A为定值，则dG A＝N A dA＝N A（aΩdz）（2－46）式中dA——微元填料层内的传质面积，m2；a——单位体积填料层所提供的有效接触面积，m2／m3；Ω一塔的横截面积，m2。
微元填料层中的吸收速率方程式可写为：N A＝K Y（Y－Y*）N A＝K X（X*－X）将上二式分别代人式2－46，得到：dG A＝K Y（Y－Y*）（aΩdz）及dG A＝K X（X*－X）（aΩd z）再将上二式与式2－45联立，可得：VdY＝K Y（Y－Y*）（aΩdz）及LdX ＝K X （X*－X ）（aΩdz ）整理上二式，分别得到：dz V K Y Y dY Y Ω=-α* （2－47）及 dz L K X X dX X Ω=-α* （2－48）对于定态操作吸收塔，L 、V 、a 及Ω皆不随时间而变，且不随塔截面位置而变。
