图形规律
- 格式:docx
- 大小:304.79 KB
- 文档页数:19


二年级奥数:《发现图形规律》(预热)前铺知识一、找规律画图1、形状变化【例1】根据规律,画出下一个图形.答案:解析:本组图的规律就是正方形、三角形、圆形三个不同形状的图形为一组,重复出现.2、数量变化【例2】根据规律,在横线上画出适当的图形.答案:解析:本组图的规律是圆形的数量发生了变化,依次增加1个.3、颜色变化【例3】根据规律,画出下一个图形答案:解析:本组图的规律是圆形的颜色发生了变化,红蓝黄绿四种颜色的三角形为一组重复出现.4、位置变化【例4】根据规律,在横线上画出适当的图形.答案:解析:本题的规律是第一组的第一个图形移动到最后一个位置,其它图形依次往前移一小格就变成了第二组图.第二组的第一个图形移动到最后一个位置,其它图形依次往前移一小格就变成了第三组图.第三组的第一个图形移动到最后一个位置,其它图形依次向前移一小格,就变成了.5、方向变化【例5】根据规律,在横线上画出适当的图形.答案:解析:本组图的规律就是箭头的方向发生了变化,每次向顺时针方向旋转90度.6、组合【例6】根据规律,在问号处应该画什么图形.?答案:解析:本组图既要观察图形的形状,又要观察颜色,是一种组合规律题.观察发现,这些图形都分为上下两部分.其中第一行,上部分的形状分别是三角形和半圆环形,颜色为绿色和蓝色,下部分分别为红色的圆环和长方形.第二行,上部分没有变化,下部分的颜色变成了黄色,因此为答案所示图形.【例7】根据规律,在空白处应该画什么图形.答案:解析:本题中,图形的形状、颜色以及位置都在发生变化.但实际上可以将此组图中的每一个大圆内的图形看成一个整体,则下一个图形就是上一个大圆按顺时针依次旋转90度得来的.【例8】根据规律,在问号处应该画什么图形.?答案:解析:观察后可发现,每一横行中,第一个图形叠到第二个图形中间,就组成了第三个图形.课前思考1、要想发现一组图形的规律,你知道可以从哪些角度去观察吗?2、如果颜色、形状、方向等都无法帮助你找到规律,你会如何思考呢?如何预习?第四讲的知识非常的有趣,小朋友们可以尽情的享受找规律的乐趣.在一年级秋季的课程中,我们已经接触过了找规律画图,知道了数学中图形的规律有好多种,例如形状变化的规律,还有颜色变化、数量变化、位置变化、方向变化以及组合出现的规律.在学习二年级秋季第四讲《发现图形规律》这一讲之前,小朋友们可以回顾一下这些知识,为第四讲的课堂学习做一个铺垫.对于应当如何预习,潘老师在这里提醒一下各位小朋友,预习的时间不要过早,应该尽量安排在距离下次上课较近的时间里.预习的时候,不要过于关注做新的题目,对于全新的知识,可以把它们保留到课堂上再去思考、学习.相较于自己去摸索新的知识,不如先把与本讲次内容相关的以前学过的知识再拿出来回顾一下,这样的效果也许会更好哦~当然了,还有几句老话要啰嗦一下,预习的时间不宜过长,内容也不宜过多过细.在预习的时候要边看边做并且边思考,最好能带着你自己的问题去上课.《发现图形规律》知识点精讲【知识点总结】1、单一变化:颜色、形状、方向、大小、数量、位置……2、多样变化【例】按规律画出空白处的图形.这些图案有外部、有内部,它们的变化既有形状、方向的变化,又有数量的变化,因此要分不同的部分来找规律.外部:正三角形→正方形→正五边形→正六边形内部:1条横线→2条竖线→3条横线→4条竖线3、拼组:(1)简单:拼起来【例】根据下面图形排列的规律,问号的地方应该选择哪个图形?经观察,发现每一行、每一列的图形都有同样一个变化规律:第一个与第三个图形拼组在一起就是中间的图形.(2)复杂:组合消失【例】根据下面图形排列的规律,问号的地方应该选择哪个图形?方法1:横着看,每行的任意两个图形拼组到一起,重合部分消失,就变成了另外一个图形. 方法2:竖着看,每列的任意两个图形拼组到一起,重合部分消失,也变成了另外一个图形. (因为这题要求的是最右下角的图形,所以不论是横看还是竖看,最快的方法是通过第一个和第二个的图形拼组在一起,重合部分消失来得到.)4、缺什么补什么【例】下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个娃娃头画出来.经观察,发现在每一行每一列,这些娃娃头都由头发(一毛、两毛和三毛)、脸(圆脸、方脸和三角形脸)、眼睛(黑眼、白眼和黑白眼)、嘴巴(一个白三角嘴、两个黑三角嘴)组成,因此可以用缺什么补什么的方法,并且要分部分来看.不管是横着看还是竖着看,最右下角缺的娃娃头是三毛、方脸、黑白眼、白三角嘴.【例】观察图形的变化规律,按照这种变化规律,在空格中画上应有的图形.观察,每个田字格中有4种图形,从第一个田字格变到第二个田字格,每个小图形的位置改变了,并且有些图形自身的形状也改变了.先看位置的变化:每个图形都按逆时针方向旋转.再看图形自身方向的变化:每个图形自身也都在按逆时针方向旋转.(圆形与正方形在本题中旋转后与原先没有区别.)(实际上本题也可以理解成整个田字格在按着顺时针方向旋转.)《发现图形规律》补充题1、根据规律,问号处应填什么图形?2、根据规律,画出空白处的图形.3、根据规律,画出问号处的图形.4、按规律画出空白处的图形.5、下面一组图形的阴影变化是有规律的,请根据这个规律把第四幅图的阴影部分画出来.6、按规律填图.7、根据A~F这几个人的排列规律,接下来应该排列的是G、H、I中的哪一个?答案1、(1)(2)【解析】:两小题中的图形都是依次按逆时针方向旋转90度.2、【解析】:本题中图形排列的规律是每一行的第一个图形和第三个图形合在一起就是第二个图形.3、【解析】:本题可以竖着来看,每一列的图形都是依次按顺时针方向旋转90度.4、(1)【解析】:通过观察,不难发现,图形从左到右的变化规律是:外面是正方形、圆形边框在交替出现,里面是箭头的数量依次加1,并且箭头的方向是一正一反出现.(2)【解析】:每一组都有三种图形,分别是圆形、箭头和三角形,我们可以依次来观察.圆形始终不变,箭头是按顺时针方向旋转,三角形是按逆时针方向旋转.(3)【解析】:观察第一至第三组字母排列变化的规律是:字母D在中间不动,其余字母从左往右依次移动1个位置,最右边的字母则移动到最左边.移动中如果遇到字母C就跳过去.5、【解析】:经观察可发现,每个图形中都有四个阴影格子,依次向右上方向推移.第二个图形中,向上推移后只有3个阴影格子,则还需要1个,注意要在左下方的对角的地方寻找.第三个图形中,继续向上推移只有2个阴影格子,则还需要2个,那么就在另一个对角上寻找到两个.第四个图形,则应该向右上方推移到只有1个阴影格子,则剩下的三个在左下方如图所示位置.注意,两个阴影格子之间没有共用的边,只有一个角相连.6、【解析】:题目给出的例子中,有三种图形,我们可以从上往下依次来观察.左图上部外面的白色圆形变成了右图上部缩小了的黑色圆形,颜色与大小都改变,位置没变,还是在上部.左图上部里面的黑色正方形变成了右图下部的白色正方形,颜色与位置改变,大小不变.左图下部的三角形变成了右图上部的三角形,颜色大小不变,位置改变.同样的规律运用到题目中,可知题目里上部外面的菱形将改变颜色和大小,放置在上部的中心,而上部里面的圆形将不改变大小,改变颜色,放置在下部.而下部的梯形将不改变颜色和大小,放置在上部.7、【解析】:观察可以发现,从第一个火柴人开始,到B增加2条线,到C拿走1条线,到D增加3条线,到E拿走2条线,到F增加4条线,按规律继续往下画在F的基础上应该拿走3条线,应该选择G.。

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:⑴图形数量的变化; ⑵图形形状的变化; ⑶图形大小的变化; ⑷图形颜色的变化; ⑸图形位置的变化; ⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.模块一、图形规律——数量规律【例 1】 观察这几个图形的变化规律,在横线上画出适当的图形.【考点】图形找规律 【难度】1星 【题型】填空【解析】 几个图形的边数依次增加,因此横线上应为一个七边形. 【答案】七边形【例 2】 请找出下面哪个图形与其他图形不一样.(1)(2)(3)(4)(5)【考点】图形找规律 【难度】1星 【题型】填空【解析】 这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个六边形,而其它几个都是四边形,这样,只有(4)与其它不一样【答案】(4)【例 3】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【考点】图形找规律 【难度】2星 【题型】填空例题精讲知识点拨4-1-2.图形找规律【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【答案】【例4】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按5、4、3、?、1的顺序变化的,显然“?”处应填一个圆形.(方法二)竖着看,圆形由左而右依次减少,而三角形由左而右依次增加,圆形按照5、4、?、2、1的顺序变化,也可以看出“?”处应是圆形.【答案】圆形【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【考点】图形找规律【难度】2星【题型】填空【解析】(方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出“?”处应是三角形△.【答案】△【例5】观察下面的图形,按规律在“?”处填上适当的图形.(4)?【考点】图形找规律 【难度】2星 【题型】填空【解析】 本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【答案】七个黑三角形【例 6】 观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【考点】图形找规律 【难度】2星 【题型】填空【解析】 第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:【答案】【例 7】 观察下图中的点群,请回答:(1) 方框内的点群包含 个点;(2) 推测第10个点群中包含 个点;(3)前10个点群中,所有点的总数是 。

几何变化规律1、正方形边长扩大(缩小)a倍,周长扩大(缩小)a倍。
面积扩大(缩小)a×a(a2)倍。
2、长方形长和宽同时扩大(缩小)a倍,周长扩大(缩小)a倍,面积扩大(缩小)a×a(a2)倍。
3、正方体棱长扩大(缩小)a倍,棱长之和扩大(缩小)a倍。
表面积扩大(缩小)a×a(a2)倍。
体积扩大(缩小)a×a×a(a3)倍。
4、长方体长、宽、高同时扩大(缩小)a倍,棱长之和扩大(缩小)a倍。
表面积扩大(缩小)a×a(a2)倍。
体积扩大(缩小)a×a×a(a3)倍。
5、长方形拉成平行四边形周长不变,高变短,面积变小。
平行四边形拉成长方形周长不变,高变长,面积变大。
6、周长一定正方形面积最大,长方形次之,平行四边形面积最小。
7、n个长、正方体拼在一起成为长方体新长方体最大表面积=【单个长、正方体表面积–最小面积(两个最小数的乘积)】×(n-1)×2新长方体最小表面积=【单个长、正方体表面积–最大面积(两个最小数的乘积)】×(n-1)×28、边长1分米的的正方体,体积是1立方分米,能分成体积是1立方厘米的小正方体1000个,把这些小正方体排成一行,新的长方体长是1000厘米、高是1厘米、宽是1厘米。
9、煅造和分割都是体积不变,表面积变。
解题时要抓住体积相等进行解答。
10、正方体棱长=正方体棱长之和÷12 正方体一个面面积=正方体表面积÷6长方体(长+宽+高)=棱长之和÷4 长方体高=长方体体积÷底面积11、有一组对面是正方形的长方体,四个侧面面积相等。
表面积=边长×边长×2+边长×高×4上、下 4个侧面。

方法:①观察变化的规律。
②抓住每次变化的规律与图形次数的关系。
一.照这样摆下去。
(n表示的是图形的个数)除了第1根小棒,观察到每摆一个三角形就多2根小棒,也就1. ……是摆几个这样的三角形,就要用几个2根小棒。
同时别忘了,开头的第1根没算进去。
可得,摆n个三角形就有(2n+1)根小棒。
①照这样摆下去,20个三角形要几根小棒?②154根小棒最多可以摆几个这样的三角形?20×2+1= 41(根)(154-1)÷2=76(个)…… 1(根)答:20个三角形要41根小棒。
答:152根小棒最多可以摆76个这样的三角形。
除了第1根小棒,观察到每摆一个正方形就多3根小棒,也就2. ……是摆几个这样的正方形,就要用几个3根小棒。
同时别忘了,开头的第1根没算进去。
可得,摆n个正方形就有(3n+1)根小棒。
①照这样摆下去,20个正方形要几根小棒?②154根小棒最多可以摆几个这样的三角形?20×3+1= 61(根)(154-1)÷3 = 51(个)答:20个三角形要61根小棒。
答:153根小棒最多可以摆51个这样的正方形。
……规律同上3. ……除了第1根小棒,观察到每摆一个正五边形就多4根小棒,也就是摆几个这样的正五形,就要用几个4根小棒。
同时别忘了,开头的第1根没算进去。
可得,摆n个正方形就有(4n+1)根小棒。
①照这样摆下去,20个正五边形要几根小棒?②154根小棒最多可以摆几个这样的正五边形?20×4+1= 81(根)(154-1)÷4 = 38(个)…… 1(根)答:20个正五边形要81根小棒。
答:153根小棒最多可以摆20个这样的正五边形。
4. ……除了第1根小棒,观察到每摆一个正六边形就多5根小棒,也就是摆几个这样的正六边形,就要用几个5根小棒。
同时别忘了,开头的第1根没算进去。
可得,摆n个正六边形就有(5n+1)根小棒。
①照这样摆下去,20个六边形要几根小棒?②154根小棒最多可以摆几个这样的六边形?20×5+1= 101(根)(154-1)÷5 = 30(个)…… 3(根)答:20个正六边形要101根小棒。
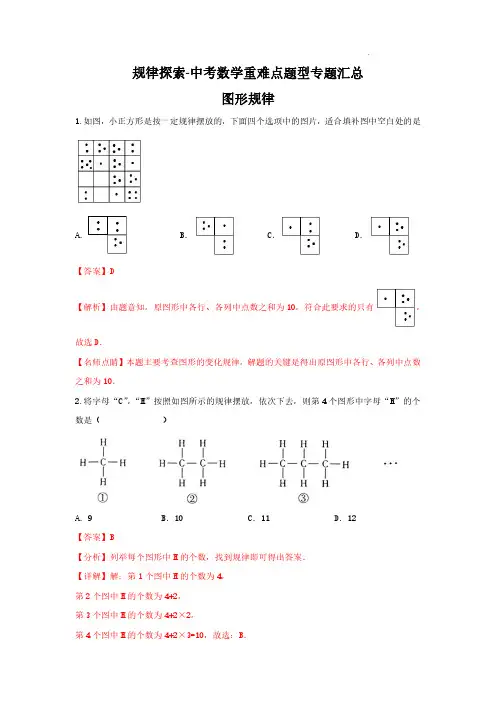
规律探索-中考数学重难点题型专题汇总图形规律1.如图,小正方形是按一定规律摆放的,下面四个选项中的图片,适合填补图中空白处的是A.B.C.D.【答案】D【解析】由题意知,原图形中各行、各列中点数之和为10,符合此要求的只有,故选D.【名师点睛】本题主要考查图形的变化规律,解题的关键是得出原图形中各行、各列中点数之和为10.2.将字母“C”,“H”按照如图所示的规律摆放,依次下去,则第4个图形中字母“H”的个数是()A.9B.10C.11D.12【答案】B【分析】列举每个图形中H的个数,找到规律即可得出答案.【详解】解:第1个图中H的个数为4,第2个图中H的个数为4+2,第3个图中H的个数为4+2×2,第4个图中H的个数为4+2×3=10,故选:B.【点睛】本题考查了规律型:图形的变化类,通过列举每个图形中H 的个数,找到规律:每个图形比上一个图形多2个H 是解题的关键.3.把菱形按照如图所示的规律拼图案,其中第①个图案中有1个菱形,第②个图案中有3个菱形,第③个图案中有5个菱形,…,按此规律排列下去,则第⑥个图案中菱形的个数为()A.15B.13C.11D.9【答案】C 【分析】根据第①个图案中菱形的个数:1;第②个图案中菱形的个数:123+=;第③个图案中菱形的个数:1225+⨯=;…第n 个图案中菱形的个数:()121n +-,算出第⑥个图案中菱形个数即可.【详解】解:∵第①个图案中菱形的个数:1;第②个图案中菱形的个数:123+=;第③个图案中菱形的个数:1225+⨯=;…第n 个图案中菱形的个数:()121n +-,∴则第⑥个图案中菱形的个数为:()126111+⨯-=,故C 正确.故选:C.【点睛】本题主要考查的是图案的变化,解题的关键是根据已知图案归纳出图案个数的变化规律.4.如图是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为()A.148B.152C.174D.202【分析】观察各图可知,后一个图案比前一个图案多2(n+3)枚棋子,然后写成第n个图案的通式,再取n=10进行计算即可求解.【解析】根据图形,第1个图案有12枚棋子,第2个图案有22枚棋子,第3个图案有34枚棋子,…第n个图案有2(1+2+…+n+2)+2(n﹣1)=n2+7n+4枚棋子,故第10个这样的图案需要黑色棋子的个数为102+7×10+4=100+70+4=174(枚).故选:C.5.把黑色三角形按如图所示的规律拼图案,其中第①个图案中有1个黑色三角形,第②个图案中有3个黑色三角形,第③个图案中有6个黑色三角形,…,按此规律排列下去,则第⑤个图案中黑色三角形的个数为()A.10B.15C.18D.21n个图案中黑色三角形的个数为1+2+3+4+……+n,据此可得第⑤个图案中黑色三角形的个数.【解析】∵第①个图案中黑色三角形的个数为1,第②个图案中黑色三角形的个数3=1+2,第③个图案中黑色三角形的个数6=1+2+3,……∴第⑤个图案中黑色三角形的个数为1+2+3+4+5=15,故选:B.Y Y-=()6.观察下列树枝分杈的规律图,若第n个图树枝数用n Y表示,则94A.4152⨯B.4312⨯C.4332⨯D.4632⨯【答案】B【分析】根据题目中的图形,可以写出前几幅图中树枝分杈的数量,从而可以发现树枝分杈的变化规律,进而得到规律21nn Y =-,代入规律求解即可.【详解】解:由图可得到:11223344211213217211521n n Y Y Y Y Y =-==-==-==-==-则:9921Y =-,∴944942121312Y Y -=--+=⨯,故答案选:B.【点睛】本题考查图形规律,解答本题的关键是明确题意,利用数形结合的思想解答.7.用正方形按如图所示的规律拼图案,其中第①个图案中有5个正方形,第②个图案中有9个正方形,第③个图案中有13个正方形,第④个图案中有17个正方形,此规律排列下去,则第⑨个图案中正方形的个数为()A.32B.34C.37D.41【分析】第1个图中有5个正方形,第2个图中有9个正方形,第3个图中有13个正方形,……,由此可得:每增加1个图形,就会增加4个正方形,由此找到规律,列出第n 个图形的算式,然后再解答即可.【详解】解:第1个图中有5个正方形;第2个图中有9个正方形,可以写成:5+4=5+4×1;第3个图中有13个正方形,可以写成:5+4+4=5+4×2;第4个图中有17个正方形,可以写成:5+4+4+4=5+4×3;...第n 个图中有正方形,可以写成:5+4(n-1)=4n+1;当n=9时,代入4n+1得:4×9+1=37.故选:C.【点睛】本题主要考查了图形的变化规律以及数字规律,通过归纳与总结结合图形得出数字之间的规律是解决问题的关键.8.在平面直角坐标系中,等边AOB ∆如图放置,点A 的坐标为()1,0,每一次将AOB ∆绕着点О逆时针方向旋转60︒,同时每边扩大为原来的2倍,第一次旋转后得到11AOB ∆,第二次旋转后得到22A OB ∆,…,依次类推,则点2021A 的坐标为()A.()202020202,2-B.()202120212,2C.()202020202,2⨯D.()201120212,2-【答案】C【分析】由题意,点A 每6次绕原点循环一周,利用每边扩大为原来的2倍即可解决问题.解:由题意,点A 每6次绕原点循环一周,20216371......5÷= ,2021A ∴点在第四象限,202120212OA =,202160xOA ∠=︒,∴点2020A 的横坐标为20212020122=2⨯,纵坐标为20212020=3222-⨯-,()2020202020212,2A ∴,故选:C.【点睛】本题考查坐标与图形变化-旋转,规律型问题,解题的关键是理解题意,学会探究规律的方法,属于中考常考题型.9.如图,用大小相同的小正方形拼大正方形,拼第1个正方形需要4个小正方形,拼第2个正方形需要9个小正方形…,按这样的方法拼成的第(n+1)个正方形比第n 个正方形多个小正方形.【分析】观察不难发现,所需要的小正方形的个数都是平方数,然后根据相应的序数与正方形的个数的关系找出规律解答即可.【解析】∵第1个正方形需要4个小正方形,4=22,第2个正方形需要9个小正方形,9=32,第3个正方形需要16个小正方形,16=42,…,∴第n+1个正方形有(n+1+1)2个小正方形,第n 个正方形有(n+1)2个小正方形,故拼成的第n+1个正方形比第n 个正方形多(n+2)2﹣(n+1)2=2n+3个小正方形.故答案为:2n+3.10.观察下列图中所示的一系列图形,它们是按一定规律排列的,依照此规律,第2019个图形中共有__________个〇.【答案】6058【解析】由图可得,第1个图象中〇的个数为:1+3×1=4,第2个图象中〇的个数为:1+3×2=7,第3个图象中〇的个数为:1+3×3=10,第4个图象中〇的个数为:1+3×4=13,…∴第2019个图形中共有:1+3×2019=1+6057=6058个〇,故答案为:6058.【名师点睛】本题考查图形的变化类,解答本题的关键是明确题意,发现图形中〇的变化规律,利用数形结合的思想解答.11.如图,每一图中有若干个大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,如果第n幅图中有2019个菱形,则n=__________.【答案】1010【解析】根据题意分析可得:第1幅图中有1个.第2幅图中有2×2-1=3个.第3幅图中有2×3-1=5个.第4幅图中有2×4-1=7个.…可以发现,每个图形都比前一个图形多2个.故第n幅图中共有(2n-1)个.当图中有2019个菱形时,2n-1=2019,n=1010,故答案为:1010.【名师点睛】本题考查规律型中的图形变化问题,难度适中,要求学生通过观察,分析、归纳并发现其中的规律.12.观察下列图形规律,当图形中的“○”的个数和“.”个数差为2022时,n的值为____________.【答案】不存在【分析】首先根据n=1、2、3、4时,“•”的个数分别是3、6、9、12,判断出第n 个图形中“•”的个数是3n;然后根据n=1、2、3、4,“○”的个数分别是1、3、6、10,判断出第n 个“○”的个数是()12n n +;最后根据图形中的“○”的个数和“.”个数差为2022,列出方程,解方程即可求出n 的值是多少即可.【详解】解:∵n=1时,“•”的个数是3=3×1;n=2时,“•”的个数是6=3×2;n=3时,“•”的个数是9=3×3;n=4时,“•”的个数是12=3×4;……∴第n 个图形中“•”的个数是3n;又∵n=1时,“○”的个数是1=1(11)2⨯+;n=2时,“○”的个数是32=n=3时,“○”的个数是3(31)62⨯+=,n=4时,“○”的个数是4(41)102⨯+=,……∴第n 个“○”的个数是()12n n +,由图形中的“○”的个数和“.”个数差为2022()1320222n n n +∴-=①,()1320222n n n +-=②解①得:无解解②得:1255,22n n +-==故答案为:不存在【点睛】本题考查了图形类规律,解一元二次方程,找到规律是解题的关键.13.将黑色圆点按如图所示的规律进行排列,图中黑色圆点的个数依次为:1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为___________.【答案】1275【分析】首先得到前n个图形中每个图形中的黑色圆点的个数,得到第n个图形中的黑色圆点的个数为()12n n+,再判断其中能被3整除的数,得到每3个数中,都有2个能被3整除,再计算出第33个能被3整除的数所在组,为原数列中第50个数,代入计算即可.【详解】解:第①个图形中的黑色圆点的个数为:1,第②个图形中的黑色圆点的个数为:()1222+⨯=3,第③个图形中的黑色圆点的个数为:()1332+⨯=6,第④个图形中的黑色圆点的个数为:()1442+⨯=10,第n个图形中的黑色圆点的个数为()1 2n n+,则这列数为1,3,6,10,15,21,28,36,45,55,66,78,91,,其中每3个数中,都有2个能被3整除,33÷2=161,16×3+2=50,则第33个被3整除的数为原数列中第50个数,即50512⨯=1275,故答案为:1275.【点睛】此题考查了规律型:图形的变化类,关键是通过归纳与总结,得到其中的规律.14.如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有______个交点【答案】190【分析】根据题目中的交点个数,找出n条直线相交最多有的交点个数公式:1(1) 2n n-.【详解】解:2条直线相交有1个交点;3条直线相交最多有1123322+==⨯⨯个交点;4条直线相交最多有11236432++==⨯⨯个交点;5条直线相交最多有1123410542+++==⨯⨯个交点;⋯20条直线相交最多有12019190 2⨯⨯=.故答案为:190.【点睛】本题考查的是多条直线相交的交点问题,解答此题的关键是找出规律,即n条直线相交最多有1(1) 2n n-.15.如图,用火柴棍拼成一个由三角形组成的图形,拼第一个图形共需要3根火柴棍,拼第二个图形共需要5根火柴棍;拼第三个图形共需要7根火柴棍;……照这样拼图,则第n 个图形需要___________根火柴棍.【答案】2n+1【分析】分别得到第一个、第二个、第三个图形需要的火柴棍,找到规律,再总结即可.【详解】解:由图可知:拼成第一个图形共需要3根火柴棍,拼成第二个图形共需要3+2=5根火柴棍,拼成第三个图形共需要3+2×2=7根火柴棍,拼成第n 个图形共需要3+2×(n-1)=2n+1根火柴棍,故答案为:2n+1.【点睛】此题考查图形的变化规律,找出图形之间的联系,得出运算规律解决问题.16.如图都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第___个图形共有210个小球.【答案】20【分析】根据已知图形得出第n 个图形中黑色三角形的个数为1+2+3+ +n=()12n n +,列一元二次方程求解可得.【详解】解:∵第1个图形中黑色三角形的个数1,第2个图形中黑色三角形的个数3=1+2,第3个图形中黑色三角形的个数6=1+2+3,第4个图形中黑色三角形的个数10=1+2+3+4,……∴第n 个图形中黑色三角形的个数为1+2+3+4+5+ +n=()12n n +,当共有210个小球时,()12102n n +=,解得:20n =或21-(不合题意,舍去),∴第20个图形共有210个小球.故答案为:20.【点睛】本题考查了图形的变化规律,解一元二次方程,解题的关键是得出第n 个图形中黑色三角形的个数为1+2+3+……+n.17.如图,由两个长为2,宽为1的长方形组成“7”字图形ABCDEF,其中顶点A 位于x 轴上,顶点B,D 位于y 轴上,O 为坐标原点,则OB OA的值为__________.(2)在(1)的基础上,继续摆放第二个“7”字图形得顶点F 1,摆放第三个“7”字图形得顶点F 2,依此类推,…,摆放第n 个“7”字图形得顶点F n-1,…,则顶点F 2019的坐标为__________.【答案】(1)12;(2)606255(,【解析】(1)∵∠ABO+∠DBC=90°,∠ABO+∠OAB=90°,∴∠DBC=∠OAB,∵∠AOB=∠BCD=90°,∴△AOB∽△BCD,∴OB DC OA BC =,∵DC=1,BC=2,∴OB OA =12,故答案为:12.(2过C 作CM⊥y 轴于M,过M 1作M 1N⊥x 轴,过F 作FN 1⊥x 轴.根据勾股定理易证得BD ==CM=OA=5,DM=OB=AN=5,∴C(5),∵AF=3,M 1F=BC=2,∴AM 1=AF-M 1F=3-2=1,∴△BOA≌ANM 1(AAS),∴NM 1=OA=255,∵NM 1∥FN 1,∴1111251553M N AM FN AF FN ==,,∴FN 1=655,∴AN 1=355,∴ON 1=OA+AN 1=253555555+=,∴F(555,655),同理,F 1(857555,F 2(55,),F 3(1459555,),F 4(17510555,),…F 2019),即(【名师点睛】此题考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳并发现其中的规律,并应用规律解决问题是解题的关键18.如图,正方形1ABCB 中,AB =,AB 与直线l 所夹锐角为60︒,延长1CB 交直线l 于点1A ,作正方形1112A B C B ,延长12C B 交直线l 于点2A ,作正方形2223A B C B ,延长23C B 交直线l 于点3A ,作正方形3334A B C B ,…,依此规律,则线段20202021A A =________.【答案】20203【分析】利用tan30°计算出30°角所对直角边,乘以2得到斜边,计算3次,找出其中的规律即可.【详解】∵AB 与直线l 所夹锐角为60︒,正方形1ABCB 中,AB =,∴∠11B AA =30°,∴11B A =1B A∴111=2=2(3AA -;∵11B A =1,∠122B A A =30°,∴22B A =11B A tan30°=33133⨯=,∴2112=23A A -⨯;∴线段20202021A A =202112020332(33-⨯=,故答案为:2020)3.【点睛】本题考查了正方形的性质,特殊角三角函数值,含30°角的直角三角形的性质,规律思考,熟练进行计算,抓住指数的变化这个突破口求解是解题的关键.19.如图,菱形ABCD 中,120ABC ∠=︒,1AB =,延长CD 至1A ,使1DA CD =,以1AC 为一边,在BC 的延长线上作菱形111ACC D ,连接1AA ,得到1ADA ∆;再延长11C D 至2A ,使1211D A C D =,以21A C 为一边,在1CC 的延长线上作菱形2122A C C D ,连接12A A ,得到112A D A ∆……按此规律,得到202020202021A D A ∆,记1ADA ∆的面积为1S ,112A D A ∆的面积为2S ……202020202021A D A ∆的面积为2021S ,则2021S =_____.【答案】40382【分析】由题意易得60,1BCD AB AD CD ∠=︒===,则有1ADA ∆为等边三角形,同理可得112A D A ∆…….202020202021A D A ∆都为等边三角形,进而根据等边三角形的面积公式可得134S =,2S =242n n S -=,然后问题可求解.【详解】解:∵四边形ABCD 是菱形,∴1AB AD CD ===,//,//AD BC AB CD ,∵120ABC ∠=︒,∴60BCD ∠=︒,∴160ADA BCD ∠=∠=︒,∵1DA CD =,∴1DA AD =,∴1ADA ∆为等边三角形,同理可得112A D A ∆…….202020202021A D A ∆都为等边三角形,过点B 作BE⊥CD 于点E,如图所示:∴3sin 2BE BC BCD =⋅∠=,∴1121133244A D BE A S D =⋅==,同理可得:2222133244S A D ==⨯=,2233233444S A D ==⨯=∴由此规律可得:242n n S -=,∴2202144038202122S ⨯-==⋅;故答案为40382【点睛】本题主要考查菱形的性质、等边三角形的性质与判定及三角函数,熟练掌握菱形的性质、等边三角形的性质与判定及三角函数是解题的关键.20.将一些相同的“〇”按如图所示的规律依次摆放,观察每个“龟图”的“〇”的个数,则第30个“龟图”中有___________个“〇”.【答案】875【分析】设第n 个“龟图”中有a n 个“〇”(n 为正整数),观察“龟图”,根据给定图形中“〇”个数的变化可找出变化规律“a n =n 2−n+5(n 为正整数)”,再代入n=30即可得出结论.【详解】解:设第n 个“龟图”中有a n 个“〇”(n 为正整数).观察图形,可知:a 1=1+2+2=5,a 2=1+3+12+2=7,a 3=1+4+22+2=11,a 4=1+5+32+2=17,…,∴a n =1+(n+1)+(n −1)2+2=n 2−n+5(n 为正整数),∴a 30=302−30+5=875.故答案是:875.【点睛】n =n 2−n+5(n 为正整数)”是解题的关键.21.下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形…,依此规律,则第n 个图形中三角形个数是_______.【答案】21n n +-【分析】此题只需分成上下两部分即可找到其中规律,上方的规律为(n-1),下方规律为n 2,结合两部分即可得出答案.【详解】解:将题意中图形分为上下两部分,则上半部规律为:0、1、2、3、4……n-1,下半部规律为:12、22、32、42……n 2,∴上下两部分统一规律为:21n n +-.故答案为:21n n +-.【点睛】本题主要考查的图形的变化规律,解题的关键是将图形分为上下两部分分别研究22.如图是一组有规律的图案,它们是由边长相等的正三角形组合而成,第1个图案有4个三角形,第2个图案有7个三角形,第3个图案有10个三角形…按此规律摆下去,第n 个图案有个三角形(用含n 的代数式表示).【分析】根据图形的变化发现规律,即可用含n 的代数式表示.【解析】第1个图案有4个三角形,即4=3×1+1第2个图案有7个三角形,即第3个图案有10个三角形,即10=3×3+1…按此规律摆下去,第n 个图案有(3n+1)个三角形.故答案为:(3n+1).23.如图,四边形ABCD 是矩形,延长DA 到点E,使AE=DA,连接EB,点F 1是CD 的中点,连接EF 1,BF 1,得到△EF 1B;点F 2是CF 1的中点,连接EF 2,BF 2,得到△EF 2B;点F 3是CF 2的中点,连接EF 3,BF 3,得到△EF 3B;…;按照此规律继续进行下去,若矩形ABCD 的面积等于2,则△EF n B 的面积为.(用含正整数n 的式子表示)【分析】先求得△EF 1D 的面积为1,再根据等高的三角形面积比等于底边的比可得EF 1F 2的面积,EF 2F 3的面积,…,EF n﹣1F n 的面积,以及△BCF n 的面积,再根据面积的和差关系即可求解.【解析】∵AE=DA,点F 1是CD 的中点,矩形ABCD 的面积等于2,∴△EF 1D 和△EAB 的面积都等于1,∵点F 2是CF 1的中点,∴△EF 1F 2的面积等于12,同理可得△EF n﹣1F n 的面积为12n−1,∵△BCF n 的面积为2×12n ÷2=12n ,∴△EF n B 的面积为2+1﹣1−12−⋯−12n−1−12n =2﹣(1−12n )=2n +12n .故答案为:2n +12n .。

图形推理的规律1.大小变化2.方向旋转3.笔画增减(数字、线条数)4.图形求同5.相同部份去掉6.图形叠加(简单叠加、合并叠加、去同叠加)7.图形组合变化(如:首尾两个图形中都包含中间图形)8.对应位置阴影变化(两图相同或不同则第三图对应位置变阴影或变空白)9.顺时针或逆时针旋转10.总笔画成等差数列11.由内向外逐步包含12.相同部件,上下、左右组合13.类似组合(如平行、图形个数一样等)14.横竖线条之比有规律(如横线3条竖线4条、横线4条竖线5条等)15.缺口相似或变化趋势相似(如逐步远离或靠近)16.图形运动变化(同一个图形从各个角度看的不同样子)17.图形拆分(有三个图构成,后两个图为第一个图的构成部件)18.线条交点数有规律19.方向规律(上、下、左、右)20.相隔一个图形分别对称(如:以第三个图为中心,1和5对称,2和4对称) 21.含义依据条件而变(如一个错号,可以表“一划”,也可以表示“两划”)22.图形趋势明显(点或图形从左到右、从上到下变化等)23.图形的上、中、下部分分别变化(求同,重叠,或去同叠加)24.相似类(包含、平行、覆盖、相交、不同图形组成、含同一图形等)25.上、中、下各部分别翻转变化26.角的度数有规律27.阴影重合变空白28.翻转、叠加、再翻转30.与特定线的交点数相同(如:与折线的交点数有规律,有直线的交点数不用考虑)31.图形有多条对称轴,且有共同交点,轴对称图形(如正三角形、正方形)32.平行、上下移动33.图形翻转对称34.图形边上角的个数增多或减少35.不同图形叠加形成新图36.图形中某条线均为长线或短线(寻找共同部分)37.线段间距离共性(如:直线上有几个点,分成几条线段,上部覆盖有另一个图形,如圆、三角形等,但是上面的图形占的位置都不大于最外面两点间的距离)38.图形外围,内部分别顺或逆时针旋转(内外部变化相反)39.特殊位置变化有规律(如当水平时、垂直时图形有一规律)40.各图形组成部件属于同一类(如:均为三条曲线相交)41.以第几幅图为中心进行变化(如:旋转、走近、相反等)42.求共同部分再加点变化(如:提出共同部分,然后让共同部分都变黑什么的)43.除去共同部分有规律44.数线段出头数,有规律(成等差数列,或有明显规律)45.每行图形被分割成的空间数相同46.以中间图形为中心,上下、对角分别成对称47.先递增再递减规律48.整套图形横着看,或竖着看,分别有规律49.注意考虑图形部分变化(如:分别为上下不变中间变化,然后上中下一起变化,左右分别变化,左右一起变化等)50.顺着次序变化(如:原来在内部的放大变为外部图形,内部图形相应变化。

数学篇解题指南图形变化问题就是观察一组由简到繁的图形的变化过程,然后归纳猜想,找出一般规律,进而列出通用的代数式的一类问题.我们在解答这类问题时,需从第1、2、3个甚至更多个简单图形开始,分析其变化规律,然后借助代数式推算出后面更复杂图形的变化形式,从而得出结果.图形规律题通常分为“同增幅”与“变增幅”两大类,下面举例予以说明.一、“同增幅”图形的变化规律“同增幅”图形是指相邻两个图形增加的量是相同的,即增幅相等.我们可以借助“做标记”的方法找出相同增幅,从而将图形变化规律转化为数字变化规律,并将数量关系用代数式表示出来.1.单一增加型单一增加型是指图形的变化是以某一个小整体依次连续不断的增加组成的.解答的策略即先观察分析递增的组合图,然后用作差法确定图形变化的增幅,进而探寻图形的变化规律.例1图1为一组有规律的图案,第1个图案由4个基础图形构成,第2个图案由7个基础图形构成,……,第n(n 为正整数)个图案中由__________个基础图形构成.图1分析:该图案每两个之间增加的图形是相同的,即其增加的“幅度”是相等的.可以通过“做标记”(如图1-1所示)的方法将其增加部分表示出来.这样就可以清楚地看出增加的部分是相同的.然后利用归纳和推理找出其中的规律.图1-1解:通过观察和归纳发现:第1个图案:4个基本图形;第2个图案:4个基本图形+3个基本图形(阴影标注),共4+3个基本图形;第3个图案:4个基本图形+3个基本图形(阴影标注)+3个基本图形(空心标注),共4+3+3=4+2×3个基本图形;……由此可以推理出:第n 个图案:4个基本图形+3个基本图形+…+3个基本图形,共4+3+…+3=4+(n -1)×3=3n +1个基本图形;所以,第n 个图案由(3n +1)个基本图形组成.评注:单一增加型图形的变化规律比较明显,同学们只需要耐心地画出两个相连图案之间的增幅,通过观察、归纳和整理即可解题.2.成倍增加型这类图形不是以图形的整体增加组成,而是图形各部分依次成倍地增加,通常很难快速找出增量,需要仔细观察,慢慢分析才可以找到突破口.解答这类问题应分步思考:第一步,把每次增加的部分表示出来;第二步,各部分相加表示出整体;第三步,确定增幅,找出规律.例2如图2,每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n ≥2)个棋子,每个图案的棋子总数为S ,按下图的分布规律推断,S 与n之间的关系可以用式子_________去表示.19数学篇数苑纵横图2分析:此题的图案是正方形,仔细观察图形可以发现,第2个图案四条边各增加一个棋子,第3个图案每条边各增加2个棋子,增量构成了边长为“2”的正方形.各图案间的增幅构成规则的正方形,且相邻图形的增量是相等的,因此,此题可以转化为求正方形周长问题.图2-1解:用空心圆标注图案“增幅”如图2-1所示.第1图案:4个棋子第2图案:4个棋子+4棋子(空心),即共4+4个棋子;第3图案:4个棋子+4棋子(空心)+4棋子(空心),即共4+2×4棋子;第4图案:4个棋子+4棋子(空心)+4棋子(空心)+4棋子(空心),即共4+3×4个棋子;……由此可以推算出:第n 图案:4个棋子+4棋子(空心)+…+4棋子(空心),即共4+(n -1)×4=4n 个棋子;所以,S =4n.评注:此类题的增幅虽然是“相同”的,但很容易让人产生增幅不等的错觉,同学们在研究分析图形变化规律时,要准确找出相邻图案间的“增幅”.二、“变增幅”图形的变化规律“变增幅”图形变化规律是指相邻两个图形增加的量是不同的.这类问题比较复杂,我们需要仔细观察图案,首先借助“做标记”的方法找到相邻图形之间的变化,并确定变化的增幅,然后找出增幅的数字变化规律,最后例3将一些半径雷同的小圆按如下图的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有_________个小圆.第n 个图形呢?图3分析:此题图案比较复杂,但细细观察可以发现,每个图案的四个角的小圆数量相等,属于不变量.因此我们只需要找出中间小圆的变化规律即可解题.再次观察图案发现,中间的小球相邻的图案每增加一行,同时增加一列,构成一个矩形,如图3-1所示.图3-1解:第1图案:4个球+2球(中间),即共4+2=4+1×2个球;第2图案:4个球+2×3球(中间矩形),即共4+2×3个球;第3图案:4个球+3×4球(中间矩形),即共4+3×4个球;第4图案:4个球+4×5球(中间矩形),即共4+4×5个球;……由此可以推算出:第6图案:4个球+6×7球(中间矩形),即共4+6×7=46个球……第n 图案:4个球+n ×(n +1)球(中间矩形)4+n ×(n +1)=n 2+n +4个球.评注:“变增幅”图形比较复杂,规律比较难寻,但只要我们仔细观察,找出“变”与“不变”的量,问题便可迎刃而解.在解答图形规律题时,同学们要多罗列出前几个图形的变化情况,找出变化趋势,然。

三年级奥数:图形规律知识定位找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.知识梳理一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:(1)图形数量的变化;(2)图形形状的变化;(3)图形大小的变化;(4)图形颜色的变化;(5)图形位置的变化;(6)图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.关于解决图形规律问题的常用方法:1、从图形数量、位置变化出发观察思考几何图形的规律2、从图形形状、大小变化发现寻找图形的变化规律3、掌握寻找复杂图形变化规律的方法图形规律问题的分类:1、从图形形状、大小、颜色变化发现寻找图形的变化规律2、从图形数量、位置变化出发观察思考几何图形的规律3、复杂图形变化规律竞赛考点挖掘1.从图形形状、大小、颜色变化发现寻找图形的变化规律题目2.从图形数量、位置变化出发观察思考几何图形的规律题目3.复杂图形变化规律题目例题精讲【题目】请找出下面哪个图形与其他图形不一样.【题目】根据左边图形的关系,画出右边图形的另一半.(1)(2)(3)【题目】在下面图形中找出一个与众不同的.【题目】按照下列图形的变化规律,空白处应是什么样的图形??【题目】如图,根据图中已知3个方格表中阴影的规律,在空白的方格表中也填上相应的阴影.【题目】观察图形变化规律,在右边补上一幅,使它成为一个完整系列【题目】观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.【题目】请观察下图中已有的几个图形,并按规律填出空白处的图形.【题目】下图中的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形.【题目】观察下列各组图的变化规律,并在“?”处画出相关的图形. (1)(2)【题目】观察下图中的点群,请回答:(1) 方框内的点群包含多少个点? (2) 推测第10个点群中包含多少个点? (3) 前10个点群中,所有点的总数是多少????ihgfedcba【题目】仔细观察下图中图形的变化规律,并在“?”处填入合适的图形.【题目】将“猫”“狗”“兔”“鸡”“猴”“虎”六个动物名称分别写在六个正方体的六个面上,从下面三种不同摆法中,判断这个正方体上哪些动物名名称分别写在相对面上.edcba??【题目】图10—1是由9个小人排列的方阵,但有一个小人没有到位,请你从下面图10—2中的6个小人中,选一位小人放到问号的位置,你认为最合适的人选是几号?【题目】四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第十次交换位子后,小兔坐在第几号位子上?习题演练【题目】顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形【题目】根据下列图形的变化规律,接着画下去.【题目】请找出下面哪个图形与其他图形不一样【题目】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【题目】仔细观察下列图形的变化,请先回答:(1)在方框(4)中应画出怎样的图形?(2)再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?。
找规律
一、找规律(图形变化规律)
1. 图形重复出现的规律:一般有2组或
2组以上的循环组才是有规律地排列。
重复出现的每组都和第一组相同。
图形组成的规律题型,通常可以分为两类:单一图形组成,多种图形组成。
2.图形排列规律的方法:
(1
)按照颜色重复的规律。
(
2)按照形状重复的规律。
3.找物体的摆放规律,仔细观察一组图形,并找出这组图形是按什么规律排列的,从而可以接着排列图形;也有图形的排列规律不再是重复出现,而是依次增加或者减少几个图形。
4.图形涂色题,要想好“循环组”,即每组有几个图形,分别涂什么颜色,涂几个这样的循环组。
二、图形规律习题:
4
5.根据规律画出被挡住部分的珠子。
6.划去不符合规律的图形和文字,圈出正确的。
7.找规律,填数。
图形规律1.大小变化2.方向旋转3.笔画增减(数字,线条数)4.图形求同5.相同部份去掉6.图形叠加(简单叠加,合并叠加,去同叠加)7.图形组合变化(如:首尾两个图形中都包含中间图形)8.对应位置阴影变化(两图相同或不同则第三图对应位置变阴影或变空白)9.顺时针或逆时针旋转10.总笔画成等差数列11.由内向外逐步包含12.相同部件,上下,左右组合13.类似组合(如平行,图形个数一样等)14.横竖线条之比有规律(如横线3条竖线4条,横线4条竖线5条等)15.缺口相似或变化趋势相似(如逐步远离或靠近)16.图形运动变化(同一个图形从各个角度看的不同样子)17.图形拆分(有三个图构成,后两个图为第一个图的构成部件)18.线条交点数有规律19.方向规律(上,下,左,右)20.相隔一个图形分别对称(如:以第三个图为中心,1和5对称,2和4对称)21.含义依据条件而变(如一个错号,可以表"划",也可以表示"两划")22.图形趋势明显(点或图形从左到右,从上到下变化等)23.图形的上,中,下部分分别变化(求同,重叠,或去同叠加)24.相似类(包含,平行,覆盖,相交,不同图形组成,含同一图形等)25.上,中,下各部分别翻转变化26.角的度数有规律27.阴影重合变空白28.翻转,叠加,再翻转30.与特定线的交点数相同(如:与折线的交点数有规律,有直线的交点数不用考虑)31.图形有多条对称轴,且有共同交点,轴对称图形(如正三角形,正方形)32.平行,上下移动33.图形翻转对称34.图形边上角的个数增多或减少35.不同图形叠加形成新图36.图形中某条线均为长线或短线(寻找共同部分)37.线段间距离共性.(如:直线上有几个点,分成几条线段,上部覆盖有另一个图形,如圆,三角形等,但是上面的图形占的位置都不大于最外面两点间的距离)38.图形外围,内部分别顺或逆时针旋转(内外部变化相反)39.特殊位置变化有规律(如当水平时,垂直时图形有一规律)40.各图形组成部件属于同一类(如:均为三条曲线相交)41.以第几幅图为中心进行变化(如:旋转,走近,相反等)42.求共同部分再加点变化(如:提出共同部分,然后让共同部分都变黑什么的)43.除去共同部分有规律44.数线段出头数,有规律(成等差数列,或有明显规律)45.图形每行空间数相同46.以中间图形为中心,上下,对角分别成对称47.先递增再递减规律48.整套图形横着看,或竖着看,分别有规律.49.注意考虑图形部分变化(如:分别为上下不变中间变化,然后上中下一起变化,左右分别变化,左右一起变化等)50.顺着次序变化.(如:原来在内部的放大变为外部图形,内部图形相应变化.左右组成的图,上一个右边图等于下个左边图,右边再加个新图,如此循环)第三部分、判断推理最关键的地方,看清题目,问的是不能还是能,加强还是削弱(是否有“除了”这个词)一.最多与最少概念之间的关系主要可以分为三大类:一是包含,如“江苏人”与“南京人”;二是交叉,如“江苏人”与“学生”;三是全异,如“江苏人”与“北京人”。
图形推理解题规律总结【1】【解析】左边一组中图形分别是上面小下面大(三角型),中间宽2头窄(圆),上面大下面小(倒三角型)。
所以第2组里也是一样的道理。
符合上面大下面小要求的是D。
【3】【解析】左边图形规律分别是1条虚线和1条实线相交以及2条虚线和2条实线相交。
右边的图形前2个图的规律是1条实线和1条虚线不相交。
第3个图就是答案便是2条实线和2条虚线不相交。
【4】【解析】左边图形的第1个变为第2个规律是横着的2条线移动其中1条消失,第2个边到第3个规律是一样,竖着的2条线移动到中间并去掉其中一条,而横着的线也被去掉,这样右边的图形一样的推拉。
右边图1到图2是2条线都移动并都去掉1条,这样到第3个图也就是答案便是都去掉。
答案是B。
【5】【解析】这道题规律是2个图形重合的地方全部去掉。
左边的图形先把2个图形合并就成为一个正方形里含个X。
但这个X是由2个X合并的。
所以并不是去掉X。
而是去掉正方形里的整个内部。
所以最后变成了一个正方形。
右边图形也是把重合的整块都去掉。
就是去掉长方形里的整块。
所以就剩下了2个三角形。
答案是C、【6】【解析】前4个图我们看到在正方形4个面。
伸出来的线条是有规律的。
分别是11,10,9,8条线伸出到正方形的外面,所最后一个图对应应该是7条伸出来的线,答案是C。
【7】【解析】2个图形同样的部分去掉,右边的图相同的去掉后便是一个三角形,答案是C。
【8】【解析】左边的图形是左右对称,右边的图形是以45度的角度的2边对称,只有C是这样对称的。
【9】【解析】规律是图形里的角的个数加上图形里点的个数都是8个,答案里只有D符合这个规律。
【10】【解析】旧字的一竖向中间移动就成了甲字,旦字下的一横想上移动就成了目字,答案是C。
【11】在左边的图形中【解析】第一个图去掉右半部分后正好是第二个图。
而第三个图正好是第一个图的右半部分与第二个图的上下结合(去掉重叠的边线)所以依照这个规律,答案选C【12】按笔画算左边一组笔画分别是1,3,5成等差右边的前2个笔画分别2,4。
类型二图形规律针对演练一、图形累加规律探索1. (2016荆州)如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案.若第n个图案中有2017个白色纸片,则n的值为()第1题图A. 671B. 672C. 673D. 6742. 下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有6个小圆圈,第②个图形中一共有9个小圆圈,第③个图形中一共有12个小圆圈,…,按此规律排列,则第⑦个图形中小圆圈的个数为()第2题图A. 21B. 24C. 27D. 303. (2016重庆B卷)观察下列一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是()第3题图A. 43B. 45C. 51D. 534. (2015曲靖)用火柴棒按如图所示的方式摆大小不同的“H”,依此规律,摆出第9个“H”需用火柴棒________根.第4题图5. (2015深圳)观察下列图形,它们是按照一定规律排列的,依照此规律,第五个图有________个太阳.第5题图6. (2016安顺)观察下列砌钢管的横截面图:第6题图则第n个图的钢管数是__________(用含n的式子表示).【答案】1.B【解析】对于每个图中的白色纸片的个数,依次是4,7=4+3,10=4+3×2,…,那么,第n个图中的白色纸片的个数为4+3×(n-1)=3n+1,令3n+1=2017,解得n=672.2.B【解析】第①个图形有6个小圆圈,第②个图形有6+3=9个小圆圈,第③个图形有6+3×2=12个小圆圈,…,按照这个规律,第个图形有6+3(n-1)=3n+3个小圆圈,故第⑦个图形一共有3×7+3=24个小圆圈.3.C【解析】图形①中星星的颗数为:2=1+(2×1-1),图形②中星星的颗数为:6=(1+2)+(2×2-1),图形③中星星的颗数为:11=(1+2+3)+(2×3-1),图形④中星星的颗数为:17=(1+2+3+4)+(2×4-1),…,图形中星星的颗数为:(1+2+…+n)+(2n-1)=n(n+1)2+2n-1,所以图形⑧中星星的颗数为:8×(8+1)2+2×8-1=51.4.29【解析】∴第9个“H ”所需的火柴棒的数量为3×9+2=29根.5.21 【解析】∵所有图形中,第一行太阳的个数分别为1,2,3,4,…,n ,∴第五个图形第一行太阳的个数为5,∵所有图形中,第二行太阳的个数分别为1,2,4,8,…,2n -1,∴第五个图形第二行太阳的个数为24=16个太阳,∴第五个图形共有5+16=21个太阳.6.32n 2+32n 【解析】由表可知,第n 个图的钢管数是3n (n +1)2=32n 2+32n .(2016重庆八中初三(下)第三次月考)下列是由一些火柴搭成的图案:图①用了5根火柴,图②用了9根火柴,图③用了13根火柴,按照这种方式摆下去,摆第⑧个图案用火柴棒的根数为 ( )第2题图A. 33B.32C. 31D. 303. (2015重庆B卷)下列图形都是由几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,依此规律,图⑩中黑色正方形的个数是()第3题图A.32B. 29C. 28D. 264. (2014重庆B卷)下列图形都是按照一定规律组成,第一个图形中共有2个三角形,第二个图形中共有8个三角形,第三个图形中共有14个三角形,…,依此规律,第五个图形中三角形的个数是()第4题图A. 22B. 24C. 26D. 285. 如图,下列图形是由边长为2的等边三角形按照一定规律排列而成,第①个图形的周长为6,第②个图形的周长为8,第③个图形的周长为10,第④个图形的周长为12,按照这样的规律来摆放,则第⑧个图形的周长为()第5题图A. 18B. 19C. 20D. 216. (2016天水改编)将一些相同的“○”按如图所示的规律依次摆放,其中图①中“○”的个数为5个,图②中“○”的个数为7个,图③中“○”的个数为11个,图④中“○”的个数为17个,…,若图○,n)中有245个“○”,则n=()第6题图A. 10B. 12C. 14D. 167. (2016重庆外国语学校二诊)下列图案均是用长度相同的小木棒按一定的规律拼搭而成,拼搭第(1)个图案需4根小木棒,拼搭第(2)个图案需10根小木棒,…,依此规律,拼搭第(6)个图案需小木棒的根数是()第7题图A. 53B. 54C. 55D. 568. (2016重庆江津中学初三下半期考试)用同样大小的黑色五角星按如图所示的方式摆图案,按照这样的规律摆下去,第⑬个图案需要的黑色五角星的个数是()第8题图A. 18B. 19C. 21D. 229. (2016重庆十一中一诊)下列图形是将正三角形按一定规律排列,则第④个图形中所有正三角形的个数有()第9题图A. 160B. 161C. 162D. 16310. (2016重庆巴蜀一诊)如图,每个图形都由同样大小的矩形按照一定的规律组成,其中第①个图形的面积为6 cm2,第②个图形的面积为18 cm2,第③个图形的面积为36 cm2,…,那么第⑥个图形的面积为()第10题图A. 84 cm2B. 90 cm2C. 126 cm2D. 168 cm211. (2016重庆西大附中第九次月考)下列图形都是用同样大小的♥按一定规律组成的,则第(8)个图形中♥共有()A. 80个B. 73个C. 64个D. 72个12. (2016重庆一中三模)如图所示,图①中含“〇”的矩形有1个,图②“〇”的矩形有7个,图③中含“〇”的矩形有17个,按此规律,图⑥中含“〇”的矩形个数为()A. 70B. 71C. 72D. 7313. (2016大渡口区诊断性检测)如图是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要棋子的枚数为()第13题图A. 115B. 122C. 127D. 13914. (2016重庆一中二模)下列图形都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有1个空心小圆圈,第②个图形中一共有6个空心小圆圈,第③个图形中一共有13个空心小圆圈,…,按此规律排列,则第⑦个图形中空心小圆圈的个数为()第14题图A. 61B. 63C. 76D. 7815. (2016重庆巴蜀中学保送生考试)如图,各图都由同样大小的图形①按一定规律组成,其中第①个图形中共有一个完整菱形,第②个图形中共有5个完整菱形,第③个图形中共有13个完整菱形,…,则第⑥个图形中完整菱形的个数为()A. 60B. 61C. 62D. 6316. (2016重庆一中第一次定时作业)已知四边形ABCD对角线相交于点O,若在线段BD上任意取一点(不与点B、O、D重合),并与A、C连接,如图①,则三角形个数为15个;若在线段BD上任意取两点(不与点B、O、D重合),如图②,则三角形个数为24个;若在线段BD上任意取三点(不与点B、O、D重合),如图③,则三角形个数为35个;…;以此规律,则图⑤中三角形的个数为()第16题图A. 48B. 56C. 61D. 6317. (2016徐州)如图,每个图案都由大小相同的正方形组成.按照此规律,第n 个图案中这样的正方形的总个数可用含n的代数式表示为________.第17题图18. (2016安顺改编)观察下列砌钢管的横截面图:第18题图则第5个图形中钢管数为________个.19. 如图,是由相同的花盆按一定的规律组成的形如正多边形的图案,其中第1个图案中花盆的个数为6个,第2个图案中花盆的个数为12个,第3个图案中花盆的个数为20个,…,则第8个图案中花盆的个数为________.第19题图20. (2016龙岩改编)用棱长为1的小正方体按照如图所示的摆放规律,逐个排成若干个无缝隙的几何体,图①几何体表面积为6,图②几何体表面积为18,则图④中所示几何体的表面积为________.第20题图答案类型一探索图形累加规律1. B【解析】每个图形中白色纸片的个数依次是4,7,10,13,….那么,第n 个图形中白色纸片的个数为3n+1,∴第12个图形中白色纸片的个数为3×12+1=37.2. A【解析】∵图①用了5根火柴,即5=5+4×0;图②用了9根火柴,即9=5+4×1;图③用了13根火柴,即13=5+4×2;…;以此规律,第○n个图形中,火柴的根数为5+4(n-1),故第⑧个图案用火柴棒的根数为5+4×(8-1)=33.3. B【解析】图①有2+3×0=2个黑色正方形;图②有2+3×1=5个黑色正方形;图③有2+3×2=8个黑色正方形;图④有2+3×3=11个黑色正方形,…,按照这个规律,图○n有2+3(n-1)个黑色正方形,故图⑩一共有2+3×9=29个黑色正方形.4. C【解析】第一个图形中有2个三角形:6×1-4=2;第二个图形中有8个三角形:6×2-4=8;第三个图形中有14个三角形:6×3-4=14;…;第n 个图形中三角形的个数为:6n-4,故第五个图形中三角形的个数为:6×5-4=26.5. C【解析】第①个图形的周长为6+0×2=6,第②个图形的周长为6+1×2=8,第③个图形的周长为6+2×2=10,第④个图形的周长为6+3×2=12,…,依此规律,可知第○n个图形的周长为6+(n-1)×2,所以第⑧个图形的周长为6+7×2=20.6. D【解析】图①中有1×(1-1)+5=5个“○”,图②中有2×(2-1)+5=7个“○”,图③中有3×(3-1)+5=11个“○”,图④中有4×(4-1)+5=17个“○”,…,据此得出:图○n中有n(n-1)+5个“○”,则可得方程n(n-1)+5=245,解得n1=16,n2=-15(不合题意,舍去).7. B【解析】观察图形可知,每个图案都是由横排小木棒和纵排小木棒搭建而成,且横排和纵排数相同,其中第(1)个图案有2横排,每排有1个小木棒;第(2)个图案有3横排,每排的小木棒个数分别为2,2,1;第(3)个图案有4横排,每排的小木棒个数分别为3,3,2,1;第(4)个图案有5横排,每排的小木棒个数分别为4,4,3,2,1,…;由此可推测第(n )个图案共有n +1横排,每排木棒个数分别为n ,n ,n -1,n -2,…,2,1,故第(6)个图案共有7横排,每排的小木棒个数分别为6,6,5,4,3,2,1,共有27根,则对应的纵排也有27根小木棒,则搭建第(6)个图案共需要小木棒54根.8. C 【解析】观察图形可以发现图①中黑色五角星的个数为1+2=3,图②中黑色五角星个数为1+2+1=4,图③中黑色五角星个数为1+2+1+2=6,图④中黑色五角星个数为1+2+1+2+1=7,图⑤中黑色五角星个数为1+2+1+2+1+2=9,…,则图○n 中,当n 为奇数时,黑色五角星个数为2)1(3+n ,当n 为偶数时,黑色五角星个数为123+n ,∴第⑬个图案需要的黑色五角星的个数为3×(13+1)2=21个. 9. B 【解析】第①个图形中正三角形的个数为:1+4,第②个图形中正三角形的个数为:1+4+3×4,第③个图形中正三角形的个数为:1+4+3×4+9×4,…,第○n 个图形中正三角形的个数为:1+4+3×4+9×4+…+3n -1×4,∴第④个图形中正三角形的个数为1+4+3×4+9×4+34-1×4=1+4+12+36+108=161.10. C 【解析】∵所有的小矩形都是大小相同的,第①个图形是由2个小矩形组成,面积为6,∴每个小矩形的面积是3,∵第①个图形中有2个小矩形,第②个图形中有6个小矩形,第③个图形中有12个小矩形,12=2+4+6=2×(1+2+3),第④个图形中有20个小矩形,20=2+4+6+8=2×(1+2+3+4),则第○n 个图形中有2×(1+2+…+n )个小矩形,故第⑥个图形中小矩形的个数为2×(1+2+3+4+5+6)=42个,则其面积为42×3=126 cm 2.11. A 【解析】第(1)个图形中♥的个数为3=22-1;第(2)个图形中♥的个数为8=32-1;第(3)个图形中♥的个数为15=42-1;第(4)个图形中♥的个数为24=52-1;…,于是,第(n )个图形中♥的个数为(n +1)2-1,所以第(8)个图形中♥的个数为92-1=80(个),故选A.12. B 【解析】图①中含“○”的矩形有1=2×12-1个,图②中含“○”的矩形有7=2×22-1个,图③中含“○”的矩形有17=2×32-1个,…,按此规律,则图○n 中含“○”的矩形个数为2n 2-1,所以图⑥中含“○”的矩形有2×62-1=71个,故选B.13. C 【解析】由题意可知,摆第1个图案需要7=1+6枚棋子,摆第2个图案需要19=1+6+6×2枚棋子,摆第3个图案需要37=1+6+6×2+6×3枚棋子,…,则摆第n 个图案需要1+6+6×2+6×3+…+6n =3n (n +1)+1枚棋子,所以摆第6个图案需要:3×6×(6+1)+1=127枚棋子,故选C.14. A 【解析】∵第①个图形中空心小圆圈个数为:4×1-3+1×0=1个;第②个图形中空心小圆圈个数为:4×2-4+2×1=6个;第③个图形中空心小圆圈个数为:4×3-5+3×2=13个;…,依此规律,第○n个图形中空心小圆圈个数为:4n-(n+2)+n(n-1),∴第⑦个图形中空心小圆圈个数为:4×7-9+7×6=61个.15. B【解析】∵第①个图形中菱形个数为02+12=1个;第②个图形中菱形个数为12+22=5个;第③个图形中菱形个数为22+32=13个;第④个图形中菱形个数为32+42=25个,…,依此规律第○n个图形中菱形个数为(n-1)2+n2个,∴第⑥个图形中菱形个数为52+62=61个.16. D【解析】在图①中,线段BD上共有4个点,所得三角形的个数共15个,15=16-1=42-1;图②中,线段BD上共5个点,所得三角形的个数共24个,24=25-1=52-1;图③中,线段BD上共6个点,所得三角形的个数共35个,35=36-1=62-1,…,由此可猜想,图○n中,线段BD上共有n+3个点,所得三角形的个数为(n+3)2-1,∴图⑤中三角形的个数为(5+3)2-1=63.17. n(n+1)【解析】由题图知,第1、2、3个图案对应的小正方形的个数分别为2=1×2、6=2×3、12=3×4,…,∴第n个图案所对应的小正方形的个数为n(n+1).19. 90【解析】观察可得,第1个图案:正三角形每条边上有3个花盆,共计32-3个花盆;第2个图案:正四边形每条边上有4个花盆,共计42-4个花盆;第3个图案:正五边形每条边上有5个花盆,共计52-5个花盆;…;由此可知第n个图案:正(n+2)边形每条边上有(n+2)个花盆,共计(n+2)2-(n+2)个花盆,则第8个图案中花盆的个数为(8+2)2-(8+2)=90.20. 60【解析】图①几何体的表面积为:6=6×1;图②几何体的表面积为:18=6×(1+2);图③几何体的表面积为:6×(1+2+3)=36.由此规律得,图④几何体的表面积为:6×(1+2+3+4)=60.二、图形成倍递变规律探索2. 下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2016个梅花图案中,共有________个“”图案.3. 如图,正五边形五个顶点标有数字1、2、3、4、5,一只青蛙在五个顶点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若它停在偶数点上,则下一次沿逆时针方向跳一个点;若青蛙从标有数字5的顶点开始跳,第一次跳后落在标有数字2的顶点上,第二次跳后落在标有数字1的顶点上,…,则第2017次跳后所停的顶点对应的数字为__________.第3题图4. (2016三明)如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P60的坐标是________.第4题图第5题图5. (2016聊城)如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2,再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3,以此类推…,则正方形OB2015B2016C2016的顶点B2016的坐标是________.【答案】1.B【解析】∵菱形OABC的顶点坐标为O(0,0),点B的坐标是(2,2),∴BO与x轴的夹角为45°,∵菱形的对角线互相垂直平分,∴点D是线段OB的中点,∴点D的坐标是(1,1),∵菱形绕点O逆时针旋转,每秒旋转45°,360°÷45°=8,∴每旋转8秒,菱形的对角线交点D就回到原来的位置(1,1),∵60÷8=7……4,∴第60秒时是把菱形绕点O逆时针旋转了7周回到原来位置后,又旋转了4秒,即又旋转了4×45°=180°,∴点D的对应点落在第三象限,且对应点与点D关于原点O成中心对称,∴第60秒时,菱形的对角线交点D的坐标为(-1,-1).2.504【解析】观察图形可知,“”图案方向依次向下、向左、向上、向右,每四个为一个循环周期.∵2016÷4=504,∴前2016个梅花图案中,有504个“”图案.3.2【解析】由5起跳,5是奇数,沿顺时针下一次能跳2个点,落在2上.由2起跳,2是偶数,沿逆时针下一次只能跳一个点,落在1上,1是奇数,沿顺时针跳两个点,落在3上.由3起跳,是奇数,沿顺时针跳两个点,落在5上.2-1-3-5-2,周期为4,∵又由2017=4×504+1,∴经过2017次跳后它停在的点所对应的数为2.4.(20,0)【解析】将点P的横纵坐标分开来看,P n的横坐标始终在变化且逐渐增大,而P n的纵坐标变化呈周期变化,即1,1,0,-1,-1,0,所以每6个点P的纵坐标为一个循环,显然60÷6=10,恰好能够整除,所以点P60的纵坐标为0,即在x轴上,显然P6,P12,P18,…,这些点的横坐标为:2,4,6,…,所以点P6k的纵坐标为2k,∴点P60的横坐标为20,∴点P60的坐标为(20,0).5.(21008,0)【解析】∵点B的位置依次落在第一象限、y轴正半轴、第二象限、x轴负半轴、第三象限、y轴负半轴、第四象限、x轴正半轴,…,每8次一循环,2016÷8=252,∴点B2016落在x轴正半轴,故B2016的纵坐标是0;OB n是正方形的对角线,OB1=2,OB2=2=(2)2,OB3=22=(2)3,…,∴OB2016=(2)2016=21008,∴点B2016的坐标为(21008,0).类型二探索图形循环规律针对演练1. 如图所示,两个全等的等边三角形的边长为1 m,一个微型机器人由A点开始按A→B→C→D→B→E→A的顺序沿等边三角形的边循环运动,行走2017 m 停下,则这个微型机器人停在()第1题图A. A点B. B点C. C点D. E点2.(2016重庆八中强化训练一)将正六边形ABCDEF的各边按如图所示延长,从射线F A开始,分别在各射线上标记点O1,O2,O3,…,按此规律,则点O2016所在射线是()第2题图A. ABB. DEC. BCD. EF3. 下列一串梅花图案是按一定规律排列的,请你仔细观察,在前2017个梅花图案中,共有________个“”图案.第3题图4. 有一个正六面体骰子,放在桌面上,将骰子沿如图所示的顺时针方向滚动,每滚动90°算一次,则滚动第2014次后,骰子朝下一面的点数是________.第4题图5.如图,在平面直角坐标系中,已知点A(1, 1),B(-1, 1),C(-1, -2),D(1, -2),把一根长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在A处,并按A→B→C→D→A…的规律紧绕在矩形ABCD的边上,则细线的另一端落在________线段上第5题图答案类型二探索图形循环规律1. B【解析】∵两个全等的等边三角形的边长为1 m,∴机器人由A点开始按A→B→C→D→B→E→A的顺序沿等边三角形的边循环运动一圈,即为6 m,∵2017÷6=336……1,即正好行走了336圈多1米,到第二个点,∴行走2017 m 停下,则这个微型机器人停在B点.2. C【解析】观察图形可知12个点依次排列在射线F A、CD、AB、DE、BC、EF、CD、F A、DE、AB、EF、BC上,依此规律循环,又因2016÷12=168,则点O2016在第12条射线BC上,故选C.3. 505【解析】观察题图可知,“”图案方向依次向上、向右、向下、向左,每四个图案为一个循环周期.∵2017÷4=504……1,∴前2017个梅花图案中,共有505个“”图案.4. 3【解析】观察可知,点数3与点数4相对,点数2与点数5相对,且循环周期为4. ∵2014÷4=503……2,∴滚动2014次后与第二次相同,∴骰子朝下一面的点数为3.5. CD 【解析】∵矩形四个顶点的坐标分别为:A (1,1),B (-1,1),C (-1,-2),D (1,-2),∴AB =CD =2,BC =AD =3,∴矩形的周长为2+3+2+3=10,则循环一周所需的单位长度是10,∵2016÷10=201……6,∴细线的另一端落在绕矩形第202圈的第6个单位长度的位置,即是点C 与点D 的中间位置,即在线段CD 上.拓展类型 数式规律针对演练1. (2016张家界)观察下列等式:71=7,72=42+92=97,73=343,74=2401,75=16807,76=117649,…,那么:71+72+73+…+72016的末位数字是( )A. 9B. 7C. 6D. 02. (2016丹东)观察下列数据:-2,52,-103,174,-265,…,它们是按一定规律排列的,依照此规律,第11个数据是________.3. (2016贵港)已知a 1=t t -1,a 2=11-a 1,a 3=11-a 2,…,a n +1=11-a n(n 为正整数,且t ≠0,1),则a 2016=________(用含有t 的代数式表示).4. (2016泉州)指出下列各图形中数的规律,依此,a 的值为________.第4题图5. (2016南宁)观察下列等式:第1层 1+2=3第2层 4+5+6=7+8第3层 9+10+11+12=13+14+15第4层 16+17+18+19+20=21+22+23+24…在上述数字宝塔中,从上往下数,2016在第________层.答案拓展类型 数式规律1. D 【解析】根据题意,7的幂的最终结果的末位数字是以7,9,3,1为循环,其和结果的末位数字是0,因为2016÷4=504,所以71+72+73+…+72016的末位数字是0.2. -12211 【解析】∵-2=-12+11,52=22+12,-103=-32+13,174=42+14,-265=-52+15,…,∴第11个数据是:-112+111=-12211. 3. t 1【解析】∵a 1=1-t t ,a 2=111--t t =1-t ,a 3=t +-111=t 1,a 4=t111-=1-t t ,…,∴每3个一次循环,∵2016÷3=672,∴a 2016的值为t1. 4. 226 【解析】观察可得:2=1×0+2,10=2×3+4,26=4×5+6,50=6×7+8,…,可以得到规律:右下角三角形中的数字等于左下角三角形中的数字与正上方三角形中数字的积加上中间三角形中的数字,故a =14×15+16=226.5. 44 【解析】根据题中给出的式子,观察得出规律,第一层第一个数为12,第2层第一个数为22,第3层第一个数为32,…,∵442=1936,452=2025,且442<2016<452,∴2016位于第44层.。