四边形动点压轴题

1(黄冈市) 20．（本题满分14分）已知：如图，在直角梯形COAB中，OC AB∥，以O为原点建立平面直角坐标系，ABC，，三点的坐标分别为(80)(810)(04)ABC，，，，，，点D为线段BC的中点，动点P从点O出发，以每秒1个单位的速度，沿折线OABD的路线移动，移动的时间为t秒．（1）求直线BC的解析式；（2）若动点P在线段OA上移动，当t为何值时，四边形OPDC的面积是梯形COAB 面积的27？（3）动点P从点O出发，沿折线OABD的路线移动过程中，设OPD△的面积为S，请直接写出S与t的函数关系式，并指出自变量t的取值范围；（4）当动点P在线段AB上移动时，能否在线段OA上找到一点Q，使四边形CQPD 为矩形？请求出此时动点P的坐标；若不能，请说明理由．（义乌市）23. (本题10分) 如图1，已知双曲线y=xk(k>0)与直线y=k′x交于A，B两点，点A在第一象限.试解答下列问题：(1)若点A的坐标为(4，2).则点B的坐标为；若点A的横坐标为m，则点B的坐标可表示为；（2）如图2，过原点O作另一条直线l，交双曲线y=xk(k>0)于P，Q两点，点P在第一象限.①说明四边形APBQ一定是平行囚边形；②设点A.P的横坐标分别为m，n，四边形APBQ可能是短形吗?可能是正方形吗?若可能，直接写出mn应满足的条件；若不可能，请说明理由.A B D C O P x yABDCO xy（此题备用）2（2008年青岛市）24．（本小题满分12分）已知：如图①，在RtACB△中，90C??，4cmAC?，3cmBC?，点P由B 出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C 匀速运动，速度为2cm/s；连接PQ．若设运动的时间为(s)t（02t??），解答下列问题：（1）当t为何值时，PQBC∥？（2）设AQP△的面积为y（2cm），求y与t之间的函数关系式；（3）是否存在某一时刻t，使线段PQ恰好把Rt ACB△的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；（4）如图②，连接PC，并把PQC△沿QC翻折，得到四边形PQPC?，那么是否存在某一时刻t，使四边形PQPC?为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．（2009年崇明）24、（本题满分12分）如图，抛物线32???bxaxy与y轴交于点C，与x轴交于A、B两点，31tan??OCA，6??ABC S．（1）求点B的坐标；（2）求抛物线的解析式及顶点坐标；（3）设点E在x轴上，点F在抛物线上，如果A、C、E、F构成平行四边形，请写出点E的坐标（不必书写计算过程）．A QC PB 图①A QCPB P 图②CABOyx3 （2009年普陀区）25．如图，在平面直角坐标xO中为原点点A、C的坐标分别为（2，0）、（13.将△AOC绕AC的中点旋转180°，点O到点B的位置，抛物线xax322?经点A，点D是该抛物线的顶点.（1）求证：四边形ABCO是平行四边形；（2）求a的值并说明点B在抛物线上；（3）若点P是线段OA上一点，且∠APD=∠OAB，求点P的坐标；(4) 若点P是x轴上一点，以P、A、D为顶点作平行四边形，该平行四边形的另一顶点在y轴上，写出点P的坐标.（2009年青浦区）24．（本题满分12分）如图，在平面直角坐标系中，直线bkxy??分别与x轴负半轴交于点A，与y轴的正半轴交于点B，⊙P经过点A、点B（圆心P在x轴负半轴上），已知AB=10，425?AP. （1）求点P到直线AB的距离；（2）求直线bkxy??的解析式；（3）在⊙P上是否存在点Q，使以A、P、B、Q为顶点的四边形是菱形？若存在，请求出点Q的坐标；若不存在，请说明理由．BCD第25题 Axy OyOxBAP4（2009年徐汇区）24．（本题满分12分）如图，抛物线cbxaxy???2与y轴正半轴交于点C，与x轴交于点），（、04)0,1(BA，OBCOCA???．（1）求抛物线的解析式；（3分）（2）在直角坐标平面内确定点M，使得以点CBAM、、、为顶点的四边形是平行四边形，请直接写出点M的坐标；（3分）（3）如果⊙P过点CBA、、三点，求圆心的坐标分（2009年江西省）24．如图，抛物线223yxx 与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D.（1）直接写出A、B、C三点的坐标和抛物线的对称轴；（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PFDE∥交抛物线于点F，设点P的横坐标为m；①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？②设BCF△的面积为S，求S与m的函数关系式.A BCOyxxy D C AOB（第24题）5 （2009年莆田市）。

中考数学压轴题专题解析---平行四边形动点问题这节课我们学什么1.动点平行四边形三定一动方法；2.动点平行四边形两定两动方法；知识框图典型例题分析1、动点平行四边形三定一动方法；例1.已知抛物线，过点，，三点2(0)y ax bx c a =++≠)0,3(-A )0,1(B )3,0(C （1）求抛物线的解析式；（2）若抛物线的顶点为，求正切值；P PAC ∠（3）若以、、、为顶点的四边形是平行四边形，求点的坐标．A P C M M 【答案：（1）由题意得：解得：∴⎪⎩⎪⎨⎧==++=+-30039c c b a c b a ⎪⎩⎪⎨⎧=-=-=321c b a 322+--=x x y （2）∴∴，，322+--=x x y 4)1(2++-=x )4,1(-P 52=PA 2=PC 23=AC ∵∴∴222AC PC PA +=090=∠PCA 31232tan ===∠AC PC PAC （3）∵直线的解析式是：AC 3+=x y 直线的解析式是：AP 62+=x y 直线的解析式是：PC 3+-=x y 当是平行四边形的一条对角线时：直线的解析式是：AC MC 32+=x y 直线的解析式是：∴AM 3--=x y )1,2(--M 当是平行四边形的一条对角线时：同理可得∴PC )7,2(M 当是平行四边形的一条对角线时：∴AP )1,4(-M∴或或】)1,2(--M )7,2(M )1,4(-M 例2.如图，在平面直角坐标系xOy 中，直线与x 轴、y 轴分别交于点243y mx m =-A 、B ，点C 在线段AB 上，且．2AOB AOC S S ∆∆=（1）求点C 的坐标（用含有m 的代数式表示）；（2）将沿x 轴翻折，当点C 的对应点C ′恰好落在抛物线AOC ∆上时，求该抛物线的表达式；223y x mx m =++（3）设点M 为（2）中所求抛物线上一点，当以A 、O 、C 、M 为顶点的四边形为平行四边形时，请直接写出所有满足条件的点M 的坐标．【答案：（1）(3,2)Cm -（2）该抛物线的表达式为2y x x =（3）点M的坐标为(3,或(-或】2、动点平行四边形两定两动方法；例3.如图，抛物线与轴交于点C ，与x 轴交于A 、B 两点，32++=bx ax y y ，．31tan =∠OCA 6=∆ABC S （1）求点B 的坐标；（2）求抛物线的解析式及顶点坐标；（3）设点E 在x 轴上，点F 在抛物线上，如果A 、C 、E 、F 构成平行四边形，请写出点E 的坐标（不必书写计算过程）．【答案：（1）(3,0)B -（2）把,顶点坐标223y x x =--+(1,4)-（3）①AC 为平行四边形的一边时123(1,0),(2(2E E E ---②AC 为平行四边形的对角线时E 4(3，0）】例4.如图，在平面直角坐标系xOy 中，O 为原点，点A 、C 的坐标分别为．将绕AC 的中点旋转180°，点O 落到点B 的位置，抛AOC ∆物线经过点A ，点D 是该抛物线的顶点．x ax y 322-=（1）求证：四边形ABCO 是平行四边形；（2）求a 的值并说明点B 在抛物线上；（3）若点P 是线段OA 上一点，且，求点P 的坐标；APD OAB ∠=∠（4）若点P 是x 轴上一点，以P 、A 、D 为顶点作平行四边形，该平行四边形的另一顶点在y 轴上，写出点P 的坐标．【答案：（1）证明：∵绕AC 的中点旋转180°，AOC ∆点O 落到点B 的位置，∴C AOC AB≅∆∆∴，,AO C CB A O B ==∴四边形ABCO 是平行四边形．（2）解： ，．3=a x x y 3232-=点B 的坐标为（3，3）,满足此函数解析式，点B 在此抛物3线上．（3）点P 的坐标为（，0）．34（4），，】)0,1(1P )0,1(2-P 3(3,0)P 例5.在平面直角坐标系xOy 中，经过点的抛物线与y 轴交(1,0)A -23y x bx =-++于点C ，点B 与点A 、点D 与点C 分别关于该抛物线的对称轴对称．（1）求b 的值以及直线AB 与x 轴正方形的夹角；（2）如果点E 是抛物线上一动点，过E 作EF 平行于x 轴交直线AD 于点F ，且F 在E 的右边，过点E 作与点G ，设E 的横坐标为m ，的周长EG AD ⊥EFG ∆为l ，试用m 表示l ；（3）点M 是该抛物线的顶点，点P 是y 轴上一点，Q 是坐标平面内一点，如果以点A 、M 、P 、Q 为顶点的四边形是矩形，求该矩形的顶点Q 的坐标．【答案：（1），夹角为2b =45（2）21)1)2l m m =-++++ （3）】123417(0,2(0,2(2,),(2,22Q Q Q Q +-例6.在平面直角坐标系中，已知点A （4，0），点B （0，3）．点P 从点A 出发，以每秒1个单位的速度向右平移，点Q 从点B 出发，以每秒2个单位的速度向右平移，又P 、Q 两点同时出发．（1）联结AQ ，当是直角三角形时，求点Q 的坐标；ABQ ∆（2）当P 、Q 运动到某个位置时，如果沿着直线AQ 翻折，点P 恰好落在线段AB 上，求这时的度数；AQP ∠（3）过点A 作，AC 交射线PQ 于点C ，联结BC ，D 是BC 的中AC AB ⊥点．在点P 、Q 的运动过程中，是否存在某时刻，使得以A 、C 、Q 、D 为顶点的四边形是平行四边形，若存在，试求出这时的值；若不存在，试说明理由．ABC ∠cot【答案：（1） 1225(,3),(4,3)4Q Q （2）45AQP ∠=︒（3）当点C 在线段PQ 上时，延长BQ 与AC 的延长线交于点F ，∵AC AB⊥∴AOB FHA∆∆ ∴即FH AO FA AB =345=FA ∴415=FA ∵，DQ =AC ，且D 为BC 中点//DQ AC ∴FC=2DQ=2AC∴45=AC 在中，=4Rt BAC ∆ABC ∠cot 当点C 在PQ 的延长线上时，记BQ 与AC 的交点为F ，记AD 与BQ 的交点为G ，∵，CQ =AD 且D 为BC 中点//CQ AD ∴AD=CQ=2DG∴CQ=2AG=2PQ ∴FC=2AF∴在中，】445=AC Rt BAC ∆94cot =∠ABC课后练习练1.如图，抛物线经过直线与坐标轴的两个交点A 、B ，此c bx x y -+=23-=x y 抛物线与x 轴的另一个交点为C ，抛物线的顶点为D ．（1）求此抛物线的解析式；（2）点P 为抛物线上的一个动点，求使的点P 的坐标；:5:4APC ACD S S ∆∆=（3）点M 为平面直角坐标系上一点，写出使点M 、A 、B 、D 为平行四边形的点M 的坐标．【答案：（1）抛物线的解析式是．322--=x x y （2）点P 的坐标为．12(4,5),(2,5)P P -（3）点M 的坐标为 】123(2,1),(2,7),(4,1)M M M ---练2.如图，点A （2，6）和点B （点B 在点A 的右侧）在反比例函数的图像上，点C 在y 轴上，轴，，二次函数的图像经过A 、B 、C 三点．//BC x 2tan =∠ACB（1）求反比例函数和二次函数的解析式；（2）如果点D 在轴的正半轴上，点E 在反比例函数的图像上，四边形ACDEx 是平行四边形，求边CD的长．【答案：（1）反比例函数的解析式为． x y 12=二次函数的解析式为．23212++-=x x y （2）延长AC 交x 轴于G ，作轴，垂足为H ．．】EH x⊥CD =课后小测验1.已知一个二次函数的图像经过、、三点．()0,3A ()4,3B ()1,0C （1）求这个二次函数的解析式;（2）求tan 的值；BAC ∠（3）若点在轴上，点在（1）中所求出的二次函数的图像上，且以点D x E A、、、为顶点的四边形是平行四边形，求点、的坐标．C D E D E 【答案：（1）243y x x =-+（2）tan tan 3BAC ACO ∠=∠=（3）或(5,0),(4,3)D E (3,0),(4,3)D E -。

四边形中的动点问题1、如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠EFB＝60°，则矩形ABCD的面积是_____________2、如图，在四边形ABCD中，对角线AC⊥BD，垂足为O，点E，F，G，H分别为边AD，AB，BC，CD的中点．若AC＝8，BD＝6，则四边形EFGH 的面积为________3、如图，正方形ABCD的边长为4，点P在DC边上，且DP＝1，点Q是AC上一动点，则DQ＋PQ的最小值为____________4、如图，在Rt△ABC中，∠B＝90°，AC＝60 cm，∠A＝60°，点D从点C出发沿CA方向以4 cm/s 的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是t s(0 < t ≤15)．过点D作DF⊥BC于点F，连接DE，EF.(1)求证：AE＝DF；(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；(3)当t为何值时，△DEF为直角三角形？请说明理由5、如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t. （1）连接EF，当EF经过AC边的中点D时，（1）求证：△ADE≌△CDF；：（2）当t为______s时，四边形ACFE是菱形；6、在菱形ABCD中，∠B=60°，点E在射线BC上运动，∠EAF=60°，点F在射线CD上（1）当点E在线段BC上时（如图1），（1）求证：EC+CF=AB；（2）当点E在BC的延长线上时（如图2），线段EC、CF、AB有怎样的相等关系？写出你的猜想，不需证明7、如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．（1）求证：四边形AMDN是平行四边形；（2）填空：①当AM的值为______时，四边形AMDN是矩形；②当AM的值为______时，四边形AMDN是菱形．8、如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．（1）探究：线段OE与OF的数量关系并加以证明；（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由．9、如图，已知菱形ABCD中，∠ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D重合）分别向直线AB、AD作垂线，垂足分别为E、F．（1）BD的长是______；（2）连接PC，当PE+PF+PC取得最小值时，此时PB的长是______10、如图，∠MON=90°，矩形ABCD的顶点A、B分别在边OM，ON上，当B在边ON上运动时，A 随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O的最大距离为______．11、如图，已知矩形ABCD，AD=4，CD=10，P是AB上一动点，M、N、E分别是PD、PC、CD的中点．（1）求证：四边形PMEN是平行四边形；（2）请直接写出当AP为何值时，四边形PMEN是菱形；（3）四边形PMEN有可能是矩形吗？若有可能，求出AP的长；若不可能，请说明理由．12、如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F是AC上两动点，分别从A，C两点以相同的速度向C、A运动，其速度为0.5cm／s。

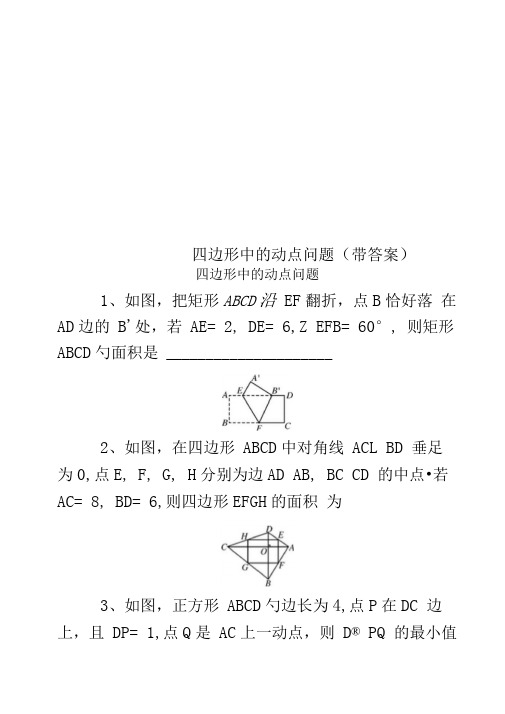
四边形中的动点问题（带答案）四边形中的动点问题1、如图，把矩形ABCD沿 EF翻折，点B恰好落在AD边的B'处，若AE= 2, DE= 6,Z EFB= 60°, 则矩形ABCD勺面积是 _____________________2、如图，在四边形ABCD中对角线ACL BD 垂足为0,点E, F, G, H分别为边AD AB, BC CD 的中点•若AC= 8, BD= 6,则四边形EFGH的面积为3、如图，正方形ABCD勺边长为4,点P在DC 边上，且DP= 1,点Q是AC上一动点，则D® PQ 的最小值为 _____________________4、如图，在Rt△ ABC中，/ B= 90°,AC= 60 cm Z A= 60°，点D从点C出发沿CA方向以4 cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2 cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D, E 运动的时间是t s(0 < t < 15) •过点D作DF 丄BC于点F,连接DE EF.(1)求证：AE= DF;(2)四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，请说明理由；(3)当t为何值时，△ DEF为直角三角形？请说明理由5、如图，在等边三角形ABC中，BC=6cm射线AG// BC,点E从点A出发沿射线AG以1cm/s的速度运动，同时点F从点B出发沿射线BC以2cm/s的速度运动，设运动时间为t. (1)连接EF当EF经过AC边的中点D时，(1)求证：△ ADE^A CDF：6、在菱形ABCD中，/ B=60°,点E在射线BC上运动，/ EAF=60，点F在射线CD上(1)当点E在线段BC上时(如图1)( 1)求证：EC+CF=A； (2) 当点E在BC的延长线上时(如图2),线段EC CFAB有怎样的相等关系？写出你的猜想，不需证明图1 027、如图，在菱形ABC［中, AB=2 / DAB=60 , 点E 是AD边的中点.点M是AB边上一动点（不与点A重合）,延长ME交射线CD于点N 连接MD AN（1）求证：四边形AMDI是平行四边形；（2）填空：①当AM的值为时，四边形AMD是矩形；②当AM的值为时，四边形AMD是菱形.D8 如图，△ ABC中，点0是边AC上一个动点，过0作直线MN BC 设MN交/ BCA的平分线于点E, 交/ BCA 的外角平分线于点F.(1)探究：线段0E与OF的数量关系并加以证明；(2)当点0运动到何处，且△ ABC满足什么条件时，四边形AECF是正方形？(3)当点0在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由.9、如图，已知菱形ABC［中, / ABC=60 , AB=8 过线段BD上的一个动点P (不与B、D重合)分别向直线AB AD作垂线，垂足分别为E、F.(1)BD的长是______ ;(2)连接PC当PE+PF+P(取得最小值时，此时PB的长是_______10、如图，/ MON=9°,矩形ABCD勺顶点A B 分别在边OM ON上，当B在边ON上运动时，A随之在OMk运动，矩形ABCD勺形状保持不变，其中AB=2 BC=1运动过程中，点D到点O的最大距离为 __________________ .11、如图，已知矩形ABCD AD=4 CD=10 P是AB上一动点，M N E分别是PD PC CD的中点.(1)求证：四边形PMEI是平行四边形；(2)请直接写出当AP为何值时，四边形PMEN 是菱形；(3)四边形PMEf有可能是矩形吗？若有可能,求出AP的长；若不可能，请说明理由.12、如图，在平行四边形ABCD中，对角线BD=12cm AC=16cm AC BD相交于点0,若E, F 是AC上两动点，分别从A, C两点以相同的速度向C、A 运动，其速度为0.5cm/s。

四边形中的动点问题1、如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B′处，若AE＝2，DE＝6，∠ EFB ＝2、如图，在四边形ABCD中，对角线AC⊥BD，垂足为O，点E，F，G，H 分别为边AD，AB，BC，CD的中点．若AC＝8，BD＝6，则四边形EFGH的面积为 _____3、如图，正方形ABCD的边长为4，点P在DC边上，且DP＝1，点Q是AC上一动点，则DQ ＋PQ 的最小值为___________4、如图，在Rt△ABC中，∠ B＝90°，AC＝60cm，∠A＝60°，点 D 从点C出发沿CA方向以4cm/s 的速度向点A匀速运动，同时点E从点 A 出发沿AB 方向以2cm/s 的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts(0<t ≤15)．过点 D 作DF⊥ BC于点F，连接DE，EF.(1) 求证：AE＝DF；(2) 四边形AEFD能够成为菱形吗如果能，求出相应的t 值；如果不能，请说明理由；(3)当t 为何值时，△ DEF为直角三角形请说明理由5、如图，在等边三角形ABC中，BC=6cm．射线AG∥BC，点E从点 A 出发沿射线AG以1cm/s 的速度运动，同时点 F 从点 B 出发沿射线BC以2cm/s 的速度运动，设运动时间为t.（1）连接EF，当EF经过AC边的中点 D 时，（1）求证：△ ADE≌△ CDF；：（2）当t 为____ s 时，四边形ACFE是菱形；6、在菱形ABCD中，∠ B=60°，点E在射线BC上运动，∠ EAF=60°，点 F 在射线CD上（1）当点E在线段BC上时（如图1），（1）求证：EC+CF=AB；（2）当点 E 在BC的延长线上时（如图2），线段EC、CF、AB 有怎样的相等关系写出你的猜想，不需证明7、如图，在菱形ABCD中，AB=2，∠ DAB=60°，点E是AD边的中点．点M 是AB边上一动点不与点 A 重合），延长ME交射线CD于点N，连接MD、AN．（1）求证：四边形AMDN 是平行四边形；（2）填空：①当AM 的值为____ 时，四边形AMDN 是矩形；②当AM 的值为____ 时，四边形AMDN 是菱形．8、如图，△ ABC中，点O 是边AC上一个动点，过O 作直线MN ∥BC，设MN 交∠ BCA的平分线于点E，交∠ BCA 的外角平分线于点F．（1）探究：线段OE与OF 的数量关系并加以证明；（2）当点O 运动到何处，且△ ABC满足什么条件时，四边形AECF是正方形（3）当点O 在边AC上运动时，四边形BCFE会是菱形吗若是，请证明，若不是，则说明理由．9、如图，已知菱形ABCD中，∠ ABC=60°，AB=8，过线段BD上的一个动点P（不与B、D 重合）分别向直线AB、AD 作垂线，垂足分别为E、F．（1）BD的长是___ ；（2）连接PC，当PE+PF+PC取得最小值时，此时PB 的长是__10、如图，∠ MON=90°，矩形ABCD的顶点A、B分别在边OM，ON 上，当B在边ON 上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB=2，BC=1，运动过程中，点D到点O 的最大距离为_____ ．11、如图，已知矩形ABCD，AD=4，CD=10，P 是AB上一动点，M、N、E分别是PD、PC、CD的中点．（1）求证：四边形PMEN 是平行四边形；（2）请直接写出当AP为何值时，四边形PMEN 是菱形；（3）四边形PMEN有可能是矩形吗若有可能，求出AP 的长；若不可能，请说明理由．12、如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F 是AC上两动点，分别从A，C两点以相同的速度向C、A 运动，其速度为／s。

通用版2021年中考数学三轮冲刺复习最后压轴题精选：四边形的动点问题1.如图，在矩形ABCD中，AD＝2 √5，AB＝4 √5，DM⊥AC于点M ，在对角线AC上取一点N ，使得2CN＝3AM ，连接DN并延长交BC于点E ，F是AB上一点，连接EF ，MF ．当点P从点E匀速运动到点F时，点Q恰好从点M匀速运动到点N ．（1）求AM ，CE的长．（2）若EF∥AC ，记EP＝x ，AQ＝y ．①求y关于x的函数表达式．②连接PQ ，当直线PQ平行于四边形DEFM的一边时，求所有满足条件的x的值．（3）在运动过程中，当直线PQ同时经过点B和D时，记点Q的运动速度为v1，记点P的运动速度为v2，求v1v2的值．2.如图，在平面直角坐标系xOy中，四边形OABC是矩形，点B的坐标是(8,6)，点M为OA边上的一动点（不与点O、A重合），连接CM，过点M作直线l⊥CM，交AB于点D，在直线l上取一点E（点E在点M右侧），使得CMME =43，过点E作EF//AO，交BO于点F，连接BE，设OM=m(0<m<8)．（1）填空：点E的坐标为________（用含m的代数式表示）；（2）判断线段EF的长度是否随点M的位置的变化而变化？并说明理由；（3）①当m为何值时，四边形BCME的面积最小，请求出最小值；②在x轴正半轴上存在点G，使得△GEF是等腰三角形，请直接写出3个符合条件的点G的坐标（用含m的代数式表示）．3.如图，在矩形ABCD中，点O是边AD的中点，点E是边BC上的一个动点，延长EO到F，使得OE=OF .（1）当点E运动到什么位置时，四边形AEDF是菱形？（直接写出答案）（2）若矩形ABCD的周长为20，求四边形AEDF的面积的最大值；（3）若AB=m，且存在点E，使四边形AEDF能成为一个矩形，求BC的取值范围.4.在平面直角坐标系中，矩形OABC的顶点A ，C分别在x轴、y轴上，点B的坐标为(2,2√3)，将矩形OABC绕点A顺时针旋转α，得到矩形O1AB1C1，点O ，B ，C的对应点分别为O1,B1,C1．（1）如图①，当α=45°时，O1C1与AB相交于点E ，求点E的坐标；（2）如图②，当点O1落在对角线OB上时，连接BC1，四边形OAC1B是何特殊的四边形？并说明理由；（3）连接BC1，当BC1取得最小值和最大值时，分别求出点B1的坐标（直接写出结果即可）．5.如图，在平面直角坐标系中，点O为坐标原点，AB //OC，点B，C的坐标分别为（15，8），（21，0），动点M从点A沿A→B以每秒1个单位的速度运动;动点N从点C沿C→O以每秒2个单位的速度运动.M，N同时出发，设运动时间为t秒.（1）在t＝3时，M点坐标________，N点坐标________;（2）当t为何值时，四边形OAMN是矩形？（3）运动过程中，四边形MNCB能否为菱形？若能，求出t的值;若不能，说明理由.6.如图，四边形OABC为矩形，其中O为原点，A、C两点分别在x轴和y轴上，B点的坐标是（4，6），将矩形沿直线DE折叠，使点C落在AB边上点F处，折痕分别交OC，BC于点E、D，且D点坐标是，6）.（52（1）求F点的坐标；（2）如图2，P点在第二象限，且△PDE≌△CED，求P点的坐标；（3）若M点为x轴上一动点，N点为直线DE上一动点，△FMN为以FN为底边的等腰直角三角形，求N点的坐标.7.已知矩形ABCD中，AB=4，BC=8．（1）如图1，点P从点D开始沿D→A以每秒1个单位的速度移动，同时另一个点Q从点B开始在线段BC上以每秒3个单位的速度往返移动．设P，Q运动时间为t秒，当0<t≤8时，是否存在这样的时刻，四边形DCQP为平行四边形？若存在，请求出t的值；若不存在，请说明理由；（2）如图2，将矩形ABCD折叠，使点B与点D重合，点A与点E重合，展平后折痕为MF，一动点N从点D出发，沿D→A→B→C→D，以每秒1个单位的速度移动一周，设N运动的时间为x秒，请直接写出当△MFN为直角三角形时x的值．8.已知：如图，在矩形ABCD中，AB=6cm，BC=8cm，对角线AC，BD交于点O．点P从点A出发，沿AD方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延点也长，交BC于点E，过点Q作QF//AC，交BD于点F．设运动时间为t(s)(0<t<6)，解答下列问题：（1）当t=2时，FQ=________；（2）当t为何值时，△AOP是等腰三角形?（3）设五边形OECQF的面积为S(cm2)，试确定S与t的函数关系式；（4）在运动过程中，是否存在某一时刻t，使OD平分∠COP?若存在，直接写出t的值；若不存在，请说明理由．9.如图在△ABC中，CD⊥AB ，AB = 6，AD = 2，CD = 4，点E为边BC的中点．动点P从点A 出发，以5cm/s的速度沿边AB向终点B运动．当点P不与点A、B重合时，过点P作PQ⊥AC于点Q ，连结PE ，以PE、PQ为边作平行四边形PQFE ．设点P的运动时间为t（s）．（1）sin∠APQ=________．（2）用含t的代数式表示线段CQ的长度．（3）当∠EPQ为锐角时，求t的取值范围．（4）当△ABC的角平分线CM恰好可以将平行四边形PQFE的面积等分时，求t的值．10.如图，正方形ABCD（四边相等，四个角都是直角）的边长为4，点P从点A出发，以每秒1个单位长度的速度沿射线AD向点D运动；点Q从点D同时出发，以相同的速度沿射线AD方向向右运动，当点P到达点D时，点Q也停止运动，连接BP，过点P作BP的垂线交过点Q平行于CD的直线l于点E，BE于CD相交于点F，连接PF，设点P运动时间为t（s），（1）求∠PBE的度数；（2）当t为何值时，△PQF是以PF为腰的等腰三角形？（3）试探索在运动过程中△PDF的周长是否随时间t的变化而变化？若变化，说明理由；若不变，试求这个定值.11.如图，在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A出发沿AB以1cm/s的速度向点B 移动；同时，点Q从点B出发沿BC以2cm/s的速度向点C移动.设运动时间为t秒.（1）当t＝2时，△DPQ的面积为________cm2；（2）在运动过程中△DPQ的面积能否为26cm2？如果能，求出t的值，若不能，请说明理由；（3）运动过程中，当A、P、Q、D四点恰好在同一个圆上时，求t的值；（4）运动过程中，当以Q为圆心，QP为半径的圆，与矩形ABCD的边共有4个交点时，直接写出t的取值范围.12.如图①，四边形OABC是一张放在平面中的矩形纸片，OA=10,OC=8．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处．（1）AE=________，BE=________；（2）求CD的长；（3）如图②，若AD上有一动点P（不与A,D重合）自A点沿AD向终点D匀速运动，运动的速度为每秒√5个单位长度，设运动的时间为t秒，连结PE，设w=PE2，①直接写出w与时间t之间的函数关系式；②当以点P,D,E为顶点的三角形为等腰三角形时，求时间t的值．13.如图，矩形ABCD中，AB＝8cm，BC＝6cm，点O为对角线的中点，点P从点A出发，沿折线AD-DO-OC，以每秒2厘米的速度向终点运动，当点P与点A不重合时，过点P作PQ⊥AB于点Q，以PQ为边向右作正方形PQMN，点P运动的时间为t（秒）.（1）求点N落在BD上时t的值；（2）当点O在正方形PQMN内部时，t的取值范围________；（3）当直线DN平分△BCD面积时求出t的值.14.如图，正方形OABC的边OA，OC在坐标轴上，点B的坐标为（﹣2，2）.点P从点A出发，以每秒1个单位长度的速度沿x轴向点O运动；点Q从点O同时出发，以相同的速度沿x轴正方向运动，过点Q作直线l垂直x轴.当点P到达点O时，点Q也停止运动.连接BP，作PD⊥BP交直线l于点D.连结BD交y轴于点E，连接PE.设点P的运动时间为t（s）.（1）①点D的坐标为________（用含t的代数式表示）.②当0＜t≤2时，∠PED的大小范围是________.（2）当0＜t＜2时，△POE的周长C是否随t的变化而变化？若变化，求出C关于t的关系式；若不变，求出C的值.（3）当t＝________秒时，△PBE为等腰三角形（直接给出答案）.15.如图1，在矩形ABCD中，AB＝5，BC＝8，点E，F分别为AB，CD的中点.（1）求证：四边形AEFD是矩形；（2）如图2，点P是边AD上一点，BP交EF于点O，点A关于BP的对称点为点M，当点M落在线段EF上时，则有OB＝OM.请说明理由；（3）如图3，若点P是射线AD上一个动点，点A关于BP的对称点为点M，连接AM，DM，当△AMD 是等腰三角形时，求AP的长.16.如图，已知菱形ABCD中，对角线AC、BD相交于点O ，且AC=12cm，BD=16cm，点P从点D出发，沿DA方向匀速向点A运动，速度为2cm/s；同时，点E从点B出发，沿BO方向匀速向点O运动，速度为1cm/s，EF∥BC ，交OC于点F ．当点P、E中有一点停止运动时，另一点也停止运动，线段EF也停止运动，连接PE、DF（0<t<5）．解答下列问题：（1）当t为何值时，PE∥AB？（2）设四边形EFDP的面积为y（cm2），求y与t之间的函数关系式．（3）是否存在某一时刻t ，使得S四边形EFDP:S菱形ABCD=21:48？若存在，求出t的值；若不存在，请说明理由．（4）连接FP ，是否存在某一时刻t ，使得FP⊥AD？若存在，求出t的值；若不存在，请说明理由．17.如图①，在平行四边形ABCD中，AB＝8，BC＝6，∠ABC＝60°．AE平分∠BAD交CD于点F．动点P从点A出发沿AD向点D以每秒1个单位长度的速度运动．过点P作PQ⊥AD，交射线AE 于点Q，以AP、AQ为邻边作平行四边形APMQ，平行四边形APMQ与△ADF重叠部分面积为S．当点P与点D重合时停止运动，设P点运动时间为t秒．（t＞0）（1）用含t的代数式表示QF的长；（2）当点M落到CD边上时，求t的值；（3）求S与t之间的函数关系式；（4）连结对角线AM与PQ交于点G，对角线AC与BD交于点O（如图②）．直接写出当GO与△ABD 的边平行时t的值．18.如图，在平面直角坐标系中，四边形OABC是矩形，OA＝4，OC＝3．动点P从点C出发，沿射线CB方向以每秒2个单位长度的速度运动；同时，动点Q从点O出发，沿x轴正半轴方向以每秒1个单位长度的速度运动．设点P、Q的运动时间为t秒（1）当t＝2秒时，求tan∠QPA的值；（2）当线段PQ与线段AB相交于点M，且BM＝2AM时，求t的值；（3）连结CQ，当点P，Q在运动过程中，记△CQP与矩形OABC重叠部分的面积为S，求S与t的函数关系式；（4）直接写出∠OAB的角平分线经过△CQP边上中点时的t值．19.如图，已知在矩形ABCD中，AD=10cm，AB=4cm，动点P从点A出发，以2cm/s的速度沿AD 向终点D移动，设移动时间为t（s）．连接PC，以PC为一边作正方形PCEF，连接DE、DF．（1）求正方形PCEF的面积（用含t的代数式来表示，不要求化简），并求当正方形PCEF的面积为25 cm2时t的值；（2）设△DEF的面积为S（cm2），求S与t之间的函数关系式，并求当t为何值时？△DEF的面积取得最小值，这个最小值是多少？（3）求当t为何值时？△DEF为等腰三角形．20.如图，BD是▱ABCD的对角线，AB=7，BD=4√2，∠ABD=45°，动点P、Q分别从A、D同时出发，点P沿折线AB−BC向终点C运动，在AB上的速度为每秒7个单位，在BC 上的速度为每秒5个单位，点Q以每秒2√2个单位的速度沿DB向终点B运动．连结PQ，以DQ、PQ为边作▱DEPQ，设点P的运动时间为t(s)(t>0)．（1）当点P在边AB上时，用含t的代数式表示点P到BD的距离．（2）当点E落在边CD上时，求t的值．（3）设▱DEPQ与▱ABCD重叠部分图形的面积为S，求S与t之间的函数关系式．（4）连结EQ，直接写出直线EQ与直线BD所夹锐角的正切值．21.如图，矩形ABCD中，AB＝6，AD＝8.动点E，F同时分别从点A，B出发，分别沿着射线AD和射线BD的方向均以每秒1个单位的速度运动，连接EF，以EF为直径作⊙O交射线BD于点M，设运动的时间为t.（1）当点E在线段AD上时，用关于t的代数式表示DE，DM.（2）在整个运动过程中，①连结CM，当t为何值时，△CDM为等腰三角形.②圆心O处在矩形ABCD内（包括边界）时，求t的取值范围，并直接写出在此范围内圆心运动的路径长.22.如图①，在矩形ABCD中，已知BC=8cm，点G为BC边上一点，满足BG=AB=6cm，动点E以1cm／s的速度沿线段BG从点B移动到点G，连接AE，作EF⊥AE，交线段CD于点F。

1．如图①,在矩形ABCD中,已知BC＝8cm,点G为BC边上一点,满足BG＝AB＝6cm,动点E以1cm/s的速度沿线段BG从点B移动到点G,连接AE,作EF⊥AE,交线段CD于点F．设点E移动的时间为t(s),CF的长度为y(cm),y与t的函数关系如图②所示．(1)图①中,CG＝ 2 cm,图②中,m＝ 2 ；(2)点F能否为线段CD的中点？若可能,求出此时t的值,若不可能,请说明理由；(3)在图①中,连接AF,AG,设AG与EF交于点H,若AG平分△AEF的面积,求此时t的值．解:(1)∵BC＝8cm,BG＝AB＝6cm,∴CG＝2cm,∵EF⊥AE,∴∠AEB+∠FEC＝90°,且∠AEB+∠BAE＝90°,∴∠BAE＝∠FEC,且∠B＝∠C＝90°,∴△ABE∽△ECF,∴,∵t＝6,∴BE＝6cm,CE＝2cm,∴∴CF＝2cm,∴m＝2,故答案为:2,2；(2)若点F是CD中点,∴CF＝DF＝3cm,∵△ABE∽△ECF,∴,∴∴EC2﹣8EC+18＝0∵△＝64﹣72＝﹣8＜0,∴点F不可能是CD中点；(3)如图①,过点H作HM⊥BC于点M,∵∠C＝90°,HM⊥BC,∴HM∥CD,∴△EHM∽△EFC,∴∵AG平分△AEF的面积,∴EH＝FH,∴EM＝MC,∵BE＝t,EC＝8﹣t,∴EM＝CM＝4﹣t,∴MG＝CM﹣CG＝2﹣,∵,∴∴CF＝∵EM＝MC,EH＝FH,∴MH＝CF＝∵AB＝BG＝6,∴∠AGB＝45°,且HM⊥BC,∴∠HGM＝∠GHM＝45°,∴HM＝GM,∴＝2﹣,∴t＝2或t＝12,且t≤6,∴t＝2．2．问题提出:(1)如图1,△ABC的边BC在直线n上,过顶点A作直线m∥n,在直线m上任取一点D,连接BD、CD,则△ABC的面积＝△DBC的面积．问题探究:(2)如图2,在菱形ABCD和菱形BGFE中,BG＝6,∠A＝60°,求△DGE的面积；问题解决:(3)如图3,在矩形ABCD中,AB＝12,BC＝10,在矩形ABCD内(也可以在边上)存在一点P,使得△ABP的面积等于矩形ABCD的面积的,求△ABP周长的最小值．解:问题提出:(1)∵两条平行线间的距离一定,∴△ABC与△DBC同底等高,即△ABC的面积＝△DBC的面积,故答案为:＝；问题探究:(2)如图2,连接BD,∵四边形ABCD,四边形BGFE是菱形,∴AD∥BC,BC∥EF,AD＝AB,BG＝BE,∴∠A＝∠CBE＝60°,∴△ADB是等边三角形,△BGE是等边三角形,∴∠ABD＝∠GBE＝60°,∴BD∥GE,∴S△DGE＝S△BGE＝BG2＝9；(3)如图3,过点P作PE∥AB,交AD于点E,∵△ABP的面积等于矩形ABCD的面积的,∴×12×AE＝×12×10∴AE＝8,作点A关于PE的对称点A',连接A'B交PE于点P,此时△ABP周长最小, ∴A'E＝AE＝8,∴AA'＝16,∴A'B＝＝＝20,∴△ABP周长的最小值＝AP+AB+PB＝A'P+PB+AB＝20+12＝32．3．(1)方法感悟:如图①,在正方形ABCD中,点E、F分别为DC、BC边上的点,且满足∠EAF＝45°,连接EF．将△ADE绕点A顺时针旋转90°得到△ABG,易证△GAF≌△EAF,从而得到结论:DE+BF＝EF．根据这个结论,若CD＝6,DE＝2,求EF的长．(2)方法迁移:如图②,若在四边形ABCD中,AB＝AD,∠B+∠D＝180°,E、F分别是BC、CD上的点,且∠EAF＝∠BAD,试猜想DE,BF,EF之间有何数量关系,证明你的结论．(3)问题拓展:如图③,在四边形ABCD中,AB＝AD,∠B+∠ADC＝180°,E、F分别是边BC、CD延长线上的点,且∠EAF＝∠BAD,试探究线段EF、BE、FD之间的数量关系,请直接写出你的猜想(不必说明理由)．解:(1)方法感悟:∵将△ADE绕点A顺时针旋转90°得到△ABG,∴GB＝DE＝2,∵△GAF≌△EAF∴GF＝EF,∵CD＝6,DE＝2∴CE＝4,∵EF2＝CF2+CE2,∴EF2＝(8﹣EF)2+16,∴EF＝5；(2)方法迁移:DE+BF＝EF,理由如下:如图②,将△ADE绕点A顺时针旋转90°得到△ABH,由旋转可得,AH＝AE,BH＝DE,∠1＝∠2,∠D＝∠ABH,∵∠EAF＝∠DAB,∴∠HAF＝∠1+∠3＝∠2+∠3＝∠BAD,∴∠HAF＝∠EAF,∵∠ABH+∠ABF＝∠D+∠ABF＝180°,∴点H、B、F三点共线,在△AEF和△AHF中,∴△AEF≌△AHF(SAS),∴EF＝HF,∵HF＝BH+BF,∴EF＝DE+BF．(3)问题拓展:EF＝BF﹣FD,理由如下:在BC上截取BH＝DF,∵∠B+∠ADC＝180°,∠ADC+∠ADF＝180°,∴∠B＝∠ADF,且AB＝AD,BH＝DF,∴△ABH≌△ADF(SAS)∴∠BAH＝∠DAF,AH＝AD,∵∠EAF＝∠BAD,∴∠DAE+∠BAH＝∠BAD,∴∠HAE＝∠BAD＝∠EAF,且AE＝AE,AH＝AD,∴△HAE≌△FAE(SAS)∴HE＝EF,∴EF＝HE＝BE﹣BH＝BE﹣DF．4．如图1,在▱ABCD中,AB＝3cm,BC＝5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s；同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图2,设移动时间为t(s)(0＜＜4),连结PQ,MQ,解答下列问题:(1)当t为何值时,PQ∥MN？(2)当t为何值时,∠CPQ＝45°？(3)当t为何值时,PQ⊥MQ？解:(1)∵AB＝3cm,BC＝5cm,AC⊥AB,∴AC＝＝4cm,∵MN∥AB,PQ∥MN,∴PQ∥AB,∴,∴,∴t＝s(2)如图2,过点Q作QE⊥AC,则QE∥AB,∴,∴,∴CE＝,QE＝t,∵∠CPQ＝45°,∴PE＝QE＝t,∴t+t+t＝4,∴t＝s(3)如图2,过点P作PF⊥BC于F点,过点M作MH⊥BC,交BC延长线于点H, ∴四边形PMHF是矩形,∴PM＝FH＝5,∵∠A＝∠PFC＝90°,∠ACB＝∠PCF,∴△ABC∽△FPC,∴,∴＝∴PF＝,CF＝,∴QH＝5﹣FQ＝5﹣(CF﹣CQ)＝,∵PQ⊥MQ,∴∠PQF+∠MQH＝90°,且∠PQF+∠FPQ＝90°,∴∠FPQ＝∠MQH,且∠PFQ＝∠H＝90°,∴△PFQ∽△QHM,∴,∴∴t＝s．5．问题背景:如图1,在正方形ABCD的内部,作∠DAE＝∠ABF＝∠BCG＝∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得四边形EFGH是正方形．类比探究:如图2,在正△ABC的内部,作∠1＝∠2＝∠3,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)．(1)△ABD,△BCE,△CAF是否全等？如果是,请选择其中一对进行证明；(2)△DEF是否为正三角形？请说明理由；(3)如图3,进一步探究发现,△ABD的三边存在一定的等量关系,设BD＝a,AD＝b,AB＝c,请探索a,b,c满足的等量关系．(1)△ABD≌△BCE≌△CAF；理由如下:∵△ABC是正三角形,∴∠CAB＝∠ABC＝∠BCA＝60°,AB＝BC＝AC,又∵∠1＝∠2＝∠3,∴∠ABD＝∠BCE＝∠CAF,在△ABD、△BCE和△CAF中,,∴△ABD≌△BCE≌△CAF(ASA)；(2)△DEF是正三角形；理由如下:∵△ABD≌△BCE≌△CAF,∴∠ADB＝∠BEC＝∠CFA,∴∠FDE＝∠DEF＝∠EFD,∴△DEF是正三角形；(3)c2＝a2+ab+b2．作AG⊥BD于G,如图所示:∵△DEF是正三角形,∴∠ADG＝60°,在Rt△ADG中,DG＝b,AG＝b,在Rt△ABG中,c2＝(a+b)2+(b)2,∴c2＝a2+ab+b2．6．如图,在四边形ABCD中,AC是对角线,∠ABC＝∠CDA＝90°,BC＝CD,延长BC交AD的延长线于点E．(1)求证:AB＝AD；(2)若AE＝BE+DE,求∠BAC的值；(3)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P,连接PB．设PB＝a,点O是直线AE上的动点,当MO+PO的值最小时,点O与点E是否可能重合？若可能,请说明理由并求此时MO+PO的值(用含a的式子表示)；若不可能,请说明理由．(1)证明:∵∠ABC＝∠CDA＝90°,∵BC＝CD,AC＝AC,∴Rt△ABC≌Rt△ADC(HL)．∴AB＝AD．(2)解:∵AE＝BE+DE,又∵AE＝AD+DE,∴AD＝BE．∵AB＝AD,∴AB＝BE．∴∠BAD＝∠BEA．∵∠ABC＝90°,∴∠BAD═45°．∵由(1)得△ABC≌△ADC,∴∠BAC＝∠DAC．∴∠BAC═22.5°．(3)解:当MO+PO的值最小时,点O与点E可以重合,理由如下: ∵ME∥AB,∴∠ABC＝∠MEC＝90°,∠MAB＝∠EMA．∵MP⊥DC,∴∠MPC＝90°．∴∠MPC＝∠ADC＝90°．∴PM∥AD．∴∠EAM＝∠PMA．由(1)得,Rt△ABC≌Rt△ADC,∴∠EAC＝∠MAB,∴∠EMA＝∠AMP．即MC平分∠PME．又∵MP⊥CP,ME⊥CE,∴PC＝EC．如图,连接PB,连接PE,延长ME交PD的延长线于点Q．设∠EAM＝α,则∠MAP＝α．在Rt△ABE中,∠BEA＝90°﹣2α．在Rt△CDE中,∠ECD＝90°﹣∠BEA＝2α．∵PC＝EC,∴∠PEB＝∠EPC＝∠ECD＝α．∴∠PED＝∠BEA+∠PEB＝90°﹣α．∵ME∥AB,∴∠QED＝∠BAD＝2α．当∠PED＝∠QED时,∵∠PDE＝∠QDE,DE＝DE,∴△PDE≌△QDE(ASA)．∴PD＝DQ．即点P与点Q关于直线AE成轴对称,也即点M、点E、点P关于直线AE的对称点Q,这三点共线,也即MO+PO的值最小时,点O与点E重合．因为当∠PED＝∠QED时,90°﹣α＝2α,也即α＝30°．所以,当∠ABD＝60°时,MO+PO取最小值时的点O与点E重合．此时MO+PO的最小值即为ME+PE．∵PC＝EC,∠PCB＝∠ECD,CB＝CD,∴△PCB≌△ECD(SAS)．∴∠CBP＝∠CDE＝90°．∴∠CBP+∠ABC＝180°．∴A,B,P三点共线．当∠ABD＝60°时,在△PEA中,∠PAE＝∠PEA＝60°．∴∠EPA＝60°．∴△PEA为等边三角形．∵EB⊥AP,∴AP＝2AB＝2a．∴EP＝AE＝2a．∵∠EMA＝∠EAM＝30°,∴EM＝AE＝2a．∴MO+PO的最小值为4a．7．已知:如图,在正方形ABCD中,点E在AD边上运动,从点A出发向点D运动,到达D点停止运动．作射线CE,并将射线CE绕着点C逆时针旋转45°,旋转后的射线与AB边交于点F,连接EF．(1)依题意补全图形；(2)猜想线段DE,EF,BF的数量关系并证明；(3)过点C作CG⊥EF,垂足为点G,若正方形ABCD的边长是4,请直接写出点G运动的路线长．解:(1)补全图形如图1所示:(2)线段DE,EF,BF的数量关系为:EF＝DE+BF．理由如下: 延长AD到点H,使DH＝BF,连接CH,如图2所示:∵四边形ABCD是正方形,∴∠BCD＝∠ADC＝∠B＝90°,BC＝DC,∴∠CDH＝90°＝∠B,在△CDH和△CBF中,,∴△CDH≌△CBF(SAS)．∴CH＝CF,∠DCH＝∠BCF．∵∠ECF＝45°,∴∠ECH＝∠ECD+∠DCH＝∠ECD+∠BCF＝45°．∴∠ECH＝∠ECF＝45°．在△ECH和△ECF中,,∴△EC H≌△ECF(SAS)．∴EH＝EF．∵EH＝DE+DH,∴EF＝DE+BF；(3)由(2)得:△ECH≌△ECF(SAS),∴∠CEH＝∠CEF,∵CD⊥AD,CG⊥EF,∴CD＝CG＝4,∴点G的运动轨迹是以C为圆心4为半径的弧DB,∴点G运动的路线长＝＝2π．8．如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE．连接DE并延长交射线AP于点F,连接BF．(1)若∠BAP＝α,直接写出∠ADF的大小(用含α的式子表示)；(2)求证:BF⊥DF；(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明．(1)解:由轴对称的性质得:∠EAP＝∠BAP＝α,AE＝AB,∵四边形ABCD是正方形,∴∠BAD＝90°,AB＝AD,∴∠DAE＝90°﹣2α,AD＝AE,∴∠ADF＝∠AED＝(180°﹣∠DAE)＝(90°+2α)＝45°+α；(2)证明:∵四边形ABCD是正方形,∴∠BAD＝90°,AB＝AD,∵点E与点B关于直线AP对称,∴∠AEF＝∠ABF,AE＝AB．∴AE＝AD．∴∠ADE＝∠AED．∵∠AED+∠AEF＝180°,∴在四边形ABFD中,∠ADE+∠ABF＝180°,∴∠BFD+∠BAD＝180°,∴∠BFD＝90°∴BF⊥DF；(3)解:线段AF,BF,CF之间的数量关系为AF＝BF+CF,理由如下: 过点B作BM⊥BF交AF于点M,如图所示:∵四边形ABCD是正方形,∴AB＝CB,∠ABC＝90°,∴∠ABM＝∠CBF,∵点E与点B关于直线AP对称,∠BFD＝90°,∴∠MFB＝∠MFE＝45°,∴△BMF是等腰直角三角形,∴BM＝BF,FM＝BF,在△AMB和△CFB中,,∴△AMB≌△CFB(SAS),∴AM＝CF,∵AF＝FM+AM,∴AF＝BF+CF．9．如图1,已知等腰Rt△ABC中,E为边AC上一点,过E点作EF⊥AB于F点,以为边作正方形,且AC＝3,EF＝．(1)如图1,连接CF,求线段CF的长；(2)将等腰Rt△ABC绕点旋转至如图2的位置,连接BE,M点为BE的中点,连接MC,MF,求MC与MF关系．解:(1)如图1,∵△ABC是等腰直角三角形,AC＝3,∴AB＝3,过点C作CM⊥AB于M,连接CF,∴CM＝AM＝AB＝,∵四边形AGEF是正方形,∴AF＝EF＝,∴MF＝AM﹣AF＝﹣,在Rt△CMF中,CF＝＝＝；(2)CM＝FM,CM⊥FM,理由:如图2,过点B作BH∥EF交FM的延长线于H,连接CF,CH,∴∠BHM＝∠EFM,∵四边形AGEF是正方形,∴EF＝AF∵点M是BE的中点,∴BM＝EM,在△BMH和△EMF中,,∴△BMH≌△EMF(AAS),∴MH＝MF,BH＝EF＝AF∵四边形AGEF是正方形,∴∠FAG＝90°,EF∥AG,∵BH∥EF,∴BH∥AG,∴∠BAG+∠ABH＝180°,∴∠CBH+∠ABC+∠BAC+∠CAG＝180°．∵△ABC是等腰直角三角形,∴BC＝AC,∠ABC＝∠BAC＝45°,∴∠CBH+∠CAG＝90°,∵∠CAG+∠CAF＝90°,∴∠CBH＝∠CAF,在△BCH和△ACF中,,∴△BCH≌△ACF(SAS),∴CH＝CF,∠BCH＝∠ACF,∴∠HCF＝∠BCH+∠BCF＝∠ACF+∠BCF＝90°,∴△FCH是等腰直角三角形,∵MH＝MF,∴CM＝FM,CM⊥FM；10．如图将正方形ABCD绕点A顺时针旋转角度α(0°＜α＜90°)得到正方形AB′C′D′．(1)如图1,B′C′与AC交于点M,C′D′与AD所在直线交于点N,若MN∥B′D′,求α；(2)如图2,C′B′与CD交于点Q,延长C′B′与BC交于点P,当α＝30°时．①求∠DAQ的度数；②若AB＝6,求PQ的长度．解:(1)如图1中,∵MN∥B′D′,∴∠C′MN＝∠C′B′D′＝45°,∠C′NM＝∠C′D′B′＝45°,∴∠C′MN＝∠C′NM,∴C′M＝C′N,∵C′B′＝C′D′,'∴MB′＝ND′,∵AB′＝AD′,∠AB′M＝∠AD′N＝90°,∴△AB′M≌△AD′N(SAS),∴∠B′AM＝∠D′AN,∵∠B′AD′＝90°,∠MAN＝45°,∴∠B′AM＝∠D′AN＝22.5°,∵∠BAC＝45°,∴∠BAB′＝22.5°,∴α＝22.5°．(2)①如图2中,∵∠AB′Q＝∠ADQ＝90°,AQ＝AQ,AB′＝AD,∴Rt△AQB′≌Rt△AQD(HL),∴∠QAB′＝∠QAD,∵∠BAB′＝30°,∠BAD＝90°,∴∠B′AD＝30°,∴∠QAD＝∠B′AD＝30°．②如图2中,连接AP,在AB上取一点E,使得AE＝EP,连接EP．设PB＝a．∵∠ABP＝∠AB′P＝90°,AP＝AP,AB＝AB′,∴Rt△APB≌Rt△APB′(HL),∴∠BAP＝∠PAB′＝15°,∵EA＝EP,∴∠BEP＝∠EAP+∠EPA＝30°,∴PE＝AE＝2a,BE＝a,∵AB＝6,∴2a+a＝6,∴a＝6(2﹣)．∴PB＝6(2﹣),∴PC＝BC﹣PB＝6﹣6(2﹣)＝6﹣6,∵∠CPQ+∠BPB′＝180°,∠BAB′+∠BPB′＝180°,∴∠CPQ＝∠BAB′＝30°,∴PQ＝＝＝12﹣4．11．已知,如图1,在边长为2的正方形ABCD中,E是边AB的中点,点F在边AD上,过点A 作AG⊥EF,分别交线段CD、EF于点G、H(点G不与线段CD的端点重合)．(1)如图2,当G是边CD中点时,求AF的长；(2)设AF＝x,四边形FHGD的面积是y,求y关于x的函数关系式,并写出x的取值范围；(3)联结ED,当∠FED＝45°时,求AF的长．解:(1)∵E是AB的中点,AB＝2,∴AE＝AB＝1,同理可得DG＝1,∵AG⊥EF,∴∠AHF＝∠HAF+∠AFH＝90°,∵四边形ABCD是正方形,∴∠ADG＝90°＝∠DAG+∠AGD,∴∠AFH＝∠AGD,∴△EAF∽△ADG,∴,即,∴AF＝；(2)如图1,由(1)知:△EAF∽△ADG,∴,即,∴DG＝2x,∵∠HAF＝∠DAG,∠AHF＝∠ADG＝90°,∴∠AHF∽△ADG,∴＝,∴＝,∴AH＝＝,FH＝＝, ∴y＝S△ADG﹣S△AFH,＝,＝2x﹣,如图2,当G与C重合时,∵EF⊥AG,∴∠AHE＝90°,∵∠EAH＝45°,∴∠AEH＝45°,∴AF＝AE＝1,∴0＜x＜1；∴y关于x的函数关系式为:y＝2x﹣(0＜x＜1)；(3)如图3,过D作DM⊥AG,交BC于M,连接EM,延长EA至N,使AN＝CM,连接DN,设CM＝a,则AN＝a,∵AD＝CD,∠NAD＝∠DCM＝90°,∴△NAD≌△MCD(SAS),∴∠ADN＝∠CDM,DN＝DM,∵EF⊥AG,DM⊥AG,∴EF∥DM,∴∠EDM＝∠FED＝45°,∴∠ADE+∠CDM＝∠EDM＝45°,∴∠NDA+∠ADE＝∠NDE＝∠EDM,∵ED＝ED,∴△NDE≌△MDE(SAS),∴EN＝EM＝a+1,∵BM＝2﹣a,在Rt△EBM中,由勾股定理得:BE2+BM2＝EM2,∴12+(2﹣a)2＝(a+1)2,a＝,∵∠AEF+∠EAG＝∠EAG+∠DAG,∴∠AEF＝∠DAG＝∠CDM,∴tan∠AEF＝tan∠CDM,∴,∴,∴AF＝．12．如图1,对角线互相垂直的四边形叫做垂美四边形．(1)概念理解:如图2,在四边形ABCD中,AB＝AD,CB＝CD,问四边形ABCD是垂美四边形吗？请说明理由；(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD．试证明:AB2+CD2＝AD2+BC2；(3)解决问题:如图3,△ACB中,∠ACB＝90°,AC⊥AG且AC＝AG,AB⊥AE且AE＝AB,连结CE、BG、GE．已知AC＝4,AB＝5,求GE的长．解:(1)四边形ABCD是垂美四边形,理由如下:连接AC,BD,∵AB＝AD,∴点A在线段BD的垂直平分线上,∵CB＝CD,∴点C在线段BD的垂直平分线上,∴AC是线段BD的垂直平分线,∴四边形ABCD是垂美四边形；(2)∵AC⊥BD,∴∠AOD＝∠AOB＝∠BOC＝∠COD＝90°,由勾股定理得,AD2+BC2＝AO2+DO2+BO2+CO2,AB2+CD2＝AO2+BO2+CO2+DO2,∴AD2+BC2＝AB2+CD2；故答案为:AB2+CD2＝AD2+BC2；(3)∵∠CAG＝∠BAE＝90°,∴∠CAG+∠BAC＝∠BAE+∠BAC,即∠GAB＝∠CAE, 在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG＝∠AEC,又∠AEC+∠AME＝90°,∴∠ABG+∠AME＝90°,即CE⊥BG,∴四边形CGEB是垂美四边形,由(2)得,CG2+BE2＝CB2+GE2,∵AC＝4,AB＝5,∴BC＝3,CG＝4,BE＝5,∴GE2＝CG2+BE2﹣CB2＝73,∴GE＝．13．如图1,四边形ACEB,连接BC,∠ACB＝∠BEC＝90°,D在AB上,连接CD,∠ACD＝∠ABC,BE＝CD．(1)求证:四边形CDBE为矩形；(2)如图2,连接DE,DE交BC于点O,若tan∠A＝2,在不添加任何辅助线和字母的情况下,请直接写出图中所有长度与AD的长度相等的线段．(1)证明:∵∠ACB＝90°,∴∠A+∠ABC＝90°,∵∠ACD＝∠ABC,∴∠A+∠ACD＝90°,∴∠ADC＝90°,∴∠BDC＝180°﹣90°＝90°＝∠BEC,在Rt△BCD和Rt△CBE中,,∴Rt△BCD≌Rt△CBE(HL),∴BD＝CE,∵CD＝BE,∴四边形CDBE是平行四边形,又∵∠BEC＝90°,∴四边形CDBE为矩形；(2)解:图中所有长度与AD的长度相等的线段为AC＝OC＝OB＝OD＝OE＝AD ．理由如下:由(1)得:四边形CDBE为矩形,∠ADC＝90°,∴BC＝DE,OD＝OE,OB＝OC,∴OC＝OB＝OD＝OE＝BC,∵∠ADC＝∠ACB＝90°,∴tan∠A＝2＝＝,∴CD＝2AD,BC＝2AC,∴AC＝＝＝AD,∴DE＝BC＝2AC,∴OC＝OB＝OD＝OE＝BC＝AC＝AD,∴AC＝OC＝OB＝OD＝OE＝AD．14．如图在直角坐标系中,四边形ABCO为正方形,A点的坐标为(a,0),D点的坐标为(0,b),且a,b满足(a﹣3)2+|b﹣|＝0．(1)求A点和D点的坐标；(2)若∠DAE＝∠OAB,请猜想DE,OD和EB的数量关系,说明理由．(3)若∠OAD＝30°,以AD为三角形的一边,坐标轴上是否存在点P,使得△PAD为等腰三角形,若存在,直接写出有多少个点P,并写出P点的坐标,选择一种情况证明．解:(1)∵(a﹣3)2+|b﹣|＝0,∴a＝3,b＝,∴D(0,),A(3,0)；(2)DE＝OD+EB；理由如下:如图1,在CO的延长线上找一点F,使OF＝BE,连接AF, 在△AOF和△ABE中,,∴△AOF≌△ABE(SAS),∴AF＝AE,∠OAF＝∠BAE,又∵∠OAB＝90°,∠DAE＝,∴∠BAE+∠DAO＝45°,∴∠DAF＝∠OAF+∠DAO＝45°,∴∠DAF＝∠EAD,在△AFD和△AED中,,∴△AFD≌△AED(SAS),∴DF＝DE＝OD+EB；(3)有3种情况共6个点:①当DA＝DP时,如图2,Rt△ADO中,OD＝,OA＝3,∴AD＝＝＝2, ∴P1(﹣3,0),P2(0,3),P3(0,﹣)；②当AP4＝DP4时,如图3,∴∠ADP4＝∠DAP4＝30°,∴∠OP4D＝60°,Rt△ODP4中,∠ODP4＝30°,OD＝,∴OP4＝1,∴P4(1,0)；③当AD＝AP时,如图4,∴AD＝AP5＝AP6＝2,∴P5(3+2,0),P6(3﹣2,0),综上,点P的坐标为:∴P(﹣3,0)或(0,3)或(0,﹣)或(1,0)或(3+2,0)或(3﹣2,0)．证明:P5(3+2,0),∵∠OAD＝30°且△ADO是直角三角形,又∵AO＝3,DO＝,∴DA＝2,而P5A＝|3+2﹣3|＝2,∴P5A＝DA,∴△P5AD是等腰三角形．15．已知,在四边形ABCD中,点M、N、P、Q分别为边AB、AD、CD、BC的中点,连接MN、NP、PQ、MQ．(1)如图1,求证:四边形MNPQ为平行四边形；(2)如图2,连接AC,AC分别交MN、PQ于点E、F,连接BD,BD分别交MQ、NP于点G、H,AC与BD交于点O,且AC⊥BD,若tan∠ADB＝,在不添加任何辅助线的情况下,请直接写出图2中所有长度等于OD的线段．(1)证明:如图1,连接BD．∵Q,P分别是BC,CD的中点,所以PQ∥BD,PQ＝BD．∵M,N分别是AB,AD的中点．∴MN∥BD,MN＝BD．∴PQ∥MN,且PQ＝MN．∴四边形MNPQ是平行四边形．(2)解:∵四边形MNPQ是平行四边形,AC⊥BD,∴四边形MNPQ是矩形,∴四边形NHOE和四边形EOGM都是矩形,∴NH＝OE＝MG＝AE＝,∵tan∠ADB＝,∴,∴NH＝OE＝MG＝AE＝．即长度等于OD的线段有NH,OE,MG,AE．。

中考数学压轴题：“动点产生的平行四边形问题”训练及解析先思考三个问题：1．已知A、B、C三点，以A、B、C、D为顶点的平行四边形有几个，怎么画？2．在坐标平面内，如何理解平行四边形ABCD的对边AB与DC平行且相等？3．在坐标平面内，如何理解平行四边形ABCD的对角线互相平分？图1 图2 图3 如图1，过△ABC的每个顶点画对边的平行线，三条直线两两相交，产生三个点D．如图2，已知A(0, 3)，B(－2, 0)，C(3, 1)，如果四边形ABCD是平行四边形，怎样求点D的坐标呢？点B先向右平移2个单位，再向上平移3个单位与点A重合，因为BA与CD平行且相等，所以点C(3, 1) 先向右平移2个单位，再向上平移3个单位得到点D(5, 4)．如图3，如果平行四边形ABCD的对角线交于点G，那么过点G画任意一条直线（一般与坐标轴垂直），点A、C到这条直线的距离相等，点B、D到这条直线的距离相等．关系式x A＋x C＝x B＋x D和y A＋y C＝y B＋y D有时候用起来很方便．我们再来说说压轴题常常要用到的数形结合．如图4，点A是抛物线y＝－x2＋2x＋3在x轴上方的一个动点，AB⊥x轴于点B，线段AB交直线y＝x－1于点C，那么点A的坐标可以表示为(x,－x2＋2x＋3)，点C的坐标可以表示为(x, x－1)，线段AB的长可以用点A的纵坐标表示为AB＝y A＝－x2＋2x＋3，线段AC的长可以用A、C两点的纵坐标图4表示为AC＝y A－y C＝(－x2＋2x＋3)－(x－1)＝－x2＋x＋2．通俗地说，数形结合就是：点在图象上，可以用图象的解析式表示点的坐标，用点的坐标表示点到坐标轴的距离．例 24 2014年湖南省岳阳市中考第24题如图1，抛物线经过A (1, 0)、B (5, 0)、C 10(0,)3三点．设点E (x , y )是抛物线上一动点，且在x 轴下方，四边形OEBF 是以OB 为对角线的平行四边形． （1）求抛物线的解析式；（2）当点E (x , y )运动时，试求平行四边形OEBF的面积S 与x 之间的函数关系式，并求出面积S 的最大值；（3）是否存在这样的点E ，使平行四边形OEBF 为正方形？若存在，求点E 、F 的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“14岳阳24”，拖动点E 运动，可以体验到，当点E 运动到抛物线的顶点时，S 最大．当点E 运动到OB 的垂直平分线上时，四边形OEBF 恰好是正方形． 思路点拨1．平行四边形OEBF 的面积等于△OEB 面积的2倍．2．第（3）题探究正方形OEBF ，先确定点E 在OB 的垂直平分线上，再验证EO ＝EB ． 图文解析（1）因为抛物线与x 轴交于A (1, 0)、B (5, 0)两点，设y ＝a (x －1)(x －5)． 代入点C 10(0,)3，得1053a =．解得23a =． 所以抛物线的解析式为22210(1)(5)4333y x x x x =--=-+． （2）因为S ＝S 平行四边形OEBF ＝2S △OBE ＝OB ·(－y E ) ＝22105(4)33x x --+＝210(65)3x x --+＝21040(3)33x --+． 所以当x ＝3时，S 取得最大值，最大值为403．此时点E 是抛物线的顶点（如图2）． （3）如果平行四边形OEBF 是正方形，那么点E 在OB 的垂直平分线上，且EO ＝EB ． 当x ＝52时，22355(1)(5)()33222y x x =--=⨯⨯-=-．此时E 55(,)22-． 如图3，设EF 与OB 交于点D ，恰好OB ＝2DE ． 所以△OEB 是等腰直角三角形．所以平行四边形OEBF 是正方形．所以当平行四边形OEBF 是正方形时，E 55(,)22-、F 55(,)22．图2 图3考点伸展既然第（3）题正方形OEBF 是存在的，命题人为什么不让探究矩形OEBF 有几个呢？ 如图4，如果平行四边形OEBF 为矩形，那么∠OEB ＝90°．根据EH 2＝HO ·HB ，列方程22(1)(5)(5)3x x x x ⎡⎤---=-⎢⎥⎣⎦． 或者由DE ＝12OB ＝52，根据DE 2＝254，列方程225225()(1)(5)234x x x ⎡⎤-+---=⎢⎥⎣⎦． 这两个方程整理以后都是一元三次方程4x 3－28x 2＋53x －20＝0，这个方程对于初中毕业的水平是不好解的． 事实上，这个方程可以因式分解，51(4)()()022x x x ---=．如图3，x ＝52；如图4，x ＝4；如图5，x ＝12，但此时点E 在x 轴上方了． 这个方程我们也可以用待定系数法解： 设方程的三个根是52、m 、n ，那么4x 3－28x 2＋53x －20＝54()()()2x x m x n ---． 根据恒等式对应项的系数相等，得方程组441028,1010453,1020.m n m n mn mn ++=⎧⎪++=⎨⎪=⎩解得4,1.2m n =⎧⎪⎨=⎪⎩图4 图5例 25 2014年湖南省益阳市中考第20题如图1，直线y＝－3x＋3与x轴、y轴分别交于点A、B，抛物线y＝a(x－2)2＋k经过A、B两点，并与x轴交于另一点C，其顶点为P．（1）求a，k的值；（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求点Q的坐标；（3）在抛物线及其对称轴上分别取点M、N，使以A、C、M、N为顶点的四边形为正方形，求此正方形的边长．】图1动感体验请打开几何画板文件名“14益阳20”，可以体验到，点Q在线段AB的垂直平分线上．还可以体验到，正方形的对角线为AC，有一个顶点恰为抛物线的顶点．思路点拨1．第（2）题的等腰三角形只考虑QA＝QB的情形．2．第（3）题的正方形不可能AC为边，只存在AC为对角线的情形．图文解析（1）由y＝－3x＋3，得A(1, 0)，B(0, 3)．将A(1, 0)、B(0, 3)分别代入y＝a(x－2)2＋k，得0,4 3.a ka k+=⎧⎨+=⎩解得a＝1，k＝－1．（2）如图2，抛物线的对称轴为直线x＝2，设点Q的坐标为(2, m)．已知A(1, 0)、B(0, 3)，根据QA2＝QB2，列方程12＋m2＝22＋(m－3)2．解得m＝2．所以Q(2, 2)．（3）点A(1, 0)关于直线x＝2的对称点为C(3, 0)，AC＝2．如图3，如果AC为正方形的边，那么点M、N都不在抛物线或对称轴上．如图4，当AC为正方形的对角线时，M、N中恰好有一个点是抛物线的顶点(2,－1) ．因为对角线AC＝2．图2 图3 图4考点伸展如果把第（3）题中的正方形改为平行四边形，那么符合条件的点M有几个？①如果AC为对角线，上面的正方形AMCN是符合条件的，M(2,－1)．②如图5，如果AC为边，那么MN//AC，MN＝AC＝2．所以点M的横坐标为4或0．此时点M的坐标为(4, 3)或(0, 3)．第（2）题如果没有限制等腰三角形ABQ的底边，那么符合条件的点Q有几个？①如图2，当QA＝QB时，Q(2, 2)．②如图6，当BQ＝BA B为圆心，BA为半径的圆与直线x＝2有两个交点．m=根据BQ2＝10，列方程22＋(m－3)2＝10，得3此时Q(2,3或(2,3．③如图7，当AQ＝AB时，以A为圆心，AB为半径的圆与直线x＝2有两个交点，但是点(2,－3)与A、B三点共线，所以Q(2, 3)．图5 图6 图7例 26 2014年湖南省邵阳市中考第25题准备一张矩形纸片（如图1），按如图2操作：将△ABE 沿BE 翻折，使点A 落在对角线BD 上的点M ，将△CDF 沿DF 翻折，使点C 落在对角线BD 上的点N ．（1）求证：四边形BFDE 是平行四边形；（2）若四边形BFDE 是菱形，AB ＝2，求菱形BFDE 的面积．图1图2动感体验请打开几何画板文件名“14邵阳25”，拖动点D 可以改变矩形ABCD 的形状，可以体验到，当EM 与FN 在同一条直线上时，四边形BFDE 是菱形，此时矩形的直角被三等分． 思路点拨1．平行四边形的定义和4个判定定理都可以证明四边形BFDE 是平行四边形．2．如果平行四边形BFDE 是菱形，那么对角线平分一组对角，或者对角线互相垂直．用这两个性质都可以解答第（2）题．图文解析（1）如图3，因为AB //DC ，所以∠ABD ＝∠CDB ．又因为∠1＝∠2，∠3＝∠4，所以∠1＝∠3．所以BE //FD ．又因为ED //BF ，所以四边形BFDE 是平行四边形．图3 图4（2）如图4，如果四边形BFDE 是菱形，那么∠1＝∠5．所以∠1＝∠2＝∠5．由于∠ABC ＝90°，所以∠1＝∠2＝∠5＝30°．所以BD ＝2AB ＝4，AE ＝3．所以ME ＝3．所以S 菱形BFDE ＝2S △BDE ＝BD ·ME ＝3．考点伸展第（1）题的解法，我们用平行四边形的定义作为判定的依据，两组对边分别平行的四边形叫平行四边形．还可以这样思考：证明四边形BFDE 的两组对边分别相等；证明ED 与BF 平行且相等；证明四边形BFDE 的两组对角分别相等．这三种证法，都要证明三角形全等，而全等的前提，要证明∠1＝∠2＝∠3＝∠4． 这样其实就走了弯路，因为由∠1＝∠3，直接得到BE //FD ，根据平行四边形的定义来得快．能不能根据BD 与EF 互相平分来证明呢？也是可以的：如图5，设EF 与BD 交于点O ，根据“角角边”证明△EMO ≌△FNO ，得到EF 与MN 互相平分．又因为BM ＝DN ，于是得到EF 与BD 互相平分．图5 图6第（2）题的解法，我们用了菱形的性质：对角线平分每组对角，得到30°的角． 我们也可以根据菱形的对角线互相垂直平分来解题：如图6，如果四边形BFDE 是菱形，那么对角线EF ⊥BD ，此时垂足M 、N 重合． 因此BD ＝2DC ．这样就得到了∠5＝30°．事实上，当四边形BFDE 是菱形时，矩形ABCD 被分割为6个全等的直角三角形．由AB ＝2，得AD ＝ABCD 的面积为菱形面积占矩形面积的23．。

九年级中考数学动点问题压轴题专题训练1. 如图1，在平面直角坐标系中，四边形OABC各顶点的坐标分别为O(0，0)，A(3，33)，B(9，53)，C(14，0)．动点P与Q同时从O点出发，运动时间为t秒，点P沿OC方向以1单位长度/秒的速度向点C运动，点Q沿折线OA－AB－BC运动，在OA，AB，BC上运动的速度分别为3，3，52(单位长度/秒)．当P，Q中的一点到达C点时，两点同时停止运动．(1)求AB所在直线的函数表达式．(2)如图2，当点Q在AB上运动时，求△CPQ的面积S关于t的函数表达式及S 的最大值．(3)在P，Q的运动过程中，若线段PQ的垂直平分线经过四边形OABC的顶点，求相应的t值．图1 图22. 如图，抛物线y=-x2+bx+c与x轴交于A，B两点(A在B的左侧)，与y轴交于点N，过A点的直线l:y=kx+n与y轴交于点C，与抛物线y=-x2+bx+c的另一个交点为D，已知A(-1，0)，D(5，-6)，P点为抛物线y=-x2+bx+c上一动点(不与A，D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时，过P点作PE∥x轴交直线l于点E，作PF∥y轴交直线l于点F，求PE+PF的最大值;(3)设M为直线l上的点，探究是否存在点M，使得以点N，C，M，P为顶点的四边形为平行四边形.若存在，求出点M的坐标;若不存在，请说明理由.3. 如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋c经过A(－2, －4 )、O(0, 0)、B(2, 0)三点．（1）求抛物线y＝ax2＋bx＋c的解析式；（2）若点M是该抛物线对称轴上的一点，求AM＋OM的最小值．4. 设直线l1：y＝k1x＋b1与l2：y＝k2x＋b2，若l1⊥l2，垂足为H，则称直线l1与l2是点H的直角线．（1）已知直线①122y x =-+；②2y x =+；③22y x =+；④24y x =+和点C (0，2)，则直线_______和_______是点C 的直角线（填序号即可）；（2）如图，在平面直角坐标系中，直角梯形OABC 的顶点A (3，0)、B (2，7)、C (0，7)，P 为线段OC 上一点，设过B 、P 两点的直线为l 1，过A 、P 两点的直线为l 2，若l 1与l 2是点P 的直角线，求直线l 1与l 2的解析式．5. 如图①，在平面直角坐标系xOy 中，已知抛物线y=ax 2-2ax -8a 与x 轴相交于A ，B 两点(点A 在点B 的左侧)，与y 轴交于点C (0，-4).(1)点A 的坐标为 ，点B 的坐标为 ，线段AC 的长为 ，抛物线的解析式为 .(2)点P 是线段BC 下方抛物线上的一个动点.如果在x 轴上存在点Q ，使得以点B ，C ，P ，Q 为顶点的四边形是平行四边形，求点Q 的坐标.①6. 如图，已知抛物线211(1)444by x b x =-++（b 是实数且b ＞2）与x 轴的正半轴分别交于点A 、B （点A 位于点B 是左侧），与y 轴的正半轴交于点C ．（1）点B 的坐标为______，点C 的坐标为__________（用含b 的代数式表示）； （2）请你探索在第一象限内是否存在点P ，使得四边形PCOB 的面积等于2b ，且△PBC 是以点P 为直角顶点的等腰直角三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）请你进一步探索在第一象限内是否存在点Q ，使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点Q 的坐标；如果不存在，请说明理由．7. 如图，已知A 、B 是线段MN 上的两点，4=MN ，1=MA ，1>MB ．以A 为中心顺时针旋转点M ，以B 为中心逆时针旋转点N ，使M 、N 两点重合成一点C ，构成△ABC ，设x AB =． （1）求x 的取值范围；（2）若△ABC 为直角三角形，求x 的值； （3）探究：△ABC 的最大面积？8. 如图，已知抛物线y＝－x2＋bx＋c经过A(0, 1)、B(4, 3)两点．（1）求抛物线的解析式；（2）求tan∠ABO的值；（3）过点B作BC⊥x轴，垂足为C，在对称轴的左侧且平行于y轴的直线交线段AB于点N，交抛物线于点M，若四边形MNCB为平行四边形，求点M的坐标．9. 在平面直角坐标系中，反比例函数与二次函数y＝k(x2＋x－1)的图象交于点A(1,k)和点B(－1,－k)．（1）当k＝－2时，求反比例函数的解析式；（2）要使反比例函数与二次函数都是y随x增大而增大，求k应满足的条件以及x的取值范围；（3）设二次函数的图象的顶点为Q，当△ABQ是以AB为斜边的直角三角形时，求k的值．10. 如图，已知抛物线y＝ax2＋bx＋4(a≠0)的对称轴为直线x＝3，抛物线与x轴相交于A，B两点，与y轴相交于点C，已知B点的坐标为(8，0)．(1)求抛物线的解析式；(2)点M为线段BC上方抛物线上的一点，点N为线段BC上的一点，若MN∥y 轴，求MN的最大值；(3)在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．11. 如图，直线y＝2x＋6与反比例函数y＝kx(k＞0)的图象交于点A(m，8)，与x轴交于点B，平行于x轴的直线y＝n(0＜n＜6)交反比例函数的图象于点M，交AB于点N，连接BM.(1)求m的值和反比例函数的解析式；(2)观察图象，直接写出当x＞0时不等式2x＋6－kx＞0的解集；(3)直线y＝n沿y轴方向平移，当n为何值时，△BMN的面积最大？最大值是多少？12. 如图，在平面直角坐标系xOy中，顶点为M的抛物线y＝ax2＋bx（a＞0）经过点A和x轴正半轴上的点B，AO＝BO＝2，∠AOB＝120°．（1）求这条抛物线的表达式；（2）连结OM，求∠AOM的大小；（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．13. 在直角梯形OABC中，CB//OA，∠COA＝90°，CB＝3，OA＝6，BA＝35．分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系．（1）求点B的坐标；（2）已知D、E分别为线段OC、OB上的点，OD＝5，OE＝2EB，直线DE交x轴于点F．求直线DE的解析式；（3）点M是（2）中直线DE上的一个动点，在x轴上方的平面内是否存在另一点N，使以O、D、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．14. 如图，已知一次函数y ＝－x ＋7与正比例函数43y x 的图象交于点A ，且与x 轴交于点B ．（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l //y 轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O —C —A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x 轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P 和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形？若存在，求t 的值；若不存在，请说明理由．15. 如图，二次函数y ＝a (x 2－2mx －3m 2)（其中a 、m 是常数，且a ＞0，m ＞0）的图像与x 轴分别交于A 、B （点A 位于点B 的左侧），与y 轴交于点C (0,－3)，点D 在二次函数的图像上，CD //AB ，联结AD ．过点A 作射线AE 交二次函数的图像于点E ，AB 平分∠DAE ． （1）用含m 的式子表示a ；（2）求证：AD为定值；AE（3）设该二次函数的图像的顶点为F．探索：在x轴的负半轴上是否存在点G，联结GF，以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G即可，并用含m的代数式表示该点的横坐标；如果不存在，请说明理由．16. 如图，二次函数y=-x2+4x+5的图象的顶点为D，对称轴是直线l，一次函数y=x+1的图象与x轴交于点A，且与直线DA关于l的对称直线交于点B.(1)点D的坐标是.(2)直线l与直线AB交于点C，N是线段DC上一点(不与点D，C重合)，点N 的纵坐标为n.过点N作直线与线段DA，DB分别交于点P，Q，使得△DPQ与△DAB 相似.①当n=时，求DP的长;②若对于每一个确定的n的值，有且只有一个△DPQ与△DAB相似，请直接写出n的取值范围.17. 已知直线y ＝3x －3分别与x 轴、y 轴交于点A ，B ，抛物线y ＝ax 2＋2x ＋c 经过点A ，B ．（1）求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；（2）记该抛物线的对称轴为直线l ，点B 关于直线l 的对称点为C ，若点D 在y 轴的正半轴上，且四边形ABCD 为梯形． ①求点D 的坐标；②将此抛物线向右平移，平移后抛物线的顶点为P ，其对称轴与直线y ＝3x －3交于点E ，若73tan =∠DPE ，求四边形BDEP 的面积．18. 如图，在平面直角坐标系xOy 中，二次函数y ＝－x 2＋2x ＋8的图象与一次函数y ＝－x ＋b 的图象交于A 、B 两点，点A 在x 轴上，点B 的纵坐标为－7.点P是二次函数图象上A 、B 两点之间的一个动点(不与点A 、B 重合)，设点P 的横坐标为m ，过点P 作x 轴的垂线交AB 于点C ，作PD ⊥AB 于点D . (1)求b 及sin ∠ACP 的值；(2)用含m 的代数式表示线段PD 的长；(3)连接PB ，线段PC 把△PDB 分成两个三角形，是否存在适合的m 值，使这两个三角形的面积之比为1∶2？如果存在，直接写出m 的值；如果不存在，请说明理由．19. 如图，抛物线233384y x x =--+与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ． （1）求点A 、B 的坐标；（2）设D 为已知抛物线的对称轴上的任意一点，当△ACD 的面积等于△ACB 的面积时，求点D 的坐标；（3）若直线l 过点E (4, 0)，M 为直线l 上的动点，当以A 、B 、M 为顶点所作的直角三角形有且只有．．．．三个时，求直线l 的解析式．20. 已知平面直角坐标系中两定点A(－1, 0)、B(4, 0)，抛物线y＝ax2＋bx－2（a≠0）过点A、B，顶点为C，点P(m, n)（n＜0）为抛物线上一点．（1）求抛物线的解析式和顶点C的坐标；（2）当∠APB为钝角时，求m的取值范围；（3）若m＞32，当∠APB为直角时，将该抛物线向左或向右平移t（0＜t＜52）个单位，点C、P平移后对应的点分别记为C′、P′，是否存在t，使得顺次首尾连接A、B、P′、C′所构成的多边形的周长最短？若存在，求t的值并说明抛物线平移的方向；若不存在，请说明理由．2021中考数学压轴专题训练之动点问题-答案一、解答题（本大题共20道小题）1. 【答案】【思维教练】(1)设一次函数解析式，将已知点A、B的坐标值代入求解即可；(2)S△CPQ＝12·CP·Q y，CP＝14－t，点Q在AB上，Q y即为当x＝t时的y值，代入化简得出S与t的函数关系式，化为顶点式得出最值；(3)垂直平分线过顶点需以时间为临界点分情况讨论，当Q在OA上时，过点C；当Q在AB上时，过点A；当Q在BC上时，过点C和点B，再列方程并求解．解图1解：(1)把A(3，33)，B(9，53)代入y ＝kx ＋b ，得⎩⎪⎨⎪⎧3k ＋b ＝33，9k ＋b ＝53，解得⎩⎨⎧k ＝33，b ＝23， ∴y ＝33x ＋23；(3分) (2)在△PQC 中，PC ＝14－t ，∵OA ＝32＋（33）2＝6且Q 在OA 上速度为3单位长度/s ， AB ＝62＋（23）2＝43且Q 点在AB 上的速度为3单位长度/s ， ∴Q 在OA 上时的横坐标为t ，Q 在AB 上时的横坐标为32t ， PC 边上的高线长为33t ＋2 3.(6分)所以S ＝12(14－t )(32t ＋23)＝－34t 2＋532t ＋143(2≤t ≤6)．当t ＝5时，S 有最大值为8134.(7分)解图2(3)①当0＜t ≤2时，线段PQ 的中垂线经过点C(如解图1)． 可得方程(332t )2＋(14－32t )2＝(14－t )2. 解得t 1＝74，t 2＝0(舍去)，此时t ＝74.(8分)解图3②当2＜t ≤6时，线段PQ 的中垂线经过点A(如解图2)． 可得方程(33)2＋(t －3)2＝[3(t －2)]2.解得t 1＝3＋572，∵t 2＝3－572(舍去)，此时t ＝3＋572. ③当6＜t ≤10时，(1)线段PQ 的中垂线经过点C(如解图3)． 可得方程14－t ＝25－52t ，解得t ＝223.(10分)解图4(2)线段PQ 的中垂线经过点B(如解图4)． 可得方程(53)2＋(t －9)2＝[52(t －6)]2. 解得t 1＝38＋2027，t 2＝38－2027(舍去)．此时t ＝38＋2027.(11分)综上所述，t 的值为74，3＋572，223，38＋2027.(12分)【难点突破】解决本题的关键点在于对PQ 的垂直平分线过四边形顶点的情况进行分类讨论，在不同阶段列方程求解．2. 【答案】[分析] (1)将点A，D的坐标分别代入直线表达式、抛物线的表达式，即可求解;(2)设出P点坐标，用参数表示PE，PF的长，利用二次函数求最值的方法.求解;(3)分NC是平行四边形的一条边或NC是平行四边形的对角线两种情况，分别求解即可.解:(1)将点A，D的坐标代入y=kx+n得:解得:故直线l的表达式为y=-x-1.将点A，D的坐标代入抛物线表达式，得解得故抛物线的表达式为:y=-x2+3x+4.(2)∵直线l的表达式为y=-x-1，∴C(0，-1)，则直线l与x轴的夹角为45°，即∠OAC=45°，∵PE∥x轴，∴∠PEF=∠OAC=45°.又∵PF∥y轴，∴∠EPF=90°，∴∠EFP=45°.则PE=PF.设点P坐标为(x，-x2+3x+4)，则点F(x，-x-1)，∴PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2)2+18，∵-2<0，∴当x=2时，PE+PF有最大值，其最大值为18.(3)由题意知N(0，4)，C(0，-1)，∴NC=5，①当NC是平行四边形的一条边时，有NC∥PM，NC=PM.设点P 坐标为(x ，-x 2+3x +4)，则点M 的坐标为(x ，-x -1)， ∴|y M -y P |=5，即|-x 2+3x +4+x +1|=5， 解得x=2±或x=0或x=4(舍去x=0)，则点M 坐标为(2+，-3-)或(2-，-3+)或(4，-5);②当NC 是平行四边形的对角线时，线段NC 与PM 互相平分. 由题意，NC 的中点坐标为0，，设点P 坐标为(m ，-m 2+3m +4)， 则点M (n'，-n'-1)， ∴0==，解得:n'=0或-4(舍去n'=0)， 故点M (-4，3).综上所述，存在点M ，使得以N ，C ，M ，P 为顶点的四边形为平行四边形，点M 的坐标分别为: (2+，-3-)，(2-，-3+)，(4，-5)，(-4，3).3. 【答案】（1）212y x x =-+。

九年级上册四边形压轴题2一．解答题〔共30小题〕1．〔2009•临沂〕数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF交正方形外角∠DCG的平分线CF于点F，求证：AE=EF．经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF．在此基础上，同学们作了进一步的研究：〔1〕小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上〔除B，C外〕的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；〔2〕小华提出：如图3，点E是BC的延长线上〔除C点外〕的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．2．〔2009•宁德〕如图〔1〕，已知正方形ABCD在直线MN的上方，BC在直线MN上，E 是BC上一点，以AE为边在直线MN的上方作正方形AEFG．〔1〕连接GD，求证：△ADG≌△ABE；〔2〕连接FC，观察并猜测∠FCN的度数，并说明理由；〔3〕如图〔2〕，将图〔1〕中正方形ABCD改为矩形ABCD，AB=a，BC=b〔a、b为常数〕，E是线段BC上一动点〔不含端点B、C〕，以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变？假设∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；假设∠FCN的大小发生改变，请举例说明．3．〔2009•黄石〕如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．〔1〕探究：线段OE与OF的数量关系并加以证明；〔2〕当点O在边AC上运动时，四边形BCFE会是菱形吗？假设是，请证明；假设不是，则说明理由；〔3〕当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？4．〔2009•无锡校级二模〕如图，在平面直角坐标系中，点A、点C同时从点O出发，分别以每秒2个单位、1个单位的速度向x轴、y轴的正半轴方向运动，以OA、OC为边作矩形OABC．以M〔4，0〕，N〔9，0〕为斜边端点作直角△PMN，点P在第一象限，且，当点A出发时，△PMN同时以每秒0.5个单位的速度沿x轴向右平移．设点A运动的时间为t秒，矩形OABC与△PMN重叠部分的面积为S．〔1〕求运动前点P的坐标；〔2〕求S与t的函数关系式，并写出自变量t的取值范围；〔3〕假设在运动过程中，要使对角线AC上始终存在点Q，满足∠OQM=90°，请直接写出符合条件的t的值或t的取值范围．5．〔2008•北京〕请阅读以下材料：问题：如图1，在菱形ABCD和菱形BEFG中，点A，B，E在同一条直线上，P是线段DF 的中点，连接PG，PC．假设∠ABC=∠BEF=60°，探究PG与PC的位置关系及的值．小聪同学的思路是：延长GP交DC于点H，构造全等三角形，经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决以下问题：〔1〕写出上面问题中线段PG与PC的位置关系及的值；〔2〕将图1中的菱形BEFG绕点B顺时针旋转，使菱形BEFG的对角线BF恰好与菱形ABCD 的边AB在同一条直线上，原问题中的其他条件不变〔如图2〕．你在〔1〕中得到的两个结论是否发生变化？写出你的猜想并加以证明；〔3〕假设图1中∠ABC=∠BEF=2α〔0°＜α＜90°〕，将菱形BEFG绕点B顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出的值〔用含α的式子表示〕．6．〔2008•厦门〕已知：如下图的一张矩形纸片ABCD〔AD＞AB〕，将纸片折叠一次，使点A与C重合，再展开，折痕EF交AD边于E，交BC边于F，分别连接AF和CE．〔1〕求证：四边形AFCE是菱形；〔2〕假设AE=10cm，△ABF的面积为24cm2，求△ABF的周长；〔3〕在线段AC上是否存在一点P，使得2AE2=AC•AP？假设存在，请说明点P的位置，并予以证明；假设不存在，请说明理由．7．〔2008•嘉兴〕小丽参加数学兴趣小组活动，提供了下面3个有联系的问题，请你帮助解决：〔1〕如图1，正方形ABCD中，作AE交BC于E，DF⊥AE交AB于F，求证：AE=DF；〔2〕如图2，正方形ABCD中，点E，F分别在AD，BC上，点G，H分别在AB，CD上，且EF⊥GH，求的值；〔3〕如图3，矩形ABCD中，AB=a，BC=b，点E，F分别在AD，BC上，且EF⊥GH，求的值．8．〔2008•宁夏〕如图，在边长为4的正方形ABCD中，点P在AB上从A向B运动，连接DP交AC于点Q．〔1〕试证明：无论点P运动到AB上何处时，都有△ADQ≌△ABQ；〔2〕当点P在AB上运动到什么位置时，△ADQ的面积是正方形ABCD面积的；〔3〕假设点P从点A运动到点B，再继续在BC上运动到点C，在整个运动过程中，当点P运动到什么位置时，△ADQ恰为等腰三角形．9．〔2008•昌平区二模〕如图，已知△ABC的顶点B、C为定点，A为动点〔不在直线BC 上〕，B′是点B关于直线AC的对称点，C′是点C关于直线AB的对称点，连接BC′、CB′、BB′、CC′．〔1〕猜想线段BC′与CB′的数量关系，并证明你的结论；〔2〕当点A运动到怎样的位置时，四边形BCB′C′为菱形？这样的位置有几个？请用语言对这样的位置进行描述〔不用证明〕；〔3〕当点A在线段BC的垂直平分线〔BC的中点及到BC的距离为的点除外上运动时，判断以点B、C、B′、C′为顶点的四边形的形状，画出相应的示意图．〔不用证明〕10．〔2007•常德〕如图1，已知四边形ABCD是菱形，G是线段CD上的任意一点时，连接BG交AC于F，过F作FH∥CD交BC于H，可以证明结论成立．〔考生不必证明〕〔1〕探究：如图2，上述条件中，假设G在CD的延长线上，其它条件不变时，其结论是否成立？假设成立，请给出证明；假设不成立，请说明理由；〔2〕计算：假设菱形ABCD中AB=6，∠ADC=60°，G在直线CD上，且CG=16，连接BG 交AC所在的直线于F，过F作FH∥CD交BC所在的直线于H，求BG与FG的长．〔3〕发现：通过上述过程，你发现G在直线CD上时，结论还成立吗？11．〔2007•宜昌〕如图1，在△ABC中，AB=BC=5，AC=6．△ECD是△ABC沿BC方向平移得到的，连接AE．AC和BE相交于点O．〔1〕判断四边形ABCE是怎样的四边形，说明理由；〔2〕如图2，P是线段BC上一动点〔图2〕，〔不与点B、C重合〕，连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R．①四边形PQED的面积是否随点P的运动而发生变化？假设变化，请说明理由；假设不变，求出四边形PQED的面积；②当线段BP的长为何值时，△PQR与△BOC相似．12．〔2007•潍坊〕已知等腰△ABC中，AB=AC，AD平分∠BAC交BC于D点，在线段AD上任取一点P〔A点除外〕，过P点作EF∥AB，分别交AC，BC于E，F点，作PM∥AC，交AB于M点，连接ME．〔1〕求证：四边形AEPM为菱形；〔2〕当P点在何处时，菱形AEPM的面积为四边形EFBM面积的一半？13．〔2007•永州〕在梯形ABCD中，AB∥CD，∠ABC=90°，AB=5，BC=10，tan∠ADC=2．〔1〕求DC的长；〔2〕E为梯形内一点，F为梯形外一点，假设BF=DE，∠FBC=∠CDE，试判断△ECF的形状，并说明理由．〔3〕在〔2〕的条件下，假设BE⊥EC，BE：EC=4：3，求DE的长．14．〔2007•常州〕已知，如图，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD边AB，CD，DA上，AH=2，连接CF．〔1〕当DG=2时，求△FCG的面积；〔2〕设DG=x，用含x的代数式表示△FCG的面积；〔3〕判断△FCG的面积能否等于1，并说明理由．15．〔2007•海南〕如图，在正方形ABCD中，点F在CD边上，射线AF交BD于点E，交BC的延长线于点G．〔1〕求证：△ADE≌△CDE；〔2〕过点C作CH⊥CE，交FG于点H，求证：FH=GH；〔3〕设AD=1，DF=x，试问是否存在x的值，使△ECG为等腰三角形？假设存在，请求出x的值；假设不存在，请说明理由．16．〔2007•哈尔滨〕如图1，在正方形ABCD中，对角线AC与BD相交于点E，AF平分∠BAC，交BD于点F．〔1〕求证：EF+AC=AB；〔2〕点C1从点C出发，沿着线段CB向点B运动〔不与点B重合〕，同时点A1从点A出发，沿着BA的延长线运动，点C1与A1的运动速度相同，当动点C1停止运动时，另一动点A1也随之停止运动．如图2，A1F1平分∠BA1C1，交BD于点F1，过点F1作F1E1⊥A1C1，垂足为E1，请猜想E1F1，A1C1与AB三者之间的数量关系，并证明你的猜想；〔3〕在〔2〕的条件下，当A1E1=3，C1E1=2时，求BD的长．17．〔2006•河南〕如图△ABC中，∠ACB=90度，AC=2，BC=3．D是BC边上一点，直线DE⊥BC于D，交AB于点E，CF∥AB交直线DE于F．设CD=x．〔1〕当x取何值时，四边形EACF是菱形？请说明理由；〔2〕当x取何值时，四边形EACD的面积等于2？18．〔2006•温州〕如图，在▱ABCD中，对角线AC⊥BC，AC=BC=2，动点P从点A出发沿AC向终点C移动，过点P分别作PM∥AB交BC于M，PN∥AD交DC于N．连接AM．设AP=x〔1〕四边形PMCN的形状有可能是菱形吗？请说明理由；〔2〕当x为何值时，四边形PMCN的面积与△ABM的面积相等？19．〔2006•沈阳〕如图1，在正方形ABCD中，点E、F分别为边BC、CD的中点，AF、DE相交于点G，则可得结论：①AF=DE，②AF⊥DE〔不须证明〕．〔1〕如图②，假设点E、F不是正方形ABCD的边BC、CD的中点，但满足CE=DF，则上面的结论①、②是否仍然成立；〔请直接答复“成立”或“不成立”〕〔2〕如图③，假设点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上，且CE=DF，此时上面的结论①、②是否仍然成立？假设成立，请写出证明过程；假设不成立，请说明理由．〔3〕如图④，在〔2〕的基础上，连接AE和EF，假设点M、N、P、Q分别为AE、EF、FD、AD的中点，请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种，并写出证明过程．20．〔2006•成都〕已知：如图，在正方形ABCD中，AD=12，点E是边CD上的动点〔点E 不与端点C，D重合〕，AE的垂直平分线FP分别交AD，AE，BC于点F，H，G，交AB 的延长线于点P．〔1〕设DE=m〔0＜m＜12〕，试用含m的代数式表示的值；〔2〕在〔1〕的条件下，当时，求BP的长．21．〔2006•汾阳市〕如图，点E在正方形ABCD的边CD上运动，AC与BE交于点F．〔1〕如图1，当点E运动到DC的中点时，求△ABF与四边形ADEF的面积之比；〔2〕如图2，当点E运动到CE：ED=2：1时，求△ABF与四边形ADEF的面积之比；〔3〕当点E运动到CE：ED=3：1时，写出△ABF与四边形ADEF的面积之比；当点E运动到CE：ED=n：1〔n是正整数〕时，猜想△ABF与四边形ADEF的面积之比〔只写结果，不要求写出计算过程〕；〔4〕请你利用上述图形，提出一个类似的问题22．〔2005•资阳〕阅读以下短文，然后解决以下问题：如果一个三角形和一个矩形满足条件：三角形的一边与矩形的一边重合，且三角形的这边所对的顶点在矩形这边的对边上，则称这样的矩形为三角形的“友好矩形”，如图①所示，矩形ABEF即为△ABC的“友好矩形”，显然，当△ABC是钝角三角形时，其“友好矩形”只有一个．〔1〕仿照以上表达，说明什么是一个三角形的“友好平行四边形”；〔2〕如图②，假设△ABC为直角三角形，且∠C=90°，在图②中画出△ABC的所有“友好矩形”，并比较这些矩形面积的大小；〔3〕假设△ABC是锐角三角形，且BC＞AC＞AB，在图③中画出△ABC的所有“友好矩形”，指出其中周长最小的矩形并加以证明．23．〔2005•重庆〕已知四边形ABCD中，P是对角线BD上的一点，过P作MN∥AD，EF∥CD，分别交AB、CD、AD、BC于点M、N、E、F，设a=PM•PE，b=PN•PF，解答以下问题：〔1〕当四边形ABCD是矩形时，见图1，请判断a与b的大小关系，并说明理由；〔2〕当四边形ABCD是平行四边形，且∠A为锐角时，见图2，〔1〕中的结论是否成立？并说明理由；〔3〕在〔2〕的条件下，设，是否存在这样的实数k，使得？假设存在，请求出满足条件的所有k的值；假设不存在，请说明理由．24．〔2005•大连〕如图，操作：把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上〔CG＞BC〕，取线段AE的中点M．探究：线段MD、MF的关系，并加以证明．说明：〔1〕如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路写出来〔要求至少写3步〕；〔2〕在你经历说明〔1〕的过程后，可以从以下①、②、③中选取一个补充或更换已知条件，完成你的证明．注意：选取①完成证明得10分；选取②完成证明得7分；选取③完成证明得5分．①DM的延长线交CE于点N，且AD=NE；②将正方形CGEF6绕点C逆时针旋转45°〔如图〕，其他条件不变；③在②的条件下，且CF=2AD．附加题：将正方形CGEF绕点C旋转任意角度后〔如图〕，其他条件不变．探究：线段MD、MF的关系，并加以证明．25．〔2005•湖州〕如图，四边形ABCD和BEFG均为正方形，则=．〔结果不取近似值〕26．〔2005•郴州〕附加题：E是四边形ABCD中AB上一点〔E不与A、B重合〕．〔1〕如图，当四边形ABCD是正方形时，△ADE、△BCE和△CDE的面积之间有着怎样的关系？证明你的结论．〔2〕假设四边形ABCD是矩形时，〔1〕中的结论是否仍然成立？为什么？ABCD是平行四边形呢？〔3〕当四边形ABCD是梯形时，〔1〕中的结论还成立吗？请说明理由．27．〔2005•深圳校级自主招生〕如图，将一三角板放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于Q．探究：设A、P两点间的距离为x．〔1〕当点Q在边CD上时，线段PQ与PB之间有怎样的数量关系？试证明你的猜想；〔2〕当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数关系，并写出函数自变量x的取值范围；〔3〕当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置．并求出相应的x值，如果不可能，试说明理由．28．〔2004•贵阳〕如图，四边形ABCD中，AC=6，BD=8且AC⊥BD．顺次连接四边形ABCD 各边中点，得到四边形A1B1C1D1；再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2…如此进行下去得到四边形A n B n C n D n．〔1〕证明：四边形A1B1C1D1是矩形；〔2〕写出四边形A1B1C1D1和四边形A2B2C2D2的面积；〔3〕写出四边形A n B n C n D n的面积；〔4〕求四边形A5B5C5D5的周长．29．〔2004•无为县〕〔1〕如图〔1〕，在正方形ABCD中，对角线AC、BD相交于点O，易知AC⊥BD，=；〔2〕如图〔2〕，假设点E是正方形ABCD的边CD的中点，即，过D作DG⊥AE，分别交AC、BC于点F、G．求证：；〔3〕如图〔3〕，假设点P是正方形ABCD的边CD上的点，且〔n为正整数〕，过点D作DN⊥AP，分别交AC、BC于点M、N，请你先猜想CM与AC的比值是多少，然后再证明你猜想的结论．30．〔2004•佛山〕如果正方形的一边落在三角形的一边上，其余两个顶点分别在三角形的另外两条边上，则这样的正方形叫做三角形的内接正方形．〔1〕如图①，在△ABC中，BC=a，BC边上的高AD=h a，EFGH是△ABC的内接正方形．设正方形EFGH的边长是x，求证：；〔2〕在Rt△ABC中，AB=4，AC=3，∠BAC=90度．请在图②，图③中分别画出可能的内接正方形，并根据计算答复哪个内接正方形的面积最大；〔3〕在锐角△ABC中，BC=a，AC=b，AB=c，且a＜b＜c．请问这个三角形的内接正方形中哪个面积最大？并说明理由．九年级上册四边形压轴题2参考答案与试题解析一．解答题〔共30小题〕1．〔2009•临沂〕数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点．∠AEF=90°，且EF交正方形外角∠DCG的平分线CF于点F，求证：AE=EF．经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证△AME≌△ECF，所以AE=EF．在此基础上，同学们作了进一步的研究：〔1〕小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上〔除B，C外〕的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；〔2〕小华提出：如图3，点E是BC的延长线上〔除C点外〕的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．考点：正方形的性质；全等三角形的判定与性质；角平分线的性质．专题：几何综合题；压轴题．分析：〔1〕在AB上取一点M，使AM=EC，连接ME，根据已知条件利用ASA判定△AME≌△ECF，因为全等三角形的对应边相等，所以AE=EF．〔2〕在BA的延长线上取一点N，使AN=CE，连接NE，根据已知利用ASA判定△ANE≌△ECF，因为全等三角形的对应边相等，所以AE=EF．解答：解：〔1〕正确．证明：在AB上取一点M，使AM=EC，连接ME．∴BM=BE，∴∠BME=45°，∴∠AME=135°，∵CF是外角平分线，∴∠DCF=45°，∴∠ECF=135°，∴∠AME=∠ECF，∵∠AEB+∠BAE=90°，∠AEB+∠CEF=90°，∴∠BAE=∠CEF，∴△AME≌△ECF〔ASA〕，∴AE=EF．〔2〕正确．证明：在BA的延长线上取一点N．使AN=CE，连接NE．∴BN=BE，∴∠N=∠NEC=45°，∵CF平分∠DCG，∴∠FCE=45°，∴∠N=∠ECF，∵四边形ABCD是正方形，∴AD∥BE，∴∠DAE=∠BEA，即∠DAE+90°=∠BEA+90°，∴∠NAE=∠CEF，∴△ANE≌△ECF〔ASA〕，∴AE=EF．点评：此题主要考查学生对正方形的性质，角平分线的性质及全等三角形的判定方法的掌握情况．2．〔2009•宁德〕如图〔1〕，已知正方形ABCD在直线MN的上方，BC在直线MN上，E 是BC上一点，以AE为边在直线MN的上方作正方形AEFG．〔1〕连接GD，求证：△ADG≌△ABE；〔2〕连接FC，观察并猜测∠FCN的度数，并说明理由；〔3〕如图〔2〕，将图〔1〕中正方形ABCD改为矩形ABCD，AB=a，BC=b〔a、b为常数〕，E是线段BC上一动点〔不含端点B、C〕，以AE为边在直线MN的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变？假设∠FCN的大小不变，请用含a、b的代数式表示tan∠FCN的值；假设∠FCN的大小发生改变，请举例说明．考点：正方形的性质；全等三角形的判定与性质；矩形的性质．专题：压轴题；动点型．分析：〔1〕根据三角形判定方法进行证明即可．〔2〕作FH⊥MN于H．先证△ABE≌△EHF，得到对应边相等，从而推出△CHF是等腰直角三角形，∠FCH的度数就可以求得了．〔3〕此题也是通过构建直角三角形来求度数，作FH⊥MN于H，∠FCH的正切值就是FH：CH．解答：〔1〕证明：∵四边形ABCD和四边形AEFG是正方形，∴AB=AD，AE=AG，∠BAD=∠EAG=90°，∴∠BAE+∠EAD=∠DAG+∠EAD，∴∠BAE=∠DAG，∴△BAE≌△DAG．〔2〕解：∠FCN=45°，理由是：作FH⊥MN于H，∵∠AEF=∠ABE=90°，∴∠BAE+∠AEB=90°，∠FEH+∠AEB=90°，∴∠FEH=∠BAE，又∵AE=EF，∠EHF=∠EBA=90°，∴△EFH≌△ABE，∴FH=BE，EH=AB=BC，∴CH=BE=FH，∵∠FHC=90°，∴∠FCN=45°．〔3〕解：当点E由B向C运动时，∠FCN的大小总保持不变，理由是：作FH⊥MN于H，由已知可得∠EAG=∠BAD=∠AEF=90°，结合〔1〕〔2〕得∠FEH=∠BAE=∠DAG，又∵G在射线CD上，∠GDA=∠EHF=∠EBA=90°，∴△EFH≌△GAD，△EFH∽△ABE，∴EH=AD=BC=b，∴==；在Rt△FEH中，tan∠FCN===，∴当点E由B向C运动时，∠FCN的大小总保持不变，tan∠FCN=．点评：此题考查了正方形，矩形的判定及全等三角形的判定方法等知识点的综合运用，其重点是通过证三角形全等或相似来得出线段的相等或成比例．3．〔2009•黄石〕如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．〔1〕探究：线段OE与OF的数量关系并加以证明；〔2〕当点O在边AC上运动时，四边形BCFE会是菱形吗？假设是，请证明；假设不是，则说明理由；〔3〕当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？考点：正方形的判定；平行线的性质；角平分线的性质；等腰三角形的性质；菱形的判定．专题：几何综合题；压轴题．分析：〔1〕利用平行线的性质由角相等得出边相等；〔2〕假设四边形BCFE，再证明与在同一平面内过同一点有且只有一条直线与已知直线垂直相矛盾；〔3〕利用平行四边形及等腰直角三角形的性质证明四边形AECF是正方形．解答：解：〔1〕OE=OF．证明如下：∵CE是∠ACB的平分线，∴∠1=∠2．∵MN∥BC，∴∠2=∠3．∴OE=OC．同理可证OC=OF．∴OE=OF．〔3分〕〔2〕四边形BCFE不可能是菱形，假设四边形BCFE为菱形，则BF⊥EC，而由〔1〕可知FC⊥EC，在平面内过同一点F不可能有两条直线同垂直于一条直线．〔3分〕〔3〕当点O运动到AC中点时，且△ABC是直角三角形〔∠ACB=90°〕时，四边形AECF是正方形．理由如下：∵O为AC中点，∴OA=OC，∵由〔1〕知OE=OF，∴四边形AECF为平行四边形；∵∠1=∠2，∠4=∠5，∠1+∠2+∠4+∠5=180°，∴∠2+∠5=90°，即∠ECF=90°，∴▱AECF为矩形，又∵AC⊥EF．∴▱AECF是正方形．∴当点O为AC中点且△ABC是以∠ACB为直角三角形时，四边形AECF是正方形．〔3分〕点评：此题考查的是平行线、角平分线、正方形、平行四边形的性质与判定，涉及面较广，在解答此类题目时要注意角的运用，一般通过角判定一些三角形，多边形的形状，需同学们熟练掌握．4．〔2009•无锡校级二模〕如图，在平面直角坐标系中，点A、点C同时从点O出发，分别以每秒2个单位、1个单位的速度向x轴、y轴的正半轴方向运动，以OA、OC为边作矩形OABC．以M〔4，0〕，N〔9，0〕为斜边端点作直角△PMN，点P在第一象限，且，当点A出发时，△PMN同时以每秒0.5个单位的速度沿x轴向右平移．设点A运动的时间为t秒，矩形OABC与△PMN重叠部分的面积为S．〔1〕求运动前点P的坐标；〔2〕求S与t的函数关系式，并写出自变量t的取值范围；〔3〕假设在运动过程中，要使对角线AC上始终存在点Q，满足∠OQM=90°，请直接写出符合条件的t的值或t的取值范围．考点：矩形的性质；圆周角定理；切线的性质．专题：压轴题；动点型．分析：〔1〕过点P作PH⊥x轴于H，可求出MH的长即点P的横坐标，再根据tan∠PMN=，及勾股定理便可求出点P的坐标．〔2〕因为点A；点C同时从点O出发，点M〔4，0〕，△PMN同时以每秒0.5个单位的速度沿x轴向右平移，运动t秒后，OA=2t，OM=4+0.5t，①当0＜OA≤OM，即0＜2t≤时，两图形无交点；②当OM＜OA≤OH，即4+0.5t＜2t≤8+0.5t时，即＜t≤时，矩形OABC与△PMN重叠部分的面积为S等于重叠的三角形的面积．③当OH＜OA≤ON，即8+0.5t＜2t≤9+0.5t，即＜t≤6时，矩形OABC与△PMN重叠矩部分的面积为S等于△MNP的面积减去不重叠的三角形的面积．④当OA＞ON，即2t＞9+0.5t，t＞6时，矩形OABC与△PMN重叠矩部分的面积为S等于△MNP的面积．〔3〕根据圆周角定理可知，当以OM为直径的圆与AC有公共点时，公共点即是符合条件的点Q，即可求出t的取值范围．解答：解：〔1〕如图，过点P作PH⊥x轴于H．∵MN=9﹣4=5，tan∠PMN=，∴PM=，PN=，∴PH=2，MH=4，NH=1．∴P〔8，2〕．〔2〕运动t秒后，OA=2t，OC=t，OM=4﹣0.5t．当0＜t≤时，S=0；当＜t≤时，S=t2﹣3t+4；当＜t≤6时，S=﹣t2+27t﹣76；当t＞6时，S=5．〔3〕当以OM为直径的圆与AC有公共点时，公共点即是符合条件的点Q．当以OM为直径的圆与AC相切时，t=，∴t的取值范围是：0＜t≤．点评：此题是典型的动点问题，比较复杂，考查了同学们对圆及三角形，矩形，等相关知识的掌握情况，有一定的难度．5．〔2008•北京〕请阅读以下材料：问题：如图1，在菱形ABCD和菱形BEFG中，点A，B，E在同一条直线上，P是线段DF 的中点，连接PG，PC．假设∠ABC=∠BEF=60°，探究PG与PC的位置关系及的值．小聪同学的思路是：延长GP交DC于点H，构造全等三角形，经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决以下问题：〔1〕写出上面问题中线段PG与PC的位置关系及的值；〔2〕将图1中的菱形BEFG绕点B顺时针旋转，使菱形BEFG的对角线BF恰好与菱形ABCD 的边AB在同一条直线上，原问题中的其他条件不变〔如图2〕．你在〔1〕中得到的两个结论是否发生变化？写出你的猜想并加以证明；〔3〕假设图1中∠ABC=∠BEF=2α〔0°＜α＜90°〕，将菱形BEFG绕点B顺时针旋转任意角度，原问题中的其他条件不变，请你直接写出的值〔用含α的式子表示〕．考点：菱形的性质；全等三角形的判定与性质；锐角三角函数的定义．专题：压轴题．分析：〔1〕根据题意可知小聪的思路为，通过判定三角形DHP和PGF为全等三角形来得出证明三角形HCG为等腰三角形且P为底边中点的条件；〔2〕思路同上，延长GP交AD于点H，连接CH，CG，此题中除了如〔1〕中证明△GFP≌△HDP〔得到P是HG中点〕外还需证明△HDC≌△GBC〔得出三角形CHG是等腰三角形〕．〔3〕∠ABC=∠BEF=2α〔0°＜α＜90°〕，那么∠PCG=90°﹣α，由〔1〕可知：PG：PC=tan 〔90°﹣α〕．解答：解：〔1〕∵CD∥GF，∠PDH=∠PFG，∠DHP=∠PGF，DP=PF，∴△DPH≌△FGP，∴PH=PG，DH=GF，∵CD=BC，GF=GB=DH，∴CH=CG，∴CP⊥HG，∠ABC=60°，∴∠DCG=120°，∴∠PCG=60°，∴PG：PC=tan60°=，∴线段PG与PC的位置关系是PG⊥PC，=；〔2〕猜想：〔1〕中的结论没有发生变化．证明：如图2，延长GP交AD于点H，连接CH，∵P是线段DF的中点，∴FP=DP，∵AD∥GF，∴∠HDP=∠GFP，∵∠GPF=∠HPD，∴△GFP≌△HDP〔ASA〕，∴GP=HP，GF=HD，∵四边形ABCD是菱形，∴CD=CB，∠HDC=∠ABC=60°，∵∠ABC=∠BEF=60°，菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上，∴∠GBF=60°，∴∠HDC=∠GBF，∵四边形BEFG是菱形，∴GF=GB，∴HD=GB，∴△HDC≌△GBC，∴CH=CG，∠HCD=∠GCB∴PG⊥PC〔到线段两端点距离相等的点在线段的垂直平分线上〕∵∠ABC=60°∴∠DCB=∠HCD+∠HCB=120°∵∠HCG=∠HCB+∠GCB∴∠HCG=120°∴∠GCP=60°∴=tan∠GCP=tan60°=；〔3〕∵∠ABC=∠BEF=2α〔0°＜α＜90°〕，∴∠PCG=90°﹣α，由〔1〕可知：PG：PC=tan〔90°﹣α〕，∴=tan〔90°﹣α〕．点评：此题是一道探究性的几何综合题，主要考查菱形的性质，全等三角形的判定及三角函数的综合运用．6．〔2008•厦门〕已知：如下图的一张矩形纸片ABCD〔AD＞AB〕，将纸片折叠一次，使点A与C重合，再展开，折痕EF交AD边于E，交BC边于F，分别连接AF和CE．〔1〕求证：四边形AFCE是菱形；〔2〕假设AE=10cm，△ABF的面积为24cm2，求△ABF的周长；〔3〕在线段AC上是否存在一点P，使得2AE2=AC•AP？假设存在，请说明点P的位置，并予以证明；假设不存在，请说明理由．考点：菱形的判定；勾股定理；矩形的性质；相似三角形的判定与性质．专题：压轴题；开放型；存在型．分析：〔1〕因为是对折所以AO=CO，利用三角形全等证明EO=FO，四边形便是菱形；〔2〕因为面积是24，也就是AB、BF的积可以求出，所以求周长只要求出AB、BF 的和就可以，而结合勾股定理它们和的平方减去乘积二倍就是AF的平方；〔3〕因为AC=AO所以可以从与△AOE相似的角度考虑，即过E作EP⊥AD．解答：〔1〕证明：连接EF交AC于O，当顶点A与C重合时，折痕EF垂直平分AC，∴OA=OC，∠AOE=∠COF=90°〔1分〕∵在矩形ABCD中，AD∥BC，∴∠EAO=∠FCO，∴△AOE≌△COF〔ASA〕．∴OE=OF〔2分〕∴四边形AFCE是菱形．〔3分〕〔2〕解：四边形AFCE是菱形，∴AF=AE=10．设AB=x，BF=y，∵∠B=90，∴〔x+y〕2﹣2xy=100①又∵S△ABF=24，∴xy=24，则xy=48．②〔5分〕由①、②得：〔x+y〕2=196〔6分〕∴x+y=14，x+y=﹣14〔不合题意舍去〕∴△ABF的周长为x+y+AF=14+10=24．〔7分〕〔3〕解：过E作EP⊥AD交AC于P，则P就是所求的点．〔9分〕证明：由作法，∠AEP=90°，由〔1〕得：∠AOE=90°，又∠EAO=∠EAP，∴△AOE∽△AEP，∴=，则AE2=AO•AP〔10分〕∵四边形AFCE是菱形，∴AO=AC，AE2=AC•AP〔11分〕∴2AE2=AC•AP〔12分〕即P的位置是：过E作EP⊥AD交AC于P．点评：此题主要考查〔1〕菱形的判定方法“对角线互相垂直且平分的四边形”，〔2〕相似三角形的判定和性质．7．〔2008•嘉兴〕小丽参加数学兴趣小组活动，提供了下面3个有联系的问题，请你帮助解决：〔1〕如图1，正方形ABCD中，作AE交BC于E，DF⊥AE交AB于F，求证：AE=DF；〔2〕如图2，正方形ABCD中，点E，F分别在AD，BC上，点G，H分别在AB，CD上，且EF⊥GH，求的值；〔3〕如图3，矩形ABCD中，AB=a，BC=b，点E，F分别在AD，BC上，且EF⊥GH，求的值．考点：矩形的性质；全等三角形的判定与性质；正方形的性质；相似三角形的判定与性质．专题：几何综合题；压轴题．分析：〔1〕证明AE=DF，只要证明三角形ABE和DAF全等即可．它们同有一个直角，且AB=AD，又因为∠AEB=90°﹣∠BAE=∠AFD，这样就构成了全等三角形判定中的AAS，两三角形就全等了；〔2〕可通过构建与已知条件相关的三角形来求解．作AM∥EF交BC于M，作DN∥GH 交AB于N，那么AM=EF，DN=GH，〔1〕中我们已证得△ABM、△DAN全等，那么AM=DN，即EF=GH，它们的比例也就求出来了；〔3〕做法同〔2〕也是通过构建三角形来求解．作AM∥EF交BC于M，作DN∥GH 交AB于N，只不过证明三角形全等改为了证明其相似．解题思路和步骤是一样的．解答：〔1〕证明：∵DF⊥AE∴∠AEB=90°﹣∠BAE=∠AFD又∵AB=AD，∠ABE=∠DAF=90°∴△ABE≌△DAF，∴AE=DF；〔2〕解：作AM∥EF交BC于M作DN∥GH交AB于N则AM=EF，DN=GH由〔1〕知，AM=DN∴EF=GH，即〔3〕解：作AM∥EF交BC于M作DN∥GH交AB于N则AM=EF，DN=GH∵EF⊥GH∴AM⊥DN∴∠AMB=90°﹣∠BAM=∠AND又∵∠ABM=∠DAN=90°∴△ABM∽△DAN∴∴．点评：此题中〔1〕〔2〕和〔3〕虽然所求不一样，但是解题思路和步骤是一样的，都是通过构建与已知和所求的条件相关的三角形，然后证明其全等或相似来得出线段间的相等或比例关系．。

专题03特殊平行四边形中的三种几何动点问题类型一、面积问题例．如图，在四边形ABCD 中，AB CD ∥，90BCD ∠= ，10cm AB AD ==，=8cm BC ．点P 从点A 出发，以每秒3cm 的速度沿折线ABC 方向运动，点Q 从点D 出发，以每秒2cm 的速度沿线段DC 方向向点C 运动．已知动点P ，Q 同时发，当点Q 运动到点C 时，P ，Q 运动停止，设运动时间为t ．(1)直接写出CD 的长（cm ）；(2)当四边形PBQD 为平行四边形时，直接写出四边形PBQD 的周长（cm ）；(3)在点P 、点Q 的运动过程中，是否存在某一时刻，使得BPQ V 的面积为215cm ？若存在，请求出所有满足条件的t 的值；若不存在，请说明理由．【变式训练1】如图，在四边形ABCD 中，,90,120,12cm,15cm AD BC A B ADC AD BC ∠=∠=︒∠=︒==∥，点P 自点A 沿折线AD DC -以1cm/s 的速度运动，点Q 自点C 沿向CB BA -以1cm/s 的速度运动．点P ，Q 同时出发，其中一个点到达终点，另一个点也停止运动．设运动时间为(s)t ．(1)当P 在AD 边上，点Q 在BC 边上时，如图1．①用含t 的代数式表示：DP =___________，BQ =___________；②若四边形APQB 是平行四边形，求t 的值？(2)求BPQ V 的面积S 与运动时间t 之间的数量关系式，并写出t 的取值范围．【变式训练2】如图，在矩形ABCD 中，AB =12，BC =18，点P 从点A 出发，以每秒2个单位长度的速度沿类型二、几何图形存在性问题长的速度向点A 匀速运动，同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D E ，运动的时间是t 秒()0t >．过点D 作DF BC ⊥于点F ，连接DE ，EF ．(1)求AB AC ，的长；(2)求证：AE DF =；(3)当t 为何值时，DEF 为直角三角形？请说明理由．例2．如图，已知正方形ABCD 的边长为4cm ，动点P 从点B 出发，以2cm /s 的速度沿B C D →→方向向点D 运动，动点Q 从点A 出发，以1cm /s 的速度沿A B →方向向点B 运动，若P 、Q 两点同时出发运动时间为s t ．(1)连接PD 、PQ 、DQ ，求当t 为何值时，PQD △的面积为27cm ？(2)当点P 在BC 上运动时，是否存在这样的t 使得PQD △是以PD 为一腰的等腰三角形？若存在，请求出符合条件的t 的值；若不存在，请说明理由．例3．如图，在四边形ABCD 中，AD ∥BC ，∠B ＝90°，AB ＝8cm ，AD ＝12cm ，BC ＝18cm ，点P 从点A 出发以1cm/s 的速度向点D 运动；点Q 从点C 同时出发，以2cm/s 的速度向点B 运动，当点Q 到达点B 时，(1)填空：AB =；菱形ABCD 的面积S =；菱形的高h =．(2)若点M 的速度为每秒1个单位，点N 的速度为每秒a 个单位（其中52a <），当4t =时在平面内存在点得以A ，M ，N ，E 为顶点的四边形为菱形，请求出所有满足条件的a 的值．类型三、直线位置关系问题例1．如图，在Rt ABC △中，90ABC ∠=︒，5AC =，4BC =，点D 是边AB 的中点，动点P 从点A 出发(1)直接写出AB的长．(2)当点Q落在AB边上时，用含t的代数式表示(1)分别求BD和BE的长度；(2)连接PQ，当95t=时，判断PQ与AD是否垂直，并说明理由；(3)试判断是否存在t的值，使得以P，Q，C，DC 点以1cm /s 的速度运动，动点Q 从点B 开始沿BA 向A 点以3cm /s 的速度运动，P ，Q 分别从点D ，B 同时出发，当其中一点到达终点时，另一点也随之停止运动，运动的时间为t 秒．(1)t 为何值时，四边形DPQA 为矩形？(2)t 为何值时，四边形PQBC 为平行四边形？2．如图，在ABC 中，6cm AC =，=8cm BC ，点O 以每秒1cm 的速度由点A 向点C 运动(不与点C 重合)，过点O 作直线MN BC ∥，BCA ∠的外角平分线CF 于点F ，ACB ∠的平分线CE 于点.E 设运动时间为t 秒．发现：(1)在点O 的运动过程中，OE 与OF 的关系是______，请写出理由．(2)当=2t 时，=EF ______cm ．探究：当=t ______时，四边形AECF 是矩形，并证明你的结论．拓展：若点O 在运动过程中，能使四边形AECF 是正方形，试写出线段AB 的长度．(直接写出结论即可)3．已知正方形ABCD 中，8AB BC CD DA ====，90A B C D ∠=∠=∠=∠=︒．动点P 以每秒2个单位速度从点B 出发沿线段BC 方向运动，动点Q 同时以每秒8个单位速度从B 点出发沿正方形的边(1)当运动时间为秒时，点P与点Q相遇；∥时，求线段DQ的长度；(2)当BQ PD全等时，求t的值．(3)连接PA，当PAB和QAD(1)CB的长为______．(2)用含t的代数式表示线段QB的长．(3)连接PQ，=；(1)求证：PE DQ(1)=a______cm，b=______cm；(2)t为何值时，EP把四边形BCDE的周长平分？(1)当2t =时，BP =___________cm ；(2)当t 为何值时，连接,,CP DP CDP △是等腰三角形；(3)Q 为AD 边上的点，且6DQ =，P 与Q 不重合，当t 为何值时，以长方形的两个顶点及点P 为顶点的三角形与DCQ 全等．。

2020年中考数学二轮专项复习——四边形、动点、最值问题压轴题型1、如图，在正方形ABCD中，E，F分别为AD，BC的中点，P为对角线BD上的一个动点，则下列线段的长等于AP+EP最小值的是。

解：【分析】连接CP，当点E，P，C在同一直线上时，AP+PE的最小值为CE长，依据△ABF≌△CDE，即可得到AP+EP最小值等于线段AF的长．如图，连接CP，由AD＝CD，∠ADP＝∠CDP＝45°，DP＝DP，可得△ADP≌△CDP，∴AP＝CP，∴AP+PE＝CP+PE，∴当点E，P，C在同一直线上时，AP+PE的最小值为CE长，此时，由AB＝CD，∠ABF＝∠CDE，BF＝DE，可得△ABF≌△CDE，∴AF＝CE，∴AP+EP最小值等于线段AF的长，【点评】本题考查的是轴对称，最短路线问题，根据题意作出A关于BD的对称点C是解答此题的关键．2、【猜想】如图1，在平行四边形ABCD中，点O是对角线AC的中点，过点O的直线分别交AD．BC于点E．F．若平行四边形ABCD的面积是8，则四边形CDEF的面积是．【探究】如图2，在菱形ABCD中，对角线相交于点O，过点O的直线分别交AD，BC于点E，F，若AC＝5，BD＝10，求四边形ABFE的面积．【应用】如图3，在Rt△ABC中，∠BAC＝90°，延长BC到点D，使DC＝BC，连结AD，若AC＝3，AD＝2，则△ABD的面积是．解：猜想：∵四边形ABCD是平行四边形，∴AD∥BC，OA＝OC．∴∠EAO＝∠FCO，∠AEO＝∠CFO，在△AOE和△COF中，，∴△AEO≌△CFO（AAS），∴四边形CDEF的面积＝S△ACD＝▱ABCD的面积＝4；故答案为：4；探究：∵四边形ABCD是菱形，∴AD∥BC，AO＝CO AC＝2.5，BO＝BD＝5，∠AOD＝90°，∴AB＝AC＝，∠OAE＝∠OCF，∠OEA＝∠OFC，在△AOE于△COF中，，∴△AOE≌△COF（AAS），∵AC⊥BD，∴S四边形ABFE＝S△ABC＝AC•BO＝××5＝．应用：延长AC到E使CE＝AC＝3，在△ABC与△CDE中，，∴△ABC≌△CDE（SAS），∴∠E＝∠BAC＝90°，∴DE＝，∴S△ABD＝S△ADE＝AE•DE＝×6×2＝6．故答案为：63、如图，正方形ABCD的边长是2，点E是CD边的中点，点F是边BC上不与点B，C重合的一个动点，把∠C 沿直线EF折叠，使点C落在点C′处．当△ADC′为等腰三角形时，FC的长为．【分析】首先证明DC′≠DA，只要分两种情形讨论即可：①如图1中，当AD＝AC′＝2时，连接AE．构建方程即可；②如图2中，当点F在BC中点时，易证AC′＝DC′，满足条件；【解答】解：由题意DE＝EC＝EC′＝1，∴DC′＜1+1∴DC′≠DA，只要分两种情形讨论即可：①如图1中，当AD＝AC′＝2时，连接AE．∵AE＝AE，AD＝AC′，DE＝DC′，∴△ADE≌△AC′E，∴∠ADE＝∠AC′E＝90°，∵∠C＝∠FC′E＝90°，∴∠AC′E+∠FC′E＝180°，∴A、C′、F共线，设CF＝x，则BF＝2﹣x，AF＝2+x，在Rt△ABF中，22+（2﹣x）2＝（2+x）2，解得x＝．②如图2中，当点F在BC中点时，易证AC′＝DC′，满足条件，此时CF＝1．综上所述，满足条件的CF的长为或1．故答案为或1．【点评】本题考查翻折变换、正方形的性质、全等三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是学会用分类讨论的首先思考问题，属于中考填空题中的压轴题．4、如图1，在平面直角坐标系中，一次函数y＝﹣2x+8的图象与x轴，y轴分别交于点A，点C，过点A作AB ⊥x轴，垂足为点A，过点C作CB⊥y轴，垂足为点C，两条垂线相交于点B．（1）线段AB，BC，AC的长分别为AB＝，BC＝，AC＝；（2）折叠图1中的△ABC，使点A与点C重合，再将折叠后的图形展开，折痕DE交AB于点D，交AC于点E，连接CD，如图2．请从下列A、B两题中任选一题作答，我选择题．A：①求线段AD的长；②在y轴上，是否存在点P，使得△APD为等腰三角形？若存在，请直接写出符合条件的所有点P的坐标；若不存在，请说明理由．B：①求线段DE的长；②在坐标平面内，是否存在点P（除点B外），使得以点A，P，C为顶点的三角形与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．解：（1）∵一次函数y＝﹣2x+8的图象与x轴，y轴分别交于点A，点C，∴A（4，0），C（0，8），∴OA＝4，OC＝8，∵AB⊥x轴，CB⊥y轴，∠AOC＝90°，∴四边形OABC是矩形，∴AB＝OC＝8，BC＝OA＝4，在Rt△ABC中，根据勾股定理得，AC＝＝4，故答案为：8，4，4；（2）A、①由（1）知，BC＝4，AB＝8，由折叠知，CD＝AD，在Rt△BCD中，BD＝AB﹣AD＝8﹣AD，根据勾股定理得，CD2＝BC2+BD2，即：AD2＝16+（8﹣AD）2，∴AD＝5，②由①知，D（4，5），设P（0，y），∵A（4，0），∴AP2＝16+y2，DP2＝16+（y﹣5）2，∵△APD为等腰三角形，∴Ⅰ、AP＝AD，∴16+y2＝25，∴y＝±3，∴P（0，3）或（0，﹣3）Ⅱ、AP＝DP，∴16+y2＝16+（y﹣5）2，∴y＝，∴P（0，），Ⅲ、AD＝DP，25＝16+（y﹣5）2，∴y＝2或8，∴P（0，2）或（0，8）．B、①、由A①知，AD＝5，由折叠知，AE＝AC＝2，DE⊥AC于E，在Rt△ADE中，DE＝＝，②、∵以点A，P，C为顶点的三角形与△ABC全等，∴△APC≌△ABC，或△CPA≌△ABC，∴∠APC＝∠ABC＝90°，∵四边形OABC是矩形，∴△ACO≌△CAB，此时，符合条件，点P和点O重合，即：P（0，0），如图3，过点O作ON⊥AC于N，易证，△AON∽△ACO，∴，∴，∴AN＝，过点N作NH⊥OA，∴NH∥OA，∴△ANH∽△ACO，∴，∴，∴NH＝，AH＝，∴OH＝，∴N（，），而点P2与点O关于AC对称，∴P2（，），同理：点B关于AC的对称点P1，同上的方法得，P1（﹣，），即：满足条件的点P的坐标为：（0，0），（，），（﹣，）．5、如图，在平面直角坐标系中，以坐标原点O为圆心，2为半径画圆，P是⊙O上一动点且在第一象限内，过点P作⊙O的切线，与x、y轴分别交于点A、B．（1）求证：△OBP与△OPA相似；（2）当点P为AB中点时，求出P点坐标；（3）在⊙O上是否存在一点Q，使得以Q，O，A、P为顶点的四边形是平行四边形．若存在，试求出Q点坐标；若不存在，请说明理由．解：（1）证明：∵AB是过点P的切线，∴AB⊥OP，∴∠OPB＝∠OPA＝90°；（1分）∴在Rt△OPB中，∠1+∠3＝90°，又∵∠BOA＝90°∴∠1+∠2＝90°，∴∠2＝∠3；（1分）在△OPB中△APO中，∴△OPB∽△APO．（2分）（2）∵OP⊥AB，且PA＝PB，∴OA＝OB，∴△AOB是等腰三角形，∴OP是∠AOB的平分线，∴点P到x、y轴的距离相等；（1分）又∵点P在第一象限，∴设点P（x，x）（x＞0），∵圆的半径为2，∴OP＝，解得x＝或x＝﹣（舍去），（2分）∴P点坐标是（，）．（1分）（3）存在；①如图设OAPQ为平行四边形，∴PQ∥OA，OQ∥PA；∵AB⊥OP，∴OQ⊥OP，PQ⊥OB，∴∠POQ＝90°，∵OP＝OQ，∴△POQ是等腰直角三角形，∴OB是∠POQ的平分线且是边PQ上的中垂线，∴∠BOQ＝∠BOP＝45°，∴∠AOP＝45°，设P（x，x）、Q（﹣x，x）（x＞0），（2分）∵OP＝2代入得，解得x＝，∴Q点坐标是（﹣，）；（1分）②如图示OPAQ为平行四边形，同理可得Q点坐标是（，﹣）．（1分）6、如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连结AD，以AD为一边且在D的右侧作正方形ADEF，解答下列问题：（1）如果AB＝AC，∠BAC＝90°．①当点D在线段BC上时（与点B不重合），如图2，线段CF，BD之间的位置关系为，数量关系为；②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，为什么？（2）如果AB≠AC，∠BAC≠90°，点D在线段BC上运动（如图4）当∠ACB＝时，CF⊥BC（点C，F 重合除外）？（3）若AC＝4，BC＝3．在（2）的条件下，设正方形ADEF的边DE与线段CF相交于点P，求线段CP长的最大值．解：（1）CF⊥BD，CF＝BD，理由如下：∵四边形ADEF是正方形，∴∠DAF＝90°，AD＝AF，∵AB＝AC，∠BAC＝90°，∴∠BAD+∠DAC＝∠CAF+∠DAC＝90°，∴∠BAD＝∠CAF，在△BAD和△CAF中，，∴△BAD≌△CAF（SAS），∴CF＝BD，∴∠B＝∠ACF，∴∠B+∠BCA＝90°，∴∠BCA+∠ACF＝90°，即CF⊥BD；故答案为：CF⊥BD，CF＝BD；②当点D在BC的延长线上时，①的结论仍成立．如图2，由正方形ADEF得：AD＝AF，∠DAF＝90°．∵∠BAC＝90°，∴∠DAF＝∠BAC．∴∠DAB＝∠FAC．又∵AB＝AC，∴△DAB≌△FAC（SAS）．∴CF＝BD，∠ACF＝∠ABD．∵∠BAC＝90°，AB＝AC，∴∠ABC＝45°，∴∠ACF＝45°．∴∠BCF＝∠ACB+∠ACF＝90°，∴CF⊥BD；（2）当∠BCA＝45°时，CF⊥BD；理由如下：如图3，过点A作AC的垂线与CB所在直线交于G，∵∠ACB＝45°，∴△AGC等腰直角三角形，∴AG＝AC，∠AGC＝∠ACG＝45°，∵AG＝AC，AD＝AF，∵∠GAD＝∠GAC﹣∠DAC＝90°﹣∠DAC，∠FAC＝∠FAD﹣∠DAC＝90°﹣∠DAC，∴∠GAD＝∠FAC，∴△GAD≌△CAF（SAS），∴∠ACF＝∠AGD＝45°，∴∠GCF＝∠GCA+∠ACF＝90°，∴CF⊥BC；故答案为：45°；（3）过点A作AQ⊥BC交CB的延长线于点Q，如图4所示：∵DE与CF交于点P时，此时点D位于线段CQ上，∵∠BCA＝45°，AC＝4，∴△ACQ是等腰直角三角形，∴AQ＝CQ＝4．设CD＝x，则DQ＝4﹣x，∵∠ADB+∠ADE+∠PDC＝180°且∠ADE＝90°，∴∠ADQ+∠PDC＝90°，又∵在直角△PCD中，∠PDC+∠DPC＝90°∴∠ADQ＝∠DPC，∵∠AQD＝∠DCP＝90°∴△AQD∽△DCP，∴＝，即＝．解得：CP＝﹣x2+x＝﹣（x﹣1）2+1．∵0＜x≤3，∴当x＝1时，CP有最大值1，即线段CP长的最大值为1．7、如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点（与点O不重合），作AF⊥BE，垂足为G，交BC于F，交BO于H，连接OG，CG．（1）求证：AH＝BE；（2）试探究：∠AGO的度数是否为定值？请说明理由；（3）若OG⊥CG，BG＝2，求S△OGC的值．解析：（1）证明：∵四边形ABCD是正方形，∴OA＝OB，∠AOB＝∠BOE＝90°，∵AF⊥BE，∴∠GAE+∠AEG＝∠OBE+∠AEG＝90°．∴∠GAE＝∠OBE，在△AOH和△BOE中，，∴△AOH≌△BOE（ASA），∴AH＝BE．（2）解：∠AGO的度数为定值，理由如下：∵∠AOH＝∠BGH＝90°，∠AHO＝∠BHG，∴△AOH∽△BGH，∴＝，∴＝，∵∠OHG＝∠AHB，∴△OHG∽△AHB，∴∠AGO＝∠ABO＝45°，即∠AGO的度数为定值．（3）解：∵∠ABC＝90°，AF⊥BE，∴∠BAG＝∠FBG，∠AGB＝∠BGF＝90°，∴△ABG∽△BFG，∴＝，∴AG•GF＝BG2＝20，∵△AHB∽△OHG，∴∠BAH＝∠GOH＝∠GBF．∵∠AOB＝∠BGF＝90°，∴∠AOG＝∠GFC，∵∠AGO＝45°，CG⊥GO，∴∠AGO＝∠FGC＝45°．∴△AGO∽△CGF，∴＝，∴GO•CG＝AG•GF＝20．∴S△OGC＝CG•GO＝10．8、已知，如图，在长方形ABCD中，AB＝4，AD＝6．延长BC到点E，使CE＝3，连接DE．（1）DE的长为．（2）动点P从点B出发，以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P运动的时间为t秒，求当t为何值时，△ABP和△DCE全等？（3）若动点P从点B出发，以每秒1个单位的速度仅沿着BE向终点E运动，连接DP．设点P运动的时间为t秒，是否存在t，使△PDE为等腰三角形？若存在，请直接写出t的值；否则，说明理由．解：（1）∵四边形ABCD是矩形∴AB＝CD＝4，AD＝BC＝6，CD⊥BC在Rt△DCE中，DE＝＝＝5 故答案为5．（2）若△ABP与△DCE全等∴BP＝CE或AP＝CE当BP＝CE＝3时，则t＝＝3秒当AP＝CE＝3时，则t＝＝13秒∴求当t为3秒或13秒时，△ABP和△DCE全等．（3）若△PDE为等腰三角形则PD＝DE或PE＝DE或PD＝PE当PD＝DE时，∵PD＝DE，DC⊥BE∴PC＝CE＝3∵BP＝BC﹣CP＝3∴t＝＝3当PE＝DE＝5时，∵BP＝BE﹣PE∴BP＝9﹣5＝4∴t＝＝4当PD＝PE时，∴PE＝PC+CE＝3+PC∴PD＝3+PC在Rt△PDC中，DP2＝CD2+PC2．∴（3+PC）2＝16+PC2∴PC＝∵BP＝BC﹣PC∴BP＝∴t＝＝综上所述：当t＝3秒或4秒或秒时，△PDE为等腰三角形．9、在平面直角坐标系中，BC∥OA，BC＝3，OA＝6，AB＝3（1）直接写出点B的坐标；（2）已知D、E分别为线段OC、OB上的点，OD＝5，OE＝2BE，直线DE交x轴于点F，求直线DE的解析式；（3）在（2）的条件下，点M是直线DE上的一点，在x轴上方是否存在另一个点N，使以O、D、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．【分析】（1）过B作BG⊥OA于点G，在Rt△ABG中，利用勾股定理可求得BG的长，则可求得B点坐标；（2）由条件可求得E点坐标，利用待定系数法可求得直线DE的解析式；（3）当OD为边时，则MO＝OD＝5或MD＝OD＝5，可求得M点坐标，由MN∥OD，且MN＝OD可求得N点坐标；当OD为对角线时，则MN垂直平分OD，则可求得M、N的纵坐标，则可求得M的坐标，利用对称性可求得N点坐标．【解答】解：（1）如图1，过B作BG⊥OA于点G，∵BC＝3，OA＝6，∴AG＝OA﹣OG＝OA﹣BC＝6﹣3＝3，在Rt△ABG中，由勾股定理可得AB2＝AG2+BG2，即（3）2＝32+BG2，解得BG＝6，∴OC＝6，∴B（3，6）；（2）由OD＝5可知D（0，5），∵B（3，6），OE＝2BE，∴E（2，4），设直线DE的解析式是y＝kx+b把D（0，5）E（2，4）代入得，∴直线DE的解析式是y＝﹣x+5；（3）当OD为菱形的边时，则MN＝OD＝5，且MN∥OD，∵M在直线DE上，∴设M（t，﹣t+5），①当点N在点M上方时，如图2，则有OM＝MN，∵OM2＝t2+（﹣t+5）2，∴t2+（﹣t+5）2＝52，解得t＝0或t＝4，当t＝0时，M与D重合，舍去，∴M（4，3），∴N（4，8）；②当点N在点M下方时，如图3，则有MD＝OD＝5，∴t2+（﹣t+5﹣5）2＝52，解得t＝2或t＝﹣2，当t＝2时，N点在x轴下方，不符合题意，舍去，∴M（﹣2，+5），∴N（﹣2，）；当OD为对角线时，则MN垂直平分OD，∴点M在直线y＝2.5上，在y＝﹣x+5中，令y＝2.5可得x＝5，∴M（5，2.5），∵M、N关于y轴对称，∴N（﹣5，2.5），综上可知存在满足条件的点N，其坐标为（4，8）或（﹣5，2.5）或（﹣2，）．【点评】本题为一次函数的综合应用，涉及勾股定理、待定系数法、菱形的性质、分类讨论及方程思想．在（2）中求得E点坐标是解题的关键，在（3）中求得M点的坐标是解题的关键，注意分类讨论．本题考查知识点较多，综合性较强，难度较大．10、如图1，已知正方形ABCD的边长为6，E是CD边上一点（不与点C重合），以CE为边在正方形ABCD的右侧作正方形CEFG，连接BF、BD、FD．计算：（1）当点E与点D重合时，△BDF的面积为；当点E为CD的中点时，△BDF的面积为．证明：（2）当E是CD边上任意一点（不与点C重合）时，猜想S△BDF与S正方形ABCD之间的关系，并证明你的猜想；运用：（3）如图2，设BF与CD相交于点H，若△DFH的面积为，求正方形CEFG的边长．解：计算：（1）∵当点E与点D重合时，∴CE＝CD＝6，∵四边形ABCD，四边形CEFG是正方形，∴DF＝CE＝AD＝AB＝6，∴S△BDF＝×DF×AB＝18，如图，连接CF，∵四边形ABCD和四边形CEFG均为正方形；∴∠CBD＝∠GCF＝45°，∴BD∥CF，∴S△BDF＝S△BDC＝S正方形ABCD＝×36＝18，故答案为：18，18；证明：（2）S△BDF＝S正方形ABCD，理由：连接CF．∵四边形ABCD和四边形CEFG均为正方形，∴∠CBD＝∠GCF＝45°，∴BD∥CF，∴S△BDF＝S△BDC＝S正方形ABCD；运用：（3）如图2，∵S△BDF＝S正方形ABCD＝×36＝18，且S△BDF＝S△BDH+S△DFH，∴S△BDH＝18﹣＝，∴×DH×6＝，∴DH＝，∴S△BDH＝××EF＝，∴EF＝4∴正方形CEFG的边长为4．11、已知如图，点C、D在线段AF上，AD＝CD＝CF，∠ABC＝∠DEF＝90°，AB∥EF．（1）若BC＝2，AB＝2，求BD的长；（2）求证：四边形BCED是平行四边形．（1）解：∵∠ABC＝90°，∴AC＝＝＝2，∵AD＝CD，∴BD＝AC＝；（2）证明：∵AD＝CD＝CF，∴DF＝AC＝2，∵∠DEF＝90°，∴CE＝DF＝，∴BD＝CE，∵AB∥EF，∴∠A＝∠F，在△ABC和△FED中，，∴△ABC≌△FED（AAS），∴BC＝ED，∵BD＝CE，∴四边形BCED是平行四边形．12、如图，在矩形ABCD中，M是BC上一点，EF垂直平分AM，分别交BC，AM，AD于点E，O，F，连接AE，MF．（1）求证：四边形AEMF是菱形；（2）若AB＝6，H为AB的中点，连接OH交AE于点P，OH+OA＝9，求△OPE的周长．（1）证明：∵EF垂直平分AM，∴AE＝EM，OA＝OM．∵四边形ABCD是矩形，∴AD∥BC．∴∠AFO＝∠MEO，在△OF和△MOE中，，∴△AOF≌△MOE（AAS）．∴OF＝OE．∴四边形AEMF是平行四边形．∵AE＝EM．∴四边形AEMF是菱形；（2）解：∵O、H分别为AM、AB的中点，∴BM＝2OH，AM＝2OA，∴AM+BM＝2OA+2OH＝18．设BM＝x，则AM＝18﹣x，在Rt△ABM中，由勾股定理得：62+x2＝（18﹣x）2，解得：x＝8，∴BM＝8，AM＝10．∴OA＝AM＝5，设EM＝m，则BE＝8﹣m，AE＝EM＝m，在Rt△ABE中，由勾股定理得：62+（8﹣m）2＝m2，解得：m＝，∴AE＝EM＝在Rt△AOE中，EO＝＝＝．∵OP∥EM，∴＝＝1，∴AP＝PE，∴OP＝EM＝，∵PE＝AE＝，∴△OPE的周长＝EO+PE+OP＝++＝10．。

九年级中考数学复习四边形压轴题专题练习1、已知：如图，平行四边形ABCD，对角线AC与BD相交于点E，点G为AD 的中点，连接CG，CG的延长线交BA的延长线于点F，连接FD．（1）求证：AB=AF；（2）若AG=AB，∠BCD=120°，判断四边形ACDF的形状，并证明你的结论．2、如图，点E是菱形ABCD对角线CA的延长线上任意一点，以线段AE为边作一个菱形AEFG，且菱形AEFG∽菱形ABCD，连接EC，GD．（1）求证：EB=GD；（2）若∠DAB=60°，AB=2，AG=，求GD的长．3、已知：如图，在▱ABCD中，E，F分别是边AD，BC上的点，且AE=CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点0．（1）求证：△ABE≌△CDF；（2）连接DG，若DG=BG，则四边形BEDF是什幺特殊四边形？请说明理由．4、如图，在直角梯形ABCD中，AB∥CD,AD⊥AB,60AB=,4BC=，B∠=︒,10点P沿线段AB从点A向点B运动，设AP x=．（1）求AD的长；（2）点P在运动过程中，是否存在以A P D、、为顶、、为顶点的三角形与以P C B点的三角形相似？若存在，求出x的值；若不存在，请说明理由；（3）设ADP∆与PCB∆的外接圆的面积分别为1S、2S，若12=+，求S的最小S S S值．5、如图，矩形ABCD中，AB=3，AD=4，E为AB上一点，AE=1，M为射线AD上一动点，AM=a（a为大于0的常数），直线EM与直线CD交于点F，过点M作MG⊥EM，交直线BC于G．（1）若M为边AD中点，求证：△EFG是等腰三角形；（2）若点G与点C重合，求线段MG的长；（3）请用含a的代数式表示△EFG的面积S，并指出S的最小整数值．6、在一次课题学习中，老师让同学们合作编题，某学习小组受赵爽弦图的启发，编写了下面这道题，请你来解一解：如图，将矩形的四边、、、分别延长至、、、，使得，，连接，，，. (1) 求证：四边形为平行四边形；(2) 若矩形是边长为1的正方形，且，，求的长.7、（1）如图，正方形ABCD 中，点E ，F 分别在边BC ，CD 上，∠EAF=45°，延长CD 到点G ，使DG=BE ，连结EF ，AG ．求证：EF=FG ．（2）如图，等腰直角三角形ABC 中，∠BAC=90°，AB=AC ，点M ，N 在边BC 上，且∠MAN=45°，若BM=1，CN=3，求MN 的长．ABCD BA CB DC AD E F G H AE CG BF DH EF FG GH HE EFGH ABCD 45FEB ∠°tan 2AEH ∠AE8、已知：如图，四边形ABCD，AB∥DC，CB⊥AB，AB=16cm，BC=6cm，CD=8cm，动点P从点D开始沿DA边匀速运动，动点Q从点A开始沿AB边匀速运动，它们的运动速度均为2cm/s．点P和点Q同时出发，以QA、QP为边作平行四边形AQPE，设运动的时间为t（s），0＜t＜5．根据题意解答下列问题：（1）用含t的代数式表示AP；（2）设四边形CPQB的面积为S（cm2），求S与t的函数关系式；（3）当QP⊥BD时，求t的值；（4）在运动过程中，是否存在某一时刻t，使点E在∠ABD的平分线上？若存在，求出t的值；若不存在，请说明理由9、猜想与证明：如图1摆放矩形纸片ABCD 与矩形纸片ECGF ，使B 、C 、G 三点在一条直线上，CE 在边CD 上，连接AF ，若M 为AF 的中点，连接DM 、ME ，试猜想DM 与ME 的关系，并证明你的结论． 拓展与延伸：（1）若将”猜想与证明“中的纸片换成正方形纸片ABCD 与正方形纸片ECGF ，其他条件不变，则DM 和ME 的关系为_____________．（2）如图2摆放正方形纸片ABCD 与正方形纸片ECGF ，使点F 在边CD 上，点M 仍为AF 的中点，试证明（1）中的结论仍然成立．10、如图①所示,已知A 、B 为直线l 上两点,点C 为直线l 上方一动点,连接AC 、BC ,分别以AC 、BC 为边向ABC ∆外作正方形CADF 和正方形CBEG ,过点D 作1DD l ⊥于点1D ,过点E 作1EE l ⊥于点1E .(1)如图②,当点E 恰好在直线l 上时(此时1E 与E 重合),试说明1DD AB =；(2)在图①中,当D 、E 两点都在直线l 的上方时,试探求三条线段1DD 、1EE 、AB之间的数量关系,并说明理由；(3)如图③,当点E 在直线l 的下方时,请直接写出三条线段1DD 、1EE 、AB 之间的数量关系.(不需要证明)11、如图，四边形ABCD 是边长为23的正方形，长方形AEFG 的宽27=AE ,长327=EF ．将长方形AEFG 绕点A 顺时针旋转15°得到长方形AMNH (如图7)，这时BD 与MN 相交于点O ．（1）求DOM ∠的度数；（2）在图7中，求N D 、两点间的距离；（3）若把长方形AMNH 绕点A 再顺时针旋转15°得到长方形ARTZ ,请问此时点B在矩形ARTZ 的内部、外部、还是边上？并说明理由．12、如图1，在梯形ABCD中，AB∥CD，∠B＝90º，AB＝2，CD＝1，BC＝m，P为线段BC上的一动点，且和B、C不重合，连接P A，过P作PE⊥P A交CD 所在直线于E．设BP＝x，CE＝y．(1)求y与x的函数关系式；(2)若点P在线段BC上运动时，点E总在线段．．CD上，求m的取值范围．(3)如图2，若m＝4，将△PEC沿PE翻折至△PEG位置，∠BAG= 90º，求BP长．13、已知正方形的对角线，相交于点．（1）如图1，，分别是，上的点，与的延长线相交于点．若，求证：；（2）如图2，是上的点，过点作，交线段于点，连结交于点，交于点．若， ①求证：； ②当时，求的长．14、如图，在矩形ABCD 中，AB =3，BC =4，将矩形ABCD 绕点C 按顺时针方向旋转α角，得到矩形A 'B 'C 'D '，B 'C 与AD 交于点E ，AD 的延长线与A 'D '交于点F ．CD AB C A D B O E G OB C O C E DG F DF C ⊥E G OE =O H C B H C EH ⊥B OB E D H C E F C O G G OE =O DG C ∠O =∠O E 1AB =CH（1）如图①，当α=60°时，连接DD'，求DD'和A'F的长；（2）如图②，当矩形A'B'CD'的顶点A'落在CD的延长线上时，求EF的长；（3）如图③，当AE=EF时，连接AC，CF，求AC•CF的值．15、已知：如图，在矩形ABCD中，Ab=6cm，BC=8cm，对角线AC，BD交于点0．点P从点A出发，沿方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动时，另一个点也停止运动．连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F．设运动时间为t（s）（0＜t ＜6），解答下列问题：（1）当t为何值时，△AOP是等腰三角形？（2）设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；（3）在运动过程中，是否存在某一时刻t，使S五边形S五边形OEC Q F：S△AC D=9：16？若存在，求出t的值；若不存在，请说明理由；（4）在运动过程中，是否存在某一时刻t，使OD平分∠COP？若存在，求出t的值；若不存在，请说明理由．16、如图，将矩形纸片ABCD沿直线MN折叠，顶点B恰好与CD边上的动点P重合（点P不与点C，D重合），折痕为MN，点M，N分别在边AD，BC上，连接MB，MP，BP，BP与MN相交于点F．（1）求证：△BFN∽△BCP；（2）①在图2中，作出经过M，D，P三点的⊙O（要求保留作图痕迹，不写做法）；②设AB=4，随着点P在CD上的运动，若①中的⊙O恰好与BM，BC同时相切，求此时DP的长．17、如图，在矩形ABCD中，AD=4，M是AD的中点，点E是线段AB上一动点，连结EM并延长交线段CD的延长线于点F．18、已知：如图1，图形①满足AD=AB，MD=MB，∠A=72°，∠M=144°．图形②与图形①恰好拼成一个菱形（如图2）．记AB的长度为a，BM的长度为b．（1）图形①中∠B=°，图形②中∠E=°；（2）小明有两种纸片各若干张，其中一种纸片的形状及大小与图形①相同，这种纸片称为“风筝一号”；另一种纸片的形状及大小与图形②相同，这种纸片称为“飞镖一号”．①小明仅用“风筝一号”纸片拼成一个边长为b的正十边形，需要这种纸片5张；②小明若用若干张“风筝一号”纸片和“飞镖一号”纸片拼成一个“大风筝”（如图3），其中∠P=72°，∠Q=144°，且PI=PJ=a+b，IQ=JQ．请你在图3中画出拼接线并保留画图痕迹．（本题中均为无重叠、无缝隙拼接）19、如图1，矩形MNPQ中，点E，F，G，H分别在NP，PQ，QM，MN上，若∠=∠，则称四边形EFGH为矩形MNPQ的反射四边形．图2，图3，∠=4=321∠图4中，四边形ABCD为矩形，且AB=4，BC=8．理解与作图：（1）在图2，图3中，点E，F分别在BC，CD边上，试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH．计算与猜想：（2）求图2，图3中反射四边形EFGH的周长，并猜想矩形ABCD的反射四边形的周长是否为定值？启发与证明：（3）如图4，为了证明上述猜想，小华同学尝试延长GF交BC的延长线于M，试利用小华同学给我们的启发证明（2）中的猜想．。

中考数学几何必考点-四边形中的动点问题-压轴题详解总结典型例题分析1：定义：若以一条线段为对角线作正方形，则称该正方形为这条线段的“对角线正方形”．例如，图①中正方形ABCD即为线段BD的“对角线正方形”．如图②，在△ABC中，∠ABC=90°，AB=3cm，BC=4cm，点P从点C出发，沿折线CA﹣AB以5cm/s的速度运动，当点P与点B不重合时，作线段PB的“对角线正方形”，设点P的运动时间为t（s），线段PB的“对角线正方形”的面积为S（cm2）．（1）如图③，借助虚线的小正方形网格，画出线段AB的“对角线正方形”．（2）当线段PB的“对角线正方形”有两边同时落在△ABC的边上时，求t的值．（3）当点P沿折线CA﹣AB运动时，求S与t之间的函数关系式．（4）在整个运动过程中，当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时，直接写出t的值．典型例题分析2：已知四边形ABCD是菱形，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB，DC相交于点E，F，且∠EAF=60°．（1）如图1，当点E是线段CB的中点时，直接写出线段AE，EF，AF之间的数量关系；（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE=CF；（3）如图3，当点E在线段CB的延长线上，且∠EAB=15°时，求点F到BC的距离．考点分析：四边形综合题．题干分析：（1）结论AE=EF=AF．只要证明AE=AF即可证明△AEF是等边三角形．（2）欲证明BE=CF，只要证明△BAE≌△CAF即可．（3）过点A作AG⊥BC于点G，过点F作FH⊥EC于点H，根据FH=CF•cos30°，因为CF=BE，只要求出BE即可解决问题．解题反思：本题考查四边形综合题、菱形的性质、等边三角形的判定、全等三角形的判定和性质等知识，解题的关键是灵活应用这些知识解决问题，学会添加常用辅助线，属于中考压轴题．典型例题分析3：如图1，在矩形ABCD中，BC＞AB，∠BAD的平分线AF与BD、BC分别交于点E、F，点O是BD的中点，直线OK∥AF，交AD于点K，交BC于点G．（1）求证：①△DOK≌△BOG；②AB+AK=BG；（2）若KD=KG，BC=4﹣√2．①求KD的长度；②如图2，点P是线段KD上的动点（不与点D、K重合），PM∥DG交KG于点M，PN∥KG交DG于点N，设PD=m，当S△PMN=√2/4时，求m的值．考点分析：四边形综合题；全等三角形的判定；矩形的性质；相似三角形的判定与性质．题干分析：（1）①先根据AAS判定△DOK≌△BOG，②再根据等腰三角形ABF和平行四边形AFKG的性质，得出结论BG=AB+AK；（2）①先根据等量代换得出AF=KG=KD=BG，再设AB=a，根据AK=FG列出关于a的方程，求得a的值，进而计算KD的长；②先过点G作GI⊥KD，求得S△DKG的值，再根据四边形PMGN是平行四边形，以及△DKG∽△PKM∽△DPN，求得S△DPN和S△PKM的表达式，最后根据等量关系S平行四边形PMGN=S△DKG﹣S△DPN﹣S△PKM，列出关于m的方程，求得m的值即可．解题反思：本题主要考查了矩形的性质以及平行四边形的性质，解题时需要运用全等三角形的判定与性质．解答此题的关键是运用相似三角形的面积之比等于相似比的平方这一性质，并根据图形面积的等量关系列出方程进行求解，难度较大，具有一定的综合性．。

2022年中考数学：几何专题复习之四边形压轴（一）1．如图，面积为4的平行四边形ABCD中，AB＝4，过点B作CD边的垂线，垂足为点E，点E正好是CD的中点，点M、点N分别是AB、AC．上的动点，MN的延长线交线段DE于点P，若点P是唯一使得线段∠MPB＝45°的点，则线段BM长x的取值范围是．2．如图，正方形ABCD中，点E是BC的中点，点F是CD上一点，分别以AE、AF为对称轴，折叠△ABE、△ADF，使得AB和AD与AG重合，连接BG交AE于点H，连接CG．（1）HE：AH＝；（2）S△AFE：S正方形ABCD＝．3．如图，线段AB的长为10，点D在AB上，△ACD是边长为3的等边三角形，过点D 作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH 的对角线交点为O，连接OB，则线段BO的最小值为．4．已知，在矩形ABCD中，AB＝3，BC＝5，点E在DC上，将矩形沿AE折叠，使点D 落在BC边上F处，则tan∠DAE＝；点G在BF上，将矩形沿AG 折叠，使点B落在AF上点H处，延长GH交AE于M，连接MF，则MF ＝．5．如图，在矩形ABCD中，AC，BD相交于点O，过点B作BF⊥AC于点M，交CD于点F，过点D作DE∥BF交AC于点N．交AB于点E，连接FN，EM．有下列结论：①四边形NEMF为平行四边形；②DN2＝MC•NC；③△DNF为等边三角形；④当AO＝AD时，四边形DEBF是菱形．其中，正确结论的序号．6．如图，∠BOD＝45°，BO＝DO，点A在OB上，四边形ABCD是矩形，连接AC，BD 交于点E，连接OE交AD于点F．下列4个判断：①OE⊥BD；②∠ADB＝30°；③DF ＝AF；④若点G是线段OF的中点，则△AEG为等腰直角三角形，其中，判断正确的是．（填序号）7．如图，已知矩形ABCD，连接BD，EO垂直平分BD，连接BE，∠ABD＝∠EFO，AE＝3EF，CD＝，求OD＝．8．已知：正方形ABCD中，E为BC的中点，BP＝2AP，F为AD上一点，EF交CP于O，∠POF＝45°，若△APF的面积为，则线段EF的长为．9．如图，正方形ABCD的对角线相交于点O，点E在边BC上，点F在CB的延长线上，∠EAF＝45°，AE交BD于点G，tan∠BAE＝，BF＝2，则FG＝．10．如图，在▱ABCD中，AD＝5，AB＝12，sin A＝．过点D作DE⊥AB，垂足为E，则sin∠BCE＝．11．如图，在正方形ABCD中，点O是对角线BD的中点，点P在线段OD上，连接AP 并延长交CD于点E，过点P作PF⊥AP交BC于点F，连接AF、EF，AF交BD于G，现有以下结论：①AP＝PF；②DE+BF＝EF；③PB﹣PD＝BF；④S△AEF为定值；⑤S 四边形PEFG＝S△APG．以上结论正确的有（填入正确的序号即可）．12．如图，矩形OABC中，点A，点C分别在x轴，y轴上，D为边BC上的一动点，现把△OCD沿OD对折，C点落在点P处．已知点B的坐标为（2，2）．（1）在点D沿BC从点C运动至点B的过程中，设点P经过的路径长度为l，则l的值；（2）在点D沿BC从点C运动至点B的过程中，若点P落在同一条直线y＝kx+4上的次数为2次，请直接写出k的取值范围．13．如图，在矩形ABCD中，点E在边AB上，△BEC与△FEC关于直线EC对称，点B的对称点F在边AD上，G为CD中点，连结BG分别与CE，CF交于M，N两点．若BM＝BE，MG＝1，则BN的长为，sin∠AFE的值为．14．图1是邻边长为2和6的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图2），则图1中所标注的d的值为；记图1中小正方形的中心为点A，B，C，图2中的对应点为点A′，B′，C′．以大正方形的中心O为圆心作圆，则当点A′，B′，C′在圆内或圆上时，圆的最小面积为．15．如图，在正方形ABCD中，F在AB上，E在BC的延长线上，AF＝CE，连接DF、DE、EF，EF交对角线BD于点N，M为EF的中点，连接MC，下列结论：①△DEF为等腰直角三角形；②∠FDB＝∠FEC；③直线MC是BD的垂直平分线；④若BF＝2，则MC ＝；其中正确结论的有．16．如图，矩形ABCD中，M是边CD的中点，连接AM，取AM的中点N，连接BN．若AB＝2，BC＝3，则BN的长为．17．如图，在正方形ABCD中，AB＝2．G为对角线BD的延长线上一点，E为线段CD的中点，BF⊥AE，连接OF．已知∠DAG＝15°，下列说法正确的是．（将正确答案的序号填写下来）①AG＝BD；②BF＝；③；④S△POF＝；⑤若E点为线段CD上一动点，当AE＝EC+CQ时，AQ＝4．18．如图，P为正方形ABCD的边BC的中点，BG⊥AP于点G，在AP的延长线上取点E，使AG＝GE，若正方形的边长为2，则CE＝．19．如图，在正方形ABCD中，AB＝4，AC与BD交于点O，点P，Q分别在线段AO，BC上，且满足BQ＝AP，以PQ为斜边作等腰直角三角形PQM，使点M与B位于PQ的两侧，当点P从点A运动到点O时，点M的运动路径长是．20．在平行四边形ABCD中，AF平分∠BAD交BC于点F，∠BAC＝90°，点E是对角线AC上的点，连接BE．（1）如图1，若AB＝AE＝AF，点G是BE的中点，则＝．（2）如图2，以点E为直角顶点，在BE的右下方作等腰直角△BEQ，若点E从点A出发，沿AC运动到点C停止，设在点E运动过程中，BQ的中点T，经过的路径长为a，AC的长为b，则＝．参考答案1．解：∵平行四边形ABCD的面积为4，AB＝4，BE⊥CD，∴BE＝1，∵点P是唯一使得线段∠MPB＝45°的点，则可看成弦MB所对的圆周角∠MPB＝45°，设△MBP外接圆的圆心为O，则∠MOB＝90°，∴，∵CD与AB之间的距离为1，∴，∴x≥，又∵MB≤4，∴．故答案为：2﹣2≤x≤4．2．解：（1）∵AE为对称轴，∴△AEG≌△AEB，BG⊥AE，∴∠GHE＝∠BHE＝90°，又∵∠HEB＝∠BEA，∴△HEB∽△BEA，∴＝，在正方形ABCD中，设边长为2x，则BE＝x，AB＝2x，∴AE＝＝＝x，∴HE＝＝＝x，∴AH＝AE﹣HE＝x﹣x＝x，∴HE：AH＝x：x＝1：4．故答案为：1：4；（2）设正方形ABCD的边长为2，则S正方形ABCD＝4，∵S△AFE＝（S正方形ABCD﹣S△FCE），CE＝BE＝GE＝1，设FG＝DF＝x，则EF＝1+x，CF＝2﹣x，在△EFC中，∵EF2＝CE2+CF2，∴（1+x）2＝（2﹣x）2+1，解得：x＝，∴CE＝2﹣x＝，∴S△CFE＝×CE×CF＝××1＝，∴S△AFE＝×（4﹣）＝，∴S△AFE：S正方形ABCD＝：4＝5：12．故答案为：5：12．3．解：连接AO，∵四边形CDGH是矩形，∴CG＝DH，OC＝CG，OD＝DH，∴OC＝OD，∵△ACD是等边三角形，∴AC＝AD，∠CAD＝60°，在△ACO和△ADO中，，∴△ACO≌△ADO（SSS），∴∠OAB＝∠CAO＝30°，∴点O一定在∠CAB的平分线上运动，∴当OB⊥AO时，OB的长度最小，∵∠OAB＝30°，∠AOB＝90°，∴OB＝AB＝×10＝5，即OB的最小值为5．故答案为：5．4．解：∵四边形ABCD为矩形，AB＝3，BC＝5，∴AB＝DC＝3，BC＝AD＝5，∠B＝∠C＝∠D＝90°，∵矩形沿AE折叠，使点D落在BC边上F处，∴∠DAE＝∠FAE，AD＝AF＝5，DE＝EF，在Rt△ABF中，AB＝3，AF＝5，由勾股定理得：BF＝＝4，∴FC＝BC﹣BF＝1，设DE＝EF＝x，则EC＝3﹣x，在Rt△CEF中，由勾股定理得，EC2+FC2＝EF2，即（3﹣x）2+12＝x2，解得：x＝，则DE＝EF＝，在Rt△ADE中，AD＝5，DE＝，∴tan∠DAE＝＝，∵矩形沿AG折叠，使点B落在AF上点H处，∴AB＝AH＝3，∠B＝∠AHG＝90°，∴∠AHM＝90°，∵∠DAE＝∠FAE，∴tan∠DAE＝tan∠FAE＝＝，∵AH＝3，∴MH＝1，HF＝AF﹣AH＝2，在Rt△FHM中，由勾股定理得，MF＝＝，∴故答案为：，．5．解：∵四边形ABCD是矩形，∴AD＝BC，AD∥BC，CD∥AB∴∠DAN＝∠BCM，∵BF⊥AC，DE∥BF，∴DE⊥AC，∴∠DNA＝∠BMC＝90°，在△ADN和△CBM中，，∴△ADN≌△CBM（AAS），∴DN＝BM，∵DF∥BE，DE∥BF，∴四边形DFBE是平行四边形，∴DE＝BF，∴EN＝FM，∵NE∥FM，∴四边形NEMF是平行四边形，故①正确，∵△ADN≌△CBM，∴AN＝CM，∴CN＝AM，∵∠AMB＝∠BMC＝∠ABC＝90°，∴∠ABM+∠CBM＝90°，∠CBM+∠BCM＝90°，∴∠ABM＝∠BCM，∴△AMB∽△BMC，∴＝，∵DN＝BM，AM＝CN，∴DN2＝CM•CN，故②正确，若△DNF是等边三角形，则∠CDN＝60°，∠ACD＝30°，这个与题目条件不符合，故③错误，∵四边形ABCD是矩形，∴OA＝OD，∵AO＝AD，∴AO＝AD＝OD，∴△AOD是等边三角形，∴∠ADO＝∠DAN＝60°，∴∠ABD＝90°﹣∠ADO＝30°，∵DE⊥AC，∴∠ADN＝ODN＝30°，∴∠ODN＝∠ABD，∴DE＝BE，∵四边形DEBF是平行四边形，∴四边形DEBF是菱形；故④正确．故答案为：①②④．6．解：①∵四边形ABCD是矩形，∴EB＝ED，∵BO＝DO，∴OE平分∠BOD，故①正确；②∵∠BOD＝45°，BO＝DO，∴∠ABD＝（180°﹣45°）＝67.5°，∴∠ADB＝90°﹣27.5°＝22.5°，故②错误；③∵四边形ABCD是矩形，∴∠OAD＝∠BAD＝90°，∴∠ABD+∠ADB＝90°，∵OB＝OD，BE＝DE，∴OE⊥BD，∴∠BOE+∠OBE＝90°，∴∠BOE＝∠BDA，∵∠BOD＝45°，∠OAD＝90°，∴∠ADO＝45°，∴AO＝AD，∴△AOF≌△ABD（ASA），∴OF＝BD，∴AF＝AB，连接BF，如图1，∴BF＝AF，∵BE＝DE，OE⊥BD，∴DF＝BF，∴DF＝AF，故③正确；④根据题意作出图形，如图2，∵G是OF的中点，∠OAF＝90°，∴AG＝OG，∴∠AOG＝∠OAG，∵∠AOD＝45°，OE平分∠AOD，∴∠AOG＝∠OAG＝22.5°，∴∠FAG＝67.5°，∠ADB＝∠AOF＝22.5°，∵四边形ABCD是矩形，∴EA＝ED，∴∠EAD＝∠EDA＝22.5°，∴∠EAG＝90°，∵∠AGE＝∠AOG+∠OAG＝45°，∴∠AEG＝45°，∴AE＝AG，∴△AEG为等腰直角三角形，故④正确；∴判断正确的是①③④．故答案为：①③④．7．解：如图，过点O作OM⊥BE，ON⊥DE于点M，N，∵EO是BD的垂直平分线，∴BE＝DE，∴EO平分∠BED，∴∠MEO＝∠NEO，∵OM⊥BE，ON⊥DE，∴∠EMO＝∠ENO，∵EO＝EO，∴△MEO≌△NEO（AAS），∴OM＝ON，EM＝EN，且点N是AD的中点，∵∠BDC+∠ADB＝∠OED+∠ADB＝90°，∴∠BDC＝∠OED＝∠OEF，∵∠ABD＝∠EFO，∴∠OFE＝∠ABD＝∠BDC，∴∠OEF＝∠OFE，∴OE＝OF，∴由三线合一得，ME＝MF＝EF，∵AE＝3EF，设EF＝2a，则AE＝6a，FM＝EM＝EN＝a，∴DN＝AN＝AE+EN＝7a，∴BE＝DE＝DN+NE＝8a，∴AD＝14a，在Rt△ABE中，根据勾股定理得，BE2＝AE2+AB2，即（8a）2＝（6a）2+（2）2，解得a＝1，∴AD＝14a＝14，∴在Rt△ABD中，根据勾股定理得，BD＝＝＝4．∴OD＝BD＝2．故答案为：2．8．解：如图：过E作EM⊥OC，垂足为M，过点O作ON⊥BC，垂足为N，过点F作FP⊥BC，垂足为G，设EM＝x，∴∠CME＝∠CBP＝90°，∴△CME∽△BPC，∵BP＝2AP＝CB，∴＝＝＝，∴CM＝x，又∵∠EOC＝∠POF＝45°，∴OM＝x，OE＝x，∴OC＝OM+CM＝x，CE＝＝x，∴正方形的边长为2CE＝x，∴AP＝x，在△COE中，S△COE＝OC•BM＝ON•EC，解得：ON＝x，∴NE＝＝x，∵ON⊥BC，GF⊥BC，∴ON∥FG，∴△EON∽△EFG，∴＝，∴EG＝x，∴BG＝BE﹣EG＝（）x＝x，∵AB∥FPGAF∥BG，∴四边形ABGF为矩形，∴AF＝BG＝x，∴S△APF＝AP•AF＝••x••x＝，解得：x＝，∵△EON∽△EFG，∴＝，∴EF＝××＝．故答案为：．9．解：如图，过点E作EH⊥AC于点H，则△EHC是等腰直角三角形，设EH＝a，则CH＝a，CE＝a，在Rt△ABE中，∠ABE＝90°，∴tan∠BAE＝＝，∴BE＝AB，∴BE＝CE＝a，∴AB＝BC＝2a，∴AC＝4a，AH＝3a，∴tan∠EAH＝＝，∵∠EAF＝∠BAC＝45°，∴∠BAF＝∠EAH，∴tan∠BAF＝tan∠EAH＝，∵BF＝2，∴AB＝6，BE＝CE＝3，∴AE＝3，AF＝2，∴EF＝5，∵AD∥BC，∴AD：BE＝AG：GE＝2：1，∴GE＝，∵EF：GE＝5：＝：1，AE：BE＝3：3＝：1，∠GEF＝∠BEA，∴EF：GE＝AE：BE，∴△GEF∽△BEA，∴∠EGF＝∠ABE＝90°，∴∠AGF＝90°，∴△AGF是等腰直角三角形，∴FG＝AF＝2．故答案为：2．10．解：如图，过点B作BF⊥EC于点F，∵DE⊥AB，AD＝5，sin A＝＝，∴DE＝4，∴AE＝＝3，在▱ABCD中，AD＝BC＝5，AB＝CD＝12，∴BE＝AB﹣AE＝12﹣3＝9，∵CD∥AB，∴∠DEA＝∠EDC＝90°，∠CEB＝∠DCE，∴tan∠CEB＝tan∠DCE，∴＝＝＝，∴EF＝3BF，在Rt△BEF中，根据勾股定理，得EF2+BF2＝BE2，∴（3BF）2+BF2＝92，解得，BF＝，∴sin∠BCE＝＝＝．故答案为：．11．解：取AF的中点T，连接PT，BT．∵AP⊥PF，四边形ABCD是正方形，∴∠ABF＝∠APF＝90°，∠ABD＝∠CBD＝45°，∵AT＝TF，∴BT＝AT＝TF＝PT，∴A，B，F，P四点共圆，∴∠PAF＝∠PBF＝45°，∴∠PAF＝∠PFA＝45°，∴PA＝PF，故①正确，将△ADE绕点A顺时针旋转90°得到△ABM，∵∠ADE＝∠ABM＝90°，∠ABC＝90°，∴∠ABC+∠ABM＝180°，∴C，B，M共线，∵∠EAF＝45°，∴∠MAF＝∠FAB+∠BAM＝∠FAB+∠DAE＝45°，∴∠FAE＝∠FAM，在△FAM和△FAE中，，∴△FAM≌△FAE（SAS），∴FM＝EF，∵FM＝BF+BM＝BF+DE，∴EF＝DE+BF，故②正确，连接PC，过点P作PG⊥CF于G，过点P作PW⊥CD于W，则四边形PGCW是矩形，在△PBA和PCB中，，∴△PBA≌△PBC（SAS），∴PA＝PC，∵PF＝PA，∴PF＝PC，∵PG⊥CF，∴FG＝GC，∵PB＝BG，PD＝PW＝CG＝FG，∴PB﹣PD＝（BG﹣FG）＝BF，故③正确，∵△AEF≌△AMF，∴S△AEF＝S△AMF＝FM•AB，∵FM的长度是变化的，∴△AEF的面积不是定值，故④错误，∵A，B，F，P四点共圆，∴∠APG＝∠AFB，∵△AFE≌△AFM，∴∠AFE＝∠AFB，∴∠APG＝∠AFE，∵∠PAG＝∠EAF，∴△PAG∽△FAE，∴＝（）2＝（）2＝，∴S四边形PEFG＝S△APG，故⑤正确，故答案为：①②③⑤．12．（1）如图1，∵在运动过程中，OP＝OC始终成立，∴OP＝2为定长，∴点P在以点O为圆心，以2为半径的圆上，∵点B的坐标为（2，2），∴tan∠COB＝＝，∴∠COB＝60°，∠COP＝120°，∴l＝×2π×2＝π．（2）在图1的基础上，取点E（0，4），过点E作⊙O（弧CP段）的切线EP′，切点为P′，连接PP′，如图2所示．∵OE＝4，OP′＝2，∴sin∠OEP′＝＝，∴∠OEP′＝30°，∴∠EOP′＝60°．∵∠COP＝120°，∴∠POP′＝60°．∵OP＝OP′，∴△OPP′为等边三角形，∵OP＝2，∴P（，﹣1），P′（，1）．当点P在直线y＝kx+4上时，有﹣1＝k+4，∴k＝﹣；当点P′在直线y＝kx+4上时，有1＝k+4，∴k＝﹣．综上可知：若点P落在同一条直线y＝kx+4上的次数为2次，则k的取值范围为﹣≤k＜﹣．13．解：∵BM＝BE，∴∠BEM＝∠BME，∴∠BEM＝∠GCM，又∵∠BME＝∠GMC，∴∠GCM＝∠GMC，∴MG＝GC＝1，∵G为CD中点，∴CD＝AB＝2．连接BF,FM，由翻折可得∠FEM＝∠BEM，BE＝EF, ∴BM＝EF，∵∠BEM＝∠BME，∴∠FEM＝∠BME，∴EF∥BM，∴四边形BEFM为平行四边形，∵BM＝BE，∴四边形BEFM为菱形，∵∠EBC＝∠EFC＝90°，EF∥BG，∴∠BNF＝90°，∵BF平分∠ABN，∴Rt△ABF≌Rt△NBF(HL)，∴BN＝AB＝2．∵FE＝FM,FA＝FN，∠A＝∠BNF＝90°，∴Rt△AEF≌Rt△NMF(HL)，∴AE＝NM，设AE＝NM＝x，则BE＝FM＝2﹣x，NG＝MG﹣NM＝1﹣x，∵FM∥GC，∴△FMN∽△CGN，∴＝,即＝,解得x＝2+(舍)或x＝2﹣，∴EF＝BE＝2﹣x＝，∴sin∠AFE＝＝＝﹣1．故答案为：2；﹣1．14．解：如图，连接FW，由题意可知点A′，O，C′在线段FW上，连接OB′，B′C′，过点O作OH⊥B′C′于H．∵大正方形的面积＝12，∴FG＝GW＝2，∵EF＝WK＝2，∴在Rt△EFG中，tan∠EGF＝＝＝，∴∠EGF＝30°，∵JK∥FG，∴∠KJG＝∠EGF＝30°，∴d＝JK＝GK＝（2﹣2）＝6﹣2，∵OF＝OW＝FW＝，C′W＝，∴OC′＝﹣，∵B′C′∥QW，B′C′＝2，∴∠OC′H＝∠FWQ＝45°，∴OH＝HC′＝﹣1，∴HB′＝2﹣（﹣1）＝3﹣，∴OB′2＝OH2+B′H2＝（﹣1）2+（3﹣）2＝16﹣8，∵OA′＝OC′＜OB′，∴当点A′，B′，C′在圆内或圆上时，圆的最小面积为（16﹣8）π．故答案为：6﹣2，（16﹣8）π．15．解：正方形ABCD中，AD＝CD，在△ADF和△CDE中，，∴△ADF≌△CDE（SAS），∴DE＝DF，∠ADF＝∠CDE，∴∠EDF＝∠FDC+∠CDE＝∠FDC+∠ADF＝∠ADC＝90°，∴△DEF是等腰直角三角形，故①正确；∴∠DFE＝45°,∵正方形ABCD,BD为对角线，∴∠NBE＝45°,∵∠FDN+∠DFN+∠DNF＝∠NBE+∠BNE+∠NEB＝180°,∠NBE＝∠DFE＝45°,∠DNF＝∠BNE,∴∠FDB＝∠FEB,故②正确；连接BM、DM，∵M是EF的中点，△BEF、△DEF是直角三角形，∴BM＝DM＝EF，又∵BC＝CD，∴直线CM是BD的垂直平分线，过点M作MH⊥BC于H，则∠MCH＝45°，∵M是EF的中点，BF⊥BC，MH⊥BC，∴MH是△BEF的中位线，∴MH＝BF＝1，∴CM＝MH＝，故④正确；综上所述，正确的结论有①②③④．故答案为：①②③④．16．解：过点N作GH∥AB，分别交BC于点G，交AD于点H，如图，∵矩形ABCD，∴AB＝CD，AD＝BC，∠C＝∠ABG＝90°，AB∥CD，∴四边形CDHG，四边形GHAB为矩形，∴∠BGN＝90°，GH＝CD＝AB，GH∥CD∥AB，∴＝＝，∵N为AM中点，∴MN＝AN，DH＝HA，∴CG＝GB＝BC＝，H为DA的中点，∴NH为△AMD的中位线，∴NH＝MD，∵M是CD的中点，∴MD＝CD＝AB＝1，∴NH＝，∴GN＝GH﹣NH＝AB﹣NH＝，在Rt△BGN中，由勾股定理得，BN＝＝，故答案为：．17．解：①∵∠DAG＝15°，∴∠GAO＝∠DAG+∠DAO＝60°，∴∠G＝30°，AG＝2AO，∵BD＝2AO，∴AG＝BD，∴①正确，符合题意．②∵E为CD中点，∴DE＝CD，∵∠DAE+∠BAF＝90°，∠BAF+∠ABF＝90°，∴∠BAF＝∠DAE，∴tan∠BAF＝tan∠DAE＝＝＝，∴BF＝2AF，在Rt△ABF中，由勾股定理得：AB＝＝AF＝2，∴AF＝，BF＝2AF＝，∴②错误，不符合题意．③∵E为CD中点，EC∥AB，∴EC为△ABQ的中位线，C为BQ中点，∴BQ＝2BC＝2AD，∵AD∥BQ，∴△ADP∽△QBP，∴＝＝，∴＝，∴DP＝BD，OP＝OD﹣DP＝BD﹣BD＝BD，∴＝＝＝，∴③正确，符合题意．④∵AB＝2，BQ＝2AB＝4，∴AQ＝＝2，∵＝＝，∴AP＝AQ＝，∴＝＝，∴＝1﹣＝，即S△POF＝S△AOP，∵＝，∴S△AOP＝S△AOD＝×S正方形ABCD＝，∴S△POF＝S△AOP＝，∴④错误，不符合题意．⑤设ED＝x，EC＝2﹣x，则＝，即＝，∴CQ＝，∴AE＝EC+CQ＝2﹣x+＝，在Rt△ADE中，由勾股定理得：AE＝＝，∴＝，解得x＝或x＝﹣（舍）．∴AE＝＝，∵AD∥BQ，∴∠DAE＝∠BQA，∴sin∠DAE＝sin∠BQA＝＝，∴AQ＝2AB＝4，∴⑤正确，符合题意．故答案为：①③⑤．18．解：如图，过C作CH⊥AE于H，∵AG＝GE，∴AB＝BE，∴∠BAE＝BEA，∵BG⊥AE，∴∠BGP＝∠CHP＝90°，∵P为BC的中点，∴BP＝CP，在△BGP和△CHP中，，∴△BGP≌△CHP（AAS），∴BG＝CH，∠GBP＝∠PCH，∵四边形ABCD是正方形，∴AB＝BC，∴BC＝BE，∴∠BCE＝∠BEC，∵∠ABC＝∠ABG+∠GBP＝90°，∠ABG+∠BAG＝90°，∴∠GBP＝∠BAG，∴∠PCH＝∠BEP，∴∠HCE＝∠HEC，∴CH＝EH，∵∠CHE＝90°，∴CE＝CH，即CE＝BG，在Rt△ABP中，AB＝2，BP＝BC＝1，∴AP＝＝，∵S△ABP＝AB•BP＝AP•BG，∴BG＝＝，∴CE＝×＝，故答案为．19．解：在正方形ABCD中，AB＝4，∴AB＝BC＝，∴AC＝＝8，∴AO＝4，①当P1在A点时，AP＝0，∴BQ＝AP＝0，∴Q点在B点处，此时，∠BAO＝∠ABO＝45°，∠AOB＝90°，即M1点在O点处；②当P3在O点时，AP3＝4＝AO，∴BQ＝AP＝4，∴Q3点在C点处，此时，∠ACD＝∠CP3M3＝45°，∠P3M3C＝90°，即M3点在DC的中点处；③当P2在AO中点时，AP2＝2，∴BQ＝AP＝2，∴Q2点在BC中点处，M2点在P3M3中点处，证明如下：当M2点在P3M3中点处，且P2M2Q2＝90°，连接P3Q2，∵P3、Q2为中点，∴OQ2⊥BC，∴四边形OQ2Q3M3是正方形，∵OQ2＝AB＝2＝OM3，∴OM2＝＝，∴Q2M2＝＝＝，过点P2作P2G⊥BC，此时P2为AO的中点，且P2G∥AB，即在△ABC中，，∵CP2＝AC﹣AP2＝6，即，∴P2G＝3，同理可得，CG＝3，GQ2＝，∴P2Q2＝＝＝，∴P2M2＝＝，故M2点在OM3是中点处，即M点在OM3上运动，∴OM3＝DC＝2．20．解：（1）∵AF平分∠BAD，∴∠BAF＝∠DAF，∵AD∥BC，∴∠DAF＝∠AFB，∴∠BAF＝∠AFB，∴AB＝BF，∵AB＝AE＝AF，∴AB＝AF＝BF，∴△ABF是等边三角形，∴∠ABF＝∠BAF＝∠AFB＝60°，设AB＝AE＝AF＝x，则BF＝x，∵∠BAE＝90°，点G是BE的中点，∴BE＝x，BG＝AG＝GE＝x，∠BAG＝∠ABG＝45°，∴∠GAF＝∠GBF＝15°，＝，∴△BGF∽△BFE，∴＝＝，故答案为：；（2）如图2中，在AC上取一点N，使得AN＝AB，连接BN，NQ，取BN的中点J，连接TJ．∵△ABN，△BEQ都是等腰直角三角形，∴BN＝AB，BQ＝BE，∠ABN＝∠EBQ＝45°，∴，∠ABE＝∠NBQ，∴△ABE∽△NBQ，∴＝，∠AEB＝∠BQN，∵∠AEB+∠BEC＝180°，∴∠BQN+∠BEC＝180°，∴∠EBQ+∠ENQ＝180°，∵∠EBQ＝∠ENQ＝45°，∴∠ENQ＝135°，∠BNQ＝90°，∵BJ＝JN，BT＝TQ，∴TJ∥NQ，TJ＝NQ，∴∠BJT＝∠BNQ＝90°，∴点T的运动轨迹是线段JT，∴a＝JT＝NQ＝AE，∵点E从A运动到C时，AE＝AC＝b，∴a＝b，∴＝，故答案为．。

人教版八年级下册数学期末平行四边形动点压轴题训练1．如图，在△ABC 中，BA＝BC＝10，sin B＝45点 D 为边BC 的中点．动点P 从点B出发，沿折线BA —AC 向点C 运动，在BA、AC 上的速度分别为每秒5 个单位长度和每秒P 不与点A 重合时，连接PD，以P A、PD 为邻边作△APDE．设点P 的运动时间为t 秒（t＞0）．(1)△线段AC 的长为_____．△用含t 的代数式表示线段AP 的长．(2)当点E 在△ABC 内部时，求t 的取值范围．(3)当APDE是菱形时，求t 的值．(4)作点B 关于直线PD 的对称点B′，连接B′D，当B′D△BC 时，直接写出t 的值．2．如图1，正方形ABCD边长为4，点P是直线BC上的一动点，连接DP，以DP为边在直线DP右侧作等边三角形DPE．(1)请直接写出正方形ABCD的面积；(2)当BP为何值时，点C落在DPE的边上；(3)如图2，若点P在线段BC上从B向C运动，当BP为何值时，线段CE的长度最小？请求出CE的最小值，并直接写出点E所经过的路径的长度．3．在长方形ABCD中，AB＝4，BC＝8，点P、Q为BC边上的两个动点（点P位于点Q的左侧，P、Q均不与顶点重合），PQ＝2(1)如图△，若点E为CD边上的中点，当Q移动到BC边上的中点时，求证：AP＝QE；(2)如图△，若点E为CD边上的中点，在PQ的移动过程中，若四边形APQE的周长最小时，求BP的长；(3)如图△，若M、N分别为AD边和CD边上的两个动点（M、N均不与顶点重合），当BP＝3，且四边形PQNM的周长最小时，求此时四边形PQNM的面积．4．如图1，正方形ABCD的边长为a，E为边CD上一动点（点E与点C、D不重合），连接AE交对角线BD于点P，过点P作PF△AE交BC于点F．（1）求证：P A＝PF；（2）如图2，过点F作FQ△BD于Q，在点E的运动过程中，PQ的长度是否发生变化？若不变，求出PQ的长；若变化，请说明变化规律．（3）请写出线段AB、BF、BP之间满足的数量关系，不必说明理由．5．如图1，有一张矩形纸条ABCD ，边AB 、BC 的长分别是方程27100x x -+=的两个根()AB BC >，E 为CD 上一点，1CE =． （1）连接AE ，BE ，试说明90AEB =︒∠．（2）如图2，M 为边AB 上一个动点，将四边形BCEM 沿ME 折叠，使点B ，C 分别落在点B ′，C '上，边MB '与边CD 交于点N ． △如图3，当点M 与点A 重合时，求N 到ME 的距离．△在点M 从点A 运动到点B 的过程中，求点N 相应运动的路径长（路程）．6．如图，长方形ABCD 中，AD △BC ，△B ＝90°，AD ＝BC ＝20，AB ＝8，动点P 从点B 出发，以每秒2cm 的速度沿B →A → D 的方向，向终点D 运动；动点Q 从点B 出发以每秒2cm 的速度沿B →C 的方向向终点C 运动．以PQ 为边向右上方作正方形PQMN ，其中一个动点到达终点时，另一个动点也随之停止运动，设点 P 、Q 同时出发，运动时间为t 秒（t ＞0）．（1）AP ＝ （用含t 的代数式表示）； （2）当点N 落在AD 边上时，求t 的值；（3）当正方形PQMN 与长方形ABCD 的重叠部分为四边形时，求重叠部分的面积S （用含t 的代数式表示）；（4）请直接写出当t 满足什么条件时，正方形PQMN 与长方形ABCD 的重叠部分为三角形．7．如图，在Rt △ABC 中，△C ＝90°，△ABC ＝30°，D ，E 是斜边AB 上的两个动点（不与点A ，B 重合），过E 作EF △BC 于点F ，设BD ＝m ，EF ＝n ，且m ＝12﹣4n ，连结DF ．（1）当m ＝8时， △求DE 长； △求△BDF 的面积．（2）是否存在点P ，使得以D ，E ，F ，P 四点为顶点的四边形是菱形，若存在，请求出n 的值，若不存在，请说明理由；（3）当点B 关于直线DF 的对称点B '落在直线EF 上时，请直接写出n 的值．8．如图，在四边形ABCD 中，//AD BC ，90B ∠=︒，8cm AB =，12cm AD =，18cm BC =，点P 从点A 出发，以1cm/s 的速度向点D 运动；点Q 从点C 同时出发，以2cm/s 的速度向点B 运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设点P ，Q 运动的时间为ts ．（1）CD 边的长度为________cm ，t 的取值范围为________． （2）从运动开始，当t =________时，PQ CD =．（3）在整个运动过程中是否存在t 值，使得四边形PQCD 是菱形．若存在，请求出t 值；若不存在，请说明理由．9．如图，点P为正方形ABCD的对角转AC上一动点，过点P作PE△PB交射线DC 于点E．（1）如图1，当点E在边CD上时，求证：PB＝PE；（2）如图2，当点E在DC的延长线上时，探求线段P A、PC、CE的数量关系并加以证明；（3）如图3，在（1）的条件下，连接BE交AC于点F，若正方形ABCD的边长为4，当点E为CD的中点，则PF＝（请直接写出结果）．10．如图，△ABC是边长为6的等边三角形，P是AC边上一动点（与A，C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），连接PQ交AB于D．（1）设AP的长为x，则PC＝，QC＝；（2）当∠BQD＝30°时，求AP的长；（3）过点Q作QF⊥AB交AB延长线于点F，过点P作PE⊥AB交AB延长线于点E，则EP，QF有怎样的关系？说明理由；（4）在运动过程中，线段ED的长是否发生变化？如果不变，求出线段ED的长11．如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PE=PB，连接PD，O为AC中点．（1）如图1，当点P在线段AO上时，试猜想PE与PD的数量关系和位置关系．（2）△如图2，当点P在线段OC上时，（1）中的猜想还成立吗？请说明理由．△图2，试用等式来表示PB、BC、CE之间的数量关系，并证明．12．已知平行四边形ABCD中，AD＝2AB．（1）作△ABC的平分线BM交AD于M，连CM．△如图1，求△BMC的度数；△如图2，若△ADC＝90°，点P是AD延长线上一点，BP交CM于N，CG△BP垂足为H，交AD于G，求证：BN＝CG+GN；（2）如图3，若△ADC＝60°，AB＝4，E是AB的中点，P是BC边上一动点，将EP 逆时针旋转90°得到线段EQ，连DQ，直接写出DQ的最小值．13．如图，P是正方形ABCD边BC上一个动点，线段AE与AD关于直线AP对称，连接EB并延长交直线AP于点F，连接CF．（1）如图1，30BAP ∠=︒， △求AFE ∠的大小； △求证：BC =；（2）如图2，试猜想线段BE 与CF 之间的数量关系，并证明你的结论．14．在正方形ABCD 中，4AB =，点E 是边AD 上一动点，以CE 为边，在CE 的右侧作正方形CEFG ，连结BF ．（1）如图1，当点E 与点A 重合时，则BF 的长为________． （2）如图2，当1AE =时，求点F 到AD 的距离和BF 的长． （3）当BF 最短时，请直接写出此时AE 的长．15．如图，平行四边形ABCD 中，4cm,2cm,60AB AD C ==∠=︒．点P 以2cm/s 的速度从顶点A 出发沿折线A B C --向点C 运动，同时点Q 以1cm/s 的速度从顶点A 出发沿折线A D C --向点C 运动，当其中一个动点到达末端停止运动时，另一点也停止运动．设运动时间为s t ．（1）求平行四边形ABCD 的面积； （2）求当1s t =时，APQ 的面积；（3）当APQ 的面积是平行四边形ABCD 面积的38时，求t 的值．16．在矩形ABCD 中，10,8CD AD ==．（1）P 为BC 边上的一点，如图，将ABP △沿直线翻折至AEP △的位置（点B 落在点E 处）△当点E 落在CD 边上时，直接写出此时DE 的长度________．△若点P 为BC 的中点，连接CE ，则CE 与AP 有何位置关系？请说明理由；（2）点Q 为射线DC 上的一个动点，将ADQ △沿AQ 翻折，点D 恰好落在直线BQ 上的点D 处，求DQ 的长为_________．17．已知矩形ABCD 的一条边8AD =，将矩形ABCD 折叠，使得顶点B 落在CD 边上的点P 处．（1）如图1，已知折痕与边BC 交于点O ，连结AP ，OP ，OA ，若4PC =，求边AB 的长；（2）如图2，若点P 恰好是边CD 的中点，求AOB ∠的度数；（3）如图3，在（1）的条件下，擦去折痕AO 、线段OP ，连接BP ，动点M 在线段AP 上（点M 与点P 、A 不重合），动点N 在线段AB 的延长线上，且BN PM =，连接MN 交PB 于点F ，作ME BP ⊥于点E ．试问当动点M 、N 在移动的过程中，线段EF的长度是否发生变化？若变化，说明理由．若不变，求线段EF的长度．18．如图，平行四边形ABCD中，8cm,4cm,30==∠=︒，点P以4cm/s的速度从AB AD C--向点C运动，同时点Q以2cm/s的速度从顶点A出发沿折顶点A出发沿折线A B C--向点C运动，当其中一个动点到达末端停止运动时，另一点也停止运动，线A D C设运动时间为t秒．（1）求平行四边形ABCD的面积；t=时，APQ的面积；（2）求当0.5s时，求t的值．（3）当APQ的面积是平行四边形ABCD面积的3819．如图，在直角坐标系中，点O是坐标原点，四边形OABC是平行四边形，∠=︒，点A的坐标为(6,0)，点B的坐标为．动点P从点O出发，沿射COA60线OA方向以每秒1个单位的速度匀速运动；动点Q同时从点A出发，到达点B之后，继续沿射线BC运动，以每秒2个单位的速度匀速运动，设点P运动的时间为t秒t>）．（0APQ的面积．（1）写出．．点C的坐标；当运动2秒时，求（2）在整个运动过程中，是否存在这样的t，使以A，P，Q，C为顶点的四边形是矩形？若存在，请求出t的值，若不存在，请改变点P的运动速度，使以A，P，Q，C 为顶点的四边形是矩形，求出此时点P的速度．（3）在整个运动过程中，t 为何值时，以A ，P ，Q ，C 为顶点的四边形是平行四边形？20．已知，平行四边形ABCD 中，一动点P 在AD 边上，以每秒1cm 的速度从点A 向点D 运动．（1）如图△，运动过程中，若CP 平分BCD ∠，且满足CD CP =，求ABC ∠的度数． （2）如图△，在（1）问的条件下，连接BP 并延长，与CD 的延长线交于点F ，连接AF ，若4cm AB =，求APF 的面积．（3）如图△，另一动点Q 在BC 边上，以每秒4cm 的速度从点C 出发，在BC 间往返运动，两个点同时出发，当点P 到达点D 时停止运动（同时Q 点也停止），若18cm AD =，则t 为何值时，以P ，D ，Q ，B 四点组成的四边形是平行四边形．参考答案：1．(1)△△105AP AB PB t =-=-或AP =-(2)12t ＜＜或t 2＜＜3 (3)1514或3712(4)57或1962．(1)16(2)4或4343或4(3)4-；2；E 所经过的路线的长度是43．(1)见解析(2)4(3)44．（1）见解析；（2）PQ 的长不变，见解析；（3）AB +BF5．（1）见解析；（2）；326．（1）82t -()04t ≤≤，或28t -()414t <≤；（2）2t =；（3）28S t =()02t <≤，或22248S t t =-+-()610t <<；（4）46t ≤≤，或10t =，．7．（1）△6；△（2）存在，127或125；（38．（1）10，09t ≤≤；（2）4或8；（3）不存在，9．（2）AP ﹣PC ．（3 10．（1）6x -，6x + ；（2）2；（3）EP FQ =，//QF PE ；（4）不变，3ED =． 11．（1）PD =PE 且PD △PE ，（2）△（1）中猜想成立；△2222BC CE PB +=，12．（1）△90°（2）13．（1）△45°；（2）BE CF ，14．（1）BF =（2）3（3）2AE =15．（1）2；（22；（33 16．（1）△6；△EC △P A ；（2）4和1617．（1）10；（2）60°；（3）不变，18．（1）16cm2；（2）12cm2；（3319．（1）C(4,，（2）不存在，点P的速度为每秒23个单位；（3）203s或8s20．（1）60°；（2）（3）4s或7.2s或12s或14.4s。