6—3电容、电感元件的串联与并联

电路基础原理电感与电容的串联与并联电路基础原理：电感与电容的串联与并联引言：电路是现代科技发展中不可或缺的一部分，而电路中的元件起着至关重要的作用。

本文将重点讨论电感与电容这两种重要的电路元件，并探讨它们在串联与并联电路中的特性和应用。

一、电感的基本原理与特性电感是一种能够储存能量的元件，它由线圈组成，当电流通过时，会产生磁场。

电感的特性主要有两点：首先，电感的储能能力与线圈中的线圈数目和电流大小成正比。

其次，电感对交流电具有阻碍作用，即它能够阻碍电流变化的速度。

这种阻碍导致了电感在滤波器和振荡器等电路中的广泛应用。

二、电容的基本原理与特性电容也是一种储存能量的元件，它由两个导体板之间的电介质隔开。

当电容器两端的电位差发生变化时，电容器会储存或释放电荷。

电容的特性包括两个方面：首先，电容的储能能力与导体板面积和电介质相对介电常数成正比；其次，电容对直流电具有阻抗作用，而对交流电具有通过作用。

这种特性使得电容器在蓄电池、滤波器和调谐器等电路中有重要应用。

三、电感与电容的串联串联是指将电感和电容依次连接在同一电路中。

在串联中，电感和电容之间的作用互相影响，产生不同的电路特性。

首先，串联会使电感和电容的电流大小相同，但相位不同。

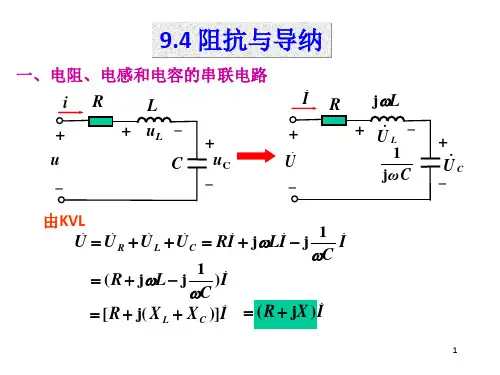
其次，串联电路的复阻抗等于电阻与电感复阻抗之和。

最后，串联电路中的电压在电感和电容上分布。

四、电感与电容的并联并联是指将电感和电容同时连接在一个电路中。

在并联中，电感和电容之间的作用互相影响，同样会产生不同的电路特性。

首先，并联会使电感和电容的电压相同，但电流不同。

其次，并联电路的复阻抗等于电阻与电容的复阻抗之和。

最后，并联电路中的电流分布在电感和电容上。

结论：电感和电容是电路中常见的元件，它们在电路中的串联与并联有不同的特性和应用。

串联电路中，电感和电容的电流大小相同但相位不同，而并联电路中，电感和电容的电压相同但电流不同。

了解电感和电容的特性和应用，对于电路设计和实际应用都具有重要意义。

第六章 储能元件§6-1 §6-2 §6-3电容元件 电感元件 电容、电感元件的串联和并联z 重点： 重点： z1. 电容元件的特性； 2. 电感元件的特性； 3. 电容、电感元件在串并联时的 等效参数。

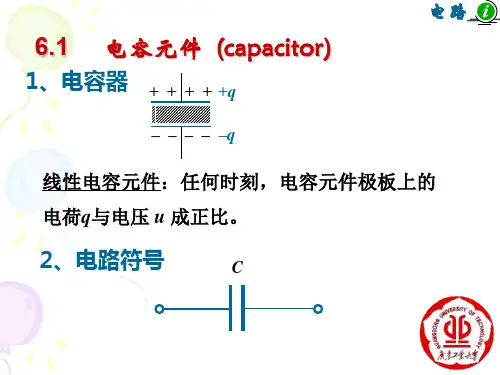
§6-1电容器电容元件在外电源作用下，两极板上分 别带上等量异号电荷，并在介质中 建立电场而具有电场能。

撤去电 源，板上电荷仍可长久地集聚下 去，电场继续存在。

q +εq -电容器是一种能存储电荷或存储电场能量的部件。

电容元件就是反映这种物理现象的电路模型。

1. 线性电容元件(1) 电路符号 (2) 库伏特性C q + i + u -q -任何时刻，极板上的电荷q与电压u成正比。

q = CuC称为电容器的电容，是一个正实常数。

单位：F(法)，常用µF，pF等表示。

q = Cu线性电容元件的库伏特性( q～u )是过原点的直线。

库伏特性qαOu(3) 线性电容元件的电压、电流关系 电流和电压取关联参考方向C q + i + u -q -dq d (Cu ) du i= = =C dt dt dtCdu 由式 i = C 可知 dtq + i + u-q -(1) 电流与电压的大小无关，而与电压的变化率成正 比。

即电压与电流具有动态关系，电容是动态元件； (2) 当电压不随时间变化，即u为常数(直流)时，电流 为零。

电容相当于开路，电容有隔断直流作用； (3) 实际电路中通过电容的电流i为有限值，则电容 电压u必定是时间的连续函数。

Cdq 由式 i = C 得 dtt t0q + i +t t0-q u tq(t ) = ∫ idξ = ∫ idξ + ∫ idξ = q(t 0) + ∫ idξ−∞ −∞ t0上式的物理意义是：t时刻具有的电荷量等于t0时 的电荷量加以t0到t时间间隔内增加的电荷量。

指定t0为时间起点并设为零( t0=0 )，上式写为q(t ) = q(0) + ∫ idξ0tC因 u = q /C 由i +q + u或t-q t 0q(t) = q(t 0) + ∫ idξt0q(t ) = q(0) + ∫ idξ1 t u(t ) = u(0) + ∫ idξ C 0得1 t u(t) = u(t 0) + ∫ idξ C t0或可见，电容电压除与0到t的电流值有关外，还与 u(0)值有关，因此，电容是一种有“记忆”的元件。

高三物理串联和并联知识点在物理学中，串联和并联是电路中常见的两种连接方式。

在本文中，我们将详细介绍高三物理中与串联和并联相关的知识点。

一、串联电路1. 定义串联电路是指电流依次通过电阻、电容或电感等元件的连接方式。

在串联电路中，电流只有一条路径可以流通，元件依次连接，两端接入外部电源。

2. 特点(1) 电流：在串联电路中，电流大小相等，分别通过每个元件。

(2) 电压：在串联电路中，总电压等于各个元件电压之和。

(3) 电阻：在串联电路中，总电阻等于各个元件电阻之和。

(4) 亮度：在串联电路中，灯泡等元件亮度与其电压成正比。

(5) 电容和电感：在串联电路中，总电容等于各个电容之和，总电感等于各个电感之和。

3. 应用(1) 家用电路中的串联电路：例如房间内的灯泡串联连接，灯泡一个接一个地连接在电源上。

(2) 电子电路中的串联电路：例如调节电压的稳压电路、分压电路等。

二、并联电路1. 定义并联电路是指电流同时通过多个支路的连接方式。

在并联电路中，电流可选择不同的路径进行流通，支路之间的连接点相同，两端接入外部电源。

2. 特点(1) 电流：在并联电路中，总电流等于各支路电流之和。

(2) 电压：在并联电路中，各支路电压相等，等于总电压。

(3) 电阻：在并联电路中，总电阻小于各支路电阻的最小值。

(4) 亮度：在并联电路中，灯泡等元件亮度与其电流成正比。

(5) 电容和电感：在并联电路中，总电容等于各个电容之和，总电感等于各个电感之和。

3. 应用(1) 家用电路中的并联电路：例如平行连接的灯泡，电路中的各灯泡可以独立控制。

(2) 电子电路中的并联电路：例如多台电器连接在同一个插座上。

三、串并联结合1. 定义在实际电路中，常常会出现串联与并联结合的情况。

即多个元件同时存在串联和并联连接的关系。

2. 特点和应用串并联结合的电路可以根据实际情况灵活调整，以满足特定的需求。

(1) 家用电路中的串并联：例如多个插座串联连接，每个插座内部的电器又是并联连接。

交流电路电感电容串联和并联的计算交流电路中的电感和电容元件在串联和并联时具有不同的计算方法。

首先我们来看一下电感和电容的特点以及串联和并联的基本概念。

1.电感和电容的特点电感（L）和电容（C）是被动元件，用于储存和处理电能。

电感储存电能的方式是通过产生磁场，而电容则通过储存电荷的方式储存电能。

电感的单位是亨利（H），表示当通过一个电流变化速率为1安培/秒时，其产生的磁通量变化速率为1韦伯/亨利。

电感对交流电的元件具有阻抗特性，即在交流电路中电感对电流具有阻碍作用，其阻抗（ZL）与频率（f）成正比。

电容的单位是法拉（F），表示当电容器两极板间的电压变化速率为1伏特/秒时，其充放电时存储或释放的电荷量为1库仑。

电容对交流电的元件具有容抗特性，即在交流电路中电容对电流具有阻碍作用，其容抗（ZC）与频率（f）成反比。

2.串联电感和电容的计算串联是指将电感和电容元件按顺序连接在一起，形成一个串联电路。

串联电感和电容的总阻抗是各元件阻抗之和。

对于串联电感元件，其总阻抗（ZL_total）可通过下式计算：ZL_total = ZL1 + ZL2 + … + ZLn对于串联电容元件，其总阻抗（ZC_total）可通过下式计算：ZC_total = (1/ZC1 + 1/ZC2 + … + 1/ZCn)^-13.并联电感和电容的计算并联是指将电感和电容元件同时连接到一个节点上，形成一个并联电路。

并联电感和电容的总阻抗是各元件阻抗的倒数之和的倒数。

对于并联电感元件，其总阻抗（ZL_total）可通过下式计算：ZL_total = (1/ZL1 + 1/ZL2 + … + 1/ZLn)^-1对于并联电容元件，其总阻抗（ZC_total）可通过下式计算：ZC_total = ZC1 + ZC2 + … + ZCn4.并联电感和电容的共振在一些特定频率下，电感和电容的串联和并联可能会产生共振现象。

共振频率是指电路中电感和电容元件共同产生最大电压或最大电流时的频率。

《电路A 》教学大纲two-terminal networks. After this course, students should be fluent in electric circuit theorem and techniques of circuit analysis, be able to find the current, voltage and power of direct current circuits, alternating current circuits and two-terminal networks, be able to analysis transient response of dynamic circuits.三、课程内容（一）课程教学目标1）通过学习掌握电路基本理论基本分析方法和初步的实验技能，为后续课程奠定基础。

2）通过学习树立严谨的科学作风和工程观点，培养科学思维能力和实验研究能力。

（二）基本教学内容第一章、电路模型和电路定律教学目的与要求：1．理解电路模型和理想电路元件的概念。

2．理解电流和电压参考方向的含义，理解关联方向和非关联方向的区别。

3．掌握功率计算的方法。

4．理解电阻元件的定义及端口伏安关系。

5．理解独立源（电压源、电流源）的定义及其端口伏安关系。

6．理解受控源的定义及其端口伏安关系。

7．掌握基尔霍夫定律。

掌握KCL及KVL方程的列写方法。

教学重点：1．电压、电流的参考方向；2．电阻元件和电源元件的特性；3．基尔霍夫定律教学难点：电压、电流的参考方向；电源元件的特性；基尔霍夫定律教学内容：§1-1 电路和电路模型§1-2 电流和电压的参考方向§1-3 电功率和能量§1-4 电路元件§1-5 电阻元件§1-6 电压源和电流源§1-7 受控电源§1-8 基尔霍夫定律学时分配：6第二章、电阻电路的等效变换教学目的与要求：1．理解电路等效变换的概念。

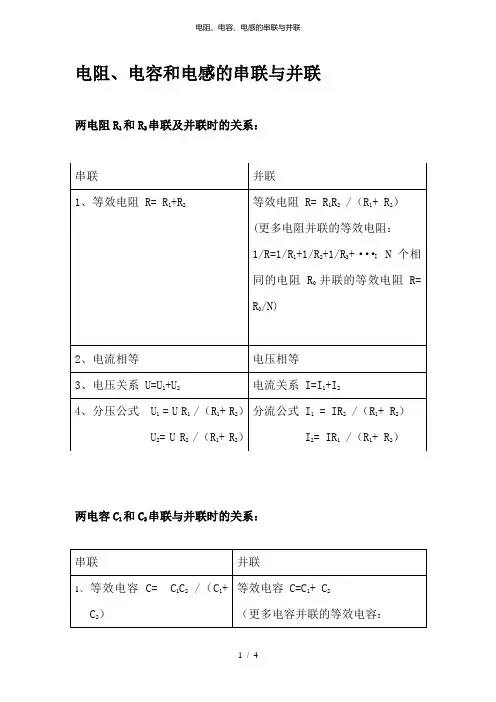
电阻、电容和电感的串联与并联两电阻R1和R2串联及并联时的关系：两电容C1和C2串联与并联时的关系：无互感的线圈的串联与并联：两线圈串联：L= L 1+ L 2两线圈并联：L= L 1L 2/（L 1+ L 2）有互感的线圈的串联与并联：有互感两线圈顺串（异名端相接）：L （顺） = L 1+ L 2+2M 有互感两线圈反串（同名端相接）：L （反）= L 1+ L 2 -2M L （顺）-L （反） =4M ， M= [L （顺） -L （反）]/4有互感两线圈并联：L （并）=（L 1 L 2-M 2）/（L 1+ L 22M ）（更多电容串联的等效电容： 1/C=1/C 1+1/C 2+1/C 3+···； N 个相同的电容C 0串联的等效电容C= C 0/N) C=C 1+C 2+C 3+···；N 个相同的电容C 0串联的等效电容C= NC 0）2、电流相等 电压相等3、电压关系 U=U 1+U 2电流关系 I=I 1+I 2 （对交流电而言） 4、分压公式 U 1 = U C 2/（C 1+ C 2）U 2= U C 1 /（C 1+ C 2）分流公式 I 1 = IC 1 /（C 1+ C 2）（对交流电而言）I 2= IC 2 /（C 1+ C 2）（对交流电而言）（2M项前的符号：同名端接在同一侧时取-，异名端接在同一侧时取+。

）（L1 L2-M2）≧0，M≤LL21M（最大）=LL21互感的耦合系数：K= M/LL21电桥直流电桥由4个电阻首尾相接构成菱形，共4端，A、C端接电源，B、D端之间为零位检测（检流计）。

上下两臂平衡时，B、D端电压差为零，检流计电流读数为0。

电桥平衡的条件：R1/R3= R2/R N（或R1R N= R2R3）R1、R2、和R3为阻值已知标准电阻，被测电阻R N = R2R3 / R1将4个电阻换为阻抗，即得到交流电桥。

869 电路（含40%电力系统基础）复习大纲--------------------------------------------------------------------------------869电路（含40%电力系统基础）复习大纲注：本考纲适用范围080802第一部分：电路教材：《电路》第五版邱关源，罗先觉高等教育出版社1、基本电路元件电压、电流特性和基尔霍夫定律；2、等效变换条件，各种类型的等效电路；对称电路；3、电路方程法和电路定理（叠加、替代、戴维南、最大功率）；4、一阶电路的三要素法和阶跃响应；5、正弦稳态电路电压、电流和功率的计算；谐振；6、耦合电感元件特性及去耦等效电路；理想变压器特性方程和阻抗变换；7、对称三相电路的计算。

第一章电路模型和电路定律§1-1 电路和电路模型§1-2 电流和电压的参考方向§1-3 电功率和能量§1-4 电路元件§1-5 电阻元件§1-6 电压源和电流源§1-7 受控电源§1-8 基尔霍夫定律第二章电阻电路的等效变换§2-1 引言§2-2 电路的等效变换§2-3 电阻的串联和并联§2-4 电阻的Y形连接和△形连接的等效变换§2-5 电压源、电流源的串联和并联§2-6 实际电源的两种模型及其等效变换§2-7 输入电阻第三章电阻电路的一般分析§3-3 支路电流法§3-4 网孔电流法§3-5 回路电流法§3-6 结点电压法第四章电路定理§4-1 叠加定理§4-2 替代定理§4-3 戴维宁定理和诺顿定理§4-4 最大功率传输定理第六章储能元件§6-1 电容元件§6-2 电感元件§6-3 电容、电感元件的串联与并联第七章一阶电路和二阶电路的时域分析§7-1 动态电路的方程及其初始条件§7-2 一阶电路的零输入响应§7-3 一阶电路的零状态响应§7-4 一阶电路的全响应§7-7 一阶电路的阶跃响应第八章相量法§8-1 复数§8-2 正弦量§8-3 相量法的基础§8-4 电路定律的相量形式第九章正弦稳态电路的分析§9-1 阻抗和导纳§9-3 正弦稳态电路的分析§9-4 正弦稳态电路的功率§9-5 复功率§9-6 最大功率传输第十章含有耦合电感的电路§10-1 互感§10-2 含有耦合电感的电路§10-5 理想变压器第十一章电路的频率响应§11-1 网络函数§11-2 RLC串联电路的谐振§11-4 RLC并联谐振电路第十二章三相电路§12-1 三相电路§12-2 线电压(电流)和相电压(电流)的关系§12-3 对称三相电路的计算§12-5 三相电路的功率第二部分：40%电力系统基础参考书目：（1）电路系统分析理论，刘天琪、邱晓燕，北京：科学出版社（2）电力系统分析（上下册，第三版），何仰赞等，华中科技大学出版社1、电力系统概述涉及的基本概念，如：电力系统的基本组成及其特性；电力系统运行特点和基本要求；额定电压和额定频率；负荷和负荷曲线等；2、电力系统元件参数的计算及元件模型和网络模型的建立；3、电力系统稳态运行的电压和功率分布计算，电力网的功率损耗和电能损耗；4、电力系统有功功率平衡和频率调整；5、电力系统无功功率平衡和电压调整；6、电力系统有功功率的最优分配；7、电力系统三相短路的分析计算；8、电力系统简单不对称故障的分析计算；9、电力系统稳定性分析原理和方法。

交流电路电感电容串联和并联的计算摘要：一、理解交流电路中电感、电容、电阻的基本概念及性质二、掌握电感、电容、电阻串联和并联的计算方法三、应用实例分析正文：在交流电路中，电感、电容和电阻的串联和并联计算是电气工程中常见的任务。

以下将详细介绍如何计算这两种情况。

一、电感、电容、电阻串联计算1.分别求出电感、电容、电阻的感抗、容抗和阻抗。

2.计算串联电路的总阻抗，使用欧姆定律计算电压、电流和阻抗的关系。

实例：设电感XL=10Ω，电容XC=10Ω，电阻R=10Ω，电压U=100V，则总阻抗Z=√(RXL+RXC)=√(100×10+100×10)=100Ω电流I=U/Z=100V/100Ω=1A二、电感、电容、电阻并联计算1.计算电感、电容、电阻的等效阻抗，分别用欧姆定律计算电压、电流和阻抗的关系。

2.计算并联电路的总电流，根据电流分配定律计算各元件的电流。

实例：设电感XL=10Ω，电容XC=10Ω，电阻R=10Ω，电压U=100V，则电感的等效阻抗XL"=XL/(1+jωC)=10/(1+j×10×10)=10Ω电容的等效阻抗XC"=1/(jωC)=1/(j×10×10)=1/100Ω并联电路的总阻抗Z"=1/(1/XL"+1/XC")=1/(1/10Ω+1/100Ω)=100Ω总电流I"=U/Z"=100V/100Ω=1A电阻的电流I1=I"×R/Z"=1A×10Ω/100Ω=0.1A电感的电流I2=I"×XL"/Z"=1A×10Ω/100Ω=0.1A电容的电流I3=I"×XC"/Z"=1A×1/100Ω/100Ω=0.01A通过以上计算，我们可以看出在交流电路中，电感、电容、电阻的串联和并联计算方法具有一定的规律。

电感的串联和并联公式推导
电感的串联和并联公式可以通过电磁感应定律和基本电路理论推导得出。

首先我们来看电感的串联公式推导。

假设有两个电感分别为L1和L2的电感器串联连接在电路中。

根据基本电路理论，串联电感器的总电感可以表示为两个电感的总和，即L = L1 + L2。

这是因为串联连接意味着电流只能依次通过每个电感器，因此总电感等于各个电感的电感之和。

现在我们来看电感的并联公式推导。

假设有两个电感分别为L1和L2的电感器并联连接在电路中。

根据基本电路理论，并联电感器的总电感可以表示为它们的倒数之和的倒数，即1/L = 1/L1 + 1/L2。

这是因为并联连接意味着电流可以选择通过其中任何一个电感器，因此总电感等于各个电感的倒数之和的倒数。

通过上述推导，我们得到了电感的串联和并联公式。

串联电感的总电感为各个电感的电感之和，而并联电感的总电感为它们的倒数之和的倒数。

这些公式在电路设计和分析中起着重要的作用，能
够帮助工程师们有效地计算和预测电路中的电感数值。

同时，这些公式也是基础电路理论中重要的内容，对于理解电路中电感器的相互作用和影响具有重要意义。

电路基础原理电容与电感的串联与并联电路基础原理：电容与电感的串联与并联在学习电路基础原理时，电容与电感是两个非常重要的概念。

它们在电路中起着不可或缺的作用。

本文将探讨电容与电感的串联与并联，以及它们在实际电路中的应用。

1. 电容与电感的基本概念首先，我们来简单了解一下电容与电感的基本概念。

电容是指一种储存电荷的装置，它由两个导体板和介质组成。

当电容器上施加电压时，正负电荷将在导体板之间积累，形成电荷分布。

而电感则是由线圈或电线圈制成的装置，当电流通过线圈时，会产生磁场，并储存能量。

2. 串联与并联的定义与特点在电路中，串联与并联是两种常见的连接方式。

串联是指将电容或电感依次连接在一起，形成一个电路路径。

而并联则是将电容或电感同时连接在一起，形成多个并行的电路路径。

串联与并联的主要特点如下：- 串联电路的总电容或总电感等于各个电容或电感的总和；- 串联电路的总电压等于各个电容或电感电压之和；- 并联电路的总电容或总电感等于各个电容或电感的倒数之和；- 并联电路的总电压等于各个电容或电感电压的平均值。

3. 电容与电感的串联与并联接下来，我们将重点讨论电容与电感的串联与并联。

3.1 电容的串联与并联首先，我们先来看电容的串联与并联。

当两个电容C1和C2串联时，它们的总电容C串等于它们的倒数之和：1/C串 = 1/C1 + 1/C2。

而当两个电容C1和C2并联时，它们的总电容C并等于它们的总和：C并 =C1 + C2。

实际应用中，电容的串联与并联可以实现不同的电路功能。

比如，在交流电路中，串联电容可以形成低通滤波器，将高频信号滤除，只保留低频信号。

而并联电容则可以形成高通滤波器，将低频信号滤除，只保留高频信号。

3.2 电感的串联与并联接着，我们再来看电感的串联与并联。

当两个电感L1和L2串联时，它们的总电感L串等于它们的总和：L串 = L1 + L2。

而当两个电感L1和L2并联时，它们的总电感L并等于它们的倒数之和：1/L并 = 1/L1+ 1/L2。

交流电路基础电阻电感和电容的串并联交流电路基础：电阻、电感和电容的串联和并联在交流电路中，电阻、电感和电容是三种基本的元件。

它们在电路中起着不同的作用，能够对电流和电压产生不同的影响。

本文将介绍电阻、电感和电容的基本概念，以及它们在串联和并联电路中的运用。

一、电阻的基本概念电阻是电路中最常见的元件之一，它用来限制电流的流动。

电阻的单位是欧姆（Ω），通常用符号R表示。

电阻的大小与材料的导电性质和尺寸相关，导体材料电阻小，绝缘材料电阻大。

在交流电路中，电阻对电流的影响主要表现为阻碍电流通过，使电流的大小与电压成正比，符合欧姆定律。

在电阻的两端，存在电压降，这个电压降与电阻值和电流大小有关。

二、电感的基本概念电感是电路中另一个重要的元件，它起着储存和释放能量的作用。

电感的单位是亨利（H），通常用符号L表示。

电感的大小与线圈的匝数、线圈的长度和截面积有关。

在交流电路中，电感对电流的影响主要表现为抵抗电流的变化，使电流的大小与电压成反比。

当电流变化时，电感中产生感应电动势，抵抗电流的变化，这称为自感现象。

三、电容的基本概念电容是电路中另一种重要的元件，它能够储存电荷。

电容的单位是法拉（F），通常用符号C表示。

电容的大小与电容器的电极面积、电极间距和介质介电常数有关。

在交流电路中，电容对电流的影响主要表现为储存和释放电荷。

当电流变化时，电容器会储存和释放电荷，使电流的大小与电压成正比。

电容器具有频率依赖性，对不同频率的信号有不同的阻抗。

四、电阻、电感和电容的串联和并联在实际的交流电路中，电阻、电感和电容的串联和并联是非常常见的情况。

串联是指将多个元件连接在一起，形成一个独立的电路路径；并联是指将多个元件同时连接到同一个节点上。

1. 电阻的串联和并联电阻的串联是指将多个电阻连接在一起，电流在各个电阻之间依次流动。

电阻的串联时，总电阻等于各个电阻之和，电压分配根据电阻值比例进行。

电阻的并联是指将多个电阻同时连接到同一个节点上，电流在各个电阻之间分流。

串联并联比例-回复串联并联比例是电路中常用的概念，它描述了电路中电阻、电容、电感等元件的连接方式。

本文将逐步解释串联与并联的概念、计算方法及其应用。

1. 串联和并联的概念在电路中，串联是指将元件依次连接在一起，形成一个电流路径，而并联则是将元件连接在一起，形成一个电压路径。

串联和并联连接方式主要应用于电阻、电容和电感等元件。

2. 串联的计算方法当电阻（或电容、电感）元件串联时，它们共享相同的电流，而电压在元件间分配。

假设有n个串联的元件，它们的电阻（或电容、电感）分别为R1，R2，...，Rn，则总电阻（或总电容、总电感）为它们的直接相加：总电阻（或总电容、总电感）= R1 + R2 + ... + Rn3. 并联的计算方法当电阻（或电容、电感）元件并联时，它们共享相同的电压，而电流在元件间分配。

假设有n个并联的元件，它们的电阻（或电容、电感）分别为R1，R2，...，Rn，则总电阻（或总电容、总电感）的倒数为它们的直接相加的倒数：1/总电阻（或总电容、总电感）= 1/R1 + 1/R2 + ... + 1/Rn4. 应用举例（1）电阻的串联和并联：假设有两个电阻R1和R2，串联连接时，总电阻为R1 + R2；并联连接时，总电阻为1/(1/R1 + 1/R2)。

举例：如果R1=2欧姆，R2=3欧姆，那么串联连接时总电阻为5欧姆，而并联连接时总电阻为1/(1/2 + 1/3) = 1.2欧姆。

（2）电容的串联和并联：假设有两个电容C1和C2，串联连接时，总电容为C1 + C2；并联连接时，总电容为C1 + C2。

举例：如果C1=2微法，C2=3微法，那么串联连接时总电容为5微法，而并联连接时总电容为2 + 3 = 5微法。

（3）电感的串联和并联：假设有两个电感L1和L2，串联连接时，总电感为L1 + L2；并联连接时，总电感为1/(1/L1 + 1/L2)。

举例：如果L1=2亨利，L2=3亨利，那么串联连接时总电感为5亨利，而并联连接时总电感为1/(1/2 + 1/3) ≈1.2亨利。

判断串联和并联的方法
电路中的串联和并联是两个常见的电路连接方式，掌握它们的判
断方法对于电路设计和维护都有很大的帮助。

本文将会详细介绍如何
判断电路中的串联和并联。

首先，我们需要明确串联和并联的定义。

串联是指电路中多个电阻、电容或电感器依次连接在一起，电流只能依次经过其中的每一个
器件才能流回电源。

而并联则是指电路中多个电阻、电容或电感器同
时连接在一起，电流可以自由地分流流过其中的每一个器件，最终再
汇集到电源处。

接下来分别介绍串联和并联的判断方法：
串联判断方法：
1. 将电路图表达出来，找到电阻、电容或电感器等电路元件；
2. 确认它们的连接方式是依次串联在一起，即是否是接到一起
的两个元件只有一处连接；
3. 如果是，则认为它们是串联的。

并联判断方法：
1. 将电路图表达出来，找到所有与电源接触的起始元件；
2. 检查这些元件是否都与一个集合点相连（集合点可以是电源
的另一个空位，或者是连接电源的电线）；
3. 如果是，则认为它们是并联的。

需要注意的是，有时候并联关系并不显而易见，此时可以采取计
算电路参数的方法进行判断。

比如，对于电阻的并联，可以通过计算
其总电阻值是否比单个电阻值小来判断，而对于电容和电感器的并联，则需要计算其总电容值和总电感值是否比单个电容或电感器的值大来
判断。

最后，需要强调的是，正确判断电路中的串联和并联是电路设计
和维护的关键，只有掌握了正确的判断方法，才能保证电路的性能和
稳定性。