七年级数学上册沪科版习题讲评课件：难点探究专题：有理数中的规律探究(选做)(共15张PPT)

可编辑修改精选全文完整版2019年沪科版7（上）有理数——数轴、相反数、绝对值【要点梳理】要点一、正数与负数像+3、+1.5、12+、+584等大于0的数，叫做正数；像－3、－1.5、12-、－584等在正数前面加“－”号的数，叫做负数．要点诠释：（1）一个数前面的“+”“-”是这个数的性质符号，“+”常省略，但“-”不能省略. （2）用正数和负数表示具有相反意义的量时，哪种为正可任意选择，但习惯把“前进、上升”等规定为正，而把“后退、下降”等规定为负．（3）0既不是正数也不是负数，它是正数和负数的“分水岭”．要点二、有理数的分类（1）按定义分类：（2）按性质符号分类：要点诠释：（1）有理数都可以写成分数的形式，整数也可以看作是分母为1的数.（2）分数与有限小数、无限循环小数可以互化，所以有限小数和无限循环小数可看作分数，但无限不循环小数不是分数，例如π．（3）正数和零统称为非负数；负数和零统称为非正数；正整数、0、负整数统称整数．【典型例题】1．下面说法中正确的是( )．A．非负数一定是正数．B．有最小的正整数，有最小的正有理数．C．a-一定是负数． D ．正整数和正分数统称正有理数．2．请把下列各数填入它所属于的集合的大括号里.1, 0.0708, -700, -3.88, 0, 3.14159265,723-，.正整数集合:{ …}，负整数集合:{ …}，整数集合:{ …}，正分数集合:{ …}，负分数集合:{ …}，分数集合:{ …}，非负数集合：{ …}，非正数集合：{ …}.【要点梳理】要点一、数轴1.定义：规定了原点、正方向和单位长度的直线叫做数轴.要点诠释：（1）原点、正方向和单位长度是数轴的三要素，三者缺一不可.（2）长度单位与单位长度是不同的，单位长度是根据需要选取的代表“1”的线段，而长度单位是为度量线段的长度而制定的单位．有km、m、dm、cm等．（3）原点、正方向、单位长度可以根据实际灵活选定，但一经选定就不能改动．2. 数轴与有理数的关系：任何一个有理数都可以用数轴上的点来表示，但数轴上的点不都表示有理数，还可以表示其他数，比如 .要点诠释：（1）一般地，数轴上原点右边的点表示正数，左边的点表示负数；反过来也对，即正数用数轴上原点右边的点表示，负数用原点左边的点表示，零用原点表示.（2）在数轴上表示的两个数，右边的数总比左边的数大.要点二、相反数1.定义：只有符号不同的两个数互为相反数，0的相反数是0.要点诠释：（1）“只”字是说仅仅是符号不同，其它部分完全相同；（2）“0的相反数是0”是相反数定义的一部分，不能漏掉；（3）相反数是成对出现的，单独一个数不能说是相反数；（4）求一个数的相反数，只要在它的前面添上“-”号即可.2.性质：（1）互为相反数的两数的点分别位于原点的两旁，且与原点的距离相等（这两个点关于原点对称）.（2）互为相反数的两数和为0.要点三、多重符号的化简多重符号的化简，由数字前面“-”号的个数来确定，若有偶数个时，化简结果为正，如-{-[-(-4)]}=4 ；若有奇数个时，化简结果为负，如-{+[-(-4)]}=-4 .要点诠释：（1）在一个数的前面添上一个“＋”，仍然与原数相同，如＋5＝5，＋（－5）＝－5. （2）在一个数的前面添上一个“－”，就成为原数的相反数.如－（－3）就是－3的相反数，因此，－（－3）＝3.【典型例题】1.数轴上点A、B的位置如图所示，若点B关于点A的对称点为C，则点C表示的数为2.（1）如果a ＝－13，那么－a ＝______；(2) 如果 －a ＝－5.4，那么a ＝______；(3) 如果－x ＝－6，那么x ＝______；(4) －x ＝9，那么x ＝______.3. －4的倒数的相反数是（ ）A ．－4B ．4C ．－D ． 4.填空：(1) －(－2.5)的相反数是 ；(2) 是-100的相反数；(3) 155-是 的相反数； (4) 的相反数是-1.1；(5)8.2和 互为相反数；（6）a 和 互为相反数.（7）______的相反数比它本身大， ______的相反数等于它本身．5. 已知21m -与172m -互为相反数，求m 的值.6．化简：（1）﹣{+[﹣（+3）]}； （2）﹣{﹣[﹣（﹣|﹣3|）}．【要点梳理】要点一、绝对值1.定义：一般地，数轴上表示数a 的点与原点的距离叫做数a 的绝对值，记作|a|. 要点诠释：（1）绝对值的代数意义：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．即对于任何有理数a 都有：（2）绝对值的几何意义：一个数的绝对值就是表示这个数的点到原点的距离，离原点的距离越远，绝对值越大；离原点的距离越近，绝对值越小．（3）一个有理数是由符号和绝对值两个方面来确定的．2.性质：绝对值具有非负性，即任何一个数的绝对值总是正数或0．要点二、有理数的大小比较41411.数轴法：在数轴上表示出这两个有理数，左边的数总比右边的数小. 如：a 与b 在数轴上的位置如图所示，则a ＜b ．2.法则比较法： 两个数比较大小，按数的性质符号分类，情况如下： 两数同号 同为正号：绝对值大的数大 同为负号：绝对值大的反而小 两数异号正数大于负数 －数为0 正数与0：正数大于0负数与0：负数小于0要点诠释：利用绝对值比较两个负数的大小的步骤：（1）分别计算两数的绝对值；（2） 比较绝对值的大小；（3）判定两数的大小．3. 作差法：设a 、b 为任意数，若a-b ＞0，则a ＞b ；若a-b ＝0，则a ＝b ；若a-b ＜0，a ＜b ；反之成立．4. 求商法：设a 、b 为任意正数，若1a b >，则a b >；若1a b =，则a b =；若1a b<，则a b <；反之也成立． 若a 、b 为任意负数，则与上述结论相反．5. 倒数比较法：如果两个数都大于0，那么倒数大的反而小.【典型例题】1．计算：（1）145-- （2）|-4|+|3|+|0| （3）-|+(-8)|2．若|a ﹣1|=1﹣a ，则a 的取值范围是（ ）A. a ≥1B. a ≤1C. a ＜1D. a ＞13. 若a ＞3，则|6﹣2a|= （用含a 的代数式表示）．4. 如果数轴上的点A 到原点的距离是6，则点A 表示的数为 ．如果｜x －2｜＝1，那么x ＝ ；如果｜x ｜＞3，那么x 的范围是 ．5.化简||||x x x +的结果是 . 6. 比大小：（1） －0.3 31- （2）⎪⎭⎫ ⎝⎛--91 101--．7. 若m ＞0，n ＜0，且|m|＞|n|，用“＞”把m ，-m ，n ，-n 连接起来．8. 已知有理数a ，b ，c 在数轴上对应的点的位置如图所示：化简：.9. 已知|a －2|＋|b －3|＝0，求a －b 的值.10. 已知b 为正整数，且a 、b 满足，求的值．【练习】1、下列说法中，错误的个数有（ ）.①绝对值是它本身的数有两个：0和1②一个有理数的绝对值必为正数③0.5的倒数的相反数的绝对值是2④任何有理数的绝对值都不是负数A 、1个B 、2个C 、3个D 、4个2、在－(－2.5)，3，0，－5，－0.25，中正整数有( )．A ．1个B ．2个C ．3个D ．4个3、在数轴上表示－2的点离开原点的距离等于( )．A ．2B ．－2C ．±2D ．44、有理数a 在数轴上的位置如图所示：化简1+a 的结果是（ ）12-A 、b a +B 、1+-aC 、1-aD 、1--a5、若两个有理数a 、b 在数轴上表示的点如图所示，则下列各式中正确的是( )．A ．a ＞bB ．|a |＞|b |C ．-a ＜-bD ．-a ＜|b |6、若a ，b 互为相反数，c ，d 互为倒数，x 的绝对值等于2，则x 2＋5(a ＋b )－8c d ＝______. 7、若实数a ，b 满足|3a －1|＋(b －2)2＝0，则a b ＝______.8、（1）当x ＝______时，|x －3|＋1有最小值为_______；（2）当x ＝______时，2－|x －1|有最大值为________.9、已知|a|＝4，|b|＝2，且ab ＜0，则a ＋b ＝_________.10、若|m －n|＝n －m ，且|m|＝4，|n|＝3，则m ＋n ＝_________.11、若x =8-，则=x ；若8-=-x ，则x = .12、若a a -=-，则=a .13、13=-x ，则=x .14、如果a ＜0，b ＞0且|a|＜|b|，则a ＋b 0.15、已知|x ＋2|＋(2y －3)²＝0，求x ＋2y 的值.【思考题】求的最小值．。

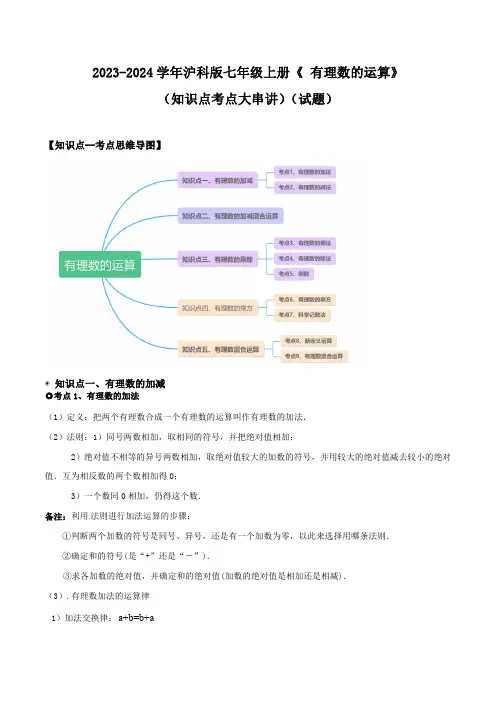
2023-2024学年沪科版七年级上册《有理数的运算》（知识点考点大串讲）（试题）【知识点--考点思维导图】◉知识点一、有理数的加减◎考点1、有理数的加法（1）定义：把两个有理数合成一个有理数的运算叫作有理数的加法．（2）法则：1）同号两数相加，取相同的符号，并把绝对值相加；2）绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值．互为相反数的两个数相加得0；3）一个数同0相加，仍得这个数．备注：利用法则进行加法运算的步骤：①判断两个加数的符号是同号、异号，还是有一个加数为零，以此来选择用哪条法则．②确定和的符号(是“+”还是“－”)．③求各加数的绝对值，并确定和的绝对值(加数的绝对值是相加还是相减)．（3）.有理数加法的运算律1）加法交换律：a+b=b+a2）加法结合律：(a+b)+c=a+(b+c)例1．（2021·湖南中考真题）计算-1+3的结果是（）A ．2B ．-2C ．4D ．-4练习1．（2021·北京九年级二模）有理数a ，b 在数轴上的对应点的位置如图所示，则结论正确的是（）A ．4a <-B ．0ab >C ．0a b +>D ．||||a b >练习2．（2021·湖北七年级期末）2020年12月30日是“二九”的第一天，这天樊城区凌晨的气温是-6℃，中午上升了7℃，则中午的气温是（）A ．-13℃B ．13℃C ．1℃D ．-1℃练习3．（2019·全国七年级课时练习）下列各式中正确使用了加法运算律的是()A ．(＋5)＋(－7)＋(－5)＝(＋5)＋(－5)＋(－7)B ．1()2-＋1()3+＝1(3-＋1()2+C ．(－1)＋(－2)＋(＋3)＝(－3)＋(＋l)＋(－2)D ．(－1.5)＋(＋2.5)＝(－2.5)＋(＋1.5)◎考点2、有理数的减法（1）定义：已知两个数的和与其中一个加数，求另一个加数的运算，叫做减法，例如：(-5)+?＝7，求？，减法是加法的逆运算．备注：1）任意两个数都可以进行减法运算．2）几个有理数相减，差仍为有理数，差由两部分组成：①性质符号；②数字即数的绝对值．（2）法则：减去一个数，等于加这个数的相反数，即有：()a b a b -=+-例1．（2021·湖北九年级一模）数轴上表示2-的点到原点的距离是（）A ．2B ．2-C ．12D ．12-练习1．（2021·四川德阳市·九年级二模）计算12--=（）A ．1-B ．1C ．3-D ．3练习2．（2021·广东佛山市·九年级一模）数轴上表示﹣6和4的点分别是A 和B ，则线段AB 的长度是（）A ．﹣2B ．2C ．﹣10D ．10练习3．（2020·武汉市六中位育中学七年级月考）下列运算正确的是（）A．11(3)(422---=B．11((2)12÷-⨯-=C．0－（－6）＝6D．（－3）÷（－6）＝2◉知识点二、有理数的加减混合运算例1．（2021·河北中考真题）能与3645⎛⎫--⎪⎝⎭相加得0的是（）A．3645--B．6354+C．6354-+D．3645-+练习1．（2019·全国）计算5372688⎛⎫-+- ⎪⎝⎭的值为（）A．23-B．5212-C．1324-D．111424-练习2．（2021·西安建筑科技大学附属中学七年级期末）A为数轴上表示3的点，将点A沿数轴向左平移7个单位到点B，再由B向右平移6个单位到点C，则点C表示的数是（）A．0B．1C．2D．3练习3．（2021·河南七年级期末）如图，乐乐将﹣3，﹣2，﹣1，0，1，2，3，4，5分别填入九个空格内，使每行、每列、每条对角线上的三个数之和相等，现在a、b、c分别标上其中的一个数，则－2（3a－2b－c）的值为（）A．－12B．12C．4D．20知识点三：有理数的乘除◎考点3、有理数的乘法（1）.有理数的乘法法则：①两数相乘，同号得正，异号得负，并把绝对值相乘；②任何数同0相乘，都得0．备注：①不为0的两数相乘，先确定符号，再把绝对值相乘．②当因数中有负号时，必须用括号括起来，如-2与-3的乘积，应列为(-2)×(-3)，不应该写成-2×-3．（2）有理数的乘法运算律：①乘法交换律：两个数相乘，交换因数的位置，积相等，即：ab=ba.②乘法结合律：三个数相乘，先把前两个数相乘，或者先把后两个数相乘，积相等．即：abc=(ab)c=a(bc)．③乘法分配律：一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加．即：a(b+c)=ab+ac ．备注：①在交换因数的位置时，要连同符号一起交换．②乘法运算律可推广为：三个以上的有理数相乘，可以任意交换因数的位置，或者把其中的几个因数相乘．如abcd=d(ac)b ．一个数同几个数的和相乘，等于把这个数分别同这几个数相乘，再把积相加．如a(b+c+d)=ab+ac+ad ．③运用运算律的目的是“简化运算”，有时，根据需要可以把运算律“顺用”，也可以把运算律“逆用”．例1．（2021·天津九年级三模）计算1(9)3-⨯的结果是（）A ．3B ．27C ．27-D ．3-练习1．四个各不相等的整数a b c d 、、、，满足9abcd =，则+++a b c d 的值为（）A ．0B ．4C ．10D ．无法确定练习2．（2020·重庆文德中学校七年级期中）一部手机原价2400元，先提价18，再降价18出售．现价和原价相比，结论是（）A ．现价高B ．原价高C ．价格相同D ．无法比较练习3．（2020·重庆一中七年级月考）已知数a ，b 在数轴上表示的点的位置如图所示，则下列结论正确的是（）A ．a+b ＞0B ．a ﹣b ＞0C ．﹣a ＞﹣b ＞aD ．ab ＞0◎考点4、有理数的除法有理数除法法则：法则一：除以一个不等于0的数，等于乘这个数的倒数，即1(0)a b ab b÷=≠.法则二：两数相除，同号得正，异号得负，并把绝对值相除．0除以任何一个不等于0的数，都得0.备注：①一般在不能整除的情况下应用法则一，在能整除时应用法则二方便些．②因为0没有倒数，所以0不能当除数．③法则二与有理数乘法法则相似，两数相除时先确定商的符号，再确定商的绝对值．例1．（2021·温州外国语学校九年级三模）计算：()62÷-的结果是（）A ．3-B ．3C ．4-D ．4练习1．（2021·山东九年级期中）下列各式中，计算结果为－4的是（）A ．－（－4）B ．－|－4|C ．（－2）2D ．8÷（－12）练习2．下列各式中计算正确的有（）①(24)(8)3-÷-=-；②(8)(2.5)20-⨯-=-；③44155⎛⎫⎛⎫-÷-= ⎪ ⎪⎝⎭⎝⎭；④33(1.25)34⎛⎫-÷-=- ⎪⎝⎭A ．1个B ．2个C ．3个D ．4个练习3．（2020·全国课时练习）格兰仕微波炉降价25%后，每台售价a 元，则这种微波炉的原价为每台（）A ．0.75a 元B ．0.25a 元C ．0.25a 元D ．0.75a 元◎考点5：倒数（1）倒数的意义：乘积是1的两个数互为倒数．备注：①“互为倒数”的两个数是互相依存的.如-2的倒数是12-，-2和12-是互相依存的；②0和任何数相乘都不等于1，因此0没有倒数；③倒数的结果必须化成最简形式，使分母中不含小数和分数；④互为倒数的两个数必定同号(同为正数或同为负数)．例1．（2021·湖北九年级二模）212⎛⎫-- ⎪⎝⎭的倒数是（）A ．－4B ．14-C ．14D ．4练习1．（2021·河南九年级三模）25的倒数是（）A ．0.4B ．2.5C ．4D ．25-练习2．（2021·江苏九年级一模）-3的倒数为（）A ．13-B ．13C ．-3D ．3练习3．（2021·黑龙江九年级三模）916-的倒数是（）A ．916B ．916-C ．169D ．169-◉知识点四、有理数的乘方◎考点6：有理数的乘方（1）乘方的概念求n 个相同因数的积的运算，叫做乘方，乘方的结果叫做幂。

小学七年级数学上册难点探究专题：有理数中的规律探究（选做）——从特殊到一般，探寻多方规律◆类型一 一列数中的规律1.找规律，并按规律填上第5个数：－32，54，－78，916， . 2.（济宁中考）按一定规律排列的一列数：12，1，1， ，911，1113，1317，…，请你仔细观察，按照此规律方框内的数字应为 Ｗ.3.（随州月考）给定一列按规律排列的数：12，25，310，417，…，则这列数的第6个数是（ ）A.637B.635C.531D.739◆类型二 计算中的规律一、四则运算中的规律4.（河北模拟）某数学活动小组的20位同学站成一列做报数游戏，规则是：从前面第一位同学开始，每位同学依自己顺序数的倒数加1，第1位同学报⎝⎛⎭⎫11＋1，第2位同学报⎝⎛⎭⎫12＋1，第3位同学报⎝⎛⎭⎫13＋1，这样得到的前20个数的积为 . 5.（无锡校级月考）若“！”是一种数学运算符号，并且1！＝1，2！＝2×1＝2，3！＝3×2×1＝6，4！＝4×3×2×1＝24，…，则5！＝ ＝ ，100！98！＝ .6.（咸阳校级月考）计算：1－3＋5－7＋9－11＋…＋97－99.二、乘方运算中的规律7.（深圳模拟）观察下列算式：21＝2，22＝4，23＝8，24＝16，25＝32，26＝64，27＝128，28＝256，用你所发现的规律得出22016的末位数字是 .8.（孝感中考）观察下列等式：1＝12，1＋3＝22，1＋3＋5＝32，1＋3＋5＋7＝42，…，则1＋3＋5＋7＋…＋2015＝ .三、图形中与数的计算的有关规律9.（泉州中考）找出下列各图形中数的规律，依此，a 的值为 .10.（北京中考）百子回归图是由1，2，3，…，100无重复排列而成的正方形数表，它是一部数化的澳门简史，如：中央四位“19 99 12 20”表示澳门回归日期，最后一行中间两位“23 50”表示澳门面积，…，同时它也是十阶幻方，即其每行10个数之和，每列10个数之和，每条对角线10个数之和均相等，则这个和为.◆类型三 数轴中的规律11.（石家庄模拟）如图，在数轴上点A 表示1，现将点A 沿数轴做如下移动：第一次点A 向左移动3个单位长度到达点A 1，第二次将点A 1向右移动6个单位长度到达点A 2，第三次将点A 2向左移动9个单位长度到达点A 3，按照这种移动规律，则点A 13，A 14之间的距离是.参考答案与解析1．－1132 2.293.A 4．21 解析：⎝⎛⎭⎫11＋1⎝⎛⎭⎫12＋1⎝⎛⎭⎫13＋1…⎝⎛⎭⎫120＋1＝2×32×43×…×2120＝21. 5．5×4×3×2×1 120 99006．解：1－3＋5－7＋9－11＋…＋97－99＝(1－3)＋(5－7)＋(9－11)＋…＋(97－99)＝－2×502＝－50. 7．6 8.100829．226 解析：根据题意得出规律a ＝15×16－14＝226.10．505 解析：1～100的总和为（1＋100）×1002＝5050，一共有10行，且每行10个数之和均相等，所以每行10个数之和为5050÷10＝505.11．42 解析：因为第一次点A 向左移动3个单位长度至点A 1，则A 1表示的数为1－3＝－2，第2次从点A1向右移动6个单位长度至点A2，则A2表示的数为－2＋6＝4，所以A1A2＝4－(－2)＝6＝2×3.因为第3次从点A2向左移动9个单位长度至点A3，则A3表示的数为4－9＝－5，所以A2A3＝4－(－5)＝9＝3×3.因为第4次从点A3向右移动12个单位长度至点A4，则A4表示的数为－5＋12＝7，所以A3A4＝7－(－5)＝12＝4×3，…，所以A13A14＝(13＋1)×3＝42.。