第三章 贝叶斯估计
- 格式:pdf
- 大小:604.09 KB
- 文档页数:9


贝叶斯估计法贝叶斯估计法是统计学中常用的一种方法,它是基于贝叶斯定理的推论而来的,可以用于估计一个未知参数的值。
其核心思想是先假设一个先验分布,然后根据已知的样本数据和假设的先验分布,通过贝叶斯定理计算后验分布,最终得到对未知参数的估计。
在使用贝叶斯估计法时,我们需要首先定义以下概念:先验分布:指在未观测到数据前,对参数的概率分布的估计。
常见的先验分布有均匀分布、正态分布等。
似然函数:指在已知参数下,给定样本的条件下所有样本出现的概率密度函数,是样本数据给出参数信息的度量。
后验分布:指在已知数据后,对参数的概率分布的估计。
它是在先验分布和似然函数的基础上,通过贝叶斯公式计算得到的。
在实际数据分析中,我们需要对先验分布做出适当的假设,通过先验分布的假设来反映我们对参数的先验认知。
然后根据已知数据和似然函数,计算出参数的后验分布,并用其来估计未知参数。
贝叶斯估计法与点估计法的区别贝叶斯估计法与点估计法是统计学中常用的两种估计方法,它们之间的区别在于:点估计法:通常是求得一个能代表总体参数未知数的值作为估计,例如样本的平均数、中位数等。
点估计法估计参数时,只考虑来自样本的信息。
贝叶斯估计法:将样本和先验信息结合在一起,通过后验分布对未知参数进行估计。
在贝叶斯估计法中,我们对参数的先验知识和数据信息进行综合考虑,最终得到一个更加准确的估计值。
因此,相比于点估计法,贝叶斯估计法更加具有弹性,它不仅可以考虑已知数据的影响,还可以利用专家知识或先验信息来修正估计值,从而提高估计的准确性。
为了说明贝叶斯估计法的实际应用,我们以估计某测试设备的故障率为例进行说明。
假设我们已经收集了100个设备的测试数据,其中有5个出现故障。
我们希望用贝叶斯估计法来估计设备的故障率。
首先,我们需要对故障率做出一个先验分布的估计。
由于我们缺乏关于该设备故障率的信息,因此我们选择假设故障率服从0到1之间的均匀分布,即先验分布为P(θ)=1。



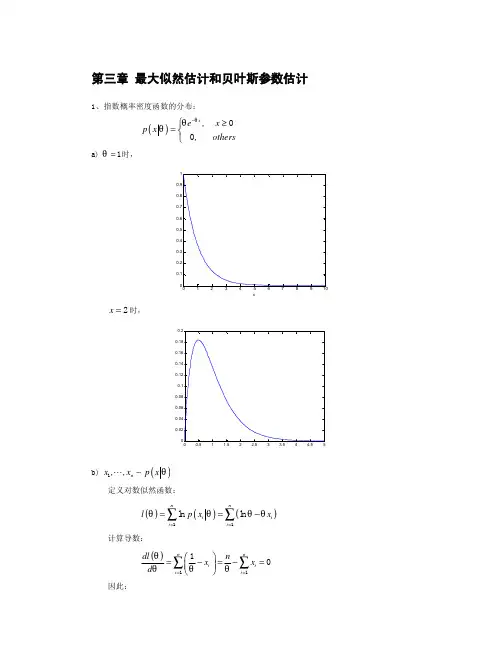


贝叶斯先验概率贝叶斯估计你有没有想过,我们每天做的决定背后,其实有很多不确定性?我们做的选择是根据过去的经验,也我们选择的结果并不完全能预测。
举个例子,假设你早上出门前看了天气预报,说今天有50%的可能下雨。
那么问题来了,你是带伞呢,还是不带呢?如果你经历了好几次天气预报错得离谱,是不是就会开始怀疑这些概率的准确性了?这时候,你可能会觉得,自己的经验比这些预测更靠谱。
嘿,这其实就跟贝叶斯估计有点关系!贝叶斯估计的核心思想就是:把我们的“信念”或者说“先入为主”的看法,结合新的信息,做出更合理的判断。
拿天气预报来说,假如你这几年过得比较顺风顺水,基本上从来没遇到过下雨的预报被错过过,天公作美,你心里可能会觉得今天下雨的可能性更小些。
这时候,你的“先验知识”就开始发挥作用了。
你并不是完全相信50%的下雨几率,而是结合自己以往的经验,觉得这50%的概率其实没那么准确,可能实际下雨的几率还得往低的方向调整。
对,先验概率,这名字听起来有点高深,但其实说白了,就是你在面对不确定的事物时,最初的判断和看法。
举个例子,假设你今天第一次见到一个人,想知道他是不是喜欢看足球。
你完全不了解他,只知道他长得高大,看起来像个运动员。
你的“先验”就是——他可能喜欢足球。
这个先验的看法,源自你对运动员的刻板印象。
可是,如果你后来得知,这个人其实从不碰球,反而热衷于下围棋,那你的想法肯定得做调整。
你会慢慢抛开原本的看法,开始根据实际信息重新评估他的兴趣。
贝叶斯估计的巧妙之处就在于,它鼓励你做这种“更新”。
每当有新的信息进来时,你就该重新调整自己原本的“信念”。
在上面的例子中,一开始你完全凭直觉判断这个人爱足球,结果一查,他竟然喜欢围棋,那你就得调整看法了,把新的信息加进来,改成一个更加准确的估计。
更有意思的是,贝叶斯估计的魅力不仅在于它能够帮助我们调整决策,还在于它不要求我们一开始就知道真相。
嘿,谁能一开始就知道自己做的决定百分之百正确呢?生活就是这样,充满了不确定。



独创性声明本人声明所呈交的学位论文是我个人在导师指导下进行的研究工作及取得的研究成果。
尽我所知,除文中已经标明引用的内容外,本论文不包含任何其他个人或集体已经发表或撰写过的研究成果。
对本文的研究做出贡献的个人和集体,均已在文中以明确方式标明。
本人完全意识到本声明的法律结果由本人承担。
学位论文作者签名:日期:年月日学位论文版权使用授权书本学位论文作者完全了解学校有关保留、使用学位论文的规定,即:学校有权保留并向国家有关部门或机构送交论文的复印件和电子版,允许论文被查阅和借阅。
本人授权华中科技大学可以将本学位论文的全部或部分内容编入有关数据库进行检索,可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
保密□,在年解密后适用本授权书。
本论文属于不保密□。
(请在以上方框内打 “ √ ” )学位论文作者签名:指导教师签名:日期:年月日日期:年月日1 绪论1.1 选题背景一位统计学家曾经这样说过:作为一名统计工作者,不论其是否是贝叶斯学派的支持者,都应该了解贝叶斯统计方法的思想,并将贝叶斯统计推断作为其统计推断的基本讨论之一。
特别是在现代统计分析中,综合各种不同资源、条件,从中寻找信息变得越来越重要,贝叶斯方法和经验贝叶斯方法就是达到这一目标的有力工具。
另外,贝叶斯方法由于计算上的优势更易于实现,而且,贝叶斯模型与贝叶斯过程通常显示出更好的性质。
因此,贝叶斯方法在各个学科领域的应用越来越广泛,特别是在社会科学和经济商业活动中,贝叶斯方法取得了成功,形成了一股不容忽视的力量,受到了更多统计工作者的重视。
客观世界具有多样性,自然现象呈现错综复杂的景象,了解真相需要统计工作者充分、完全地利用各方面的有用信息。
经典的统计方法直接利用样本信息,这样的经典推断大多不考虑所作的推断将被应用的领域。
而贝叶斯分析将先验信息正式地纳入统计学中并探索如何利用这种信息的。
贝叶斯方法可以在实践中检验正确性,并不断地完善。
虽然,很多实践证明这些先验信息可以帮助做出更好统计推断,但是先验的寻找和确定并不是一件容易的事情。
§3.2 经典线性计量经济学模型的贝叶斯估计Bayesian EstimationBayesian Econometrics(教材§3.3)一、贝叶斯定理二、正态线性单方程计量经济学模型的贝叶斯估计0 引子•在《Econometric Analysis》(第3版)中:•Chapter 6 The Classical Multiple Linear Regression Model—Specification and Estimation • 6.9 Bayesian Estimation•在《Econometric Analysis》(第5版)中:•Chapter 16 Estimation Frameworks in Econometrics•16.2 Parametric Estimation•16.2.2 Bayesian Estimation•作为一类估计方法,其原理是重要的。
•在实际应用中,由于先验信息难以获得,该估计方法很难应用。
•贝叶斯统计是由T.R.Bayes于19世纪创立的数理统计的一个重要分支,20世纪50年代,以H.Robbins 为代表提出了在计量经济学模型估计中将经验贝叶斯方法与经典方法相结合,引起了广泛的重视。
•贝叶斯估计对经典计量经济学模型估计方法的扩展在于,它不仅利用样本信息,同时利用非样本信息。
一、贝叶斯定理•后验信息正比于样本信息与先验信息的乘积。
•可以通过样本信息对先验信息的修正来得到更准确的后验信息。
⒉单方程计量经济学模型贝叶斯估计的过程•确定模型的形式,指出待估参数•给出待估参数的先验分布•利用样本信息,修正先验分布•利用待估参数的后验密度函数,进一步推断出待估参数的点估计值,或进行区间估计与假设检验•预测二、正态线性单方程计量经济学模型的贝叶斯估计⒋区间估计•根据B的后验密度函数进行区间估计。
•需要引入最高后验密度区间的概念:区间内每点的后验密度函数值大于区间外任何一点的后验密度函数值,这样的区间称为最高后验密度区间(HPD区间)。