线段和最小值问题

线段和的最值小值问题第8课时线段和、差的最值问题是一类综合性较强的问题，主要归于两个几何模型：1．求“变动的线段之和的最小值”时，可归于“两点之间线段最短（或三角形两边之和大于第三边）”．如图，在直线l 上确定一点P ，使PB PA最小．一、选择题1．下列说法中正确提（ ）（A ）到直线l 的距离相等的两点关于直线l 对称 （B ）角是轴对称图形，对称轴是角平分线 （C ）圆是轴对称图形，有无数条对称轴 （D ）有一个内角是60º的三角形是轴对称图形 2．已知△ABC 和△ADC 关于直线AC 轴对称，若 ∠BAD +∠BCD =170º，那么△ABC 是（ ）（A ）直角三角形（B ）等腰三角形 （C ）钝角三角形 （D ）锐角三角形 3．如图，点P 、Q 在直线AB 外，点O 在直线AB 上从左往右运动形成无数个三角形：△O 1PQ 、△O 2PQ 、△O 3PQ 、…，在这样的运动变化过程中，这些三角形的周长（ ）（A ）不断变大（B ）不断变小 （C ）先变小再变大 （D ）先变大再变小4．如图所示，在正方形网格中有格点A 、B ，在数轴上找一点P A ，使P 到点A 和点B 的距离之和最小．则点P 所对应的数为（ ）（A ）−2 （B ）0 （C ）2 （D ）3 二、填空题5．如图，点D 、E 分别在△ABC 的边AB 、AC 上，且DE ∥BC ，沿DE 折叠△ABC 后，点A 落在点A ′处，若∠C =120º，∠A =26º，则∠A ′DB = º．6．在△ABC 中，AC 边的垂直平分线l 交AC 于D ，BC =4，点P 在直线l 上，则P A +PB 的最小值是 ． 7．如图所示，点A 、B 均在由边长为1的相同小正方形组成的网格的格点上，若要在直线l 上找一点，使得P A 与PB 的差最大，那么P 点应在 点处． 8．如图，点P 在∠AOB 的内部， 点M 、N 分别点P 关于直线OA 、 OB 的对称点，线段MN 交OA 、 OB 于点E 、F ．若△PMN 的周 长为20cm ，PG =2cm ，PH =4cm ， 则△PEF 的周长为 cm ． 三、解答题9．（1）如图①，等边△ABC 中，点E 是AB 的中点，AD 是高，P 为AD 上一点，当BP +PE 的值最小时，画出图形说明P 点的位置．知识要点APQO 1O 2O 3B第3题第4题第7题ABC lD P 第6题A′ B C 第5题DEAO B P GM EFN HlB A（2）如图②，四边形ABCD 中，∠A =∠D =90°，在AD 上确定点P ，使△PBC 的周长最小．10．已知：如图，四边形ABCD 中，AB=BC ，对角线BD 平分∠ABC ，E 是BC 的中点，P 是对角线BD 上的一个动点，则当PE +PC 的最小值时，试确定P 点的位置（画出图形说明理由）．一、填空题11．如图，在四边形ABCD 中，∠A =90º，AD =5，对角线BD ⊥CD ，∠ADB =∠C ．P 是BC 边上一动点，连结PD ，则PD 的最小值为12．如图，在Rt △ABC 中，D 、E 为斜边AB 上两点，且BD =BC ，AE =AC ，则∠DCE 的大小为 º． 13．如图，等腰三角形ABC 的面积为48cm 2，底边BC 的长为8cm ，腰AB 的垂直平分线EF 交AC 于F ，若D 是BC 边的中点，M 为线段EF 上一动点，则△BDM 的周长的最小值为 cm ．二、解答题14．如图，已知两点P 、Q 在锐角∠AOB 内，分别在OA 、OB 上求作点M 、N ，使四边形PMNQ 的周长最小（简要说明作法及理由）．15．如图①，在∠AOB 内有一点P ，先作点P 关于直线OA 的对称点P 1，再作点P 关于直线OB 的对称点P 2． （1）猜想∠P 1OP 2与∠AOB 的数量关系，并证明； （2）当点P 在∠AOB 外部时，上述结论还成立吗？请在图②中画出相应的图形并说明理由．A图①DCBA图②DAB C P 第11题C 第12题第13题ABC F E MD DA能力提升P图① 图②A。

两定点到圆上一动点的线段和最小值1. 引言大家好！今天我们聊聊一个有趣的几何问题，那就是“两定点到圆上一动点的线段和的最小值”。

这个问题看似复杂，但其实非常有趣。

让我们一起揭开这个谜团，看看怎么找到这个最小值吧！2. 问题背景2.1. 定义问题设想我们有一个圆和两个定点A和B。

在这个圆上，有一个点P在移动，我们关心的是，从点A到点P的线段长度加上从点P到点B的线段长度的和，也就是AP + PB的和。

这种情况下，我们想找出这个和的最小值。

2.2. 问题的意义这个问题在现实生活中其实有点像“走最短的路”。

比如你在城市里走路，要从家到公司，你会选择最短的路径，减少走的距离。

在几何中，这个最小值也就是我们要寻找的目标。

3. 方法探讨3.1. 对称性分析先来简单理解一下，对称性是如何帮助我们解决问题的。

我们可以把点A和点B看成两个固定的点，圆上的点P可以移动。

如果我们把圆外的点A和B连接起来，形成一条线段，然后再考虑圆的对称性，这样我们可以发现，从点P到A和B的总距离，其实可以用镜像反射的技巧来简化。

3.2. 反射法来个小窍门，设想把圆以点P为对称中心，进行镜像反射。

这样，圆上的点P变成了圆外的点P'。

这时候，我们可以得到从点A到点P加上从点P到点B的最短路径等于从点A到点P'的直线距离。

听起来是不是很简单？4. 解决过程4.1. 几何直观好啦，现在我们开始具体计算了。

通过反射，我们就可以知道最短路径的长度是线段AP' + P'B。

因为线段AP'是直线段，而圆上的任何点到这个直线段的距离都不会比直线段的长度长。

所以最短的总和就是AP' + P'B，也就是我们最初所说的最小值。

4.2. 代数验证为了更加确信，我们也可以通过代数方法来验证一下。

假设圆心为O，半径为r，那么AP + PB的最小值就等于A和B之间的距离。

这个距离可以通过简单的几何公式或者代数运算得出，结果是最小值等于线段AB的长度。

线段之和的最小值问题（七年级下册）如图，要在街道旁修建一个奶站，向居民区A 、B 提供牛奶，奶站应建在什么地方，才能使它到A ，B 的距离之和最小？【温馨提示】基本图形:两点一线，定动点；基本思路:利用轴对称的性质设M 是边长为2的正△ABC 的边AB 上的中点，P 是边BC 上的任意一点，求PA ＋PM 的最小值．如图，正方形ABCD 中，AB=2, P 是对角线AC 上任意一点.（1）若M 是AB 边上的中点，求PM+PB 的最小值.（2）若M 是AB 边上的中点，N 是BC 边上的点，且AB CN 31 ,求PM+PN 的最小值. （3）若M 、N 分别是AB ，BC 边上的点，且AM=CN=1/3AB,求PM+PN 的最小值.（1） （2） （3）【温馨提示】找出基本图形：两点一线，定动点如图，正方形ABCD 中，AB=2,Q 是AB 中点，连结QC ，点P 、M 是QC 、BC 上任意点，求PM+PB 的最小值.如图，在四边形ABCD 中，∠BAD ＝120°， ∠B ＝∠D ＝90°，AB ＝1，AD ＝2，在BC 、CD 上分别找一点M 、N ，使得△AMN 的周长最小，则△AMN 的最小周长是_______．1.如图，在直角坐标系xoy 中，x 轴上的动点M （X ，0）到定点P （5，5）和到Q （2，1）的距离分别为MP 和MQ ，那么当MP+MQ 取最小值时，点M 的横坐标为 .在反比例函数xy 6=上有两点A(3,2),B(6,1)，在直线x y -=上有动点P,那么当PA+PB 最小时，求P 点的坐标.已知抛物线225212+-=x x y 若一个动点Ｍ自Ｐ出发，先到达对称轴上某点（设为点F ），最后运动到点A 。

确定使点M 运动的总路径最短的点F 的位置，并求出这个最短路程的长.若一个动点Ｍ自Ｐ出发，先到达x 轴上的某点（设为点E ），再到达抛物线的对称轴上某点（设为点F ），最后运动到点A.确定使点M 运动的总路径最短的点E 、点F 的位置，并求出这个最短路程的长.。

线段角度的最大值与线段长度的最小值问题引言本文讨论了线段角度的最大值与线段长度的最小值问题。

我们将首先定义线段的角度和长度，然后探讨如何找到具有最大角度和最小长度的线段。

定义- 线段：两个点之间的直线段，由两个端点确定。

- 线段角度：线段与x轴正方向之间的夹角。

- 线段长度：线段的物理长度。

线段角度的最大值要找到具有最大角度的线段，我们可以遍历所有线段并计算它们的角度。

具体步骤如下：1. 遍历每个线段。

2. 计算每个线段与x轴正方向之间的夹角。

3. 保存具有最大角度的线段。

4. 返回具有最大角度的线段。

以下是示例代码实现这个算法：max_angle = 0max_angle_segment = Nonefor segment in segments:angle = calculate_angle(segment)if angle > max_angle:max_angle = anglemax_angle_segment = segmentreturn max_angle_segment线段长度的最小值要找到具有最小长度的线段，我们可以遍历所有线段并比较它们的长度。

具体步骤如下：1. 遍历每个线段。

2. 计算每个线段的长度。

3. 保存具有最小长度的线段。

4. 返回具有最小长度的线段。

以下是示例代码实现这个算法：min_length = float('inf')min_length_segment = Nonefor segment in segments:length = calculate_length(segment)if length < min_length:min_length = lengthmin_length_segment = segmentreturn min_length_segment结论通过上述算法，我们可以找到具有最大角度和最小长度的线段。

143最值问题——用轴对称解决线段和的最小值问题一：【情景引入】如图：要在河边修建一个水泵站,分别向张村A 和李庄B 送水,问水泵站应修建在河边的什么地方,可使使用的水管最短?图①图②二：【精选例题】 如图：在正方形ABCD 中, E 在BC 上, 且 BE=2, CE=1, 点P 在线段BD 上运动, 求PE+PC 的最小值为多少？三：【巩固练习】1、如下图：E 在菱形ABCD 中，∠DAB=120°,E 为DC 中点，点O 是BD 上一动点，若AB=2，则PE+PC 的最小值是___________________A B2、如右上图：⊙O 的半径为1, 点A 是半圆上一个三等分点，点B 是弧AN 的中点， 点P 是直径MN 上一动点，则PA ＋PB 的最小值为_________________________．1443、若抛物线y= x 2 + bx + c 与x 轴交于A (1, 0 ) 、B (3, 0 ) 两点．①求出抛物线的解析式。

②设此抛物线交y 轴于C 点，在该抛物线的对称轴上是否存在点Q ，使得△QAC 的周长最小?若存在，求出Q 点坐标；若不存在，请说明理由．四：拓展与提高已知在平面直角坐标系xoy 中，A 、B 两点的坐标分别为A(2,-3)、B(4,-1).①若P (x,0 )是x 轴上的一个动点, 则当x 为何值时,△PAB 的周长最短？②设M 、N 分别为x 轴和y 轴上的动点, 请问:是否存在这样的点M(m,0)、N(0,n), 使四边形 ABMN 的周长最短? 若存在, 求出m 、n 的值；若不存在,说明理由。

③若C (a , 0 )、D (a+3 , 0 )是x 轴上的两个动点, 则当a 为何值 时,四边形ABDC 的周长最短；。

“求两线段长度值和最小”问题全解析在近几年的中考中.经常遇到求PA+PB最小型问题.为了让同学们对这类问题有一个比较全面的认识和了解.我们特此编写了“求两线段长度值和最小”问题全解析.希望对同学们有所帮助．一、在三角形背景下探求线段和的最小值1.1 在锐角三角形中探求线段和的最小值例1如图1.在锐角三角形ABC中.AB=4,∠BAC=45°.∠BAC的平分线交BC于点D.M,N分别是AD和AB上的动点.则BM+MN的最小值为．分析：在这里.有两个动点.所以在解答时.就不能用我们常用对称点法．我们要选用三角形两边之和大于第三边的原理加以解决．解：如图 1.在AC上截取AE=AN.连接BE．因为∠BAC的平分线交BC于点 D.所以∠EAM=∠NAM.又因为AM=AM. 所以△AME≌△AMN.所以ME=MN．所以BM+MN=BM+ME≥BE．因为BM+MN有最小值．当BE是点B到直线AC的距离时.BE取最小值为4.以BM+MN的最小值是4．故填4．1.2在等边三角形中探求线段和的最小值例2（2010 山东滨州）如图4所示.等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为 .分析：要求线段和最小值.关键是利用轴对称思想.找出这条最短的线段.后应用所学的知识求出这条线段的长度即可．解：因为等边△ABC的边长为6,AD是BC边上的中线,所以点C与点B关于AD对称.连接BE交AD于点M.这就是EM+CM最小时的位置.如图5所示.因为CM=BM.所以EM+CM=BE.过点E作EF⊥BC.垂足为F.因为AE=2.AC=6.所以EC=4.在直角三角形EFC中.因为EC=4, ∠ECF=60°.∠FEC=30°.所以FC=2,EF==2．因为BC=6.FC=2.所以BF=4．在直角三角形BEF中.BE==.二、在四边形背景下探求线段和的最小值2.1在直角梯形中探求线段和的最小值例3（2010江苏扬州）如图3.在直角梯形ABCD中.∠ABC＝90°.AD∥BC.AD＝4.AB＝5.BC ＝6.点P是AB上一个动点.当PC＋PD的和最小时.PB的长为__________．分析：在这里有一个动点.两个定点符合对称点法求线段和最小的思路.所以解答时可以用对称法．解：如图3所示.作点D关于直线AB的对称点E.连接CE.交AB于点P.此时PC＋PD和最小.为线段CE．因为AD＝4.所以AE=4．因为∠ABC＝90°.AD∥BC.所以∠EAP＝90°．因为∠APE＝∠BPC,所以△APE∽△BPC.所以.因为AE=4.BC＝6.所以.所以.所以,因为AB＝5.所以PB=3.2.2在等腰梯形中探求线段和的最小值例4如图4.等腰梯形ABCD中.AB=AD=CD=1.∠ABC=60°.P是上底.下底中点EF直线上的一点.则PA+PB的最小值为．分析：根据等腰梯形的性质知道.点A的对称点是点D.这是解题的一个关键点．其次运用好直角三角形的性质是解题的又一个关键．解：如图4所示.因为点D关于直线EF的对称点为A.连接BD.交EF于点P.此时PA＋PB和最小.为线段BD．过点D作DG⊥BC.垂足为G.因为四边形ABCD是等腰梯形.且AB=AD=CD=1.∠ABC=60°.所以∠C=60°.∠GDC=30°.所以GC=,DG=．因为∠ABC＝60°.AD∥BC.所以∠BAD＝120°．因为AB=AD.所以∠ABD=∠ADB=30°.所以∠ADBC=30°.所以BD=2DG=2×=．所以PA+PB的最小值为．2.3在菱形中探求线段和的最小值例5如图5菱形ABCD中.AB=2.∠BAD=60°.E是AB的中点.P是对角线AC上的一个动点.则PE+PB的最小值为．分析：根据菱形的性质知道.点B的对称点是点D.这是解题的一个关键点．解：如图5所示.因为点B关于直线AC的对称点为D.连接DE.交AC于点P.此时PE＋PB和最小.为线段ED．因为四边形ABCD是菱形.且∠BAD=60°.所以三角形ABD是等边三角形．因为E是AB的中点.AB=2.所以AE=1.DE⊥AB.所以ED==．所以PE＋PB的最小值为．2.4在正方形中探求线段和的最小值例6如图6所示.已知正方形ABCD的边长为8.点M在DC上.且DM=2.N是AC上的一个动点.则DN+MN的最小值为．分析：根据正方形的性质知道.点B的对称点是点D.这是解题的一个关键点．解：如图6所示.因为点D关于直线AC的对称点为B.连接BM.交AC于点N.此时DN＋MN和最小.为线段BM．因为四边形ABCD是正方形.所以BC=CD=8．因为DM=2.所以MC=6.所以BM==10.所以DN+MN的最小值为10.例7（2009?达州）如图7.在边长为2cm的正方形ABCD中.点Q为BC边的中点.点P为对角线AC上一动点.连接PB、PQ.则△PBQ周长的最小值为cm．（结果不取近似值）．分析：在这里△PBQ周长等于PB+PQ+BQ.而BQ是正方形边长的一半.是一个定值1.所以要想使得三角形的周长最小.问题就转化成使得PB+PQ的和最小问题．因为题目中有一个动点P.两个定点B,Q符合对称点法求线段和最小的思路.所以解答时可以用对称法．解:如图7所示.根据正方形的性质知道点B与点D关于AC对称.连接DQ.交AC于点P.连接PB．所以BP=DP.所以BP+PQ=DP+PQ=DQ．在Rt△CDQ中.DQ== .所以△PBQ的周长的最小值为：BP+PQ+BQ=DQ+BQ= +1．故答案为+1．三、在圆背景下探求线段和的最小值例8（2010年荆门）如图8.MN是半径为1的⊙O的直径.点A在⊙O上.∠AMN＝30°.B 为AN弧的中点.P是直径MN上一动点.则PA＋PB的最小值为( )(A)2 (B) (C)1 (D)2分析：根据圆的对称性.作出点A的对称点D.连接DB.则线段和的最小值就是线段DB 的长度．解：如图8.作出点A的对称点D.连接DB.OB,OD．因为∠AMN＝30°.B为AN弧的中点.所以弧AB的度数为30°.弧AB的度数为30°.弧AN的度数为60°．根据圆心角与圆周角的关系定理得到：∠BON＝30°．由垂径定理得：弧DN的度数为60°．所以∠BOD＝∠BON+∠DON= 30°+60°=90°.所以DB==.所以选择B．四、在反比例函数图象背景下探求线段和的最小值例9（2010山东济宁）如图9.正比例函数y=x的图象与反比例函数y=（k≠0）在第一象限的图象交于A点.过A点作x轴的垂线.垂足为M.已知三角形OAM的面积为1.（1）求反比例函数的解析式；（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合）.且B点的横坐标为1.在x轴上求一点P.使PA+PB最小.分析：利用三角形的面积和交点坐标的意义.确定出点A的坐标是解题的第一个关键．要想确定出PA+PB的最小值.关键是明白怎样才能保证PA+PB的和最小.同学们可以联想我们以前学过的对称作图问题.明白了最小的内涵.解题的过程就迎刃而解了．解：（1）设点A的坐标为（x.y）.且点A在第一象限.所以OM=x,AM=y．因为三角形OAM的面积为1.所以所以xy=2.所以反比例函数的解析式为y=．（2）因为y=x与y=相交于点A.所以=x.解得x=2.或x=-2.因为x＞0.所以x=2.所以y=1.即点A的坐标为（2.1）．因为点B的横坐标为1.且点B在反比例函数的图像上.所以点B的纵坐标为2.所点B的坐标为（1.2）.所以点B关于x轴的对称点D的坐标为（1.-2）．设直线AD的解析式为y=kx+b.所以.解得k=3.b=-5.所以函数的解析式为y=3x-5.当y=0时.x=.所以当点P在（.0）时.PA+PB的值最小．五、在二次函数背景下探求线段和的最小值例10（2010年玉溪改编）如图10.在平面直角坐标系中.点A的坐标为（1.） .△AOB 的面积是.（1）求点B的坐标；（2）求过点A、O、B的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C.使△AOC的周长最小？若存在.求出点C的坐标；若不存在.请说明理由；分析：在这里△AOC周长等于AC+CO+AO.而A,O是定点.所以AO是一个定长.所以要想使得三角形的周长最小.问题就转化成使得AC+CO的和最小问题．因为题目中有一个动点C.两个定点A,O符合对称点法求线段和最小的思路.所以解答时可以用对称法．解：（1）由题意得:所以OB=2．因为点B在x轴的负半轴上.所以点B 的坐标为（-2.）；（2）因为B(-2,0),O(0,0),所以设抛物线的解析式为：y=ax（x+2）.将点A的坐标为（1.）代入解析式得：3a=.所以a=.所以函数的解析式为y=+x．（3）存在点C. 如图10.根据抛物线的性质知道点B与点O是对称点.所以连接AB与抛物线的对称轴x= - 1交AC于点C.此时△AOC的周长最小.设对称轴与x轴的交点为E．过点A作AF垂直于x轴于点F.则BE=EO=EF=1.因为△BCE∽△B AF,所以, 所以.所以CE=．因为点C在第二象限.所以点C的坐标为（-1.）．六、在平面直角坐标系背景下探求线段和的最小值例11（2010年天津）如图11.在平面直角坐标系中.矩形的顶点O在坐标原点.顶点A、B分别在x轴、y轴的正半轴上.OA=3.OB=4.D为边OB的中点.（1）若E为边OA上的一个动点.当△CDE的周长最小时.求点E的坐标；（2）若E、F为边OA上的两个动点.且EF=2.当四边形CDEF的周长最小时.求点E、F 的坐标.分析：本题的最大亮点是将一个动点求最小值和两个动点求最小值问题糅合在一起.并很好的运用到平面直角坐标系中．解：（1）如图12.作点D关于x轴的对称点.连接C与x轴交于点E.连接DE.若在边OA上任取点（与点E不重合）.连接C、D、.由D+ C=+ C＞C= D+CE=DE+CE.所以△的周长最小.因为在矩形OACB中.OA=3,OB=4, D为OB的中点.所以 BC=3.DO=O=2.所以点C的坐标为（3.4）.点的坐标为（0.-2）.设直线C的解析式为y=kx+b.则.解得k=2.b=-2.所以函数的解析式为y=2x-2.令y=0.则x=1.所以点E的坐标为（1.0）；（2）如图13.作点D关于x轴的对称点.在CB边上截取CG=2.连接G与x轴交于点E.在EA上截EF=2.因为GC∥EF.GC=EF.所以四边形GEFC为平行四边形.有GE=CF.又 DC、EF的长为定值.所以此时得到的点E、F使四边形CDEF的周长最小.因为在矩形OACB中.OA=3,OB=4, D为OB的中点.CG=2,所以 BC=3.DO=O=2,BG=1.所以点G的坐标为（1.4）.点的坐标为（0.-2）.设直线G的解析式为y=kx+b.则.解得k=6.b=-2.所以函数的解析式为y=6x-2.令y=0.则x=.所以点E的坐标为（.0）,所以点F的坐标为（+2.0）即F的坐标为（.0）。

两定点到圆上一动点的线段和最小值哎呀，这道题目可真是让人头疼啊！不过，既然咱们来了，那就得好好聊聊这个话题。

话说，两定点到圆上一动点的线段和最小值，这个问题可是涉及到了数学的奥秘哦！不过，别担心，我这个“数学小白”也会尽力给大家讲解清楚的。

咱们得明确一下这个问题的背景。

假设我们有两个定点A和B,以及一个圆心O。

我们需要找到一条线段AB,使得这条线段经过圆心O,并且它的长度最短。

这个问题的解决方法其实很简单，就是利用勾股定理和三角函数来求解。

我们需要知道圆心O到两个定点A和B的距离。

假设OA和OB分别是两个距离，那么根据勾股定理，我们可以得到AB的长度为：AB = sqrt(OA^2 + OB^2)接下来，我们需要找到一条线段AB,使得它经过圆心O。

这其实也很简单，因为圆心O到两个定点A和B的距离已经给出了，所以我们只需要找到一个角度θ，使得cos(θ) = (OA/AB) / (OB/AB)。

这样一来，我们就可以得到线段AB的长度了。

我们需要找到这条线段AB的长度的最小时值。

这个问题的解决方法其实也很简单，就是利用三角函数来求解。

我们知道，sin(θ) = 对边/斜边，cos(θ) = 邻边/斜边。

所以，我们可以得到：AB^2 = OA^2 + OB^2 2 * OA * OB * cos(θ)将上面的公式代入cos(θ)的表达式，我们可以得到：AB^2 = OA^2 + OB^2 2 * OA * OB * (OA/AB) / (OB/AB)化简一下，我们可以得到：AB^2 = OA^2 + OB^2 2 * OA * OB * (OA^2 + OB^2) / (OA * AB + OB * AB)这就是我们要找的线段AB的最短长度公式啦！这个公式还有一个变形版本，就是：AB^2 = (OA^2 + OB^2) * (1 + sin^2(θ)) / (1 + sin^2(θ))这个公式可以用来求解任意两个定点A和B之间的最短距离。

线段差的最大值与线段和的最小值问题有关线段差的最大值与线段和的最小值问题的主要应用原理是：1、两点这间线段最短。

2、三角形的任意两边之和大于第三边（找和的最小值）。

3、三角形的任意两边之差小于第三边（找差的最大值）。

作图找点的关键：充分利用轴对称，找出对称点，然后，使三点在一条直线上。

即利用线段的垂直平分线定理可以把两条线段、三条线段、四条线段搬在同一条直线上。

证明此类问题，可任意另找一点，利用以上原理来证明。

一两条线段差的最大值：（1）两点同侧：如图，点P在直线L上运动，画出一点P，使︱PA－PB︱取最大值。

作法：连结AB并延长AB交直线L于点P。

点P即为所求。

︱PA－PB︱=AB证明：在直线L上任意取一点P。

，连结PA、PB，︱PA－PB︱＜AB（2两点异侧：如图，如图，点P在直线L上运动，画出一点P，使︱PA－PB︱取最大值。

作法：1、作B关于直线L的对称点B。

2、连结AB并延长AB交直线L于点P。

点P即为所求。

︱PA－PB︱=AB证明：在直线L上任意取一点P。

，连结PA、PB、PB。

︱PA－PB︱=︱PA－PB︱＜AB（三角形任意两边之差小于第三边）二、两条线段和的最小值问题：（1））两点同侧：如图，点P在直线L上运动，画出一点P使P A＋PB取最小值。

（三角形的任意两边之和大于第三边（找和的最小值），P A＋PB=AB（2）两点异侧：如图，点P在直线L上运动，画出一点P使P A＋PB取最小值。

（两点之间线段最短）三、中考考点：08年林金钟老师的最后一题：如图，在矩形ABCO中，B（3，2），E（3，1），F（1，2）在X轴与Y轴上是否分别存在点M、N，使得四边形EFNM的周长最小？若存在，请求出周长的最小值，若不存在，请说明理由。

提示：EF长不变。

即求F N＋NM＋MF的最小值。

利用E关于X轴的对称点E，F的对称点F，把这三条线段搬到同一条直线上。

一、以正方形为载体，求线段和的最小值例1. 如图1，四边形ABCD是正方形，边长是4，E是BC上一点，且CE＝1，P是对角线BD上任一点，则PE＋PC的最小值是_____________。

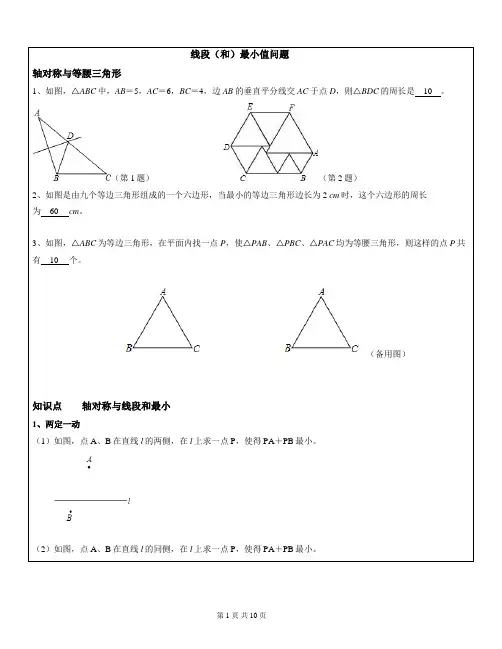
线段（和）最小值问题轴对称与等腰三角形1、如图，△ABC中，AB＝5，AC＝6，BC＝4，边AB的垂直平分线交AC于点D，则△BDC的周长是 10 。

（第1题）（第2题）2、如图是由九个等边三角形组成的一个六边形，当最小的等边三角形边长为2 cm时，这个六边形的周长为 60 cm。

3、如图，△ABC为等边三角形，在平面内找一点P，使△PAB、△PBC、△PAC均为等腰三角形，则这样的点P共有 10 个。

（备用图）知识点轴对称与线段和最小1、两定一动（1）如图，点A、B在直线l的两侧，在l上求一点P，使得PA＋PB最小。

（2）如图，点A、B在直线l的同侧，在l上求一点P，使得PA＋PB最小。

2、三定一动平面直角坐标系中有三点A（6，4）、B（4，6）、C（0，2），在x轴上找一点D，使得四边形ABCD的周长最小，则点D的坐标应该是（2，0）。

3、一定两动型如图，点A是∠MON内部一点，在∠MON的两边OM、ON上各取一点B、C，与点A组成三角形，使△ABC的周长最小。

4、两定两动型（1）AB是∠MON内部一条线段，在∠MON的两边OM、ON上各取一点C、D组成四边形，使四边形周长最小。

（2）平面直角坐标系中有两点A（6，4）、B（4，6），在y轴上找一点C，在x轴上找一点D，使得四边形ABCD的周长最小，则点C的坐标应该是（0，2），点D的坐标应该是（2，0）。

5、定点与定长线段点M、N在直线l同侧，请你在直线l上画出两点O、P，使得OP＝1cm，且MO＋OP＋PN的值最小。

（轴对称与平移的结合）【例题精讲一】例1：1、如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是（0，3）。

2、如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：（用直尺画图）（1）画出格点△ABC（顶点均在格点上）关于直线DE对称的△A1B1C1；（2）在DE上画出点P，使PB1＋PC最小；（3）在DE上画出点Q，使QA＋QC最小。

线段斜率的最大值与线段长度的最小值问题背景在几何学中，线段是由两个端点组成的有限直线段。

研究线段的特性对于解决各种问题非常重要，其中包括线段斜率的最大值与线段长度的最小值问题。

线段斜率的最大值线段斜率是指线段上两个端点之间的斜率。

线段的斜率可通过直线的斜率公式计算得出。

根据数学原理，线段的斜率的最大值即为线段所在直线的斜率的最大值。

因此，要求线段斜率的最大值，就需要找到线段所在直线的斜率的最大值。

线段长度的最小值线段的长度是指线段上两个端点之间的距离。

计算线段的长度可以使用两点间距离公式。

要求线段长度的最小值，就需要找到线段两个端点之间的最短距离。

可以通过找到端点间距离的最小值来实现。

解决问题的策略为了求解线段斜率的最大值与线段长度的最小值问题，可以采用以下简单的策略：1. 首先，确定线段的两个端点的坐标。

这可以通过观察或测量来获得。

2. 然后，计算线段所在直线的斜率。

使用斜率公式，将两个端点的坐标代入，得到直线的斜率。

3. 接下来，比较多个线段所在直线的斜率，找到其中的最大值。

这将给出线段斜率的最大值。

4. 同时，计算线段的长度。

使用两点间距离公式，将两个端点的坐标代入，得到线段的长度。

5. 最后，比较多个线段的长度，找到其中的最小值。

这将给出线段长度的最小值。

注意事项在解决线段斜率的最大值与线段长度的最小值问题时，需要注意以下事项：- 确保计算斜率和长度时使用正确的公式，避免错误结果。

- 如果涉及到多个线段进行比较，可以使用合适的算法或编程语言来简化计算。

- 在实际应用中，可能还需要考虑其他因素，如约束条件或实际问题的限制。

总结线段斜率的最大值与线段长度的最小值问题在几何学和计算数学中有广泛的应用。

通过采用简单的策略，可以找到线段斜率的最大值和线段长度的最小值，从而解决具体问题，并应用于实际情境中。

在解决问题过程中，需要确保正确选择计算公式和注意事项，以获得准确和有效的结果。

2017中考专题复习
----线段和的最小值问题
复习目标：1 题型归类触类旁通。

2 学会分析思考问题，实现问题的转化。

3 体会在解决问题过程中蕴含的数学思想，方法。

复习重点：求线段和的最小值。

复习难点：任何实现线段和的转化，从而解决问题。

核心知识点：1 轴对称。

2 两点之间线段最短。

3 垂线段最短。

复习过程：例1如图，已知C（1，0），直线Y=-X+7与两坐标轴分别交于A,B两点，D,E分别是AB,OA上的动点，求三角形CDE周长的最小值？（图见投影）
分析提示：解决问题的关键是利用轴对称找到满足条件的点的位置。

学生充分思考，探究后交流做法。

教师点评，强调。

例2 在三角形ABC中，角ABC=45度，BC=4,BD平分角ABC交AC于D,M,N分别是BD,BC上的动点，求CM+MN的最小值？（图见投影）
分析提示:把线段和转化成一条线段，再确定这条线段最短的位置。

学生思考探究，口答解法。

教师点评，归纳。

巩固提升：在扇形OAB中角AOB=90度，OA=6,C为OA中点，D是OB上一点，OD=5,P是弧AB上一动点，求PC+1/2PD的最小值？（图见投影）。

方法一：利用几何性质解决问题知识点1：垂线段最短（点到直线的距离，垂线段最短）知识点2：两点之间线段最短（即“将军饮马”问题）知识点3：利用“画圆”来确定动点问题解决最值问题运用画圆解决问题有两种情况：情况1：动点到某一定点的距离是定值（圆上的点到圆心的距离恒等于半径）情况2：动点为90°固定角的顶点（直径所对的圆周角恒定为90°）在中考中最常用的是“知识点2”、“知识点3”方法二：利用代数法直接证明知识点1：利用配方法求三次二项式的最值知识点2：运用二次函数中顶点求最值代数方法较为常见，所以我们本篇暂时不会涉及.接下来，我们来简单看一下每个几何知识点对应的问题知识点1：垂线段最短常出现几何图形问题中，通常在初二会见到，中考中不会涉及。

例：如图，在△ABC中有一点D在AC上移动，若AB=AC=5，BC=6则AD+BD+CD的最小值为_______.分析:题目中问“AD+BD+CD”的最小值，通过图形我们可以知道“AD+CD”是定值，所以问题可以转换为求BD的最小值.那么求BD的最小值即为求一点B到某一直线AC上的最小值，所以可以利用“垂线段最短”的性质来求解.过点B作AC垂线即可解决问题.知识点2：两点之间线段最短这类问题常出现在函数的大题中，考生如果函数知识不过关也不能拿到满分，因为仅作出图形别不能得出答案，还需要利用函数知识进行求点坐标.解题思路：通常做定点关于动点所在直线的对称点（两个动点所在直线就做两个对称点），然后连接对称点与另一点与动点所在直线的交点即为动点位置。

例1.如图，在直角坐标系中，点A、B的坐标分别为（1，3）和（2，0），点C是y轴上的一个动点，且A、B、C三点不在同一条直线上，当△ABC的周长最小时，点C的坐标是______.分析：典型的“将军饮马”问题。

通过作点B关于y轴的对称点即可解决问题.例2：如图所示，直线y=x+2与两坐标轴分别交于A、B两点，点C 是OB的中点，D、E分别是直线AB、y轴上的动点，则△CDE周长的最小值是_______.分析：本题中存在两个动点，分别是点D、点E所以我们只需要做点C关于直线AB、关于y轴的对称点即可解决问题.知识点3：利用“画圆”来确定动点问题解决最值问题例1：如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=6，点D是边BC的中点，点E是边AB上的任意一点（点E不与点B重合），沿DE翻折△DBE使点B落在点F处，连接AF，则线段AF长的最小值是________.分析：由翻折得到，DF=DB=3.所以点F在以点D为圆心以3为半径的圆上.连接A与圆心D，AD与圆的交点即为F'所以AF的最小值是AD-DF'=5-3=2.例2：如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是________.分析：根据正方形的性质可得AB=AD=CD，∠BAD=∠CDA，∠ADG=∠CDG，然后利用“边角边”证明△ABE和△DCF全等，根据全等三角形对应角相等可得∠1=∠2，利用“SAS”证明△ADG和△CDG 全等，根据全等三角形对应角相等可得∠2=∠3，从而得到∠1=∠3，然后求出∠AHB=90°.所以点H在以AB为直径的圆上，所以以AB中点为圆心，以AB长的一半为半径画圆，连接D与圆心交点即为点H.所以DH'=OD-OH'中考中常见的求最值方法就是上面所提到的这些。