2019年高考试题汇编：三角函数

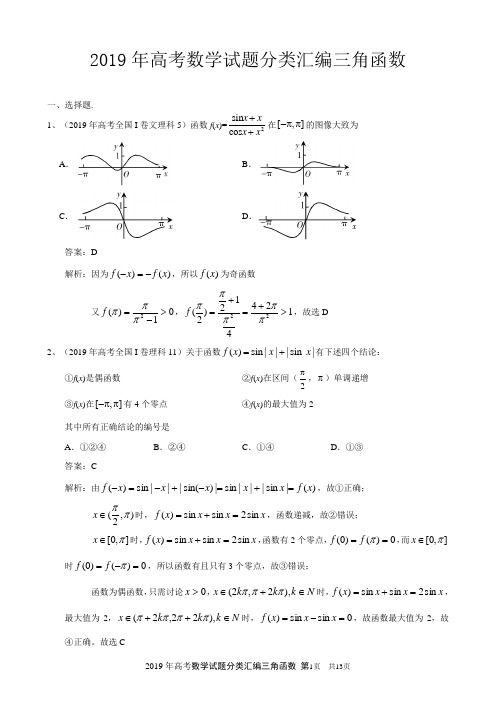
2019年高考试题分类汇编（三角函数）考法1 三角函数的图像及性质1．（2019·全国卷Ⅰ·文科）tan 225=A．2-．2-+．2 D．22.（2019·全国卷Ⅱ·文科）若14x π=，234x π=是函数()sin f x x ω=（0ω>）两个相邻的极值点，则ω=A ．2B ．32C ．1D ．123．（2019·全国卷Ⅲ·文科）函数()2sin sin2f x x x =-在[0,2]π的零点个数为A ．2B ．3C ．4D ．54.（2019·全国卷Ⅰ·文理科）函数2sin ()cos x x f x x x +=+在[,]ππ-的图像大致为5.（2019·全国卷Ⅰ·理科）关于函数()sin sin f x x x =+有以下四个结论： ①()f x 是偶函数 ②()f x 在区间(,)2ππ单调递增 ③()f x 在[,]ππ-有个零点 ④()f x 有最大值为2其中所有正确结论的编号是A ．①②④B ．②④C ．①④D ．①③6.（2019·全国卷Ⅱ·理科）下列函数中，以2π为周期且在区间(,)42ππ单调递增的是A ．()cos2f x x =B ．()sin 2f x x =C ．()cos f x x =D ．()sin f x x =7.（2019·北京卷·理科）函数f (x )=sin 22x 的最小正周期是 .8.（2019·全国卷Ⅱ·理科）已知(0,)2πα∈，2sin 2cos21αα=+，则sin α=A ．15B 9．（2019·全国卷Ⅰ·文科）函数3π()sin(2)3cos 2f x x x =+-的最小值为 ． 10.（2019·全国卷Ⅲ·理科）设函数()sin()5f x x ωπ=+(0ω>)，已知()f x 在[0,2]π有且仅有5个零点，下述四个结论：①()f x 在(0,2π)有且仅有3个极大值点②()f x 在(0,2π)有且仅有2个极小值点③()f x 在(0,10π)单调递增④ω的取值范围是1229[)510， 其中所有正确结论的编号是A ．①④B ．②③C ．①②③D ．①③④11.（2019·天津卷·文理科）已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数，将()y x =的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为()g x .若()g x 的最小正周期为2π，且()4g π=，则3()8f π=A.2-B. D.212.（2019·浙江卷）设函数()sin f x x =，x R ∈.（Ⅰ）已知[0,2)θ∈π，函数()f x θ+是偶函数，求θ的值； （Ⅱ）求函数22[()][()]124y f x f x ππ=+++的值域． 考法2 解三角形1．（2019·浙江卷）在ABC ∆中，90ABC ∠=︒，4AB =，3BC =，点D 在线段AC 上，若45BDC ∠=︒，则BD = ，cos ABD ∠= ．2．（2019·全国卷Ⅰ·文科）ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin sin 4sin a A b B c C -=，14cos A =-，则b c =A ．6B ．5C ．4D ．33.（2019·全国卷Ⅰ·理科）ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c .设22(sin sin )sin B C A -=-sin sin B C .（Ⅰ）求A ；2b c +=，求sin C .4.（2019·全国卷Ⅲ·文理科）ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c .已知sin sin 2A C a b A +=． （Ⅰ）求B ；（Ⅱ）若ABC ∆为锐角三角形，且1c =，求ABC ∆面积的取值范围．5.（2019·北京卷·文理科）在ABC ∆中，a =3，b -c =2，1cos 2B =-． （Ⅰ）求b ,c 的值；（Ⅱ）求sin()B C -的值.6.（2019·天津卷·文理科）在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c .已知2b c a +=，3sin c B =4sin a C . （Ⅰ）求cos B 的值； （Ⅱ）求sin(2)6B π+的值.。

2019年高考数学试题分项版——三角函数（解析版）1、（2019年高考新课标Ⅰ卷文）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知5a ，2c ，2cos 3A，则b=（A ）2（B ）3（C ）2 （D ）3【答案】D 【解析】试题分析：由由余弦定理得3222452b b，解得3b（31b舍去），选 D.2、（2019年高考新课标Ⅰ卷文）若将函数y=2sin (2x+π6)的图像向右平移14个周期后，所得图像对应的函数为（A ）y=2sin(2x+π4) （B ）y=2sin(2x+π3) （C ）y=2sin(2x –π4) （D ）y=2sin(2x –π3)【答案】D 【解析】试题分析：函数y2sin(2x)6的周期为，将函数y2sin(2x)6的图像向右平移14个周期即4个单位，所得函数为y2sin[2(x))]2sin(2x)463，故选 D.3、（2019年高考新课标Ⅰ卷文）若函数1()sin 2sin 3f x x -x a x 在,单调递增，则a 的取值范围是（A ）1,1（B ）11,3（C ）11,33（D ）11,3【答案】C 【解析】试题分析：用特殊值法：取1a ，1sin 2sin 3f x xx x，21cos 2cos 3f x x x，但2201133f ，不具备在,单调递增，排除A ，B ，D ．故选C ．4、（2019年高考新课标Ⅰ卷理）已知函数()sin()(0),24f x x+x，为()f x 的零点，4x为()y f x 图像的对称轴，且()f x 在51836，单调，则的最大值为（A ）11 （B ）9 （C ）7 （D ）5 【答案】B 【解析】试题分析：因为4x为()f x 的零点，4x为()f x 图像的对称轴，所以()444T kT ，即41412244k k T，所以41(*)k kN ，又因为()f x 在5,1836单调，所以5236181222T，即12，由此的最大值为9.故选B.5、（2019年高考新课标Ⅱ卷文）函数=sin()y A x 的部分图像如图所示，则（A ）2sin(2)6y x（B ）2sin(2)3yx（C ）2sin(2+)6yx （D ）2sin(2+)3yx 【答案】A6、（2019年高考新课标Ⅱ卷理）若将函数y=2sin 2x 的图像向左平移π12个单位长度，则平移后图象的对称轴为（A ）ππ26k x k Z （B ）ππ26k x k Z （C ）ππ212Zk xk（D ）ππ212Zk xk【答案】B考点：三角函数的图象变换与对称性.【名师点睛】平移变换和伸缩变换都是针对x 而言，即x 本身加减多少值，而不是依赖于ωｘ加减多少值．7、（2019年高考新课标Ⅱ卷理）若π3cos45，则sin 2= （A ）725（B ）15（C ）15（D ）725【答案】D 【解析】试题分析：2237cos 22cos12144525，且cos 2cos2sin 242，故选 D.8、（2019年高考新课标Ⅲ卷文）若，则（）（A ）（B ）（C ）（D ）【答案】D考点：1、同角三角函数间的基本关系；2、二倍角．9、（2019年高考新课标Ⅲ卷文理）在中，，BC 边上的高等于,则tan13cos 245151545ABC △π4B =13BC sin A =（A ）（B ）（C ）（D ）【答案】D 【解析】试题分析：设边上的高线为，则，所以．由正弦定理，知，即，解得，故选D ．[来源:学科网ZXXK]10、（2019年高考新课标Ⅲ卷理）若，则(A)(B)(C) 1 (D)【答案】A 【解析】试题分析：由，得或，所以，故选A ．考点：1、同角三角函数间的基本关系；2、倍角公式．11、(2019年高考北京卷理) 将函数图象上的点向左平移（）个单位长度得到点，若位于函数的图象上，则（）A.，的最小值为B.，的最小值为[来源:Z 。

2019届高考数学总复习分类试卷三角函数、解三角形、平面向量(时间:120分钟总分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知sin(88°+θ)=23,则cos(178°+θ)=()A.23B.-23C.√53D.-√532.设P是△ABC所在平面内的一点,且CP⃗⃗⃗⃗ =2PA⃗⃗⃗⃗ ,则△PAB与△PBC的面积的比值是( )A.13B.12C.23D.343.在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsin A=3csin B,a=3,cos B=23,则b=( ) A.14 B.6 C.√14 D.√64.函数f(x)=cos(x+π4)-cos(x-π4)是( )A.周期为π的偶函数B.周期为2π的偶函数C.周期为π的奇函数D.周期为2π的奇函数5.函数y=2sin(π6-2x)(x∈[-π,0])的单调递增区间是( )A.[-π,-5π6] B.[-π3,0] C.[-2π3,-π6] D.[-π3,-π6]6.已知函数y=sin ωx(ω>0)在区间[0,π2]上为增函数,且图象关于点(3π,0)对称,则ω的取值集合为( )A.{13,23,1} B.{16,13} C.{13,23} D.{16,23}7.若把函数y=sin(ωx-π6)的图象向左平移π3个单位,所得到的图象与函数y=cos ωx的图象重合,则ω的一个可能取值是( )A.2B.32C.23D.128.在△ABC中,A=π3,AB=2,AC=3,CM⃗⃗⃗⃗⃗ =2MB⃗⃗⃗⃗⃗⃗ ,则AM⃗⃗⃗⃗⃗ ·BC⃗⃗⃗⃗ =( )A.-113B.-43C.43D.1139.在△ABC中,内角A,B,C所对的边分别是a,b,c.若c2=(a-b)2+6,C=π3,则△ABC的面积是( )A.3B.9√32C.3√32D.3√310.在△ABC中,内角A,B,C的对边分别为a,b,c,若△ABC的面积为S,且2S=(a+b)2-c2,则tan C 等于( )A.34B.43C.-43D.-3411.已知△ABC是边长为1的等边三角形,则(AB⃗⃗⃗⃗⃗ -2BC⃗⃗⃗⃗ )·(3BC⃗⃗⃗⃗ +4CA⃗⃗⃗⃗ )=( )A.-132B.-112C.-6-√32D.-6+√3212.将函数f(x)=2sin(ωx-π3)(ω>0)的图象向左平移π3ω个单位,得到函数y=g(x)的图象.若y=g(x)在[0,π4]上为增函数,则ω的最大值为( )A.1B.2C.3D.41 2 3 4 5 6 7 8 9 10 11 12 得分二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中的横线上)13.若单位向量e1,e2的夹角为π3,向量a=e1+λe2(λ∈R),且|a|=√32,则λ=.14.△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的面积为S,若4√3S=(a+b)2-c2,则角C的大小为.15.已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<π2),y=f(x)的部分图象如图,则f(π24)= .16.在平面四边形ABCD中,若AB=1,BC=2,∠B=60°,∠C=45°,∠D=120°,则AD= .三、解答题(本大题共6小题,共70分,解答时写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)已知函数f(x)=√3sin 2ωx+cos4ωx-sin4ωx+1(其中0<ω<1),若点(-π6,1)是函数f(x)图象的一个对称中心.(1)求f(x)的解析式,并求距y轴最近的一条对称轴的方程;(2)先列表,再作出函数f(x)在区间[-π,π]上的图象.18.(本小题满分12分)已知函数f(x)=2√3sin(x+π4)·cos(x+π4)+sin 2x+a的最大值为1.(1)求函数f(x)的单调递增区间;(2)将函数f(x)的图象向左平移π6个单位,得到函数g(x)的图象,若方程g(x)=m在x∈[0,π2]上有解,求实数m的取值范围.19.(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,a+1a=4cos C,b=1.(1)若A=90°,求△ABC的面积;(2)若△ABC的面积为√32,求a,c.20.(本小题满分12分)设△ABC的内角A,B,C的对边分别为a,b,c,满足2asin A=(2sin B-√3sinC)b+(2sin C-√3sin B)c.(1)求角A的大小;(2)若a=2,b=2√3,求△ABC的面积.21.(本小题满分12分)已知函数f(x)=2cos(2x+2π3)+√3sin 2x.(1)求函数f(x)的最小正周期和最大值;(2)设△ABC的三个内角分别是A,B,C,若f(C2)=-12,且AC=1,BC=3,求sin A的值.22.(本小题满分12分)已知函数f(x)=2√3sin xcos x-3sin 2x-cos 2x+2. (1)当x ∈[0,π2]时,求f(x)的值域;(2)若△ABC 的内角A,B,C 的对边分别为a,b,c,且满足ba =√3,sin(2A+C)sinA=2+2cos(A+C),求f(B)的值.三角函数、解三角形、平面向量一、选择题1.B ∵sin(88°+θ)=23,∴cos(178°+θ)=cos(90°+88°+θ)=-sin(88°+θ)=-23.2.B ∵CP ⃗⃗⃗⃗ =2PA ⃗⃗⃗⃗⃗ ,∴|CP ⃗⃗⃗⃗⃗ ||PA ⃗⃗⃗⃗⃗ |=2,又△PAB 边PA 上的高与△PBC 边PC 上的高相等,∴S △PAB S△PBC=|PA ⃗⃗⃗⃗⃗||CP ⃗⃗⃗⃗⃗ |=12. 3.D 在△ABC 中,由asinA =bsinB,可得bsin A=asin B,又bsin A=3csin B,所以a=3c,又a=3,故c=1.由b 2=a 2+c 2-2accos B,cos B=23,可得b=√6.故选D.4.D f(x)=cos (x +π4)-cos (x -π4)=-√2sin x,所以函数f(x)是周期为2π的奇函数. 5.C 因为y=2sin (π6-2x)=-2sin (2x -π6),所以函数y=2sin (π6-2x)的单调递增区间就是函数y=sin (2x -π6)的单调递减区间.由π2+2kπ≤2x-π6≤3π2+2kπ(k∈Z ),解得π3+kπ≤x ≤5π6+kπ(k∈Z ),即函数y=2sin (π6-2x)的单调递增区间为[π3+kπ,5π6+kπ](k ∈Z ),又x ∈[-π,0],所以k=-1,故函数y=2sin (π6-2x)(x ∈[-π,0])的单调递增区间为[-2π3,-π6].6.A 由题意知{π2ω≥π2,3ωπ=kπ,k ∈Z,即{0<ω≤1,ω=k 3,k ∈Z,则ω=13或ω=23或ω=1.7.A 把函数y=sin (ωx -π6)的图象向左平移π3个单位得函数y=sin [ω(x +π3)-π6]=sin [ωx +(π3ω-π6)]的图象,由题意,得π3ω-π6=2kπ+π2(k ∈Z ),所以ω=6k+2(k∈Z ),所以ω的一个可能取值是2,故选A.8.C 因为AM ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +CM ⃗⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +23CB ⃗⃗⃗⃗⃗ =AC ⃗⃗⃗⃗⃗ +23(AB ⃗⃗⃗⃗⃗ -AC ⃗⃗⃗⃗⃗ )=13AC ⃗⃗⃗⃗⃗ +23AB ⃗⃗⃗⃗⃗ ,所以AM ⃗⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ =(13AC ⃗⃗⃗⃗⃗ +23AB ⃗⃗⃗⃗⃗ )·(AC ⃗⃗⃗⃗⃗ -AB ⃗⃗⃗⃗⃗ )=13×32-23×22+13AB ⃗⃗⃗⃗⃗ ·AC ⃗⃗⃗⃗⃗ =13+13×3×2cos π3=43,故选C. 9.C c 2=(a-b)2+6,即c 2=a 2+b 2-2ab+6①.∵C=π3,∴由余弦定理得c 2=a 2+b 2-ab②,由①和②得ab=6,∴S △ABC =12absin C=12×6×√32=3√32,故选C.10.C 由2S=(a+b)2-c 2得2×12absin C=a 2+b 2-c 2+2ab,得absin C=2abcos C+2ab,sin C-2cos C=2,∴sin 2C+4cos 2C-4sin Ccos C=4, ∴tan 2C -4tanC+4tan 2C+1=4,∴tan C=-43或0(舍去),故选C.11.B (AB ⃗⃗⃗⃗⃗ -2BC ⃗⃗⃗⃗⃗ )·(3BC ⃗⃗⃗⃗⃗ +4CA ⃗⃗⃗⃗⃗ )=3AB ⃗⃗⃗⃗⃗ ·BC ⃗⃗⃗⃗⃗ -6BC ⃗⃗⃗⃗⃗ 2+4AB ⃗⃗⃗⃗⃗ ·CA ⃗⃗⃗⃗⃗ -8BC ⃗⃗⃗⃗⃗ ·CA ⃗⃗⃗⃗⃗ =3|AB ⃗⃗⃗⃗⃗ |·|BC⃗⃗⃗⃗⃗ |cos 120°-6|BC ⃗⃗⃗⃗⃗ |2+4|AB ⃗⃗⃗⃗⃗ |·|CA ⃗⃗⃗⃗⃗ |cos 120°-8|BC ⃗⃗⃗⃗⃗ |·|CA ⃗⃗⃗⃗⃗ |cos 120°=3×1×1×(-12)-6×12+4×1×1×(-12)-8×1×1×(-12)=-32-6-2+4=-112,故选B. 12.B 将函数f(x)=2sin (ωx -π3)(ω>0)的图象向左平移π3ω个单位,得g(x)=2sin ω(x +π3ω)-π3=2sin (ωx +π3-π3)=2sin ωx 的图象,当x ∈[0,π4]时,ωx∈[0,ωπ4],要使y=g(x)在[0,π4]上为增函数,需满足ωπ4≤π2,即ω≤2,故ω的最大值为2.二、填空题 13.答案 -12解析 由题意可得e 1·e 2=12,|a |2=(e 1+λe 2)2=1+2λ×12+λ2=34,化简得λ2+λ+14=0,解得λ=-12. 14.答案π3解析 由4√3S=a 2+b 2-c 2+2ab 可得,2√3absin C=2abcos C+2ab,即√3sin C-cos C =2sin (C -π6)=1,sin (C -π6)=12,由题意知0<C<π,∴-π6<C-π6<56π,∴C -π6=π6,解得C=π3. 15.答案 √3解析 由题图可知:T=2(3π8-π8)=π2, ∴ω=2,∴2×π8+φ=kπ+π2,k ∈Z ,又|φ|<π2, ∴φ=π4.又f(0)=1,∴Atan π4=1, 得A=1,∴f(x)=tan (2x +π4),∴f (π24)=tan (π12+π4)=tan π3=√3. 16.答案√6-√22解析 连接AC.在△ABC 中,AC 2=BA 2+BC 2-2BA ·BC ·cos 60°=3,所以AC=√3,又AC 2+BA 2=4=BC 2,所以△ABC 是直角三角形,且∠BAC=90°.在四边形ABCD 中,∠BAD=360°-(60°+45°+120°)=135°,因此∠CAD=∠BAD-∠BAC=45°,所以∠ACD=180°-∠CAD-∠D=15°.在△ACD 中,由ADsin ∠ACD =ACsin ∠D,即ADsin15°=√3sin120°,得AD=√3sin15°sin120°=√3×(√6-√2)4×√3=√6-√22. 三、解答题17.解析 (1)f(x)=√3sin 2ωx+(cos 2ωx -sin 2ωx)(cos 2ωx+sin 2ωx)+1=√3sin 2ωx+cos 2ωx+1 =2sin (2ωx +π6)+1.∵点(-π6,1)是函数f(x)图象的一个对称中心,∴-ωπ3+π6=kπ,k∈Z ,∴ω=-3k+12,k ∈Z . ∵0<ω<1,∴ω=12,∴f(x)=2sin (x +π6)+1.由x+π6=kπ+π2,k ∈Z ,得x=kπ+π3,k ∈Z ,令k=0,得距y 轴最近的一条对称轴方程为x=π3.(2)由(1)知, f(x)=2sin (x +π6)+1,当x ∈[-π,π]时,列表如下:x+π6-5π6-π2π2π 7π6 x-π -2π3 -π6π3 5π6 π f(x) 0 -1 13 1则函数f(x)在区间[-π,π]上的图象如图所示.18.解析 (1)f(x)=√3sin (2x +π2)+sin 2x+a=√3cos 2x+sin 2x+a=2sin (2x +π3)+a,由题意知2+a=1,解得a=-1. 由-π2+2kπ≤2x+π3≤π2+2kπ,k∈Z , 解得-5π12+kπ≤x ≤π12+kπ,k∈Z ,∴函数f(x)的单调递增区间是[-5π12+kπ,π12+kπ],k ∈Z .(2)∵将函数f(x)的图象向左平移π6个单位,得到函数g(x)的图象,∴g(x)=f (x +π6)=2sin [2(x +π6)+π3]-1=2sin (2x +2π3)-1,当x ∈[0,π2]时,2x+2π3∈[2π3,5π3],当2x+2π3=2π3时,sin (2x +2π3)=√32,g(x)取最大值√3-1; 当2x+2π3=3π2时,sin (2x +2π3)=-1,g(x)取最小值-3.∴-3≤m ≤√3-1. 19.解析 (1)∵b=1, ∴a+1a =4cos C=4×a 2+b 2-c 22ab=2(a 2+1−c 2)a,∴2c 2=a 2+1.又A=90°,∴a 2=b 2+c 2=c 2+1, ∴2c 2=a 2+1=c 2+2,解得c=√2, ∴S △ABC =12bcsin A=12bc=12×1×√2=√22.(2)∵S △ABC =12absin C=12asin C=√32, ∴sin C=√3a ,∵a+1a=4cos C,∴[14(a +1a)]2+(√3a)2=1, 化简得(a 2-7)2=0,∴a=√7, ∴cos C=2√77. 由余弦定理得c 2=a 2+b 2-2ab ·cos C =7+1-2×√7×1×2√77=4,从而c=2.20.解析 (1)由已知及正弦定理可得2a 2=(2b-√3c)b+(2c-√3b)c,整理得b 2+c 2-a 2=√3bc,所以cos A =√32. 又A ∈(0,π),故A=π6. (2)由a sinA=b sinB ,a=2,b=2√3,A=π6, 得sin B=√32. 又B ∈(0,5π6),故B=π3或2π3. 若B=π3,则C=π2,于是S △ABC =12ab=2√3; 若B=2π3,则C=π6,于是S △ABC =12absin C=√3. 21.解析 (1)f(x)=2cos (2x +2π3)+√3sin 2x=-cos 2x,∴函数f(x)的最小正周期T=π,函数f(x)的最大值为1. (2)由(1)知f(x)=-cos 2x, ∴f (C2)=-cos C=-12,可得cos C=12. ∵C∈(0,π),∴sin C=√32. 由余弦定理可得,AB 2=AC 2+BC 2-2AC ·BC ·cos C=1+9-2×1×3×12=7, ∴AB=√7.第 11 页 共 11 页 ∴由正弦定理可得,sin A=BC ·sinC AB =3×√32√7=3√2114. 22.解析 (1)f(x)=2√3sin xcos x-3sin 2x-cos 2x+2 =√3sin 2x-2sin 2x+1=√3sin 2x+cos 2x=2sin (2x +π6).∵x∈[0,π2],∴2x+π6∈[π6,7π6], ∴sin (2x +π6)∈[-12,1],∴f(x)在x ∈[0,π2]上的值域是[-1,2]. (2)由题意可知sin[A+(A+C)]=2sin A+2sin Acos(A+C),即sin Acos(A+C)+cos Asin(A+C)=2sin A+2sin Acos(A+C), 化简可得sin C=2sin A,由正弦定理可得c=2a,∵b=√3a,∴cos B=a 2+c 2-b 22ac =a 2+4a 2-3a 22a ·2a =12, ∵0<B<π,∴B=π3.∴f(B)=2sin (2×π3+π6)=1.。

三角函数及解三角形专题1．【2019年高考全国Ⅰ卷文数】函数f (x )=在[,]-ππ的图像大致为A ．B ．C ．D ．【答案】D 【解析】由22sin()()sin ()()cos()()cos x x x xf x f x x x x x-+----===--+-+，得()f x 是奇函数，其图象关于原点对称，排除A ．又22π1π42π2()1,π2π()2f ++==>2π(π)01πf =>-+，排除B ，C ，故选D ． 【名师点睛】本题考查函数的性质与图象，渗透了逻辑推理、直观想象和数学运算素养，采取性质法或赋值法，利用数形结合思想解题．解答本题时，先判断函数的奇偶性，得()f x 是奇函数，排除A ，再注意到选项的区别，利用特殊值得正确答案． 2．【2019年高考全国Ⅰ卷文数】tan255°=A ．−2B ．−C ．2D ．【答案】D【解析】tan 255tan(18075)tan 75tan(4530)︒=︒+︒=︒=︒+︒=tan 45tan 301tan 45tan 30︒+︒-︒︒12+==+故选D. 【名师点睛】本题主要考查三角函数的诱导公式、两角和与差的三角函数、特殊角的三角函数值、运算求解能力．首先应用诱导公式，将问题转化成锐角三角函数的计算，进一步应用两角和的正切公式2sin cos ++x xx x计算求解．题目较易，注重了基础知识、基本计算能力的考查．3．【2019年高考全国Ⅰ卷文数】△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知a sin A −b sin B =4c sin C ，cos A =−14，则b c=A ．6B ．5C ．4D ．3【答案】A【解析】由已知及正弦定理可得2224a b c -=，由余弦定理推论可得2222214131cos ,,,422424b c a c c c A bc bc b +---==∴=-∴=3462b c ∴=⨯=，故选A ． 【名师点睛】本题考查正弦定理及余弦定理推论的应用．先利用余弦定理推论得出a ，b ，c 关系，再结合正弦定理边角互换列出方程，解出结果. 4．【2019年高考全国Ⅱ卷文数】若x 1=4π，x 2=43π是函数f (x )=sin x ω(ω>0)两个相邻的极值点，则ω= A ．2 B ．32C ．1D ．12【答案】A【解析】由题意知，()sin f x x ω=的周期232()44T ωπππ==-=π，解得2ω=．故选A ． 【名师点睛】本题考查三角函数的极值和周期，渗透了直观想象、逻辑推理和数学运算素养．利用周期公式，通过方程思想解题．5．【2019年高考全国Ⅱ卷文数】已知a ∈（0，π2），2sin2α=cos2α+1，则sin α=A ．15BCD 【答案】B 【解析】2sin 2cos21αα=+，24sin cos 2cos .0,,cos 02αααααπ⎛⎫∴⋅=∈∴> ⎪⎝⎭，sin 0,α>2sin cos αα∴=，又22sin cos 1αα+=，2215sin 1,sin 5αα∴==，又sin 0α>，sin 5α∴=，故选B ．【名师点睛】本题是对三角函数中二倍角公式、同角三角函数基本关系式的考查，中等难度，判断正余弦的正负，运算准确性是关键，题目不难，需细心，解决三角函数问题，研究角的范围后得出三角函数值的正负很关键，切记不能凭感觉．解答本题时，先利用二倍角公式得到正余弦关系，再利用角范围及正余弦平方和为1关系得出答案．6．【2019年高考全国Ⅲ卷文数】函数()2sin sin2f x x x =-在[0，2π]的零点个数为 A ．2 B ．3 C ．4D ．5【答案】B【解析】由()2sin sin 22sin 2sin cos 2sin (1cos )0f x x x x x x x x =-=-=-=， 得sin 0x =或cos 1x =，[]0,2πx ∈，0π2πx ∴=、或．()f x ∴在[]0,2π的零点个数是3，故选B ．【名师点睛】本题考查在一定范围内的函数的零点个数，渗透了直观想象和数学运算素养．令()0f x =，得sin 0x =或cos 1x =，再根据x 的取值范围可求得零点.7．【2019年高考北京卷文数】设函数f （x ）=cos x +b sin x （b 为常数），则“b =0”是“f （x ）为偶函数”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C【解析】0b =时，()cos sin cos f x x b x x =+=，()f x 为偶函数；()f x 为偶函数时，()=()f x f x -对任意的x 恒成立，即()cos()sin()cos sin f x x b x x b x -=-+-=-，cos sin cos sin x b x x b x +=-，得sin 0b x =对任意的x 恒成立，从而0b =.从而“0b =”是“()f x 为偶函数”的充分必要条件，故选C.【名师点睛】本题较易，注重基础知识、逻辑推理能力的考查.根据定义域为R 的函数()f x 为偶函数等价于()=()f x f x -恒成立进行判断.8．【2019年高考北京卷文数】如图，A ，B 是半径为2的圆周上的定点，P 为圆周上的动点，APB ∠是锐角，大小为β.图中阴影区域的面积的最大值为A ．4β+4cos βB ．4β+4sin βC ．2β+2cos βD ．2β+2sin β【答案】B【解析】设圆心为O ，如图1，连接OA ，OB ，AB ，OP ，则22AOB APB ∠=∠=β，所以22242OABS ⨯==扇形ββ，因为ABP AOB OAB S S S S =+-△△阴影扇形，且AOB OAB S S △扇形，都已确定， 所以当ABP S △最大时，阴影部分面积最大.观察图象可知，当P 为弧AB 的中点时（如图2），阴影部分的面积S 取最大值，此时∠BOP =∠AOP =π−β，面积S 的最大值为ABP AOB OAB S S S S =+-△△阴影扇形=4β+S △POB + S △POA =4β+12|OP ||OB |sin （π−β）+12|OP ||OA |sin （π−β）=4β+2sin β+2sin β=4β+4 sin β，故选B. 【名师点睛】本题主要考查阅读理解能力、数学应用意识、数形结合思想及数学式子变形和运算求解能力，有一定的难度.关键是观察分析区域面积最大时的状态，并将面积用边角等表示.9．【2019年高考天津卷文数】已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数，且()f x 的最小正周期为π，将()y f x =的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为()g x .若π4g ⎛⎫= ⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭A ．−2B ．C D ．2【答案】C【解析】∵()f x 为奇函数，∴(0)sin 0,=π,,0,f A k k k ϕϕ==∴∈∴=Z 0ϕ=； ∵()f x 的最小正周期为π，2ππ,T ∴==ω∴2ω=，∴1()sin sin ,2g x A x A x ==ω又π()4g =2A =，∴()2sin 2f x x =，3π()8f = 故选C.【名师点睛】本题主要考查函数的性质和函数的求值问题，解题关键是求出函数()g x ，结合函数性质逐步得出,,A ωϕ的值即可.10．【2019年高考全国Ⅰ卷文数】函数3π()sin(2)3cos 2f x x x =+-的最小值为___________． 【答案】4-【解析】23π()sin(2)3cos cos 23cos 2cos 3cos 12f x x x x x x x =+-=--=--+ 23172(cos )48x =-++，1cos 1x -≤≤，∴当cos 1x =时，min ()4f x =-，故函数()f x 的最小值为4-．【名师点睛】本题首先应用诱导公式，转化得到二倍角的余弦，进一步应用二倍角的余弦公式，得到关于cos x 的二次函数，从而得解.注意解答本题的过程中，部分考生易忽视1cos 1x -≤≤的限制，而简单应用二次函数的性质，出现运算错误．11．【2019年高考全国Ⅱ卷文数】ABC △的内角A ，B ，C 的对边分别为a ，b ，c ．已知b sin A +a cos B =0，则B =___________. 【答案】3π4【解析】由正弦定理，得sin sin sin cos 0B A A B +=．(0,),(0,)A B ∈π∈π，sin 0,A ∴≠∴sin cos 0B B +=，即tan 1B =-，3.4B π∴=【名师点睛】本题考查利用正弦定理转化三角恒等式，渗透了逻辑推理和数学运算素养．采取定理法，利用转化与化归思想解题．本题容易忽视三角形内角的范围致误，三角形内角均在(0,π)范围内，化边为角，结合三角函数的恒等变化求角．12．【2019年高考江苏卷】已知tan 2π3tan 4αα=-⎛⎫+ ⎪⎝⎭，则πsin 24α⎛⎫+ ⎪⎝⎭的值是 ▲ .【答案】10【解析】由()tan 1tan tan tan 2tan 1πtan 13tan 1tan 4αααααααα-===-++⎛⎫+ ⎪-⎝⎭，得23tan 5tan 20αα--=， 解得tan 2α=，或1tan 3α=-. πππsin 2sin 2cos cos 2sin 444ααα⎛⎫+=+ ⎪⎝⎭()22222sin cos cos sin sin 2cos 2=22sin cos αααααααα⎛⎫+-=+ ⎪+⎝⎭222tan 1tan =2tan 1ααα⎫+-⎪+⎝⎭， 当tan 2α=时，上式222212==22110⎛⎫⨯+- ⎪+⎝⎭ 当1tan 3α=-时，上式=22112()1()33[]=1210()13⨯-+--⨯-+综上，πsin 2410α⎛⎫+= ⎪⎝⎭ 【名师点睛】本题考查三角函数的化简求值，渗透了逻辑推理和数学运算素养.采取转化法，利用分类讨论和转化与化归思想解题.由题意首先求得tan α的值，然后利用两角和的正弦公式和二倍角公式将原问题转化为齐次式求值的问题，最后切化弦求得三角函数式的值即可.13．【2019年高考浙江卷】在ABC △中，90ABC ∠=︒，4AB =，3BC =，点D 在线段AC 上，若45BDC ∠=︒，则BD =___________，cos ABD ∠=___________．【解析】如图，在ABD △中，由正弦定理有：sin sin AB BD ADB BAC =∠∠，而3π4,4AB ADB =∠=,5AC ，34sin ,cos 55BC AB BAC BAC AC AC ∠==∠==，所以BD =.ππcos cos()cos cos sin sin 44ABD BDC BAC BAC BAC ∠=∠-∠=∠+∠=.【名师点睛】本题主要考查解三角形问题，即正弦定理、三角恒等变换、数形结合思想及函数方程思想.在ABD △中应用正弦定理，建立方程，进而得解.解答解三角形问题，要注意充分利用图形特征. 14．【2019年高考全国Ⅲ卷文数】ABC △的内角A 、B 、C 的对边分别为a 、b 、c ．已知sin sin 2A Ca b A +=． （1）求B ；（2）若△ABC 为锐角三角形，且c =1，求△ABC 面积的取值范围．【答案】（1）B =60°；（2）. 【解析】（1）由题设及正弦定理得sin sinsin sin 2A CA B A +=．因为sin A ≠0，所以sinsin 2A CB +=． 由180A BC ︒++=，可得sincos 22A C B +=，故cos 2sin cos 222B B B=． 因为cos02B ≠，故1sin 22B =，因此B =60°． （2）由题设及（1）知△ABC的面积ABC S =△． 由正弦定理得()sin 120sin 1sin sin 2tan 2C c A a C C C ︒-===+．由于△ABC 为锐角三角形，故0°<A <90°，0°<C <90°，由（1）知A +C =120°，所以30°<C <90°，故122a <<，从而82ABC S <<△． 因此，△ABC面积的取值范围是⎝⎭．【名师点睛】这道题考查了三角函数的基础知识，以及正弦定理的使用（此题也可以用余弦定理求解），最后考查V ABC 是锐角三角形这个条件的利用，考查的很全面，是一道很好的考题. 15．【2019年高考北京卷文数】在△ABC 中，a =3，–2b c =，cos B =12-． （1）求b ，c 的值； （2）求sin （B +C ）的值． 【答案】（1）7b =，5c =；（2【解析】（1）由余弦定理2222cos b a c ac B =+-，得2221323()2b c c =+-⨯⨯⨯-．因为2b c =+，所以2221(2)323()2c c c +=+-⨯⨯⨯-． 解得5c =．所以7b =． （2）由1cos 2B =-得sin 2B =．由正弦定理得sin sin 14a A Bb ==． 在ABC △中，B C A +=π-．所以sin()sin B C A +==【名师点睛】本题主要考查余弦定理、正弦定理的应用，两角差的正弦公式的应用等知识，意在考查学生的转化能力和计算求解能力.16．【2019年高考天津卷文数】在ABC △中，内角,,A B C 所对的边分别为,,a b c .已知2b c a +=，3sin 4sin c B a C =.（1）求cos B 的值； （2）求sin 26πB ⎛⎫+⎪⎝⎭的值. 【答案】（1）14-；（2）716+-. 【解析】（1）在ABC △中，由正弦定理sin sin b cB C=，得sin sin b C c B =， 又由3sin 4sin c B a C =，得3sin 4sin b C a C =，即34b a =．又因为2b c a +=，得到43b a =，23c a =． 由余弦定理可得222222416199cos 22423a a a a cb B ac a a +-+-===-⋅⋅．（2）由（1）可得sin B ==，从而sin 22sin cos B B B ==，227cos 2cos sin 8B B B =-=-，故71sin 2sin 2cos cos 2sin 66682B B B πππ⎛⎫+=+=⨯= ⎪⎝⎭． 【名师点睛】本小题主要考查同角三角函数的基本关系，两角和的正弦公式，二倍角的正弦与余弦公式，以及正弦定理、余弦定理等基础知识．考查运算求解能力．17．【2019年高考江苏卷】在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．（1）若a =3c ，b ，cos B =23，求c 的值； （2）若sin cos 2A B a b =，求sin()2B π+的值．【答案】（1）c =（2.【解析】（1）因为23,3a cb B ===，由余弦定理222cos 2a c b B ac +-=，得2222(3)323c c c c+-=⨯⨯，即213c =.所以c =（2）因为sin cos 2A Ba b =， 由正弦定理sin sin a b A B =，得cos sin 2B Bb b=，所以cos 2sin B B =. 从而22cos (2sin )B B =，即()22cos 41cos B B =-，故24cos 5B =.因为sin 0B >，所以cos 2sin 0B B =>，从而cos B =.因此πsin cos 2B B ⎛⎫+== ⎪⎝⎭【名师点睛】本小题主要考查正弦定理、余弦定理、同角三角函数关系、诱导公式等基础知识，考查运算求解能力.18．【2019年高考江苏卷】如图，一个湖的边界是圆心为O 的圆，湖的一侧有一条直线型公路l ，湖上有桥AB （AB 是圆O 的直径）．规划在公路l 上选两个点P 、Q ，并修建两段直线型道路PB 、QA ．规划要求：线段PB 、QA 上的所有点到点O 的距离均不小于圆．．．．O 的半径．已知点A 、B 到直线l 的距离分别为AC 和BD （C 、D 为垂足），测得AB =10，AC =6，BD =12（单位：百米）． （1）若道路PB 与桥AB 垂直，求道路PB 的长；（2）在规划要求下，P 和Q 中能否有一个点选在D 处？并说明理由；（3）在规划要求下，若道路PB 和QA 的长度均为d （单位：百米）.求当d 最小时，P 、Q 两点间的距离．【答案】（1）15（百米）；（2）见解析；（3）17+.【解析】解法一：（1）过A 作AE BD ⊥，垂足为E .由已知条件得，四边形ACDE 为矩形，6, 8DE BE AC AE CD =====.'因为PB ⊥AB ， 所以84cos sin 105PBD ABE ∠=∠==. 所以12154cos 5BD PB PBD ===∠. 因此道路PB 的长为15（百米）.（2）①若P 在D 处，由（1）可得E 在圆上，则线段BE 上的点（除B ，E ）到点O 的距离均小于圆O 的半径，所以P 选在D 处不满足规划要求.②若Q 在D 处，连结AD ，由（1）知10AD ==， 从而2227cos 0225AD AB BD BAD AD AB +-∠==>⋅，所以∠BAD 为锐角. 所以线段AD 上存在点到点O 的距离小于圆O 的半径.因此，Q 选在D 处也不满足规划要求.综上，P 和Q 均不能选在D 处.（3）先讨论点P 的位置.当∠OBP <90°时，线段PB 上存在点到点O 的距离小于圆O 的半径，点P 不符合规划要求；当∠OBP ≥90°时，对线段PB 上任意一点F ，OF ≥OB ，即线段PB 上所有点到点O 的距离均不小于圆O 的半径，点P 符合规划要求.设1P 为l 上一点，且1PB AB ⊥，由（1）知，1P B =15， 此时11113sin cos 1595PD PB PBD PB EBA =∠=∠=⨯=； 当∠OBP >90°时，在1PPB △中，115PB PB >=. 由上可知，d ≥15.再讨论点Q 的位置. 由（2）知，要使得QA ≥15，点Q 只有位于点C 的右侧，才能符合规划要求.当QA =15时，1CQ =此时，线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上，当PB ⊥AB ，点Q 位于点C 右侧，且CQ =时，d 最小，此时P ，Q 两点间的距离PQ =PD +CD +CQ =17+因此，d 最小时，P ，Q 两点间的距离为17+.解法二：（1）如图，过O 作OH ⊥l ，垂足为H.以O 为坐标原点，直线OH 为y 轴，建立平面直角坐标系.因为BD =12，AC =6，所以OH =9，直线l 的方程为y =9，点A ，B 的纵坐标分别为3，−3.因为AB 为圆O 的直径，AB =10，所以圆O 的方程为x 2+y 2=25.从而A （4，3），B （−4，−3），直线AB 的斜率为34.因为PB ⊥AB ，所以直线PB 的斜率为43-， 直线PB 的方程为42533y x =--.所以P （−13，9），15PB ==.因此道路PB 的长为15（百米）.（2）①若P 在D 处，取线段BD 上一点E （−4，0），则EO =4<5，所以P 选在D 处不满足规划要求. ②若Q 在D 处，连结AD ，由（1）知D （−4，9），又A （4，3），所以线段AD ：36(44)4y x x =-+-剟.在线段AD 上取点M （3，154），因为5OM =<=， 所以线段AD 上存在点到点O 的距离小于圆O 的半径.因此Q 选在D 处也不满足规划要求.综上，P 和Q 均不能选在D 处.（3）先讨论点P 的位置.当∠OBP <90°时，线段PB 上存在点到点O 的距离小于圆O 的半径，点P 不符合规划要求；当∠OBP ≥90°时，对线段PB 上任意一点F ，OF ≥OB ，即线段PB 上所有点到点O 的距离均不小于圆O 的半径，点P 符合规划要求.设1P 为l 上一点，且1PB AB ⊥，由（1）知，1P B =15，此时1P （−13，9）； 当∠OBP >90°时，在1PPB △中，115PB PB >=. 由上可知，d ≥15.再讨论点Q 的位置.由（2）知，要使得QA≥15，点Q 只有位于点C 的右侧，才能符合规划要求.当QA =15时，设Q （a ，9），由15(4)AQ a ==>，得a =4+Q （4+9），此时，线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上，当P （−13，9），Q （4+9）时，d 最小，此时P ，Q 两点间的距离4(13)17PQ =+-=+.因此，d 最小时，P ，Q 两点间的距离为17+.【名师点睛】本小题主要考查三角函数的应用、解方程、直线与圆等基础知识，考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.19．【2019年高考浙江卷】设函数()sin ,f x x x =∈R .（1）已知[0,2),θ∈π函数()f x θ+是偶函数，求θ的值；（2）求函数22[()][()]124y f x f x ππ=+++的值域． 【答案】（1）π2θ=或3π2；（2）[1-+． 【解析】（1）因为()sin()f x x θθ+=+是偶函数，所以，对任意实数x 都有sin()sin()x x θθ+=-+， 即sin cos cos sin sin cos cos sin x x x x θθθθ+=-+，故2sin cos 0x θ=，所以cos 0θ=．又[0,2π)θ∈，因此π2θ=或3π2． （2）2222ππππsin sin 124124y f x f x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ππ1cos 21cos 213621cos 2sin 222222x x x x ⎛⎫⎛⎫-+-+ ⎪ ⎪⎛⎫⎝⎭⎝⎭=+=-- ⎪ ⎪⎝⎭π123x ⎛⎫=+ ⎪⎝⎭．因此，函数的值域是[1+． 【名师点睛】本题主要考查三角函数及其恒等变换等基础知识，同时考查运算求解能力.20．【重庆西南大学附属中学校2019届高三第十次月考数学试题】已知角α的顶点在坐标原点，始边与x 轴正半轴重合，终边经过点(1)P ，则cos2=αAB ．13C ．13- D．3-【答案】B【解析】因为角α的顶点在坐标原点，始边与x 轴正半轴重合，终边经过点(1)P ，所以cos3==-α， 因此21cos 22cos 13=-=αα.故选B. 【名师点睛】本题主要考查三角函数的定义，以及二倍角公式，熟记三角函数的定义与二倍角公式即可，属于常考题型.解答本题时，先由角α的终边过点(1)P ，求出cos α，再由二倍角公式，即可得出结果.。

2019年高考数学真题分类汇编专题15：三角函数（综合题）一、解答题1.（2019•江苏）在△ABC中，角A，B，C的对边分别为a，b，c．（1）若a=3c，b= ，cos B= ，求c的值；（2）若，求的值．2.[选修4-4：坐标系与参数方程]在极坐标系中，已知两点，直线l的方程为.（1）求A，B两点间的距离；（2）求点B到直线l的距离.3.（2019•江苏）如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB（AB 是圆O的直径）．规划在公路l上选两个点P、Q，并修建两段直线型道路PB、QA．规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位:百米）．（1）若道路PB与桥AB垂直，求道路PB的长；（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；（3）对规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．4.（2019•浙江）设函数f（x）=sinx，x R。

（1）已知θ=[0，2x），函数f（x+θ）是偶函数，求θ的值（2）求函数y=[f（x）+ ]2+[f（x+ ）]2的值域5.（2019•天津）在中，内角所对的边分别为.已知，.（Ⅰ）求的值；（Ⅱ）求的值.6.（2019•全国Ⅲ）△ABC的内角A、B、C的对边分别为a，b，c，已知（1）求B；（2）若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围.7.（2019•北京）在△ABC中，a=3，b-c=2，cosB=- .（I）求b，c的值：（II）求sin（B+C）的值.8.（2019•北京）在△ABC中，a=3，b-c=2，cosB=- .（I）求b，c的值；（II）求sin（B-C）的值.9.（2019•卷Ⅰ）∆ABC的内角A，B，C的对边分别为a，b，c.设(sinB-sinC)2=sin2A-sinBsinC。

专题四 三角函数与三角形1.【2018高考新课标1，理2】o o o o sin 20cos10cos160sin10- =( )（A ） （B （C ）12- （D ）12【答案】D【解析】原式=o o o o sin 20cos10cos 20sin10+ =o sin 30=12，故选D. 【考点定位】三角函数求值.【名师点睛】本题解题的关键在于观察到20°与160°之间的联系，会用诱导公式将不同角化为同角，再用两角和与差的三角公式化为一个角的三角函数，利用特殊角的三角函数值即可求出值，注意要准确记忆公式和灵活运用公式.2.【2018高考山东，理3】要得到函数sin 43y x π⎛⎫=-⎪⎝⎭的图象，只需要将函数sin 4y x =的图象（ ） （A ）向左平移12π个单位 （B ）向右平移12π个单位（C ）向左平移3π个单位 （D ）向右平移3π个单位 【答案】B【解析】因为sin 4sin 4312y x x ππ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭ ，所以要得到函数sin 43y x π⎛⎫=- ⎪⎝⎭的图象，只需将函数sin 4y x = 的图象向右平移12π个单位.故选B.【考点定位】三角函数的图象变换.【名师点睛】本题考查了三角函数的图象，重点考查学生对三角函数图象变换规律的理解与掌握，能否正确处理先周期变换后相位变换这种情况下图象的平移问题，反映学生对所学知识理解的深度.3.【2018高考新课标1，理8】函数()f x =cos()x ωϕ+的部分图像如图所示，则()f x 的单调递减区间为( )(A)13(,),44k k k Z ππ-+∈ (B)13(2,2),44k k k Z ππ-+∈ (C)13(,),44k k k Z -+∈ (D)13(2,2),44k k k Z -+∈【答案】D【考点定位】三角函数图像与性质【名师点睛】本题考查函数cos()y A x ωϕ=+的图像与性质，先利用五点作图法列出关于ωϕ，方程，求出ωϕ，，或利用利用图像先求出周期，用周期公式求出ω，利用特殊点求出ϕ，再利用复合函数单调性求其单调递减区间，是中档题，正确求ωϕ，使解题的关键.4.【2018高考四川，理4】下列函数中，最小正周期为且图象关于原点对称的函数是（ ）()cos(2)2A y x π=+ ()sin(2)2B y x π=+ ()sin 2cos 2C y x x =+ ()sin cos D y x x =+【答案】A【解析】对于选项A ，因为2sin 2,2y x T ππ=-==，且图象关于原点对称，故选A. 【考点定位】三角函数的性质.【名师点睛】本题不是直接据条件求结果，而是从4个选项中找出符合条件的一项，故一般是逐项检验，但这类题常常可采用排除法.很明显，C 、D 选项中的函数既不是奇函数也不是偶函数，而B 选项中的函数是偶函数，故均可排除，所以选A.5.【2018高考重庆，理9】若tan 2tan 5πα=，则3cos()10sin()5παπα-=-（ ）A 、1B 、2C 、3D 、4 【答案】C 【解析】由已知，3cos()10sin()5παπα-=-33cos cos sin sin 1010sin cos cos sin 55ππααππαα+-33cos tan sin 1010tan cos sin 55ππαππα+=-33cos 2tan sin 105102tan cos sin555ππππππ+=- 33cos cos 2sin sin 510510sin cos 55ππππππ+=＝155(cos cos )(cos cos )21010101012sin 25πππππ++-3cos103cos 10ππ==，选C. 【考点定位】两角和与差的正弦（余弦）公式，同角间的三角函数关系，三角函数的恒等变换.【名师点晴】三角恒等变换的主要题目类型是求值，在求值时只要根据求解目标的需要，结合已知条件选用合适的公式计算即可．本例应用两角和与差的正弦（余弦）公式化解所求式子，利用同角关系式使得已知条件可代入后再化简，求解过程中注意公式的顺用和逆用．6.【2018高考陕西，理3】如图，某港口一天6时到18时的水深变化曲线近似满足函数3sin()6y x k πϕ=++，据此函数可知，这段时间水深（单位：m ）的最大值为（ ）A ．5B ．6C ．8D ．10【答案】C【解析】由图象知：min 2y =，因为min 3y k =-+，所以32k -+=，解得：5k =，所以这段时间水深的最大值是max 3358y k =+=+=，故选C ． 【考点定位】三角函数的图象与性质．【名师点晴】本题主要考查的是三角函数的图象与性质，属于容易题．解题时一定要抓住重要字眼“最大值”，否则很容易出现错误．解三角函数求最值的试题时，我们经常使用的是整体法．本题从图象中可知sin 16x πϕ⎛⎫+=- ⎪⎝⎭时，y 取得最小值，进而求出k 的值，当sin 16x πϕ⎛⎫+= ⎪⎝⎭时，y 取得最大值． 7.【2018高考安徽，理10】已知函数()()sin f x x ωϕ=A +（A ，ω，ϕ均为正的常数）的最小正周期为π，当23x π=时，函数()f x 取得最小值，则下列结论正确的是（ ） （A ）()()()220f f f <-< （B ）()()()022f f f <<- （C ）()()()202f f f -<< （D ）()()()202f f f <<- 【答案】A【考点定位】1.三角函数的图象与应用；2.函数值的大小比较.【名师点睛】对于三角函数中比较大小的问题，一般的步骤是：第一步，根据题中所给的条件写出三角函数解析式，如本题通过周期判断出ω，通过最值判断出ϕ，从而得出三角函数解析式；第二步，需要比较大小的函数值代入解析式或者通过函数图象进行判断，本题中代入函数值计算不太方便，故可以根据函数图象的特征进行判断即可.【2018高考湖南，理9】将函数()sin 2f x x =的图像向右平移(0)2πϕϕ<<个单位后得到函数()g x 的图像，若对满足12()()2f x g x -=的1x ，2x ，有12min3x x π-=，则ϕ=（ ）A.512π B.3π C.4π D.6π 【答案】D. 【解析】试题分析：向右平移ϕ个单位后，得到)22sin()(ϕ-=x x g ，又∵2|)()(|21=-x g x f ，∴不妨ππk x 2221+=，ππϕm x 22222+-=-，∴πϕπ)(221m k x x -+-=-，又∵12min 3x x π-=，∴632πϕπϕπ=⇒=-，故选D.【考点定位】三角函数的图象和性质.【名师点睛】本题主要考查了三角函数的图象和性质，属于中档题，高考题对于三角函数的考查，多以)sin()(ϕω+=x A x f 为背景来考查其性质，解决此类问题的关键：一是会化简，熟悉三角恒等变形，对三角函数进行化简；二是会用性质，熟悉正弦函数的单调性，周期性，对称性，奇偶性等.【2018高考上海，理13】已知函数()sin f x x =．若存在1x ，2x ，⋅⋅⋅，m x 满足1206m x x x π≤<<⋅⋅⋅<≤，且()()()()()()1223112n n f x f x f x f x f x f x --+-+⋅⋅⋅+-=（2m ≥，m *∈N ），则m 的最小值 为 ． 【答案】8【解析】因为()sin f x x =，所以()()max min ()()2m n f x f x f x f x -≤-=，因此要使得满足条件()()()()()()1223112n n f x f x f x f x f x f x --+-+⋅⋅⋅+-=的m 最小，须取123456783579110,,,,,,,6,222222x x x x x x x x πππππππ========即8.m = 【考点定位】三角函数性质【名师点睛】三角函数最值与绝对值的综合，可结合数形结合解决.极端位置的考虑方法是解决非常规题的一个行之有效的方法.8.【2018高考天津，理13】在ABC ∆ 中，内角,,A B C 所对的边分别为,,a b c ，已知ABC ∆的面积为 ，12,cos ,4b c A -==- 则a 的值为 .【答案】8【解析】因为0A π<<，所以sin A ==又1sin 242ABC S bc A bc ∆===∴=，解方程组224b c bc -=⎧⎨=⎩得6,4b c ==，由余弦定理得 2222212cos 64264644a b c bc A ⎛⎫=+-=+-⨯⨯⨯-= ⎪⎝⎭，所以8a =.【考点定位】同角三角函数关系、三角形面积公式、余弦定理.【名师点睛】本题主要考查同角三角函数关系、三角形面积公式、余弦定理.解三角形是实际应用问题之一，先根据同角三角关系求角A 的正弦值，再由三角形面积公式求出24bc =，解方程组求出,b c 的值，用余弦定理可求边a 有值.体现了综合运用三角知识、正余弦定理的能力与运算能力，是数学重要思想方法的体现. 【2018高考上海，理14】在锐角三角形C AB 中，1tan 2A =，D 为边C B 上的点，D ∆AB 与CD ∆A 的面积分别为2和4．过D 作D E ⊥AB 于E ，DF C ⊥A 于F ，则D DF E ⋅= ． 【答案】1615-【考点定位】向量数量积，解三角形【名师点睛】向量数量积的两种运算方法(1)当已知向量的模和夹角时，可利用定义法求解，即a·b＝|a||b|cos<a ，b>．(2)当已知向量的坐标时，可利用坐标法求解，即若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a·b＝x 1x 2＋y 1y 2.向量夹角与三角形内角的关系，可利用三角形解决；向量的模与三角形的边的关系，可利用面积解决.9.【2018高考广东，理11】设ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，若a = 1sin 2B =，6C =π，则b = . 【答案】1． 【解析】因为1sin 2B =且()0,B π∈，所以6B π=或56B π=，又6C π=，所以6B π=，23A B C ππ=--=，又a =sin sin a b A B =sin 36bπ=解得1b =，故应填入1． 【考点定位】三角形的内角和定理，正弦定理应用．【名师点睛】本题主要考查三角形的内角和定理、运用正弦定理解三角形，属于容易题，解答此题要注意由1sin 2B =得出6B π=或56B π=时，结合三角形内角和定理舍去56B π=． 10.【2018高考北京，理12】在ABC △中，4a =，5b =，6c =，则sin 2sin AC= ．【答案】1【解析】222sin 22sin cos 2sin sin 2A A A a b c a C C c bc+-==⋅2425361616256⨯+-=⋅=⨯⨯ 考点定位：本题考点为正弦定理、余弦定理的应用及二倍角公式，灵活使用正弦定理、余弦定理进行边化角、角化边.【名师点睛】本题考查二倍角公式及正弦定理和余弦定理，本题属于基础题，题目所求分式的分子为二倍角正弦，应用二倍角的正弦公式进行恒等变形，变形后为角的正弦、余弦式，灵活运用正弦定理和余弦定理进行角化边，再把边长代入求值.11.【2018高考湖北，理12】函数2π()4cos cos()2sin |ln(1)|22x f x x x x =---+的零点个数为 ．【答案】2【解析】因为2π()4cos cos()2sin |ln(1)|22x f x x x x =---+ |)1ln(|sin 2sin )cos 1(2+--+=x x x x |)1ln(|2sin +-=x x所以函数)(x f 的零点个数为函数x y 2sin =与|)1ln(|+=x y 图象的交点的个数， 函数x y 2sin =与|)1ln(|+=x y 图象如图，由图知，两函数图象有2个交点， 所以函数)(x f 有2个零点.【考点定位】二倍角的正弦、余弦公式，诱导公式，函数的零点.【名师点睛】数形结合思想方法是高考考查的重点. 已知函数的零点个数，一般利用数形结合转化为两个图象的交点个数，这时图形一定要准确。

1 +2 = 4 + 2π> 1, f (π) = 排除 A ．又 f ( ) =( )2π专题 06 三角函数及解三角形1．【2019 年高考全国Ⅰ卷文数】函数 f(x)= sinx + x在 [-π, π] 的图像大致为cosx + x 2A ．B ．C ．D ．【答案】D【解析】由 f (- x ) = sin(- x) + (- x) cos(- x ) + (- x )2 - sin x - x= = - f ( x ) ，得 f ( x ) 是奇函数，其图象关于原点对称，cos x + x 2π 2 π22π π -1 + π2 > 0 ，排除 B ，C ，故选 D ．【名师点睛】本题考查函数的性质与图象，渗透了逻辑推理、直观想象和数学运算素养，采取性质法或赋值法，利用数形结合思想解题．解答本题时，先判断函数的奇偶性，得f ( x ) 是奇函数，排除 A ，再注意到选项的区别，利用特殊值得正确答案．2．【2019 年高考全国Ⅰ卷文数】tan255°=A ．−2− 3C ．2− 3【答案】DB ．−2+ 3D ．2+ 3【解析】 tan 255︒ = tan(180︒ + 75︒) = tan 75︒ = tan(45 ︒ + 30︒) =tan 45︒ + tan 30︒ 1 - tan 45︒ tan 30︒= 1 +1 -33 = 2 + 3. 故选 D. 33【名师点睛】本题主要考查三角函数的诱导公式、两角和与差的三角函数、特殊角的三角函数值、运1，x 2= 是函数 f(x)= sin ω x ( ω >0)两个相邻的极值点，则ω = ω = 2(2sin 2α = cos2 α +1 ， ∴ 4sin α ⋅ cos α = 2cos 2 α . α ∈ 0, ⎪ ,∴ cos α > 0 ， sin α > 0,计算求解．题目较易，注重了基础知识、基本计算能力的考查．3．【2019 年高考全国Ⅰ卷文数】△ABC 的内角 A ，B ，C 的对边分别为 a ，b ，c ，已知 asinA −b sinB =4csinC ，cosA =− 1 4 ，则 bc =A ．6C ．4B ．5D ．3【答案】A【解析】由已知及正弦定理可得 a 2 - b 2 = 4c 2 ，1 b2 + c 2 - a 2 c 2 - 4c 2 1 3c 1由余弦定理推论可得 - = cos A = , ∴ = - , ∴ = ,4 2bc 2bc 4 2b 4b 3∴ = ⨯ 4 = 6 ，故选 A ．c 2【名师点睛】本题考查正弦定理及余弦定理推论的应用．先利用余弦定理推论得出 a ，b ，c 关系，再结合正弦定理边角互换列出方程，解出结果.4．【2019 年高考全国Ⅱ卷文数】若 x 1= π 3π 4 4A ．2 C ．1【答案】AB ．D ．32 12【解析】由题意知， f ( x ) = sin ω x 的周期 T = 2π 3π π- ) = π ，解得 ω = 2 ．故选 A ．4 4【名师点睛】本题考查三角函数的极值和周期，渗透了直观想象、逻辑推理和数学运算素养．利用周期公式，通过方程思想解题．5．【2019 年高考全国Ⅱ卷文数】已知 a ∈（0，π ），2sin2α=cos2α+1，则 sin α= 2A ．15B ．5 5C ．33【答案】BD ．2 5 5【解析】⎛ π ⎫ ⎝ 2 ⎭∴2sin α = cos α ，又sin 2 α + cos 2 α = 1 ，∴ 5sin 2α = 1,sin 2α = ，又sin α >0 ，∴ s in α =15 5 5，故选 B ．【名师点睛】本题是对三角函数中二倍角公式、同角三角函数基本关系式的考查，中等难度，判断正余弦的正负，运算准确性是关键，题目不难，需细心，解决三角函数问题，研究角的范围后得出三角函数值的正负很关键，切记不能凭感觉．解答本题时，先利用二倍角公式得到正余弦关系，再利用角范围及正余弦平方和为 1 关系得出答案．6．【2019年高考全国Ⅲ卷文数】函数 f ( x ) = 2sinx - sin2 x 在[0，2π]的零点个数为A ．2C ．4B ．3D ．5【答案】B【解析】由 f ( x ) = 2sin x - sin 2 x = 2sin x - 2sin x cos x = 2sin x(1- cos x) = 0 ，得 sin x = 0 或 cos x = 1 ，x ∈[0,2 π]，∴ x = 0、π或2π ．∴ f ( x ) 在 [0,2 π]的零点个数是 3，故选 B ．【名师点睛】本题考查在一定范围内的函数的零点个数，渗透了直观想象和数学运算素养．令 f ( x ) = 0 ，得 sin x = 0 或 cos x = 1 ，再根据 x 的取值范围可求得零点.7．【2019 年高考北京卷文数】设函数 f （x ）=cosx +b sinx （b 为常数），则“b =0”是“f （x ）为偶函数”的A ．充分而不必要条件C ．充分必要条件B ．必要而不充分条件D ．既不充分也不必要条件【答案】C【解析】 b = 0 时， f ( x ) = cos x + b s in x = cos x ， f ( x ) 为偶函数；f ( x ) 为偶函数时，f (- x )=f ( x ) 对任意的 x 恒成立，即 f (- x ) = cos(- x ) + b s in(- x ) = cos x - b s in x ，cos x + b s in x = cos x - b s in x ，得 b s in x = 0 对任意的 x 恒成立，从而 b = 0 .从而“ b = 0 ”是“ f ( x ) 为偶函数”的充分必要条件，故选 C.【名师点睛】本题较易，注重基础知识、逻辑推理能力的考查.根据定义域为 R 的函数 f ( x ) 为偶函数等2价于 f (- x )=f ( x ) 恒成立进行判断.8．【2019 年高考北京卷文数】如图，A ，B 是半径为 2 的圆周上的定点，P 为圆周上的动点， ∠APB 是锐角，大小为 β.图中阴影区域的面积的最大值为A ．4β+4cos βC ．2β+2cos βB ．4β+4sin βD ．2β+2sin β【答案】B【解析】设圆心为 O ，如图 1，连接 OA ，OB ，AB ，OP ，则 ∠AOB = 2∠APB = 2β ，所以 S扇形OAB2β ⨯ 22= = 4β ，2因为 S 阴影 = S 扇形OAB + S △ABP - S △AOB ，且 S 扇形OAB ，S △AOB 都已确定，所以当 S △ABP 最大时，阴影部分面积最大.观察图象可知，当 P 为弧 AB 的中点时（如图 2），阴影部分的面积 S 取最大值，此时∠BOP =∠AOP =π−β，面积 S 的最大值为 S 阴影 = S 扇形OAB + S △ABP - S △AOB =4β+△S POB + △S POA =4β+1|OP||OB|sin （π−β）+ 12|OP||OA|sin （π−β）=4β+2sin β+2sin β=4β+4 sin β，故选 B.【名师点睛】本题主要考查阅读理解能力、数学应用意识、数形结合思想及数学式子变形和运算求解对应的函数为g(x).若g ⎪=2，则f ⎪=.ω=π,∴ω=2，能力，有一定的难度.关键是观察分析区域面积最大时的状态，并将面积用边角等表示9．【2019年高考天津卷文数】已知函数f(x)=A s in(ωx+ϕ)(A>0,ω>0,|ϕ|<π)是奇函数，且f(x)的最小正周期为π，将y=f(x)的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象⎛π⎫⎛3π⎫⎝4⎭⎝8⎭A．−2 C．2B．-2 D．2【答案】C【解析】∵f(x)为奇函数，∴f(0)=A s inϕ=0,∴ϕ=kπ,k∈Z,∴k=0,ϕ=0；∵f(x)的最小正周期为π，∴T=2π∴g(x)=A s in 12ωx=A s in x,π又g()=2，∴A=2，4∴f(x)=2sin2x，f(3π8)= 2.故选C.【名师点睛】本题主要考查函数的性质和函数的求值问题，解题关键是求出函数g(x)，结合函数性质逐步得出A,ω,ϕ的值即可.10．【2019年高考全国Ⅰ卷文数】函数f(x)=sin(2x+【答案】-43π2)-3cos x的最小值为___________．【解析】f(x)=sin(2x+317 =-2(cos x+)2+，483π2)-3cos x=-cos2x-3cos x=-2cos2x-3cos x+1-1≤cos x≤1，∴当cos x=1时，f(x)min=-4，故函数f(x)的最小值为-4．【名师点睛】本题首先应用诱导公式，转化得到二倍角的余弦，进一步应用二倍角的余弦公式，得到关于cos x的二次函数，从而得解.注意解答本题的过程中，部分考生易忽视-1≤cos x≤1的限制，而简单应用二次函数的性质，出现运算错误．⎛ α π ⎫ 3 ，则 sin 2α + ⎪ 的值是 ▲ . tan + ⎪ ⎝ 4 ⎭ π ⎫ tan α + 1tan α + 13 ，得 3tan 2α - 5tan α - 2 = 0 ，tan α + ⎪ tan α (1 - tan α )sin2α + ⎪ = sin 2α cos + cos 2α sin 2 (sin 2α + cos 2α )=2 2 ⎝ sin 2 α + cos 2 α⎭2 ⎝tan 2 α + 1⎭=； 当 tan α = 2 时，上式 = ⎪ ⎝ 22 + 1 ⎭ 10 1 3 3 ]= 2 .⨯ [2 ⨯ (- ) + 1 - (- )2 当 tan α = - 时，上式=111．【2019 年高考全国Ⅱ卷文数】 △ABC 的内角 A ，B ，C 的对边分别为 a ，b ，c ．已知 b sinA +acosB =0，则 B=___________. 【答案】3π4【 解 析 】 由 正 弦 定 理 ， 得 sin B s in A + sin A c os B = 0 ．A ∈ (0, π),B ∈ (0, π) ， ∴ s in A ≠ 0, ∴sin B + cos B = 0 ，即 tan B = -1，∴ B =3π 4.【名师点睛】本题考查利用正弦定理转化三角恒等式，渗透了逻辑推理和数学运算素养．采取定理法，利用转化与化归思想解题．本题容易忽视三角形内角的范围致误，三角形内角均在 (0, π) 范围内，化边为角，结合三角函数的恒等变化求角．12．【2019 年高考江苏卷】已知【答案】210tan α 2=- ⎛ π ⎫⎝ 4 ⎭ 【解析】由解得 tan α = 2 ，或 tan α = -13.⎛π ⎫ π π ⎝4 ⎭ 4 4==2 ⎛ 2sin α cos α + cos 2 α - sin 2 α ⎫ ⎪2 ⎛ 2 tan α + 1 - tan 2 α ⎫ ⎪ ，2 ⎛ 2 ⨯ 2 + 1 - 22 ⎫ 2 21 1 23 2 10 (- )2 + 1 36综上，sin2π【答案】122【解析】如图，在△ABD中，由正弦定理有：ABAC=AB2+BC2=5，sin BACBC3AB4122【B2410.【名师点睛】本题考查三角函数的化简求值，渗透了逻辑推理和数学运算素养.采取转化法，利用分类讨论和转化与化归思想解题.由题意首先求得tan的值，然后利用两角和的正弦公式和二倍角公式将原问题转化为齐次式求值的问题，最后切化弦求得三角函数式的值即可.13．【2019年高考浙江卷】在△ABC中，ABC90，AB4，BC3，点D在线段AC上，若BDC45，则BD___________，cos ABD___________．72，510BD3π，而AB4,ADB,sin ADB sin BAC4,cos BAC，所以BDAC5AC55.ππ72cos ABD cos(BDC BAC)cos cos BAC sin sin BAC4410.【名师点睛】本题主要考查解三角形问题，即正弦定理、三角恒等变换、数形结合思想及函数方程思想.在△ABD中应用正弦定理，建立方程，进而得解.解答解三角形问题，要注意充分利用图形特征. 14．2019年高考全国Ⅲ卷文数】△ABC的内角A、、C的对边分别为a、b、c．已知a sin （1）求B；（2）若△ABC为锐角三角形，且c=1，求△ABC面积的取值范围．33【答案】（1）B=60°；（2）(,).82【解析】（1）由题设及正弦定理得s inA sinA CsinB sinA．2A C2bsinA．因为 cos B sin (120︒ - C)从而 3△ABC <因此，△ABC 面积的取值范围是 8 , 2 ⎪⎭.c因为sinA ≠ 0，所以 sin A + C= sin B ．2由 A + B + C = 180︒ ，可得 sin A + C B B B B= cos ，故 cos = 2sin cos ．2 2 2 2 2B 1≠ 0 ，故 sin = ，因此B =60°．2 2 2（2）由题设及（1△）知 ABC 的面积 S△ABC = 3 4a ．c sin A3 1由正弦定理得 a = == + ． sin Csin C2 tan C 2△由于 ABC 为锐角三角形，故0°<A <90°，0°<C <90°，由（1）知A +C =120°，所以30°<C <90°，故 1< a < 2 ， 23 < S 8 2．⎛ 3 3 ⎫ ．⎝【名师点睛】这道题考查了三角函数的基础知识，以及正弦定理的使用（此题也可以用余弦定理求解），最后考查 V ABC 是锐角三角形这个条件的利用，考查的很全面，是一道很好的考题15．【2019 年高考北京卷文数】在△ABC 中，a =3， b – = 2 ，cosB = -（1）求 b ，c 的值；（2）求 sin （B +C ）的值．1 2．【答案】（1） b = 7 ， c = 5 ；（2）3 3 14.【解析】（1）由余弦定理 b 2 = a 2 + c 2 - 2ac cos B ，得1b 2 = 32 +c 2 - 2 ⨯ 3 ⨯ c ⨯ (- ) ．2因为 b = c + 2 ，1所以 (c + 2)2= 32+ c 2- 2 ⨯ 3 ⨯ c ⨯ (- ) ．2解得 c = 5 ．（2）由 cos B = - 得 sin B =6 ⎭⎛⎫ 【答案】（1） - 1【解析】（1）在 △ABC 中，由正弦定理ba 2 + c 2 -b 2 a 2 + a 2 - a 29 92 2 ⋅ a ⋅ a（ 2 ） 由 （ 1 ） 可 得 sin B = 1 - cos 2 B =15sin 2B + ⎪ = sin 2B cos + cos 2B sin =- ⨯ - ⨯ =-所以 b = 7 ．1 32 2．由正弦定理得 s in A = a 3 3 sin B = b 14．在 △ABC 中， B + C = π- A ．所以 sin( B + C ) = sin A = 3 314．【名师点睛】本题主要考查余弦定理、正弦定理的应用，两角差的正弦公式的应用等知识，意在考查学生的转化能力和计算求解能力.16．【 2019 年高考天津卷文数】在 △ABC 中，内角 A, B, C 所对的边分别为 a, b , c .已知 b + c = 2 a ，3c s in B = 4a sin C .（1）求 cos B 的值；（2）求 sin 2 B + ⎝π ⎪ 的值.3 5 + 7；（2） -4 16.c= ，得 b s in C = c sin B ， sin B sin C又由 3c s in B = 4a sin C ，得 3b s in C = 4a sin C ，即 3b = 4a ．4 2又因为 b + c = 2a ，得到 b = a ， c = a ．3 3 由余弦定理可得 cos B =4 16 1 = =- ．2ac 4315， 从 而 sin 2 B = 2sin B cos B = - ，487cos 2B = cos 2 B - sin 2 B = - ，故8⎛ π⎫ π π 15 3 7 1 3 5 + 7 ⎝6 ⎭ 6 6 8 2 8 2 16．【名师点睛】本小题主要考查同角三角函数的基本关系，两角和的正弦公式，二倍角的正弦与余弦公（2）若 sin A ( ) 从而 cos 2 B = (2sin B)2 ，即 cos 2 B = 4 1 - cos 2 B ，故 cos 2 B = .= = 因此 sin B + ⎪ = cos B = ⎫ 要求：线段 PB 、QA 上的所有点到点 O 的距离均不小于圆 O 的半径．已知点 A 、B 到直线 l 的距离分式，以及正弦定理、余弦定理等基础知识．考查运算求解能力．17．【2019 年高考江苏卷】在△ABC 中，角 A ，B ，C 的对边分别为 a ，b ，c ．（1）若 a =3c ，b = 2 ，cosB = 23，求 c 的值；cos B π= ，求 sin(B + ) 的值．a 2b 2【答案】（1） c =3 2 5 ；（2）3 5.【解析】（1）因为 a = 3c, b =2,cos B = 23，a 2 + c 2 -b 22 (3c)2 + c 2 - ( 2) 21 由余弦定理 cos B =，得 = ，即 c 2 = .2ac3 2 ⨯ 3c ⨯ c3所以 c =3 3.（2）因为 sin A cos B= ，a 2ba b cos B sin B由正弦定理 ，得 ，所以 cos B = 2sin B .sin A sin B 2b b45因为 sin B > 0 ，所以 cos B = 2sin B > 0 ，从而 cos B = 2 5 5.⎛ π 2 5⎝2 ⎭ 5.【名师点睛】本小题主要考查正弦定理、余弦定理、同角三角函数关系、诱导公式等基础知识，考查运算求解能力.18．【2019 年高考江苏卷】如图，一个湖的边界是圆心为 O 的圆，湖的一侧有一条直线型公路 l ，湖上有桥 AB （AB 是圆 O 的直径）．规划在公路 l 上选两个点 P 、Q ，并修建两段直线型道路 PB 、QA ．规划．．．．别为 AC 和 BD （C 、D 为垂足），测得 AB =10，AC =6，BD =12（单位：百米）．（1）若道路 PB 与桥 AB 垂直，求道路 PB 的长；（2）在规划要求下，P 和 Q 中能否有一个点选在 D 处？并说明理由；所以cos∠PBD=sin∠ABE=8（3）在规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．【答案】（1）15（百米）；（2）见解析；（3）17+321（百米）.【解析】解法一：（1）过A作AE⊥BD，垂足为E.由已知条件得，四边形ACDE为矩形，DE=BE=AC=6,AE=CD=8.'因为PB⊥AB，4=.105所以PB=BD12==15cos∠PBD4.5因此道路PB的长为15（百米）.（2）①若P在D处，由（1）可得E在圆上，则线段BE上的点（除B，E）到点O的距离均小于圆O的半径，所以P选在D处不满足规划要求.②若Q在D处，连结AD，由（1）知AD=AE2+ED2=10，AD2+AB2-BD27从而cos∠BAD==>0，所以∠BAD为锐角.2A D⋅AB25所以线段AD上存在点到点O的距离小于圆O的半径.因此，Q选在D处也不满足规划要求.51 1 12 2 .1综上，P 和Q 均不能选在D 处.（3）先讨论点P 的位置.当∠OBP <90°时，线段PB 上存在点到点O 的距离小于圆O 的半径，点P 不符合规划要求；当∠OBP ≥90°时，对线段PB 上任意一点F ，OF ≥OB ，即线段PB 上所有点到点O 的距离均不小于圆O 的半径，点P 符合规划要求.设 P 为l 上一点，且 PB ⊥ AB ，由（1）知， P B =15，3 此时 PD = PB sin ∠PBD = PB cos ∠EBA = 15 ⨯= 9 ；1 111当∠OBP >90°时，在 △PPB 中， PB > PB = 15 .11由上可知，d ≥15.再讨论点Q 的位置.由 （ 2 ） 知 ， 要 使 得 QA ≥15 ， 点 Q 只 有 位 于 点 C 的 右 侧 ， 才 能 符 合 规 划 要 求 . 当 QA =15 时 ，CQ = QA - AC = 1 5 2 -6 2 = 3 2 此时，线段QA 上所有点到点O 的距离均不小于圆O 的半径.综 上 ， 当 PB ⊥ AB ， 点 Q 位 于 点 C 右 侧 ， 且 CQ = 3 21 时 ， d 最 小 ， 此 时 P ， Q 两 点 间 的 距 离PQ =PD +CD +CQ =17+ 3 21 .因此，d 最小时，P ，Q 两点间的距离为17+ 3 21 （百米）.解法二：（1）如图，过O 作OH ⊥l ，垂足为H.以O 为坐标原点，直线OH 为y 轴，建立平面直角坐标系.因为BD =12，AC =6，所以OH =9，直线l 的方程为y =9，点A ，B 的纵坐标分别为3，−3.因为AB 为圆O 的直径，AB =10，所以圆O 的方程为x 2+y 2=25.从而A （4，3），B （−4，−3），直线AB 的斜率为34.在线段AD 上取点M （3， ），因为 OM = 32 +⎪ < 32 + 42 = 5 ， ⎝ 4 ⎭1 1 1 1因为PB ⊥AB ，所以直线PB 的斜率为 -4 25直线PB 的方程为 y =- x -.334 3，所以P （−13，9）， PB =(-13 + 4)2 + (9 + 3)2 = 15 .因此道路PB 的长为15（百米）.（2）①若P 在D 处，取线段BD 上一点E （−4，0），则EO =4<5，所以P 选在D 处不满足规划要求.②若Q 在D 处，连结AD ，由（1）知D （−4，9），又A （4，3）， 所以线段AD ： y = - 3x + 6(-4剟x 4) .415⎛ 15 ⎫24所以线段AD 上存在点到点O 的距离小于圆O 的半径.因此Q 选在D 处也不满足规划要求.综上，P 和Q 均不能选在D 处.（3）先讨论点P 的位置.当∠OBP <90°时，线段PB 上存在点到点O 的距离小于圆O 的半径，点P 不符合规划要求；当∠OBP ≥90°时，对线段PB 上任意一点F ，OF ≥OB ，即线段PB 上所有点到点O 的距离均不小于圆O 的半径，点P 符合规划要求.设 P 为l 上一点，且 PB ⊥ AB ，由（1）知， P B =15，此时 P （−13，9）；当∠OBP >90°时，在 △PPB 中， PB > PB = 15 .1 1由上可知，d ≥15.再讨论点Q 的位置.由（2）知，要使得QA≥15，点Q 只有位于点C 的右侧，才能符合规划要求.当QA =15时，设Q （a ，9），由 AQ = (a - 4)2 + (9 - 3)2 = 15(a > 4) ，得a = 4 + 3 21 ，所以Q （ 4 + 3 21 ，9），此时，线段QA上所有点到点O 的距离均不小于圆O 的半径.综上，当P （−13，9），Q （ 4 + 3 21 ，9）时，d 最小，此时P ，Q 两点间的距离PQ = 4 + 3 21 - (-13) = 17 + 3 21 .因此，d 最小时，P ，Q 两点间的距离为17 + 3 21 （百米）.)]2+ [ f ( x + )]2 的值域．又 θ ∈ [0, 2π) ，因此θ =π（2） y = ⎢ f x + ⎪⎥ + ⎢ f x + ⎪⎥ = sin 2 x + + sin 2 x + ⎪ ⎝12 ⎭⎦ ⎣ ⎝ ⎝ 12 ⎭ ⎝ 4 ⎭⎦ 4 ⎭ 1 - cos 2 x + ⎪ 1 - cos 2 x + ⎪= + = 1 - cos 2 x - sin 2 x ⎪⎪π ⎫ 6 ⎭ cos 2 x + ⎪ ．.【3B ．C ． - 1【名师点睛】本小题主要考查三角函数的应用、解方程、直线与圆等基础知识，考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.19．【2019 年高考浙江卷】设函数 f ( x ) = sinx, x ∈ R .（1）已知θ ∈ [0,2 π), 函数 f ( x + θ ) 是偶函数，求θ 的值；（2）求函数 y = [ f ( x + π π 12 4【答案】（1）θ = π 3π 3 3或 ；（2） [1- ,1 + ] ．2 2 2 2【解析】（1）因为 f ( x + θ ) = sin( x + θ ) 是偶函数，所以，对任意实数x 都有 sin( x + θ ) = sin( - x + θ) ，即 sin x cos θ + cos x s in θ = - s in x cos θ + cos x sin θ ，故 2sin x cos θ = 0 ，所以 cos θ = 0 ．3π或 ． 2 2⎡ ⎣ ⎛ π ⎫⎤ 2 ⎡ ⎛ π ⎫⎤ 2⎛ π ⎫ ⎛ π ⎫ ⎪⎛ ⎛ π ⎫ ⎝⎝ 2 ⎭ 1 ⎛ 3 3 ⎫ 2 2 2 ⎝ 2 2⎭= 1 - 3 2⎛ π ⎫⎝ 3 ⎭因此，函数的值域是[1- 3 3,1 + ] ．2 2【名师点睛】本题主要考查三角函数及其恒等变换等基础知识，同时考查运算求解能力20． 重庆西南大学附属中学校 2019 届高三第十次月考数学试题】已知角 α 的顶点在坐标原点，始边与 x 轴正半轴重合，终边经过点 P(- 2，1) ，则 cos2α =A ． 2 21 33D ． -2 2 3tan α - ⎪=cos α = - , a ∈ (- π,0 )，∴ α ∈ - π, -⎪ ，π ⎫ tan α - 1 4 1 则 tan α - ⎪ = = = - .故选 C ． 4 ⎭ 1 + tan α 73 1 + ，将函数图象向左平移 个单位得到函数 g ( x ) 的图象，则 g ( x ) =【答案】B【解析】因为角α 的顶点在坐标原点，始边与 x 轴正半轴重合，终边经过点 P(- 2，1) ，所以 cos α = - 2 2 + 1=- 6 3，因此 cos 2α = 2cos 2α - 1 = 13.故选 B.【名师点睛】本题主要考查三角函数的定义，以及二倍角公式，熟记三角函数的定义与二倍角公式即可，属于常考题型.解答本题时，先由角α 的终边过点 P(- 2，1) ，求出 cos α ，再由二倍角公式，即可得出结果.21．【四川省宜宾市 2019 届高三第三次诊断性考试数学试题】已知 c os α = - 4， α ∈ (-π,0 )，则5⎛ π ⎫ ⎝4 ⎭A ．1 7B ．7C ． -17D ． -7【答案】C【解析】3 3∴ s in α = - , tan α = ，5 43- 1⎛⎝4【名师点睛】本题主要考查了同角三角函数关系式及两角差的正切公式的简单应用，属于基础题．解答本题时，根据已知 cos α 的值，结合同角三角函数关系式可求 tan α，然后根据两角差的正切公式即可求解．22．【广东省韶关市 2019 届高考模拟测试（4 月）数学文试题】已知函数 f ( x ) = sin(ω x +π 6) (ω > 0)的相邻对称轴之间的距离为π A ． sin( x + ) 3 π π2 6 πB ． sin(2 x + )3) + ] = sin 2 x + + ⎪ = cos 2 x 的图象，故选 C ． ⇒ > ,∴ω <C ． cos2 x【答案】C【解析】由函数 f ( x ) = sin(ω x + πD ． cos(2 x + )3π π T π)(ω > 0) 的相邻对称轴之间的距离为 ，得 = ，即 T = π ，所6 2 2 2以 π =2πω ，解得 ω = 2 ，π π将函数 f ( x ) = sin(2 x + ) 的图象向左平移 个单位，6 6得到 g ( x ) = sin[2( x + π 6 π ⎛ 6 ⎝ π π ⎫ 3 6 ⎭【名师点睛】本题考查的知识要点：三角函数关系式的平移变换和伸缩变换的应用，正弦型函数性质的应用，主要考查学生的运算能力和转换能力，属于基础题型．解答本题时，首先利用函数的图象求出函数的关系式，进一步利用图象的平移变换的应用求出结果．23．【河南省郑州市 2019 届高三第三次质量检测数学试题】已知函数 f (x ) = A s in (ωx + ϕ )，A > 0,ω > 0, ϕ < π的部分图象如图所示，则使 f (a + x )- f (a - x ) = 0 成立的 a 的最小正值为2A ．C ．π12 π 4B ．D ．π 6 π 3【答案】B【解析】由图象易知， A = 2 ， f (0) = 1 ，即 2sin ϕ = 1 ，且 ϕ <π π，即 ϕ = ， 2 6由图可知， f ( 11π 11π π 11π π 12k - 2) = 0, 所以 sin( ⋅ ω + ) = 0,∴ ⋅ ω + = k π, k ∈ Z ，即 ω = , k ∈ Z ，12 12 6 12 6 1111π 2π 11π 24又由图可知，周期T >，且 ω > 0 ， 12 ω 12 11所以由五点作图法可知 k = 2, ω = 2 ，所以函数 f ( x ) = 2sin(2 x + π) ，6C的对边，若△ABC的面积为S，且43S=(a+b)2-c2，则sin C+⎪= 4D．即3sin C-cos C=1，即2sin C-6⎭=1，则sin C-⎪=，则sin C+4⎭+=sin cos+cos sin=3⨯2+⨯2=6+2 =sin⎝34⎭222243434因为f(a+x)-f(a-x)=0，所以函数f(x)关于x=a对称，即有2a+ππkππ=kπ+,k∈Z，所以可得a=+,k∈Z，6226π所以a的最小正值为.6故选B.【名师点睛】本题考查了三角函数的图象和性质，熟练运用三角函数的图象和周期对称性是解题的关键，属于中档题.解答本题时，先由图象，求出A,ϕ,ω，可得函数f(x)的解析式，再由f(a+x)-f(a-x)=0易知f(x)的图象关于x=a对称，即可求得a的值.24．【山东省实验中学等四校2019届高三联合考试数学试题】在△ABC中，a，b，c分别为角A，B，⎛π⎫⎝4⎭A．1B．C．6-2【答案】D 226+2 4【解析】由43S=(a+b )2-c2，得43⨯12ab sin C=a2+b2-c2+2ab，∵a2+b2-c2=2ab cos C，∴23ab sin C=2ab cos C+2ab，⎛⎝π⎫⎪⎛⎝π⎫16⎭2∵0<C<π，∴-ππ5ππππ<C-<，∴C-=，即C=，666663⎛⎝π⎫⎪⎛ππ⎫ππππ1⎪，故选D．【名师点睛】本题主要考查解三角形的应用，结合三角形的面积公式以及余弦定理求出C的值以及利用两角和差的正弦公式进行计算是解决本题的关键．解答本题时，根据三角形的面积公式以及余弦定理进行化简求出C的值，然后利用两角和的正弦公式进行求解即可．25．【山东省烟台市2019届高三3月诊断性测试（一模）数学试题】在△ABC中，角A，B，C的对边【分别为 a ， b ， c ，若 a = 1 ， 3 sin A cos C + ( 3 sin C + b ) cos A = 0 ，则角 A =A ．C ．2π 3 π 6B ．D ．π 3 5π 6【答案】D【解析】∵ a = 1 ， 3 sin A cos C + ( 3 sin C + b ) cos A = 0 ，∴ 3 sin A cos C + 3 sin C cos A = -b cos A ，∴ 3 sin( A + C ) = 3 sin B = -b cos A ，∴ 3a sin B = -b cos A ，由正弦定理可得： 3 sin A s in B = - sin B cos A ，∵ sin B > 0 ，∴ 3 sin A = - cos A ，即 tan A = - 3 3，∵ A ∈ (0, π) ，∴ A = 5π 6.故选 D ．【名师点睛】本题主要考查解三角形，熟记正弦定理，两角和的正弦公式即可，属于基础题．解答本题时，由 3 sin A cos C + ( 3 sin C + b ) cos A = 0 ，可得 3a sin B = -b cos A ，再由正弦定理得到tan A = -3 ，结合 A ∈ (0, π) ，即可求得 A 的值．326． 广东省韶关市 2019 届高考模拟测试（4 月）数学试题】在 △ABC 中，a 、b 、c 分别是内角 A 、 B 、C 的对边，且 3b cos A = sin A(a cos C + c cos A) .（1）求角 A 的大小；（2）若 a = 2 3 ， △ABC 的面积为5 3 4，求 △ABC 的周长．【答案】（1） A =π 3；（2） 5 3 .【解析】（1）∵ 3b cos A = sin A(a cos C + c cos A) ，∴由正弦定理可得：3 sin B cos A = sin A(sin A cos C + sin C cos A) = sin A s in( A + C ) = sin A s in B ，， a = 2 3 ， △ABC 的面积为， （2）当 x ∈ [0, ] 时，不等式 c < f ( x ) < c + 2 恒成立，求实数 c 的取值范围．【 = =即 3 sin B cos A = sin A s in B ，∵ sin B ≠ 0 ，∴ tan A = 3 ，∵ A ∈ (0, π) ，∴ A = π3．（2）∵ A = π 5 33 41 3 5 3∴ bc sin A = bc =2 4 4，∴ bc = 5 ，∴由余弦定理可得： a 2 = b 2 + c 2 - 2bc cos A ，即12 = b 2 + c 2 - bc = (b + c)2 - 3bc = (b + c)2 - 15 ，解得： b + c = 3 3 ，∴ △ABC 的周长为 a + b + c = 2 3 + 3 3 = 5 3 .【名师点睛】本题主要考查了正弦定理，两角和的正弦函数公式，三角形的面积公式，余弦定理在解三角形中的综合应用，考查了计算能力和转化思想，属于基础题．（1）由正弦定理，两角和的正弦函数公式化简已知等式可得 3 sin B cos A = sin A s in B ，由nisB0≠ ，可求 tan A = 3 ，结合 A ∈ (0, π) ，可求 A = π 3．（2）利用三角形的面积公式可求bc = 5 ，进而根据余弦定理可得b + c = 3 3 ，即可计算△ABC 的周长的值．27． 北京市昌平区 2019 届高三 5 月综合练习（二模）数学试题】已知函数 f ( x ） cos x( 3 sin x - cos x)+π（1）求 f ( ) 的值；3π21【答案】（1）1；（2） (-1,- ) .21【解析】（1） f ( x ）3 sin x cos x - cos 2 x + 21 2.sin 2 x - 所以 - ≤ sin （2 x - ）≤ 1 . ⎪⎩c + 2 > 1 （2）首先求得函数 f (x )在区间 ⎢0, ⎥ 上的值域，然后结合恒成立的结论得到关于 c 的不等式组，求 2= 31 cos2 x 2 2π =sin(2 x - ) ， 6 π 所以 f ( ) = 1 . 3 （2）因为 0 ≤ x ≤ π 2， π π 5π 所以 - ≤ 2 x - ≤ ， 6 6 6 1 π 2 6 ⎧ 1 ⎪ c <- 1 由不等式 c < f ( x ) < c + 2 恒成立，得 ⎨ 2 ，解得 -1 < c < - . 21 所以实数 c 的取值范围为 (-1,- ) . 2【名师点睛】本题主要考查三角函数的性质及其应用，恒成立问题的处理方法等知识，意在考查学生的转化能力和计算求解能力.（1）首先整理函数的解析式，然后结合函数的解析式求解函数值即可；⎡ π ⎤ ⎣ ⎦解不等式组可得 c 的取值范围.20。

2，π）单调递增5B．3D．专题三角函数及解三角形1．【2019年高考全国Ⅰ卷理数】函数f(x)=sinx+x在[-π,π]的图像大致为cosx+x2A．B．C．D．2．【2019年高考全国Ⅰ卷理数】关于函数f(x)=sin|x|+|sin x|有下述四个结论：①f(x)是偶函数②f(x)在区间（π③f(x)在[-π,π]有4个零点其中所有正确结论的编号是A．①②④C．①④3．【2019年高考全国Ⅱ卷理数】下列函数中，以④f(x)的最大值为2B．②④D．①③π2为周期且在区间(π4，π2)单调递增的是A．f(x)=|cos2x|C．f(x)=cos|x|4．【2019年高考全国Ⅱ卷理数】已知α∈(0，B．f(x)=|sin2x|D．f(x)=sin|x|π2)，2sin2α=cos2α+1，则sinα=5A．15C．3255 5．【2019年高考全国Ⅲ卷理数】设函数f(x)=sin（ωx+个零点，下述四个结论：①f(x)在（0,2π）有且仅有3个极大值点②f(x)在（0,2π）有且仅有2个极小值点π5）(ω＞0)，已知f(x)在[0,2π]有且仅有5④ ω 的取值范围是[ ， )【2π ，且 g ⎛ ⎫⎪= 2 ，则 f ⎛ ⎪= = - ，则 sin 2α + ⎪ 的值是 ▲ . ⎛ αtan + ⎪【 B b c③ f (x )在（ 0, π 10）单调递增12 295 10其中所有正确结论的编号是A ．①④C ．①②③B ．②③D ．①③④6． 2019 年高考天津卷理数】已知函数 f ( x ) = A s in(ω x + ϕ )( A > 0, ω > 0,| ϕ |< π) 是奇函数，将 y = f (x )的图象上所有点的横坐标伸长到原来的 2 倍（纵坐标不变），所得图象对应的函数为g (x )．若 g (x )的最小正周期为A ． -2C ． 2⎝ 4 ⎭ ⎝ 8 ⎭π 3π ⎫ B ． - 2D ． 27．【2019 年高考北京卷理数】函数 f （x ）=sin 22x 的最小正周期是__________．8．【2019 年高考全国Ⅱ卷理数】 △ABC 的内角 A, B, C 的对边分别为 a, b , c .若 b = 6, a = 2c, B = π3△ABC 的面积为_________．，则9．【2019 年高考江苏卷】已知tan α 2 ⎛ π ⎫π ⎫ 3 ⎝ 4 ⎭⎝ 4 ⎭10．【2019 年高考浙江卷】在△ABC 中， ∠ABC = 90︒ ， AB = 4 ， BC = 3，点 D 在线段 AC 上，若∠BDC = 45︒ ，则 BD = ___________， cos ∠ABD = ___________．11．【2019 年高考全国Ⅰ卷理数】△ABC 的内角 A ，B ，C 的对边分别为 a ，b ，c ，设(sin B - sin C )2 = sin 2 A - sin B sin C ．（1）求 A ；（2）若 2a + b = 2c ，求 sinC ．12． 2019 年高考全国Ⅲ卷理数】△ABC 的内角 A ， ，C 的对边分别为 a ， ， ，已知 a sin（1）求 B ； A + C2b sin A．（2）求 sin2B + ⎪ 的值．（△2）若 ABC 为锐角三角形，且 c △=1，求 ABC 面积的取值范围．13．【2019 年高考北京卷理数】在△ABC 中，a =3，b −c =2，cosB = -（1）求 b ，c 的值；（2）求 sin （B –C ）的值．1 2 ．14．【2019 年高考天津卷理数】在 △ABC 中，内角 A, B, C 所对的边分别为 a, b , c ．已知 b + c = 2a ，3c s in B = 4a sin C ．（1）求 cos B 的值；⎛ ⎝π⎫ 6⎭15．【2019 年高考江苏卷】在△ABC 中，角 A ，B ，C 的对边分别为 a ，b ，c ．（1）若 a =3c ，b = 2 ，cosB = 2 3，求 c 的值；（2）若sin A要求：线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分)]2+[f(x+)]2的值域．【cos Bπ=，求sin(B+)的值．a2b216．【2019年高考江苏卷】如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P、Q，并修建两段直线型道路PB、QA．规划．．．．别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位：百米）．（1）若道路PB与桥AB垂直，求道路PB的长；（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；（3）在规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．17．【2019年高考浙江卷】设函数f(x)=sinx,x∈R.（1）已知θ∈[0,2π),函数f(x+θ)是偶函数，求θ的值；（2）求函数y=[f(x+ππ12418．重庆西南大学附属中学校2019届高三第十次月考数学试题】已知角α的顶点在坐标原点，始边与x轴正半轴重合，终边经过点P(-2，1)，则cos2α=3B．C．-1tan α-⎪=20．【广东省韶关市2019届高考模拟测试（4月）数学文试题】已知函数f(x)=sin(ωx+)(ω>0)的相，将函数图象向左平移个单位得到函数g(x)的图象，则g(x)= C的对边，若△ABC的面积为S，且43S=(a+b)2-c2，则sin C+⎪=A．22133D．-22319．【四川省宜宾市2019届高三第三次诊断性考试数学试题】已知c osα=-4，α∈(-π,0)，则5⎛π⎫⎝4⎭1A．B．77C．-17D．-7π6邻对称轴之间的距离为ππ26A．sin(x+C．cos2xπ3)πB．sin(2x+)3πD．cos(2x+)321．【河南省郑州市2019届高三第三次质量检测数学试题】已知函数f(x)=A s in(ωx+ϕ)，A>0,ω>0,ϕ<π的部分图象如图所示，则使f(a+x)-f(a-x)=0成立的a的最小正值为2A．C．π12π4B．D．π6π322．【山东省实验中学等四校2019届高三联合考试数学试题】在△ABC中，a，b，c分别为角A，B，⎛π⎫⎝4⎭4D ．【（2）当 x ∈ [0, ] 时，不等式 c < f ( x ) < c + 2 恒成立，求实数 c 的取值范围．【 =A ．1B ．22C ． 6 - 26 + 2423．【山东省烟台市 2019 届高三 3 月诊断性测试（一模）数学试题】在△ABC 中，角 A ， B ， C 的对边分别为 a ， b ， c ，若 a = 1 ， 3 sin A cos C + ( 3 sin C + b ) cos A = 0 ，则角 A =A ．C ．2π3 π 6B ．D ．π 3 5π 624． 广东省韶关市 2019 届高考模拟测试（4 月）数学试题】在 △ABC 中，a 、b 、c 分别是内角 A 、 B 、C 的对边，且 3b cos A = sin A(a cos C + c cos A) .（1）求角 A 的大小；（2）若 a = 2 3 ， △ABC 的面积为5 3 4，求 △ABC 的周长．25． 北京市昌平区 2019 届高三 5 月综合练习（二模）数学试题】已知函数 f ( x ） cosx( 3 sin x - cos x)+π（1）求 f ( ) 的值；3π21 2.【解析】由 f (- x ) = sin(- x) + (- x) 2 1 + 2 = 4 + 2π > 1, f (π) = 排除 A ．又 f ( ) = ( )2π 2 -1 + π2 ， π ）单调递增答 案1．【2019 年高考全国Ⅰ卷理数】函数 f(x)= sinx + xcosx + x 2在 [-π, π] 的图像大致为A ．B ．C ．D ．【答案】D- sin x - x== - f ( x ) ，得 f ( x ) 是奇函数，其图象关于原点对称， cos(- x ) + (- x ) cos x + x 2π π 2 π22π> 0 ，排除 B ，C ，故选 D ．【名师点睛】本题考查函数的性质与图象，渗透了逻辑推理、直观想象和数学运算素养，采取性质法或赋值法，利用数形结合思想解题．解答本题时，先判断函数的奇偶性，得f ( x ) 是奇函数，排除 A ，再注意到选项的区别，利用特殊值得正确答案．2．【2019 年高考全国Ⅰ卷理数】关于函数 f ( x ) = sin | x | + | sin x | 有下述四个结论：①f(x)是偶函数②f(x)在区间（π③f(x)在 [-π, π] 有 4 个零点 其中所有正确结论的编号是A ．①②④C ．①④④f(x)的最大值为 2B ．②④D ．①③【答案】C【解析】Q f (- x ) = sin - x + sin (- x ) = sin x + sin x = f (x ) , ∴ f (x )为偶函数，故①正确．当π⎛π<x<π时，f(x)=2sin x，它在区间 ,π⎪单调递减，故②错误．作出y=sin2x的图象如图3，由图象知，其周期为，在区间(，)单调递减，排除B，⎫2⎝2⎭当0≤x≤π时，f(x)=2sin x，它有两个零点：0,π；当-π≤x<0时，f(x)=sin(-x)-sin x =-2sin x，它有一个零点：-π，故f(x)在[-π,π]有3个零点：-π,0,π，故③错误．当x∈[2kπ,2kπ+π](k∈N*)时，f(x)=2sin x；当x∈[2kπ+π,2kπ+2π](k∈N*)时，f(x)=sin x-sin x=0，又f(x)为偶函数，∴f(x)的最大值为2，故④正确．综上所述，①④正确，故选C．【名师点睛】本题也可画出函数f(x)=sin x+sin x的图象（如下图），由图象可得①④正确．3．【2019年高考全国Ⅱ卷理数】下列函数中，以A．f(x)=|cos2x|C．f(x)=cos|x|π2为周期且在区间(B．f(x)=|sin2x|D．f(x)=sin|x|π4，π2)单调递增的是【答案】A【解析】作出因为y=sin|x|的图象如下图1，知其不是周期函数，排除D；因为y=cos x=cos x，周期为2π，排除C；作出y=cos2x图象如图2，由图象知，其周期为πππ，在区间(，)单调递增，A正确；242πππ242故选A．图12 )，2sin2α=cos2α+1，则 sin α=5B ．3D ． 【 解 析 】 Q 2sin 2α = cos2 α +1 ， ∴ 4sin α ⋅ cos α = 2cos 2 α .Q α ∈ 0, ⎪ ,∴ cos α > 0 ， sin α > 0,∴2sin α = cos α ，又sin 2α + cos 2α = 1 ，∴ 5sin 2 α = 1,sin 2α = ，又sin α > 0 ，∴ s in α =图 2图 3【名师点睛】本题主要考查三角函数的图象与性质，渗透直观想象、逻辑推理等数学素养，画出各函数图象，即可作出选择．本题也可利用二级结论：①函数 y = f ( x ) 的周期是函数 y = f ( x ) 周期的一半；② y = sin ω x 不是周期函数.4．【2019 年高考全国Ⅱ卷理数】已知 α∈(0，πA ．1C ．3【答案】B552 55⎛ ⎝ π⎫ 2 ⎭15 5 5，故选 B ．【名师点睛】本题是对三角函数中二倍角公式、同角三角函数基本关系式的考查，中等难度，判断正余弦的正负，运算准确性是关键，题目不难，需细心，解决三角函数问题，研究角的范围后得出三角函数值的正负很关键，切记不能凭感觉．解答本题时，先利用二倍角公式得到正余弦关系，再利用角范围及正余弦平方和为 1 关系得出答案．④ω的取值范围是[，)ππkπ-④当f(x)=sin（ωx+）=0时，ωx+=kπ（k∈Z），所以5，所以当k=5时，5π-12296π-5≤2π，当k=6时，x=5105>2π，解得5．【2019年高考全国Ⅲ卷理数】设函数f(x)=sin（ωx+个零点，下述四个结论：①f(x)在（0,2π）有且仅有3个极大值点②f(x)在（0,2π）有且仅有2个极小值点π5）(ω＞0)，已知f(x)在[0,2π]有且仅有5③f (x)在（0,π10）单调递增1229510其中所有正确结论的编号是A．①④C．①②③B．②③D．①③④【答案】D【解析】①若f(x)在[0,2π]上有5个零点，可画出大致图象，由图1可知，f(x)在(0,2π)有且仅有3个极大值点.故①正确；②由图1、2可知，f(x)在(0,2π)有且仅有2个或3个极小值点.故②错误；π55x=ω因为f(x)在[0,2π]上有5个零点，x=ωππω≤ω<，③函数f(x)=sin（ωx+）的增区间为：-+2kπ<ωx+<+2kπ，2k-π+2k⎪π10⎭10<x<⎝⎭.7⎫综上可得，f(x)在 0,⎝10⎭【最小正周期为2π，且g ⎪=2，则f ⎪=又g(x)=A s inωx,∴T=42，∴A=2，故④正确.ππππ5252⎛⎛3⎫⎪⎝ωω取k=0，当ω=1271时，单调递增区间为-π<x<π，52482973当ω=时，单调递增区间为-π<x<π，102929⎛π⎫⎪单调递增.故③正确.所以结论正确的有①③④.故本题正确答案为D.【名师点睛】本题为三角函数与零点结合问题，难度大，可数形结合，分析得出答案，要求高，理解深度高，考查数形结合思想．注意本题中极小值点个数是动态的，易错，正确性考查需认真计算，易出错．6．2019年高考天津卷理数】已知函数f(x)=A s in(ωx+ϕ)(A>0,ω>0,|ϕ|<π)是奇函数，将y=f(x)的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为g(x)．若g(x)的A．-2 C．2⎛π⎫⎝4⎭⎛3π⎫⎝8⎭B．-2D．2【答案】C【解析】∵f(x)为奇函数，∴f(0)=A s inϕ=0,∴ϕ=kπ,k∈Z,∴k=0,ϕ=0；又g(π)=12π21ω2=2π,∴ω=2，∴f(x)=2sin2x，f(3π8)= 2.故选C.【名师点睛】本题主要考查函数的性质和函数的求值问题，解题关键是求出函数g(x)，再根据函数性【解析】函数 f (x ) = sin 2 2x = 1 - cos 4 x .=1= - ，则 sin 2α + ⎪ 的值是 ▲ .⎛ α tan + ⎪= = = - ，得 3tan 2 α - 5tan α - 2 = 0 ，tan α + ⎪ tan α (1 - tan α )sin 2α + ⎪ = sin 2α cos + cos 2α sin质逐步得出 A, ω,ϕ 的值即可.7．【2019 年高考北京卷理数】函数 f （x ）=sin 22x 的最小正周期是__________．【答案】π2π，周期为 .2 2【名师点睛】本题主要考查二倍角的三角函数公式 三角函数的最小正周期公式，属于基础题.将所给的函数利用降幂公式进行恒等变形，然后求解其最小正周期即可8．【2019 年高考全国Ⅱ卷理数】 △ABC 的内角 A, B, C 的对边分别为 a, b , c .若 b = 6, a = 2c, B =π3△ABC 的面积为_________．【答案】 6 3，则【解析】由余弦定理得 b 2 = a 2 + c 2 - 2ac cos B ，所以 (2c)2 + c 2 - 2 ⨯ 2c ⨯ c ⨯解得 c = 2 3, c = -2 3 （舍去），1 3所以 a = 2c = 4 3 ， Sac sin B = ⨯ 4 3 ⨯ 2 3 ⨯= 6 3.22 2 12 = 62 ，即 c 2 = 12 ，【名师点睛】本题易错点往往是余弦定理应用有误或是开方导致错误．解答此类问题，关键是在明确方法的基础上，准确记忆公式，细心计算．本题首先应用余弦定理，建立关于 c 的方程，应用 a, c 的关系、三角形面积公式计算求解，本题属于常见题目，难度不大，注重了基础知识、基本方法、数学式子的变形及运算求解能力的考查．9．【2019 年高考江苏卷】已知【答案】210tanα 2 ⎛ π ⎫ π ⎫ 3 ⎝ 4 ⎭ ⎝ 4 ⎭【解析】由 tan α tan α 2⎛ π ⎫ tan α + 1 tan α + 1 3⎝ 4 ⎭ 1 - tan α解得 tan α = 2 ，或 tan α = -13.⎛π ⎫ π π ⎝4 ⎭ 4 42 (sin 2α + cos 2α )=22 ⎝sin 2 α + cos 2 α ⎭ 2 ⎝ tan 2 α + 1 ⎭= ； 当 tan α = 2 时，上式 = ⎪ ⎝ 2 2 + 1 ⎭10 13 3 ]= 2 .⨯ [2 ⨯ (- ) + 1 - (- )2 当 tan α = - 时，上式=1π ⎫ 2 = .4 ⎭ 10⎛【答案】 12 2 . .【解析】如图，在△ABD 中，由正弦定理有：AB= ,cos ∠BAC = = ，所以 BD ===2 ⎛ 2sin α cos α + cos 2 α - sin 2 α ⎫ ⎪2 ⎛ 2 tan α + 1 - tan 2 α ⎫⎪ ，2 ⎛ 2 ⨯ 2 + 1 - 22 ⎫ 2 21 123 210(- )2 + 13综上， sin 2α + ⎝⎪【名师点睛】本题考查三角函数的化简求值，渗透了逻辑推理和数学运算素养采取转化法，利用分类讨 论和转化与化归思想解题.由题意首先求得 tan α 的值，然后利用两角和的正弦公式和二倍角公式将原问题转化为齐次式求值的问题，最后切化弦求得三角函数式的值即可 10．【2019 年高考浙江卷】在 △ABC 中， ∠ABC = 90︒ ， AB = 4 ， BC = 3 ，点 D 在线段 AC 上，若∠BDC = 45︒ ，则 BD = ___________， cos ∠ABD = ___________．7 2 ，5 10BD 3π= ，而 AB = 4, ∠ADB =sin ∠ADB sin ∠BAC 4,AC = AB 2 + BC 2 = 5 ， sin ∠BAC =BC 3 AB 4 12 2 AC 5 AC 5 5.π π 7 2cos ∠ABD = cos(∠BDC - ∠BAC ) = cos cos ∠BAC + sin sin ∠BAC =4 4 10.【名师点睛】本题主要考查解三角形问题，即正弦定理、三角恒等变换、数形结合思想及函数方程思( )cos C + sin C = 2sin C ，可得 cos (C + 60︒ )= - 【 B b c想.在 △ABD 中应用正弦定理，建立方程，进而得解.解答解三角形问题，要注意充分利用图形特征.11．【2019 年高考全国Ⅰ卷理数】△ABC 的内角 A ，B ，C 的对边分别为 a ，b ，c ，设(sin B - sin C )2 = sin 2 A - sin B sin C ．（1）求 A ；（2）若 2a + b = 2c ，求 sinC ．【答案】（1） A = 60︒ ；（2） sin C =6 + 2 4.【解析】（1）由已知得 s in 2 B + sin 2 C - sin 2 A = sin B s in C ，故由正弦定理得 b 2 + c 2 - a 2 = bc ．b 2 +c 2 - a 2 1 由余弦定理得 cos A = = ．2bc 2因为 0︒ < A < 180︒ ，所以 A = 60︒ ．（2）由（1）知 B = 120︒ - C ，由题设及正弦定理得 2 sin A + sin 120︒ - C = 2sin C ，即 6 3 1 2 +2 2 2 2．由于 0︒< C < 120︒，所以 sin(C + 60︒)=2 2，故sin C = sin (C + 60︒ - 60︒ )= sin (C + 60︒ )cos60 ︒ - cos (C + 60︒ )sin 60︒= 6 + 2 4．【名师点睛】本题考查利用正弦定理、余弦定理解三角形的问题，涉及到两角和差正弦公式、同角三角函数关系的应用，解题关键是能够利用正弦定理对边角关系式进行化简，得到余弦定理的形式或角之间的关系.12． 2019 年高考全国Ⅲ卷理数】△ ABC 的内角 A ， ，C 的对边分别为 a ， ， ，已知 a sin（1）求 B ；（2△）若 ABC 为锐角三角形，且 c =1△，求 ABC 面积的取值范围．A + C 2= b sin A ．【答案】（1）B =60°；（2） ( 3因为 cos B 从而3△ABC<．因此，△ ABC 面积的取值范围是 8 , 2 ⎪⎭ .b 2 = 32 +c 2 - 2 ⨯ 3 ⨯ c ⨯ - ⎪.3, ) . 8 2【解析】（1）由题设及正弦定理得 s in A s in A + C= sin B sin A ．2因为sinA ≠ 0，所以 sin A + C= sin B ．2由 A + B + C = 180︒ ，可得 sin A + C B B B B= cos ，故 cos = 2sin cos ．2 2 2 2 2B 1≠ 0 ，故 sin = ，因此B =60°．2 2 2（2）由题设及（1△）知 ABC 的面积 S△ABC = 3 4a ．c sin A sin (120︒ - C )3 1由正弦定理得 a = = = + ．sin C sin C 2 tan C 2△由于 ABC 为锐角三角形，故0°<A <90°，0°<C <90°，由（1）知A +C =120°，所以30°<C <90°，故 1< a < 2 ，23< S82⎛ 3 3 ⎫ ⎪ ．⎝【名师点睛】这道题考查了三角函数的基础知识，以及正弦定理的使用（此题也可以用余弦定理求解），最后考查 V ABC 是锐角三角形这个条件的利用，考查的很全面，是一道很好的考题13．【2019 年高考北京卷理数】在△ ABC 中，a =3，b −c =2，cosB = -（1）求 b ，c 的值；（2）求 sin （B –C ）的值．1 2 ．【答案】（1） b = 7 ， c = 5 ；（2）4 73 .【解析】（1）由余弦定理 b 2 = a 2 + c 2 - 2ac cos B ，得⎛ 1 ⎫ ⎝ 2 ⎭所以 (c + 2)2 = 32 + c 2 - 2 ⨯ 3 ⨯ c ⨯ - ⎪ . （2）由 cos B = - 得 sin B = ⎪ 的值．⎛ （ 得 3b s in C = 4a sin C ，即 3b = 4a ．又因为 b + c = 2a ，得到 b = a ， c = a ．由余弦定理可得a 2 + c 2 -b 2 a 2 + a 2 - a 21 cos B = = =- ．2因为 b = c + 2 ，⎛ 1 ⎫ ⎝ 2 ⎭解得 c = 5 .所以 b = 7 .1 32 2.由正弦定理得 s in C = c 5 3 sin B = b 14.在 △ABC 中，∠B 是钝角，所以∠C 为锐角.所以 cos C = 1 - sin 2 C = 11 14.所以 sin( B - C ) = sin B cos C - cos B sin C = 4 3 7.【名师点睛】本题主要考查余弦定理、正弦定理的应用，两角差的正弦公式的应用等知识，意在考查学生的转化能力和计算求解能力.14．【2019 年高考天津卷理数】在 △ABC 中，内角 A, B, C 所对的边分别为 a, b , c ．已知 b + c = 2a ，3c s in B = 4a sin C ．（1）求 cos B 的值；（2）求 sin 2B + ⎝π⎫6⎭【答案】（1） - 1 4 3 5 + 7；（2） - .16【解析】 1）在 △ABC 中，由正弦定理 b c=sin B sin C，得 b s in C = c s in B ，又由 3c sin B = 4a sin C ，4 23 34 169 92ac 42 ⋅ a ⋅ a3sin 2B + ⎪ = sin 2B cos + cos 2B sin =- ⨯ - ⨯ =- （2）若 sin A 3 2 ⨯ 3c ⨯ c ，得 ( ) π⎫ 2 5= cos B = 2 ⎭ 5⎛（ 2 ） 由 （ 1 ） 可 得 sin B = 1 - cos 2 B =7cos 2B = cos 2 B - sin 2 B = - ，故815 15， 从 而 sin 2 B = 2sin B cos B = - ， 4 8⎛ π⎫ π π 15 3 7 1 3 5 + 7 ⎝6 ⎭ 6 6 8 2 8 2 16．【名师点睛】本小题主要考查同角三角函数的基本关系，两角和的正弦公式，二倍角的正弦与余弦公式，以及正弦定理、余弦定理等基础知识．考查运算求解能力．15．【2019 年高考江苏卷】在△ABC 中，角 A ，B ，C 的对边分别为 a ，b ，c ．（1）若 a =3c ，b = 2 ，cosB = 23，求 c 的值；cos B π= ，求 sin(B + ) 的值．a 2b 2【答案】（1） c =3 2 5；（2） . 3 5【解析】（1）因为 a = 3c, b =2,cos B = 23，a 2 + c 2 -b 2 2 (3c)2 +c 2 - ( 2) 2 1由余弦定理 cos B = ，得 = ，即 c 2 = .2ac 3所以 c =3 3.（2）因为 sin A cos B =a 2b， 由正弦定理 a b cos B sin B= =sin A sin B 2b b，所以 cos B = 2sin B .4从而 cos 2 B = (2sin B)2 ，即 cos 2 B = 4 1 - cos 2 B ，故 cos 2 B = .5因为 sin B > 0 ，所以 cos B = 2sin B > 0 ，从而 cos B = 2 55.因此 sin B + ⎝⎪ .【名师点睛】本小题主要考查正弦定理、余弦定理、同角三角函数关系、诱导公式等基础知识，考查运算求解能力.要求：线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分16．【2019年高考江苏卷】如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P、Q，并修建两段直线型道路PB、QA．规划．．．．别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位：百米）．（1）若道路PB与桥AB垂直，求道路PB的长；（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；（3）在规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．【答案】（1）15（百米）；（2）见解析；（3）17+321（百米）.【解析】解法一：（1）过A作AE⊥BD，垂足为E.由已知条件得，四边形ACDE为矩形，DE=BE=AC=6,AE=CD=8.'因为PB⊥AB，所以cos∠PBD=sin∠ABE=84=.105所以PB=BD12==15.cos∠PBD45因此道路PB的长为15（百米）.（2）①若P在D处，由（1）可得E在圆上，则线段BE上的点（除B，E）到点O的距离均小于圆O的半径，所以P选在D处不满足规划要求.5②若Q 在D 处，连结AD ，由（1）知 AD = AE 2 + ED 2 = 10 ，从而 cos ∠BAD = AD 2 + AB 2 - BD 2 7= > 0 ，所以∠BAD 为锐角.2 A D ⋅ AB 25所以线段AD 上存在点到点O 的距离小于圆O 的半径.因此，Q 选在D 处也不满足规划要求.综上，P 和Q 均不能选在D 处.（3）先讨论点P 的位置.当∠OBP <90°时，线段PB 上存在点到点O 的距离小于圆O 的半径，点P 不符合规划要求；当∠OBP ≥90°时，对线段PB 上任意一点F ，OF ≥OB ，即线段PB 上所有点到点O 的距离均不小于圆O 的半径，点P 符合规划要求.设 P 为l 上一点，且 PB ⊥ AB ，由（1）知， P B =15，1 1 1此时 PD = PB sin ∠PBD = PB cos ∠EBA = 15 ⨯ 3 = 9 ；1111当∠OBP >90°时，在 △PPB 中， PB > PB = 15 .1 1由上可知，d ≥15.再讨论点Q 的位置.由 （ 2 ） 知 ， 要 使 得 QA ≥15 ， 点 Q 只 有 位 于 点 C 的 右 侧 ， 才 能 符 合 规 划 要 求 . 当 QA =15 时 ，CQ = QA 2 - AC 2 = 152 - 62 = 3 21 .此时，线段QA 上所有点到点O 的距离均不小于圆O 的半径.综 上 ， 当 PB ⊥AB ， 点 Q 位 于 点 C 右 侧 ， 且 CQ = 3 21 时 ， d 最 小 ， 此 时 P ， Q 两 点 间 的 距 离PQ =PD +CD +CQ =17+ 3 21 .因此，d 最小时，P ，Q 两点间的距离为17+ 3 21 （百米）.解法二：（1）如图，过O 作OH ⊥l ，垂足为H.以O 为坐标原点，直线OH 为y 轴，建立平面直角坐标系.在线段AD 上取点M （3， ），因为 OM = 32 + ⎪ < 32 + 42 = 5 ，因为BD =12，AC =6，所以OH =9，直线l 的方程为y =9，点A ，B 的纵坐标分别为3，−3.因为AB 为圆O 的直径，AB =10，所以圆O 的方程为x 2+y 2=25.从而A （4，3），B （−4，−3），直线AB 的斜率为 3 4.因为PB ⊥AB ，所以直线PB 的斜率为 -4 25直线PB 的方程为 y =- x -.334 3，所以P （−13，9）， PB =(-13 + 4)2 + (9 + 3)2 = 15 .因此道路PB 的长为15（百米）.（2）①若P 在D 处，取线段BD 上一点E （−4，0），则EO =4<5，所以P 选在D 处不满足规划要求.②若Q 在D 处，连结AD ，由（1）知D （−4，9），又A （4，3）， 所以线段AD ： y = - 3x + 6(-4剟x 4) .415 ⎛ 15 ⎫24⎝ 4 ⎭所以线段AD 上存在点到点O 的距离小于圆O 的半径.因此Q 选在D 处也不满足规划要求.综上，P 和Q 均不能选在D 处.（3）先讨论点P 的位置.当∠OBP <90°时，线段PB 上存在点到点O 的距离小于圆O 的半径，点P 不符合规划要求；当∠OBP ≥90°时，对线段PB 上任意一点F ，OF ≥OB ，即线段PB 上所有点到点O 的距离均不小于圆O 的半径，点P 符合规划要求.设 P 为l 上一点，且 PB ⊥ AB ，由（1）知， P B =15，此时 P （−13，9）；1111当∠OBP >90°时，在 △PPB 中， PB > PB = 15 .1 1由上可知，d ≥15.（2）求函数 y = [ f ( x + π )]2 + [ f ( x + )]2的值域． 又 θ ∈ [0, 2π) ，因此θ =π（2） y = ⎢ f x + + ⎢ f x + ⎪⎥ = sin 2 x + 12 ⎭⎥⎦ 4 ⎭⎦ ⎝ + sin 2 x + ⎪ 12 ⎭ ⎝ 4 ⎭ 1 - cos 2 x + ⎪ 1 - cos 2 x + ⎪= + = 1 - cos 2 x - sin 2 x ⎪π ⎫ 6 ⎭ cos 2 x + ⎪ ．再讨论点Q 的位置.由（2）知，要使得QA≥15，点Q 只有位于点C 的右侧，才能符合规划要求.当QA =15时，设Q （a ，9），由 AQ = (a - 4)2 + (9 - 3)2 = 15(a > 4) ，得a = 4 + 3 21 ，所以Q （ 4 + 3 21 ，9），此时，线段QA上所有点到点O 的距离均不小于圆O 的半径.综上，当P （ 13，9），Q （ 4 + 3 21 ，9）时，d 最小，此时P ，Q 两点间的距离PQ = 4 + 3 21 - (-13) = 17 + 3 21 .因此，d 最小时，P ，Q 两点间的距离为17 + 3 21 （百米）.【名师点睛】本小题主要考查三角函数的应用、解方程、直线与圆等基础知识，考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力.17．【2019 年高考浙江卷】设函数 f ( x ) = sinx, x ∈ R .（1）已知θ ∈ [0,2 π), 函数 f ( x + θ ) 是偶函数，求θ 的值；π 12 4【答案】（1）θ = π 3π或 ；（2） [1-2 23 3 ,1 + ] ． 2 2【解析】（1）因为 f ( x + θ ) = sin( x + θ ) 是偶函数，所以，对任意实数x 都有 sin( x + θ ) = sin( - x + θ ) ，即 sin x cos θ + cos x sin θ = - s in x cos θ + cos x sin θ ，故 2sin x cos θ = 0 ，所以 cos θ = 0 ．3π或 ． 2 2⎡ ⎣ ⎛ π ⎫⎤ 2 ⎡ ⎛ π ⎫⎤ 2 ⎛ ⎪ ⎝ ⎣ ⎝ π ⎫ ⎛ π ⎫ ⎪⎛ ⎛ π ⎫ ⎝ ⎝2 ⎭ 1 ⎛3 3 ⎫ 2 2 2 ⎝ 2 2⎭= 1 - 3 2⎛ π ⎫⎝ 3 ⎭因此，函数的值域是[1-3.【3B．tan α-⎪=【解析】Q cosα=-,a∈(-π,0)，∴α∈⎛-π,-π⎫⎪，3,1+]．22【名师点睛】本题主要考查三角函数及其恒等变换等基础知识，同时考查运算求解能力18．重庆西南大学附属中学校2019届高三第十次月考数学试题】已知角α的顶点在坐标原点，始边与x轴正半轴重合，终边经过点P(-2，1)，则cos2α=A．2213C．-13D．-223【答案】B【解析】因为角α的顶点在坐标原点，始边与x轴正半轴重合，终边经过点P(-2，1)，所以cosα=-22+1=-63，因此cos2α=2cos2α-1=13.故选B.【名师点睛】本题主要考查三角函数的定义，以及二倍角公式，熟记三角函数的定义与二倍角公式即可，属于常考题型.解答本题时，先由角α的终边过点P(-2，1)，求出cosα，再由二倍角公式，即可得出结果.19．【四川省宜宾市2019届高三第三次诊断性考试数学试题】已知c osα=-4，α∈(-π,0)，则5⎛π⎫⎝4⎭A．17B．7C．-17D．-7【答案】C45⎝2⎭33∴s inα=-,tanα=，54π ⎫ tan α - 1 4 1 则 tan α - ⎪ == = - .故选 C ． 4 ⎭ 1 + tan α 7 3 1 +20．【广东省韶关市 2019 届高考模拟测试（4 月）数学文试题】已知函数 f ( x ) = sin(ω x + ) (ω > 0) 的相，将函数图象向左平移 个单位得到函数 g ( x ) 的图象，则 g ( x ) =) + ] = sin 2 x + + ⎪ = cos 2 x 的图象，故选 C ．3- 1 ⎛⎝4【名师点睛】本题主要考查了同角三角函数关系式及两角差的正切公式的简单应用，属于基础题．解答本题时，根据已知 c os α 的值，结合同角三角函数关系式可求 tan α，然后根据两角差的正切公式即可求解．π6邻对称轴之间的距离为 π π2 6A ． sin( x +C ． cos2 x π 3 ) πB ． sin(2 x + )3πD ． cos(2 x + )3【答案】C【解析】由函数 f ( x ) = sin(ω x +π π T π)(ω > 0) 的相邻对称轴之间的距离为 ，得 = ，即 T = π ，所6 2 2 2以 π =2πω ，解得 ω = 2 ，π π将函数 f ( x ) = sin(2 x + ) 的图象向左平移 个单位，6 6得到 g ( x ) = sin[2( x + π 6 π ⎛ 6 ⎝ π π ⎫ 3 6 ⎭【名师点睛】本题考查的知识要点：三角函数关系式的平移变换和伸缩变换的应用，正弦型函数性质的应用，主要考查学生的运算能力和转换能力，属于基础题型．解答本题时，首先利用函数的图象求出函数的关系式，进一步利用图象的平移变换的应用求出结果．21．【河南省郑州市 2019 届高三第三次质量检测数学试题】已知函数 f (x ) = A s in (ωx + ϕ )，A > 0,ω > 0, ϕ < π的部分图象如图所示，则使 f (a + x )- f (a - x ) = 0 成立的 a 的最小正值为 2⇒>,∴ω<所以a的最小正值为.C的对边，若△ABC的面积为S，且43S=(a+b)2-c2，则sin C+⎪=4D．A．C．π12π4B．D．π6π3【答案】B【解析】由图象易知，A=2，f(0)=1，即2sinϕ=1，且ϕ<ππ，即ϕ=，26由图可知，f(11π11ππ11ππ12k-2 )=0,所以sin(⋅ω+)=0,∴⋅ω+=kπ,k∈Z，即ω=,k∈Z，1212612611 11π2π11π24又由图可知，周期T>，且ω>0，12ω1211所以由五点作图法可知k=2,ω=2，π所以函数f(x)=2sin(2x+)，6因为f(a+x)-f(a-x)=0，所以函数f(x)关于x=a对称，即有2a+ππkππ=kπ+,k∈Z，所以可得a=+,k∈Z，6226π6故选B.【名师点睛】本题考查了三角函数的图象和性质，熟练运用三角函数的图象和周期对称性是解题的关键，属于中档题.解答本题时，先由图象，求出A,ϕ,ω，可得函数f(x)的解析式，再由f(a+x)-f(a-x)=0易知f(x)的图象关于x=a对称，即可求得a的值.22．【山东省实验中学等四校2019届高三联合考试数学试题】在△ABC中，a，b，c分别为角A，B，⎛π⎫⎝4⎭A．1B．C．6-2【答案】D 226+2 4【解析】由43S=(a+b )2-c2，得43⨯12ab sin C=a2+b2-c2+2ab，∵a2+b2-c2=2ab cos C，∴23ab sin C=2ab cos C+2ab，即 3 sin C - cos C = 1 ，即 2sin C - 6 ⎭ = 1 ，则 sin C - ⎪ = ，+ = sin cos + cos sin = 3 ⨯ 2 + ⨯ 2 = 6 + 2 sin C + = sin ⎝ ⎝ 3 4 ⎭ 2 2 2 2 44 ⎭ 3 4 3 4 π ⎫⎛⎝ π ⎫ ⎪ ⎛ ⎝π ⎫ 1 6 ⎭ 2∵ 0 < C < π ，∴ - π π 5π π π π< C - < ， ∴ C - = ，即 C = ，6 6 6 6 6 3则 ⎛ ⎛ π π ⎫ π π π π 1 ⎪ ⎪，故选 D ．【名师点睛】本题主要考查解三角形的应用，结合三角形的面积公式以及余弦定理求出C 的值以及利用两角和差的正弦公式进行计算是解决本题的关键．解答本题时，根据三角形的面积公式以及余弦定理进行化简求出 C 的值，然后利用两角和的正弦公式进行求解即可．23．【山东省烟台市 2019 届高三 3 月诊断性测试（一模）数学试题】在△ABC 中，角 A ， B ， C 的对边分别为 a ， b ， c ，若 a = 1 ， 3 sin A cos C + ( 3 sin C + b ) cos A = 0 ，则角 A =A ．C ．2π 3 π 6B ．D ．π 3 5π 6【答案】D【解析】∵ a = 1 ， 3 sin A cos C + ( 3 sin C + b ) cos A = 0 ，∴ 3 sin A cos C + 3 sin C cos A = -b cos A ，∴ 3 sin( A + C ) = 3 sin B = -b cos A ，∴ 3a sin B = -b cos A ，由正弦定理可得： 3 sin A s in B = - sin B cos A ，∵ sin B > 0 ，∴ 3 sin A = - cos A ，即 tan A = - 3 3，∵ A ∈ (0, π) ，∴ A = 5π 6.故选 D ．【名师点睛】本题主要考查解三角形，熟记正弦定理，两角和的正弦公式即可，属于基础题．解答本题时，由 3 sin A cos C + ( 3 sin C + b ) cos A = 0 ，可得 3a sin B = -b cos A ，再由正弦定理得到tan A = -3 ，结合 A ∈ (0, π) ，即可求得 A 的值．3【， a = 2 3 ， △ABC 的面积为，24． 广东省韶关市 2019 届高考模拟测试（4 月）数学试题】在 △ABC 中，a 、b 、c 分别是内角 A 、 B 、C 的对边，且 3b cos A = sin A(a cos C + c cos A) .（1）求角 A 的大小；（2）若 a = 2 3 ， △ABC 的面积为5 3 4，求 △ABC 的周长．【答案】（1） A =π 3；（2） 5 3 .【解析】（1）∵ 3b cos A = sin A(a cos C + c cos A) ，∴由正弦定理可得：3 sin B cos A = sin A(sin A cos C + sin C cos A) = sin A s in( A + C ) = sin A s in B ，即 3 sin B cos A = sin A s in B ，∵ sin B ≠ 0 ，∴ tan A = 3 ，∵ A ∈ (0, π) ，∴ A = π3．（2）∵ A = π 5 33 41 3 5 3∴ bc sin A = bc =2 4 4，∴ bc = 5 ，∴由余弦定理可得： a 2 = b 2 + c 2 - 2bc cos A ，即12 = b 2 + c 2 - bc = (b + c)2 - 3bc = (b + c)2 - 15 ，解得： b + c = 3 3 ，∴ △ABC 的周长为 a + b + c = 2 3 + 3 3 = 5 3 .【名师点睛】本题主要考查了正弦定理，两角和的正弦函数公式，三角形的面积公式，余弦定理在解三角形中的综合应用，考查了计算能力和转化思想，属于基础题．（1）由正弦定理，两角和的正弦函数公式化简已知等式可得 3 sin B cos A = sin A s in B ，由 sin B ≠ 0 ，（2）当 x ∈ [0, ] 时，不等式 c < f ( x ) < c + 2 恒成立，求实数 c 的取值范围．【 = = sin 2 x - 所以 - ≤ sin （2 x - ）≤ 1 .⎪⎩c + 2 > 1 所以实数 c 的取值范围为 (-1,- ) .（2）首先求得函数 f (x )在区间 ⎢0, ⎥ 上的值域，然后结合恒成立的结论得到关于 c 的不等式组，求可求 tan A = 3 ，结合 A ∈ (0, π) ，可求 A =π3．（2）利用三角形的面积公式可求bc = 5 ，进而根据余弦定理可得b + c = 3 3 ，即可计算△ABC 的周长的值．25． 北京市昌平区 2019 届高三 5 月综合练习（二模）数学试题】已知函数 f ( x ） cos x( 3 sin x - cos x)+π（1）求 f ( ) 的值；3π21【答案】（1）1；（2） (-1,- ) .21【解析】（1） f ( x ）3 sin x cos x - cos 2 x + 2= 31cos 2 x2 2π=sin(2 x - ) ，6 π所以 f ( ) = 1 .31 2.（2）因为 0 ≤ x ≤ π 2，π π 5π所以 - ≤ 2 x - ≤ ，6 6 6 1 π2 6⎧1 ⎪ c <- 1由不等式 c < f ( x ) < c + 2 恒成立，得 ⎨2 ，解得 -1 < c < - . 212【名师点睛】本题主要考查三角函数的性质及其应用，恒成立问题的处理方法等知识，意在考查学生的转化能力和计算求解能力.（1）首先整理函数的解析式，然后结合函数的解析式求解函数值即可；⎡ π ⎤ ⎣ 2 ⎦解不等式组可得 c 的取值范围.。

2019全国各地高考数学重点试题分类解析汇编7：三角函数注意事项：认真阅读理解，结合历年的真题，总结经验，查找不足！重在审题，多思考，多理解！【江西省新钢中学2018届高三第一次考试】设函数)(|,3sin |3sin )(x f x x x f 则+=为A 、周期函数，最小正周期为23πB 、周期函数，最小正周期为3πC 、周期函数，最小正周期为π2D 、非周期函数【答案】A 【解析】：2sin3,sin30()sin3|sin3|0,sin30x x f x x x x ≥⎧=+=⎨<⎩ ，周期不变【江西省新钢中学2018届高三第一次考试】5、E ，F 是等腰直角△ABC 斜边AB 上的三等分点，那么tan ECF ∠=A 、1627B 、23C、3D 、 34【答案】D【解析】考查三角函数的计算、解析化应用意识。

解法1：约定AB=6,AC=BC=由余弦定理再由余弦定理得4cos 5ECF ∠=，解得3tan 4ECF ∠=解法2：坐标化。

约定AB=6,AC=BC=〔0,3〕利用向量的夹角公式得4cos 5ECF ∠=，解得3tan 4ECF ∠=。

【江西省新钢中学2018届高三第一次考试】6、假设02πα<<，02πβ-<<，1cos()43πα+=，cos()423πβ-=cos()2βα+= A、D、 【答案】 C 【解析】：()()2442βππβαα+=+--cos()cos[()()]2442βππβαα∴+=+--cos()cos()442ππβα=+-sin()sin()442ππβα+++13===应选C【江西省新钢中学2018届高三第一次考试】7、如图，在△ABC 中，D 是边AC 上的点，且,2,2AB AD AB BC BD ===，那么sin C 的值为ABCD 【答案】D【解析】设BDa =,那么由题意可得:2,BC a =AB AD ==,在ABD ∆中,由余弦定理得：222cos 2AB AD BDA AB AD +-==⋅2232a a⨯-=13，所以sin A=3，在△ABC中，由正弦定理得，sin sin ABBC C A=，所以2sina C =，解得sin C =6应选D.【江西省新钢中学2018届高三第一次考试】12.,2)4tan(=+πx 那么xx 2tan tan 的值为__________ 【答案】49【解析】因为22tan()4tan 2()41tan ()4x x x πππ++==-+22212⨯=-43-,而tan(2)2x π+=-cot2x,所以3tan 24x =-,又因为tan 1tan()241tan x x x π++==-,所以解得1tan 3x =,所以x x 2tan tan 的值为49.【江西省新钢中学2018届高三第一次考试】13、在ABC ∆中，60,B AC ==2AB BC +的最大值为 。

2019年高考数学试题分项版——三角函数（解析版）一、选择题1．(2019·全国Ⅰ文，7)tan 255°等于()A．－2－B．－2＋C．2－D．2＋答案 D解析tan 255°＝tan(180°＋75°)＝tan 75°＝tan(45°＋30°)＝＝＝2＋.2．(2019·全国Ⅰ文，11)△ABC的内角A，B，C的对边分别为a，b，c，已知a sin A－b sin B＝4c sin C，cos A＝－，则等于()A．6 B．5 C．4 D．3答案 A解析∵a sin A－b sin B＝4c sin C，∴由正弦定理得a2－b2＝4c2，即a2＝4c2＋b2.由余弦定理得cos A＝＝＝＝－，∴＝6.3．(2019·全国Ⅱ文，8)若x1＝，x2＝是函数f(x)＝sin ωx(ω>0)两个相邻的极值点，则ω等于()A．2 B.C．1 D.答案 A解析由题意及函数y＝sin ωx的图象与性质可知，T＝－，∴T＝π，∴＝π，∴ω＝2.4．(2019·全国Ⅱ文，11)已知α∈，2sin 2α＝cos 2α＋1，则sin α等于()A. B. C. D.答案 B解析由2sin 2α＝cos 2α＋1，得4sin αcos α＝1－2sin2α＋1，即2sin αcos α＝1－sin2α.因为α∈，所以cos α＝，所以2sin α＝1－sin2α，解得sin α＝，故选B.5．(2019·全国Ⅲ文，5)函数f(x)＝2sin x－sin 2x在[0,2π]上的零点个数为()A．2 B．3 C．4 D．5答案 B解析令f(x)＝0，得2sin x－sin 2x＝0，即2sin x－2sin x cos x＝0，∴2sin x(1－cos x)＝0，∴sin x＝0或cos x＝1.又x∈[0,2π]，∴由sin x＝0得x＝0，π或2π，由cos x＝1得x＝0或2π.故函数f(x)的零点为0，π，2π，共3个．6．(2019·北京文，6)设函数f(x)＝cos x＋b sin x(b为常数)，则“b＝0”是“f(x)为偶函数”的() A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案 C解析∵f(x)＝cos x＋b sin x为偶函数，∴对任意的x∈R，都有f(－x)＝f(x)，即cos(－x)＋b sin(－x)＝cos x＋b sin x，∴2b sin x＝0.由x的任意性，得b＝0.故f(x)为偶函数⇒b＝0.必要性成立．反过来，若b＝0，则f(x)＝cos x是偶函数，充分性成立．∴“b＝0”是“f(x)为偶函数”的充分必要条件．7.(2019·北京文，8)如图，A，B是半径为2的圆周上的定点，P为圆周上的动点，∠APB是锐角，大小为β.图中阴影区域的面积的最大值为()A．4β＋4cos βB．4β＋4sin βC．2β＋2cos βD．2β＋2sin β答案 B解析方法一如图①，图①设圆心为O，连接OA，OB，OP.∵∠APB＝β，∴∠AOB＝2β，∴S阴影＝S△AOP＋S△BOP＋S扇形AOB＝×2×2sin∠AOP＋×2×2sin∠BOP＋×2β×22＝2sin∠AOP＋2sin∠BOP＋4β＝2sin∠AOP＋2sin(2π－2β－∠AOP)＋4β＝2sin∠AOP－2sin(2β＋∠AOP)＋4β＝2sin∠AOP－2(sin 2β·cos∠AOP＋cos 2β·sin∠AOP)＋4β＝2sin∠AOP－2sin 2β·cos∠AOP－2cos 2β·sin∠AOP＋4β＝2(1－cos 2β)sin∠AOP－2sin 2β·cos∠AOP＋4β＝2×2sin2β·sin∠AOP－2×2sin β·cos β·cos∠AOP＋4β＝4sin β(sin β·sin∠AOP－cos β·cos∠AOP)＋4β＝4β－4sin β·cos(β＋∠AOP)．∵β为锐角，∴sin β>0.∴当cos(β＋∠AOP)＝－1，即β＋∠AOP＝π时，阴影区域面积最大，为4β＋4sin β. 方法二如图②，图②设圆心为O，连接OA，OB，OP，AB，则阴影区域被分成弓形AmB和△ABP.∵∠APB＝β，∴∠AOB＝2β.∵弓形AmB的面积是定值，∴要使阴影区域面积最大，则只需△ABP面积最大．∵△ABP底边AB长固定，∴只要△ABP的底边AB上的高最大即可．由图可知，当AP＝BP时，满足条件，此时S阴影＝S扇形AOB＋S△AOP＋S△BOP＝×2β·22＋2××22·sin－＝4β＋4sin β.即为阴影区域面积的最大值．8．(2019·天津文，7)已知函数f(x)＝A sin(ωx＋φ)(A＞0，ω＞0，|φ|＜π)是奇函数，且f(x)的最小正周期为π，将y＝f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象对应的函数为g(x)．若g＝，则f 等于()A．－2 B．－ C.D．2答案 C解析∵函数f(x)为奇函数，且|φ|＜π，∴φ＝0.又f(x)的最小正周期为π，∴＝π，解得ω＝2，∴f(x)＝A sin 2x.由题意可得g(x)＝A sin x，g＝，即A sin ＝，解得A＝2.故f(x)＝2sin 2x.∴f ＝2sin ＝.9．(2019·全国Ⅰ理，11)关于函数f(x)＝sin|x|＋|sin x|有下述四个结论：①f(x)是偶函数；②f(x)在区间上单调递增；③f(x)在[－π，π]上有4个零点；④f(x)的最大值为2.其中所有正确结论的编号是()A．①②④B．②④C．①④D．①③答案 C解析f(－x)＝sin|－x|＋|sin(－x)|＝sin|x|＋|sin x|＝f(x)，∴f(x)为偶函数，故①正确；当<x<π时，f(x)＝sin x＋sin x＝2sin x，∴f(x)在上单调递减，故②不正确；f(x)在[－π，π]上的图象如图所示，由图可知函数f(x)在[－π，π]上只有3个零点，故③不正确；∵y＝sin|x|与y＝|sin x|的最大值都为1且可以同时取到，∴f(x)可以取到最大值2，故④正确．综上，正确结论的编号是①④.故选C.10．(2019·全国Ⅱ理，9)下列函数中，以为周期且在区间上单调递增的是() A．f(x)＝|cos 2x| B．f(x)＝|sin 2x|C．f(x)＝cos|x| D．f(x)＝sin|x|答案 A解析A中，函数f(x)＝|cos 2x|的周期为，当x∈时，2x∈，函数f(x)单调递增，故A正确；B中，函数f(x)＝|sin 2x|的周期为，当x∈时，2x∈，函数f(x)单调递减，故B不正确；C中，函数f(x)＝cos|x|＝cos x的周期为2π，故C不正确；D中，f(x)＝sin|x|＝由正弦函数图象知，在x≥0和x<0时，f(x)均以2π为周期，但在整个定义域上f(x)不是周期函数，故D不正确．故选A.11．(2019·全国Ⅱ理，10)已知α∈，2sin 2α＝cos 2α＋1，则sin α等于()A. B. C. D.答案 B解析由2sin 2α＝cos 2α＋1，得4sin αcos α＝1－2sin2α＋1，即2sin αcos α＝1－sin2α.因为α∈，所以cos α＝2sin α＝1－sin2α，解得sin α＝，故选B.12．(2019·全国Ⅲ理，12)设函数f(x)＝sin(ω>0)，已知f(x)在[0,2π]上有且仅有5个零点．下述四个结论：①f(x)在(0,2π)上有且仅有3个极大值点；②f(x)在(0,2π)上有且仅有2个极小值点；③f(x)在上单调递增；④ω的取值范围是.其中所有正确结论的编号是()A．①④B．②③C．①②③D．①③④答案 D解析如图，根据题意知，x A≤2π<x B，根据图象可知函数f(x)在(0,2π)有且仅有3个极大值点，所以①正确；但可能会有3个极小值点，所以②错误；根据x A≤2π<x B，有≤2π<，得≤ω<，所以④正确；当x∈时，<ωx＋<＋，因为≤ω<，所以＋<<，所以函数f(x)在上单调递增，所以③正确．13．(2019·天津理，7)已知函数f(x)＝A sin(ωx＋φ)(A＞0，ω＞0，|φ|＜π)是奇函数，将y＝f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象对应的函数为g(x)．若g(x)的最小正周期为2π，且g＝，则f 等于()A．－2 B．－ C.D．2答案 C解析由f(x)为奇函数可得φ＝kπ(k∈Z)，又|φ|＜π，所以φ＝0，所以g(x)＝A sin .由g(x)的最小正周期为2π，可得＝2π，故ω＝2，g(x)＝A sin x，g＝A sin ＝，所以A＝2，所以f(x)＝2sin 2x，故f ＝2sin ＝.二、填空题1．(2019·全国Ⅰ文，15)函数f(x)＝sin－3cos x的最小值为________．答案－4解析∵f(x)＝sin－3cos x＝－cos 2x－3cos x＝－2cos2x－3cos x＋1，令t＝cos x，则t∈[－1,1]，∴f(t)＝－2t2－3t＋1.又函数f(t)图象的对称轴t＝－∈[－1,1]，且开口向下，∴当t＝1时，f(t)有最小值－4.综上，f(x)的最小值为－4.2．(2019·全国Ⅱ文，15)△ABC的内角A，B，C的对边分别为a，b，c.已知b sin A＋a cos B ＝0，则B＝________.答案解析∵b sin A＋a cos B＝0，∴＝，由正弦定理，得－cos B＝sin B，∴tan B＝－1，又B∈(0，π)，∴B＝.3．(2019·天津文，14)在四边形ABCD中，AD∥BC，AB＝2，AD＝5，∠A＝30°，点E 在线段CB的延长线上，且AE＝BE，则·＝________.答案－1解析方法一在等腰△ABE中，易得∠BAE＝∠ABE＝30°，故BE＝2，则·＝(－)·(＋)A＝·＋·－2－·＝5×2×cos 30°＋5×2×cos 180°－12－2×2×cos 150°＝15－10－12＋6＝－1.方法二在△ABD中，由余弦定理可得BD＝＝，所以cos∠ABD＝＝－，则sin ∠ABD＝.设与的夹角为θ，则cos θ＝cos(180°－∠ABD＋30°)＝－cos(∠ABD－30°)＝－cos∠ABD·cos 30°－sin∠ABD·sin 30°＝－，在△ABE中，易得AE＝BE＝2，故·＝×2×＝－1.4．(2019·浙江，14)在△ABC中，∠ABC＝90°，AB＝4，BC＝3，点D在线段AC上．若∠BDC＝45°，则BD＝________，cos∠ABD＝________.答案解析在Rt△ABC中，易得AC＝5，sin C＝＝.在△BCD中，由正弦定理得BD＝×sin∠BCD×＝，sin∠DBC＝sin [π－(∠BCD＋∠BDC)]＝sin(∠BCD＋∠BDC)＝sin∠BCD·cos∠BDC＋cos∠BCD·sin∠BDC＝×＋×＝.又∠ABD＋∠DBC ＝，所以cos∠ABD＝sin∠DBC＝.5．(2019·江苏，13)已知＝－，则sin的值是____________________．答案解析＝＝＝－，解得tan α＝2或tan α＝－，当tan α＝2时，sin 2α＝＝＝，cos 2α＝＝＝－，此时sin 2α＋cos 2α＝，同理当tan α＝－时，sin 2α＝－，cos 2α＝，此时sin 2α＋cos 2α＝，所以sin＝(sin 2α＋cos 2α)＝.6．(2019·全国Ⅱ理，15)△ABC的内角A，B，C的对边分别为a，b，c.若b＝6，a＝2c，B ＝，则△ABC的面积为________．答案6解析 方法一 因为a ＝2c ，b ＝6，B ＝，所以由余弦定理b 2＝a 2＋c 2－2ac cos B ，得62＝(2c )2＋c 2－2×2c ×c cos，得c ＝2 ，所以a ＝4 ，所以△ABC 的面积S ＝ac sin B ＝×4 ×2 ×sin＝6 .方法二 因为a ＝2c ，b ＝6，B ＝，所以由余弦定理b 2＝a 2＋c 2－2ac cos B ，得62＝(2c )2＋c 2－2×2c ×c cos，得c ＝2 ，所以a ＝4 ，所以a 2＝b 2＋c 2，所以A ＝，所以△ABC 的面积S ＝×2 ×6＝6 .7．(2019·北京理，9)函数2()sin 2f x x =的最小正周期是 ．【思路分析】用二倍角公式可得11()cos(4)22f x x =-+，然后用周期公式求出周期即可．【解析】：2()sin (2)f x x =，11()cos(4)22f x x ∴=-+，()f x ∴的周期2T π=，故答案为：2π．【归纳与总结】本题考查了三角函数的图象与性质，关键是合理使用二倍角公式，属基础题． 三、解答题1．(2019·全国Ⅲ文，18)△ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知a sin＝b sinA . (1)求B ；(2)若△ABC 为锐角三角形，且c ＝1，求△ABC 面积的取值范围． 解 (1)由题设及正弦定理， 得sin A sin＝sin B sin A .因为sin A ≠0，所以sin＝sin B .由A ＋B ＋C ＝180°，可得sin＝cos，故cos＝2sincos.因为cos ≠0，故sin ＝，因此B ＝60°. (2)由题设及(1)知△ABC 的面积S △ABC ＝a . 由正弦定理，得a ＝＝＝＋. 由于△ABC 为锐角三角形，故0°<A <90°，0°<C <90°.由(1)知A ＋C ＝120°，所以30°<C <90°，故<a <2， 从而<S △ABC <.因此，△ABC 面积的取值范围是.2．(2019·北京文，15)在△ABC中，a＝3，b－c＝2，cos B＝－.(1)求b，c的值；(2)求sin(B＋C)的值．解(1)由余弦定理b2＝a2＋c2－2ac cos B，得b2＝32＋c2－2×3×c×.因为b＝c＋2，所以(c＋2)2＝32＋c2－2×3×c×，解得c＝5.所以b＝7.(2)由cos B＝－，得sin B＝.由正弦定理，得sin A＝sin B＝.在△ABC中，B＋C＝π－A，所以sin(B＋C)＝sin A＝.3．(2019·天津文，16)在△ABC中，内角A，B，C所对的边分别为a，b，c，已知b＋c＝2a,3c sin B＝4a sin C.(1)求cos B的值；(2)求sin的值．解(1)在△ABC中，由正弦定理＝，得b sin C＝c sin B，又由3c sin B＝4a sin C，得3b sin C＝4a sin C，又sin C≠0，所以3b＝4a.又因为b＋c＝2a，所以b＝a，c＝a，由余弦定理可得cos B＝＝＝－.(2)由(1)可得sin B＝＝，从而sin 2B＝2sin B cos B＝－，cos 2B＝cos2B－sin2B＝－，故sin＝sin 2B cos ＋cos 2B sin ＝－×－×＝－.4．(2019·浙江，18)设函数f(x)＝sin x，x∈R.(1)已知θ∈[0,2π)，函数f(x＋θ)是偶函数，求θ的值；(2)求函数y＝2＋2的值域．解(1)因为f(x＋θ)＝sin(x＋θ)是偶函数，所以，对任意实数x都有sin(x＋θ)＝sin(－x＋θ)，即sin x cos θ＋cos x sin θ＝－sin x cos θ＋cos x sin θ，故2sin x cos θ＝0，所以cos θ＝0.又θ∈[0,2π)，因此θ＝或.(2)y＝2＋2＝sin2＋sin2＝＋＝1－＝1－cos.因此，函数的值域是.5．(2019·江苏，15)在△ABC中，角A，B，C的对边分别为a，b，c.(1)若a＝3c，b＝，cos B＝，求c的值；(2)若＝，求sin的值．解(1)因为a＝3c，b＝，cos B＝，由余弦定理cos B＝，得＝，即c2＝.所以c＝.(2)因为＝，由正弦定理＝，得＝，所以cos B＝2sin B.从而cos2B＝(2sin B)2，即cos2B＝4(1－cos2B)，故cos2B＝.因为sin B>0，所以cos B＝2sin B>0，从而cos B＝.因此sin＝cos B＝.6．(2019·全国Ⅰ理，17)△ABC的内角A，B，C的对边分别为a，b，c，设(sin B－sin C)2＝sin2A－sin B sin C.(1)求A；(2)若a＋b＝2c，求sin C.解(1)由已知得sin2B＋sin2C－sin2A＝sin B sin C，故由正弦定理得b2＋c2－a2＝bc，由余弦定理得cos A＝＝，因为0°<A<180°，所以A＝60°.(2)由(1)知B＝120°－C，由题设及正弦定理得sin A＋sin(120°－C)＝2sin C，即＋cos C＋sin C＝2sinC，可得cos(C＋60°)＝－.由于0°<C<120°，所以sin(C＋60°)＝，故sin C＝sin(C＋60°－60°)＝sin(C＋60°)cos 60°－cos(C＋60°)sin 60°＝.7．(2019·全国Ⅲ理，18)△ABC的内角A，B，C的对边分别为a，b，c.已知a sin ＝b sinA.(1)求B；(2)若△ABC为锐角三角形，且c＝1，求△ABC面积的取值范围．解(1)由题设及正弦定理，得sin A sin＝sin B sin A.因为sin A≠0，所以sin ＝sin B.由A＋B＋C＝180°，可得sin ＝cos ，故cos ＝2sin cos .因为cos ≠0，故sin ＝，因此B＝60°.(2)由题设及(1)知△ABC的面积S△ABC＝a.由正弦定理，得a＝4＝＝＋.由于△ABC为锐角三角形，故0°<A<90°，0°<C<90°.由(1)知A＋C＝120°，所以30°<C<90°，故<a<2，从而<S△ABC<.因此，△ABC面积的取值范围是.8．(2019·北京理，15)（13分）在ABC∆中，3a=，2b c-=，1 cos2B=-．（Ⅰ）求b，c的值；（Ⅱ）求sin()B C-的值．【思路分析】（Ⅰ）利用余弦定理可得2222cosb ac ac B=+-，代入已知条件即可得到关于b 的方程，解方程即可；（Ⅱ）sin()sin cos cos sin B C B C B C -=-，根据正弦定理可求出sin C ，然后求出cos C ，代入即可得解．【解析】：（Ⅰ）3a =，2b c -=，1cos 2B =-． ∴由余弦定理，得2222cos b a c ac B =+-219(2)23(2)()2b b =+--⨯⨯-⨯-， 7b ∴=，25c b ∴=-=；（Ⅱ）在ABC ∆中，1cos 2B =-，sin B ∴=， 由正弦定理有：sin sin c b C B =，∴5sin 2sin 7c B C b === b c >，B C ∴>，C ∴为锐角，11cos 14C ∴=， sin()sin cos cos sin B C B C B C ∴-=-111()142=--=． 【归纳与总结】本题考查了正弦定理余弦定理和两角差的正弦公式，属基础题．9．(2019·天津理，15)在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知b ＋c ＝2a,3c sin B ＝4a sin C .(1)求cos B 的值；(2)求sin的值． 解 (1)在△ABC 中，由正弦定理 ＝ ，得b sin C ＝c sin B ，又由3c sin B ＝4a sin C ，得3b sin C ＝4a sin C ，又sin C ≠0，所以3b ＝4a .又因为b ＋c ＝2a ，所以b ＝ a ，c ＝ a ，由余弦定理可得cos B ＝ ＝＝－ . (2)由(1)可得sin B ＝ ＝， 从而sin 2B ＝2sin B cos B ＝－，cos 2B ＝cos 2B －sin 2B ＝－ ， 故sin ＝sin 2B cos ＋cos 2B sin＝－ × － × ＝－ .。

(2019全国1理)11.关于函数()sin sin f x x x =+有下述四个结论： ①()f x 是偶函数 ②()f x 在区间(,)2ππ单调递增③()f x 在[],ππ-有4个零点 ④()f x 的最大值为2 其中所有正确结论的编号是（ ）A.①②④B.②④C.①④D.①③ 答案：C 解答：因为()sin sin()sin sin ()f x x x x x f x -=-+-=+=，所以()f x 是偶函数，①正确， 因为52,(,)632ππππ∈，而52()()63f f ππ<，所以②错误， 画出函数()f x 在[],ππ-上的图像，很容易知道()f x 有3零点，所以③错误， 结合函数图像，可知()f x 的最大值为2，④正确，故答案选C.(2019全国1理)17.ABC ∆的内角,,A B C 的对边分别为,,a b c .设()22sin sin sin sin sin B C A B C -=-. （1）求A ；（22b c +=，求sin C . 答案：（1）由()22sin sin sin sin sin B C A B C -=-得222sin sin sin sin sin B C A B C +-= 结合正弦定理得222b c a bc +-=∴2221cos =22b c a A b c +-=⋅⋅又(0,)A π∈，∴=3A π.（22b c +=sin 2sin A B C +=,()sin 2sin A A C C ++=∴sin()2sin 23C C π++=,1cos 22C C -=∴sin()6C π-=又203C π<<∴662C πππ-<-< 又sin()06C π->∴062C ππ<-<∴cos 62C π⎛⎫-= ⎪⎝⎭，∴sin sin()66C C ππ=-+=sin cos cos sin 6666C C ππππ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭4=.(2019全国2理)9. 下列函数中，以2π为周期且在区间,42ππ⎛⎫⎪⎝⎭单调递增的是（ ） A.|2cos |)(x x f = B.|2sin |)(x x f = C.||cos )(x x f = D.||sin )(x x f = 答案：A解答：对于A,函数|2cos |)(x x f =的周期2T π=,在区间,42ππ⎛⎫⎪⎝⎭单调递增,符合题意； 对于B,函数|2sin |)(x x f =的周期2T π=,在区间,42ππ⎛⎫⎪⎝⎭单调递减,不符合题意； 对于C ，函数x x x f cos ||cos )(==，周期2T π=,不符合题意； 对于D,函数||sin )(x x f =的周期T π=,不符合题意.(2019全国2理)10. 已知(0,)2πα∈，2sin 2cos21αα=+，则sin α=（ ）A.15答案：B 解析：(0,)2πα∈，22sin 2cos 214sin cos 2cos ααααα=+⇒=，则12sin cos tan 2ααα=⇒=，所以cos α==所以sin α==.(2019全国2理)15. ABC ∆的内角C B A ,,的对边分别为c b a ,,，若,3,2,6π===B c a b 则ABC ∆的面积为_____. 答案：36解析：21436423cos cos 222222=-+=-+==cc c ac b c a B π, 3623323421sin 21,34,32=⨯⨯⨯==∴==∴B ac S a c（2019全国3理）12.设函数()()sin 05f x x πωω⎛⎫=+> ⎪⎝⎭，已知()f x 在[]02π，有且仅有5个零点，下述四个结论：○1()f x 在()0,2π有且仅有3个极大值点 ○2()f x 在()0,2π有且仅有2个极小值点 ○3()f x 在0,10π⎛⎫⎪⎝⎭单调递增 ○4ω的取值范围是1229,510⎡⎫⎪⎢⎣⎭其中所有正确结论的编号是A. ○1○4B.○2○3C.○1○2○3D.○1○3○4 答案： D解析：根据题意，画出草图，由图可知[)122,x x π∈，由题意可得，125565x x πωππωπ⎧+=⎪⎪⎨⎪+=⎪⎩，解得12245295x x πωπω⎧=⎪⎪⎨⎪=⎪⎩，所以2429255πππωω≤<，解得1229510ω≤<，故○4对； 令52x ππω+=得3010x πω=>，∴图像中y 轴右侧第一个最值点为最大值点，故○1对； ∵[)122,x x π∈，∴()f x 在()0,2π有2个或3个极小值点，故○2错； ∵1229510ω≤<，∴1149251051002πππππω≤⋅+<<，故○3对. （2019全国3理）18.ABC ∆的内角A B C ，，的对边分别为,,a b c .已知sinsin 2A Ca b A +=.(1求B; (2) 若ABC ∆为锐角三角形，且1c =，求ABC ∆面积的取值范围.答案：（1）3π（2）见解析 解析：因为s i ns i n s i ns i n2BA B A π-=；结合正弦定理sin sinsin sin 2BA B Aπ-=,得cossin 2sin cos 222B B B B ==,即1sin 22B =；得到,263B B ππ==；（2）因为23A C π+=,0,2A π<<0,2C π<<20,32C ππ<-<所以,62C ππ<<又因为s i n s i ns i nabcA B C ==,11sin sin sin 122sin 24sin c A S ac B A C C ==⋅⋅⋅⋅=;又因为s i n 1(,2)s i n 2A C ∈（因为2,3A C π+=,A C 为锐角，若A 越大sin A 越大，则C 越小sin C 越小；sin sin A C 越大）；所以sin 1(,2)sin 2A C ∈，所以S ∈.（2019北京理）9.函数f (x )=sin 22x 的最小正周期是__________．【答案】2π.【解析】将所给的函数利用降幂公式进行恒等变形，然后求解其最小正周期即可. 【详解】函数()2sin 2f x x ==142cos x -,周期为2π【点睛】本题主要考查二倍角的三角函数公式､三角函数的最小正周期公式，属于基础题. （2019北京理）15.在△ABC 中，a =3，b −c =2，cos B =12-． （Ⅰ）求b ，c 的值； （Ⅱ）求sin （B –C ）的值．【答案】(Ⅰ) 375a b c =⎧⎪=⎨⎪=⎩；(Ⅱ) 【解析】 (Ⅰ)由题意列出关于a ,b ,c 的方程组，求解方程组即可确定b ,c 的值； (Ⅱ)由题意结合正弦定理和两角和差正余弦公式可得()sin B C -的值.【详解】(Ⅰ)由题意可得：2221cos 2223a c b B ac b c a ⎧+-==-⎪⎪⎪-=⎨⎪=⎪⎪⎩，解得：375a b c =⎧⎪=⎨⎪=⎩.(Ⅱ)由同角三角函数基本关系可得：sin 2B ==， 结合正弦定理sin sin b c B C =可得：sin sin c B C b == 很明显角C为锐角，故11cos 14C ==， 故()sin sin cos cos sin B C B C B C -=-=【点睛】本题主要考查余弦定理、正弦定理的应用，两角和差正余弦公式的应用等知识，意在考查学生的转化能力和计算求解能力.（2019天津理）7.已知函数()sin()(0,0,||)f x A x A ωϕωϕπ=+>><是奇函数，将()y f x =的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图像对应的函数为()g x .若()g x 的最小正周期为2π，且4g π⎛⎫= ⎪⎝⎭38f π⎛⎫= ⎪⎝⎭（ ） A. 2-B.C.D. 2【答案】C【解析】只需根据函数性质逐步得出,,A ωϕ值即可。

2019年高考试题分类汇编(三角函数) 2019年高考试题分类汇编（三角函数）考法1 三角函数的图像及性质1.（2019·全国卷Ⅰ·文科）已知tan225= tan(180°+45°)=-tan45°=-1，故选A。

2.（2019·全国卷Ⅱ·文科）由f(x)的定义可知，当x=π/4时，f(x)=sin(πω/4)，当x=3π/4时，f(x)=sin(3πω/4)。

因为x1和x2是相邻的极值点，所以f(x1)=f(x2)=0，即sin(πω/4)=sin(3πω/4)=0.因为ω>0，所以πω/4=0或π，3πω/4=π/2或5π/2.解得ω=8或16，故选B。

3.（2019·全国卷Ⅲ·文科）f(x)=2sinx-sin2x=2sinx-2sinxcosx=2sinx(1-cosx)，所以f(x)的零点为x=0,π和2π。

故选B。

4.（2019·全国卷Ⅰ·文理科）由于cosx在[-π,π]上单调递减，所以cosx的最小值为cos(-π)=-1，最大值为cos(π)=1.因此，当x=-π或x=π时，f(x)的值最小，为-2/π；当x=0时，f(x)的值最大，为2.故选B。

5.（2019·全国卷Ⅰ·理科）①f(x)是偶函数，③f(x)在[-π,π]上有一个零点，故①和③正确。

当00，即f(x)在(0,π)单调递增，故②正确。

当x=π/2时，f(x)=2，又因为f(x)是偶函数，所以当x=-π/2时，f(x)也等于2，故④正确。

因此，选A。

6.（2019·全国卷Ⅱ·理科）由f(x)的定义可知，f(x+π/2)=cos2x，f(x+π)=cos(2x+π)=-cos2x，f(x+3π/2)=-cos2x，f(x+2π)=cos2x。

因此，f(x)的周期为π，而且f(x)在(0,π)单调递增，故选B。

2019年高考数学试题分类汇编三角函数一、选择题.1、（2019年高考全国I 卷文理科5）函数f (x )=2sin cos ++x xx x在[,]-ππ的图像大致为 A ．B ．C ．D ．答案：D解析：因为)()(x f x f -=-，所以)(x f 为奇函数又01)(2>-=πππf ，124412)2(22>+=+=πππππf ，故选D 2、（2019年高考全国I 卷理科11）关于函数()sin |||sin |f x x x =+有下述四个结论：①f (x )是偶函数②f (x )在区间（2π，π）单调递增③f (x )在[,]-ππ有4个零点 ④f (x )的最大值为2其中所有正确结论的编号是 A ．①②④ B ．②④C ．①④D ．①③答案：C解析：由)(|sin |||sin |)sin(|||sin )(x f x x x x x f =+=-+-=-，故①正确；),2(ππ∈x 时，x x x x f sin 2sin sin )(=+=，函数递减，故②错误；],0[π∈x 时，x x x x f sin 2sin sin )(=+=，函数有2个零点，0)()0(==πf f ，而],0[π∈x 时0)()0(=-=πf f ，所以函数有且只有3个零点，故③错误；函数为偶函数，只需讨论0>x ，N k k k x ∈+∈),2,2(πππ时，x x x x f sin 2sin sin )(=+=，最大值为2，N k k k x ∈++∈),22,2(ππππ时，0sin sin )(=-=x x x f ，故函数最大值为2，故④正确。

故选C3、（2019年高考全国I 卷文科7）tan255°= A ．-2B ．-C ．2D ．答案：D解析：32)4530tan(75tan )75180tan(255tan +=︒+︒=︒=︒+︒=︒故选D4、（2019年高考全国I 卷文科11）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知a sin A -b sin B =4c sin C ，cos A =-14，则b c=A ．6B ．5C ．4D ．3答案：A解析：由正弦定理C B b A a sin 4sin sin =-,角化边得2224c b a +=又412)4(cos 2222-=+-+=bc c b c b A ，联立求得6=c b 故选A5、（2019年高考全国II 卷理科4）019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆，我国航天事业取得又一重大成就，实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系．为解决这个问题，发射了嫦娥四号中继星“鹊桥”，鹊桥沿着围绕地月拉格朗日2L 点的轨道运行．2L 点是平衡点，位于地月连线的延长线上．设地球质量为M １，月球质量为M ２，地月距离为R ，2L 点到月球的距离为r ，根据牛顿运动定律和万有引力定律，r 满足方程：121223()()M M M R r R r r R +=++.设r Rα=，由于α的值很小，因此在近似计算中34532333(1)ααααα++≈+，则r 的近似值为 ABCD答案：D 解析：Rr=α则R r α=，代入121223()()M M M R r R r r R +=++得12322)1(1)1(M M ααα+-+=即3254322312)1(33)1(1)1(αααααααα≈+++=+-+=M M所以R M M r 3123=.故答案选D 6、（2019年高考全国II 卷理科9）下列函数中，以2π为周期且在区间(4π，2π)单调递增的是A ．f (x )=│cos2x │B ．f (x )=│sin 2x │C ．f (x )=cos│x │D ．f (x )= sin │x │答案：A解析：将|2cos |)(x x f =的图像变换，“下翻上”，如图可知在区间)2,4(ππ上是增函数.故答案选A 7、（2019年高考全国II 卷理科10，文科11）已知α∈(0，2π)，2sin 2α=cos 2α+1，则sin α=A ．15B 5C 3D 5答案：B解析：ααα2cos 212cos 2sin 2=+=，与αααcos sin 22sin =联立求得21tan =α 又)2,0(πα∈，所以55sin =α故答案选B 8、（2019年高考全国II 卷文科8）若x 1=4π，x 2=43π是函数f (x )=sin x ω(ω>0)两个相邻的极值点，则ω=A ．2B ．32C ．1D ．12答案：A 解析：πππ=-=T T ,4432,又ωπ2=T ,所以2=ω。

专题10 三角函数求值【母题来源一】【2019年高考全国Ⅱ卷理数】已知α∈(0，2π)，2sin 2cos21αα=+，则sin α=A ．15B ．5C ．3D ．5【答案】B【母题来源二】【2018年高考全国Ⅱ理数】已知sin cos 1αβ+=，cos sin 0αβ+=，则sin()αβ+=_____________．【答案】12-【命题意图】1．和与差的三角函数公式（1）会用向量的数量积推导出两角差的余弦公式．（2）能利用两角差的余弦公式导出两角差的正弦、正切公式．（3）能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式，导出二倍角的正弦、余弦、正切公式，了解它们的内在联系． 2．简单的三角恒等变换能运用上述公式进行简单的恒等变换（包括导出积化和差、和差化积、半角公式，但对这三组公式不要求记忆）． 3．通过考查三角恒等变换公式等相关知识，考查转化思想和运算求解能力． 【命题规律】一般以选择题或填空题的形式考查，主要从公式的变用、逆用以及角度的关系等角度，考查方程思想和运算求解能力．试题难度不大，多为低档题． 【答题模板】 1．给角求值给角求值中一般所给出的角都是非特殊角，从表面上来看是很难的，但仔细观察会发现非特殊角与特殊角之间总有一定的关系．解题时，要利用观察得到的关系，结合公式将非特殊角的三角函数转化为特殊角的三角函数，从而得解．2．给值求值已知三角函数值，求其他三角函数式的值的一般思路： （1）先化简所求式子．（2）观察已知条件与所求式子之间的联系(从三角函数名及角入手)． （3）将已知条件代入所求式子，化简求值． 3．给值求角通过求角的某种三角函数值来求角，在选取函数时，有以下原则： （1）已知正切函数值，则选正切函数．（2）已知正、余弦函数值，则选正弦或余弦函数．若角的范围是π(0,)2，则选正、余弦皆可；若角的范围是(0，π)，则选余弦较好；若角的范围为ππ(,)22-，则选正弦较好． （3）在解决给值求角问题时，不仅要注意已经明确给出的有关角的范围，还要结合有关角的三角函数值尽可能地缩小角的范围． 【方法总结】1．两角和与差的正弦、余弦、正切公式（1）()C αβ-：cos()αβ-=cos cos sin sin αβαβ+ （2）()C αβ+：cos()cos cos sin sin αβαβαβ+=- （3）()S αβ+：sin()αβ+=sin cos cos sin αβαβ+ （4）()S αβ-：sin()αβ-=sin cos cos sin αβαβ- （5）()T αβ+：tan()αβ+=tan tan π(,,π,)1tan tan 2k k αβαβαβαβ++≠+∈-Z（6）()T αβ-：tan()αβ-=tan tan π(,,π,)1tan tan 2k k αβαβαβαβ--≠+∈+Z2．二倍角公式（1）2S α：sin 2α=2sin cos αα（2）2C α：cos2α=2222cos sin 12sin 2cos 1αααα-=-=- （3）2T α：tan 2α=22tan πππ(π,)1tan 224k k k αααα≠+≠+∈-Z 且3．公式的常用变形（1）tan tan tan()(1tan tan )αβαβαβ±=±m ；tan tan tan tan tan tan 11tan()tan()αβαβαβαβαβ+-=-=-+-（2）降幂公式：21cos 2sin2αα-=；21cos 2cos 2αα+=；1sin cos sin 22ααα= （3）升幂公式：21cos 22cos αα+=；21cos 22sin αα-=；21sin 2(sin cos )ααα+=+；21sin 2(sin cos )ααα-=-（4）辅助角公式：sin cos a x b x +)x ϕ=+，其中cos ϕϕ==tan baϕ=4．半角公式（1）sin2α=；（2）cos2α=；（3）tan2α=sin 1cos 1cos sin αααα-==+． 5．积化和差公式 （1）1cos cos [cos()cos()]2αβαβαβ=++-； （2）1sin sin [cos()cos()]2αβαβαβ=-+--； （3）1sin cos [sin()sin()]2αβαβαβ=++-； （4）1cos sin [sin()sin()]2αβαβαβ=+--． 6．和差化积公式（1）sin sin 2sin cos22αβαβαβ+-+=； （2）sin sin 2cossin22αβαβαβ+--=； （3）cos cos 2coscos22αβαβαβ+-+=； （4）cos cos 2sin sin22αβαβαβ+--=-．7．常见的角的变换 （1）已知角表示未知角例如：()()ααββββα=+-=--，()()()()2,2ααβαββαβαβ=++-=+--，(2)αβαβα+=++，(2)αβαβα-=-+，22αβαβα+-=+，22αβαββ+-=-．（2）互余与互补关系 例如：π3π()()π44αα++-=，πππ()()362αα++-=． （3）非特殊角转化为特殊角 例如：15°=45°−30°，75°=45°＋30°．1．【陕西省榆林市2019届高考模拟第三次测试】已知tan 2α=-，则tan()4απ+= A ．13-B ．13C ．3-D ．3【答案】A2．【重庆西南大学附属中学校2019届高三第十次月考】已知角α的顶点在坐标原点，始边与x 轴正半轴重合，终边经过点(1)P ，则cos2=αA ．3B ．13C ．13-D ．3-【答案】B3．【四川省宜宾市2019届高三第三次诊断性考试】已知4cos 5=-α，(π,0)α∈-，则πtan()4α-= A ．17 B ．7 C ．17-D ．7-【答案】C4．【陕西省2019届高三年级第三次联考】已知sin 2cos αα=，则cos2α=A ．45- B ．35-C ．35±D ．45±【答案】B5．【宁夏石嘴山市第三中学2019届高三下学期一模】已知2sin23α=，则1tan tan αα+= A ．1 B ．2 C ．3D ．4【答案】C6．【吉林省吉林市普通中学2018-2019学年度高中毕业班第三次调研】已知角α的终边经过点(P -，则sin 2α=A ．2B ．2-C ．12-D ．【答案】B7．【东北三省三校（哈尔滨师大附中、东北师大附中、辽宁省实验中学）2019届高三第二次模拟】已知1cos()63απ+=，则sin(2)6απ-= A ．79- B ．79C ．89D ．89-【答案】B8．【吉林省延边州2019届高三2月复习质量检测】已知1sin()3απ+=，||2απ<，则cos()6απ+=A ．6B ．16C D 【答案】B9．【黑龙江省哈尔滨市第三中学2019届高三第二次模拟】已知α是第二象限角，且3sin()5απ+=-，则tan 2α的值为A ．45 B ．237-C ．247-D ．249-【答案】C10．【重庆市2019届高三学业质量调研抽测4月二诊】已知2απ<<π，且1sin cos 5αα+=，则tan 2α的值为 A ．247- B ．247C ．724-D ．724【答案】B11．【甘肃省2019届高三第二次高考诊断】已知sin 2sin 0,(,)2αααπ+=∈π，则tan()4απ+=A ．2-B ．2C ．2-D ．2【答案】C12．【黑龙江省哈尔滨师范大学附属中学2019届高三上学期期中考试】已知2sin cos 0θθ+=，则2sin cos cos θθθ-的值 A ．65- B ．35- C ．35D ．65【答案】A13．【辽宁省丹东市2019届高三总复习质量测试二】若tan()34απ+=-，则2sin 2cos αα-=A ．35B ．25-C ．1-D ．3【答案】A14．【黑龙江省哈尔滨市第六中学2019届高三第二次模拟】若4cos 25α=-，(,)2απ∈π，则tan()4απ+= A ．2- B ．12- C ．2D ．12【答案】B15．【新疆维吾尔自治区2019年普通高考第二次适应性检测】已知x ∈R ，sin 3cos x x -=tan2x =A ．43 B ．34 C ．34-D ．43-【答案】A16．【新疆维吾尔自治区2019年普通高考第一次适应性检测】若sin()(0,)4ααπ+=∈π，则cos α的值为A BCD 【答案】D17．【吉林省四平一中2019届高三下学期第二次联合模拟】若tan(2)2αβ+=，tan 3β=-，则tan α=______________． 【答案】1218．【甘青宁2019届高三3月联考】若tan(2)2αβ+=，tan 3β=-，则tan()αβ+=______________．【答案】1-19．【齐鲁名校教科研协作体湖北、山东部分重点中学2019届高三第一次联考】若(0,)2απ∈，且sin22cos22αα-=，则tan α=______________． 【答案】220．【新疆乌鲁木齐2019届高三第二次质量检测】已知1sin()34απ+=，则os 3(c 2)2απ+的值为______________． 【答案】7821．【安徽省合肥市2019届高三第二次教学质量检测】若1sin()23απ+=，则cos2cos αα+=______________． 【答案】49-22．【辽宁省朝阳市普通高中2019届高三第三次模拟】若tan 3α=，(0,)2απ∈，则cos()4απ-=______________．23．【黑龙江省大庆市2019届高三第二次模拟】已知α，β为锐角，且(1)(1)4αβ=，则αβ+=______________． 【答案】23π24．【甘肃省2019届高三第一次高考诊断】已知α，β均为锐角，4cos 5α=，1tan()3αβ-=-，则cos β=______________．【答案】5025．【新疆乌鲁木齐市2019届高三第二次诊断性测试】已知4sin()45απ+=，3(,)44αππ∈，则tan α=______________． 【答案】7。

专题09 三角函数1．【2019年高考全国Ⅰ卷理数】函数f (x )=2sin cos ++x xx x 在的图像大致为[,]-ππA ．B ．C ．D ．【答案】D【解析】由，得是奇函数，其图象关于原点对称，22sin()()sin ()()cos()()cos x x x xf x f x x x x x-+----===--+-+()f x 排除A ．又，排除B ，C ，故选D ．22π1π42π2()1,π2π()2f ++==>2π(π)01πf =>-+【名师点睛】本题考查函数的性质与图象，渗透了逻辑推理、直观想象和数学运算素养，采取性质法或赋值法，利用数形结合思想解题．解答本题时，先判断函数的奇偶性，得是奇函数，排除A ，再注()f x 意到选项的区别，利用特殊值得正确答案．2．【2019年高考全国Ⅰ卷理数】关于函数有下述四个结论：()sin |||sin |f x x x =+①f (x )是偶函数②f (x )在区间（，）单调递增2ππ③f (x )在有4个零点④f (x )的最大值为2[,]-ππ其中所有正确结论的编号是A ．①②④B ．②④C ．①④D ．①③【答案】C【解析】为偶函数，故①正确．()()()()sin sin sin sin ,f x x x x x f x f x -=-+-=+=∴ 当时，，它在区间单调递减，故②错误．ππ2x <<()2sin f x x =,2π⎛⎫π ⎪⎝⎭当时，，它有两个零点：；当时，0πx ≤≤()2sin f x x =0,ππ0x -≤<()()sin sin f x x x=--，它有一个零点：，故在有个零点：，故③错误．2sin x =-π-()f x [],-ππ30-π,,π当时，；当时，[]()2,2x k k k *∈ππ+π∈N()2sin f x x =[]()2,22x k k k *∈π+ππ+π∈N，又为偶函数，的最大值为，故④正确．()sin sin 0f x x x =-=()f x ()f x ∴2综上所述，①④正确，故选C ．【名师点睛】本题也可画出函数的图象（如下图），由图象可得①④正确．()sin sin f x x x =+3．【2019年高考全国Ⅱ卷理数】下列函数中，以为周期且在区间(，)单调递增的是2π4π2πA ．f (x )=|cos2x | B ．f (x )=|sin2x | C ．f (x )=cos|x | D ．f (x )=sin|x |【答案】A【解析】作出因为的图象如下图1，知其不是周期函数，排除D ；sin ||y x =因为，周期为，排除C ；cos cos y x x ==2π作出图象如图2，由图象知，其周期为，在区间(，)单调递增，A 正确；cos 2y x =π24π2π作出的图象如图3，由图象知，其周期为，在区间(，)单调递减，排除B ，sin 2y x =π24π2π故选A ．图1图2图3【名师点睛】本题主要考查三角函数的图象与性质，渗透直观想象、逻辑推理等数学素养，画出各函数图象，即可作出选择．本题也可利用二级结论：①函数的周期是函数周期的一半；②()y f x =()y f x =不是周期函数.sin y x ω=4．【2019年高考全国Ⅱ卷理数】已知α∈(0，)，2sin2α=cos2α+1，则sin α=2πA ．B 15C D 【答案】B【解析】，，2sin 2cos 21αα=+ 24sin cos 2cos .0,,cos 02αααααπ⎛⎫∴⋅=∈∴> ⎪⎝⎭sin 0,α>，又，，又，2sin cos αα∴=22sin cos 1αα+=2215sin 1,sin 5αα∴==sin 0α>sin α∴=选B ．【名师点睛】本题是对三角函数中二倍角公式、同角三角函数基本关系式的考查，中等难度，判断正余弦的正负，运算准确性是关键，题目不难，需细心，解决三角函数问题，研究角的范围后得出三角函数值的正负很关键，切记不能凭感觉．解答本题时，先利用二倍角公式得到正余弦关系，再利用角范围及正余弦平方和为1关系得出答案．5．【2019年高考全国Ⅲ卷理数】设函数=sin （）(＞0)，已知在有且仅有5()f x 5x ωπ+ω()f x []0,2π个零点，下述四个结论：①在（）有且仅有3个极大值点()f x 0,2π②在（）有且仅有2个极小值点()f x 0,2π③在（）单调递增()f x 0,10π④的取值范围是[)ω1229510，其中所有正确结论的编号是A ．①④B ．②③C ．①②③D ．①③④【答案】D【名师点睛】本题为三角函数与零点结合问题，难度大，可数形结合，分析得出答案，要求高，理解深度高，考查数形结合思想．注意本题中极小值点个数是动态的，易错，正确性考查需认真计算，易出错．6．【2019年高考天津卷理数】已知函数是奇函数，将()sin()(0,0,||)f x A x A ωϕωϕ=+>><π()y f x =的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），所得图象对应的函数为．若的()g x ()g x 最小正周期为，且，则2π4g π⎛⎫=⎪⎝⎭38f π⎛⎫= ⎪⎝⎭A ．B ．2-CD ．2【答案】C【解析】∵为奇函数，∴；()f x (0)sin 0,=π,,0,f A k k k ϕϕ==∴∈∴=Z 0ϕ=又∴，12π()sin,2π,122g x A x T ωω=∴==2ω=又，π(4g =2A =∴，故选C.()2sin 2f x x =3π(8f =【名师点睛】本题主要考查函数的性质和函数的求值问题，解题关键是求出函数，再根据函数性()g x质逐步得出的值即可.,,A ωϕ7．【2018年高考全国Ⅲ卷理数】若，则1sin 3α=cos 2α=A ．B ．8979C ．D ．79-89-【答案】B【解析】.2217cos 212sin 12()39αα=-=-⨯=故选B.【名师点睛】本题主要考查三角函数的求值，考查考生的运算求解能力，考查的核心素养是数学运算.8．【2018年高考全国卷II 理数】若在是减函数，则的最大值是()cos sin f x x x =-[],a a -a A ．B ．π4π2C ．D ．3π4π【答案】A【解析】因为，()πcos sin 4f x x x x ⎛⎫=-=+ ⎪⎝⎭所以由得，π02ππ2π()4k x k k +≤+≤+∈Z π3π2π2π()44k x k k -+≤≤+∈Z 因此，从而的最大值为，[]π3ππ3ππ,,,,,,044444a a a a a a a ⎡⎤-⊂-∴-<-≥-≤∴<≤⎢⎥⎣⎦a π4故选A.【名师点睛】解答本题时，先确定三角函数单调减区间，再根据集合包含关系确定的最大值.函数a 的性质：()sin (0,0)y A x B A =++>>ωϕω(1).max min =+y A B y A B =-，(2)周期2.T =πω(3)由求对称轴.()ππ2x k k +=+∈Z ωϕ(4)由求增区间；由求减区()ππ2π2π22k x k k -+≤+≤+∈Z ωϕ()π3π2π2π22k x k k +≤+≤+∈Z ωϕ间.9．【2018年高考天津理数】将函数的图象向右平移个单位长度，所得图象对应的函数sin(2)5y x π=+10πA ．在区间上单调递增B ．在区间上单调递减35[,]44ππ3[,]4ππC ．在区间上单调递增D ．在区间上单调递减53[,]42ππ3[,2]2ππ【答案】A【解析】由函数图象平移变换的性质可知：将的图象向右平移个单位长度之后的解πsin 25y x ⎛⎫=+⎪⎝⎭π10析式为.ππsin 2sin2105y x x ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦则函数的单调递增区间满足，即，()ππ2π22π22k x k k -≤≤+∈Z ()ππππ44k x k k -≤≤+∈Z 令可得一个单调递增区间为.1k =3π5π,44⎡⎤⎢⎥⎣⎦函数的单调递减区间满足：，即，()π3π2π22π22k x k k +≤≤+∈Z ()π3πππ44k x k k +≤≤+∈Z 令可得一个单调递减区间为：.1k =5π7π,44⎡⎤⎢⎥⎣⎦故选A.【名师点睛】本题主要考查三角函数的平移变换，三角函数的单调区间的判断等知识，意在考查学生的转化能力和计算求解能力.10．【2018年高考浙江卷】函数y =sin2x 的图象可能是2xA ．B ．C ．D ．【答案】D【解析】令，因为，所以()2sin2xf x x =()()(),2sin22sin2xxx f x x x f x -∈-=-=-=-R 为奇函数，排除选项A ，B ；()2sin2xf x x =因为时，，所以排除选项C ，π,π2x ⎛⎫∈ ⎪⎝⎭()0f x <故选D.【名师点睛】解答本题时，先研究函数的奇偶性，再研究函数在上的符号，即可作出判断.有π,π2⎛⎫⎪⎝⎭关函数图象的识别问题的常见题型及解题思路：（1）由函数的定义域，判断图象的左、右位置，由函数的值域，判断图象的上、下位置；（2）由函数的单调性，判断图象的变化趋势；（3）由函数的奇偶性，判断图象的对称性；（4）由函数的周期性，判断图象的循环往复．11．【2017年高考全国Ⅰ理数】已知曲线C 1：y =cos x ，C 2：y =sin (2x +)，则下面结论正确的是2π3A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得π6到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得π12到曲线C 2C ．把C 1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得12π6到曲线C 2D ．把C 1上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得12π12到曲线C 2【答案】D【解析】因为函数名不同，所以先将利用诱导公式转化成与相同的函数名，则12,C C 2C 1C ，则由上各点的横坐标缩短到原来的倍变22π2πππ:sin(2cos(2cos(2)3326C y x x x =+=+-=+1C 12为，再将曲线向左平移个单位长度得到，故选D.cos 2y x =π122C 【名师点睛】对于三角函数图象变换问题，首先要将不同名函数转换成同名函数，利用诱导公式，需要重点记住；另外，在进行图象变换时，提倡先平移后伸缩，而先ππsin cos(),cos sin()22αααα=-=+伸缩后平移在考试中也经常出现，无论哪种变换，记住每一个变换总是对变量而言.x 12．【2017年高考全国Ⅲ理数】设函数，则下列结论错误的是()π(3cos f x x =+A ．的一个周期为()f x 2π-B ．的图象关于直线对称()y f x =8π3x =C ．的一个零点为(π)f x +π6x =D ．在(，)单调递减()f x π2π【答案】D【解析】函数的最小正周期为，则函数的周期为，取，()f x 2π2π1T ==()f x ()2πT k k =∈Z 1k =-可得函数的一个周期为，选项A 正确；()f x 2π-函数图象的对称轴为，即，取，可得y =f (x )的图象关()f x ()ππ3x k k +=∈Z ()ππ3x k k =-∈Z 3k =于直线对称，选项B 正确；8π3x =，函数的零点满足，即()πππcos πcos 33f x x x ⎡⎤⎛⎫⎛⎫+=++=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦()f x ()πππ32x k k +=+∈Z ，取，可得的一个零点为，选项C 正确；()ππ6x k k =+∈Z 0k =(π)f x +π6x =当时，，函数在该区间内不单调，选项D 错误.π,π2x ⎛⎫∈ ⎪⎝⎭π5π4π,363x ⎛⎫+∈ ⎪⎝⎭()f x 故选D.【名师点睛】（1）求最小正周期时可先把所给三角函数式化为或(n )si y A x ωϕ=+(s )co y A x ωϕ=+的形式，则最小正周期为；奇偶性的判断关键是解析式是否为或2πT ω=sin y A x ω=cos y A x bω=+的形式.（2）求的对称轴，只需令，求x ；求f (x )的对()()sin 0()f x A x ωϕω+≠=()ππ2x k k ωϕ+=+∈Z 称中心的横坐标，只需令即可.π()x k k ωϕ+=∈Z 13．【2017年高考天津卷理数】设函数，，其中，．若，()2sin()f x x ωϕ=+x ∈R 0ω>||ϕ<π5(28f π=，且的最小正周期大于，则()08f 11π=()f x 2πA ．，B ．，23ω=12ϕπ=23ω=12ϕ11π=-C ．，D ．，13ω=24ϕ11π=-13ω=24ϕ7π=【答案】A【解析】由题意得，其中，所以，125282118k k ωϕωϕππ⎧+=π+⎪⎪⎨π⎪+=π⎪⎩12,k k ∈Z 2142(2)33k k ω=--又，所以，所以，，22T ωπ=>π01ω<<23ω=11212k ϕ=π+π由得，故选A ．ϕ<π12ϕπ=【名师点睛】关于的问题有以下两种题型：sin()y A x ωϕ=+①提供函数图象求解析式或参数的取值范围，一般先根据图象的最高点或最低点确定，再根据最小A 正周期求，最后利用最高点或最低点的坐标满足解析式，求出满足条件的的值；ωϕ②题目用文字叙述函数图象的特点，如对称轴方程、曲线经过的点的坐标、最值等，根据题意自己画出大致图象，然后寻求待定的参变量，题型很活，一般是求或的值、函数最值、取值范围等．ωϕ14．【2019年高考北京卷理数】函数f （x ）=sin 22x 的最小正周期是__________．【答案】π2【解析】函数，周期为.()2sin 2f x x ==1cos 42x -π2【名师点睛】本题主要考查二倍角的三角函数公式､三角函数的最小正周期公式，属于基础题.将所给的函数利用降幂公式进行恒等变形，然后求解其最小正周期即可.15．【2019年高考江苏卷】已知，则的值是 ▲ .tan 2π3tan 4αα=-⎛⎫+ ⎪⎝⎭πsin 24α⎛⎫+ ⎪⎝⎭【解析】由，得，()tan 1tan tan tan 2tan 1πtan 13tan 1tan 4αααααααα-===-++⎛⎫+ ⎪-⎝⎭23tan 5tan 20αα--=解得，或.tan 2α=1tan 3α=-πππsin 2sin 2cos cos 2sin444ααα⎛⎫+=+⎪⎝⎭)22222sin cos cos sin sin 2cos 2sin cos αααααααα⎫+-=+⎪+⎭，222tan 1tan tan 1ααα⎫+-⎪+⎭当时，上式tan 2α=22221221⎛⎫⨯+- ⎪+⎝⎭当时，上式=1tan 3α=-22112()1()33[1()13⨯-+---+综上，πsin 24α⎛⎫+= ⎪⎝⎭【名师点睛】本题考查三角函数的化简求值，渗透了逻辑推理和数学运算素养.采取转化法，利用分类讨论和转化与化归思想解题.由题意首先求得的值，然后利用两角和的正弦公式和二倍角公式将原问tan α题转化为齐次式求值的问题，最后切化弦求得三角函数式的值即可.16．【2018年高考全国Ⅰ理数】已知函数，则的最小值是_____________．()2sin sin 2f x x x =+()f x 【答案】【解析】，()()212cos 2cos 24cos 2cos 24cos 1cos 2f x x x x x x x ⎛⎫'=+=+-=+-⎪⎝⎭所以当时函数单调递减，当时函数单调递增，从而得到函数的递减区间为1cos 2x <1cos 2x >，函数的递增区间为，()5ππ2π,2π33k k k ⎡⎤--∈⎢⎥⎣⎦Z ()ππ2π,2π33k k k ⎡⎤-+∈⎢⎥⎣⎦Z 所以当时，函数取得最小值，此时，π2π,3x k k =-∈Z ()fx sin x x ==所以.()min2f x ⎛=⨯= ⎝【名师点睛】该题考查的是有关应用导数研究函数的最小值问题，在求解的过程中，需要明确相关的函数的求导公式，需要明白导数的符号与函数的单调性的关系，确定出函数的单调增区间和单调减区间，进而求得函数的最小值点，从而求得相应的三角函数值，代入求得函数的最小值.17．【2018年高考北京卷理数】设函数f （x ）=，若对任意的实数x 都成立，πcos()(0)6x ωω->π()()4f x f ≤则ω的最小值为__________．【答案】23【解析】因为对任意的实数x 都成立，所以取最大值，()π4f x f ⎛⎫≤ ⎪⎝⎭π4f ⎛⎫⎪⎝⎭所以，()()ππ22π8463k k k k -=∈∴=+∈Z Z ，ωω因为，所以当时，ω取最小值为.0>ω0k =23【名师点睛】本题主要考查三角函数的图象和性质，考查考生的逻辑推理能力以及运算求解能力，考查的核心素养是逻辑推理、数学运算.18．【2018年高考全国Ⅲ理数】函数在的零点个数为________．()πcos 36f x x ⎛⎫=+ ⎪⎝⎭[]0π，【答案】3【解析】，，由题可知，或，解0πx ≤≤ ππ19π3666x ∴≤+≤πππ3π336262x x +=+=，π5π362x +=得，或，故有3个零点.π4π,99x =7π9【名师点睛】本题主要考查三角函数的图象与性质，考查数形结合思想和考生的运算求解能力，考查的核心素养是数学运算.19．【2018年高考江苏卷】已知函数的图象关于直线对称，则的值()ππsin 2(22y x =+-<<ϕϕπ3x =ϕ是________．【答案】π6-【解析】由题意可得，所以，2sin π13⎛⎫+=± ⎪⎝⎭ϕ2πππππ()326k k k +=+=-+∈Z ，ϕϕ因为，所以ππ22-<<ϕπ0,.6k ==-ϕ【名师点睛】由对称轴得，再根据限制范围求结果.函数2πππππ()326k k k +=+=-+∈Z ，ϕϕ（A >0，ω>0）的性质：()sin y A x B =++ωϕ(1)；max min ,y A B y A B =+=-+(2)最小正周期；2πT =ω(3)由求对称轴；()ππ2x k k +=+∈Z ωϕ(4)由求增区间;由求减()ππ2π2π22k x k k -+≤+≤+∈Z ωϕ()π3π2π2π22k x k k +≤+≤+∈Z ωϕ区间.20．【2017年高考全国Ⅱ理数】函数()的最大值是.()23sin 4f x x x =+-π0,2x ⎡⎤∈⎢⎥⎣⎦【答案】1【解析】化简三角函数的解析式：，()222311cos cos cos 144f x x x x x x ⎛=-+-=-+=--+ ⎝由自变量的范围：可得：，π0,2x ⎡⎤∈⎢⎥⎣⎦[]cos 0,1x ∈当时，函数取得最大值1.cos x =()f x 【名师点睛】本题经三角函数式的化简将三角函数的问题转化为二次函数的问题，二次函数、二次方程与二次不等式统称“三个二次”，它们常结合在一起，有关二次函数的问题，数形结合，密切联系图象是探求解题思路的有效方法.一般从：①开口方向；②对称轴位置；③判别式；④端点函数值符号四个方面分析.21．【2017年高考北京卷理数】在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若，则=___________.1sin 3α=cos()αβ-【答案】79-【解析】因为和关于轴对称，所以，那么，αβy π2π,k k αβ+=+∈Z 1sin sin 3βα==cos cos αβ=-=cos cos βα=-=所以.()2227cos cos cos sin sin cossin 2sin 19αβαβαβααα-=+=-+=-=-【名师点睛】本题考查了角的对称关系，以及诱导公式，常用的一些对称关系包含：若与的终边关αβ于轴对称，则，若与的终边关于轴对称，则，若y π2π,k k αβ+=+∈Z αβx 2π,k k αβ+=∈Z α与的终边关于原点对称，则.βπ2π,k k αβ-=+∈Z 22．【2018年高考全国Ⅱ理数】已知，，则__________．sin cos 1αβ+=cos sin 0αβ+=sin()αβ+=【答案】12-【解析】因为，，所以sin cos 1+=αβcos sin 0+=αβ()()221sin cos 1,-+-=αα所以，11sin ,cos 22==αβ因此()22111111sin sin cos cos sin cos 1sin 1.224442+=+=⨯-=-+=-+=-αβαβαβαα【名师点睛】本题主要考查三角恒等变换，考查考生分析问题、解决问题的能力，考查的核心素养是数学运算.23．【2017年高考江苏卷】若则 ▲ ．π1tan(),46α-=tan α=【答案】75【解析】．故答案为．11tan()tan7644tan tan[(14451tan()tan 1446ααααππ+-+ππ=-+===ππ---75【考点】两角和的正切公式【名师点睛】三角函数求值的三种类型（1）给角求值：关键是正确选用公式，以便把非特殊角的三角函数转化为特殊角的三角函数．（2）给值求值：关键是找出已知式与待求式之间的联系及函数的差异．一般有如下两种思路：①适当变换已知式，进而求得待求式的值；②变换待求式，便于将已知式的值代入，从而达到解题的目的．（3）给值求角：实质是转化为“给值求值”，先求角的某一函数值，再求角的范围，进而确定角．24．【2019年高考浙江卷】设函数.()sin ,f x x x =∈R （1）已知函数是偶函数，求的值；[0,2),θ∈π()f x θ+θ（2）求函数的值域．22[([(124y f x f x ππ=+++【答案】（1）或；（2）．π2θ=3π2[1-【解析】（1）因为是偶函数，所以，对任意实数x 都有，()sin()f x x θθ+=+sin()sin()x x θθ+=-+即，sin cos cos sin sin cos cos sin x x x x θθθθ+=-+故，2sin cos 0x θ=所以．cos 0θ=又，[0,2π)θ∈因此或．π2θ=3π2（2）2222ππππsin sin 124124y fx f x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ππ1cos 21cos 2136212sin 22222x x x x ⎛⎫⎛⎫-+-+ ⎪ ⎪⎫⎝⎭⎝⎭=+=--⎪⎪⎭．π123x ⎛⎫=+⎪⎝⎭因此，函数的值域是．[1+【名师点睛】本题主要考查三角函数及其恒等变换等基础知识，同时考查运算求解能力.25．【2017年高考浙江卷】已知函数．22sin cos cos ()()x x x f x x x =--∈R （1）求的值．2()3f π（2）求的最小正周期及单调递增区间．()f x【答案】（1）2；（2）的最小正周期是；单调递增区间是．()f x π2[,],63k k k ππ+π+π∈Z【解析】（1）由，．2sin 3π=21cos 32π=-22211(((322f π=----得．2(23f π=（2）由与得22cos 2cos sin x x x =-sin 22sin cos x x x =()cos 22f x x x=--．2sin(2)6x π=-+所以的最小正周期是．()f x π由正弦函数的性质得，3222,262k x k k πππ+π≤+≤+π∈Z 解得，2,63k x k k ππ+π≤≤+π∈Z 所以，的单调递增区间是．()f x 2[,],63k k k ππ+π+π∈Z 【名师点睛】本题主要考查了三角函数的化简，以及函数()ϕω+=x A y sin 的性质，是高考中的常考知识点，属于基础题，强调基础的重要性；三角函数解答题中，涉及到周期，单调性，单调区间以及最值等考点时，都属于考查三角函数的性质，首先应把它化为三角函数的基本形式即()ϕω+=x A y sin ，然后利用三角函数u A y sin =的性质求解．26．【2017年高考江苏卷】已知向量(cos ,sin ),(3,[0,π].x x x ==∈a b （1）若a ∥b ，求的值；x （2）记，求的最大值和最小值以及对应的的值．()f x =⋅a b ()f x x【答案】（1）；（2）时，取到最大值3；时，取到最小值．5π6x =0x =()f x 5π6x =()f x -【解析】（1）因为，，a ∥b ，co ()s ,sin x x =a (3,=b所以．3sin x x =若，则，与矛盾，故．cos 0x =sin 0x =22sin cos 1x x +=cos 0x ≠于是tan x =又，所以．[]0πx ∈，5π6x =（2）．π(cos ,sin )(3,3cos ()6f x x x x x x =⋅=⋅==+a b 因为，所以，[]0πx ∈，ππ7π[,]666x +∈从而．π1cos(6x -≤+≤于是，当，即时，取到最大值3；ππ66x +=0x =()f x当，即时，取到最小值．π6x +=π5π6x =()f x -27．【2018年高考浙江卷】已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边过点P （）．3455-，-（1）求sin （α+π）的值；（2）若角β满足sin （α+β）=，求cos β的值．513【答案】（1）；（2）或.4556cos 65β=-16cos 65β=-【解析】（1）由角的终边过点得，α34(,)55P --4sin 5α=-所以.4sin(π)sin 5αα+=-=（2）由角的终边过点得，α34(,)55P --3cos 5α=-由得.5sin()13αβ+=12cos()13αβ+=±由得，()βαβα=+-cos cos()cos sin()sin βαβααβα=+++所以或.56cos 65β=-16cos 65β=-【名师点睛】本题主要考查三角函数的定义、诱导公式、两角差的余弦公式，考查考生分析问题、解决问题的能力，运算求解能力，考查的数学核心素养是数学运算.求解三角函数的求值问题时，需综合应用三角函数的定义、诱导公式及三角恒等变换.（1）首先利用三角函数的定义求得，然后利用诱导公式，计算sin （α+π）的值;sin α（2）根据sin （α+β）的值，结合同角三角函数的基本关系，计算的值，要注意该值的cos()+αβ正负，然后根据，利用两角差的余弦公式，通过分类讨论，求得cos β的值.()βαβα=+-28．【2018年高考江苏卷】已知为锐角，，．,αβ4tan 3=αcos()+=αβ（1）求的值；cos 2α（2）求的值．tan()-αβ【答案】（1）；（2）.725-211-【解析】（1）因为，，4tan 3=αsin tan cos =ααα所以．4sin cos 3=αα因为，22sin cos 1+=αα所以，29cos 25=α因此，．27cos 22cos 125=-=-αα（2）因为为锐角，所以．,αβ(0,)+∈παβ又因为，cos()+=αβ所以，sin()+==αβ因此．tan()2+=-αβ因为，所以，4tan 3=α22tan 24tan 21tan 7==--ααα因此，．tan 2tan()2tan()tan[2()]1tan 2tan()11-+-=-+==-++ααβαβααβααβ【名师点睛】本小题主要考查同角三角函数关系、两角和（差）及二倍角的三角函数，考查运算求解能力．三角函数求值的三种类型：（1）给角求值：关键是正确选用公式，以便把非特殊角的三角函数转化为特殊角的三角函数．（2）给值求值：关键是找出已知式与待求式之间的联系及函数的差异．一般有如下两种思路：①适当变换已知式，进而求得待求式的值；②变换待求式，便于将已知式的值代入，从而达到解题的目的．（3）给值求角：实质是转化为“给值求值”，先求角的某一函数值，再求角的范围，进而确定角．29．【2017年高考山东卷理数】设函数，其中03ω<<.已知.ππ()sin(sin()62f x x x ωω=-+-π()06f =（1）求ω；（2）将函数()y f x =的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移个单位，得到函数()y g x =的图象，求()g x 在上的最小值.π4π3π[,]44-【答案】（1）2ω=；（2）最小值为32-.【解析】（1）因为，ππ()sin(sin()62f x x x ωω=-+-所以1()cos cos 2f x x x x ωωω=--3cos 2x x ωω=-1sin )2x x ωω=.π)3x ω=-由题设知，π()06f =所以，.πππ63k -=ωk ∈Z 故62k ω=+，，k ∈Z 又03ω<<，所以2ω=.（2）由（1）得.()23f x x π⎛⎫=- ⎪⎝⎭所以.()4312g x x x πππ⎛⎫⎛⎫=+-=- ⎪ ⎪⎝⎭⎝⎭因为，π3π[,]44x ∈-所以，2,1233x πππ⎡⎤-∈-⎢⎥⎣⎦所以当，即时，()g x 取得最小值32-.123x ππ-=-4x π=-【名师点睛】此类题目是三角函数问题中的典型题目，可谓相当经典.解答本题时，关键在于能利用三角公式化简函数、进一步讨论函数的性质，本题易错点在于一是图象的变换与解析式的对应，二是忽视设定角的范围.难度不大，能较好地考查考生的基本运算求解能力及复杂式子的变形能力等.。

2019年全国高考理科数学试题分类汇编3：三角函数work Information Technology Company.2020YEAR2019年全国高考理科数学试题分类汇编3：三角函数一、选择题1 ．（2019年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））已知210cos 2sin ,=+∈αααR ,则=α2tan A.34 B. 43 C.43- D.34-【答案】C2 ．（2019年高考陕西卷（理））设△ABC 的内角A , B , C 所对的边分别为a , b , c , 若cos cos sin b C c B a A +=, 则△ABC 的形状为(A) 锐角三角形(B) 直角三角形 (C) 钝角三角形(D) 不确定【答案】B3 ．（2019年普通高等学校招生统一考试天津数学（理）试题（含答案））在△ABC 中,,2,3,4AB BC ABC π∠==则sin BAC ∠ =(A)10 10 3105 【答案】C4 ．（2019年普通高等学校招生统一考试山东数学（理）试题（含答案））将函数sin(2)y x ϕ=+的图象沿x 轴向左平移8π个单位后,得到一个偶函数的图象,则ϕ的一个可能取值为 (A) 34π (B) 4π(C)0 (D) 4π-【答案】B5 ．（2019年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））在ABC ∆,内角,,A B C 所对的边长分别为,,.a b c 1sin cos sin cos ,2a B C c B Ab +=且a b >,则B ∠=A.6πB.3πC.23πD.56π【答案】A6 ．（2019年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知函数()=cos sin 2f x x x ,下列结论中错误的是(A)()y f x =的图像关于(),0π中心对称 (B)()y f x =的图像关于直线2x π=对称(C)()f x 3(D)()f x 既奇函数,又是周期函数【答案】C7 ．（2019年普通高等学校招生统一考试山东数学（理）试题（含答案））函数cos sin y x x x =+的图象大致为【答案】D8 ．（2019年高考四川卷（理））函数()2sin(),(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是( )(A)2,3π-(B)2,6π-(C)4,6π-(D)4,3π【答案】A9 ．（2019年上海市春季高考数学试卷(含答案)）既是偶函数又在区间(0 )π，上单调递减的函数是( )(A)sin y x = (B)cos y x = (C)sin 2y x = (D)cos 2y x =【答案】B10．（2019年普通高等学校招生统一考试重庆数学（理）试题（含答案））04cos50tan 40-=( )223+3 D.221 【答案】C11．（2019年高考湖南卷（理））在锐角中ABC ∆,角,A B 所对的边长分别为,a b .若2sin 3,a B b A =则角等于A.12π B.6π C.4π D.3π 【答案】D12．（2019年高考湖北卷（理））将函数()3cos sin yx x x R =+∈的图像向左平移()0m m >个长度单位后,所得到的图像关于y 轴对称,则m 的最小值是( ) A.12π B.6π C.3π D.56π【答案】B 二、填空题13．（2019年普通高等学校招生统一考试浙江数学（理）试题（纯WORD 版））ABC ∆中,090=∠C ,M 是BC 的中点,若31sin =∠BAM ,则=∠BAC sin ________.【答案】6314．（2019年高考新课标1（理））设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=______【答案】255-. 15．（2019年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））如图ABC ∆中,已知点D在BC 边上,AD ⊥AC,22sin ,32,33BAC AB AD ∠===则BD 的长为_______________316．（2019年上海市春季高考数学试卷(含答案)）函数2sin y x =的最小正周期是_____________【答案】2π17．（2019年高考四川卷（理））设sin 2sin αα=-,(,)2παπ∈,则tan 2α的值是_________.18．（2019年高考上海卷（理））若12cos cos sin sin,sin 2sin 223x y x y x y +=+=,则sin()________x y +=【答案】2sin()3x y +=. 19．（2019年高考上海卷（理））已知△ABC的内角A 、B 、C 所对应边分别为a 、b 、c,若22232330a ab b c ++-=,则角C 的大小是_______________(结果用反三角函数值表示)【答案】1arccos 3Cπ=-20．（2019年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））已知α是第三象限角,1sin 3a =-,则cot a =____________.【答案】21．（2019年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））函数)42sin(3π+=x y 的最小正周期为___________.【答案】π22．（2019年上海市春季高考数学试卷(含答案)）在ABC ∆中,角 A B C 、、所对边长分别为 a b c 、、,若5 8 60a b B ===，，,则b=_______【答案】7 23．（2019年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））设ABC ∆的内角,,A B C 所对边的长分别为,,a b c .若2b c a +=,则3sin 5sin ,A B =则角C =_____.【答案】π3224．（2019年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））设θ为第二象限角,若1tan()42πθ+=,则sin cos θθ+=________.【答案】5-25．（2019年高考江西卷（理））函数2sin 2y x x =+的最小正周期为T 为_________.【答案】π26．（2019年上海市春季高考数学试卷(含答案)）函数4sin 3cos y x x =+的最大值是_______________【答案】5 三、解答题27．（2019年高考北京卷（理））在△ABC中,a =3,b ,∠B =2∠A .(I)求cos A 的值; (II)求c 的值.【答案】解:(I)因为a =3,b ,∠B =2∠A . 所以在△ABC 中,由正弦定理得3sin sin 2A A=.所以2sin cos sin 3A A A =.故cos 3A =.(II)由(I)知cos 3A =,所以sin 3A ==.又因为∠B=2∠A,所以21cos 2cos 13B A =-=.所以sin 3B ==.在△ABC 中,sin sin()sin cos cos sin C A B A B A B =+=+=所以sin 5sin a Cc A==.28．（2019年高考陕西卷（理））已知向量1(cos ,),,cos2),2x x x x =-=∈a b R , 设函数()·f x =a b .(Ⅰ) 求f (x)的最小正周期.(Ⅱ) 求f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】解:(Ⅰ) ()·f x =a b =)62sin(2cos 212sin 232cos 21sin 3cos π-=-=-⋅x x x x x x .最小正周期ππ==22T . 所以),62sin()(π-=x x f 最小正周期为π.(Ⅱ) 上的图像知，在，由标准函数时，当]65,6-[sin ]65,6-[)62(]2,0[ππππππx y x x =∈-∈.]1,21[)]2(),6-([)62sin()(-=∈-=πππf f x x f .所以,f (x) 在0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值分别为21,1-. 29．（2019年普通高等学校招生统一考试重庆数学（理）试题（含答案））在ABC 中,内角,,A B C 的对边分别是,,a b c ,且2222a b ab c ++=. (1)求C ; (2)设()()2cos cos 322cos cos ,5cos 5A B A B ααα++==,求tan α的值. 【答案】由题意得30．（2019年普通高等学校招生统一考试天津数学（理）试题（含答案））已知函数2()2sin 26sin cos 2cos 41,f x x x x x x π⎛⎫=-++- ⎪+⎝⎭∈R .(Ⅰ) 求f (x )的最小正周期; (Ⅱ) 求f (x )在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值和最小值.【答案】31．（2019年普通高等学校招生统一考试辽宁数学（理）试题（WORD 版））设向量()()3sin ,sin ,cos ,sinx ,0,.2a x x b x x π⎡⎤==∈⎢⎥⎣⎦(I)若.a b x =求的值； (II)设函数()(),.f x a b f x =求的最大值【答案】]32．（2019年高考上海卷（理））(6分+8分)已知函数()2sin()f x x ω=,其中常数0ω>;(1)若()y f x =在2[,]43ππ-上单调递增,求ω的取值范围;(2)令2ω=,将函数()y f x =的图像向左平移6π个单位,再向上平移1个单位,得到函数()y g x =的图像,区间[,]a b (,a b R ∈且a b <)满足:()y g x =在[,]a b 上至少含有30个零点,在所有满足上述条件的[,]a b 中,求b a -的最小值.【答案】(1)因为0ω>,根据题意有34202432ππωωππω⎧-≥-⎪⎪⇒<≤⎨⎪≤⎪⎩(2) ()2sin(2)f x x =,()2sin(2())12sin(2)163g x x x ππ=++=++1()0sin(2)323g x x x k πππ=⇒+=-⇒=-或7,12x k k Z ππ=-∈,即()g x 的零点相离间隔依次为3π和23π,故若()y g x =在[,]a b 上至少含有30个零点,则b a -的最小值为2431415333πππ⨯+⨯=. 33．（2019年普通高等学校招生统一考试大纲版数学（理）WORD 版含答案（已校对））设ABC ∆的内角,,A B C 的对边分别为,,a b c ,()()a b c a b c ac ++-+=.(I)求B(II)若31sin sin 4A C =,求C . 【答案】34．（2019年高考四川卷（理））在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且232cos cos sin()sin cos()25A B B A B B A C ---++=-. (Ⅰ)求cos A 的值; (Ⅱ)若42a =,5b =,求向量BA 在BC 方向上的投影.【答案】解:()I 由()()232cos cos sin sin cos 25A B B A B B A C ---++=-,得 ()()3cos 1cos sin sin cos 5A B B A B B B -+---=-⎡⎤⎣⎦, 即()()3cos cos sin sin 5A B B A B B ---=-,则()3cos 5A B B -+=-,即3cos 5A =-()II 由3cos ,05A A π=-<<,得4sin 5A =,由正弦定理,有sin sin a bA B=,所以,sin 2sin b A B a ==. 由题知a b >,则A B >,故4B π=.根据余弦定理,有(2223425255c c ⎛⎫=+-⨯⨯- ⎪⎝⎭,解得1c =或7c =-(舍去).故向量BA 在BC 方向上的投影为2cos 2BA B =35．（2019年普通高等学校招生统一考试山东数学（理）试题（含答案））设△ABC 的内角,,A B C 所对的边分别为,,a b c ,且6a c +=,2b =,7cos 9B =. (Ⅰ)求,a c 的值; (Ⅱ)求sin()A B -的值.【答案】解:(Ⅰ)由余弦定理2222cos ba c ac B =+-,得()222(1cos )b ac ac B =+-+,又6a c +=,2b =,7cos 9B =,所以9ac =,解得3a =,3c =.(Ⅱ)在△ABC 中,242sin 1cos 9B B =-=,由正弦定理得sin 22sin 3a B A b ==,因为a c =,所以A 为锐角,所以21cos 1sin 3A A =-=因此102sin()sin cos cos sin 27A B A B A B -=-=.36．（2019年普通高等学校招生统一考试安徽数学（理）试题（纯WORD 版））已知函数()4cos sin (0)4f x x x πϖϖϖ⎛⎫=⋅+> ⎪⎝⎭的最小正周期为π.(Ⅰ)求ϖ的值; (Ⅱ)讨论()f x 在区间[]0,2上的单调性.【答案】解:(Ⅰ)2)42sin(2)12cos 2(sin 2)cos (sin cos 22++=++=+⇒πωωωωωωx x x x x x122=⇒=⇒ωπωπ.所以1,2)42sin(2)(=++=ωπx x f (Ⅱ) ；解得，令时，当8242]4,4[)42(]2,0[ππππππππ==++∈+∈x x x x所以.]28[]8,0[)(上单调递减，上单调递增；在在πππx f y =37．（2019年普通高等学校招生统一考试福建数学（理）试题（纯WORD 版））已知函数()sin()(0,0)f x x ωϕωϕπ=+><<的周期为π,图像的一个对称中心为(,0)4π,将函数()f x 图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移2π个单位长度后得到函数()g x 的图像. (1)求函数()f x 与()g x 的解析式;(2)是否存在0(,)64x ππ∈,使得0000(),(),()()f x g x f x g x 按照某种顺序成等差数列?若存在,请确定0x 的个数;若不存在,说明理由. (3)求实数a 与正整数n ,使得()()()F x f x ag x =+在(0,)n π内恰有2019个零点.【答案】解:(Ⅰ)由函数()sin()f x x ωϕ=+的周期为π,0ω>,得2ω=又曲线()y f x =的一个对称中心为(,0)4π,(0,)ϕπ∈故()sin(2)044f ππϕ=⨯+=,得2πϕ=,所以()cos 2f x x =将函数()f x 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得cos y x =的图象,再将cos y x =的图象向右平移2π个单位长度后得到函数()sin g x x =(Ⅱ)当(,)64x ππ∈时,1sin 2x <<,10cos 22x <<所以sin cos 2sin cos 2x x x x >>问题转化为方程2cos 2sin sin cos 2x x x x =+在(,)64ππ内是否有解设()sin sin cos 22cos 2G x x x x x =+-,(,)64x ππ∈则()cos cos cos 22sin 2(2sin )G x x x x x x '=++-因为(,)64x ππ∈,所以()0G x '>,()G x 在(,)64ππ内单调递增又1()064G π=-<,()04G π=>且函数()G x 的图象连续不断,故可知函数()G x 在(,)64ππ内存在唯一零点0x ,即存在唯一的0(,)64x ππ∈满足题意(Ⅲ)依题意,()sin cos 2F x a x x =+,令()sin cos 20F x a x x =+=当sin 0x =,即()x k k Z π=∈时,cos 21x =,从而()x k k Z π=∈不是方程()0F x =的解,所以方程()0F x =等价于关于x 的方程cos 2sin xa x=-,()x k k Z π≠∈ 现研究(0,)(,2)x πππ∈时方程解的情况 令cos 2()sin xh x x=-,(0,)(,2)x πππ∈ 则问题转化为研究直线y a =与曲线()y h x =在(0,)(,2)x πππ∈的交点情况22cos (2sin 1)()sin x x h x x +'=,令()0h x '=,得2x π=或32x π= 当x 变化时,()h x 和()h x '变化情况如下表x(0,)2π 2π(,)2ππ 3(,)2ππ 32π 3(,2)2ππ ()h x '+ 0 - - 0 + ()h x1-当0x >且x 趋近于0时,()h x 趋向于-∞ 当x π<且x 趋近于π时,()h x 趋向于-∞ 当x π>且x 趋近于π时,()h x 趋向于+∞ 当2x π<且x 趋近于2π时,()h x 趋向于+∞故当1a >时,直线y a =与曲线()y h x =在(0,)π内有无交点,在(,2)ππ内有2个交点; 当1a <-时,直线y a =与曲线()y h x =在(0,)π内有2个交点,在(,2)ππ内无交点; 当11a -<<时,直线y a =与曲线()y h x =在(0,)π内有2个交点,在(,2)ππ内有2个交点 由函数()h x 的周期性,可知当1a ≠±时,直线y a =与曲线()y h x =在(0,)n π内总有偶数个交点,从而不存在正整数n ,使得直线y a =与曲线()y h x =在(0,)n π内恰有2013个交点;当1a =±时,直线y a =与曲线()y h x =在(0,)(,2)πππ内有3个交点,由周期性,20133671=⨯,所以67121342n =⨯=综上,当1a =±,1342n =时,函数()()()F x f x ag x =+在(0,)n π内恰有2013个零点38．（2019年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分14分.已知(cos ,sin )(cos ,sin )a b ααββ=＝，,παβ<<<0. (1)若||2a b -=,求证:a b ⊥;(2)设(0,1)c =,若a b c +=,求βα,的值.【答案】解:(1)∵2||=-b a ∴2||2=- 即()22222=+-=-,又∵1sin cos ||2222=+==αα,1sin cos ||2222=+==ββ∴222=-b a ∴0=b a ∴b ⊥a(2)∵)1,0()sin sin ,cos (cos =++=+βαβα ∴⎩⎨⎧=+=+1sin sin 0cos cos βαβα即⎩⎨⎧-=-=βαβαsin 1sin cos cos两边分别平方再相加得:βsin 221-= ∴21sin =β ∴21sin =α ∵παβ<<<0 ∴πβπα61,65==39．（2019年普通高等学校招生统一考试广东省数学（理）卷（纯WORD 版））已知函数()212f x x π⎛⎫=- ⎪⎝⎭,x ∈R .(Ⅰ) 求6f π⎛⎫- ⎪⎝⎭的值; (Ⅱ) 若3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,求23f πθ⎛⎫+ ⎪⎝⎭. Z#X#X#K]【答案】(Ⅰ)2221661244f πππππ⎛⎫⎛⎫⎛⎫-=--=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭; (Ⅱ) 22222cos 2sin 233124f ππππθθθθθ⎛⎫⎛⎫⎛⎫+=+-=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为3cos 5θ=,3,22πθπ⎛⎫∈ ⎪⎝⎭,所以4sin 5θ=-,所以24sin 22sin cos 25θθθ==-,227cos 2cos sin 25θθθ=-=- 所以23f πθ⎛⎫+ ⎪⎝⎭cos2sin 2θθ=-72417252525⎛⎫=---= ⎪⎝⎭.40．（2019年高考湖南卷（理））已知函数2()sin()cos().()2sin 632xf x x xg x ππ=-+-=.(I)若α是第一象限角,且33()f α=求()g α的值; (II)求使()()f x g x ≥成立的x 的取值集合.【答案】解: (I)533sin 3)(sin 3sin 23cos 21cos 21sin 23)(==⇒=++-=ααf x x x x x x f . 51cos 12sin 2)(,54cos )2,0(,53sin 2=-===⇒∈=⇒ααααπααg 且(II)21)6sin(cos 21sin 23cos 1sin 3)()(≥+=+⇒-≥⇒≥πx x x x x x g x f Z k k k x k k x ∈+∈⇒++∈+⇒],322,2[]652,62[6ππππππππ 41．（2019年普通高等学校招生全国统一招生考试江苏卷（数学）（已校对纯WORD 版含附加题））本小题满分16分.如图,游客从某旅游景区的景点A 处下山至C 处有两种路径.一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C .现有甲.乙两位游客从A 处下山,甲沿AC 匀速步行,速度为min /50m .在甲出发min 2后,乙从A 乘缆车到B ,在B 处停留min 1后,再从匀速步行到C .假设缆车匀速直线运动的速度为min /130m ,山路AC 长为m 1260,经测量,1312cos =A ,53cos =C . (1)求索道AB 的长 (2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?【答案】解:(1)∵1312cos =A ,53cos =C ∴），（、20π∈C A ∴135sin =A ,54sin =C∴[]6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B ）（）（π 根据sinB sinC AC AB =得m C ACAB 1040sin sinB== CBA(2)设乙出发t 分钟后,甲.乙距离为d,则1312)50100(1302)50100()130(222⨯+⨯⨯-++=t t t t d ∴)507037(20022+-=t t d∵13010400≤≤t 即80≤≤t ∴3735=t 时,即乙出发3735分钟后,乙在缆车上与甲的距离最短.(3)由正弦定理sinBsinA ACBC =得50013565631260sin sinB ===A AC BC (m) 乙从B 出发时,甲已经走了50(2+8+1)=550(m),还需走710 m 才能到达C 设乙的步行速度为V min /m ,则350710500≤-v ∴3507105003≤-≤-v ∴14625431250≤≤v ∴为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在⎥⎦⎤⎢⎣⎡14625,431250范围内法二:解:(1)如图作BD ⊥CA 于点D , 设BD =20k ,则DC =25k ,AD =48k ,AB =52k ,由AC =63k =1260m, 知:AB =52k =1040m.(2)设乙出发x 分钟后到达点M , 此时甲到达N 点,如图所示. 则:AM =130x ,AN =50(x +2),由余弦定理得:MN 2=AM 2+AN 2-2 AM ·AN cos A =7400 x 2-14000 x +10000, 其中0≤x ≤8,当x =3537(min)时,MN 最小,此时乙在缆车上与甲的距离最短. (3)由(1)知:BC =500m,甲到C 用时:126050 =1265(min).若甲等乙3分钟,则乙到C 用时:1265 +3=1415 (min),在BC 上用时:865(min) . 此时乙的速度最小,且为:500÷865 =125043m/min. 若乙等甲3分钟,则乙到C 用时:1265 -3=1115 (min),在BC 上用时:565 (min) .此时乙的速度最大,且为:500÷565 =62514m/min. 故乙步行的速度应控制在[125043 ,62514]范围内.42．（2019年高考湖北卷（理））在ABC∆中,角A ,B ,C 对应的边分别是a ,b ,c .已知()cos23cos 1A B C -+=.(I)求角A 的大小;(II)若ABC ∆的面积S =,5b =,求sin sin B C 的值.【答案】解:(I)由已知条件得:cos23cos 1A A +=22cos 3cos 20A A ∴+-=,解得1cos 2A =,角60A =︒(II)1sin 2S bc A ==4c ⇒=,由余弦定理得:221a =,()222228sin a R A == 25sin sin 47bc B C R ∴== 43．（2019年普通高等学校招生统一考试新课标Ⅱ卷数学（理）（纯WORD 版含答案））△ABC 在内角,,A B C 的对边分别为,,a b c ,已知cos sin a b C c B =+. (Ⅰ)求B ;(Ⅱ)若2b =,求△ABC 面积的最大值.CBAD MN【答案】。