线性系统理论课件02-第二章状态空间描述-2.1系统的状态空间描述2.2系统的状态空间表达式的分类
- 格式:ppt
- 大小:766.50 KB
- 文档页数:34





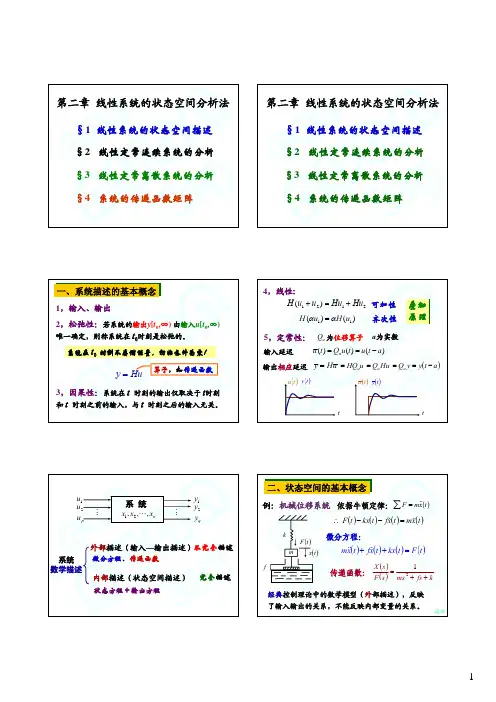
第二章 线性系统的状态空间分析法c§1 线性系统的状态空间描述§2 线性定常连续系统的分析e a第二章 线性系统的状态空间分析法§3 线性定常离散系统的分析 §4 系统的传递函数矩阵ty cc§1 线性系统的状态空间描述§2 线性定常连续系统的分析e a§3 线性定常离散系统的分析 §4 系统的传递函数矩阵ty c叠加 原理一、系统描述的基本概念 一、系统描述的基本概念1,输入、输出2,松弛性:若系统的输出y[t0,∞) 由输入u[t0,∞)唯一确定,则称系统在t0时刻是松弛的。
系统在t0 时刻不存储能量,初始条件为零!ce a4,线性: H (u1 + u 2 ) = Hu1 + Hu2 可加性5,定常性: Qa 为位移算子y = Hu算子,如传递函数3,因果性:系统在t 时刻的输出仅取决于t时刻和t 时刻之前的输入,与t 时刻之后的输入无关。
ty cy1 y2 yq输入延迟输出相应延迟 y = Hu = HQa u = Qa Hu = Qa y = y (t − a )u (t ) y (t ) u (t ) y (t )cH (αu1 ) = αH (u1 )e at齐次性a为实数u (t ) = Qa u (t ) = u (t − a )ty ct系统 数学描述cu1 u2 up外部描述(输入—输出描述)不完全描述微分方程、传递函数e aM二、状态空间的基本概念 二、状态空间的基本概念Mx 例:机械位移系统 依据牛顿定律: ∑ F = m&&(t )系 统x1 , x2 , L , xn内部描述(状态空间描述)状态方程+输出方程ty c完全描述ckmF (t )e ax (t )& ∴ F (t ) − kx(t ) − fx(t ) = m&&(t ) x微分方程:& m&&(t ) + fx(t ) + kx(t ) = F (t ) xf传递函数:X (s ) 1 = (s ) ms 2 + fs + k F经典控制理论中的数学模型(外部描述),反映 了输入输出的关系,不能反映内部变量的关系。
