矩形脉冲信号的分解和合成

综合性实验报告题目：方波的合成与分解实验课程：信号与系统学号：姓名：班级：12自动化2班指导教师：方波的分解与合成一、实验类型综合性实验二、实验目的和要求1．观察方波信号的分解。

2．用同时分析法观测方波信号的频谱，并与方波的傅利叶级数各项的频率与系数作比较。

3．掌握带通滤波器的有关特性测试方法。

4．观测基波和其谐波的合成。

三、实验条件实验仪器1．20M 双踪示波器一台。

2．信号与系统实验箱。

四、实验原理1. 信号的频谱与测量信号的时域特性和频域特性是对信号的两种不同的描述方式。

对于一个时域的周期信号)t (f ，只要满足狄利克莱(Dirichlet)条件，就可以将其展开成三角形式或指数形式的傅里叶级数。

例如，对于一个周期为T 的时域周期信号)t (f ，可以用三角形式的傅里叶级数求出它的各次分量，在区间)1,1(T t t +内表示为：)sin cos 1(0)(t n nb t n n n a a t f Ω+Ω∑∞=+=即将信号分解成直流分量及许多余弦分量和正弦分量，研究其频谱分布情况。

AA（c）图7-1 信号的时域特性和频域特性信号的时域特性与频域特性之间有着密切的内在联系，这种联系可以用图7-1来形象地表示。

其中图7-1(a)是信号在幅度--时间--频率三维座标系统中的图形；图7-1(b)是信号在幅度--时间座标系统中的图形即波形图；把周期信号分解得到的各次谐波分量按频率的高低排列，就可以得到频谱图。

反映各频率分量幅度的频谱称为振幅频谱。

图7-1(c)是信号在幅度--频率座标系统中的图形即振幅频谱图。

反映各分量相位的频谱称为相位频谱。

在本实验中只研究信号振幅频谱。

周期信号的振幅频谱有三个性质：离散性、谐波性、收敛性。

测量时利用了这些性质。

从振幅频谱图上，可以直观地看出各频率分量所占的比重。

测量方法有同时分析法和顺序分析法。

同时分析法的基本工作原理是利用多个滤波器，把它们的中心频率分别调到被测信号的各个频率分量上。

矩形脉冲的傅里叶变换引言傅里叶变换是一种重要的数学工具，可以将一个信号分解成不同频率的正弦波成分。

矩形脉冲是一种常见的信号形态，具有方波的特点。

在本文中，我们将探讨矩形脉冲的傅里叶变换及其在信号处理中的应用。

傅里叶变换简介什么是傅里叶变换傅里叶变换是一种将一个函数表示为多个正弦和余弦函数的和的方法。

它将时域函数转换为频域函数，使我们能够观察信号的不同频率成分。

傅里叶变换的数学表示对于一个连续时间信号x(t)，其傅里叶变换X(f)可以表示为：∞(t)e−j2πft dtX(f)=∫x−∞其中，f为频率，j为虚数单位，X(f)为频谱表示。

离散傅里叶变换离散傅里叶变换(DFT)是傅里叶变换在离散时间域上的扩展。

对于一个离散时间信号x[n]，其DFT可以表示为：N−1[n]e−j2πkn/NX[k]=∑xn=0其中，k为频率，X[k]为频谱表示。

矩形脉冲的定义矩形脉冲是一种具有方波形态的信号，其在一个有限时间内保持高电平，其余时间为低电平。

矩形脉冲的数学表示可以为：rect (t )={1,if −T 2≤t ≤T 2,0,otherwise .其中，T 为脉冲的周期。

矩形脉冲的频域表示为了求解矩形脉冲的频域表示，我们需要对矩形脉冲进行傅里叶变换。

对称性质矩形脉冲具有对称性质，即其频谱在频谱轴上呈现奇对称性。

具体来说，矩形脉冲的频谱X(f)满足：X (f )=X (−f )频域表示对于一个宽度为T 的矩形脉冲，其频谱X(f)可表示为 sinc 函数的线性组合形式：X (f )=sinc (Tf 2) 其中 sinc 函数定义为 sinc (x )=sin (πx )πx 。

矩形脉冲的频域特性矩形脉冲的频域特性对于信号处理具有重要意义。

通过分析矩形脉冲的频谱，我们可以了解其频率响应及滤波特性。

零点矩形脉冲的频谱在一些特定频率上为零。

这些特定频率的幅度为零，意味着矩形脉冲对这些频率的信号进行了滤波。

带宽矩形脉冲的频谱在f=±1T 处等于sinc(1/2)，即频率上升至最高并保持不变的位置。

实验十三 信号分解及合成一、 实验目的1、 了解和熟悉波形分解与合成原理。

2、 了解和掌握用傅里叶级数进行谐波分析的方法。

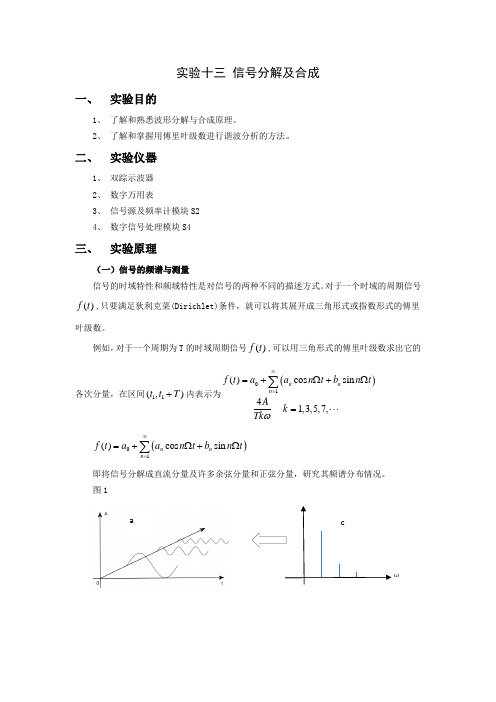
二、 实验仪器1、 双踪示波器2、 数字万用表3、 信号源及频率计模块S24、 数字信号处理模块S4三、 实验原理（一）信号的频谱与测量信号的时域特性和频域特性是对信号的两种不同的描述方式。

对于一个时域的周期信号()f t ,只要满足狄利克菜(Dirichlet)条件，就可以将其展开成三角形式或指数形式的傅里叶级数。

例如，对于一个周期为T 的时域周期信号()f t ,可以用三角形式的傅里叶级数求出它的各次分量，在区间11(,)t t T +内表示为()01()cos sin 41,3,5,7,n n n f t a a n t b n t Ak Tk ω∞==+Ω+Ω=⋅⋅⋅∑()01()cos sin n n n f t a a n t b n t ∞==+Ω+Ω∑即将信号分解成直流分量及许多余弦分量和正弦分量，研究其频谱分布情况。

图1ωca信号的时域特性和频域特性信号的时域特性与频域特性之间有着密切的内在联系，这种联系可以用图13-1来形象地表示。

其中图(a)是信号在幅度—时间—频率三维坐标系统中的图形;图(b)是信号在幅度一时间坐标系统中的图形即波形图：把周期信号分解得到的各次谐波分量按频率的高低排列，就可以得到频谱图。

反映各频率分量幅度的频谱称为振幅频谱。

图(c)是信号在幅度—频率坐标系统中的图形即振幅频谱图。

反映各分量相位的频谱称为相位频谱。

在本实验中只研究信号振幅频谱。

周期信号的振幅频谱有三个性质：离散性、谐波性、收敛性。

测量时利用了这些性质。

从振幅频谱图上，可以直观地看出各频率分量所占的比重。

测量方法有同时分析法和顺序分析法。

同时分析法的基本工作原理是利用多个滤波器，把它们的中心频率分别调到被测信号的各个频率分量上。

当被测信号同时加到所有滤波器上,中心频率与信号所包含的某次谐波分景频率-致的滤波器便有输出。

矩形脉冲信号的频谱矩形脉冲信号（也称为矩形波）在电子工程、通信和信号处理中非常常见。

它的频谱特性是分析和设计这些系统时的关键要素。

下面我们将详细介绍矩形脉冲信号的频谱特性，包括其基本概念、数学推导、重要性质以及在实际应用中的意义。

一、基本概念矩形脉冲信号是一种具有固定幅度和持续时间的信号，它在一定时间段内保持恒定的幅度，然后突然下降到零。

这种信号的时域表示非常简单明了，但在频域中却表现出复杂的特性。

通过傅里叶变换，我们可以将时域中的矩形脉冲信号转换为频域中的频谱。

二、傅里叶变换与频谱傅里叶变换是一种强大的数学工具，用于分析信号的频谱特性。

对于矩形脉冲信号，其傅里叶变换揭示了信号在频域中的分布情况。

傅里叶变换的基本思想是将复杂的时域信号分解为一系列简单的正弦波和余弦波的和。

1. 傅里叶级数对于周期性的矩形脉冲信号，我们首先可以通过傅里叶级数来进行分析。

傅里叶级数将周期信号表示为一系列正弦波和余弦波的叠加。

这些正弦波和余弦波的频率是基频的整数倍，而幅度和相位则由信号的特性和傅里叶系数决定。

2. 傅里叶变换对于非周期性的矩形脉冲信号，我们使用傅里叶变换来进行分析。

傅里叶变换将时域信号转换为频域信号，揭示了信号在不同频率下的幅度和相位信息。

对于矩形脉冲信号，其傅里叶变换的结果是一个连续的频谱，包含多个频率分量。

三、矩形脉冲信号的频谱特性1. 幅度谱和相位谱通过傅里叶变换，我们可以得到矩形脉冲信号的幅度谱和相位谱。

幅度谱表示不同频率分量的幅度大小，而相位谱则表示各频率分量的相位信息。

对于矩形脉冲信号，其幅度谱呈现出一系列离散的峰值，这些峰值对应于信号的谐波分量。

2. 带宽和主瓣宽度矩形脉冲信号的频谱带宽是指包含信号主要能量的频率范围。

带宽越宽，意味着信号包含的频率分量越多，信号的复杂性也越高。

主瓣宽度是指幅度谱中最大峰值对应的频率范围，它反映了信号的主要频率特性。

3. 旁瓣级数和旁瓣抑制除了主瓣外，矩形脉冲信号的幅度谱还包含多个旁瓣。

学号： 姓名：实验三、矩形信号的分解一、实验目的1、分析典型的矩形脉冲信号，了解矩形脉冲信号谐波分量的构成；2、观察矩形脉冲信号分解出各谐波分量的情况。

二、预备知识1.学习“周期信号的傅里叶级数分析”一节；2．复习matlab 软件的使用方法。

3．信号的滤波知识三、实验原理1、信号的频谱与测量信号的时域特性和频域特性是对信号的两种不同的描述方式。

对于一个时域的周期信号)t (f ，只要满足狄利克莱(Dirichlet)条件，就可以将其展开成三角形式或指数形式的傅里叶级数。

例如，对于一个周期为T 的时域周期信号)t (f ，可以用三角形式的傅里叶级数求出它的各次分量，在区间)T t ,t (11+内表示为)sin cos ()(10t n b t n a a t f n n n Ω+Ω+=∑∞=即将信号分解成直流分量及许多余弦分量和正弦分量，研究其频谱分布情况。

AA（c）图3-1 信号的时域特性和频域特性信号的时域特性与频域特性之间有着密切的内在联系，这种联系可以用图3-1来形象地表示。

其中图3-1(a)是信号在幅度--时间--频率三维座标系统中的图形；图3-1(b)是信号在幅度--时间座标系统中的图形即波形图；把周期信号分解得到的各次谐波分量按频率的高低排列，就可以得到频谱图。

反映各频率分量幅度的频谱称为振幅频谱。

图3-1(c)是信号在幅度--频率座标系统中的图形即振幅频谱图。

反映各分量相位的频谱称为相位频谱。

在本实验中只研究信号振幅频谱。

周期信号的振幅频谱有三个性质：离散性、谐波性、收敛性。

测量时利用了这些性质。

从振幅频谱图上，可以直观地看出各频率分量所占的比重。

测量方法有同时分析法和顺序分析法。

2、 矩形脉冲信号的频谱一个幅度为E ，脉冲宽度为τ，重复周期为T 的矩形脉冲信号，如图10-3所示。

图3-2 周期性矩形脉冲信号其傅里叶级数为：t n Tn Sa T E T E t f n i ωπτττcos )(2)(1∑=+= 该信号第n 次谐波的振幅为：Tn T n T E T n Sa T E a n /)/sin(2)(2τπτπττπτ== 由上式可见第n 次谐波的振幅与E 、T 、τ有关。

信号的几种分解形式
信号是消息的表现形式，消息则是信号的详细内容。

为了讨论信号传输与信号处理的问题，往往将一些信号分解成比较简洁的信号重量之和，信号可以从不同角度进行不同的信号分解。

一、直流重量与沟通重量
信号平均值即信号的直流重量，从原信号中去掉直流重量即得到信号的沟通重量。

设原信号为f(t)分解为直流重量fD与沟通重量fA(t)。

表示为f(t)=fD+fA(t)
信号的平均功率= 信号的直流功率+ 沟通功率
二、偶重量与奇重量
任何信号都可以分解为偶重量与奇重量两部分之和。

信号的平均功率= 偶重量功率+ 奇重量功率
这个分解方法的优点是可以分别利用偶函数与奇函数的对称性简化信号运算。

三、脉冲重量
一个信号可以近视分解为很多脉冲重量之和。

可以分解为矩形窄脉冲重量（窄脉冲组合的极限状况就是冲激信号的叠加）或者分解为阶跃信号重量的叠加。

用矩形脉冲靠近信号f（t）
这类分解的优点是基本信号元的波形简洁，响应好求，并且可以
充分利用LTI系统的叠加、比例与时不变性，便利的求解简单信号的响应。

四、正交函数重量
在频域法中，将信号分解为一系列正弦函数的和(或积分)，通过系统对正弦信号的响应求解系统对信号的响应。

矩形波产生原理矩形波是一种典型的非正弦波形，它的波形特点是在等间隔的时间内，以固定的幅值快速切换，形成一个有规则的矩形波形。

矩形波被广泛应用于各种电子设备中，如信号发生器、数字电路、电子音乐等领域。

本文将详细介绍矩形波的产生原理。

一、理论基础矩形波是一种周期性方波，可以由一组不同的正弦波叠加而成。

正弦波是一种单频振荡的波形，在物理学中，任意波形都可以看作是由一组或多组正弦波组成的。

因此矩形波也可以看作是由多个不同频率的正弦波所组成的波形。

这个过程称为傅里叶变换。

傅里叶变换能够将一个周期性的信号分解成多个不同频率的正弦波，而矩形波就是由多个正弦波叠加而成的。

二、产生原理矩形波的产生原理可以分为两类：电子学和数学。

1.电子学原理矩形波可以通过使用一个二极管和一个电容器来产生。

当电容器充电时，电压与时间之间的关系是线性的，因此输出信号将是一个正弦波。

当电容器放电时，输出信号将恒定为一个固定的电压，这是因为电容器中的电荷已经耗尽，电压不再变化。

这样，通过一个简单的电路，就可以得到一个以固定幅值快速切换的矩形波。

2.数学原理矩形波也可以通过傅里叶级数展开来产生。

一个矩形波可以看作是周期为T、幅值为A 的基本频率正弦信号的有限和。

这个信号的时间函数为：f(t)= A/2 + (A/π) ∑[ (-1)^n/(2n+1)sin(2π(2n+1)f0t)/f0 ]f0是基本频率，n是正整数。

这个公式描述了一个从-A/2到A/2范围内以1/2A的幅度快速切换的矩形波。

三、应用领域矩形波是一种常见的信号波形，在电子技术、物理学和工程学中广泛应用。

以下是一些常见的应用领域：1.信号发生器矩形波是信号发生器中最基本的波形之一。

它可以用于测试和调整其他电子设备的性能，如滤波器、调制器等。

它还可用于音频合成器或波形发生器的输出。

2.数字电路在数字电路中，矩形波用作时钟信号和数据传输。

时钟信号是微处理器和其他数字电路中的基本元素，它用于协调电路中的不同部件之间的操作。

信号与系统重点概念公式总结一、信号的基本概念：1.离散信号：在离散时间点上取值的信号，用x[n]表示。

2.连续信号：在连续时间上取值的信号，用x(t)表示。

3.周期信号：在一定时间内重复出现的信号。

4.能量信号：能量信号的能量有限，用E表示。

5.功率信号：功率信号的能量无限，用P表示。

二、时域分析：1. 时域表示：x(t) = X(t)eiωt，其中X(t)是振幅函数，ω是角频率。

2.常用信号的时域表示：- 矩形脉冲信号：rect(t/T)- 三角函数信号：acos(ωt + φ)-单位跳跃信号：u(t)-单位斜坡信号：r(t)3.信号的分解与合成：线性时不变系统能够将一个信号分解为若干个基础信号的线性组合。

4.性质：-时域平移性：如果x(t)的拉普拉斯变换是X(s)，那么x(t-t0)的拉普拉斯变换是e^(-t0s)X(s)。

-线性性：设输入信号的拉普拉斯变换为X(s)，系统的拉普拉斯变换表达式为H(s)，那么输出为Y(s)=X(s)H(s)。

-倍乘性：设输入信号拉普拉斯变换为X(s)，输出信号的拉普拉斯变换为Y(s)，那么输出信号的拉普拉斯变换为cX(s)，即输出信号的幅度放大为c倍。

-时间反转性：x(-t)的拉普拉斯变换是X(-s)。

-时间抽取性：设输入信号的拉普拉斯变换为X(s)，那么调整时间尺度为t/T的信号的拉普拉斯变换为X(s/T)。

三、频域分析：1.傅里叶级数：将周期信号表示为一系列谐波的和。

2.离散傅里叶变换（DFT）：将离散信号从时域变换到频域的过程。

3.傅里叶变换：将连续信号从时域变换到频域的过程。

4.频域表示：- 矩形函数：sinc(ωt) = sin(πωt)/(πωt)- 高斯函数：ft(x) = e^(-πx^2)5.频域滤波：系统的传输函数是H(ω)，那么输出信号的频率表示为Y(ω)=X(ω)H(ω)。

四、信号与系统的系统分析：1.系统稳定性：-意义：系统稳定指的是当输入有界时，输出有界。

矩形脉冲信号的分解和合成
脉冲信号简介矩形脉冲指阶跃时间远小于顶部持续时间的平顶脉冲。

定义1
矩形脉冲图形表达如图所示：（高度为A，宽度为a），此函数常作矩形采样窗口和平滑函数的模型。

定义2
具有轮廓近似为矩形，其上升和下降时间远小于脉冲持续时间的波形。

定义3
阶跃时间远小于顶部持续时间的平顶脉冲。

定义4
上升时间和下降时间相对于脉冲持续时间可以忽略，而且上升和下降之间的瞬时值实际上不变的单向脉冲。

本文主要介绍一下矩形脉冲信号的分解及合成，具体的跟随小编一起来看看吧。

矩形脉冲信号的分解一、实验目的
1、分析典型的矩形脉冲信号，了解矩形脉冲信号谐波分量的构成；
2、观察矩形脉冲信号通过多个数字滤波器后，分解出各谐波分量的情况。

二、实验原理
1、信号的频谱与测量
信号的时域特性和频域特性是对信号的两种不同的描述方式。

对于一个时域的周期信号f （t），只要满足狄利克莱（Dirichlet）条件，就可以将其展开成三角形式或指数形式的傅里叶级数。

例如，对于一个周期为T的时域周期信号发f（t），可以用三角形式的傅里叶级数求出它的各次分量，在区间。