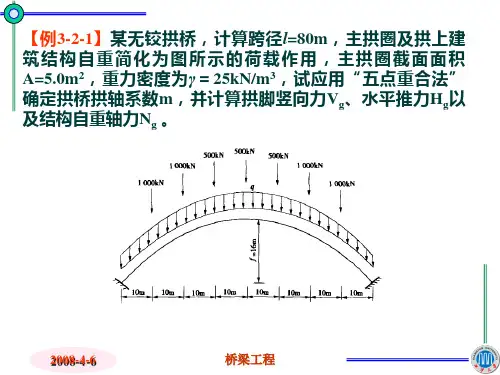
(优选)拱桥计算例题.
- 格式:ppt
- 大小:1022.50 KB
- 文档页数:12

中考数学高频考点突破:实际问题与二次函数——拱桥问题一、选择题1.有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行( )A.2.76米B.7米C.6米D.6.76米2.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=−0.01(x−20)2+4,桥拱与桥墩AC的交点C恰好位于水面,且AC⊥x轴,若OA=5米,则桥面离水面的高度AC为( )A.5米B.4米C.2.25米D.1.25米3.如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面 1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )A.4√3米B.5√2米C.2√13米D.7米二、填空题4.如图所示是一段抛物线型的拱梁,抛物线的表达式为y=ax2+bx.小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10秒时和26秒时拱梁的髙度相同,则小强骑自行车通过拱梁部分的桥面OC共需秒.5.一个拱形桥架可以近似看做是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成的.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45∘,AC1=4米,点D2的坐标为(−13,−1.69),则桥架的拱高OH=米.6.闵行体育公园的圆形喷水池的水柱(如图1),如果曲线APB表示落点B离点O最远的一条水流(如图2),其上的水珠的高度y(米)关于水平距离x(米)的函数解析式,那么圆形水池的半径至少为米时,才能使喷出的水流不落在为y=−x2+4x+94水池外.三、解答题7.如图,隧道的截面由抛物线AED和矩形ABCD构成,矩形的长BC为8m,宽AB为2m,以BC所在的直线为x轴,线段BC的中垂线为y轴,建立平面直角坐标系,y轴是抛物线的对称轴,顶点E到坐标原点O的距离为6m.(1) 求抛物线的解析式;(2) 一辆货运卡车高4.5m,宽2.4m,它能通过该隧道吗?8.如图是一个抛物线形拱桥示意图,已知河床宽度AB=40米,拱桥高度为10米.(1) 建立适当的坐标系,并求出抛物线的解析式;(2) 若测量得拱桥内水面宽度为28米,求拱桥内的水深.9.已知一条隧道的截面如图所示,它的上部是一个半圆,下部是一个矩形,且矩形的一条边长为2.5m.(1) 写出隧道截面的面积y(m2)与截面上部半圆的半径x(m)之间的函数表达式;(2) 当隧道截面上部半圆的半径为2m时,隧道截面的面积约是多少(精确到0.1m2)?10.桂林红桥位于桃花江上,是桂林两江四湖的一道亮丽的风景线,该桥的部分横截面如图所示,上方可看作是一个经过A,C,B三点的抛物线,以桥面的水平线为x轴,经过抛物线的顶点C与x轴垂直的直线为y轴,建立平面直角坐标系,已知此桥垂直于桥面的相邻两柱之间的距离为2米(图中用线段AD,FG,CO,BE等表示桥柱),CO=1米,FG=2米.(1) 求经过A,B,C三点的抛物线的函数解析式;(2) 求桥柱AD的高度.11.有一个抛物线形蔬菜大棚,将其截面放在如图所示的平面直角坐标系中,抛物线可以用函数y=ax2+bx来表示,已知OA=8米,距离O点2米处的棚高BC为9米.4(1) 求该抛物线的解析式;(2) 若借助横梁DE(DE∥OA)建一个门,要求门的高度为1.5米,则横梁DE的长度是多少米?12.如图,在喷水池的中心A处竖直安装一个水管AB.水管的顶端安有一个喷水管,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点C,高度为3m.水柱落地点D离池中心A处3m,建立适当的平面直角坐标系,解答下列问题.(1) 求水柱所在抛物线的函数解析式;(2) 求水管AB的长.13.如图为一座桥的示意图,已知桥洞的拱形是抛物线.当水面宽为12m时,桥洞顶部离水面4m.(1) 建立平面直角坐标系,并求该抛物线的函数表达式.(2) 若水面上升1m,水面宽度将减少多少?14.如图①,一个横截面为抛物线形的隧道,其底部的宽AB为8m,拱高为4m,该隧道为双向车道,且两车道之间有0.4m的隔离带,一辆宽为2m的货车要安全通过这条隧道,需保持其顶部与隧道间有不少于0.5m的空隙,以AB的中点O为原点,按如图②所示建立平面直角坐标系.(1) 求该抛物线对应的函数关系式;(2) 通过计算说明该货车能安全通过的最大高度.15.秋风送爽,学校组织同学们去颐和园秋游,昆明湖西堤六桥中的玉带桥非常令人喜爱,如图所示,玉带桥的桥拱是抛物线形,水面宽度AB=10m,桥拱最高点C到水面的距离为6m.(1) 建立适当的平面直角坐标系,求抛物线的表达式;(2) 现有一艘游船高度是 4.5m,宽度是4m,为了保证安全,船顶距离桥拱顶部至少0.5m,通过计算说明这艘游船能否安全通过玉带桥.16.如图是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.(1) 经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是(填“方案一”“方案二”或“方案三”),则B点坐标是,求出你所选方案中的抛物线的表达式.(2) 因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.17.如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系.(1) 画出直角坐标系xOy,并求出抛物线ADC的函数表达式;(2) 在抛物线型拱壁E,F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?18.如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起,据试验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.(1) 求足球开始飞出到第一次落地时,该抛物线的解析式.(2) 足球第一次落地点C距守门员多少米?(取4√3≈7)(3) 运动员乙要在第二个落地点D抢到足球,他应再向前跑多少米?(取2√6≈5)答案一、选择题1. 【答案】D【解析】设该抛物线的表达式为 y =ax 2,把 x =10,代入表达式得 −4=a ×102,解得 a =−125,故此抛物线的表达式为 y =−125x 2,∵ 桥下水面宽度不得小于 18m ,∴ 令 x =9 时,可得 y =−125×81=−3.24(m ), 此时水深 6+4−3.24=6.76(m ), 即桥下水深 6.76m 时正好通过, ∴ 超过 6.76m 时则不能通过.2. 【答案】C3. 【答案】B【解析】建立如图所示的平面直角坐标系,则 MN =4 米,EF =14 米,BC =10 米,DO =32 米,设大孔所在抛物线的解析式为 y =ax 2+32(a ≠0),∵BC =10 米, ∴ 点 B (−5,0),∴0=a ×(−5)2+32, ∴a =−350,∴ 大孔所在抛物线的解析式为 y =−350x 2+32,设点 A (b,0),则设顶点为 A 的小孔所在抛物线的解析式为 y =m (x −b )2, ∵EF =14 米,∴ 点 E 的横坐标为 −7, ∴ 点 E 的坐标为 (−7,−3625),当 m (x −b )2=−3625 时,解得 x 1=65√−1m +b ,x 2=−65√−1m +b , ∵MN =4 米, ∴∣∣∣∣65√−1m +b −(−65√−1m +b)∣∣∣∣=4, ∴m =−925,∴ 顶点为 A 的小孔所在抛物线的解析式为 y =−925(x −b )2,∵ 大孔水面宽度为 20 米,∴ 当 x =−10 时,y =−92, ∴−92=−925(x −b )2, ∴x 1=5√22+b ,x 2=−5√22+b ,∴ 当大孔水面宽度为 20 米时,单个小孔的水面宽度 =∣∣∣(5√22+b)−(−5√22+b)∣∣∣=5√2(米). 故选B .二、填空题4. 【答案】 36【解析】如图所示:设在 10 秒时到达 A 点,在 26 秒时到达 B , ∵10 秒时和 26 秒时拱梁的高度相同,∴A ,B 关于对称轴对称,则从 A 到 B 需要 16 秒,则从 A 到 D 需要 8 秒, ∴ 从 O 到 D 需要 10+8=18 秒, 从 O 到 C 需要 2×18=36 秒.5. 【答案】 7.24【解析】设抛物线 D 1OD 8 的解析式为 y =ax 2,将 x =−13,y =−1.69 代入,可得 a =−1100.因为横梁 D 1D 8=C 1C 8=AB −2AC 1=36 m ,所以点 D 1 的横坐标是 −18,代入 y =−1100x 2,得 y =−3.24. 因为 ∠A =45∘,所以 D 1C 1=AC 1=4 m ,所以 OH =3.24+4=7.24 m .6. 【答案】 92三、解答题7. 【答案】(1) 根据题意,A (−4,2),D (4,2),E (0,6),设抛物线的解析式为 y =ax 2+6(a ≠0),把 A (−4,2) 或 D (4,2) 代入得 16a +6=2,得 a =−14,抛物线的解析式为 y =−14x 2+6.(2) 根据题意,把 x =±1.2 代入解析式,得 y =5.64, ∵5.64>4.5,∴ 货运卡车能通过.【解析】(1) 方法二:设解析式为y=ax2+bx+c,代入A,D,E三点坐标得{16a−4b+c=216a+4b+c=2c=6,得{a=−14b=0c=6,抛物线的解析式为y=−14x2+6.8. 【答案】(1) 建立如图所示坐标系,设抛物线铁板式为y=ax2;由题意得,B(20,−10),∴−10=202a,解得a=−140,∴y=−140x2.(2) 由题意得,点D横坐标为28÷2=14,当x=14时,y=−140×142=−4.9,−4.9−(−10)=5.1.∴拱桥内的水深5.1米.9. 【答案】(1) y与x之间的函数表达式是y=12πx2+5x;(2) 当x=2时,y=12π×22+5×2=2π+10≈16.3(m2).所以隧道截面上部半圆的半径为2m时,隧道截面的面积约是16.3m2.10. 【答案】(1) 由题意可知:点C的坐标为(0,1),点F的坐标为(−4,2).设抛物线的函数解析式为y=ax2+c,所以{1=c,2=16a+c,解得{a=116,c=1.所以抛物线的函数解析式为y=116x2+1.(2) 点A的横坐标为−8,当x=−8时,y=5,所以桥柱AD的高度为5米.11. 【答案】(1) 由题意可得,抛物线经过(2,94),(8,0),故{64a+8b=0,4a+2b=94,解得{a=−316,b=32,故拋物线的解析式为y=−316x2+32x.(2) 由题意可得,当y=1.5时,1.5=−316x2+32x,解得x1=4+2√2,x2=4−2√2,故DE=x1−x2=4+2√2−(4−2√2)=4√2(米).12. 【答案】(1) 以池中心A为原点,竖直安装的水管为y轴,与水管垂直的方向为x轴建立平面直角坐标系.由于在距池中心的水平距离为1m时达到最高,高度为3m,则设抛物线的解析式为y =a (x −1)2+3,代入 (3,0),求得 a =−34, 故所求的函数解析式为 y =−34(x −1)2+3(0≤x ≤3).(2) 令 x =0,则 y =94=2.25.故水管 AB 的长为 2.25 m .13. 【答案】(1) 以 C 为坐标原点建立坐标系,则 A (−6,−4),B (6,−4),C (0,0),设 y =ax 2,把 B (6,−4) 代入上式,36a +4=0,解得:a =−19,∴y =−19x 2.(2) 令 y =−3 得:−19x 2=−3,解得:x =±3√3, ∴ 若水面上升 1 m ,水面宽度将减少 12−6√3.14. 【答案】(1) 如图,A (−4,0),C (0,4),设抛物线的解析式为 y =ax 2+k (a ≠0),由题意,得 {16a +k =0,k =4,解得 {a =−14,k =4,∴ 抛物线的解析式为 y =−14x 2+4.(2) 2+0.42=2.2,当 ∣x ∣=2.2 时,y =−14×2.22+4=2.79,2.79−0.5=2.29(m ).答:该货车能够安全通行的最大高度为 2.29 m .15. 【答案】(1) 以 AB 的中点为原点,建立如下的坐标系, 则点 C (0,6),点 B (5,0).设函数的表达式为 y =ax 2+c =ax 2+6(a ≠0),将点 B 的坐标代入上式,得 0=25a +6,解得 a =−625,故抛物线的表达式为 y =−625x 2+6.(2) 设船从桥的中心进入,则其最右侧点的横坐标为 2,当 x =2 时,y =−625x 2+6=−625×4+6=12625=5.04,船的顶部高为 4.5,4.5+0.5=5<5.04,故顶部通过符合要求,故这艘游船能安全通过玉带桥.16. 【答案】(1) 方案二;(10,0);由题意知,抛物线的顶点坐标为 A (5,5),且经过点 O (0,0),B (10,0), 设抛物线的解析式为 y =a (x −5)2+5(a ≠0),把点 (0,0) 代入,得 0=a (0−5)2+5,解得a=−15.∴抛物线的解析式为y=−15(x−5)2+5.(2) 在方案二的前提下,由题意知,当x=5−3=2时,−15(x−5)2+5=165,所以水面上涨的高度为165米.17. 【答案】(1) 画出直角坐标系xOy,如图:由题意可知,抛物线ADC的顶点坐标为(6,10),A点坐标为(0,4),可设抛物线ADC的函数表达式为y=a(x−6)2+10,将x=0,y=4代入得:a=−16,∴抛物线ADC的函数表达式为y=−16(x−6)2+10.(2) 由y=8得:−16(x−6)2+10=8,解得:x1=6+2√3,x2=6−2√3,则EF=x1−x2=4√3,即两盏灯的水平距离EF是4√3米.18. 【答案】(1) 根据题意,可设足球开始飞出到第一次落地时,抛物线的解析式为y=a(x−6)2+4,将点A(0,1)代入,得36a+4=1,解得a=−112,∴足球开始飞出到第一次落地时,该抛物线的解析式为y=−112(x−6)2+4.(2) 令y=0,得−112(x−6)2+4=0,解得x1=4√3+6≈13,x2=−4√3+6<0(舍去),∴足球第一次落地点C距守门员13米.(3) 如图,足球第二次弹起后的水平距离为CD,根据题意知CD=EF(即相当于将抛物线AEMFC向下平移了2个单位),∴−112(x−6)2+4=2,解得x1=6−2√6,x2=6+2√6,∴CD=x2−x1=4√6≈10(米),∴BD=13−6+10=17(米).答:运动员乙要在第二个落地点D抢到足球,他应再向前跑17米.。

拱桥一、填空题1、按照拱上建筑的型式可以将拱桥分为:实腹式和空腹式。
2、按照桥面的位置可分为:上承式、中承式、下承式。
3、按照拱圈截面形式可分为:板拱、肋拱、箱形拱、双曲拱等。
4、确定拱桥设计高程有四个,分别为:跨中结构的底面高程、起拱线的高程、基底高程和桥面高程。
5、拱桥常用的拱轴线形有悬链线、抛物线、圆弧线。
6、拱桥分类方法很多,按其结构静力图示可分为静定拱、超静定拱。
7、拱桥的矢跨比是指计算矢高与计算跨度之比。
当矢跨比增大时,拱的推力减小。
8、梁桥以受弯矩与剪力为主,拱桥主拱圈以受轴向压力为主。
9、拱上填料的作用是扩大车辆荷载分布面积的作用,减少车辆荷载的冲击作用。
10、无铰拱桥的受力状态与三铰拱桥的受力状态相比,它的主要优点内力分布均匀,整体刚度大11、当跨径、荷载和拱上建筑等情况相同时,f/L=1/3的拱桥和f/L=1/8的拱桥相比,前者的水平推力比后者_小_________。
12、混凝土砼拱桥极限跨度在__500__米左右,经济跨度___100-300_______米;钢拱桥在1200__米左右,经济跨度___300-500_______。
13、万州长江大桥采用的缆索吊装和悬臂扣挂施工方法。
14、组合体系拱桥的最重要特点是桥面结构,主拱结构形成整体共同承受荷载。
15、双曲拱桥主拱圈通常由拱肋、拱波、拱板、横向联系几部分组成。
16、迄今最大跨径的钢管混凝土拱桥是巫山长江大桥,最大跨径的石拱桥是是山西晋城丹河大桥,最大跨径的钢筋砼拱桥是万县长江大桥,最大跨径的钢拱桥是上海卢浦大桥。
17、当拱圈宽跨比B/L<1/20 时,应验算拱圈的横向稳定性。
18、双曲拱桥的建设策略是。
19、空腹式拱桥拱上建筑的腹拱墩有排架式和横墙式两种。
20、拱铰主要有弧形铰、铅垫铰、不完全铰、平铰和钢铰五种形式。
21、中下承式拱桥中的吊杆间距通常为4~10 米,可分为刚性吊杆、半刚性吊杆、柔性吊杆三种构造,其中刚性吊杆一般采用预应力混凝土矩形截面,半刚性吊杆一般采用钢管混凝土园形截面,柔性吊杆采用高强钢丝束制成。
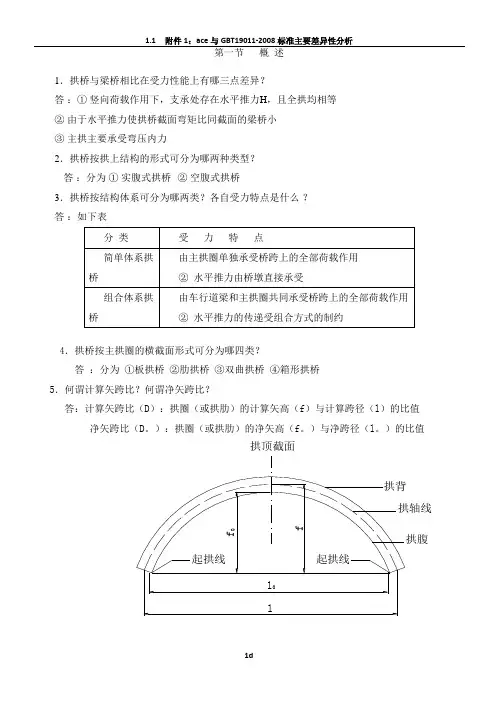
第一节概述1.拱桥与梁桥相比在受力性能上有哪三点差异?答:①竖向荷载作用下,支承处存在水平推力H,且全拱均相等②由于水平推力使拱桥截面弯矩比同截面的梁桥小③主拱主要承受弯压内力2.拱桥按拱上结构的形式可分为哪两种类型?答:分为①实腹式拱桥②空腹式拱桥3.拱桥按结构体系可分为哪两类?各自受力特点是什么?答:如下表4.拱桥按主拱圈的横截面形式可分为哪四类?答:分为①板拱桥②肋拱桥③双曲拱桥④箱形拱桥5.何谓计算矢跨比?何谓净矢跨比?答:计算矢跨比(D):拱圈(或拱肋)的计算矢高(f)与计算跨径(l)的比值净矢跨比(D。
):拱圈(或拱肋)的净矢高(f。
)与净跨径(l。
)的比值拱顶截面第二节拱桥的构造与设计1.何谓板拱?答:主拱圈为矩形实体截面的拱桥,称为板拱2.何谓肋拱桥?其上部结构由哪几部分组成?答:肋拱桥是由两条或多条分离的平行拱肋,以及在拱肋上设置的立柱和横梁支承的形成部分组成的拱桥,其上部结构由横系梁、立柱、横梁、纵梁及桥面板组成。
3.箱形拱的主要特点有哪五点?答:①截面挖空率大,减轻了自重②箱形截面的中性轴大致居中,对于抵抗正负弯矩具有几乎相等的能力,能较好地适应主拱圈各截面的正负弯矩变化的需要③由于是闭合空心截面,抗弯和抗扭刚度大,拱圈的整体性好,应力分布较均匀④单条肋箱刚度较大,稳定性好,能单箱肋成拱,便于无支架吊装⑤制作要求较高,吊装设备较多,主要用于大跨径拱桥4.箱形截面常用的组成方式有哪四种?各种的优缺点是什么?答:① U型肋组成的多室箱形截面优点:预制不需要顶模,吊装稳定性好缺点:浇筑顶层砼时需要侧模,安装不方便② I型肋组成的多室箱形截面优点:无需浇筑顶层砼(不需要侧模),施工工序少缺点:吊装稳定性差③箱形肋组成的多室箱形截面优点:吊装稳定性好,抗弯、抗扭刚度大缺点:吊装自重大5.实腹式拱上建筑的特点是什么?答:①构造简单②施工方便③填料数量较多④恒重大6.拱上侧墙、护拱的作用各是什么?答:侧墙的作用是承受拱腹填料及车辆荷载所产生的侧压力(推力)护拱的作用是加强拱脚段拱圈,同时便于在多孔拱桥中敷设防水层和排出积水7.空腹式拱上建筑的特点是什么?答:空腹式拱上建筑的最大特点是除了具有实腹拱上建筑相同构造外,还具有腹孔和腹孔墩,减轻了拱桥恒重,同时增加了美观性8.拱上腹孔的布置原则是什么?答:①应对称布置在靠拱脚侧的一定区段内②一般为奇数孔③腹孔构造宜统一,以便与施工和有利于腹孔墩的受力④腹拱高度应布置在主拱圈允许的高度内⑤应尽量减轻贡上建筑恒重,不使腹孔墩过分集中或者过分分散9.伸缩缝与变形缝的作用是什么?答:①符合受力图式②避免不规则开裂10.排除拱桥腹内积水有哪两个重要性?答:①避免含水量的增大,确保路面强度②防止雨水渗到主要结构内,使其发生冻胀破坏11.拱桥中铰按性质可分为哪两种类型?答:分为①永久性铰②临时性铰12.拱桥的主要设计标高有哪四个?答:①桥面标高(主要有三个:桥梁起点、终点及跨中点的桥面标高)②拱顶底面标高③起拱线标高④基底标高13.为什么说拱桥的主拱的矢跨比是拱轴设计中的主要参数之一?答:①拱桥的水平推力与垂直反力之比值,随矢跨比的减小而增大②当矢跨比减小时,拱的推力增大,反之则水平推力减小③无铰拱随矢跨比减小其弹性压缩、温度变化、混凝土收缩及墩台位移产生的附加内力越大④拱的矢跨比过大使拱脚段施工困难⑤矢跨比对拱桥的外形及周围景观的协调产生影响14.不等跨拱桥的主要受力特点是什么?在处理不等跨分孔时应注意控制的实质性问题是什么?如何作?答:不等跨拱桥的主要受力特点是:恒载产生的相邻跨的水平推力不等处理不等跨分孔时应注意控制的实质性问题是:尽量减小因恒载引起的不平衡推力对桥墩基底的偏心作用处理不等跨分孔的方法:采用不同的矢跨比;采取不同的起拱线标高;15.什么是拱轴线?什么是合理拱轴线?拱轴线的种类有哪些?各对应哪种荷载模式?答:拱轴线是拱圈横截面形心点的连线将恒载作用下的压力线作为主拱圈的设计拱轴线则称为合理拱轴线圆弧拱轴线:等静水压力;抛物线拱轴线:均布荷载;悬链线:与竖坐标成比例的荷载。

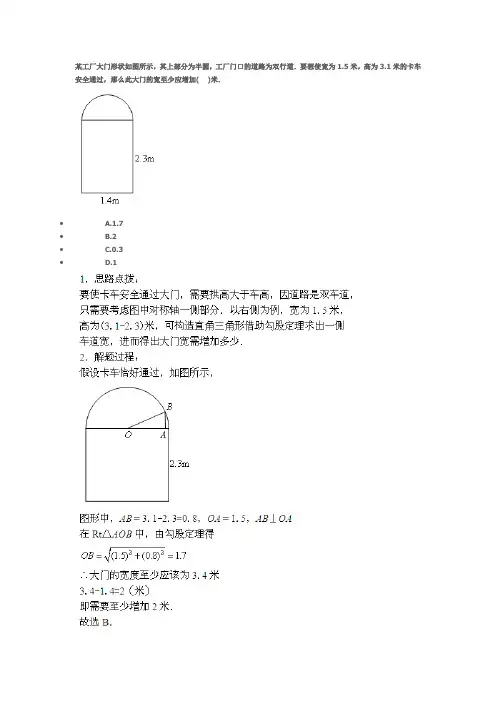
某工厂大门形状如图所示,其上部分为半圆,工厂门口的道路为双行道.要想使宽为1.5米,高为3.1米的卡车安全通过,那么此大门的宽至少应增加( )米.• A.1.7• B.2• C.0.3• D.1一辆卡车装满货物后宽3.2米,这辆卡车要通过如图所示的隧道(上方是一个半圆,下方是边长为4米的正方形),则装满货物后卡车的最大高度为( )米.• A.5.2• B.5.8• C.7.6• D.5.4如图所示,某住宅社区在相邻两楼之间修建一个上方是半圆,下方是长方形的仿古通道(AD=2.6米,AB=5米),现有一辆卡车装满家具后宽3米,卡车要通过通道,装满家具后的最大高度为____米.(上方是一个以AB为直径的半圆)如图所示,某住宅社区在相邻两楼之间修建一个上方是半圆,下方是长方形的仿古通道(AD=2.6米,AB=4米),现有一辆卡车装满家具后宽2.8米,高4米,这辆卡车能通过横截面如图所示这个通道吗?(上方是一个以AB为直径的半圆)能通过一辆装满货物的卡车,2.5米高,1.6米宽,想要开进某工厂,工厂厂门如图所示(上部分为半圆,下部分为长方形),则这辆卡车____通过.(填“能”或“不能”)答MN=1.6m,AB=2m∴OE=0.8m∵OC=OA=1m在Rt△OCE中,∴CM=2.3m+0.6m=2.9m>2.5m所以这辆卡车能通过一辆卡车装满货物后宽6.4米,这辆卡车要通过如图所示的隧道(上方是一个半圆,下方是边长为8米的正方形),则装满货物后卡车的最大高度为( )米.• A.10.4• B.11.6• C.15.2• D.10.8如图,由题意得,卡车从正中间通过的机会最大,且当卡车CDEB车顶刚好碰到隧道上方的半圆,接触点为B,E时,恰好通过,此时高度CB即为最大高度.由条件可知,,设AB为x,在Rt△OAB中,由勾股定理得,,得x=2.4,故最大高度为AB+AC=2.4+8=10.4,故选A一辆卡车装满货物后,高4米,宽2.8米.这辆卡车能通过横截面如图所示(上方是一个半圆)的隧道吗?案能通过解:∵卡车在隧道中间位置能通过的可能性最大∴如图,O为EF的中点,OE=1.4m,OG为圆的半径,OG=2m在直角△OEG中GE²=OG²-OE²=2²-1.4²=2.04∵(4-2.6)²=1.4²=1.96,2.04>1.96∴在相同宽度下隧道的高度高于卡车的高度,卡车能通过该隧道。

22.3(4.1)---(拱桥问题)一.【知识要点】1.现实生活中的抛物线:喷射的水流、投出的篮球运动轨迹、两端固定自然下垂的绳子、一些拱桥、涵洞等,都给人留下抛物线的印象。
如果把它们放到平面直角坐标系中,结合实际数据即可求解得出抛物线的解析式,再通过二次函数的性质来解决测量问题、最值问题等.二.【经典例题】1.右图是抛物线型拱桥,当拱顶离水面2m时,水面宽4m,水面下降2m,水面宽度增加__________m。
2.(6分)如右图所示,有一座拱桥圆弧形,它的跨度为60米,拱高为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,•是否采取紧急措施?三.【题库】【A】1.如图,是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯,建立适当坐标系.则两盏景观灯之间的水平距离_________.【B】1.如图,某大桥有一段抛物线形的拱梁,抛物线的解析式为y=ax2+bx,小强骑自行车从拱梁一端O沿直线匀速穿过拱梁部分的桥面OC,当小强骑自行车行驶10 s时和26 s时拱梁的高度相同,则小强骑自行车通过拱梁部分的桥面OC共需_____________ s.【C】1.一位运动员投掷铅球的成绩是14m,当铅球运行的水平距离是6m时达到最大高度4m,若铅球运行的路线是抛物线,则铅球出手时距地面的高度是m.【D】1.小明和小丽先后从A地出发沿同一直道去B地.设小丽出发第xmin时,小丽、小明离B地的距离分别为y1m,y2m,y1与x之间的函数表达式是y1=﹣180x+2250,y2与x之间的函数表达式是y2=﹣10x2﹣100x+2000.(1)小丽出发时,小明离A地的距离为m.(2)小丽出发至小明到达B地这段时间内,①两人何时相距180m?②两人何时相距最近?最近距离是多少?。

2024年中考数学高频考点专题复习-拱桥问题(实际问题与二次函数)1.某公园要修建一个截面抛物线形的拱门,其最大高度为4.5m,宽度OP为6米,现以地面(OP所在的直线)为x轴建立平面直角坐标系(如图1所示)(1)求这条抛物线的函数表达式;(2)如图所示,公园想在抛物线拱门距地面3米处钉两个钉子以便拉一条横幅,请计算该横幅的宽度为多少米?(3)为修建该拱门,施工队需搭建一个矩形“支架“ABCD(由四根木杆AB﹣BC﹣CD﹣DA组成),使B,C两点在抛物线上.A,D两点在地面OP上(如图2所示),请你帮施工队计算一下最多需要准备多少米该种木杆?2.施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明.3.如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12m,宽是4m.按照图中所示的直角坐标系,抛物线可以用y=16x2+bx+c表示,且抛物线上的点C到OB的水平距离为3m,到地面OA的距离为172m.(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?4.陕北窑洞,具有十分浓厚的民俗风情和土气息. 如图所示,某窑洞口的下部近似为矩形 OABC ,上部近似为一条抛物线. 已知 3OA =米,2AB =米,窑洞的最高点 M (抛物线的顶点)高地面 OA 的距离为 258米.(1)建立如图所示的平面直角坐标系,求抛物线的表达式;(2)若在窑洞口的上部要安装一个正方形窗户DEFG ,使得点 D E 、在矩形 OABC 的边BC 上,点 F G 、在抛物线上,那么这个正方形窗户 DEFG 的边长为多少米?5.赛龙舟是中国端午节的习俗之一,也是一项广受欢迎的民俗体育运动.某地计划进行一场划龙舟比赛,图1是比赛途中经过的一座拱桥,图2是该桥露出水面的主桥拱的示意图,可看作抛物线的一部分,建立如图所示的平面直角坐标系xOy ,桥拱上的点到水面的竖直高度y (单位:m )与到点O 的水平距离x (单位:m )近似满足函数关系()20.01309y x =--+,据调查,龙舟最高处距离水面2m ,为保障安全,通过拱桥时龙舟最高处到桥拱的竖直距离至少3m .(1)水面的宽度OA =_______m ;(2)要设计通过拱桥的龙舟赛道方案,若每条龙舟赛道宽度为9m ,求最多可设计龙舟赛道的数量.6.如图,某长为800m 的隧道的横截面顶部为拋物线形,隧道的左侧是高为4m 的墙OA ,右侧是高为5m 的墙BC ,拱壁上某处离地面的高度()m y 与其离墙OA 的水平距离()m x 之间的关系满足216y x bx c =-++.现测得,OA BC 两墙体之间的水平距离为12m .(1)求该抛物线的函数关系式,并计算出拱顶D到地面OC的距离.(2)从隧道头到隧道尾,在拋物线形拱壁上安装若干排吊灯,每排吊灯与地面的距离都不低于203m32,每相邻两排吊灯之间的水平距离为2m,每排内相邻两盏吊灯之间的距离为10m.求共需要多少盏吊灯?(3)如果隧道内设双向行车道,每条车道的宽为5m,两条车道之间是宽为1m的绿化带,一辆货车载一个长方体集装箱后高为5m、宽为4m,那么这辆货车无论从哪条车道都能安全通过吗?请说明理由.7.(1)解方程:22125x x-+=(2)如图是抛物线形拱桥,当拱顶离水面2m时,水面AB宽4m.若水面上升1m,求水面的宽度.8.某公司生产A型活动板房的成本是每个3500元.图1表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长4mAD=,宽3mAB=,抛物线的最高点E到BC的距离为4m.(1)按图1中所示的平面直角坐标系,求该抛物线的函数表达式;(2)现将A型活动板房改造成为B型活动板房.如图2,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G、M在AD上,点F、N在抛物线上,窗户的成本为150元/2m.已知2mGM=,求每个B型活动板房的成本.(每个B型活动板房的成本=每个A型活动板房的成本+一扇窗户FGMN的成本)9.现要修建一条隧道,其截面为抛物线型,如图所示,线段OE 表示水平的路面,以O 为坐标原点,以OE 所在的直线为x 轴,以过点O 作垂直于x 轴的直线为y 轴,建立平面直角坐标系.根据设计要求12m OE =,该抛物线的顶点P 到OE 的距离为9m .(1)求满足设计要求的抛物线的函数解析式;(2)现需在这一隧道内壁的同样高度的A 、B 处安装上照明灯,如图所示,若要求A 、B 两个照明灯之间的水平距离为8m ,求出此时A 、B 两个照明灯距离地面的高度.10.湘雅公园人工湖上有一座拱桥,横截面呈抛物线形状,如图所示,现对此展开研究:跨度AB 为4米,桥墩露出水面的高度AE 为0.88米,在距点A 水平距离为2米的地点,拱桥距离水面的高度为2.88米,建立如图所示的平面直角坐标系,并设抛物线的表达式为()2y a x h k =-+,其中()m x 是横截水面,()m y 是拱桥距水面的高度.(1)求抛物线的表达式;(2)公园欲开设游船项目,为安全起见,公园要在水面上的C 、D 两处设置航行警戒线,并且CE DF =,要求游船能从C 、D 两点之间安全通过,则C 处距桥墩的距离CE 至少为多少米?11.如图所示的是一座古桥,桥拱为抛物线型,桥的跨径AB 为20m ,此时水位在OC 处,在水面以上的桥墩AO BC ,都为2m ,桥拱最高点P 离水面6m .以OC 所在的直线为x 轴、AO 所在的直线为y 轴建立平面直角坐标系.(1)求此桥拱所在抛物线的表达式.(2)当水位上涨2m 时,若有一艘船在水面以上部分高3m ,宽10.8m ,问此船能否通过桥洞?请说明理由. 12.一座隧道的截面由抛物线和长方形构成,长方形的长为8m ,宽为 2m ,隧道最高点P 位于AB 的中央且距地面6m ,建立如图所示的坐标系.(1)求抛物线的表达式;(2)一辆货车高4m ,宽4m ,能否从该隧道内通过,为什么?13.即墨古城某城门横断面分为两部分,上半部分为抛物线形状,下半部分为正方形(OMNE 为正方形),已知城门宽度为4米,最高处离地面6米,如图1所示,现以O 点为原点,OM 所在的直线为x 轴,OE 所在的直线为y 轴建立直角坐标系.(1)求出上半部分抛物线的函数表达式,并写出其自变量的取值范围;(2)有一辆宽3米,高4.5米的消防车需要通过该城门进入古城,请问该消防车能否正常进入?(3)为营造节日气氛,需要临时搭建一个矩形“装饰门”ABCD ,该“装饰门”关于抛物线对称轴对称,如图2所示,其中AB ,AD ,CD 为三根承重钢支架,A 、D 在抛物线上,B ,C 在地面上,已知钢支架每米50元,问搭建这样一个矩形“装饰门”,仅钢支架一项,最多需要花费多少元?14.如图,有一座抛物线型拱桥,在正常水位时水面宽20m AB =,当水位上升3m 时,水面宽10m CD =.(1)按如图所示的直角坐标系,求此抛物线的函数表达式;km h的速度向此桥径直驶来,当船距离此桥35km,桥下水位正好在AB处,之后水位每小时上涨(2)有一条船以5/0.25m,当水位达到CD处时,将禁止船只通行.如果该船的速度不变继续向此桥行驶35km时,水面宽是多少?它能否安全通过此桥?参考答案:1.(1)213(06)2y x x x =-+≤≤(2)33)最多需要准备11米该种木杆. 2.(1)y=-16x 2+2x .(0≤x≤12);(2)不能行驶宽2.5米、高5米的特种车辆. 3.(1)抛物线的函数关系式为y =16-x 2+2x +4,拱顶D 到地面OA 的距离为10m ;(2)可以通过(3)两排灯的水平距离最小是43m .4.(1)()2132503228y x x ⎛⎫=--+≤≤ ⎪⎝⎭ (2)1米5.(1)60(2)4条.6.(1)212510096496y x ⎛⎫=--+ ⎪⎝⎭,1009m 96 (2)486盏(3)货车无论从哪条车道都能安全通过7.(1)126,4x x ==-(2)22m8.(1)2114y x =-+ (2)每个B 型活动板房的成本为3725元9.(1)21(6)94y x =--+ (2)5m10.(1)()212 2.882y x =--+; (2)C 处距桥墩的距离CE 至少为0.8米.11.(1)抛物线解析式为()2110625y x =--+ (2)此船不能通过桥洞 12.(1) 21(4)64y x =--+;(2) 货车能通过隧道 13.(1)()2124042y x x x =-++≤≤;(2)能正常进入;(3)650元 14.(1)2125y x =- (2)水面宽是15m ,它能安全通过此桥。



拱桥一、填空题1、按照拱上建筑的型式可以将拱桥分为:实腹式和空腹式。
2、按照桥面的位置可分为:上承式、中承式、下承式。
3、按照拱圈截面形式可分为:板拱、肋拱、箱形拱、双曲拱等。
4、确定拱桥设计高程有四个,分别为:跨中结构的底面高程、起拱线的高程、基底高程和桥面高程。
5、拱桥常用的拱轴线形有悬链线、抛物线、圆弧线。
6、拱桥分类方法很多,按其结构静力图示可分为静定拱、超静定拱。
7、拱桥的矢跨比是指计算矢高与计算跨度之比。
当矢跨比增大时,拱的推力减小。
8、梁桥以受弯矩与剪力为主,拱桥主拱圈以受轴向压力为主。
9、拱上填料的作用是扩大车辆荷载分布面积的作用,减少车辆荷载的冲击作用。
10、无铰拱桥的受力状态与三铰拱桥的受力状态相比,它的主要优点内力分布均匀,整体刚度大11、当跨径、荷载和拱上建筑等情况相同时,f/L=1/3的拱桥和f/L=1/8的拱桥相比,前者的水平推力比后者_小_________。
12、混凝土砼拱桥极限跨度在__500__米左右,经济跨度___100-300_______米;钢拱桥在1200__米左右,经济跨度___300-500_______。
13、万州长江大桥采用的缆索吊装和悬臂扣挂施工方法。
14、组合体系拱桥的最重要特点是桥面结构,主拱结构形成整体共同承受荷载。
15、双曲拱桥主拱圈通常由拱肋、拱波、拱板、横向联系几部分组成。
16、迄今最大跨径的钢管混凝土拱桥是巫山长江大桥,最大跨径的石拱桥是是山西晋城丹河大桥,最大跨径的钢筋砼拱桥是万县长江大桥,最大跨径的钢拱桥是上海卢浦大桥。
17、当拱圈宽跨比B/L<1/20 时,应验算拱圈的横向稳定性。
18、双曲拱桥的建设策略是将主拱圈以“化整为零”的方法按先后顺序进行施工,再以“集零为整”的方式组合成承重的整体结构。
因主拱圈分期形成,呈现组合结构的受力特征,整体性较弱,在地震荷载作用下容易破坏。
19、空腹式拱桥拱上建筑的腹拱墩有排架式和横墙式两种。
计算报告目录一、结构计算分析依据 (2)二、结构计算分析 (2)2.1 拱轴系数计算 (2)2.1.1 计算标准 (2)2.1.2 材料及其数据 (2)2.1.3 上部结构计算 (2)2.2 计算分析模型 (7)2.2.1 建立模型 (7)2.2.2 材料特性 (8)2.2.3计算分析说明 (8)2.2.4 计算分析结果 (9)2.2.4.1 主拱圈承载能力极限状态承载能力计算结果 (9)2.2.4.2 主拱圈应力计算结果 (11)2.2.4.3 主拱圈抗剪验算 (14)2.2.4.4 刚度验算 (15)2.2.4.5 桥台稳定性和抗滑移验算 (15)三、结构计算分析结论 (23)一、结构计算分析依据1、交通部《公路桥涵养护规范》(JTG H11-2004)2、交通部《公路桥涵设计通用规范》(JTG D60-2004)3、交通部《公路工程技术标准》(JTG B01-2003)4、交通部《公路工程质量检验评定标准》(JTG F80/1-2004)5、交通部《公路圬工桥涵设计规范》(JTG D61-2005)6、交通部《公路桥涵地基与基础设计规范》(JTG D63-2007)7、交通部部标准《公路砖石及混凝土桥涵设计规范(JTJ022-85》8、《公路桥涵设计手册-拱桥》(上、下册),人民交通出版社,1994年9、《公路桥涵设计手册-基本资料》,人民交通出版社,1993年二、结构计算分析2.1 拱轴系数计算2.1.1 计算标准设计荷载:公路-Ⅱ级净跨径:L0=80m净矢高:f0=13.33m桥面净宽:净4.5+2×0.5m(防撞护栏)2.1.2 材料及其数据拱顶填料厚度hd=0.62m,γ4=24KN/m3拱腔填料单位重γ3=23KN/m3腹孔结构材料单位重γ2=25KN/m3主拱圈采用C40钢筋混凝土,γ1=26KN/m3,轴心抗压强度设计值fcd=18.4MPa,弹性模量E=3.00×104MPa。
第一节概述1.拱桥与梁桥相比在受力性能上有哪三点差异答:①竖向荷载作用下,支承处存在水平推力H,且全拱均相等②由于水平推力使拱桥截面弯矩比同截面的梁桥小③主拱主要承受弯压内力2.拱桥按拱上结构的形式可分为哪两种类型答:分为①实腹式拱桥②空腹式拱桥3.拱桥按结构体系可分为哪两类各自受力特点是什么答:如下表4.拱桥按主拱圈的横截面形式可分为哪四类答:分为①板拱桥②肋拱桥③双曲拱桥④箱形拱桥5.何谓计算矢跨比何谓净矢跨比答:计算矢跨比(D):拱圈(或拱肋)的计算矢高(f)与计算跨径(l)的比值净矢跨比(D。
):拱圈(或拱肋)的净矢高(f。
)与净跨径(l。
)的比值拱顶截面第二节拱桥的构造与设计1.何谓板拱答:主拱圈为矩形实体截面的拱桥,称为板拱2.何谓肋拱桥其上部结构由哪几部分组成答:肋拱桥是由两条或多条分离的平行拱肋,以及在拱肋上设置的立柱和横梁支承的形成部分组成的拱桥,其上部结构由横系梁、立柱、横梁、纵梁及桥面板组成。
3.箱形拱的主要特点有哪五点答:①截面挖空率大,减轻了自重②箱形截面的中性轴大致居中,对于抵抗正负弯矩具有几乎相等的能力,能较好地适应主拱圈各截面的正负弯矩变化的需要③由于是闭合空心截面,抗弯和抗扭刚度大,拱圈的整体性好,应力分布较均匀④单条肋箱刚度较大,稳定性好,能单箱肋成拱,便于无支架吊装⑤制作要求较高,吊装设备较多,主要用于大跨径拱桥4.箱形截面常用的组成方式有哪四种各种的优缺点是什么答:① U型肋组成的多室箱形截面优点:预制不需要顶模,吊装稳定性好缺点:浇筑顶层砼时需要侧模,安装不方便② I型肋组成的多室箱形截面优点:无需浇筑顶层砼(不需要侧模),施工工序少缺点:吊装稳定性差③箱形肋组成的多室箱形截面优点:吊装稳定性好,抗弯、抗扭刚度大缺点:吊装自重大5.实腹式拱上建筑的特点是什么答:①构造简单②施工方便③填料数量较多④恒重大6.拱上侧墙、护拱的作用各是什么答:侧墙的作用是承受拱腹填料及车辆荷载所产生的侧压力(推力)护拱的作用是加强拱脚段拱圈,同时便于在多孔拱桥中敷设防水层和排出积水7.空腹式拱上建筑的特点是什么答:空腹式拱上建筑的最大特点是除了具有实腹拱上建筑相同构造外,还具有腹孔和腹孔墩,减轻了拱桥恒重,同时增加了美观性8.拱上腹孔的布置原则是什么答:①应对称布置在靠拱脚侧的一定区段内②一般为奇数孔③腹孔构造宜统一,以便与施工和有利于腹孔墩的受力④腹拱高度应布置在主拱圈允许的高度内⑤应尽量减轻贡上建筑恒重,不使腹孔墩过分集中或者过分分散9.伸缩缝与变形缝的作用是什么答:①符合受力图式②避免不规则开裂10.排除拱桥腹内积水有哪两个重要性答:①避免含水量的增大,确保路面强度②防止雨水渗到主要结构内,使其发生冻胀破坏11.拱桥中铰按性质可分为哪两种类型答:分为①永久性铰②临时性铰12.拱桥的主要设计标高有哪四个答:①桥面标高(主要有三个:桥梁起点、终点及跨中点的桥面标高)②拱顶底面标高③起拱线标高④基底标高13.为什么说拱桥的主拱的矢跨比是拱轴设计中的主要参数之一答:①拱桥的水平推力与垂直反力之比值,随矢跨比的减小而增大②当矢跨比减小时,拱的推力增大,反之则水平推力减小③无铰拱随矢跨比减小其弹性压缩、温度变化、混凝土收缩及墩台位移产生的附加内力越大④拱的矢跨比过大使拱脚段施工困难⑤矢跨比对拱桥的外形及周围景观的协调产生影响14.不等跨拱桥的主要受力特点是什么在处理不等跨分孔时应注意控制的实质性问题是什么如何作答:不等跨拱桥的主要受力特点是:恒载产生的相邻跨的水平推力不等处理不等跨分孔时应注意控制的实质性问题是:尽量减小因恒载引起的不平衡推力对桥墩基底的偏心作用处理不等跨分孔的方法:采用不同的矢跨比;采取不同的起拱线标高;15.什么是拱轴线什么是合理拱轴线拱轴线的种类有哪些各对应哪种荷载模式答:拱轴线是拱圈横截面形心点的连线将恒载作用下的压力线作为主拱圈的设计拱轴线则称为合理拱轴线圆弧拱轴线:等静水压力;抛物线拱轴线:均布荷载; 悬链线:与竖坐标成比例的荷载。
拱桥一、填空题1、按照拱上建筑的型式可以将拱桥分为:实腹式和空腹式。
2、按照桥面的位置可分为:上承式、中承式、下承式。
3、按照拱圈截面形式可分为:板拱、肋拱、箱形拱、双曲拱等。
4、确定拱桥设计高程有四个,分别为:跨中结构的底面高程、起拱线的高程、基底高程和桥面高程。
5、拱桥常用的拱轴线形有悬链线、抛物线、圆弧线。
6、拱桥分类方法很多,按其结构静力图示可分为静定拱、超静定拱。
7、拱桥的矢跨比是指计算矢高与计算跨度之比。
当矢跨比增大时,拱的推力减小。
8、梁桥以受弯矩与剪力为主,拱桥主拱圈以受轴向压力为主。
9、拱上填料的作用是扩大车辆荷载分布面积的作用,减少车辆荷载的冲击作用。
10、无铰拱桥的受力状态与三铰拱桥的受力状态相比,它的主要优点内力分布均匀,整体刚度大11、当跨径、荷载和拱上建筑等情况相同时,f/L=1/3的拱桥和f/L=1/8的拱桥相比,前者的水平推力比后者_小_________。
12、混凝土砼拱桥极限跨度在__500__米左右,经济跨度___100-300_______米;钢拱桥在1200__米左右,经济跨度___300-500_______。
13、万州长江大桥采用的缆索吊装和悬臂扣挂施工方法。
14、组合体系拱桥的最重要特点是桥面结构,主拱结构形成整体共同承受荷载。
15、双曲拱桥主拱圈通常由拱肋、拱波、拱板、横向联系几部分组成。
16、迄今最大跨径的钢管混凝土拱桥是巫山长江大桥,最大跨径的石拱桥是是山西晋城丹河大桥,最大跨径的钢筋砼拱桥是万县长江大桥,最大跨径的钢拱桥是上海卢浦大桥。
17、当拱圈宽跨比B/L<1/20时,应验算拱圈的横向稳定性。
18、双曲拱桥的建设策略是将主拱圈以“化整为零”的方法按先后顺序进行施工,再以“集零为整”的方式组合成承重的整体结构。
因主拱圈分期形成,呈现组合结构的受力特征,整体性较弱,在地震荷载作用下容易破坏。
19、空腹式拱桥拱上建筑的腹拱墩有排架式和横墙式两种。