当前位置：文档之家 › 第二讲 圆的一般方程

第二讲 圆的一般方程

  • 格式：doc
  • 大小：257.30 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

4.1.2圆的一般方程

4.1.2圆的一般方程

圆的方程
标准方程: ( x a ) ( y b) r
2 2 2
2 2
展开
x y 2ax 2by (a b r ) 0 圆心: (a , b) 半径: r ( r 0)
2 2 2
一般方程: 2 2 2 2 x y Dx Ey F 0 ( D E 4F 0)
（a）2+（b）2=r2 a=4 （1-a）2+（1-b）2=r2 解得 b=-3 （4-a）2+（2-b）2=r2 r=5
所求圆的方程为：
即（x-4）2+（y+3）2=25
例1： 求过三点O(0，0)，M1 (1，1) ，M2（4，2） 的方程，并求出这个圆的半径和圆心坐标. 方法二： 几何方法
分别说出下列圆的圆心与半径 (1) 圆 (x－2)2+ (y+4)2=2 圆心 (2, －4) ，半径 2 . (2) 圆 (x+1)2+ (y+2)2=m2 （m≠0） 圆心 (－1, －2) ，半径|m|
求圆的方程
几何方法
求圆心坐标 （两条直线的交点） （常用弦的中垂线）
待定系数法
( x a ) 2 ( y b) 2 r 2
的曲线是圆呢？
思考
(1) x y 2 x 4 y 1 0
2 2
配方得 ( x 1) ( y 2) 4
2 2
以（1，-2）为圆心，以2为半径的圆
(2) x y 2 x 4 y 6 0 配方得 ( x 1)2 ( y 2)2 1
2 2
不是圆
x y Dx Ey F 0

圆的标准、一般方程 2

圆的标准、一般方程 2
因为AC⊥BC，且A、B、C三点不共线，所以x≠3且x≠-1． …………………………………………………………………4分
又k AC y y ，且k BC ， 6分 x 1 x 3 y y 且k AC k BC 1 8分 ， x 1 x 3
则 x 0 x a ，y0 y (1)，
2 2
2 因为|AD|=m， 所以（x a） y2 m2 (2). …………………8分 0 0
将（1）式代入（2）式整理得 （x+3a）2+y2=4m2. …………………………………………10分 因为C不能在x轴上,所以y≠0②， …………………………11分 故所求轨迹方程为（x+3a）2+y2=4m2(y≠0). ……………12分
OC AC AO 52 42 3． 6分
2 2
所以圆心C的坐标为（3，0）或(－3，0)②,
所以所求圆的方程为(x-3)2+y2=25，
或(x+3)2+y2=25. ……………………………………………12分
典例2已知圆心为C的圆经过点A(1, 1)和B(2, －
对称的圆的标准方程.
【变式训练】若圆(x+1)2+(y-5)2=4与圆(x-3)2+(y+3)2=4关于
直线x+y-a=0对称,求实数a的值.
【解析】由题意知,两圆的圆心关于直线x+y-a=0对称，即两圆
心的中点在该直线上. 因为两圆的圆心分别为（-1，5），（3，-3）,其中点坐标为 （1，1）,所以有1+1-a=0,得a=2.
r | CM | (2 1) 2 (3 1) 2 5
所求圆的方程为(x-2)2+(y+3)2=25.

学圆与方程圆的一般方程

学圆与方程圆的一般方程

一般方程的推导方法
基于圆的定义
根据圆的标准方程和圆的定义，我们可以推导出一般 方程。首先，将标准方程中的r^2用(x^2 + y^2)替换 ，得到$(x - a)^{2} + (y - b)^{2} = x^2 + y^2$。整 理后得到一般方程为$x^{2} + y^{2} - 2ax - 2by + a^2 + b^2 - r^2 = 0$。
这个方程实际上是圆的一般形式，它可以表示所有形状的圆 ，包括实心圆和空心圆。
圆的一般方程的特点
圆的一般方程具有普遍性，它可以描述各种形状和大小的 圆。
与标准方程(x-a)²+(y-b)²=r²相比，一般方程提供了更为 灵活的表述方式，可以描述那些不以原点为中心的圆。
圆的一般方程与标准方程的异同
相同点
03
圆的一般方程与图形关系
圆的一般方程与图形形状
圆的一般方程可以描述圆的形状特征，通过方程中的系数可 以调整圆的大小、圆心位置以及半径长度。
通过解方程，可以得到圆的圆心坐标和半径，从而确定圆的 形状。
圆的一般方程与图形位置
圆的一般方程可以描述圆在空间中的位置关系，通过解方 程可以得到圆心坐标和半径，确定圆的位置。
复数中的圆函数
在复数平面上，与圆有关的函数被称 为圆函数。这些函数描述了圆的某些 性质，如圆的周长、面积和其他几何 性质的变化规律。通过对圆函数的导 数和积分运算，我们可以研究圆的性 质和变化规律。
THANK YOU.
判断点与圆的位置关系
利用一般方程，可以判断一个点是否在圆内、圆上或圆外。通过将点的坐标代入一般方程 ，求解方程的根，根据根的判别式来判断点与圆的位置关系。
圆的性质研究

第二课时 圆的一般方程

第二课时 圆的一般方程
索引
(2)并判断点M(1，2)，N(4，5)，Q(2，3)与圆的位置关系. 解 ∵M(1，2)， ∴12＋22＋4×1－4×2－2＝－1<0， ∴点M(1，2)在圆内. ∵N(4，5)， ∴42＋52＋4×4－4×5－2＝35>0， ∴点N(4，5)在圆外. ∵Q(2，3)， ∴22＋32＋4×2－4×3－2＝7>0， ∴点Q(2，3)在圆外.
索引
思维升华
方程x2＋y2＋Dx＋Ey＋F＝0表示圆的两种判断方法 (1)配方法.对形如x2＋y2＋Dx＋Ey＋F＝0的二元二次方程可以通过配方变形成 “标准”形式后，观察是否表示圆. (2)运用圆的一般方程的判断方法求解，即通过判断D2＋E2－4F是否为正，确 定它是否表示圆. 特别提醒 在利用D2＋E2－4F>0来判断二元二次方程是否表示圆时，务必注 意x2及y2的系数为1.
索引
由圆的定义，知动点C的轨迹是以D(1，0)为圆心，以2为半径长的圆(因为A，B， C三点不共线，所以应除去与x轴的交点). 设C(x，y)，则直角顶点C的轨迹方程为(x－1)2＋y2＝4(x≠3，且x≠－1).
索引
思维升华
求轨迹方程的三种常用方法 (1)直接法：根据题目条件，建立坐标系，设出动点坐标，找出动点满足的条 件，然后化简、证明. (2)定义法：当动点的运动轨迹符合圆的定义时，可利用定义写出动点的轨迹 方程. (3)代入法：若动点P(x，y)依赖于某圆上的一个动点Q(x1，y1)而运动，把x1，y1 用x，y表示，再将Q点的坐标代入到已知圆的方程中，得点P的轨迹方程. 特别提醒 在解决此类问题时易出现不符合条件的点仍在所求的轨迹上，故 应排除不合适的点.
索引
法四 由于 kAB＝－ －11－ －31＝2，kAC＝－5－ 3－31＝－21， ∴kAB·kAC＝－1， ∴AB⊥AC， ∴△ABC是以∠A为直角的直角三角形， ∴外接圆圆心为BC的中点，即(－2，2)， 半径 r＝21BC＝ 10， ∴圆的方程为(x＋2)2＋(y－2)2＝10， 即圆的一般方程为x2＋y2＋4x－4y－2＝0.

2.4.2圆的一般方程 课件(共18张PPT)

2.4.2圆的一般方程 课件(共18张PPT)
解:设M的坐标为(x, y) , 点A坐标是(x0，y0).
由于点B的坐标是(4 , 3) , 且M是线段AB
x0 4
y0 3
的中点, 所以
x
y
2
2
x0 2 x 4
因为点A在圆上运动 , 所以A的
于是有:
y0 2 y 3 坐标满足圆的方程 , 即:
( x0 1) y0 4 (2 x 4 1) (2 y 3) 4
(3)圆心(a , - 3a ), 半径 | a | .
练习：判断下列方程分别表示什么图形?
2
2
(1) x + y = 0
2
2
(2) x + y - 2 x + 4 y - 6 = 0
2
2
2
(3) x + y + 2ax - b = 0
(1)原点(0,0)
(2)表示圆 , 坐标为(1,-2) , 半径是 .
课 堂 练 习
1.写出下列各圆的圆心坐标和半径:
(1)
x y 6x 0
(2)
x y 2by 0
2
2
2
2
(3) x 2 y 2 2ax 2 3ay 3a 2 0
解: (1)圆心坐标(3, 0) ,半径为3.
(2)圆心坐标(0, b) , 半径为 |b| .
y
一点，也就是点M属于集合
| OM | 1 M
{M |
}
| AM | 2
A x
由两点间的距离公式，得
C O
x y
2
2
1
化简得 x2+y2+2x3＝0

圆的一般方程的第二课时----王婷

圆的一般方程的第二课时----王婷

整理得轨迹方程
整理得轨迹方程
的轨迹方程.
y
。B
A
P
•
•c
-6
•
。
o
3x
小结：
1.求轨迹方程思想：求出动点坐标x，y所满足的关系 2.求轨迹方程方法：
相关点法
直接法
设未知点为(x,y)， 已知点为(x0,y0)
设动点的坐标为(x,y)
根据已知点、未知点的 关系得x0=f(x),y0=g(y)
找到几何关系
代入已知点方程
用方程表示几何关系
22
4
• 用待定系数法求圆的一般方程
求轨迹方程问题：
y
M(x,y)是圆C上任意一点
Байду номын сангаас
C
(x a)2 (x b)2 r2
o
x
M(x,y)
点M的坐标 (x,y)满足的关系式
求轨迹方程即为求出曲线上一动点坐标(x，y)所满足的关 系.
求轨迹方程：
例1、已知点A、B的坐标分别是（-1，0）， （1，0），直线AM与直线BM垂直相交于点 M,且它们的斜率都存在,求动点M的轨迹方程。
第二课时《4.1.2 圆的一般方程》
复习回顾
• 理解和掌握圆的一般方程
x2+y2＋Dx+Ey+F=0 (D2 E2 4F 0)
• 根据圆的一般方程找出圆心和半径长
（x D ）2 ( y E )2 D2 E2 4F
2
2
4
圆心坐标（- D ,- E ）,半径r= D2 E2 4F
直接法
对点练习1：
已知点M与两个定点O(0,0),A(3,0)的距离的比 为 1，求动点M的轨迹方程。

圆的一般方程(2)全面版

圆的一般方程(2)全面版
图解
四、小结： 1、圆的一般方程的定义和特点
2、直线与圆的位置关系
五、作业： 1、巩固练习
例5.已知圆与直线xy 3 和两坐标轴都相切，圆 求 的标准方程.
只要我们坚持了，就没有克服不了的困难。或许，为了将来，为了自己的发展，我们会把一件事情想得非常透彻，对自己越来越严，要求越来越高，对任何机会都不曾错过，其 目的也只不过是不让自己随时陷入逆境与失去那种面对困难不曾屈服的精神。但有时，“千里之行，始于足下。”我们更需要用时间持久的用心去做一件事情，让自己其中那小 小的浅浅的进步，来击破打破突破自己那本以为可以高枕无忧十分舒适的区域，强迫逼迫自己一刻不停的马不停蹄的一直向前走，向前看，向前进。所有的未来，都是靠脚步去 丈量。没有走，怎么知道，不可能；没有去努力，又怎么知道不能实现？幸福都是奋斗出来的。那不如，生活中、工作中，就让这“幸福都是奋斗出来的”完完全全彻彻底底的 渗入我们的心灵，着心、心平气和的去体验、去察觉这一种灵魂深处的安详，侧耳聆听这仅属于我们自己生命最原始最动人的节奏。但，这种聆听，它绝不是仅限于、执着于 “我”，而是观察一种生命状态能够扩展和超脱到什么程度，也就是那“幸福都是奋斗出来的”深处又会是如何？生命不止，奋斗不息！又或者，对于很多优秀的人来说，我们 奋斗了一辈子，拼搏了一辈子，也只是人家的起点。可是，这微不足道的进步，对于我们来说，却是幸福的，也是知足的，因为我们清清楚楚的知道自己需要的是什么，隐隐约 约的感觉到自己的人生正把握在自己手中，并且这一切还是通过我们自己勤勤恳恳努力，去积极争取的!“宝剑锋从磨砺出，梅花香自苦寒来。”当我们坦然接受这人生的终局， 或许，这无所皈依的心灵就有了归宿，这生命中觅寻处那真正的幸福、真正的清香也就从此真正的灿烂了我们的人生。一生有多少属于我们的时光？陌上的花，落了又开了，开 了又落了。无数个岁月就这样在悄无声息的时光里静静的流逝。童年的玩伴，曾经的天真，只能在梦里回味，每回梦醒时分，总是多了很多伤感。不知不觉中，走过了青春年少， 走过了人世间风风雨雨。爱过了，恨过了，哭过了，笑过了，才渐渐明白，酸甜苦辣咸才是人生的真味！生老病死是自然规律。所以，面对生活中经历的一切顺境和逆境都学会 了坦然承受，面对突然而至的灾难多了一份从容和冷静。这世上没有什么不能承受的，只要你有足够的坚强！这世上没有什么不能放下的，只要你有足够的胸襟！ 一生有多少 属于我们的时光？当你为今天的落日而感伤流泪的时候，你也将错过了明日的旭日东升；当你为过去的遗憾郁郁寡欢，患得患失的时候，你也将忽略了沿途美丽的风景，淡漠了 对未来美好生活的憧憬。没有十全十美的生活，没有一帆风顺的旅途。波平浪静的人生太乏味，抑郁忧伤的人生少欢乐，风雨过后的彩虹最绚丽，历经磨砺的生命才丰盈而深刻。 见过了各样的人生：有的轻浮，有的踏实；有的喧哗，有的落寞；有的激扬，有的低回。肉体凡胎的我们之所以苦恼或喜悦，大都是缘于生活里的际遇沉浮，走不出个人心里的 藩篱。也许我们能挺得过物质生活的匮乏，却不能抵挡住内心的种种纠结。其实幸福和欢乐大多时候是对人对事对生活的一种态度，一花一世界，一树一菩提，就是一粒小小的 沙子，也有自己精彩的乾坤。如果想到我们终有一天会灰飞烟灭，一切象风一样无影亦无踪，还去争个什么？还去抱怨什么？还要烦恼什么？未曾生我谁是我？生我之时我是谁？ 长大成人方是我，合眼朦胧又是谁？一生真的没有多少时光，何必要和生活过不去，和自己过不去呢。你在与不在，太阳每天都会照常升起；你愁与不愁，生活都将要继续。时

高中数学同步教学课件 圆的一般方程 (2)

高中数学同步教学课件 圆的一般方程 (2)

∴r2＝a2＋4
2
3
2
，代入⑤并将两端平方得 a2－6a＋5＝0，解得 a1＝1，a2＝5，
∴r1＝ 13 ，r2＝ 37 .
故所求圆的方程为(x－1)2＋y2＝13 或(x－5)2＋(y－4)2＝37.
通性通法
求圆的一般方程的两种常见方法 (1)直接法：即根据条件直接求出圆心坐标和半径，得到圆 的方程．这种方法一般用在圆心比较明确，易于确定圆心 坐标的题目； (2)待定系数法：先设圆的方程(标准方程或一般方程)，根 据条件列出三个关于系数的独立方程，求出待定系数，即 可求出圆的方程．
当 a＝－1 时，方程为 x2＋y2＋4x＋8y－5＝0，配方得(x＋2)2＋(y＋4)2＝25，
则圆心坐标为(－2，－4)，半径是 5. 答案：(－2，－4) 5
2．已知曲线 C：x2＋y2－4mx＋2my＋20m－20＝0. 求证：当 m≠2 时，曲线 C 是一个圆，且圆心在一条直线上． 证明：∵D＝－4m，E＝2m，F＝20m－20， ∴D2＋E2－4F＝16m2＋4m2－80m＋80＝20(m－2)2. 又 m≠2，∴(m－2)2＞0，∴D2＋E2－4F＞0， 即曲线 C 是一个圆． 设圆心坐标为(x，y)，则由yx＝＝－2mm， 消去 m，得 x＋2y＝0， 即圆心在直线 x＋2y＝0 上．
(x＋m)2＋(y－1)2＝1－5m，
故圆心坐标为(－m，1)，半径 r＝ 1－5m .
通性通法
方程 x2＋y2＋Dx＋Ey＋F＝0 表示圆的两种判断方法 (1)配方法：对形如 x2＋y2＋Dx＋Ey＋F＝0 的二元二次方程可以通过 配方变形成“标准”形式后，观察是否表示圆； (2)运用圆的一般方程的判断方法求解，即通过判断 D2＋E2－4F 是否 为正，确定它是否表示圆． [提醒] 在利用 D2＋E2－4F>0 来判断二元二次方程是否表示圆时， 务必注意 x2 及 y2 的系数．

2.2.2 圆的一般方程 课件(北师大必修2)

2.2.2 圆的一般方程 课件(北师大必修2)

① ② ③
令y＝0，得x2＋Dx＋F＝0.
设x1、x2是方程③的两根，则x1＋x2＝－D，x1x2＝F
由|x1－x2|＝6，得(x1＋x2)2－4x1x2＝36，
有D2－4F＝36.
④
由①②④解得D＝－2，E＝－4，F＝－8，或D＝－6，
E＝－8，F＝0，
所以所求圆的方程为x2＋y2－2x－4y－8＝0 或x2＋y2－6x－8y＝0.
方程 x2＋y2＋ Dx＋Ey ＋F＝0
条件
图形
D2＋E2－4F>0
D E (－ 2 ，－ 2 ) 表示以 为圆心， 1 D2＋E2－4F 以2 为半径的圆
1．圆的一般方程与标准方程可以互化
形式
转化
标准方程
一般方程
对应关系
D＝－，E＝－2b，F＝a2＋b2－r2
形式 圆心 半径
标准方程 (a，b) r
配方，得(x＋3)2＋(y－1)2＝25.
所以其外接圆的圆心是(－3,1)，即外心坐标为(－3,1)．
1 3 法二：∵AB的中点坐标为(2，2)，斜率为 －2－5 kAB＝ 1 ＝－7. 3 1 1 ∴AB边的垂直平分线的方程为y－2＝7(x－2)， 即x－7y＋10＝0. ∵BC的中点为(－1，－3)，斜率为
[例2] 坐标．
已知△ABC的三个顶点坐标分别是A(0,5)，B(1，
－2)，C(－3，－4)，求它的外接圆的方程，并求其外心
[思路点拨] 先设其外接圆的方程是x2＋y2＋Dx＋Ey
＋F＝0，然后把三个点的坐标代入方程，得关于D，E，
F的方程组，解方程组得D，E，F的值代入原方程即可；
也可用几何法求出AB和BC的垂直平分线，进而求出圆心 坐标和半径，再利用圆的标准方程直接写出．

2.2 圆的一般方程

2.2 圆的一般方程
若已知条件涉及圆心和半径, 我们一般采用圆的标准方程较简单.
练习：求过三点A(0,0), B(6,0), C(0,8)的圆的方程.
设圆的方程为 x2 + y2 + Dx + Ey + F = 0
把点A，B，C的坐标代入得方程组
F =0
62 + 6D + F = 0
82 + 8E + F = 0
D = -6,
（1）a=-D/2，b=-E/2，r= 1 D2 + E 2 - 4F 2
（2）标准方程易于看出圆心与半径 一般方程突出形式上的特点：
x2与y2系数相同并且不等于0；
没有xy这样的二次项
练习1： 判断下列方程能否表示圆的方程, 若能写出圆心与半径
（1）x2+y2-2x+4y-4=0 是 圆心（1，-2）半径3 （2）2x2+2y2-12x+4y=0 是 圆心（3，-1）半径 10 （3）x2+2y2-6x+4y-1=0 不是 （4）x2+y2-12x+6y+50=0 不是 （5）x2+y2-3xy+5x+2y=0 不是
知识回顾：
(1) 圆的 标准方程: (x-a)2+(y-b)2=r2 特征：直接看出圆心与半径
指出下面圆的圆心和半径：
(x-1)2+(y+2)2=2 (x+2)2+(y-2)2=5 (x+a)2+(y-2)2=a2 (a≠0)
把圆的 标准方程（x-a)2+(y-b)2=r2 展开，得
x2 + y2 - 2ax - 2by + a2 + b2 - r2 = 0

解析几何：圆的方程

解析几何：圆的方程

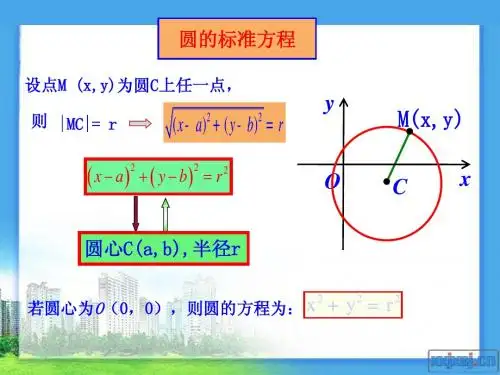
解析几何：圆的方程在解析几何中，我们经常遇到圆形。

圆是一个在平面上具有特定性质的图形，它由与圆心等距的点组成。

在数学中，我们可以通过方程来描述圆。

圆的一般方程形式为：(x - a)² + (y - b)² = r²其中，(a, b)表示圆心的坐标，r表示圆的半径。

根据圆的一般方程，我们可以推导出其他形式的圆的方程，包括标准方程、截距方程以及圆的参数方程。

一、标准方程标准方程是描述圆形最简洁的形式，形式如下：x² + y² + Dx + Ey + F = 0其中，D、E、F为实数，且D² + E² > 4F。

该方程描述的圆心坐标为(-D/2, -E/2)，半径为√(D² + E² - 4F)。

二、截距方程截距方程是描述圆形的另一种形式，形式如下：(x/a)² + (y/b)² = 1其中，a、b分别表示圆心到横轴和纵轴的截距，描述的是一个以坐标原点为圆心的圆。

三、参数方程参数方程是通过参数化描述圆形的方程，形式如下：x = a + r*cosθy = b + r*sinθ其中，(a, b)表示圆心坐标，r为半径，θ为参数角度。

四、圆的性质除了方程形式的描述，圆还具有一系列独特的性质。

1. 圆上任意两点与圆心的距离相等；2. 圆的直径是圆上任意两点之间的最大距离，直径长度为半径的两倍；3. 圆的内切圆与外接圆分别与圆相切于一个点；4. 圆的周长为2πr，面积为πr²。

五、实例分析以标准方程为例，假设有一个圆的方程为x² + y² - 6x - 4y + 9 = 0，我们可以通过比较方程与一般方程的系数来找出圆的相关信息。

将方程与一般方程形式对应，我们可以得到D = -6，E = -4，F = 9。

进一步计算得到圆心坐标为(3, 2)，半径为√(D² + E² - 4F) = √(36 + 16 - 36) = √16 = 4。

【数学】2.2.2 圆的一般方程 课件(北师大必修2)

【数学】2.2.2 圆的一般方程 课件(北师大必修2)

2 2
2
2
（1）当
D E 4F 0
2 2
时，表示圆，
D E 4F
2 2
E D 圆心 - , 2 2
r
2
（2）当 （3）当
D E 4F 0
2 2
时，表示点
E D - , 2 2
D E 4F 0
2 2
时，不表示任何图形
8
2
8E F 0
D 6, E 8， F 0.
所求圆的方程为：
2 y2 6x 8y 0 x
若已知三点求圆的方程,我们常采用圆的 一般方程用待定系数法求解.
小结
x y Dx Ey F 0
2 2
D E D E 4F x y 2 2 4
设方程为
2 2 2
求圆心坐标 （两条直线的交点） （常用弦的中垂线）
( x a ) ( y b) r
2 2
(或x y Dx Ey F 0)
求 半径 （圆心到圆上一点的距离）
列关于a，b，r（或D，E，F） 的方程组
写出圆的标准方程
解出a，b，r（或D，E，F）， 写出标准方程（或一般方程）
.
.
（-1，0）
O
.
A(3,0)
x
[简单的思考与应用] (1)已知圆 x 2 y 2 Dx Ey F 0 的圆心坐标为 (-2,3),半径为4,则D,E,F分别等于 (D)
( A ) 4 , 6 ,3
( B ) 4 , 6 ,3 ( C ) 4 , 6 , 3
( D ) 4, 6, 3

高中数学必修二圆的一般式方程

高中数学必修二圆的一般式方程
(x+ 4
3
)2+(y+
4
3
)2=
50
9
2、从圆x2+y2=9外一点P(3,2)向该圆引切线，求切线方程。 x=3和5x+12y-39=0
圆心：两条弦的中垂线的交点
半径：圆心到圆上一点
方法二：待定系数法
解：设所求圆的方程为：
( x a) ( y b) r
2 2
2
因为A(5,1),B (7,-3),C(2,8)都在圆上
(5 a ) 2 (1 b) 2 r 2 a2 2 2 2 (7 a ) (3 b) r b 3 (2 a) 2 (8 b) 2 r 2 r 5
解
设 P( x1 , y1 ) , Q( x2 , y2 )
P
O Q
x2 y 2 m 0 x y 1 0
1 m x1 x2 2
2x 2x (1 m) 0
2
1 m 同理y1 y2 2
OP OQ
x1 x2 y1 y2 0 (2)
1、求圆心C在直线 x+2y+4=0 上，且过两定点A(-1 , 1)、 B(1,-1)的圆的方程。
2
2
( D E 4 F 0)
2
思 方程Ax Bxy Cy Dx Ey F 0 考 什么时候可以表示圆? 2 2 A C 0, B 0, D E 4 AF 0.
2
[观察]：圆的标准方程与圆的一般 方程在形式上的异同点.
圆的标准方程
2 2 ( x a ) ( y b) r 2
(2) x y 2ax y a 0表示圆, 1 a R, a 则a的取值范围是 _____ 2

002圆的一般方程

002圆的一般方程

圆的一般方程的定义 形如 x 2 y 2 Dx Ey F 0 ( D 2 E 2 4F 0 )的方程为圆的一 般方程。 其中：圆心为 ( D , E ) 、半径 r = 1
2 2 2 D 2 E 2 4F
；
一般方程的特点： （1）x2 和 y2 的系数相同，都不为 0； （2）没有形如 xy 的二次项； （3） D 2 E 2 4F 0 ；
例 2、求过三点 O(0，0)，M1(1，1)，M2(4，2)的圆的方程， 并求出圆心坐标和半径。
练习：平面直角坐标系中有 A(0,1) ，B(2,1) ，C (3, 4) ，D(1, 2) 四点， 这四点能否在同一个圆上？为什么？
知识小结 （1）圆的一般方程及其特点； （2）用配方法化圆的一般方程为圆的标准方程，求圆心坐 标和半径； （3）用待定系数法求圆的方程； （4）大家考虑：D2+E2－4F 有点像什么？ 像判别式，它正是方程 x2+y2+Dx+Ey+F=0 是否是圆的 方程的判别式．
知识探究二
点与圆的位置关系
已知点 M(x0，y0)和圆的方程 x2＋y2＋Dx＋Ey＋F＝0(D2 ＋E2－4F＞0)，则其位置关系如下表：
例 1、下列方程各表示什么图形： （1）x2+y2-2x+4y-4=0； （2） x2 y 2 2by 0
练习：判断下列方程是否表示圆的方程？如果是，请求出圆 的圆心及半径. （1）x2+y2－2x+4y－4=0； （2）x2+2y2－6x+4y－1=0； （3）4x2 + 4y2 – 4x + 12y + 11 = 0；
圆的一般方程

圆的一般方程课件

圆的一般方程课件

2
2
6
x
-
a
+
y
-
b
< r2
1
1
8
2、点 M
x1,y1
在圆A外的充要条件：
2
2
10
x - a y - b
1
+
1
> r2
3、点 M
x1,y1
在圆A上2 的充要条2 件：
x - a y - b
1
+
1
= r2
r A（a,b）
M(x1,y1)
5
10
新课导入
思考一下
解的情况
无穷多解
只有一个解
无解
表示图形
方程是以
-
D 2
,-
E 2
为圆心，1 D 2 + E 2 - 4F
2
为半径的圆；
点
-
D 2
,-
E 2
不能表示任何 图形。
例题讲解
例1：已知P（-2,3）在圆C：x2 + y2 - 2x+ 2y+ m = 0 则实数m= -23 ,圆的半径r= 5 。
2
圆的方程，即
x + 1
0
+y 2=4 0 2
2
②
将① 代入②，得
2x
-
4
+
1
+
2y
-
3
=4
2
2
x -
3
2
+
y
-
3
2
=1
这是点M的轨迹方程，它表示以
3 2
,32
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二讲 圆的一般方程
一、圆的一般方程的定义
当2
2
40D E F +->时，方程220x y Dx Ey F ++++=表示一个圆，这个方程叫做圆的一般方程。

【要点】
1.220x y Dx Ey F ++++=表示的曲线不一定是圆，2
2
40D E F +-=时表示的是一个点
,22D E ⎛⎫-- ⎪⎝⎭
；22
40D E F +-<时方程没有实数解，不代表任何图形；只有当2240D E F +->时，方程才表示圆。

2.2
2
,x y 的系数相同且不等于0；方程不含xy 项。

3. 圆心坐标为,22D E ⎛⎫
-- ⎪⎝⎭
，半径长为2242D E F +-
4.圆的一般方程−−−→←−−−展开配方
圆的标准方程
考点一 由圆的一般方程求圆的圆心和半径
由圆的一般方程求圆心坐标和半径长有两种方法： 1. 通过配方法化为标准方程； 2. 直接用公式法求。

例1 圆2
2
420x y x y +-+=的圆心坐标和半径长分别是（ ）
A. ()2,1,5-
B.()2,1,5-
C.()2,1,5-
D.()2,1,5-
考点二 判断形如220Ax Bxy Cy Dx Ey F +++++=的方程是否表示圆
形如22
0Ax Bxy Cy Dx Ey F +++++=的方程表示圆必须具备的条件 1. 0A C =≠； 2. 0B =；
3. 2
2
40D E AF +->
以上三个条件需同时满足时，二元二次方程才表示圆。

例2 下列方程能否表示圆？若能，求出圆心和半径；若不能，说明理由。

（1）222750x y x +-+=； （2）22580x xy y x y -+-++=； （3）222240x y x +-=； （4）22210x y ay ++-=； （5）2220x y ax ++=.
考点三 由确定圆的条件求参数范围
二元二次方程220x y Dx Ey F ++++=表示圆的条件是2
2
40D E F +->，求参数取值范围问题可以转化为解不等式2
2
40D E F +->。

若已知二元二次方程
()2200Ax Cy Dx Ey F A C ++++==≠，则可先将22,x y 的项的系数化为1.
例 3 若方程222
22210x y a x a y a a +++++-=表示圆，则a 的取值范围是
______________.
例4 m 取什么值时，关于,x y 的方程()()
2222
21220m m x m m y m +-+-+++=的图像
表示一个圆？
考点四 由圆的一般方程判断点与圆的位置关系
已知点()00,M x y 和圆的方程22220(40)x y Dx Ey F D E F ++++=+->，其位置关系如下所示：
位置关系 代数关系
点M 在圆外 2200000x y Dx Ey F ++++> 点M 在圆上 2200000x y Dx Ey F ++++= 点M 在圆内
2200000x y Dx Ey F ++++<
例 5 若点()1,1a a +-在圆22240x y ay +--=的内部（不包括边界），则a 的取值范围是（ ）
A.1a >
B.01a <<
C.1
5
a < D.1a <
考点五 判断四点共圆
先求过其中三点的圆的方程，然后把第四个点代入，若满足方程，则四点共圆；若不满足方程，则四点不共圆。

例6 已知A （6,0），B （-2,0），C （-3,3），D （6,3），判断A ，B ，C ，D 四点是否共圆.
考点六 用待定系数法求圆的一般方程（重点）
步骤：
1. 根据题意，设出一般方程220x y Dx Ey F ++++=；
2. 根据条件列出关于D ，E ，F 的方程组；
3. 解出D ，E ，F ，代入圆的一般方程中。

两种方程的选择方法：
1. 如果已知条件和圆心坐标或半径都无直接关系，一般采用圆的一般方程，再利用待定系数法求出常数D ，E ，F.
2. 如果由已知条件容易求得圆心坐标、半径长或需利用圆心的坐标或半径长来列方程的问题，一般采用圆的标准方程。

例7 求过原点及点A （1,1）且在x 轴上截得线段长为3的圆的方程。

二、轨迹和轨迹方程
1. 轨迹和轨迹方程的定义：平面上一动点M ，按照一定规则运动，形成的曲线叫做动点M 的轨迹，在坐标系中，这个轨迹可用一个方程表示，这个方程就是轨迹方程。

2. 求轨迹方程的步骤：
（1）建系：建立适当的坐标系；
（2）设点：设出轨迹（曲线）上的任一点（动点）的坐标为（,x y ）； （3）列式：根据题中的等量关系列出关于,x y 的方程；
（4）化简：把方程化成最简形式； （5）确定轨迹的范围。

一个区别：求轨迹方程，只用求得方程即可；若是求轨迹，求得方程后，还应指出方程所表示的曲线类型。

一个技巧：如果轨迹动点P （,x y ）依赖于另一动点Q （,a b ），而Q 又按某个规律运动，则可先用,x y 表示,a b ，再把,a b 代入它满足的条件便得到动点P 的轨迹方程。

简记： 由未知表示已知，再由已知表示未知。

例8 一个动点在圆221x y +=上移动时，求它与定点（3,0）的连线中点P 的轨迹方程？
常见考点：求圆心的轨迹方程
参数法：由条件得到圆心坐标，一般是含有同一个参数，再设法消去这个参数（代入消参法），得到圆心轨迹方程。

例9 已知曲线C ：2
2
4220200x y mx my m +-++-=. 求证：当2m ≠时，曲线C 是一个圆，且圆心在一条直线上.。