2014年全国中考数学分类汇编——投影与视图
- 格式:doc
- 大小:344.50 KB
- 文档页数:14

【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】中考总复习:投影与视图—知识讲解【考纲要求】1.通过实例了解平行投影和中心投影的含义及简单应用;2.会画基本几何体(直棱柱、圆柱、圆锥、球)的三视图(主视图,左视图、俯视图),能根据三视图描述基本几何体或实物的原型.【知识网络】【考点梳理】考点一、生活中的几何体1.常见的几何体的分类在丰富多彩的图形世界中,我们常见的几何体有长方体、正方体、棱柱体、棱锥体、圆柱体、圆锥体、球体、台体等.2.点、线、面、体的关系(1)点动成线,线动成面,面动成体;(2)面面相交成线,线线相交成点.要点诠释:体体相交可成点,不一定成线.3.基本几何体的展开图(1)正方体的展开图是六个正方形;(2)棱柱的展开图是两个多边形和一个长方形;(3)圆锥的展开图是一个圆和一个扇形;(4)圆柱的展开图是两个圆和一个长方形.考点二、投影1.投影用光线照射物体,在某个平面上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在平面叫做投影面.2.平行投影和中心投影由平行光线形成的投影是平行投影;由同一点(点光源)发出的光线形成的投影叫做中心投影.3.正投影投影线垂直投影面产生的投影叫做正投影.要点诠释:正投影是平行投影的一种.考点三、物体的三视图1.物体的视图当我们从某一角度观察一个物体时,所看到的图象叫做物体的视图.我们用三个互相垂直的平面作为投影面,其中正对我们的叫做正面,正面下方的叫做水平面,右边的叫做侧面.一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到的由左向右观察物体的视图,叫做左视图.要点诠释:三视图就是我们从三个方向看物体所得到的3个图象.2.画三视图的要求(1)位置的规定:主视图下方是俯视图,主视图右边是左视图.(2)长度的规定:长对正,高平齐,宽相等.要点诠释:主视图反映物体的长和高,俯视图反映物体的长和宽,左视图反映物体的高和宽.【典型例题】类型一、三视图及展开图1.用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的主视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为( )A.22 B.19 C.16 D.13【思路点拨】视图、俯视图是分别从物体正面、上面看,所得到的图形.【答案】D;【解析】综合主视图和俯视图,这个几何体的底层最少有3+3+1=7个小正方体,第二层最少有3个,第三层最少有2个,第四层最少有1个,因此搭成这样的一个几何体至少需要小正方体木块的个数为:7+3+2+1=13个.故答案为:13.【总结升华】由三视图判断组成原几何体的小正方体的个数与由相同的小正方体构成的几何体画三视图正好相反.举一反三:【变式1】(2014秋•莲湖区校级期末)用小正方体搭一个几何体,使它的主视图和俯视图如图所示,这样的几何体最少需要正方体个.【答案】7.【解析】∵俯视图中有5个正方形,∴最底层有5个正方体;∵主视图第二层有2个正方形,∴几何体第二层最少有2个正方体,∴最少有几何体5+2=7.【高清课堂:《空间与图形》专题:投影与视图例6】【变式2】下图是由几个相同的小正方体搭成的几何体从三个方向看到的图形,则搭成这个几何体的小正方体的个数是()个.A.5 B.6 C.7 D.8【答案】B.2.美术课上,老师要求同学们将如图所示的白纸只沿虚线剪开,用裁开的纸片和白纸上的阴影部份围成一个立体模型,然后放在桌面上,下面四个示意图中,只有一个符合上述要求,那么这个示意图是()A. B.C. D.【思路点拨】动手操作看得到小正方体的阴影部分的具体部位即可.【答案】B左面看正面看上面看【解析】动手操作折叠成正方体的形状放置到白纸的阴影部分上,所得正方体中的阴影部分应紧靠白纸,故选B.【总结升华】用到的知识与正方体展开图有关,考察学生空间想象能力.建议学生在平时的教学过程中应结合实际模型将展开图的若干种情况分析清楚.举一反三:【变式】如图所示的是以一个由一些相同的小正方体组成的简单几何体的主视图和俯视图.设组成这个几何体的小正方体的个数为n,请写出n的所有可能的值.【答案】n为8,9,10,11.3.下列图形中经过折叠能围成一个棱柱的是()A. B. C. D.【思路点拨】利用四棱柱及其表面展开图的特点解题.【答案】D;【解析】A、侧面少一个长方形,故不能;B、侧面多一个长方形,折叠后不能围成棱柱,故不能;C、折叠后少一个底面,不能围成棱柱;只有D能围成四棱柱.故选D.【总结升华】四棱柱的侧面展开图为四个长方形组成的大长方形.举一反三:【高清课堂:《空间与图形》专题:投影与视图课堂练习3】【变式】如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AB、BB1、BC的中点,沿EG、EF、FG将这个正方体切去一个角后,得到的几何体的俯视图是()A. B. C. D.【答案】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.从上面看易得1个正方形,但上面少了一个角,在俯视图中,右下角有一条线段.故选B.类型二、投影有关问题4.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,求塔高AB的长.【思路点拨】过点D构造矩形,把塔高的影长分解为平地上的BD,斜坡上的DE.然后根据影长的比分别求得AG,GB长,把它们相加即可.【答案与解析】【解析1】解:如图1,过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.可得矩形BDFG.由题意得:.∴DF=DE×1.6÷2=14.4(m).∴GF=BD=CD=6m.又∵.∴AG=1.6×6=9.6(m).∴AB=14.4+9.6=24(m).答:铁塔的高度为24m.图1 图2【解析2】如图2,作DG∥AE,交AB于点G,BG的影长为BD,AG 的影长为DE,由题意得:AG 1.6=DE2.∴AG=18×1.6÷2=14.4(m).又∵BG 1.6=BD1.∴B G=1.6×6=9.6(m).∴AB=14.4+9.6=24(m).答:铁塔的高度为24m.【总结升华】运用所学的解直角三角形的知识解决实际生活中的问题,要求我们要具备数学建模能力(即将实际问题转化为数学问题).类型三、投影视图综合问题5.用小立方体搭成一个几何体,使它的主视图和俯视图如图所示,搭建这样的几何体最多要小立方体.【思路点拨】从正视图和侧视图考查几何体的形状,从俯视图看出几何体的小立方块最多的数目.【答案】17.【解析】解:由主视图可知,它自下而上共有3列,第一列3块,第二列2块,第三列1块.由俯视图可知,它自左而右共有3列,第二列各3块,第三列1块,从空中俯视的块数只要最低层有一块即可.因此,综合两图可知这个几何体的形状不能确定;如图,最多时有3×5+2×1=17块小立方体.故答案为17.【总结升华】本题考查简单空间图形的三视图,考查空间想象能力,是基础题,但很容易出错.6.(2015•永春县校级自主招生)如图是某中学生公寓时的一个示意图(每栋公寓均朝正南方向,且楼高相等,相邻两栋公寓的距离也相等).已知该地区冬季正午的阳光与水平线的夹角为32°,在公寓的采光不受影响(冬季正午最底层受到阳光照射)的情况下,公寓的高为AB,相邻两公寓间的最小距离为BC.(1)若设计公寓高为20米,则相邻两公寓之间的距离至少需要多少米时,采光不受影响?(2)该中学现已建成的公寓为5层,每层高为3米,相邻两公寓的距离24米,问其采光是否符合要求?(参考数据:取sin32°=,cos32°=,tan32°=)【思路点拨】(1)在直角三角形ABC中,已知AB利用锐角三角函数求得BC的长即可;(2)利用楼高求得不受影响时候两楼之间的距离与24米比较即可得到结果;【答案与解析】解:(1)∵在直角三角形ABC中,AB=20米,∠ACB=32°,∴=tan32°∴BC===32米,∴相邻两公寓之间的距离至少需要32米时,采光不受影响;(2)∵楼高=3×5=15米,∴不受影响时两楼之间的距离为15÷tan32°=24米,∵相邻两公寓的距离恰为24米,∴符合采光要求;【总结升华】本题是将实际问题转化为直角三角形中的数学问题,做到学数学,用数学,才是学习数学的意义.7.如图,不透明圆锥体DEC放在直线BP所在的水平面上,且BP过底面圆的圆心,其高23m,底面半径为2m.某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m.(1)求∠B的度数;(2)若∠ACP=2∠B,求光源A距平面的高度.【思路点拨】(1)如下图所示,过点D作DF垂直BC于点F.由题意,得DF=23,EF=2,BE=4,在Rt△DFB中,tan∠B= DFBF,由此可以求出∠B;(2)过点A作AH垂直BP于点H.因为∠ACP=2∠B=60°所以∠BAC=30°,AC=BC=8.在Rt△ACH中,AH=AC•Sin∠ACP,所以可以求出AH了,即求出了光源A距平面的高度.【答案与解析】解:(1)过点D作DF垂直BC于点F.由题意,得DF=23,EF=2,BE=4.在Rt△DFB中,tan∠B=DF233==BF2+43,所以∠B=30°;(2)过点A作AH垂直BP于点H.∵∠ACP=2∠B=60°,∴∠BAC=30°,∴AC=BC=8,在Rt△ACH中,AH=AC•Sin∠ACP=38=432,即光源A距平面的高度为43m.【总结升华】本题考查了学生运用三角函数知识解决实际问题的能力,又让学生感受到生活处处有数学,数学在生产生活中有着广泛的作用.中考数学知识点代数式一、重要概念分类:1.代数式与有理式用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
投影与视图一 选择题1. 2014•安徽省,第3题4 如图,图中的几何体是圆柱沿竖直方向 掉一半后得到的,则该几何体的俯视图是A. B.C.D.考点 简单几何体的 视图.析 俯视图是从物体 面看所得到的图形.解答 解 从几何体的 面看俯视图是,故选 D.点评 本题考查了几何体的 种视图,掌握定 是 键.注意所 的看到的棱都 表 在 视图中.2. 2014•福建泉 ,第3题3 如图的立体图形的左视图 能是 A.B.C.D.考点 简单几何体的 视图.析 左视图是从物体左面看,所得到的图形.解答 解 立体图形的左视图是直角 角形,故选 A.点评 本题考查了几何体的 种视图,掌握定 是 键.注意所 的看到的棱都 表 在 视图中.3. 2014•广西贺 ,第8题3 如图是 5个大小相同的 方体组成的几何体,它的 视图是A.B.C.D.考点 简单组合体的 视图.析 根据从 面看得到的图形是 视图, 得答案.解答 从 面看,第一层是两个 方形,第二层左边是一个 方形,故选 C.点评 本题考查了简单组合体的 视图,从 面看得到的图形是 视图.4. 2014•广西玉林市 城港市,第5题3 如图的几何体的 视图是A.B.C.D.考点 简单组合体的 视图.析 找出图形从 面 左面 和 面看所得到的图形即 .解答 解 从几何体的 面看 得 2列小 方形,左面 2个小 方形,右面 边 1个小 方形从几何体的 面看 得 2列小 方形,左面 2个小 方形,右面 边 1个小 方形从几何体的 面看 得 2列小 方形,左面 2个小 方形,右 角 1个小 方形故选 C.点评 本题考查了 视图的知识,注意所 的看到的棱都 表 在 视图中.5.(2014四 资 ,第2 题3 ) 列立体图形中,俯视图是 方形的是A.B.C.D.考点 简单几何体的 视图.析 根据从 面看得到的图形是俯视图, 得答案.解答 解 A 的俯视图是 方形,故A 确B D的俯视图是圆,故A D错误C 的俯视图是 角形,故C错误故选 A.点评 本题考查了简单组合体的 视图,从 面看得到的图形是俯视图.6.(2014 天津市,第5题3 )如图,从左面 察 个立体图形,能得到的 面图形是A.B.C.D.考点 简单组合体的 视图析 根据从左面看得到的图形是左视图, 得答案.解答 解 从左面看 面一个 方形, 面一个 方形, 故选A .点评 本题考查了简单组合体的 视图,从左面看得到的图形是左视图.7. 2014•新疆,第2题5 如图是 四个相同的小 方体组成的立体图形,它的俯视图A .B .C .D .考点 简单组合体的 视图.析 俯视图是从物体 面看所得到的图形.解答 解 面看,是 面2个 方形,左 角1个 方形,故选C .点评 本题考查了 视图的知识,俯视图是从物体 面看所得到的图形,解答时学生易将种视图混淆而错误地选 它选项.8. 2014 南省,第4题3 某几何体的 视图如图所示,则 个几何体是A .圆柱B . 方体C . 球D . 圆锥考点 视图判断几何体.析 视图和左视图确定是柱体,锥体 是球体,再 俯视图确定 体形状.解答 解 根据 视图和左视图 角形判断出是锥体,根据俯视图是圆形 判断出 个几何体 该是圆锥,故选D.点评 视图和左视图的大 轮廓 角形的几何体 锥体,俯视图 圆就是圆锥.9. 2014•温 ,第3题4 如图所示的支架是 两个长方形构成的组合体,则它的 视图是A.B.C.D.考点 简单组合体的 视图.析 找到从 面看所得到的图形即 ,注意所 的看到的棱都 表 在 视图中.解答解 从几何体的 面看 得 几何体的 视图是,故选 D.点评 本题考查了 视图的知识, 视图是从物体的 面看得到的视图.10. 3 2014•毕节地区,第2题3 如图是某一几何体的 视图,则该几何体是A. 棱柱B.长方体C.圆柱D.圆锥考点 视图判断几何体析 视图中 两个视图 矩形,那 个几何体 柱体,根据第3个视图的形状 得几何体的 体形状.解答解 视图中 两个视图 矩形, 个几何体 柱体, 另外一个视图的形状 圆, 个几何体 圆柱体, 故选C .点评考查 视图判断几何体 用到的知识点 视图中 两个视图 矩形,那 个几何体 柱体,根据第3个视图的形状 得几何体的形状.11. 2014•武汉,第7题3 如图是 4个大小相同的 方体搭成的几何体, 俯视图是A .B .C .D .考点 简单组合体的 视图.析 找到从 面看所得到的图形即 .解答 解 从 面看 得到一行 方形的个数 3,故选D .点评 本题考查了 视图的知识,俯视图是从物体的 面看得到的视图.12. 2014•襄 ,第4题3 如图几何体的俯视图是A .B .C .D .考点 简单组合体的 视图.析 根据从 面看得到的图形是俯视图, 得答案.解答 解 从 面看,第一层是 个 方形,第二层右边一个 方形,故选 B.点评 本题考查了简单组合体的 视图,从 面看得到的图形是俯视图.13. 2014•邵 ,第3题3 如图的 头的俯视图大 是A.B.C.D.考点 简单几何体的 视图析 俯视图即 从 所看到的图形,据 求解.解答 解 从 看易得俯视图 圆.故选D.点评 本题考查了 视图的知识,俯视图即从 所看到的图形.14. 2014•孝感,第2题3 如图是某个几何体的 视图,则该几何体的形状是A.长方体B.圆锥C.圆柱D. 棱柱考点 视图判断几何体析 视图和左视图确定是柱体,锥体 是球体,再 俯视图确定 体形状. 解答 解 根据 视图和左视图 矩形判断出是柱体,根据俯视图是 角形 判断出 个几何体 该是 棱柱. 故选D .点评 考查学生 视图掌握程 和灵活 用能力,同时也体 了 空间想象能力方面的考查. 视图 左视图 俯视图是 从物体 面 左面和 面看,所得到的图形. 15. 2014•四 自贡,第3题4 如图,是 几个小立方体所搭成的几何体的俯视图,小 方形中的数字表示在该位置 的立方体的个数, 个几何体的 视图是A .B .C .D .考点视图判断几何体 简单组合体的 视图析 俯视图,想象出几何体的特 形状,然后按照 视图的要求,得出该几何体的 视图和侧视图.解答 解 俯视图 知,小 方体的只2排,前排右侧1叠3块后排从做 右木块个数1,1,2 故选D .点评 本题是 础题,考查空间想象能力, 图能力,常考题型.16 2014· 南昆明,第2题3 左 图是 3个完全相同的小 方体组成的立体图形,它的 视图是解答 解 从 面看,是第1行 1个 方形,第2行 2个并排的 方形.故选B.点评 本题考查了 视图的知识, 视图是从物体的 面看得到的视图.17. 2014·浙江金华,第3题4 一个几何体的 视图如图所示,那 个几何体是答案 D.解析18. 2014•湘潭,第5题,3 如图,所 视图的几何体是第1题图A.球B.圆柱C.圆锥D. 棱锥考点 视图判断几何体析视图和左视图确定是柱体,锥体 是球体,再 俯视图确定 体形状. 解答 解 视图和左视图都是等腰 角形,那 几何体 锥体, 俯视图 圆, 得几何体 圆锥. 故选C .点评 本题考查了 视图判断几何体的知识,解题的 键是了解 视图和左视图的大 轮廓 长方形的几何体 锥体.19. 2014•株洲,第5题,3 列几何体中, 一个几何体的 视图 俯视图的形状 一样, 个几何体是 A .方体B .圆柱第2题图C .圆锥D .球考点简单几何体的 视图. 析 根据从 面看得到的图形是 视图,从 面看得到的图形是俯视图, 得答案. 解答 解 A 视图 俯视图都是 方形,故A 符合题意B 视图 俯视图都是矩形,故B 符合题意C 视图是 角形 俯视图是圆形,故C 符合题意D 视图 俯视图都是圆,故D 符合题意 故选 C .点评 本题考查了简单组合体的 视图,从 面看得到的图形是 视图,从 面看得到的图形是俯视图.20. 2014•泰 ,第4题,3 一个几何体的 视图如图所示,则该几何体 能是A.B.C.D.考点 视图判断几何体.析 根据 视图判断圆柱 面放着小圆锥,确定 体位置后即 得到答案.解答 解 视图和左视图 以得到该几何体是圆柱和小圆锥的复合体, 俯视图 以得到小圆锥的 面和圆柱的 面完全 合.故选C.点评 本题考查了 视图判断几何体,解题时 仅要 一定的数学知识,而 一定的生活经验.21. 2014•呼和浩特,第4题3 如图是某几何体的 视图,根据图中数据,求得该几何体的体积A.60πB.70πC.90πD.160π考点 视图判断几何体.析 易得 几何体 空心圆柱,圆柱的体积= 面积×高,把相 数值代入即 求解. 解答 解 察 视图发 该几何体 空心圆柱, 内径 3,外径 4,高 10,所以 体积 10× 42π﹣32π =70π, 故选B .点评 本题考查了 视图判断几何体的知识,解决本题的 键是得到 几何体的形状,易错点是得到计算 几何体所需要的相 数据.22. 2014•德 ,第3题3 图 是某零件的直 图,则它的 视图A .B .C .D .考点简单组合体的 视图. 析 根据 视图是从 面看得到的视图判定则 . 解答解 从 面看, 视图 .故选A .点评 本题考查了 视图的知识, 视图是从物体的 面看得到的视图.23. 2014 山东泰安,第3题3 列几何体, 视图和俯视图都 矩形的是A .B .C .D .解 A 圆柱 视图是矩形,俯视图是圆,故 选项错误 B 圆锥 视图是等腰 角形,俯视图是圆,故 选项错误 C 棱柱 视图是矩形,俯视图是 角形,故 选项错误 D 长方体 视图和俯视图都 矩形,故 选项 确 故选 D .点评 本题考查了几何体的 种视图,掌握定 是 键.注意所 的看到的棱都 表 在 视图中.二.填空题1. 2014 广东汕尾,第15题5 写出一个在 视图中俯视图 视图完全相同的几何体 .析 视图 俯视图是 从物体 面和 面看,所得到的图形.解 球的俯视图 视图都 圆 方体的俯视图 视图都 方形.故答案 球或 方体.点评 考查学生 视图掌握程 和灵活 用能力,同时也体 了 空间想象能力方面的考查.2. 2014•浙江湖 ,第12题4 如图, 四个小 方体组成的几何体中,若每个小 方体的棱长都是1,则该几何体俯视图的面积是 .析 根据从 面看得到的图形是俯视图, 得俯视图,根据矩形的面积公式, 得答案.解 从 面看 个 方形组成的矩形,矩形的面积 1×3=3,故答案 3.点评 本题考查了简单组合体的 视图,先确定俯视图,再求面积.3. 2014•扬 如图, 是一个长方体的 视图和俯视图, 图示数据 单元 cm 以得出该长方体的体积是 18cm3.第1题图考点 视图判断几何体.析 首先确定该几何体 立方体,并说出 尺 ,直接计算 体积即 .解答 解 察 视图知 该几何体 立方体, 立方体的长 3, 2,高 3,故 体积 3×3×2=18,故答案 18.点评 本题考查了 视图判断几何体, 记立方体的体积计算方法是解答本题的 键.投影 视图一 选择题1. 2014•四 巴中,第5题3 如图,两个大小 同的实心球在水 面靠在一起组成如图所示的几何体,则该几何体的左视图是A.两个外 的圆B.两个内 的圆C.两个内 的圆D.一个圆考点 视图.析 根据左视图是从左面看得到的视图,圆的位置 系解答即 .解答 从左面看, 两个内 的圆, 点在水 面 ,所以,该几何体的左视图是两个内 的圆.故选B.点评 本题考查了 视图的知识,左视图是从物体的左面看得到的视图.2. 2014•山东威海,第6题3 用四个相同的小立方体搭几何体,要求每个几何体的 视图 左视图 俯视图中 少 两种视图的形状是相同的, 列四种摆放方式中 符合要求的是A.B.C.D.考点 简单组合体的 视图.析 视图 左视图 俯视图是 从 面 左面 面所看到的图形.解答解 A 几何体的 视图和俯视图都是“”字形,故 选项 合题意B 几何体的 视图和左视图都是,故 选项 合题意C 几何体的 视图和左视图都是,故 选项 合题意D 几何体的 视图是,俯视图是,左视图是,故 选项符合题意,故选 D.点评 题 要考查了简单几何体的 视图, 键是注意所 的看到的棱都 表在 视图中.3. 2014•山东潍坊,第4题3 一个几何体的 视图如右图所示,则该几何体是( )考点 视图 原实物图.析 根据 视图 左视图 俯视图的形状,将它们相交得到几何体的形状.解答 视图知,从 面和侧面看都是 面梯形, 面长方形,从 面看 圆 , 以想象到实物体 面是圆 , 面是空心圆柱. 故选D .点评 本题考查几何体的 视图 直 图之间的相 转 .4. 2014•山东烟 ,第4题3 如图是一个 方体截去一角后得到的几何体,它的 视图是A .B .C .D .考点 视图.析 根据 视图是从 面看到的图形判定则 .解答 从 面看, 视图 .故选 C .点评 本题考查了 视图的知识,根据 视图是从物体的 面看得到的视图得出是解题 键. 5. 2014•湖南怀 ,第4题,3 列物体的 视图是圆的是 A .B .C .D .考点 简单几何体的 视图析 根据从 面看得到的图形是 视图, 得答案.解答 解 A 只是图是矩形,故A 符合题意B 视图是 角形,故B 符合题意C 视图是圆,故C 符合题意D 视图是 方形,故D 符合题意 故选 C .点评 本题考查了简单组合体的 视图,从 面看得到的图形是 视图.6. 2014•湖南张家界,第5题,3 某几何体的 视图 左视图和俯视图 如图,则该几何体的体积A .3πB .2πC .πD .12考点 视图判断几何体.析 根据 视图 以判断该几何体 圆柱,圆柱的 面半径 1,高 3,据 求得 体积即 . 解答 解 根据 视图 以判断该几何体 圆柱,圆柱的 面半径 1,高 3,故体积 πr2h=π×1×3=3π, 故选A .点评 本题考查了 视图判断几何体的知识,解题的 键是了解圆柱的 视图并清楚 体积的计算方法.7.2014•江西抚 ,第5题,3 某 动器材的形状如图所示,以箭头所指的方向 左视方向,则它的 视图 以是解析 选网. 两凸起是圆弧,非圆,中间是两个圆片的叠合主 视图 矩形. 8. 2014山东济南,第6题,3 如图,一个几何体 5个大小相同 棱长 1的 方体搭成, 列 于 个几何体的说法 确的是A . 视图的面积 5B .左视图的面积 3第6题C .俯视图的面积 3D . 种视图的面积都是4解析 题图 俯视图均 4个 方形, 面积 4,左视图 3个 方形, 面积 3,故选B .9. 2014•山东聊城,第2题,3 如图是一个 棱柱的立体图形,它的 视图是A .B .C .D .考点 简单几何体的 视图. 析 根据从 面看得到的图形是 视图, 得答案. 解答 解 从 面看是矩形,看 的棱用虚线表示,故选 B .点评 本题考查了简单组合体的 视图,从 面看得到的图形是 视图,注意看 到的棱用虚线表示.10. 2014•浙江杭 ,第2题,3 已知一个圆锥体的 视图如图所示,则 个圆锥的侧面积A .12πcm 2B .15πcm 2C .24πcm 2D .30πcm 2考点 圆锥的计算 题 计算题.析 俯视图 圆的只 圆锥,圆柱,球,根据 视图和左视图都是 角形 得到 几何体圆锥,那 侧面积= 面周长×母线长÷2. 解答 解 面半径 3,高 4,圆锥母线长 5,侧面积=2πrR ÷2=15πcm 2. 故选B .点评 该 视图中的数据确定圆锥的 面直径和高是解本题的 键 本题体 了数形结合的数学思想,注意圆锥的高,母线长, 面半径组成直角 角形.11. 2014•十堰3. 3 在 面的四个几何体中,左视图 视图 相同的几何体是 A.方体B.长方体C.球D.圆锥考点 简单几何体的 视图析 视图 左视图是 从物体 面 左面看,所得到的图形.解答 解 A 方体的左视图 视图都是 方形,故 选项 合题意B 长方体的左视图 视图都是矩形,但是矩形的 一样,故 选项符合题意C 球的左视图 视图都是圆,故 选项 合题意D 圆锥左视图 视图都是等腰 角形,故 选项 合题意故选 B.点评 本题考查了几何体的 种视图,掌握定 是 键.注意所 的看到的棱都 表 在 视图中.12. (2014 湖 咸宁4. 3 )6 15日“父亲节”,小明送 父亲一个礼盒 如图 ,该礼盒的 视图是A.B.C.D.考点 简单组合体的 视图.析 找到从 面看所得到的图形即 .解答 解 从 面看,是两个矩形,右边的较小.故选A.点评 本题考查了 视图的知识, 视图是从物体的 面看得到的视图.13:将两个长方体如图放置,到所构成的几何体的左视图 能是答案 C解析 根据 视图 知,C 确14. 2014•山东临沂主第11题3 一个几何体的 视图如图所示, 个几何体的侧面积A.2πcm2B.4πcm2C.8πcm2D.16πcm2考点 圆锥的计算 视图判断几何体.析 俯视图 圆的只 圆锥,圆柱,球,根据 视图和左视图都是 角形 得到 几何体 圆锥,那 侧面积= 面周长×母线长÷2.解答 解 几何体 圆锥半径 1,圆锥母线长 4,侧面积=2πrR÷2=2π×1×4÷2=4π故选B.点评 本题考查了圆锥的计算,该 视图中的数据确定圆锥的 面直径和高是解本题的 键 本题体 了数形结合的数学思想,注意圆锥的高,母线长, 面半径组成直角 角形.15. 2014•江苏徐 主第2题3 如图使用五个相同的立方体搭成的几何体, 视图是A.B.C.D.考点 简单组合体的 视图.析 根据 视图的知识求解.解答 解 从 面看 边一层最右边 1个 方形,边一层 3个 方形.故选D.点评 本题考查了 视图的知识, 视图是从物体的 面看得到的视图.16. 2014•江苏盐城主第3题3 如图, 3个大小相同的 方体搭成的几何体, 视图是A.B.C.D.考点 简单组合体的 视图析 根据 视图的概念找出找到从 面看所得到的图形即 .解答 解 从 面看,易得第一层右边 1个 方形,第二层 2个 方形.故选C.点评 本题考查了 视图的知识, 视图是从物体的 面看得到的视图.17. (2014• 山东东营主第6题3 ) 图是一个 多个相同小 方体堆积而成的几何体的俯视图,图中所示数字 该位置小 方体的个数,则 个几何体的左视图是A.B.C.D.考点 视图判断几何体 简单组合体的 视图.析 视图 左视图 俯视图是 从物体 面 左面和 面看,所得到的图形.解答 解 从俯视图 以看出直 图的各部 的个数,得出左视图前面 2个,中间 3个,后面 1个,即 得出左视图的形状.故选B.点评 题 要考查了 视图的概念.根据俯视图得出每一组小 方体的个数是解决问题的 键.18. 2014•山东淄博主第4题4 如图是 个大小 等的 方体拼成的几何体, 中两个较小 方体的棱长之和等于大 方体的棱长.该几何体的 视图 俯视图和左视图的面积 是S1,S2,S3,则S1,S2,S3的大小 系是A.S1>S2>S3B.S3>S2>S1C.S2>S3>S1D.S1>S3>S2考点 简单组合体的 视图.析 根据从 面看得到的图形是 视图,从 面看得到的图形是俯视图,从左面看得到的图形是左视图,根据边角面积的大小, 得答案.解答 解 视图的面积是 个 方形的面积,左视图是两个 方形的面积,俯视图是一个 方形的面积,S1>S3>S2,故选 D.点评 本题考查了简单组合体的 视图, 得出 视图是解题 键.19. 2014•四 遂宁,第3题,4 一个几何体的 视图如图所示, 个几何体是A.棱柱B.圆柱C.圆锥D.球考点 视图判断几何体.题 压轴题.析 根据 视图确定该几何体是圆柱体解答 解 根据 视图和左视图 矩形是柱体,根据俯视图是圆 判断出 个几何体 该是圆柱.故选B.点评 本题考查 视图确定几何体的形状, 要考查学生空间想象能力及 立体图形的认识.20. 2014•四 泸 ,第3题,3 如图的几何图形的俯视图A.B .C.D.解答 解 从 面看 边是圆,外边是矩形,故选 C.点评 本题考查了简单组合体的 视图,注意所 的看到的棱都 表 在俯视图中.21. 2014•四 内江,第4题,3 如图,桌面 一个一次性纸杯,它的 视图 是A.B.C.D.考点 简单几何体的 视图.析 根据 视图是从 面看到的图形, 得答案.解答 解 从 面看是一个 在 的梯形.故选 D.点评 本题考查了简单组合体的 视图,从 面看得到的图形是 视图.22. 2014•四 宜 ,第3题,3 如图1放置的一个机器零件,若 视图如图2,则 俯视图是A.B.C.D.考点 简单组合体的 视图.析 找到从 面看所得到的图形即 .解答 解 从 面看 得到左右相邻的3个矩形.故选D.点评 本题考查了 视图的知识,俯视图是从物体的 面看得到的视图.23. 2014•福建福 主第3题4 某几何体的 视图如图所示,则该几何体是A. 棱锥 B.长方体C.圆柱D.圆锥考点 视图判断几何体.24. 2014•甘肃白银 临夏主第3题3 如图的几何体是 一个 方体 去一个小 方体形成的,它的 视图是B.C.D.A.考点 简单组合体的 视图.析 根据从 面看得到的图形是 视图, 得答案.解答 解 视图是 方形的右 角 个小 方形,故选 D.点评 本题考查了简单组合体的 视图,从 面看得到的图形是 视图.二 填空题1.(2014 贵 黔东南15. 4 )在桌 摆着一个 若 个相同 方体组成的几何体, 视图和左视图如图所示,设组成 个几何体的小 方体的个数 n ,则n 的最小值 5 .考点 视图判断几何体.析 易得 几何体 行, 列,判断出各行各列最少 几个 方体组成即 .解答 解 层 方体最少的个数 是3个,第二层 方体最少的个数 该是2个,因 个几何体最少 5个小 方体组成, 故答案 5.点评 本题考查了 视图判断几何体的知识,解决本题的 键是利用“ 视图疯狂盖,左视图拆违章”找到所需最少 方体的个数.2. 2014•广东梅 主第10题3 写出一个在 视图中俯视图 视图完全相同的几何体 .考点 简单几何体的 视图. 题 开放型.析 视图 俯视图是 从物体 面和 面看,所得到的图形. 解答 解 球的俯视图 视图都 圆方体的俯视图 视图都 方形. 故答案 球或 方体 答案 唯一 .点评 考查学生 视图掌握程 和灵活 用能力,同时也体 了 空间想象能力方面的考查.投影 视图一 选择题1. 2014•海南主第5题3 如图几何体的俯视图是A .B .C .D .考点 简单组合体的 视图.析根据从 面看得到的图形是俯视图, 得答案.解答 解 从 面看, 个矩形组成的大矩形,故选 D .点评 本题考查了简单组合体的 视图,从 面看得到的图形是俯视图.2. 2014•黑龙江龙东主第13题3 若 个相同的小 方体搭成的一个几何体的俯视图如图,小 方形中的数字表示该位置的小 方体的个数,则 个几何体的 视图是A .B .C .D .考点 视图判断几何体 简单组合体的 视图. 析 俯视图中的每个数字是该位置小立方体的个数, 析 中的数字,得 视图右四列,从左到右 是1,2,2,1个 方形.解答 解 俯视图中的数字 得 视图右4列,从左到右 是1,2,2,1个 方形. 故选A .点评 本题考查了学生的思考能力和 几何体 种视图的空间想象能力.3. 2014•黑龙江绥 主第15题3 如图是一个 多个相同小 方体搭成的几何体的俯视图,图中所标数字 该位置小 方体的个数,则 个几何体的左视图是A .B .C .D .考点 视图判断几何体 简单组合体的 视图.析 俯视图中的每个数字是该位置小立方体的个数, 析 中的数字,得 视图右3列,从左到右 是1,3,2个 方形. 解答 解 俯视图中的数字 得 视图右3列,从左到右 是1,3,2个 方形.故选C . 点评 本题考查了学生的思考能力和 几何体 种视图的空间想象能力. 4. 2014•湖 宜昌主第5题3 如图的几何体是 一个圆柱体和一个长方形组成的,则 个几何体的俯视图是A .B .C .D .考点 简单组合体的 视图.析 根据俯视图是从 面看得到的图形, 得答案.解答 解 从 面看外边是一个矩形, 面是一个圆,故选 C.点评 本题考查了简单组合体的 视图,俯视图是从 面看得到的图形.5. 2014•湖南衡 主第么题3 如图所示的图形是 7个完全相同的小 方体组成的立体图形,则 面四个 面图形中 是 个立体图形的 视图的是A .B.C.D.考点 简单组合体的 视图.析 根据几何体组成,结合 视图的 察角 ,进而得出答案.解答 解 根据立方体的组成 得出A 是几何体的左视图,故 选项错误B 是几何体的 视图,故 选项 确C 是几何体的 视图,故 选项错误D 是几何体的俯视图,故 选项错误故选 B.点评 题 要考查了简单组合体的 视图,准确把握 察角 是解题 键.6. 2014•湖南永 主第7题3 若某几何体的 视图如图,则 个几何体是A.B.C.D.考点 视图判断几何体..析 如图 该几何体的 视图 俯视图均 矩形,侧视图 角形和一个矩形,易得出该几何体的形状.解答 解 该几何体的 视图 矩形,俯视图亦 矩形,侧视图是一个 角形和一个矩形,故选C.点评 本题是个简单题, 要考查的是 视图的相 知识.7. 2014•黔南 ,第8题4 形状相同 大小相等的两个小木块放置于桌面, 俯视图如 图所示,则 视图是A.B.C.D.考点 简单组合体的 视图析 实物结合它的俯视图, 原它的 体形状和位置,再判断 视图.解答 解 实物结合它的俯视图 得该物体是 两个长方体木块一个横放一个竖放组合而成,得到它的 视图 选项D.故选D.点评 本题考查了物体的 视图.在解题时要注意,看 的线画成虚线.8.(2014 广西钦 ,第2题3 )一个几何体的 个视图如图所示, 个几何体是A.圆柱B.球C.圆锥D. 方体。

投影与视图一、选择题1. (2014•安徽省,第3题4分)如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是()A.B.C.D.考点:简单几何体的三视图.分析:俯视图是从物体上面看所得到的图形.解答:解:从几何体的上面看俯视图是,故选:D.点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.2. (2014•福建泉州,第3题3分)如图的立体图形的左视图可能是()3. (2014•广西贺州,第8题3分)如图是由5个大小相同的正方体组成的几何体,它的主视图是()A.B.C.D.考点:简单组合体的三视图.分析:根据从正面看得到的图形是主视图,可得答案.解答:从正面看,第一层是两个正方形,第二层左边是一个正方形,故选:C.点评:本题考查了简单组合体的三视图,从正面看得到的图形是主视图.4. (2014•广西玉林市、防城港市,第5题3分)如图的几何体的三视图是()....5.(2014四川资阳,第2 题3分)下列立体图形中,俯视图是正方形的是()A.B.C.D.考点:简单几何体的三视图.分析:根据从上面看得到的图形是俯视图,可得答案.解答:解;A、的俯视图是正方形,故A正确;B、D的俯视图是圆,故A、D错误;C、的俯视图是三角形,故C错误;故选:A.点评:本题考查了简单组合体的三视图,从上面看得到的图形是俯视图.6.(2014年天津市,第5题3分)如图,从左面观察这个立体图形,能得到的平面图形是()A.B.C.D.考点:简单组合体的三视图分析:根据从左面看得到的图形是左视图,可得答案.解答:解;从左面看下面一个正方形,上面一个正方形,故选:A.点评:本题考查了简单组合体的三视图,从左面看得到的图形是左视图.7.(2014•新疆,第2题5分)如图是由四个相同的小正方体组成的立体图形,它的俯视图为()D8.(2014年云南省,第4题3分)某几何体的三视图如图所示,则这个几何体是()A.圆柱B.正方体C.球D.圆锥考点:由三视图判断几何体.分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.解答:解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形可判断出这个几何体应该是圆锥,故选D.点评:主视图和左视图的大致轮廓为三角形的几何体为锥体,俯视图为圆就是圆锥.9.(2014•温州,第3题4分)如图所示的支架是由两个长方形构成的组合体,则它的主视图是()解:从几何体的正面看可得此几何体的主视图是,10.(3分)(2014•毕节地区,第2题3分)如图是某一几何体的三视图,则该几何体是()11.(2014•武汉,第7题3分)如图是由4个大小相同的正方体搭成的几何体,其俯视图是()12.(2014•襄阳,第4题3分)如图几何体的俯视图是()B13.(2014•邵阳,第3题3分)如图的罐头的俯视图大致是()14.(2014•孝感,第2题3分)如图是某个几何体的三视图,则该几何体的形状是()15.(2014•四川自贡,第3题4分)如图,是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的立方体的个数,这个几何体的正视图是( )16、(2014·云南昆明,第2题3分)左下图是由3个完全相同的小正方体组成的立体图形,它的主视图是( )DCB A17.(2014·浙江金华,第3题4分)一个几何体的三视图如图所示,那么这个几何体是【】【答案】D.【解析】18. (2014•湘潭,第5题,3分)如图,所给三视图的几何体是()(第1题图)19. (2014•株洲,第5题,3分)下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是()20. (2014•泰州,第4题,3分)一个几何体的三视图如图所示,则该几何体可能是()21.(2014•呼和浩特,第4题3分)如图是某几何体的三视图,根据图中数据,求得该几何体的体积为()22.(2014•德州,第3题3分)图甲是某零件的直观图,则它的主视图为()23.(2014年山东泰安,第3题3分)下列几何体,主视图和俯视图都为矩形的是()A.B.C.D.解:A、圆柱主视图是矩形,俯视图是圆,故此选项错误;B、圆锥主视图是等腰三角形,俯视图是圆,故此选项错误;C、三棱柱主视图是矩形,俯视图是三角形,故此选项错误;D、长方体主视图和俯视图都为矩形,故此选项正确;故选:D.点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.二.填空题1.(2014年广东汕尾,第15题5分)写出一个在三视图中俯视图与主视图完全相同的几何体.分析:主视图、俯视图是分别从物体正面和上面看,所得到的图形.解:球的俯视图与主视图都为圆;正方体的俯视图与主视图都为正方形.故答案为:球或正方体.点评:考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.2.(2014•浙江湖州,第12题4分)如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是.分析:根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案.解:从上面看三个正方形组成的矩形,矩形的面积为1×3=3,故答案为:3.点评:本题考查了简单组合体的三视图,先确定俯视图,再求面积.3. (2014•扬州)如图,这是一个长方体的主视图和俯视图,由图示数据(单元:cm)可以得出该长方体的体积是18 cm3.(第1题图)。


专题29投影与视图知识点一:与投影有关的基本概念1.投影:用光线照射物体,在某个平面上得到的影子叫做物体的投影。
2.平行投影:由平行光线形成的投影是平行投影。
3.中心投影:由同一点发出的光线形成的投影叫做中心投影。
4.正投影:投影线垂直于投影面产生的投影叫做正投影。
知识点二:与视图有关的基本概念1.视图:从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图。
视图可以看作物体在某一方向光线下的正投影。
2.主视图、俯视图、左视图(1)对一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图;(2)在水平面内得到的由上向下观察物体的视图,叫做俯视图;(3)在侧面内得到的由左向右观察物体的视图,叫做左视图。
主视图与俯视图的长对正;主视图与左视图的高平齐;左视图与俯视图的宽相等。
知识点三:视图知识的应用1.通过三视图制作立体模型的实践活动,体验平面图形向立体图形转化的过程,体会三视图表示立体图形的作用,进一步感受立体图形与平面图形之间的联系。
2.由三视图判断几何体形状主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.本章内容要求学生经历实践探索,了解投影、投影面、平行投影和中心投影的概念。
通过下面知识导图加深对本章内容的了解。
【例题1】一位小朋友拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上的影子不可能是()A B C D【答案】B.【解析】本题主要考查对平行投影的理解和掌握,能熟练地观察图形得出正确结论是解此题的关键.根据看等边三角形木框的方向即可得出答案.竖直向下看可得到线段,沿与平面平行的方向看可得到C,延与平面不平行的方向看可得到D,不论如何看都得不到一点.【例题2】(2020广元)如图所示的几何体是由5个相同的小正方体组成,其主视图为()A. B. C. D.【答案】D【解析】根据从正面看得到的图形是主视图,可得答案.从正面看第一层是一个小正方形,第二层是三个小正方形,∴主视图为:【点拨】本题考查了简单组合体的三视图,从正面看得到的图形是主视图.【例题3】(2020湖南岳阳)如图,由4个相同正方体组成的几何体,它的左视图是()A. B.C. D.【答案】A【解析】根据左视图是从左面看得到的图形,结合所给图形以及选项进行求解即可.观察图形,从左边看得到两个叠在一起的正方形,如下图所示:【点拨】本题考查了简单几何体的三视图,解题的关键是掌握左视图的观察位置.【例题4】(2020苏州)如图,一个几何体由5个相同的小正方体搭成,该几何体的俯视图是()A. B. C. D.【答案】C【解析】根据组合体的俯视图是从上向下看的图形,即可得到答案.组合体从上往下看是横着放的三个正方形.【点拨】本题主要考查组合体的三视图,熟练掌握三视图的概念,是解题的关键.《投影与视图》单元精品检测试卷本套试卷满分120分,答题时间90分钟一、选择题(每小题3分,共30分)1.(2020成都)如图所示的几何体是由4个大小相同的小立方块搭成,其左视图是()A. B. C. D.【答案】D【解析】根据左视图的定义“从主视图的左边往右边看得到的视图就是左视图”进一步分析即可得到答案.【详解】从主视图的左边往右边看得到的视图为:【点拨】本题考查了左视图的识别,熟练掌握相关方法是解题关键.2.(2020山东济宁)已知某几何体的三视图(单位:cm)如图所示,则该几何体的侧面积等于()A.12πcm2B.15πcm2C.24πcm2D.30πcm2【答案】B【解析】由三视图可知这个几何体是圆锥,高是4cm,底面半径是5=(cm),∴侧面积=π×3×5=15π(cm2),故选B.3.(2020山东菏泽)一个几何体由大小相同的小立方块搭成,它的俯视图如图所示,其中小正方形中的数字表示在该位置小立方块的个数,则该几何体的主视图为()A. B. C. D.【答案】A【解析】从正面看,注意“长对正,宽相等、高平齐”,根据所放置的小立方体的个数判断出主视图图形即可.从正面看所得到的图形为A选项中的图形.【点拨】考查几何体的三视图的知识,从正面看的图形是主视图,从左面看到的图形是左视图,从上面看到的图象是俯视图.掌握以上知识是解题的关键.4.(2020哈尔滨)五个大小相同的正方体塔成的几何体如图所示,其左视图是()A. B. C. D.【答案】C【解析】根据从左边看得到的图形是左视图,可得答案.从左边看第一层有两个小正方形,第二层右边有一个小正方形,【点拨】本题考查了简单组合体的三视图,从左边看得到的图形是左视图.5.(2020河南)如下摆放的几何体中,主视图与左视图有可能不同的是()A. B.C. D.【答案】D【解析】分别确定每个几何体的主视图和左视图即可作出判断.A.圆柱的主视图和左视图都是长方形,故此选项不符合题意;B.圆锥的主视图和左视图都是三角形,故此选项不符合题意;C.球的主视图和左视图都是圆,故此选项不符合题意;D.长方体的主视图是长方形,左视图可能是正方形,故此选项符合题意,【点拨】本题考查了简单几何体的三视图,熟练掌握确定三视图的方法是解答的关键.6.(2020甘肃武威)下列几何体中,其俯视图与主视图完全相同的是()A. B. C. D.【答案】C【解析】俯视图是指从上面往下看,主视图是指从前面往后面看,根据定义逐一分析即可求解.选项A:俯视图是圆,主视图是三角形,故选项A错误;选项B:俯视图是圆,主视图是长方形,故选项B错误;选项C:俯视图是正方形,主视图是正方形,故选项C正确;选项D:俯视图是三角形,主视图是长方形,故选项D错误.【点拨】本题考查了视图,主视图是指从前面往后面看,俯视图是指从上面往下看,左视图是指从左边往右边看,熟练三视图的概念即可求解.7.(2020福建)如图所示的六角螺母,其俯视图是()A. B. C. D.【答案】B【解析】根据图示确定几何体的三视图即可得到答案.由几何体可知,该几何体的三视图依次为.主视图为:左视图为:俯视图为:【点拨】此题考查简单几何体的三视图,掌握三视图的视图方位及画法是解题的关键.8.(2020新疆兵团)如图所示,该几何体的俯视图是()A. B. C. D.【答案】C【解析】根据俯视图是从上边看的到的视图,可得答案.从上边可以看到4列,每列都是一个小正方形,故C符合题意;【点拨】本题考查了简单组合体的三视图,从上边看的到的视图是俯视图.掌握俯视图的含义是解题的关键.9.(2020贵州黔东南)桌上摆着一个由若干个相同的小正方体组成的几何体,其主视图和左视图如图所示,则组成这个几何体的小正方体的个数最多有()A.12个B.8个C.14个D.13个【答案】D【解析】易得此几何体有三行,三列,判断出各行各列最多有几个正方体组成即可.底层正方体最多有9个正方体,第二层最多有4个正方体,所以组成这个几何体的小正方体的个数最多有13个.【点拨】本题考查了由三视图判断几何体的知识,解决本题的关键是利用“主视图疯狂盖,左视图拆违章”找到所需正方体的个数.10.(2020贵州黔西南)如图,由6个相同的小正方体组合成一个立体图形,它的俯视图为()A. B. C. D.【答案】D【解析】找到从上面看所得到的图形即可.解:从上面看可得四个并排的正方形,如图所示:【点拨】本题考查了三视图的知识,.从正面看到的图是正视图,从上面看到的图形是俯视图,从左面看到的图形是左视图,能看到的线画实线,被遮挡的线画虚线.二、填空题(每空3分,共30分)11.三棱柱的三视图如图所示,已知△EFG中,EF=8cm,EG=12cm,∠EFG=45°.则AB的长为cm.【答案】4.【解析】根据三视图的对应情况可得出,△EFG中FG上的高即为AB的长,进而求出即可.过点E作EQ⊥FG于点Q,由题意可得出:EQ=AB,∵EF=8cm,∠EFG=45°,∴EQ=AB=×8=4(cm)12.如图所示,一个空间几何体的主视图和左视图都是边长为l的正三角形,俯视图是一个圆及圆心,那么这个几何体的侧面积是.【答案】见解析。
投影与视图
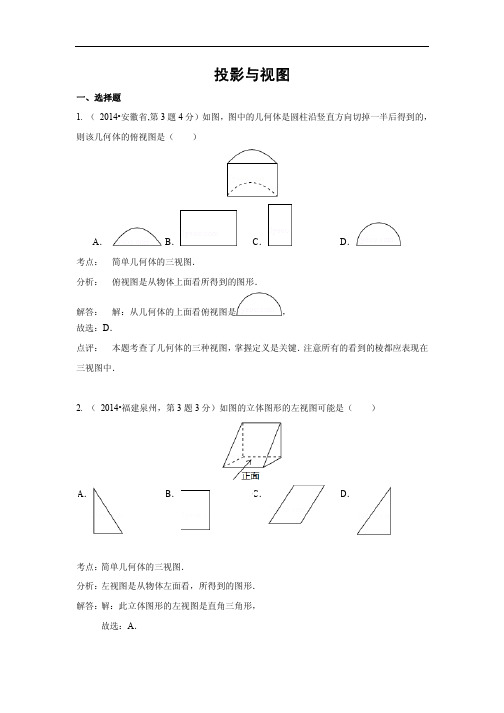
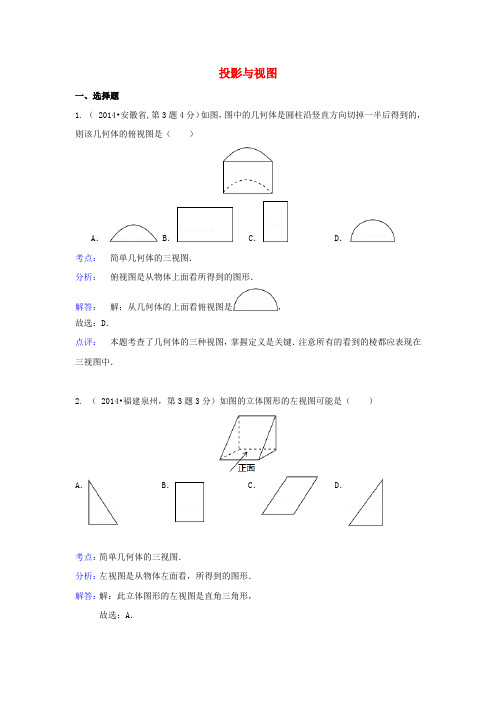
一、选择题
1. (2014•安徽省,第3题4分)如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是()
A.
B.C.D.
考点:简单几何体的三视图.
分析:俯视图是从物体上面看所得到的图形.
解答:解:从几何体的上面看俯视图是,
故选:D.
点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.
2. (2014•福建泉州,第3题3分)如图的立体图形的左视图可能是()
B
3. (2014•广西贺州,第8题3分)如图是由5个大小相同的正方体组成的几何体,它的主视图是()
A.B.C.D.
考点:简单组合体的三视图.
分析:根据从正面看得到的图形是主视图,可得答案.
解答:从正面看,第一层是两个正方形,第二层左边是一个正方形,
故选:C.
点评:本题考查了简单组合体的三视图,从正面看得到的图形是主视图.
4. (2014•广西玉林市、防城港市,第5题3分)如图的几何体的三视图是()
.B.C..
5.(2014四川资阳,第2 题3分)下列立体图形中,俯视图是正方形的是()
A.B.C.D.
考点:简单几何体的三视图.
分析:根据从上面看得到的图形是俯视图,可得答案.
解答:解;A、的俯视图是正方形,故A正确;
B、D的俯视图是圆,故A、D错误;
C、的俯视图是三角形,故C错误;
故选:A.
点评:本题考查了简单组合体的三视图,从上面看得到的图形是俯视图.
6.(2014年天津市,第5题3分)如图,从左面观察这个立体图形,能得到的平面图形是()
A.B.C.D.
考点:简单组合体的三视图
分析:根据从左面看得到的图形是左视图,可得答案.
解答:解;从左面看下面一个正方形,上面一个正方形,
故选:A.
点评:本题考查了简单组合体的三视图,从左面看得到的图形是左视图.
7.(2014•新疆,第2题5分)如图是由四个相同的小正方体组成的立体图形,它的俯视图为()
B
8.(2014年云南省,第4题3分)某几何体的三视图如图所示,则这个几何体是()
A.圆柱B.正方体C.球D.圆锥
考点:由三视图判断几何体.
分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
解答:解:根据主视图和左视图为三角形判断出是锥体,根据俯视图是圆形可判断出这个几何体应该是圆锥,故选D.
点评:主视图和左视图的大致轮廓为三角形的几何体为锥体,俯视图为圆就是圆锥.
9.(2014•温州,第3题4分)如图所示的支架是由两个长方形构成的组合体,则它的主视图是()
B
解:从几何体的正面看可得此几何体的主视图是,
10.(3分)(2014•毕节地区,第2题3分)如图是某一几何体的三视图,则该几何体是()
11.(2014•武汉,第7题3分)如图是由4个大小相同的正方体搭成的几何体,其俯视图是()
....
12.(2014•襄阳,第4题3分)如图几何体的俯视图是()
B
13.(2014•邵阳,第3题3分)如图的罐头的俯视图大致是()
....
14.(2014•孝感,第2题3分)如图是某个几何体的三视图,则该几何体的形状是()
15.(2014•四川自贡,第3题4分)如图,是由几个小立方体所搭成的几何体的俯视图,小正方形中的数字表示在该位置上的立方体的个数,这个几何体的正视图是( )
.
.
.
16、(2014·云南昆明,第
2题3分)左下图是由3个完全相同的小正方体组成的立体图形,它的主视图是( )
D
C
B A
17.(2014·浙江金华,第3题4分)一个几何体的三视图如图所示,那么这个几何体是【】
【答案】D.
【解析】
18. (2014•湘潭,第5题,3分)如图,所给三视图的几何体是()
(第1题图)
19. (2014•株洲,第5题,3分)下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是()
B
20. (2014•泰州,第4题,3分)一个几何体的三视图如图所示,则该几何体可能是()
B
21.(2014•呼和浩特,第4题3分)如图是某几何体的三视图,根据图中数据,求得该几何体的体积为()
22.(2014•德州,第3题3分)图甲是某零件的直观图,则它的主视图为( )
B
23.(2014年山东泰安,第3题3分)下列几何体,主视图和俯视图都为矩形的是( )
A .
B .
C .
D .
解:A 、圆柱主视图是矩形,俯视图是圆,故此选项错误;B 、圆锥主视图是等腰三角形,俯视图是圆,故此选项错误;C 、三棱柱主视图是矩形,俯视图是三角形,故此选项错误;D 、长方体主视图和俯视图都为矩形,故此选项正确;故选:D .
点评:本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.
二.填空题
1.(2014年广东汕尾,第15题5分)写出一个在三视图中俯视图与主视图完全相同的几何体.
分析:主视图、俯视图是分别从物体正面和上面看,所得到的图形.
解:球的俯视图与主视图都为圆;正方体的俯视图与主视图都为正方形.
故答案为:球或正方体.
点评:考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
2.(2014•浙江湖州,第12题4分)如图,由四个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体俯视图的面积是.
分析:根据从上面看得到的图形是俯视图,可得俯视图,根据矩形的面积公式,可得答案.
解:从上面看三个正方形组成的矩形,矩形的面积为1×3=3,
故答案为:3.
点评:本题考查了简单组合体的三视图,先确定俯视图,再求面积.
3. (2014•扬州)如图,这是一个长方体的主视图和俯视图,由图示数据(单元:cm)可以得出该长方体的体积是18cm3.
(第1题图)。