当前位置：文档之家 › 二次函数一般式(课堂PPT)

二次函数一般式(课堂PPT)

  • 格式：ppt
  • 大小：1.83 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

二次函数图像与性质ppt课件

二次函数图像与性质ppt课件

D．f(1)＞25
答案：A
三基能力强化
2．若函数f(x)＝ax2＋bx＋c满足 f(4)＝f(1)，那么( )
A．f(2)＞f(3) B．f(3)＞f(2) C．f(3)＝f(2) D．f(3)与f(2)的大小关系不确定 答案：C
三基能力强化
3．已知函数y＝x2－2x＋3在闭区
间[0，m]上有最大值3，最小值2，则
课堂互动讲练
【思路点拨】 (1)待定系数法．(2) 二次函数的单调性．
【解】 (1)依题意，方程f(x)＝ax2 ＋bx＝x有等根，
则有Δ＝(b－1)2＝0，∴b＝1. 2分 又f(－x＋5)＝f(x－3)， 故f(x)的图象关于直线x＝1对称， ∴－2ba＝1，解得 a＝－12，
∴f(x)＝－21x2＋x. 5 分
基础知识梳理
2．二次函数的图象及其性质
基础知识梳理
基础知识梳理
基础知识梳理
二次函数可以为奇函数吗？ 【思考·提示】 不会为奇 函数．
三基能力强化
1．已知函数f(x)＝4x2－mx＋5在
区间[－2，＋∞)上是增函数，则f(1)的
范围是( )
A．f(1)≥25
B．f(1)＝25
C．f(1)≤2＋2＝(x＋a)2＋2 －a2的对称轴为x＝－a，
∵f(x)在[－5,5]上是单调函数， ∴－a≤－5，或－a≥5， 解得a≤－5，或a≥5. 10分
规律方法总结
1．二次函数f(x)＝ax2＋bx＋c(a ＞0)在区间[m，n]上的最值．
当－2ba＜m 时，函数在区间[m， n]上单调递增，最小值为 f(m)，最大 值为 f(n)；
基础知识梳理
1．二次函数的解析式有三种常用表 达形式

《二次函数》PPT优秀课件

《二次函数》PPT优秀课件

。
• 3.观察上述函数函数关系有哪些共同之处？ 。
归纳总结
• 一般地，形如y＝ax2＋bx＋c(a，b，c为常数且a≠0)的函数，叫 做二次函数。其中x是自变量，a叫做二次项系数，b叫做一次项 系数，c叫做常数项．
• 注意：判断二次函数注意自变量最高次数为2，且二次项系数不为0
03 例题练习
例题
练习
• 1.某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率
都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y＝
．
• 2．多边形的对角线条数d与边数n之间的关系式为
为
；当d＝35时，多边形的边数n＝
．
，自变量n的取值范围是 且
练习
3.已知两个变量x，y之间的关系为y＝(m－2)xm2－2＋x－1，若x，y之间是二次函数关系， 求m的值．
4．如图，有一个长为24米的篱笆，一面利用墙(墙的最大长度a为10米)围成的中间隔有一道 篱笆的长方形花圃．设花圃的宽AB为x米，面积为S平方米． (1)求S与x的函数关系式； (2)如果要围成面积为45平方米的花圃，AB的长为多少米？
04 作业布置
作业布置
1．下列函数是二次函数的是( )
A．y＝2x＋1
二次函数
01
教学目标
目录
02 03
知识点框架
例题练习
04
作业布置
01
教学目标
掌握二次函数的定义并能根据实际问题列出二次函数解析式
02 知识点框架
二、新课讲授
• 1.设一个正方形的边长为x，则该正方形的面积y=
。
• 2.用一根长为40的铁丝围成一个半径为的扇形，求扇形的面积与它的半径之

二次函数一般式的图像与性质(与a.b.c符号)ppt课件

二次函数一般式的图像与性质(与a.b.c符号)ppt课件
5.已知二次函数y=ax2+bx+c的图象如图所示， 请根据图象判断下列各式的符号：
a < 0 ,b< 0, c > 0 ,∆ > 0 , a-b+c >0,a+b+c = 0
精选PPT课件
19
自我挑战1
1.已知y=ax2+bx+c的图象如图所示,请在下列横线 上填写“<”,“>”或“=”.
（1） a__<_0, b__<__0, c__>___0, abc__>__0 b2-4ac__>___0
为坐标原点，抛物线的对称轴为y轴，1米为数轴的
单位长度，建立平面直角坐标系， 求（1）以这一部分抛物线为图
y
象的函数解析式，并写出x的取
O
值范围；
x
（2） 有一辆宽2.8米，高1米的
农用货车（货物最高处与地面AB
的距离）能否通过此隧道？
A CB
精选PPT课件
26
探究活动:
一座拱桥的示意图如图，当水面宽12m时，桥洞顶部 离水面4m。已知桥洞的拱形是抛物线，要求该抛物线 的函数解析式，你认为首先要做的工作是什么?如果以 水平方向为x轴，取以下三个不同的点为坐标原点：
当a < 0 时开口向下 a 越大图象开口越小
a 越小图象开口越大
精选PPT课件
13
b影响 对称轴 的位置
b与图象的关系 当b=0时对称轴为y轴 当ab>0时对称轴在y轴左侧 当ab<0时对称轴在y轴右侧
精选PPT课件
14
c与图象的关系
C 确定图 象与y轴 的交点
当c＝0时图象过原点 当 c > 0时图象与y轴正半轴相交 当c < 0时图象与y轴负半轴相交

2.3 二次函数表达式的三种形式 课件(共21张PPT)

2.3 二次函数表达式的三种形式 课件(共21张PPT)
3．已知抛物线与x轴有两个交点（或已知抛物线与x
轴（交其点中的x1横, 坐x2标是）抛，物选线交与点x式轴：交y 点 (的x 横x坐1)(标x ）x2 )
但不论何种形式，最后都化为一般形x1 式。
2.抛物线y=ax²+bx+c的顶点为(2，4)，且过(1，2)点， 求抛物线的解析式．
3.二次函数y=ax²+bx+c的图象过点A(－2，5)，且当 x＝2时，y＝－3，求这个二次函数的解析式，并 判断点B(0，3)是否在这个函数的图象上．
4.抛物线y=ax²+bx+c经过(0，0)，(12，0)两点，其 顶点的纵坐标是3，求这个抛物线的解x1 析式．(要 求用多种方法)
• 求二次函数表达式的方法有很多，今 天主要学习用待定系数法来求二次函 数的表达式（解析式）
• 2015已知二次函数的图象与y轴的交点为C， 与x轴正半轴的交点为A．且．tan ACO 1
4
• (1)求二次函数的解析式；
课后练习
1.抛物线y=ax²+bx+c过(－3，0)，(1，0)两点，与y 轴的交点为(0，4)过(－3，0)，(1，0)两点，与y 轴的交点为(0，4)，求抛物线的解析式
• 3.交点式：y a(x x1)(x x2 ) (a 0)
一般式 y ax2 bx c(a )
例题1 (1) 已知二次函数图象经过点A(-1,0), B（4，5），C（0，－3），求该二次函
数的表达式．
(2) (2015牡丹江)抛物线y=x²+bx+c经过 点A(1,-4),B(3,0).求此抛物线的解析式.
二、顶点式 y a(x h)2 k
例题1 (1)(2013绥化)若二次函数图像的顶点坐 标为(-2,3），且过点（－3,5）,求此二次 函数的解析式。

高中数学二次函数ppt课件

高中数学二次函数ppt课件

【解题回顾】①在本题解题过程中，容易将f(x)=mx2+(m3)x+1看成是二次函数，从而忽视对m=0的讨论
②实系数方程ax2+bx+c=0(a≠0)的两实根异号的充要条件
为c
0 ；有两正实根的充要条件是
a
0
c
根的充要条件是
c
a
b a
0
0
a
b
a
0
0
0
；有两负实
能力·思维·方法
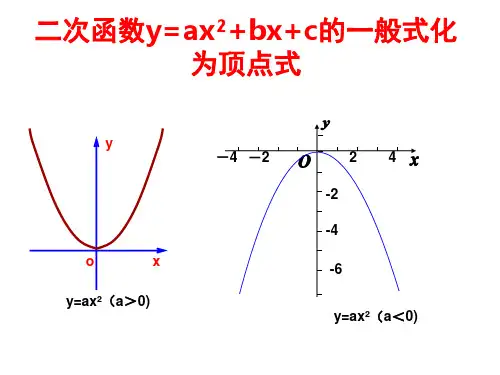
2.二次函数的图象与性质 定义域: R 单调性与值域: 奇偶性: 函数为偶函数b=0 图象:二次函数的图象是一条抛物线,对称轴方程是
x b ,当a>0 时, 图象开口向上;当a<0 时,图象开口向下.
2a
当 △>0 时, 图象与 x 轴有两个交点,两个交点的距离为 ;
|a |
当 △<0 时, 若a>0,则函数值恒正; 若a<0, 则函数值恒负.
的值都非负，求关于x的方程 x a12的根的范围.
解解题：分解 由析已：得知由3得已，知a△方2≤程0,即a(x-42aa)2|-2a4(21a|+122将)≤0x,表示为 a 的
函(数1)当 ，这3样求a2方程1时 根的，问题就原转方化程成化求为函x=数-值a2+域a+的6问题。
a22a6a1225
(2)本题是“定”二次函数，“动”区间，依照此法也可以 讨论“动”二次函数，“定”区间的二次函数问题 .
“顶点定,区间动”;
“顶点动,区间定”.
误解分析
1.在讨论方程根的分布情况时，要写出它的充要条件，注 意观察方程对应的函数图象是避免将充要条件写成必要条 件的有效办法.

二次函数的一般式化为顶点式(课堂PPT)

二次函数的一般式化为顶点式(课堂PPT)

y
···
· ·0
x
··
·
·
如何画出
y
1x2 2
6x21的图象呢?
我们知道,像y=a(x-h)2+k这样的函数, 容易确定相应抛物线的顶点为(h,k), 二次函 数 y1x2 6x21也能化成这样的形式吗
2
?
y=ax2+bx+c
b
=a(x2+ x)+c
a
= a[x2+
Hale Waihona Puke b ax+
(
b 2a
) 2 ]-
y3x212x7，那么如何将抛物线 y 3 x 2的图 像移动，得到的 y3x212x7 图像呢？
二次函数 y=2(x+3)2+5 y = -3x(x-1)2 -2 y = 4(x-3)2 +7 y = -5(2-x)2 - 6
开口方 对称轴 顶点坐标 向
向上 直线x=–3 （－3，5）
向下 直线x=1 （1，－2）
向上 直线x=3 （3，7 ） 向下 直线x=2 （2，－6）
你能说出二次函数y=-2x 2－8x-7图 像的特征吗？
如何画出 y-2x28x-7 的图象呢?
我们知道,像y=a(x+h)2+k这样的函数, 容易确定相应抛物线的顶点为(-h,k), 二次 函数y-2x28x-7 也能化成这样的形式 吗?
(
b 2a
)2
a
+c
=a(x+ b )2+ 4 a c b 2
2a
4a
2020/7/10
14
求下列二次函数图像的开口、顶点、对称轴
①y=2x2-5x+3②y=－ 1 x2+4x-9 ③y=(x-3)(x+2)

初三二次函数课件ppt课件

初三二次函数课件ppt课件

02
二次函数的解析式
一般式
总结词
最通用的二次函数形式，包含三个系数a、b和c。
详细描述
一般式为y=ax^2+bx+c，其中a、b和c为实数，且a≠0。它可以表示任意二次 函数，通过调整系数a、b和c的值，可以改变函数的形状、开口方向和大小。
顶点式
总结词
包含顶点坐标的二次函数形式。
详细描述
顶点式为y=a(x-h)^2+k，其中(h,k)为抛物线的顶点坐标。通过顶点式可以直接 读出顶点的坐标，并且可以快速判断抛物线的开口方向和对称轴。
伸缩变换
总结词
伸缩变换是指二次函数的图像在平面坐标系中沿x轴或y轴方向进行缩放。
详细描述
伸缩变换包括沿x轴方向的伸缩和沿y轴方向的伸缩。沿x轴方向的伸缩是指将图像在x轴方向上放大或 缩小，对应的函数变换是将x替换为kx(k>1表示放大，0<k<1表示缩小)。沿y轴方向的伸缩是指将图 像在y轴方向上放大或缩小，对应的函数变换是将y替换为ky(k>1表示放大，0<k<1表示缩小)。
利用二次函数求面积
详细描述
通过设定一个变量为常数，将 二次函数转化为一次函数，再 根据一次函数的性质求出面积 。
总结词
几何图形面积
详细描述
在几何图形中，如矩形、三角 形、圆等，可以利用二次函数
来求解面积。
生活中的二次函数问题
总结词
生活中的二次函数
总结词
实际应用案例
详细描述
在生活中，许多问题都可以用二次函数来 描述和解决，如速度、加速度、位移等物 理量之间的关系。
二次函数的图像
总结词
二次函数的图像是一个抛物线，其形 状由系数$a$决定。

二次函数(1)PPT课件(人教版)

二次函数(1)PPT课件(人教版)
九年级上册人教版数学
第二十二章 二次函数
22．1 二次函数的图象和性质
22．1.1 二次函数
1．一般地，形如 y＝ax2＋bx＋c(a，b，c 是常数，a≠0)的函数，叫做 __二__次__函__数_，其中 x 是自变量，a，b，c 分别是函数解析式的_二__次__项___系数、 一__次__项___系数和常数项．
14．边长为4 m的正方形中间挖去一个边长为x(m)(x＜4)的小正方形，剩 余的四方框的面积为y(m2)，则y与x之间的函数关系式为y_＝__1_6_－__x_2_(_0_＜__x_＜_，4) 它是_二__次____函数．

15．若y＝(m－1)xm2＋2m－1＋3. (1)m取什么值时，此函数是二次函数？ (2)m取什么值时，此函数是一次函数？
解 ： 降 低 x 元 后 ， 所 销 售 的 件 数 是 (500 ＋ 100x) ， 则 y ＝ (13.5 － 2.5 － x)(500＋100x)，即y＝－100x2＋600x＋5500(0＜x≤11)
18．如图，在△ABC中，∠B＝90°，AB＝12 mm，BC＝24 mm，动点P 从点A开始沿边AB向B以2 mm/s的速度移动(不与点B重合)，动点Q从点B开 始沿边BC向C以4 mm/s的速度移动(不与点C重合)．如果P，Q分别从A，B 同时出发，设运动的时间为x s，四边形APQC的面积为y mm2.
C．y＝12(x－1)(x＋4)不是二次函数 D．在 y＝1－ 2x2 中，一次项系数为 1
3．若y＝(a＋3)x2－3x＋2是二次函数，则a的取值范围是__a_≠_－__3___． 4．对于二次函数y＝1－3x＋2x2，其二次项系数、一次项系数及常数 项的和是__0__． 5．已知两个变量x，y之间的关系式为y＝(a－2)x2＋(b＋2)x－3. (1)当___a≠__2____时，x，y之间是二次函数关系； (2)当___a_＝__2_且__b_≠_－__2_____时，x，y之间是一次函数关系．

《二次函数与一元二次方程》二次函数PPT课件

《二次函数与一元二次方程》二次函数PPT课件

A. 有两个不相等的实数根
B. 有两个异号绝对值相等的实数根
C. 有两个相等的实数根
y 3
D. 没有实数根
-1
. o 1.3
x
x=－1
9.根据下列表格的对应值:
x
3.23 3.24 3.25 3.26
y=ax2+bx+c -0.06 -0.02 0.03 0.09
判断方程 ax2+bx+c =0 (a≠0,a,b,c为常数)一个解x 的范围是（ C ）
二次函数 y=ax2+bx+c的图
象和x轴交点
有两个交点
一元二次方程 ax2+bx+c= 0的根
一元二次方程 ax2+bx+c= 0根的判
别式Δ=b2-4ac
有两个不相 等的实数根
b2 – 4ac > 0
只有一个交点 有两个相等的 实数根
b2 – 4ac = 0
没有交点
没有实数根
b2 – 4ac < 0
y
O
x y
有两个相等的
解
x1=x2=
b 2a
没有实数根
O
x
1.一元二次方程 3 x2+x-10=0的两个根是 x1= -2 ,x2=5/3, 那么二次函数y= 3 x2+x-10 与x轴的交点坐标是＿(-2＿,0)＿(5＿/3＿,0).
2.抛物线y=2x2-3x-5 与x轴有无交点？若无说 出理由,若有求出交点坐标？
系? y x2 x 2
y x2 6x 9
y x2 x 1
二次函数 y x2 x 2 y x2 6x 9
与x轴交点坐标 (-2,0),(1,0)

二次函数的解析式课件

二次函数的解析式课件

弹性力学问题
在弹性力学中，二次函数 可以用于描述物体的应力 和应变关系，以及弹性体 的变形和稳定性等问题。
04
二次函数解析式的性质
二次函数的开口方向与a的关系
总结词：a的正负决定二次函数的开口方 向 a>0时，开口向上；a<0时，开口向下。
a的符号决定了二次函数的开口方向，这 是判断二次函数增减性的关键。
几何问题
二次函数与几何图形密切相关，可以 用于研究平面几何、立体几何中的一 些问题，例如抛物线、椭圆、双曲线 的性质和图像。
在物理问题中的应用
01
02
03
运动学问题
二次函数可以用于描述物 体在重力作用下的运动规 律，例如自由落体运动、 抛体运动等。
波动问题
在波动现象中，例如声波 、光波等，二次函数可以 用于描述波的传播规律和 性质。
参数的取值还影响抛物线 的顶点位置：顶点的x坐标 为-b/2a，y坐标为(4acb^2)/4a。
03
二次函数解析式的应用
在生活中的实际应用
金融领域
二次函数可以用于描述股 票价格、债券收益率等金 融数据的变动规律，帮助 投资者进行风险评估和预
测。
建筑领域
在建筑设计中，二次函数 可以用于计算结构物的受 力分析、稳定性等，以确 保建筑的安全性和稳定性
最小值为c-b^2/4a，此时二次函数开 口向上；最大值为c-b^2/4a，此时二 次函数开口向下。
二次函数的最小值或最大值在对称轴 上取得，即x=-b/2a处。
05
二次函数解析式的求解方法
配方法求解二次函数解析式
总结词
通过配方将二次函数转化为顶点式，便于分析函数的开口方向、对称轴和顶点坐标。
详细描述

《二次函数》PPT优秀课件

《二次函数》PPT优秀课件
说一说以上二次函数解析式的各项系数.
链接中考
1.下列函数解析式中，一定为二次函数的是（ C ）
A.y=3x-1 C.s=2t2-2t+1
B.y=ax2+bx+c
D.y=x2+
1
2
x
链接中考
2.已知函数 y=（m²﹣m）x²+（m﹣1）x+m+1． （1）若这个函数是一次函数，求m的值； （2）若这个函数是二次函数，则m的值应怎样？ 解：（1）根据一次函数的定义，得m2﹣m=0，
探究新知
素养考点 1 二次函数的识别
例1 下列函数中是二次函数的有 ①⑤⑥ .
①√ y= 2x2 2
×③y x2(1 x2 ) 1
最高次数是4
⑤√ y=x( x 1)
×②y 2x2 x(1 2x) a=0
×④y
1 x2
x2
√⑥y
x4 x2 x2 1
=x2
二次函数：y=ax²+bx+c（a，b，c为常数，a≠0）
素养目标
2. 能根据实际问题中的数量关系列出二次函数 解析式，并能指出二次函数的项及各项系数.
1.掌握二次函数的定义，并能判断所给函数 是否是二次函数.
探究新知
知识点 1 二次函数的概念
问题1 正方体的六个面是全等的正方形（如下图）,设正方
形的棱长为x,表面积为y,显然对于x的每一个值, y都 有一个对应值,即y是x的函数,它们的具体关系可以表 示为 y=6x2①.
探究新知
方法点拨
运用定义法判断一个函数是否为二次函数的 步骤： （1）将函数解析式右边整理为含自变量的代 数式，左边是函数（因变量）的形式； （2）判断右边含自变量的代数式是否是整式； （3）判断自变量的最高次数是否是2； （4）判断二次项系数是否不等于0.

《二次函数的图像》ppt课件

《二次函数的图像》ppt课件

二次函数的顶点及其性质
顶点坐标
指引如何求解二次函数的顶点坐 标。
凹凸性
讨论二次函数图像的凹凸性及其 与二次函数的系数关系。
图像特点
解释顶点与图像特点的关系，如 开口方向、对称轴和伸缩。
二次函数与判别式
判别式的定义
解释二次函数的判别式及其含义，如何通过判别式判断函数图像的性质。
判别式的示例
提供实际的例子，演示如何使用判别式确定二次函数图像的形状。
二次函数的图像
二次函数的概念。了解二次函数的基本定义和特点，包括函数的二次项、一 次项和常数项。
二次函数的标准式和一般式
1 标准式
介绍二次函数的标准形式，形如y=ax^2释二次函数的一般形式，形如y=ax^2+bx+c。
二次函数图像的基本性质
开口方向
讲解二次函数图像的开口方向， 以及如何通过系数判断。
对称轴
解释二次函数图像的对称轴， 如何确定并绘制。
顶点坐标
介绍二次函数图像的顶点坐标 的求法，以及其意义。
二次函数图像的平移、翻转和伸缩
1
平移
说明二次函数图像的平移，如何改变顶
翻转
2
点的横纵坐标。
讨论二次函数图像的翻转，如何改变函
数的开口方向。
3
伸缩
探讨二次函数图像的伸缩，如何调整二 次函数图像的形状和大小。
二次函数与实际问题的应用
介绍二次函数在实际问题中的应用，如抛物线的运动轨迹、物体的抛体运动 等。

二次函数复习课课件

二次函数复习课课件

对称变换
总结词
对称变换是指二次函数的图像关 于某条直线进行对称。
详细描述
对称变换包括关于x轴、y轴或原点 对称。在对称变换过程中，二次函 数的开口方向、顶点和对称轴等性 质可能发生变化。
举例
将二次函数$f(x) = x^2 - 2x$的图 像关于x轴对称，得到新的函数$f(x) = (-x)^2 - 2(-x) = x^2 + 2x$。
二次函数的图像
总结词
二次函数的图像是一个抛物线， 其形状由系数$a$决定。
详细描述
二次函数的图像是一个抛物线。 当$a > 0$时，抛物线开口向上； 当$a < 0$时，抛物线开口向下。 抛物线的对称轴是直线$x = frac{b}{2a}$，顶点位于该对称轴 上，坐标为$left(-frac{b}{2a}, fleft(-frac{b}{2a}right)right)$。
详细描述
顶点式是二次函数的一种特殊形式，它通过完全平方的形式简化了函数表达式 ，使得函数图像的顶点和对称轴更加直观。顶点式在解决与二次函数顶点相关 的问题时非常有用。
交点式
总结词
二次函数的交点式为y=a(x-x1)(x-x2)，其中x1、x2为函数与x轴的交点。
详细描述
交点式是二次函数的一种特殊形式，它通过将函数表示为两个一次因式的乘积， 突出了函数与x轴的交点。交点式在解决与二次函数与x轴交点相关的问题时非常 有用。
03
二次函数的图像变换
平移变换
总结词
平移变换是指二次函数的图像在 平面坐标系中沿x轴或y轴方向移
动。
详细描述
平移变换包括向左或向右移动图 像，以及向上或向下移动图像。 在平移过程中，二次函数的开口 方向、顶点和对称轴等性质保持
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2
b a
x
b 2a
2
b 2a
2
c
a
要记住公式哦！
a
(x
b 2a
)2
4ac - b 2
4a 2
a( x b )2 4ac b 2
2a
4a
12
y
1x2 2
-2x3
解：
a
1 2
0
开口方向：向上。
对称轴 x： 2ba22212
y
4
a cb2 4a
4213(2 421
)2
1
顶 点 坐 标 ： （ 2 ， 1 ） 13
x b 增大.2a
时，y随x的增大而
x b 2a
8
（2）：
如果a<0，当x b 时，y随x的增大而减小，
当x
b
2a 时，y随x的增大而增大.
2a
9
你能把 yax2 bxc 改写成 ya(xh)2 k吗？
用配方法
你知道吗?
10
y ax 2 bx c
a(x
2
b a
x
c) a
a
x
2
b a
与x轴的交点坐标是
(。1,0)或（3，0）
(0,3)
抛物线与y轴的交 点有什么特征？
抛物线与x轴的交 点有什么特征？
16
写出下列抛物线的开口方向、对称轴和顶点：
(1)y3x22x (2)yx22x
(3)y2x28x8
(4)y1x24x3 2
17
解 ： （ 1） 配 方 得 y=3(x+1)31 33
y
1x2 2
-2x3
（1y ） 22x-121 x3
解：
a
1 2
0
开口方向：向上。
对称轴 x： 2ba22212
y
4ቤተ መጻሕፍቲ ባይዱ
a cb2 4a
4213(2 421
)2
1
顶 点 坐 标 ： （ 2 ， 1 ） 14
y
1x2 2
-2x3
（1y ） 22x-121 x3
解：
a
1 2
0
开口方向：向上。
解： a 2 0 开口方向：向上。
x
b 2a
2
b 2a
2
c
a
a
(x
b 2a
)2
4ac - b 2
4a 2
a( x b )2 4ac b 2
2a
4a
11
∴开口方向：由a决定;
y ax 2 bx c
a(x
2
b a
x
c) a
对 称 轴x：2ba 顶 点（ 坐 2b标 a， 44 a ： a c b2)
a
x
性质
2
分析：这种函数形式并不是我们所熟 悉的二次函数，所以考虑将其变形
配方可得： y1(x6)2 3 2
3
根据前面的知识，我们知道：其变形过程如 下所示
y
1 2
x
2
向右平移6个y
单位 长度
1 2
(x
6)2向上平移3 个单位长度
y
1(x6)2 2
3
还有什么方 法平移呢
4
如果我们直接画二次函数 y1x2 6x21的图象，
22.1.4 二次函数y=ax2+bx+c的 图象和性质
早胜初中 刘鹏德
1
回顾：二次函数y=a(x-h)2+k的性质
y=a(x-h)2 +k(a≠0) 开口方向 顶点坐标 对称轴 增 减 性
极值
a>0
向上 (h ,k)
a<0
向下 (h ,k)
x=h
x=h
当x<h时，
当x<h时,
y随着x的增大而减小。 y随着x的增大而增大。
所 以 开 口 向 上 ， 对 称 轴 x1， 顶 点 （1， 1）
3
33
解 ： （ 2 ） 配 方 得 y = -( x + 1 )3+ 1
所 以 开 口 向 下 ， 对 称 轴 x 1 ， 顶 点 （ 1 ， 1 ）
解 ： （ 3 ） 配 方 得 y = -2 ( x -2 )2 所 以 开 口 向 下 ， 对 称 轴 x2 ， 顶 点 （ 2 ， 0 ）
的图象和性质吗？
6
一般的，二次函数y=ax2+bx+c可以通过配方 化成y=a(x-h)2+k的形式，即
ya(xb)24acb2 2a 4a
因此，其对称轴是： b 2a
4 ac b 2
顶点是：
4a
7
从二次函数y=ax2+bx+c的图象可以看出：
（1）： 如果a>0，当x b 时， y随x的增大而减小2，a 当
当x>h时，
当x>h时，
y随着x的增大而增大。 y随着x的增大而减小。
x=h时,y最小值=k
x=h时,y最大值=k
抛物线y=a(x-h)2+k(a≠0)的图象可由y=ax2的图象通 过上下和左右平移得到.
2
我们已经知道二次函数y=a(x-h)2+k
的图象和性质，能否利用这些知识
来讨论二次函数 y1x2 6x21图象和
可按如下步骤进行.
2
利用图形对称性列表：
x
····· 3 4 5 6 7 8 9 ·····
·
y1x2 6x21······ 2
7.5
5
3.5 3 3.5
5
7.5 ·····
描点画图：
由图象可知： （1）在对称轴左侧，抛物线从 左到右下降 （2）在对称轴右侧，抛物线从 左到右上升
5
你能用上面的方法讨论二次函数 y2x24x1
对称轴 x： 2ba22212
对 称 x 轴 2 b a ： 2 12 23
y
4
a cb2 4a
4213(2 421
)2
1
y4
acb2 4a
421432(1
22
)-
5
顶 点 坐 标-： 5 ） （ 3 ，
顶 点 坐 标 ： （ 2 ， 1 ） 15
1.抛物线y=x2-4x+3与y轴的交点坐标是 ，
解 ： （ 4） 配 方 得 y=1(x-4)2-5 2
所 以 开 口 向 上 ， 对 称 轴 x4， 顶 点 （ 4， -5）
18
19