微积分基本公式优秀课件

格式：ppt
大小：686.00 KB
文档页数：25

下载文档原格式

微积分基本公式PPT课件

xa a
x
( x a) f ( x) f (t)dt
证 F ( x)
a
(x a)2
x
只要证明 ( x a) f ( x) f (t)dt 0 即可. a
令 g( x) ( x a) f ( x)
x
f (t)dt ,
a
则 g( x) f ( x) ( x a) f ( x) f ( x)
原函数.
该定理告诉我们, 连续函数一定有原函数.
6
变限积分函数的求导：
d x f (t)dt f ( x) ，
dx a
d
b
f (t)dt
d
x f (t)dt f ( x) ，
dx x
dx b
设(x) 在[a, b]上可导,则
d
(x)
f (t)dt f [( x)]( x) .
dx a
证设 Φ( x) x f (t)dt ，则 (x) f (t)dt Φ[( x)]，
a
a
所以
d
(x)
f (t)dt Φ[ ( x)] ( x) f [( x)]( x) .
dx a
7
更一般地，设 ( x) ， ( x) 在[a, b] 上可导,则
d (x)
f (t)dt
dx ( x)
§6.3 微积分基本定理
用定义求定积分实际上是行不通的,下面介绍计算定积分的方法
原函数存在定理牛顿-莱布尼茨公式
1
原函数存在定理
定理6.3 设函数f ( x)在[a, b]上连续, 则变上限积分
x
Φ( x) a f (t)dt
在[a, b]上可导, 且
Φ( x) d
x

《微积分的基本定理》课件

物理
在物理学科中，该定理可以用来解决各种物理量如质量、速度、力等的积分问题，例如计算物体的动量、动能等。
工程
在工程领域，该定理可以用来解决各种实际问题的积分计算，例如计算电路中的电流、求解流体动力学中的压力分布等。
02 定理的证明
定理证明的思路
明确问题
首先，我们需要明确微积分的基本定理是关于什么的，以及它要解决的问题是什么。
难点2
如何利用积分运算法则简化每个小部分的积分。
关键点1
理解定积分的定义和性质，以及它们在证明定理中的作用。
关键点2
掌握导数的定义和性质，以及它们在推导原函数值增量中的应用。
03 定理的推论和扩展
推论一：积分中值定理
总结词
积分中值定理是微积分中的一个重要定理，它表明在闭区间上连续的函数一定存在至少一个点，使得该函数在此点的值为该区间上函数积分的平均值。
详细描述
积分中值定理是微积分中的一个基本定理，它表明如果一个函数在闭区间上连续，那么在这个区间内一定存在至少一个点，使得该函数在这一点处的值等于该函数在整个区间上的平均值。这个定理在解决一些微积分问题时非常有用，因为它可以帮助我们找到函数在某个点处的值，而不需要计算整个区间的积分。
推论二：洛必达法则
个定积分的值就是曲边梯形的面积。
应用实例二：求解不定积分
总结词
微积分的基本定理是求解不定积分的关键工具。
VS
详细描述
不定积分是微分学的逆运算，其求解过程需要用到微积分的基本定理。根据基本定理，不定积分∫f(x)dx = F(x) + C，其中 F(x)是f(x)的一个原函数，C是常数。通过基本定理，我们可以找到一个函数F(x)，使得F'(x) = f(x)。这样，我们就可以求解不定积分了。

微积分基本定理PPT课件

π 0
sinx dx = -cosx
π 0
= -cosπ - -cos0 = -cos2π - -cosπ = -cos2π - -cos0
=2
2π π
sinx dx = -cosx
2π π
= -2
2π 0
sinx dx = -cosx
2π 0
接下来让我们练一练吧
定积分的基本公式,又称牛顿 ----莱布尼兹公式.常表示为

b
a
f(x)dx = F(x) = F b - F a .
b a
例1. 计算 -1
3
1 解: 因为 arctanx = 1 + x2 由微积分基本定理得：
'
dx . 2 1+ x
dx 3 = arctanx -1 -1 1 + x2 = arctan 3 - arctan -1
从几何意义上看，设曲线y=y(t) 上与 t i-1 对应的点为P，PD是P点处的切线，由导数的几何意义知，切线PD的斜率等于y' ti-1 ，于是
Δs i ≈ h i = tan∠DPCgΔt = y t i-1 Δt
'
物体的总位移s
s = Δsi ≈ hi = v t i-1 Δt
教学目标
知识与能力
了解微积分的概念和推导过程以及基本思想，并能利用微积分的定义解决实际问题.
过程与方法
通过实例（如变速运动物体在某段时间内的速度与路程的关系），直观了解微积分基本定理的含义．
情感态度与价值观
微积分是大学阶段的数学必修，是高等数学的基础组成部分.高中阶段的导数是其基础.

( 人教A版)微积分基本定理课件 (共38张PPT)

2
2
答案：D
3．设 f(x)＝x22－，x0，≤1x<≤x≤1，2，
则2f(x)dx 等于________． 0
解析：2f(x)dx＝1x2dx＋2(2－x)dx
0
0
1
＝x3310 ＋(2x－x22)21
＝13＋[(2×2－222)－(2－12)]＝56.
答案：56
探究一计算简单函数的定积分
[自主梳理]
如果 f(x)是区间[a，b]上的连续函数，并且 F′(x) 内容＝ f(x)，那么bf(x)dx＝ F(b)－F(a)
a
符号
bf(x)dx＝F(x)ba ＝ F(b)－F(a)
a
二、定积分和曲边梯形面积的关系设曲边梯形在 x 轴上方的面积为 S 上，x 轴下方的面积为 S 下，则 1．当曲边梯形的面积在 x 轴上方时，如图(1)，则bf(x)dx＝ S 上．
(7)baxdx＝lnaxaba (a>0 且 a≠1)． a
1．计算下列定积分．
(1)1(x3－2x)dx； 0
(2)
2 0
(x＋cos
x)dx；
(3
解析：(1)∵(14x4－x2)′＝x3－2x，
∴1(x3－2x)dx＝(14x4－x2)10 ＝－34. 0
2．(1)若
f(x)＝x2 cos
x≤0 x－1
x>0
2．常见函数的定积分公式： (1)bCdx＝Cxba (C 为常数)．
a
(2)abxndx＝n＋1 1xn＋1ba (n≠－1)． (3)bsin xdx＝－cos xba .
a
(4)bcos xdx＝sin xba . a
(5)b1xdx＝ln xba (b>a>0)． a

课件：微积分基本公式

二、积分上限函数及其导数
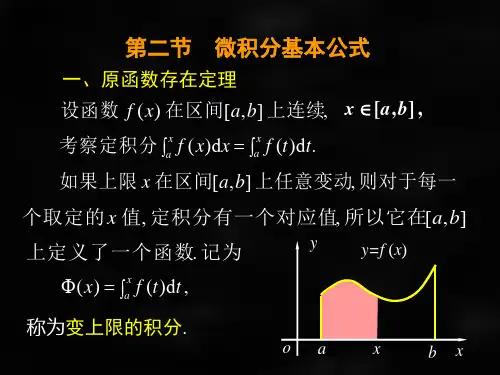
设f ( x)在[a,b]上连续, x [a,b],
记 ( x) ax f (t)dt ----积分上限函数
◆积分上限函数的重要性质：
定理1 若f ( x)在[a,b]上连续,则积分上限函数
( x) ax f (t )dt在[a,b]上可导,且x (a,b)有 :
( x)
其中: I可以为任意形式的区间.
d
x
x
f (t)dt [ f (t)dt] f (x)
dx a
a
例1 已知f ( x) 0x t 2 sin tdt,求f ( x). 解 f ( x) [0x t 2 sin tdt ] x2 sin x.
例2
已知f
(
x)
x2
0
t2
sintdt,求f
证 x (a,b),
y
( x x) axx f (t )dt
( x x) ( x)
axx f (t )dt ax f (t )dt
( x) (x)
o a x x x b x
x
f (t)dt
x x
f (t)dt
x
f (t)dt
x x
f (t)dt,
a
x
a
x
由积分中值定理得:
sin x
arctan x
xf
(t )dt ,
求g( x).
思考题解答
1. 已知f ( x)在[a,b]上连续,问ax f (t )dt与xb f (u)du 是谁的函数? 它们在[a , b]上可导吗? 如可导, 求其导数.
解: 都是x的函数; 可导;
d dx
ax

微积分的基本公式PPT幻灯片课件

一个原函数, 则
b a
f
(x)d x

F ( x)
b a

F (b)
于是
0 | F(x) | |
x x
f (t)dt |
xx
| f (t) | dt Mx
x
x
由夹逼定理及点 x 的任意性, 即可得 F (x) C([a,b]) .
7
定理1说明: 定义在区间[a,b] 上的积分上限函数是连续的.
积分上限函数是否可导?
8
由 F(x x) F(x)
xx
f (t)dt,
x
如果 f (x) C([a,b]), 则由积分中值定理, 得
xx
F(x x) F(x) x f (t)dt f ( )x ,
( 在 x 与 x x 之间)
故 lim F (x x) F (x) lim f ( )x
x0
推论2 基本初等函数在其定义域内原函数存在.
推论3 初等函数在其有定义的区间内原函数存在.
17
2. 微积分基本公式
如果 f (x) C([a,b]), 则
x
f (t)dt
为 f (x) 在[a,b] 上
a
的一个原函数.
若已知 F (x) 为 f (x) 的原函数, 则有
x
a f (t)dt F (x) C0.
( x)
F(x) ( a f (t)dt ) f ((x)) (x) .
14
例3
e1 t2 d t
计算 lim x0
cos x
x2
.
解
e1 t2 d t
cos x et2 d t

《微积分学基本定理,微积分基本公式》图文课件

b
a
f ( x )dx F ( x ) | F ( b ) F ( a )
b a
计算定积分的方法: f ( x )dx
a
b
(1)定义法 ( 2)面积法(曲边梯形面积 ) ( 3)公式法( 微积分基本定理 )F ( x ) f ( x )
/

b
a
f ( x )dx F ( x ) | F ( b ) F (a )
基本的不定积分公式: (1) K dx Kx C ; 1 ( 3) dx ln | x | C x (4) e dx e C
x x
1 n 1 ( 2) x dx x C n1
n
a (5) a dx C ln a
x
x
(6) ln xdx x ln x x C (8) sin xdx cos x C
v ( t )dt s(T2 ) s(T1 ). 其中 s(t ) v(t ). T
1
T2
三、牛顿—莱布尼茨公式
微积分基本定理
[a , b ] 上如果F ( x ) 是连续函数 f ( x ) 在区间
的一个原函数，则a f ( x )dx F (b) F (a ) .
牛顿—莱布尼茨公式
b
a f ( x )dx F (b ) F (a ) F ( x )
b
b a
微积分基本公式表明：
一个连续函数在区间[a , b] 上的定积分等于 [a , b] 上的增量. 它的任意一个原函数在区间
求定积分问题转化为求原函数的问题. 注意当a b 时， f ( x )dx F (b) F (a ) 仍成立. a

微积分第二版课件第二节微积分基本公式

y
y=f (x)
(x) ax f (t)dt ,
称为变上限的积分.
oa
x
bx
定理（微积分基本定理）
若函数f (x)在区间[a,b]上连续，则变上限函数
Φ(x)
x
f (t)dt
(a
x b)在[a,b]上具有导数，且
a
Φ '(x)
d dx
ax
f
(t
)dt
f (x)
(a x b).
即上限函数Φ(x)是f (x)在[a,b]上的一个原函数.
对应变上限积分函数还有变下限积分函数
(x) xb f (t)dt 对于变上（下）限积分函数也可以进行函数的复合，由变上限积分函数导数与复合函数求导法则有结论：
若函数 (x), (x) 可微，函数 f (x) 连续，则
(1) d dx
a x
f
(t)dt
d dx
x a
f
(t
)dt
f (x)
0
cos
t
2
d
t
x2
lim
x0
2x cos 2x
x4
lim cos
x0
x4
1
1
lim
x0
0xarctan x2
tdt
.
lim
x0
arctan 2x
x
1 2
lim
x0
1
x2
1
1. 2
二、微积分基本公式
变速直线运动的路程问题
设物体作变速直线运动其路程函数为s=s(t) , 速度
函数为v=v(t) .则在时间间隔 [T1,T2 ] 内有
根据导数的定义及函数的连续性，有

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

牛顿－莱布尼茨公式
例:求 2 x 2 d x 和 2 t 2 d t
1
1
例:求 y2cosx在 x [ 0 , ] 的平均值. 2
例:连续可导函数 f (x) 有 f (a) = 3, f (b) = 5, 求
b f ( x)dx. a
积分上限函数的导数
利用牛顿—莱布尼茨公式反过来理解积分上限函数 (注:此为非正规方式)
x
(x)a f(t)dt
就是 f (x) 在 [a , b] 上的一个原函数.即:
(x)f(x) 或 (x) f(x)dx
例:函数 f (t ) = t 的积分上限函数 (x)
x
tdt
0
(x)f(x)x
原函数存在定理
x
(x )af(t)d t (x )f(x )
证:
xx
x
(xx)(x) f(t)dt f(t)dt
例:已知
f
(x)
x x2
0 x1 ,求 1 x2
2
f ( x)dx.
0
y
f (x)
O
1 2x
例:已知
x2 f (x) ex
1 x2
,求
0 x1
2
f ( x)dx.
0
牛顿－莱布尼茨公式
例:求 cos x dx 0
例:求 sin x dx
2
例:求 1 x dx 0
2
例:求 2x 1 dx 0
F(x)(x)C, x[a,b]
当 x = a 得 F(a) (a)C,
牛顿－莱布尼茨公式
a
(a )af(x )d x0 F (a )C
( x ) F ( x ) C F ( x ) F ( a )
b
(b)af(t)dtF (b)F (a)
又因为定积分的值与积分变量字母无关,
b
dxex 2xsinx2exsinex
例:求 d
2x
cos tdt
dx ln x
积分上限函数的导数
连续积分上限函数 (x)
x
f(t)dt
满足:
a
a
(a) f(t)dt0 ,则有 a
x
lim (x)lim f(t)dt0
x a
x a a
x
sin tdt
例:求 lim x 0
0
x2
x
t(t 1)dt
a
a
xx
x f(t)dt
存在 [x,xx]可使 xxf(t)dtf()x x
( x ) lim ( x x ) ( x ) lim f() x f( x )
x 0 x
x 0 x
原函数存在定理
x
(x )af(t)d t (x )f(x )
d
例:求
xln2(t 1)dt
x2 costdt
sint
x2
sin(x2)sina
a
a
d
x2
costdt
[sin(x2)sina]
2xcosx2
dx a
积分上限函数的导数
定理: d (x)f(t)dtf[(x)](x);
dxa
例:求 d sin x e t d t
dx 0
例:求 d
x2 sin t dt
dx ห้องสมุดไป่ตู้ t
例:求 d
dx 0
d1
例:求 dx
cos tdt
x
思考:已知 x f(t)dtln(x21) , 求 f (1). 0
提示:
x
(x ) f(t)d t (x )f(x )
a
牛顿－莱布尼茨公式
定理若 F(x) 是连续函数 f (x) 在区间 [a , b] 上的
一个原函数,则
bf(x)d xF (x)bF (b )F (a).
例:求
lim
x1
1
( x 1)2
积分上限函数的导数
0
ln(t 1)dt
例:求 lim x x0
x2
cos x e t2 dt
思考: lim 1 x0
x2
2x
ln(1 t)dt
思考: lim 0 x0 1 cos x
定积分的物理意义变速直线运动的路程
a
a
例:
2
xdx
x2
2
22
02
2
0
2 22
0
例:求 2 x 2 d x 1
例:求
2
sin
xdx
2
牛顿－莱布尼茨公式
bf(x)d xF (x)bF (b )F (a).
a
a
x
证:设 F(x) 是 f (x) 的一个原函数, (x) f(t)dt a
(x)f(x), 即 Φ(x) 也是 f (x) 的原函数.
定理: d (x)f(t)dtf[(x)](x);
dxa
例:求 d
1
cos 2tdt
dx ex
例:求 d 1 ln(1t2)dt dx 2x
积分上限函数的导数定理:
d d x (( x x ))f(t)d t f[(x )](x ) f[(x )](x ).
例: d x2sintdtsin(x2)(x2)sin(ex)(ex)
设: F(t)f(t),则
(x) xf(t)dtF(t)xF(x)F(a)
a
a
(x)[F(x)F(a)]F(x)f(x)
例: (x) xcostdtsintxsinxsin0sinx
0
0
(x)cosx
积分上限函数的导数例:试用牛顿—莱布尼茨公式理解下列积分上限函数.
(x) x t2dt 1
0
(x) x costdt
(x) sinxetdt 0
x2
(x) 0 costdt
积分上限函数的导数
定理: d (x)f(t)dtf[(x)](x);
dxa
例: dx 2c o std t c o s(x 2)(x 2) 2 x c o sx 2 d xa
也可用牛顿—莱布尼茨公式理解此定理
微积分基本公式优秀课件
积分上限函数
例:函数 f (t ) = t 的积分上限函数
x
x
( x ) 0 f (t)d t 0 td t y
x2
x
(x)
2
1
1
(1) 0 td t 2
O
2
(2 ) 0 td t 2
yt
(x) xt
原函数存在定理
定理如果 f (x) 在 [a , b] 连续,则积分上限函数
b
af(x )d x af(t)d t F (b ) F (a )
牛顿－莱布尼茨公式
bf(x)d xF (x)bF (b )F (a).
a
a
例:求
1
(
x 2ex)dx
0
例:求
e
2
( x )dx
1
x
1
2
例:求 (2 x )dx
0
x
例:求 4(cosxsec2 x)dx 0
牛顿－莱布尼茨公式
2x
t tan tdt
dx 0
积分上限函数的导数
定理: d (x)f(t)dtf[(x)](x);
dxa
设 F(t)f(t) ,则
(x) f (t)dt F(t)(x) F[(x)]F(a);
a
a
d
( x)
f (t)dt {F[(x)]F(a)}
dx a
f[(x)](x).
积分上限函数的导数