积分表模板

欢迎阅读常 用 积 分 公 式（一）含有ax b +的积分(0a ≠)1．d x ax b +⎰＝1ln ax b C a ++2．()d ax b x μ+⎰＝11()(1)ax b C a μμ++++（1μ≠-）3．d x x ＝21(ln )ax b b ax b C +-++4．5．6．7．8．9．10．11．12．x x ⎰＝22232(15128105a x abx b C a-+13．x＝22(23ax b C a -+14．2x＝22232(34815a x abx b C a -+15．＝(0)(0)C b C b ⎧+>+<16．2a bx b -- 17．18．19．20．21．22．23．24．22d x x ax b +⎰＝2d x b xa a axb -+⎰ 25．2d ()x x ax b +⎰＝221ln2x C b ax b++ 26．22d ()x x ax b +⎰＝21d a xbx b ax b--+⎰27．32d ()x x ax b +⎰＝22221ln 22ax b a C b x bx +-+ 28．22d ()x ax b +⎰＝221d 2()2x xb ax b b ax b+++⎰（五）含有2ax bx c ++(0)a >的积分29．2(4)C b ac+<30．31．32．33．34．35．36．37．1ln aC a x + 38．C + 39．x 2ln(2a x C +++40．x ＝2243(25ln(88x x a a x C +++41．x ⎰C42．x x ⎰＝422(2ln(88x a x a x C +-++43．x a C +44．45．46．47．48．49．50．51．52．C +53．x 2ln 2a x C ++54．x ＝2243(25ln 88x x a a x C -+++55．x ⎰C +56．x x ⎰＝422(2ln 88x a x a x C --++57．x arccos aa C x +58．2d x x ⎰＝ln x C x-+++(0)a >的积分59．60．61．62．63．64．65．66．67．x 2arcsin 2a x C a++68．x ＝2243(52arcsin 88x xa x a C a -+69．x ⎰＝C70．xx ⎰＝422(2arcsin 88x a x x a C a-+71．x a C +72．x ＝arcsin xC a-+(0)a >的积分73．2ax b C +++74．75．76．77．78．79．80．81．82．x 2()4b a C - （十一）含有三角函数的积分 83．sin d x x ⎰＝cos x C -+ 84．cos d x x ⎰＝sin x C +85．tan d x x ⎰＝ln cos x C -+ 86．cot d x x ⎰＝ln sin x C +87．sec d x x ⎰＝ln tan(42xC π++＝ln sec tan x x C ++88．csc d x x ⎰＝ln tan2xC +＝ln csc cot x x C -+ 89．290．91．92．93．94．95．96．97．98．99．100．2()2()a b a b +-101．sin sin d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b -++-++-102．cos cos d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b ++-++-103．d sin xa b x +⎰tanxa b C ++22()a b >104．d sin x a b x +⎰C+22()a b <105．d cos xa b x +⎰)2x C +22()a b >106．107．108．109．110．⎰111．⎰112．⎰113．⎰114．⎰115．2arcsin d xx x a⎰＝3221arcsin (239x x x a C a +++116．arccos d x x a ⎰＝arccos xx C a-+117．arccos d xx x a ⎰＝22(24x a x C a --+ 118．2arccos d xx x a⎰＝3221arccos (239x x x a C a -++119．arctan d x x a ⎰＝22arctan ln()2x ax a x C a -++120．arctan d x x x a ⎰＝221()arctan 22x aa x x C a +-+121．2arctan d xx x a⎰＝33222arctan ln()366x x a a x a x C a -+++（十三）含有指数函数的积分122．d x a x ⎰＝1ln xa C a +123．ax 1ax124．125．126．127．128．129．130．131．132．133．134．135．(ln )d n x x ⎰＝1(ln )(ln )d n n x x n x x --⎰136．(ln )d m n x x x ⎰＝111(ln )(ln )d 11m n m n nx x x x x m m +--++⎰ （十五）含有双曲函数的积分137．sh d x x ⎰＝ch x C + 138．ch d x x ⎰＝sh x C +139．th d x x ⎰＝lnch x C +140．2sh d x x ⎰＝1sh224x x C -++ 141．2ch d x x ⎰＝1sh224x x C ++（十六）定积分142．cos d nx x π-π⎰＝sin d nx x π-π⎰＝0143．cos sin d mx nx x π-π⎰＝0144．π-π⎰145．π-π⎰146．0π⎰147． I I 4253I ⋅⋅ 31422I π⋅⋅⋅一、 .? ??注: 含有a) ??可令b) ?可令 c)?可令当有理分式函数中分母的阶较高时, 常采用倒代换. 三、第二换元积分法 ?????????? ,例题：凑微分法例1求不定积分.例2 求不定分例3计算不定积分.例4 计算不定积分例5求不定积分.例6例7例8例9例;??????????????? (2)?例??? (1)? ????? (2)?例求不定积分.例求不定积分.例?(1)? ????例求下列不定积分???? (1)? ??? (2) ?例16求不定积分.例17求.例18 ?用换元法求不定积分?例19 试用换元法求不定积分?例20试用换元法求不定积分例21求不定积分.例22 求不定积分?第二换元法??? 例23?求不定积分例例例例例.例?例.例.2.设,。

排球规则与比赛顺序：
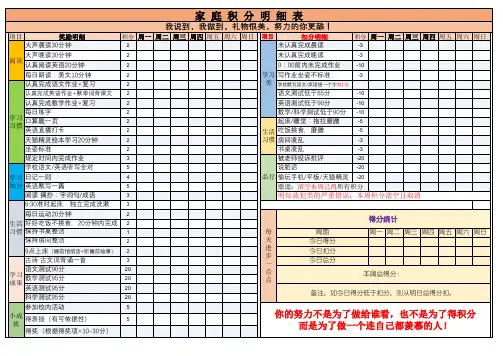
1、本次比赛采取5局三胜制，某队在先赢得25分之后为胜一
局，先胜三局的队伍则取得一场比赛的胜利。

当比赛双方
比分为24:24时,一方必须领先对方2分才能取胜。

如果比
赛已经进行了4局,比赛双方比分为2：2时.第五局比赛到
8分时，双方交换场地，比赛继续进行，先到15分的队伍，并净胜俩分为取胜。

2、此次比赛采用循环积分制,四支队伍，依次轮番比赛,进行
积分,胜一局记俩分，负一局记一分，最后按分数高低排列。

如果积分一样:A（胜局总数）/B(负局总数）=C值，C值高
者名次列前。

如C值仍相等,则采用：X（总得分数)/Y(总
失分数）=Z值，Z值高者名次列前.
3、各组出俩名裁判，一名主裁一名副裁，一名记录员。

以下
是比赛编排表。

社体三班比赛编排表
第一局第二局第三局
第一组——第三组第一组——第四组第一组——第二组第二组——第四组第三组——第二组第四组—-第三组。

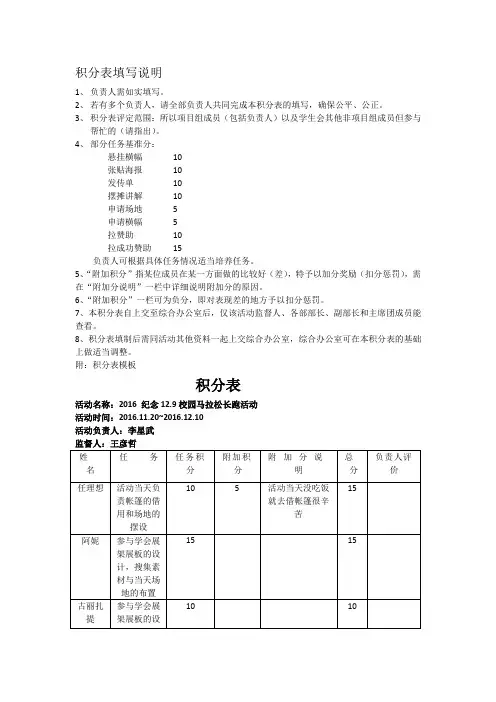
积分表填写说明
1、负责人需如实填写。

2、若有多个负责人，请全部负责人共同完成本积分表的填写，确保公平、公正。

3、积分表评定范围：所以项目组成员（包括负责人）以及学生会其他非项目组成员但参与
帮忙的（请指出）。

4、部分任务基准分：
悬挂横幅10
张贴海报10
发传单10
摆摊讲解10
申请场地5
申请横幅5
拉赞助10
拉成功赞助15
负责人可根据具体任务情况适当培养任务。

5、“附加积分”指某位成员在某一方面做的比较好（差），特予以加分奖励（扣分惩罚），需在“附加分说明”一栏中详细说明附加分的原因。

6、“附加积分”一栏可为负分，即对表现差的地方予以扣分惩罚。

7、本积分表自上交至综合办公室后，仅该活动监督人、各部部长、副部长和主席团成员能查看。

8、积分表填制后需同活动其他资料一起上交综合办公室，综合办公室可在本积分表的基础上做适当调整。

附：积分表模板
积分表
活动名称：2016 纪念12.9校园马拉松长跑活动
活动时间：2016.11.20~2016.12.10
活动负责人：李星武
填写人：李星武2016年12月15日。