条件分式求值的方法与技巧

5、有条件的分式的化简与求值给出一定的条件，在此条件下求分式的值称为有条件的分式求值．而分式的化简与求值是紧密相连的，求值之前必须先化简，化简的目的是为了求值，先化简后求值是解有条件的分式的化简与求值的基本策略． 解有条件的分式化简与求值问题时，既要瞄准目标，又要抓住条件；既要根据目标变换条件，又要依据条件来调整目标，除了要用到整式化简求值的知识方法外，还常常用到如下技巧： 1．恰当引入参数；2．取倒数或利用倒数关系； 3．拆项变形或拆分变形； 4．整体代人；5．利用比例性质等． 、【例l 】若,a d d c c b b a ===则dC b a d c b a +-+-+-的值是 (“希望杯”邀请赛试题)思路点拨 引入参数，利用参数寻找a 、b 、c 、d 的关系．【例2】如果a+b+C=0，,0312111=+++++C b a 那么++++22)2()1(b a 2)3(+C 的值为( )． A ．36 B ．16 C ．14 D ．3(2005年“CASl0杯”武汉市选拔赛试题) 思路点拨联想到(a+b+c)2的展开式，解题的关键是对条件a+b+c= 0的变形． 【例3】 已知xyz=1，x+y+z=2，,16222=++z y x 求代数式++z xy 21yzx x yz 2121+++的值．(北京市竞赛题)思路点拨 直接通分，显然较繁，由x+y+z=2，得z=2一x 一 Y ，x=2- Yz ，y=2一x —z ，从变形分母人手．【例4】 已知,1325))()(())()((=+++---a c c b b a a c c b b a 求a c c c b b b a a +++++的值． (“北京数学科普日”攻擂赛试题)思路点拨 已知条件是⋅+-+-+-ac ac c b c b b a b a 、、三个数的乘积，探求这三个数的和与这三个数的积之间的关系，从而求出ac ac FC b c b b a b a +-+--++-的值是解本例的关键． 【例5】(1)解方程：;81209112716512312222=+++++++++++x x x x x x x x(第19届江苏省竞赛题)(2)已知方程c c x x 11+=+(c 为不等于0的常数)的解是C 或,1c 求方程x+aa a x 2136412++=-的解(a 为不等于0的常数)．(第16届“希望杯”邀请赛试题)思路点拨解分式方程涉及到分式的运算、化简，对特殊分式方程常需对方程进行拆项、拆分、分步计算等变形，运用巧取倒数、整体求解等策略．对于(1)，寻找．分母的共同特征；对于(2)，在阅读理解的基础上，把方程左、右两边拆分为倒数和．1．已知x2+x 一3=0，那么1332---x x x =(淄博市中考题)2．已知abc≠0，且,a c c b b a ==则=--++cb ac b a 3223 (第16届“希望杯”邀请赛试题)3．若a 、b 、c 满足a+b+C=0，abc>0，且x=++=++)11(,||||||cb a yc c b b a a ),11()11(b a c a c b +++ 则 x十2y+3xy=(“祖冲之杯”邀请赛试题)4．已知． x2—3x+1=0，则1242++x x x 的值为(2004年重庆市竞赛题)5．若,b a b a x +-=且以≠0，则a b等于( )． x x A +-11. x x B -+11. 11.+-x x C 11.-+x x D (2005年天津市竞赛题)6．设a 、b 、c 是三个互不相同的正数，如果,abb ac b c a =+=-那么( )． A ．3b=2c B ．3a=2b C ．2b=c D ．2a=b(“祖冲之杯”邀请赛试题)7．若4x 一3y -6z=0，x+2y 一7z=0(xyz≠O)，则代数式222222103225x y x z y x ---+的值等于 ( )。

分式运算综合题1、先化简，再求值：（1-x x －11+x ）÷112-x ，其中x=22、先化简，再求值：21+-a a ·12422+--a a a ÷112-a ，其中a 满足a 2-a=12。

3、计算：223y x y x -+－222y x y x -++2232y x yx --。

4、化简：12+x x -1422-+x x ÷1222+-+x x x ，然后在不等式x ≤2的非负整数解中选择一个适当的数代入求值。

5、已知M=222y x xy -，N=2222y x y x -+，P=224x y xy-，用“＋”或“-”连接M ，N ，P 有多种不同的形式，如M+N-P 。

请你任选一种进行计算，并化简求值，其中x ：y=5:2。

6、已知abc ≠0且a+b+c=0,求a(b 1+c 1)+b(c 1+a 1)+c(a 1+b1)的值。

7、已知两个式子：A=442-x ，B=21+x ＋x-21，其中x ≠±2，则A 与B 的关系是（ ）A.相等B.互为倒数C.互为相反数D.A 大于B8、已知1＜x ＜2，则式子|2|2--x x －1|1|--x x ＋xx ||化简的结果是（ ）A.－1B.1C.2D.39、已知a2+3ab+b2=0(a ≠0,b ≠0)，则式子a b +ba= 。

10、已知a 1+b 21=3，则式子b a ab b ab a 634452--+-= 。

11、已知3-x m －2+x n =)2)(3(17+-+x x x ，求m 2+n 2的值。

12、已知a,b 为实数，且ab=1，设M=1+a a +1+b b ，N=11+a ＋11+b ，试确定M ，N 的大小关系。

13、先化简，再求值：（x-13+x x ）÷1222++-x x x ,其中x 满足x 2+x-2=0.14、已知A=（x-3）÷4)96)(2(22-+-+x x x x －1,(1)化简A; 2x-1＜x,(2)若x 满足不等式组 且x 为整数，求A 的值。

分式求值技巧
2023年中考复习
设参数k法
方法介绍
当题目给出的条件出现连比形式，或者连等式时，经常采用增设参数k的方法，用含参数k的代数式表示分式中的各字母．在化简求值过程中，参数k最终都能消去，即可求出结果．
例1：
解答：
例2：
解答：
设定主元法
方法介绍
当题目中给出2个字母，却只给出1个方程，或者给出3个字母，却只给出2个方程时，我们无法具体求出每个字母的值．因此，可以设定其中一个字母作为主元，用含主元的代数式来表示其他字母，从而可以在分式化简中，达到只含有主元的目的，最终消去主元求值．
例1：
解答：
例2：
解答：
整体同除法
方法介绍
对于有些题目，我们可以从需要求值的分式入手，将分子分母同除分式中次数最高的项，以达到让分式中出现与已知条件相关的代数式，从而可以将已知条件作为整体，代入求值．
例1：
解答：
例2：
解答：
用乘法公式
方法介绍
对于一些本身，或者通分后含平方和类型的分式，我们可以联系以前所学的乘法公式，利用配方等方法，对分式进行变形，从而更快求解．
例1：
解答：
例2：
解答：
特殊值法
方法介绍
这是最后没有办法的办法了，适用于选择填空题．对于一些无法求出具体数值的字母，我们可以根据已知条件，取字母的一组特殊值，然后代入求解．当然，如果你不确定结果是否正确，可以多代几组特殊值检验．
例1：
解答：
例2：
解答：。

分式求值的技巧点拨胡伟在分式运算中，常遇到求值问题，这类问题题型多样，技巧性强，若根据题目中分式的结构特点，采用适当方法，则可巧妙获解。

一、巧用配方法求值例1 已知01x 5x 2=+-求44x 1x +的值。

解：由0x 01x 5x 2≠=+-知，由此得5x 1x =+∴2)x1x (x 1x 22244-+=+ 5272]2)x1x [(22=--+= 说明：在求解有关分式中两数（或两式）的平方和问题时，可考虑用完全平方公式进行解答。

二、巧用因式分解法求值例2 先化简，再求值：1n mn )n m n mn n mn 2m n m (22222--+-+--。

其中231m -=，231n +=。

解：原式=1n mn ])n m )(n m ()n m (n )n m (n m [2--++--- n m mn 1n mn n m n 11n mn )n m n n m 1(--=-⋅--=----= ∵23231m --=-=，23231n +-=+=∴1)23)(23(mn -=+---=，4)23()23(n m -=+----=- ∴41n m mn -=--=原式 说明：因式分解法是一种重要的数学方法，解决很多数学问题都要用到它，尤其是在分式化简和分式的四则运算中运用较多。

因此，希望同学们对因式分解的各种方法熟练掌握。

三、巧用整体代入法求值例3 已知3b 1a 1=-，求bab 2a b 2ab 3a 2---+的值。

解：由3b1a 1=-变形得ab 3b a -=-，代入所求式得： 原式ab 2)b a (ab 3)b a (2--+-= 53ab 2ab 3ab3ab 6=--+-=说明：在解答给定条件下求分式的值这类问题时，需要把待求值的分式进行恒等变形，转化成能用已知条件表示的形式，再代入计算，或先把条件进行化简再采用上述方法求值。

四、巧设参数（辅助未知数）求值例4 已知实数x 、y 满足x:y=1:2，则=+-yx y x 3__________。

分式求值的常用技巧分式是一种特殊类型的数学表达式，它包含有一个或多个数（称为分子）除以另一个数（称为分母）。

分式可以代表有理数和算术运算，例如加法、减法、乘法和除法。

在解决分式求值问题时，有一些常用的技巧可以帮助我们简化计算和得出结果。

1.化简分式首先，我们可以通过化简分式来简化计算过程。

化简分式的目的是找到分子和分母的最大公约数，并将分子和分母都除以它，使分式更简单。

例如，考虑分式12/24，我们可以找到最大公约数为12，并将分子和分母都除以12，得到1/2、这样，原分式就被化简为最简分式。

2.找到分子和分母的公因式在一些分式中，分子和分母可能有一个或多个公因式。

我们可以通过找到它们来简化计算。

例如，考虑分式16/24，我们可以发现分子和分母都可以被2整除。

我们可以将16除以2得到8，24除以2得到12，从而得到化简后的分式8/12、然后，我们可以继续找到8和12的最大公约数，并将它们化简为最简分式。

3.交换分子和分母的位置有时候，分式的分子和分母的位置可以互换。

我们可以利用这个性质来简化计算。

例如，考虑分式1/4，我们可以将分子和分母互换，得到4/1、然后，我们可以将4除以1得到4，从而得到最简分式44.将分式转化为小数形式有时候，将分式转化为小数形式可以更便于计算。

我们可以通过将分子除以分母来得到分数的小数形式。

例如，考虑分式3/5，我们可以将3除以5得到0.6、这样，我们就得到了分式的小数形式。

5.使用乘法和除法的性质在进行分式求值时，我们可以利用乘法和除法的性质来简化计算。

例如，考虑分式(2/3)*(4/5)，我们可以将分子和分母相乘得到8/15、同样的，如果我们考虑分式(2/3)/(4/5)，我们可以将分子乘以分母的倒数得到(2/3)*(5/4)，然后进行乘法操作得到10/12，最后化简为5/66.使用加法和减法的性质在进行分式求值时，我们还可以利用加法和减法的性质来简化计算。

例如，考虑分式(2/3)+(4/5)，我们可以找到两个分数的公共分母，然后将分子相加得到一个新的分数作为结果。

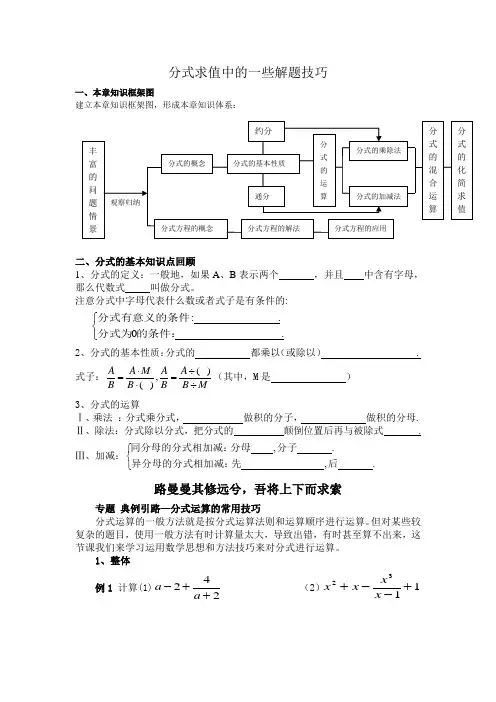
分式求值中的一些解题技巧一、本章知识框架图建立本章知识框架图，形成本章知识体系：二、分式的基本知识点回顾1、分式的定义：一般地，如果A 、B 表示两个 ，并且 中含有字母，那么代数式 叫做分式。

注意分式中字母代表什么数或者式子是有条件的:.0 .⎧⎨⎩分式有意义的条件:分式为的条件：2、分式的基本性质：分式的 都乘以（或除以） . 式子：MB A B A B M A B A ÷÷=⋅⋅=)(,) (（其中，M 是 ） 3、分式的运算 Ⅰ、乘法 ：分式乘分式， 做积的分子， 做积的分母. Ⅱ、除法：分式除以分式，把分式的 颠倒位置后再与被除式 .Ⅲ、加减：⎩⎨⎧. , . , 后先异分母的分式相加减：分子分母同分母的分式相加减：路曼曼其修远兮，吾将上下而求索专题 典例引路—分式运算的常用技巧分式运算的一般方法就是按分式运算法则和运算顺序进行运算。

但对某些较复杂的题目，使用一般方法有时计算量太大，导致出错，有时甚至算不出来，这节课我们来学习运用数学思想和方法技巧来对分式进行运算。

1、整体例1 计算(1)242++-a a （2）1132+--+x x x x观察归纳丰富的问题情景分式的概念分式方程的概念分式方程的解法 分式方程的应用分式的基本性质通分约分分式的运算分式的乘除法分式的加减法 分式的混合运算 分式的化简求值例2 .3353,511)1(的值求若yxy x yxy x y x ---+=-.111,1)2(的值求已知++++++++=c ac cb bc b a ab a abc.3515x 5,411x )3(224242的值求如果xx x x +-=++整体思想就是考虑数学问题时，不是着眼于它的局部特征，而是把注意和着眼点放在问题的整体结构上，通过对其全面深刻的观察，从宏观整体上认识问题的实质，把一些彼此独立但实质上又相互紧密联系着的量作为整体来处理的思想方法。

整体思想在处理数学问题时，有广泛的应用。

浅析有条件的分式化简与求值问题342800　江西宁都三中　李雪樱 解有条件的分式化简与求值问题时,既要瞄准目标,又要抓住条件;既要根据目标变换条件,又要依据条件来调整目标,常常用到如下解题技巧.1　引入参数法此法的运用特点是当题目所给条件为连比等式的形式时,采用引入参数法进行转换1例1　已知a+b2=b-2c3=3c-a4,求5a+6b-7c8a+9b的值.分析　审视条件和待求式,设连比值为k,则a,b,c 分别能用参数k的倍数来表示,问题可迎刃而解.解　设a+b2=b-2c3=3c-a4=k,则a+b=2k,b-2c=3k,3c-a=4k,三式联立解方程组,得a=-115k,b=21 5k,c=35k.所以,5a+6b-7c8a+9b=5×(-11k5)+6×21k5-7×3k58×(-11k5)+9×21k5=50101.点评　通过引入参数k,将条件转化为方程组,然后用k分别表示a,b,c,代入分式中求解.通过引入参数,实现将多元(a,b,c)转变为一元(k)来求解,既有条不紊又方便快捷.例2　已知abc≠0,且a+bc=b+ca=c+ab,求(a+b)(b+c)(c+a)abc的值.分析　审视条件和待求式,设连比值为k,则待求式等于k3,若能求出k,问题获解.解　设a+bc=b+ca=c+ab=k,则a+b=kc,b+c=ka,c+a=kb,三式相加得2(a+b+c)=k(a+b+c),即(a+b+c)(k-2)=0,所以k=2或a+b+c=01当k=2时,(a+b)(b+c)(c+a)abc=2c2a2babc=8;由a+b+c=0,得出k=a+bc=-1.∵a+bc=k,∴k=-11当k=-1时,(a+b)(b+c)(c+a)abc=(-c)(-a)(-b)abc=-1. 所以∠H MD=∠H MP+∠PMD=∠QBP+∠MBD +∠ACB=∠ABC+∠ACB=180°-∠A,易证∠QO P=180°-∠A,所以∠QO P=∠HMD1又因为△COP∽△BOQ,所以CPBQ =O POQ=MDH M1所以△QO P∽△HMD,由此可得∠OQ P=∠MH D,因为OQ⊥A B,∠OQ P+∠A Q P=90°,由H M∥BQ 得到∠A Q P=∠MHQ,所以∠MHD+∠MHQ=90°,即DH⊥PQ.从而问题得证.这种证明的方法是利用三角形的中位线和相似变换,简洁明了,方法更具有创新性,思维也更周密通过对问题证法的探求,我们不但发现了新的证法,而且对题目有了更深刻、更本质的认识和把握.不仅沟通了相似变换、全等变换、三角形、四边形等知识之间的联系,更可贵的是我们形成了解决中点类问题的方法和策略,体悟了运用数学方法解决规律性探索问题的策略,可谓一举多得1笔者想借用罗增儒教授的话结束本文:对“解题过程的反思”继续把解题活动作为认识的对象,不仅关注如何获得解,而且寄希望于对“解”进一步分析,增强数学能力、优化认知结构、提高思维素质,学会“数学地思维”,重点在学会怎样解题.参考文献罗增儒.中学数学解题的理论与实际[M].广西:广西教育出版社,2008,9(收稿日期3)22　(2009年第6期初中版) 解题研究.:2009040 点评　本题引进参数k表示比值,一方面使已知条件便于使用,另一方面使待求式简化,一箭双雕.2　折项相消法此法的运用特点是题目中待化简式的全部或部分分式中,其分子或分母可以通过分解因式分拆为两项,使待化简式产生容易相抵消的某些项,从而简化求解过程.例3　化简分式2a 2+3a+2a+1-a2-a-5a+2-3a2-4a-5a-2+2a2-8a+5a-31分析　直接通分,则分子中a的次数最高可达到5次,运算将十分繁杂,显然不可取.审视各分式的结构,分子a的最高次数是分母次数的2倍,可将每一个分式拆分为两项,一项含其分母中的因式,一项为常数,以简化运算.解　原式=(2a+1)(a+1)+1a+1-(a-3)(a+2)+1a+2-(3a+2)(a-2)-1a-2+2(a-1)(a-3)-1a-3=[(2a+1)+1a+1]-[(a-3)+1a+2]-[(3a+2)-1a-2]+[2(a-1)-1a-3]=1a+1-1a+2+1a-2-1a-3=1(a+1)(a+2)+-1(a-2)(a-3)=-8a+4(a+1)(a+2)(a-2)(a-3).点评　拆分时要依据分母和分子中二次项的系数和一次项的系数进行;消减有关项后,巧用分组(两式相减且分母相差1)进而再通分,通过这种分步通分来简化运算.例4　化简1(x+2005)(x+2006)+1(x+2006)(x+2007)+1(x+2007)(x+2008)1分析　审视需要化简的式子结构,每个分式具有(+)的特征,而(+)=+,问题则迎刃而解解　原式=(1x+2005-1x+2006)+(1x+2006-1x+2007)+(1x+2007-1x+2008)=1x+2005-1x+2008=3(x+2005)(x+2008).点评　利用每个分式具有同一结构特征,通过裂项(拆项),使待化简式中出现若干对“相反数”,相消某些项从而得解.这种拆项相消法是分式化简中的常用技巧.3　取倒数变形法例5　化简b-c(a-b)(a-c)+c-a(b-c)(b-a)+a-b(c-a)(c-b)-2a-b-2c-a-2b-c1分析　审视需要化简的式子的结构特征,直接通分虽然也可行,但运算量比较大.利用a-b,b-c,c-a,对分子进行添项减项的恒等变形,使分式进行简化拆分相消,进而获解.解　原式=(a-c)-(a-b)(a-b)(a-c)+(b-a)-(b-c)(b-c)(b-a)+(c-b)-(c-a)(c-a)(c-b)-2a-b-2c-a-2b-c=1a-b-1a-c+1b-c-1b-a+1c-a-1c-b-2a-b-2c-a-2b-c=01点评　根据问题的特点,对分子进行某种变形,旨在优化解题过程.4　整体代入法此法的运用特点是所给的条件式的左端,或者待求式,取倒数后可变为几项之和,使条件与待求容易沟通.例6　已知aba+b=13,bcb+c=14,aca+c=15,求abcab+bc+ca的值.分析　审查条件式的结构和待求式的结构,取倒数后由分式变为和式,通过方程组的形式可求得1a+1b+1的值,再取倒数则可得待求式的值.若瞄准目标(待求式),设法将++用表示出,考察条件,不难实现32解题研究 (2009年第6期初中版)1n n11n n11n-1n1.cab bc c a abc .解　由已知条件取倒数,得1a +1b =3,1b +1c =4,1a +1c=5,三式相加得1a+1b +1c=6.所以abc ab +bc +ca =11a +1b +1c=16.点评　瞄准目标,抓住条件,对待求式变形和对条件变形,加以灵活运用,是顺畅解题的常用策略.例7　已知x x 2+x +1=a,a ≠0且a ≠12,求x2x 4+x 2+1的值.分析　若由条件式求出x,代入待求式求值,显然繁琐.若将条件式取倒数,则可以用x +1x这个整体来关联条件与待求,化难为易.解法1　由x x 2+x +1=a 及a ≠0,得x 2+x +1x =1a ,即x +1x =1a-1,所以x 4+x 2+1x 2=x 2+1x2+1=(x +1x )2-1=(1a-1)2-1=1-2aa2.又a ≠12,所以x 2x 4+x 2+1=a 21-2a(a ≠12).若注意到x 4+x 2+1=(x 2+x +1)(x 2-x +1),也可以形成另一种巧妙解法.解法2　由xx 2+x +1=a 及a ≠0,得x 2+x +1=x a ,x 2-x +1=x (1-2a )a ,所以当a ≠12时,x 2x 4+x 2+1=a21-2a.点评　观察是解题的门户,仔细观察,善于联想,在条件与结论之间寻找最便捷的桥梁,是学习数学的理想追求.5　整体运用法此法的运用特点是待求式通过变形可用某个“整体”来表示,而所给条件通过变形又可以求出这个“整体”例　若,都是正实数,且+=,求(ba)3+(ab)3的值.分析　由待求式的特征,联想到公式a 3+b 3=(a +b)3-3ab (a +b),即可知(ba )3+(a b)3=(b a +a b)3-3ba ab (b a+a b ),若能求出b a +a b这个整体,原问题即可获解.由条件可得b a -a b =1,进而b a +ab可求.解　因为1a -1b -1a +b=0,所以1a -1b =1a +b ,a +b a -a +b b =1,即b a -a b =1,所以(b a +a b)2=(b a -ab)2+4=5,即b a +ab=5,所以(b a )3+(a b)3=(b a +a b)3-3ba ab (b a +a b)=(5)3-35=25.点评　解答数学问题,应先紧扣待求问题寻觅解题途径,然后对照条件审视该途径是否通畅,若不通畅则继续寻觅,直到条件与寻觅的途径能够有效沟通.例9　如果a 是方程x 2-3x +1=0的根,试求2a 5-5a 4+2a 3-8a2a 2+1的值.分析　由条件得a 2-3a +1=0,显然求出a 值(2个)代入待求式求值十分繁琐,此路不可取.关注待求式,分母可以化为3a,分子则以整体(a 2-3a +1)来表示它,从而降次简化分子,便可简化待求式.解　由题意a 2-3a +1=0,用长除法,得到:2a 5-5a 4+2a 3-8a2=(a 2-3a +1)(2a 3+a 2+3a )-3a,所以,原式=(a 2-3a +1)(2a 3+a 2+3a)-3a3a=-3a3a=-1.点评　在解题时,细察题目的外形,把握问题的特征,展开联想,创设整体常常会使解题思路豁然开朗.运用整体方法的具体操作中常常有:整体构造、整体观察、整体换元、整体变形、整体代入等灵活而闪耀智慧光芒的变形是学习数学所要追求的理想境界之一(收稿日期3)42　(2009年第6期初中版) 解题研究.8a b 1a -1b -1a b0..:2009027。

分式化简求值几大常用技巧分式化简求值几大常用技巧在给定的条件下求分式的值，大多数条件下难以直接代入求值，它必须根据题目本身的特点，将已知条件或所求分式适当变形，然后巧妙求解.常用的变形方法大致有以下几种：1、 应用分式的基本性质 例1 如果12x x+=，则2421x x x ++的值是多少?解：由0x ≠，将待求分式的分子、分母同时除以2x ，得 原式=.22221111112131()1x x xx===-+++-.2、倒数法 例2 如果12x x+=，则2421x x x ++的值是多少?解：将待求分式取倒数，得42222221111()1213x x x x x x x++=++=+-=-=∴原式=13. 3、平方法例3 已知12x x+=，则221x x +的值是多少？解：两边同时平方，得22221124,42 2.x x x x ++=∴+=-=4、设参数法例4 已知0235a b c ==≠，求分式2222323ab bc aca b c+-+-的值. 解：设235ab ck ===，则 2,3,5a k b k c k===.∴原式=222222323532566.(2)2(3)3(5)5353k k k k k k k k k k k ⨯+⨯⨯-⨯⨯==-+--例5 已知,a b c b c a ==求a b c a b c+--+的值. 解：设a b ck bc a===，则 ,,.a bkb ckc ak ===∴3c ak bk k ck k k ck ==⋅=⋅⋅=， ∴31,1kk ==∴a b c ==∴原式= 1.ab ca b c+-=-+ 5、整体代换法例6 已知113,x y -=求2322x xy y x xy y+---的值. 解：将已知变形，得3,y x xy -=即3x y xy -=-∴原式=2()32(3)333.()23255x y xy xy xy xy x y xy xy xy xy -+⨯-+-===-----例： 例5. 已知a b +<0，且满足a a b ba b 2222++--=，求a b a b3313+-的值。

学科: 奥数教学内容：条件分式求值的方法与技巧求条件分式的值是分式化简、计算的重要内容，解题主要有以下三个方面：一、将条件式变形后代入求值例1已知432z y x ==，z y x z y x +--+22求的值．＝3)111(-++++a b c c b a ∵ a ＋b ＋c ＝0，∴ 原式＝－3．例4已知31=+xx ，求1242++x x x ．分析：∵ 1)1(111222224-+=++=++x x xx x x x ， ∴ 可先求值式的倒数，再求求值式的值．解：∵ 1)1(12224-+=++x x xx x 8132=-=，∴12=x ． 5332323)11(2)(23=--⨯-=-----=yx y x 分析：∵ 填空题不需要写出解题过程，故可取满足已知等式的特殊值求解． 解法三：取x ＝21，y ＝－1，)31211(=+=-yx ． ∴原式.532/52/3)1()1(21221)1(2)1(213212==---⨯⨯--⨯--⨯⨯+⨯= 注意：特殊值法是解填空题或选择题常用的解题方法或技巧．取特殊值要注意满足条件等式，其原则是要便于计算．例6 已知a 2＋2a －1＝0，求分式24)44122(22+-÷++--+-a a a a a a a a 的值． 解：原式＝42])2(1)2(2[2-+⋅+--+-a a a a a a a 42)2()1()2)(2(2-+⋅+--+-=a a a a a a a a 42)2(42-+⋅+-=a a a a a aa a a 21)2(12+=+= ∵ 0122=-+a a ，∴ 122=+a a ，∴ 原式＝1．122=+a a 技巧叫做整体代入．1．已知231=-x x ，求分式221xx +的值．2．已知01342=+++x x x ，先化简后求xx x -+-3932的值． 3．化简求值43326512222-+---+÷+--a a a a a a a a ，其中a ＝－3． 4．已知abc ＝1，则111++++++++c ca c b bc b a ab a 的值为________．。

分式求值五技巧求分式的值这种题型在《分式》一章中经常出现有些求值题用一般方法直接可以解答，但有些求值题用一般的方法解起来很困难所以我们要善于总结，寻找技巧，这样才能顺利解题以下向同学们介绍了几种常用的技巧一、巧用整体代换例1：已知：x 1=2，求221x 的值 分析：用x 1表示221x ，用已知式整体代换所求式 解：由x 1=2可得 ⎝⎛⎪⎭⎫+21x x =4所以221x = ⎝⎛⎪⎭⎫+21x x -2••x 1=4-2=2二、巧用变形代入：例2：已知：n m =4求2222n mn m mn m +--的值分析：先将求值式化简，再把已知条件变形代入解：由n m=4可得m=4n 代入原式，原式=)()(2n m n m m --=n m m -=n n n -44=n n 34=34 三、巧设比值代入例3：已知：2a =3b =4c 求分式222cb a ac bc ab ++++的值 分析：已知条件2a =3b =4c 为等比形式时，常设比值为，把a ，b ，c 都用K 来表示，这样就可以求值了 解：设2a =3b =4c =则a=2b=3c=4代入求值式：原式=2221694424332k k k k k k k k k ++•+•+•=222926k k =2926 四、巧用倒数：例4：已知：a a1=5则1242++a a a 为________ 分析：由a a 1=5求出a 的值式代入1242++a a a 明显比较复杂，对求值式取倒数，并向已知条件靠拢有下列解法 解：把1242++a a a 的分子、分母倒过来即2241a a a ++=24a a 22a a 21a=a 221a 1 = ⎝⎛⎪⎭⎫+21a a -21 = ⎝⎛⎪⎭⎫+21a a -1 =52-1=24 所以，原式1242++a a a =241 五、巧选特殊值代入：例5：若x 1-y 1=31，求yxy x y xy x ---+3232的值 分析：通过条件式的一组特殊值来计算求值式的值这种特殊的方法计算起来简单快捷，但是条件中字母不能任意取值，要受限制所以我们在选值时要让它符合两个条件：（1）代入条件式和求值式中都有意义（2）尽量找整数，利于求值计算解：令=2代入已知等式得，y=6把=2，y=6代入求值式，得y xy x y xy x ---+3232=662326262322-••-•-••+•=636212364---+ 原式=4028-=-107 以上例5题还有其它的巧解方法，希望同学们在今后的学习中多找技巧，提高数学的学习兴趣，丰富自己的生活。

分式求值的几种常用方法分式求值是指解决一个分式的数值的过程。

分式由分子和分母组成，分数线表示两者的除法关系。

求解分式的数值可以使用几种常用的方法。

下面将介绍一些常用的方法。

1.分母与分子同乘（常用于消除分母中的变量）这种方法适用于分母中有变量的情况，为了简化计算，可以通过同乘一个合适的因式使分子或分母中的变量消除。

例如，对于分式(a+b)/(a-b)，可以将分子和分母都同乘(a+b)，得到(a+b)*(a+b)/(a-b)。

这样，原先的分式变为了一个更简单的形式，可以更容易地求解。

2.分子与分母同除（常用于消除分子中的变量）这种方法适用于分子中有变量的情况，同样为了简化计算，可以通过同除一个合适的因式使分子或分母中的变量消除。

例如，对于分式(a+b)/(a-b)，可以将分子和分母都同除(a+b)，得到(a+b)/(a+b)*(a+b)/(a-b)。

同样地，原先的分式变为了一个更简单的形式。

3.分解分子或分母（常用于将复杂的分式化简为简单的分式）当分子或分母中出现更复杂的表达式时，可以将其进行分解，将分式化简为简单的分式。

例如，对于分式(a+b)/(a-b)，可以将分子展开为(a+b)=a+b，将分母展开为(a-b)=a-b，然后将其带入分式，得到(a+b)/(a-b)=(a+b)/(a-b)。

这样，原先的分式变为了一个更简单的形式。

4.改变分割点（常用于化简复杂的分式）有时，将分式中的表达式写成更简单的形式，可以更好地进行计算。

例如，对于分式(a+b)/(a-b)，可以将(a+b)分别分成a和b的和，将(a-b)分别分成a和b的差，即得到a/(a-b)+b/(a-b)。

这样，原先的分式变为了两个简单分式相加的形式，可以更容易地求解。

5.用分母的乘法倒数取代除法（常用于取消除法运算）当分式中存在除法运算时，可以用乘以分母的倒数来替代除法。

例如，对于分式1/(a+b)，可以将其写为1*(a+b)^（-1），然后使用指数的乘法法则将指数变为负数，得到(a+b)^-1、这样，原先的分式变为了一个更简单的形式。

专题09 分式方程【专题目录】技巧1：分式的意义及性质的四种题型 技巧2：分式运算的八种技巧技巧3：巧用分式方程的解求字母的值或取值范围 技巧4：分式求值的方法 【题型】一、分式有意义的条件 【题型】二、分式的运算 【题型】三、分式的基本性质 【题型】四、解分式方程 【题型】五、分式方程的解 【题型】六、列分式方程 【考纲要求】1、理解分式、最简分式、最简公分母的概念，掌握分式的基本性质，能熟练地进行约分、通分．2、能根据分式的加、减、乘、除的运算法则解决计算、化简、求值等问题，并掌握分式有意义、无意义和值为零的约束条件．3、理解分式方程的概念，会解可化为一元一次(二次)方程的分式方程(方程中的分式不超过两个)。

4、了解解分式方程产生增根的原因，会检验和对分式方程出现的增根进行讨论． 【考点总结】一、分式形如AB(A 、B 是整式，且B 中含有字母，B ≠0)的式子叫做分式．A A【考点总结】二、分式方程【注意】1.约分前后分式的值要相等.2.约分的关键是确定分式的分子和分母的公因式.3.约分是对分子、分母的整体进行的，也就是分子的整体和分母的整体都除以同一个因式 分式混合运算的运算运算顺序：1.先把除法统一成乘法运算；2.分子、分母中能分解因式的多项式分解因式；3.确定分式的符号，然后约分；4.结果应是最简分式.【技巧归纳】分式乘以分式，用分子的积做积的分子，分母的积做积的分母，即a b ·c d ＝acbd .分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘，即a b ÷c d ＝a b ·d c ＝adbc在分式的加减乘除混合运算中，应先算乘除，进行约分化简后，再进行加减运算，遇到有括号的，先算括号里面的．运算结果必须是最简分式或整式．技巧1：分式的意义及性质的四种题型 【类型】一、分式的识别1．在3x 4x －2，－5x 2＋7，4x －25，2m ，x 2π＋1，2m 2m中，不是分式的式子有( )A ．1个B ．2个C ．3个D ．4个2．从a －1，3＋π，2，x 2＋5中任选2个构成分式，共有________个． 【类型】二、分式有无意义的条件3．若代数式1a －4在实数范围内有意义，则实数a 的取值范围为( )A ．a ＝4B ．a>4C ．a<4D ．a≠4 4．当x ＝________时，分式x －1x 2－1无意义． 5．已知不论x 为何实数，分式3x ＋5x 2－6x ＋m 总有意义，试求m 的取值范围．【类型】三、分式值为正、负数或0的条件6．若x ＋2x 2－2x ＋1的值为正数，则x 的取值范围是( )A ．x ＜－2B ．x ＜1C ．x ＞－2且x≠1D ．x ＞1 7．若分式3x －42－x 的值为负数，则x 的取值范围是________．8．已知分式a －1a 2－b 2的值为0，求a 的值及b 的取值范围．【类型】四、分式的基本性质及其应用 9．下列各式正确的是( )A .a b ＝a 2b 2B .a b ＝ab a ＋bC .a b ＝a ＋c b ＋cD .a b ＝ab b 2 10．要使式子1x －3＝x ＋2x 2－x －6从左到右的变形成立，x 应满足的条件是( ) A ．x ＞－2 B ．x ＝－2 C ．x ＜－2 D ．x≠－2 11．已知 x 4＝y 6＝z7≠0，求 x ＋2y ＋3z 6x －5y ＋4z 的值．12．已知x ＋y ＋z ＝0，xyz≠0，求x |y ＋z|＋y |z ＋x|＋z|x ＋y|的值． 参考答案1．C 点拨：4x －25，2m ，x 2π＋1不是分式．2．6 点拨：以a －1为分母，可构成3个分式；以x 2＋5为分母，可构成3个分式，所以共可构成6个分式． 3．D 4.±15．解：x 2－6x ＋m ＝(x －3)2＋(m －9)．因为(x －3)2≥0，所以当m －9＞0，即m ＞9时，x 2－6x ＋m 始终为正数，分式总有意义．6．C 点拨：x 2－2x ＋1＝(x －1)2.因为分式的值为正数，所以x ＋2＞0且x －1≠0.解得x ＞－2且x≠1. 7．x ＞2或x ＜438．解：因为分式a －1a 2－b 2的值为0，所以a －1＝0且a 2－b 2≠0.解得a ＝1且b≠±1.9．D 10.D11．解：设x 4＝y 6＝z7＝k(k≠0)，则x ＝4k ，y ＝6k ，z ＝7k.所以x ＋2y ＋3z 6x －5y ＋4z ＝4k ＋2×6k ＋3×7k 6×4k －5×6k ＋4×7k ＝37k 22k ＝3722.12．解：由x ＋y ＋z ＝0，xyz≠0可知，x ，y ，z 必为两正一负或两负一正．当x ，y ，z 为两正一负时，不妨设x ＞0，y ＞0，z ＜0，则原式＝x |－x|＋y |－y|＋z|－z|＝1＋1－1＝1；当x ，y ，z 为两负一正时，不妨设x ＞0，y ＜0，z ＜0，则原式＝x |－x|＋y |－y|＋z|－z|＝1－1－1＝－1.综上所述，所求式子的值为1或－1. 值的分式消元求值． 技巧2：分式运算的八种技巧 【类型】一、约分计算法 1．计算：a 2＋6a a 2＋3a －a 2－9a 2＋6a ＋9.【类型】二、整体通分法 2．计算：a －2＋4a ＋2.【类型】三、顺次相加法3．计算：1x －1＋1x ＋1＋2x x 2＋1＋4x 3x 4＋1.【类型】四、换元通分法4．计算：(3m －2n)＋（3m －2n ）33m －2n ＋1－(3m －2n)2＋2n －3m3m －2n －1.【类型】五、裂项相消法⎝⎛⎭⎫即1n （n ＋1）＝1n －1n ＋15．计算：1a （a ＋1）＋1（a ＋1）（a ＋2）＋1（a ＋2）（a ＋3）＋…＋1（a ＋99）（a ＋100）.【类型】六、整体代入法6．已知1a ＋1b ＝16，1b ＋1c ＝19，1a ＋1c ＝115，求abcab ＋bc ＋ac 的值．【类型】七、倒数求值法7．已知 x x 2－3x ＋1＝－1，求x 2x 4－9x 2＋1的值．【类型】八、消元法8．已知4x －3y －6z ＝0，x ＋2y －7z ＝0，且xyz≠0，求5x 2＋2y 2－z 22x 2－3y 2－10z 2的值．参考答案1．解：原式＝a （a ＋6）a （a ＋3）－（a ＋3）（a －3）（a ＋3）2＝a ＋6a ＋3－a －3a ＋3＝9a ＋3. 点拨：在分式的加减运算中，若分式的分子、分母是多项式，则首先把能因式分解的分子、分母分解因式，其次把分子、分母能约分的先约分，然后再计算，这样可简化计算过程． 2．解：原式＝a －21＋4a ＋2＝a 2－4a ＋2＋4a ＋2 ＝a 2a ＋2. 点拨：整式与分式相加减时，可以先将整式看成分母为1的式子，然后通分相加减． 3．解：原式＝x ＋1x 2－1＋x －1x 2－1＋2x x 2＋1＋4x 3x 4＋1＝2x x 2－1＋2x x 2＋1＋4x 3x 4＋1＝2x （x 2＋1）＋2x （x 2－1）（x 2－1）（x 2＋1）＋4x 3x 4＋1＝4x 3x 4－1＋4x 3x 4＋1＝4x 3（x 4＋1）＋4x 3（x 4－1）（x 4－1）（x 4＋1）＝8x 7x 8－1. 点拨：此类题在计算时，采用“分步通分相加”的方法，逐步递进进行计算，达到化繁为简的目的．在解题时既要看到局部特征，又要全局考虑．4．解：设3m －2n ＝x ，则原式＝x ＋x 3x ＋1－x 2－x x －1＝x （x 2－1）＋x 3（x －1）－x 2（x 2－1）－x （x ＋1）（x ＋1）（x －1）＝－2x（x ＋1）（x －1）＝4n －6m（3m －2n ＋1）（3m －2n －1）.5．解：原式＝1a －1a ＋1＋1a ＋1－1a ＋2＋1a ＋2－1a ＋3＋…＋1a ＋99－1a ＋100＝1a －1a ＋100＝100a （a ＋100）.点拨：对于分子是1，分母是相差为1的两个整式的积的分式相加减，常用1n （n ＋1）＝1n －1n ＋1进行裂项，然后相加减，这样可以抵消一些项． 6．解：1a ＋1b ＝16，1b ＋1c ＝19，1a ＋1c ＝115，上面各式两边分别相加，得⎝⎛⎭⎫1a ＋1b ＋1c ×2＝16＋19＋115， 所以1a ＋1b ＋1c ＝31180.易知abc≠0，所以abc ab ＋bc ＋ac ＝11c ＋1a ＋1b ＝18031.7．解：由xx 2－3x ＋1＝－1，知x≠0，所以x 2－3x ＋1x ＝－1.所以x －3＋1x ＝－1.即x ＋1x ＝2.所以x 4－9x 2＋1x 2＝x 2－9＋1x 2＝⎝⎛⎭⎫x ＋1x 2－11＝22－11＝－7. 所以x 2x 4－9x 2＋1＝－17.8．解：以x ，y 为主元，将已知的两个等式化为⎩⎪⎨⎪⎧4x －3y ＝6z ，x ＋2y ＝7z.解得x ＝3z ，y ＝2z. 因为xyz≠0，所以z≠0.所以原式＝5×9z 2＋2×4z 2－z 22×9z 2－3×4z 2－10z 2＝－13.点拨：此题无法直接求出x ，y ，z 的值，因此需将三个未知数的其中一个作为常数，解关于另外两个未知数的二元一次方程组，然后代入待求值的分式消元求值．技巧3：巧用分式方程的解求字母的值或取值范围 【类型】一、利用分式方程解的定义求字母的值1．已知关于x 的分式方程2x ＋4＝m x 与分式方程32x ＝1x －1的解相同，求m 2－2m 的值．【类型】二、利用分式方程有解求字母的取值范围2．若关于x 的方程x －2x －3＝mx －3＋2有解，求m 的取值范围．【类型】三、利用分式方程有增根求字母的值 3．如果解关于x 的分式方程m x －2－2x 2－x＝1时出现增根，那么m 的值为( ) A ．－2 B ．2 C ．4 D ．－44．若关于x 的方程m x 2－9＋2x ＋3＝1x －3有增根，则增根是多少？并求方程产生增根时m 的值．【类型】四、利用分式方程无解求字母的值5．若关于x 的分式方程x －ax ＋1＝a 无解，则a ＝________.6．已知关于x 的方程x －4x －3－m －4＝m3－x 无解，求m 的值．7．已知关于x 的分式方程x ＋a x －2－5x＝1.(1)若方程的增根为x ＝2，求a 的值； (2)若方程有增根，求a 的值； (3)若方程无解，求a 的值． 参考答案1．解：解分式方程32x ＝1x －1，得x ＝3.经检验，x ＝3是该方程的解． 将x ＝3代入2x ＋4＝mx ，得27＝m 3.解得m ＝67. ∴m 2－2m ＝⎝⎛⎭⎫672－2×67＝－4849.2．解：去分母并整理，得x ＋m －4＝0.解得x ＝4－m.∵分式方程有解， ∴x ＝4－m 不能为增根． ∴4－m≠3.解得m≠1.∴当m≠1时，原分式方程有解． 3．D4．解：因为原方程有增根，且增根必定使最简公分母(x ＋3)(x －3)＝0，所以x ＝3或x ＝－3是原方程的增根．原方程两边同乘(x ＋3)(x －3)，得m ＋2(x －3)＝x ＋3. 当x ＝3时，m ＋2×(3－3)＝3＋3，解得m ＝6； 当x ＝－3时，m ＋2×(－3－3)＝－3＋3， 解得m ＝12.综上所述，原方程的增根是x ＝3或x ＝－3. 当x ＝3时，m ＝6； 当x ＝－3时，m ＝12.点拨：只要令最简公分母等于零，就可以求出分式方程的增根，再将增根代入分式方程化成的整式方程，就能求出相应的m 的值．5．1或－16．解：原方程可化为(m ＋3)x ＝4m ＋8.由于原方程无解，故有以下两种情形：(1)若整式方程无实根，则m ＋3＝0且4m ＋8≠0，此时m ＝－3；(2)若整式方程的根是原方程的增根，则4m ＋8m ＋3＝3，解得m ＝1.经检验，m ＝1是方程4m ＋8m ＋3＝3的解．综上所述，m 的值为－3或1.7．解：原方程去分母并整理，得(3－a)x ＝10.(1)因为原方程的增根为x ＝2，所以(3－a)×2＝10.解得a ＝－2. (2)因为原分式方程有增根，所以x(x －2)＝0.解得x ＝0或x ＝2.因为x ＝0不可能是整式方程(3－a)x ＝10的解，所以原分式方程的增根为x ＝2.所以(3－a)×2＝10.解得a ＝－2.(3)①当3－a ＝0，即a ＝3时，整式方程(3－a)x ＝10无解，则原分式方程也无解； ②当3－a≠0时，要使原方程无解，则由(2)知，a ＝－2.综上所述，a 的值为3或－2.点拨：分式方程有增根时，一定存在使最简公分母等于0的整式方程的解．分式方程无解是指整式方程的解使最简公分母等于0或整式方程无解． 技巧4：分式求值的方法 【类型】一、直接代入法求值 1．先化简，再求值：⎝⎛⎭⎪⎫2a ＋1＋a ＋2a 2－1÷a a －1，其中a ＝5.【类型】二、活用公式求值2．已知实数x 满足x 2－5x ＋1＝0，求x 4＋1x 4的值．3．已知x ＋y ＝12，xy ＝9，求x 2＋3xy ＋y 2x 2y ＋xy 2的值．【类型】三、整体代入法求值4．已知x y ＋z ＋y z ＋x ＋z x ＋y ＝1，且x ＋y ＋z≠0，求x 2y ＋z ＋y 2z ＋x ＋z 2x ＋y 的值．【类型】四、巧变形法求值5．已知实数x 满足4x 2－4x ＋1＝0，求2x ＋12x 的值．【类型】五、设参数求值6．已知x 2＝y 3＝z4≠0，求x 2－y 2＋2z 2xy ＋yz ＋xz 的值．参考答案1．解：原式＝[2a ＋1＋a ＋2（a ＋1）（a －1）]·a －1a＝2（a －1）＋（a ＋2）（a ＋1）（a －1）·a －1a＝3a ＋1. 当a ＝5时，3a ＋1＝35＋1＝12.2．解：由x 2－5x ＋1＝0得x≠0，∴x ＋1x＝5.∴⎝⎛⎭⎫x ＋1x 2＝25.∴x 2＋1x 2＝23. ∴x 4＋1x 4＝⎝⎛⎭⎫x 2＋1x 22－2＝232－2＝527 点拨：在求解有关分式中两数(或两式)的平方和问题时，可考虑运用完全平方公式进行解答． 3．解：x 2＋3xy ＋y 2x 2y ＋xy 2＝x 2＋2xy ＋y 2＋xy xy （x ＋y ）＝（x ＋y ）2＋xyxy （x ＋y ）.因为x ＋y ＝12，xy ＝9， 所以（x ＋y ）2＋xy xy （x ＋y ）＝122＋99×12＝1712.4．解：因为x ＋y ＋z≠0，所以等式的两边同时乘x ＋y ＋z ，得x （x ＋y ＋z ）y ＋z ＋y （x ＋y ＋z ）z ＋x ＋z （x ＋y ＋z ）x ＋y＝x ＋y ＋z ，所以x 2y ＋z ＋x （y ＋z ）y ＋z ＋y 2z ＋x ＋y （z ＋x ）z ＋x ＋z 2x ＋y ＋z （x ＋y ）x ＋y ＝x ＋y ＋z.所以x 2y ＋z ＋y 2z ＋x ＋z 2x ＋y ＋x ＋y ＋z ＝x ＋y ＋z.所以x 2y ＋z ＋y 2z ＋x ＋z 2x ＋y＝0.点拨：条件分式的求值，如需对已知条件或所求条件分式变形，必须依据题目自身的特点，这样才能收到事半功倍的效果．条件分式的求值问题体现了数学中的整体思想和转化思想． 5．解：∵4x 2－4x ＋1＝0，∴(2x －1)2＝0.∴2x ＝1. ∴2x ＋12x ＝1＋11＝2.6．解：设x 2＝y 3＝z4＝k≠0，则x ＝2k ，y ＝3k ，z ＝4k.所以x 2－y 2＋2z 2xy ＋yz ＋xz＝（2k ）2－（3k ）2＋2（4k ）22k·3k ＋3k·4k ＋2k·4k＝27k 226k 2＝2726. 【题型讲解】【题型】一、分式有意义的条件例1x 的取值范围是（ ） A ．x≥4 B ．x ＞4C ．x≤4D ．x ＜4【答案】D【分析】直接利用二次根式有意义的条件分析得出答案．4﹣x ＞0，解得：x ＜4 即x 的取值范围是：x ＜4故选D ． 【题型】二、分式的运算 例2、分式222111a a a a++---化简后的结果为（ ） A ．11a a +-B ．31a a +-C ．1a a --D ．2231a a +--【答案】B【分析】根据异分母分式相加减的运算法则计算即可．异分母分式相加减，先通分，再根据同分母分式相加减的法则计算． 【详解】解：222111a a a a++--- ()()()()()21221111a a a a a a ++=-+--+ ()()()222111a a a a +++=+-()()2222111a a a a a ++++=+-()()()()3111a a a a +=++- 31a a +=- 故选：B ．【题型】三、分式的基本性质 例3、若b a b -=14，则ab的值为（ ） A ．5B ．15C ．3D ．13【答案】A 【解析】因为b a b -=14， 所以4b=a -b ．，解得a=5b① 所以a b ①55b b=. 故选A.【题型】四、解分式方程 例4、方程2152x x =+-的解是（ ） A ．1x =- B ．5x =C ．7x =D ．9x =【答案】D【分析】根据题意可知，本题考察分式方程及其解法，根据方程解的意义，运用去分母，移项的方法，进行求解． 【详解】 解：方程可化简为()225x x -=+ 245x x -=+9x =经检验9x =是原方程的解 故选D【题型】五、分式方程的解 例5、关于x 的分式方程2mx -﹣32x-＝1有增根，则m 的值（ ） A ．m ＝2 B ．m ＝1C ．m ＝3D ．m ＝﹣3【答案】D【分析】分式方程去分母转化为整式方程，由分式方程有增根，确定出m 的值即可． 【详解】解：去分母得：m +3＝x ﹣2， 由分式方程有增根，得到x ﹣2＝0，即x ＝2，把x＝2代入整式方程得：m+3＝0，解得：m＝﹣3，故选：D．【题型】六、列分式方程例6、随着快递业务的增加，某快递公司为快递员更换了快捷的交通工具，公司投递快件的能力由每周3000件提高到4200件，平均每人每周比原来多投递80件，若快递公司的快递员人数不变，求原来平均每人每周投递快件多少件？设原来平均每人每周投递快件x件，根据题意可列方程为（）A．3000420080x x=-B．3000420080x x+=C．4200300080x x=-D．3000420080x x=+【答案】D【分析】设原来平均每人每周投递快件x件，则现在平均每人每周投递快件（x+80）件，根据人数=投递快递总数量÷人均投递数量，结合快递公司的快递员人数不变，即可得出关于x的分式方程，此题得解．【详解】解：设原来平均每人每周投递快件x件，则现在平均每人每周投递快件（x+80）件，根据快递公司的快递员人数不变列出方程，得：3000420080x x=+，故选：D．分式方程（达标训练）一、单选题1．（2022·广西·富川瑶族自治县教学研究室模拟预测）关于x的分式方程3122m xx x++=--有解，则实数m应满足的条件是（）A．m=-1B．m≠-1C．m=1D．m≠1【答案】D【分析】解分式方程得：m + x-3=2-x即x=52m，由题意可知x≠2，即可得到m．【详解】解：31 22m xx x++= --方程两边同时乘以2-x得：m+x-3=2-x, 2x=5-m，x=52m①分式方程有解① x ≠2， 即52m≠2， ①m ≠1． 故选D ．【点睛】本题主要考查了分式方程的解，熟练掌握分式方程的解法，理解分式方程有意义的条件是解题的关键．2．（2022·海南省直辖县级单位·二模）分式方程211x =+的解为（ ） A ．1- B ．0 C ．1 D ．2【答案】C【分析】按照分式方程的解法求解判断即可． 【详解】①211x =+， 去分母，得2=x +1， 移项，得 x =2-1=1，经检验，x =1是原方程的根 故选C ．【点睛】本题考查了分式方程的解法，熟练掌握分式方程的解法是解题的关键． 3．（2022·天津南开·二模）化简2222432x y x yx y y x -----的结果是（ ）A ．5x y- B ．5x y+ C ．225x y -D ．223x yx y +-【答案】B【分析】利用同分母分式的加法法则计算，约分得到最简结果即可．【详解】解：2222432x y x yx y y x ----- 2222432x y x yx y x y --=+--55()()x yx y x y -=+-5()()()x y x y x y -=+-5x y=+，【点睛】本题主要考查了分式的加减，解题的关键是掌握分式混合运算顺序和运算法则． 4．（2022·贵州贵阳·三模）计算222m m m ---的结果是（ ） A ．2 B ．－2C ．1D ．－1【答案】C【分析】根据分式减法运算法则进行运算，化简即可． 【详解】解：221222m m m m m --==---， 故选：C ．【点睛】本题考查了分式的减法，正确运算是解题关键，注意运算后需要约分化简． 5．（2022·江苏淮安·一模）若分式2xx +有意义，则x 的取值范围是（ ） A ．0x ≠ B ．2x ≠- C ．2x >- D ．2x ≥-【答案】B【分析】根据分式有意义的条件：分母不为0即可得到． 【详解】要分式2xx +有意义，则20x +≠， 解得：2x ≠-． 故选：B【点睛】本题考查分式有意义的条件，掌握分式有意义的条件是解题的关键．二、填空题6．（2022·四川省遂宁市第二中学校二模）分式方程31311x x x -=-+的解为 ______． 【答案】x =-2【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．【详解】解：去分母得：3x (x +1)-(x -1)=3(x +1)(x -1)， 解得：x =-2，经检验x =-2是分式方程的解， 故答案为x =-2．【点睛】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．7．（2022·湖南怀化·模拟预测）计算52x x ++﹣32x +＝_____． 【答案】1【分析】根据同分母分式相加减，分母不变，把分子相加减计算即可． 【详解】解：52x x ++﹣32x +=532122x x x x +-+==++ 故答案为：1．【点睛】本题考查分式的加减，解题关键是熟练掌握同分母分式相加减时分母不变，分子相加减，异分母相加减时，先通分变为同分母分式，再加减．三、解答题8．（2022·浙江丽水·一模）解方程：13233x x-=--． 【答案】=5x【分析】这是一道可化为一元一次方程的分式方程，根据解分式方程的一般步骤：去分母，转化为求解整式方程，然后检验得到的解是否符合题意，最后得出结论． 【详解】两边同时乘以(3)x -，得132(3)x +=-， 去括号，得426x =-， 化简，得=5x ，检验：当=5x 时，30x -≠， ∴原分式方程的解为=5x ．【点睛】此题考查可化为一元一次方程的分式方程，熟练掌握解分式方程的方法与步骤是解此题的关键，但是要特别注意：检验是不可少的环节．分式方程（提升测评）一、单选题1．（2022·辽宁葫芦岛·一模）2022年北京冬奥会的吉祥物“冰墩墩”和“雪容融”深受国内外朋友的喜爱．某特许零售店准备购进一批吉祥物销售．已知用600元购进“冰墩墩”的数量与用500元购进“雪容融”数置相同，已知购进“冰墩墩”的单价比“雪容融”的单价多10元，设购进“冰墩墩”的单价为x 元，则列出方程正确的是（ ）A ．60050010x x=+ B ．60050010x x =+ C ．60050010x x=- D ．60050010x x =- 【答案】D【分析】设“冰墩敏”的销售单价为x ，则 “雪容融”的销售单价为（x -10）元，然后根据用600元购进“冰墩墩”的数量与用500元购进“雪容融”数置相同即可列出方程．【详解】解：设“冰墩敏”的销售单价为x ，则 “雪容融”的销售单价为（x -10）元， 根据题意，得60050010x x =-。

分式概念形如〔A、B是整式，B中含有字母〕的式子叫做分式。

其中A叫做分式的分子，B 叫做分式的分母。

且当分式的分子的次数低于分母的次数时，我们把这个分式叫做真分式；当分式的分子的次数高于分母的次数时，我们把这个分式叫做假分式。

注意：判断一个式子是否是分式，不要看式子是否是的形式，关键要满足：分式的分母中必须含有字母，分子分母均为整式。

无需考虑该分式是否有意义，即分母是否为零。

由于字母可以表示不同的数，所以分式比分数更具有一般性。

方法：数看结果，式看形。

分式条件:1.分式有意义条件：分母不为0。

2.分式值为0条件：分子为0且分母不为0。

3.分式值为正(负)数条件：分子分母同号得正，异号得负。

4.分式值为1的条件：分子=分母≠0。

5.分式值为-1的条件：分子分母互为相反数，且都不为0。

代数式分类整式和分式统称为有理式。

带有根号且根号下含有字母的式子叫做无理式。

无理式和有理式统称代数式。

分式的根本性质分式的分子和分母同时乘以〔或除以〕同一个不为0的整式，分式的值不变。

用式子表示为：〔A,B,C为整式，且B、C≠0〕运算法那么约分根据分式根本性质，可以把一个分式的分子和分母的公因式约去，这种变形称为分式的约分。

约分的关键是确定分式中分子与分母的公因式。

约分步骤：单项式或者是几个因式乘积的形式，将它们的公因式约去。

多项式，将分子和分母分别分解因式，再将公因式约去。

公因式的提取方法：系数取分子和分母系数的最大公约数，字母取分子和分母共有的字母，指数取公共字母的最小指数，即为它们的公因式。

最简分式：一个分式不能约分时，这个分式称为最简分式。

约分时，一般将一个分式化为最简分式。

通分：异分母的分式可以化成同分母的分式，这一过程叫做通分。

分式的乘法法那么：〔1〕两个分式相乘，把分子相乘的积作为积的分子，把分母相乘的积作为积的分母。

（2）两个分式相除，把除式的分子和分母颠倒位置后再与被除式相乘。

用字母表示为：分式的加减法法那么：同分母分式的加减法法那么:同分母的分式相加减，分母不变，把分子相加减。

分式求值的方法
分式求值是数学中比较常见的一种计算方法，它主要是指对于一个分数式子进行化简和计算的过程。

下面将介绍分式求值的基本方法和一些常见的技巧。

一、基本方法
1. 首先要对分式进行化简，把分子分母中的公因数约掉，使得分式的形式更加简单。

2. 然后要找到分式的最简公共分母，把分式统一为相同的分母，这样就可以进行加减乘除等运算了。

3. 进行加减乘除等运算后，最后还要对结果进行化简，把分式中的公因数约掉，得到最简形式。

二、常见技巧
1. 对于分式中含有多项式的情况，可以使用分解因式的方法进行化简。

2. 对于分式中含有根式的情况，可以使用有理化分母的方法进行化简。

3. 对于分式中含有三角函数的情况，可以使用三角恒等式进行化简。

4. 对于分式中含有指数的情况，可以使用指数运算的规律进行化简。

总之，分式求值是一种基本的数学技能，掌握了基本的方法和技巧，就可以轻松应对各种题目。