2016初等数论教学大纲

引言概述：初等数论是数学的一个重要分支，它研究整数的性质和关系，是一门基础性的课程。

本文旨在为《初等数论》课程的教学制定一份详细的大纲，以帮助教师合理安排教学内容，提高教学效果。

正文内容：一、素数与合数1.素数的定义与性质素数的定义：只能被1和自身整除的正整数。

2.合数的定义与性质合数的定义：不是素数的正整数。

二、因数与倍数1.因数的概念因数的定义：能整除一个数的整数。

因子的分类：负因数、正因数、真因数。

2.最大公因数与最小公倍数最大公因数的定义与性质：两个数公共因子中最大的一个。

最小公倍数的定义与性质：两个数公共倍数中最小的一个。

三、整数的整除性与除法算法1.整除的概念与性质整除的定义：一个数能够被另一个数整除。

整除的性质：整数除法原则、整数的对称性。

2.整数的除法算法除法算法的步骤与原理：用减法、用乘法、整数除法算法的应用。

四、余数与模运算1.余数的概念与性质余数的定义：做除法时除不尽的部分。

余数的性质：余数的范围、余数的基本性质。

2.模运算的概念与性质模运算的定义：对于整数a和正整数n，a与n的商所得的余数。

模运算的性质：模运算的加法、减法和乘法规则。

五、同余与模运算应用1.同余的定义与性质同余的定义：对于整数a、b和正整数n，当a与b对n取余相等时，称a与b模n同余。

同余的性质：同余的传递性、同余的运算性质。

2.模运算的应用模运算在代数方程中的应用：线性同余方程、模运算的性质在方程求解中的应用。

总结：本文从素数与合数、因数与倍数、整除性与除法算法、余数与模运算以及同余与模运算应用等五个大点进行阐述。

通过这些内容的学习，学生将能够了解整数的性质和关系，理解数论的基本原理，为后续数学学习打下坚实的基础。

教师在教学过程中，应注重拓展学生的数学思维、培养其解决问题的能力，并结合实际生活和其他数学知识进行应用。

通过系统的教学大纲指导，教师能够更好地组织教学内容，提高学生的学习效果。

《初等数论》教学大纲第一部分大纲说明一、课程的作用与任务“初等数论”课程是数学与应用数学专业的一门选修课。

数学与应用数学专业的学生学习一些初等数论的基础知识可以加深对数的性质的了解与认识，便于理解和学习与其相关的一些课程。

通过这门课的学习，使学生获得关于整数的整除性、不定方程、同余式、原根与指标及简单连分数的基本知识，掌握数论中的最基本的理论和常用的方法，加强他们的理解和解决数学问题的能力，为今后的学习奠定必要的基础。

二、课程的目的与要求初等数论是研究整数性质的一门学科，历史上遗留下来没有解决的大多数数论难题其问题本身容易搞懂，容易引起人的兴趣，但是解决它们却非常困难。

本课程的目的是简单介绍在初等数论研究中经常用到的若干基础知识、基本概念、方法和技巧。

通过本课程的学习，使学生加深对整数的性质的了解，更深入地理解初等数论与其它邻近学科的关系。

三、教学要求有关定义、定理、性质等概念的内容按“知道、了解和理解”三个层次要求；有关计算、解法、公式和法则等方法的内容按“会、掌握、熟练掌握”三个层次要求。

第二部分学时按排一、学时和学分1、本课程共72学时，学时分配为：2、学分本课程共3学分。

二、教学环节第三部分教学内容与要求一、整数的整除性理论（12学时）（一）教学内容1、整除性、公因数、公倍数两个整数整除的概念、剩余定理；最大公因子的概念、性质及求最大公因子的方法；最小公倍数的概念、性质及最小公倍数的求法。

2、素数与整数的素因子分解素数与合数的概念、素数的性质、整数关于素数的分解定理、素数的求法（筛法）。

3、函数[x]、{x}及其应用函数[x]与{x}的概念、性质、n!的素数分解、组合数为整数的性质。

4、抽屉原理抽屉原理的简单与一般形式、抽屉原理在构造具有特殊性质整数方面的应用。

重点：整除、公因子、素数的概念及性质，剩余定理，求最大公因子的方法，整数的素数分解定理。

难点：函数[x]、{x}的概念及其应用。

初等数论教学大纲一、课程简介初等数论是数学中的重要分支之一，研究的是自然数的性质与关系。

本课程旨在培养学生的数论思维能力和逻辑思维能力，提高他们的问题解决能力和数学推理能力。

二、教学目标1. 掌握初等数论的基本概念，如素数、合数、互质等。

2. 熟悉常见数论问题的解决方法，如质因数分解、最大公因数与最小公倍数的求法等。

3. 理解和运用模运算的概念和性质，解决相关数论问题。

4. 掌握费马小定理和欧拉定理的应用，解决与其相关的数论问题。

5. 培养学生的数论证明能力，培养其逻辑思维和数学推理能力。

三、教学内容1. 自然数的性质与关系- 质数与合数- 整除性与约数- 互质关系与最大公因数2. 质因数与分解定理- 质因数分解- 最大公因数与最小公倍数 - 公因数与公倍数3. 模运算- 同余等价关系- 同余方程- 中国剩余定理4. 费马小定理与欧拉定理- 费马小定理的证明与应用 - 欧拉函数的定义与性质- 欧拉定理的证明与应用5. 整数的奇妙性质- 数字根与数位- 数字平方舞蹈- 数字阶梯问题- 尼科彻斯定理四、教学方法1. 讲述法：结合实例，详细解释数论概念和原理，引导学生理解与掌握。

2. 分组讨论：将学生分成小组，互相讨论和解决数论问题，促进合作学习和思维碰撞。

3. 课堂练习：布置一些基础练习题和拓展题，提高学生的问题解决能力和应用能力。

4. 数论证明：鼓励学生进行数论定理的证明，培养其逻辑思维和数学推理能力。

五、评估方式1. 平时成绩：包括课堂表现、作业完成情况等。

2. 期中考试：针对课程的基础知识进行测试。

3. 期末考试：综合考察学生对数论概念、原理和问题解决方法的理解与应用能力。

六、教材与参考书主教材：《初等数论》辅助教材：《数论引论》、《数论简史》七、教学进度安排根据教学计划，完成课程内容的讲解和练习，及时反馈学生学习情况，根据实际情况进行调整。

八、教学辅助手段使用黑板、白板等教学工具进行讲解和演示，辅助教学工具包括投影仪、计算器等。

初等数论教学大纲（本科）哈尔滨师范大学数学系初等数论(本科) 教学大纲说明《初等数论》是师范本科学校数学与应用数学专业的一门重要专业课，数学与应用数学专业的学生学习一些初等数论的基础知识可以加深对数的性质的了解与认识，便于理解和学习与其相关的一些课程。

是在学生进入四年级后开设的一门课程。

通过对《初等数论》的教学，使学生掌握初等数论的最基本的内容，使学生在掌握其基本理论的同时为从事中学数学竞赛工作提供宏观理论的积累，初等数论是研究整数最基本的性质，是一门重要的数学基础课。

初等数论开设的目的：通过这门课的学习，使学生获得关于整数的整除性、不定方程、同余式、原根与指标及不定方程的基本知识，掌握数论中的最基本的理论和常用的方法，加强他们的理解和解决数学问题的能力，为今后的学习奠定必要的基础。

1、国际奥林匹克数学竞赛中所占初等数论内容很多，学好初等数论对于培养学生进行奥林匹克数竞赛的培训工作提供理论的知识储备。

2、培养学生初步的科研能力，因为初等数论是数学中理论与实践结合得最完美的基础课程，近代数学中的很多数学思想、概念、方法与技巧都是从整数的性质的深入研究而不断丰富和发展起来的。

确定《初等数论》的教学内容应依据初高中教学实际，立足于培养学生的数学思想、方法和技巧，掌握竞赛数学中初等数论的主要理论和进一步提高和学习的基本理论，因而整个课程分为整除、同余、同余式、不定方程和原根指标几部分。

这样处理有助于形成学生完善的数学知识结构，进而从根本上提高学生的素质。

根据教学计划规定，本课程教学时数为48学时，其中讲授课和习题课共48学时，本课程安排在第七学期，周学时4，具体分配如下：1．整除12学时；2．同余8学时；3．同余方程18学时；4．不定方程4学时；5．原根和指标5学时。

大纲内容一、整除（一）教学目的通过本章的教学，使学生掌握整除的性质、带余数除法、辗转相除法，掌握最大公因数和最小公倍数的基本理论，熟练掌握算术基本定理，除数和函数和完全数的概念，掌握函数［x］、｛x｝基本理论。

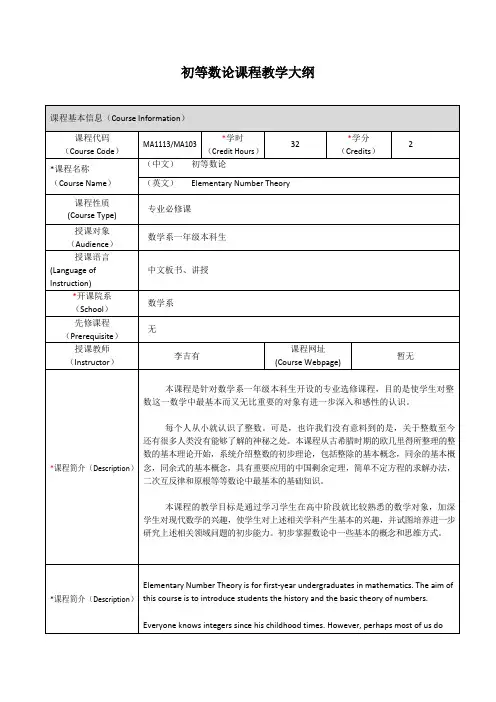
《初等数论》课程教学大纲一、教师信息二、课程基本信息课程名称（中文）：初等数论课程名称（英文）：Elementary Number Theory课程性质：□公共必修课√□专业必修课□限选课□任选课□实践性环节课程性质: √□学术知识类□方法技能类□研究探索类□实践体验类课程代码：4230070周学时： 2 总学时：32 学分: 2先修课程：高中数学授课对象：小学教育（理科）三、课程简介本课程是《小学数学课程与教学》的前修课程，是小学教育专业的本科生（理科）必不可少的基础知识之一，为以后指导小学数学教育提供有用的理论依据，并能直接指导小学数学课外活动。

首先，采用不太多的数学知识，由浅入深地介绍初等数论的基本原理和解题方法与技巧，如整数的整除理论及其在小学数学教学中的指导作用，素数的部分性质，及其同余的基本原理与同余式（组）的解法等。

其次，联系小学数学的教学内容和小学数学竞赛的辅导内容，突出讲解整除性理论在小学数学中的地位，和介绍数的K进位制的意义和计算，对整数和分数的四则运算的指导作用，以及四则运算中的运算技巧等。

再次，整除性理论中讲解奇偶性分析在解题中的作用，介绍不定方程中的著名问题“百鸡问题”、“费马问题”，同余式内容中，介绍我国古代数学书中提出的问题“韩信点兵”的“中国剩余定理”（孙子定理）等，以体现初等数论的应用性，提高学生对数学和小学数学教学的兴趣。

四、课程目标1.了解经常出现在生活中的自然数和整数的一些性质，了解初等数论与算数的关系；2.掌握整数的整除性、不定方程和同余式等基本知识；通过较系统的学习，掌握这门学科的基本数学思想和方法。

3.了解数论在我国的古代就已有极其光辉的成就，如孙子定理等。

五、课程内容与进度安排（一）课程内容第一章整数的可除性1.课时数（10）2．讲授内容主要知识点：（1）整除的概念、带余除法；（2）整除性定理；（3）奇数和偶数；（4）最大公约数和最小公倍数；（5）质数和合数（算术基本定理）重点：整除的概念、带余除法、最大公约数和辗转相除法、最小公倍数的性质、约数和算术基本定理。

初等数论教学大纲一、引言A. 数论的定义和背景B. 数论在数学中的重要性和应用领域C. 本教学大纲的目的和结构概述二、基础知识A. 自然数、整数、有理数和实数的定义和性质回顾B. 互质数和最大公因数的概念和计算方法C. 数学归纳法的原理和应用三、质数与素数A. 质数和素数的概念区别B. 质数的性质和判断方法C. 素数分解和唯一分解定理D. 质数在现代密码学中的应用四、同余与模运算A. 同余关系的定义和性质B. 模运算的基本运算法则C. 同余方程的解法和应用D. 中国剩余定理的概念和应用五、数字分割和循环小数A. 数字分割的定义和基本性质B. 循环小数的概念和判定方法C. 分数与循环小数之间的转换D. 无理数的性质和证明方法六、公约数与公倍数A. 公约数和公倍数的定义和性质B. 欧几里得算法的原理和应用C. 互质数的判定方法和应用D. 最小公倍数和最大公约数的计算方法七、数论函数与数论恒等式A. 欧拉函数和莫比乌斯函数的定义和性质B. 数论函数的计算方法和应用C. 数论恒等式的证明方法和应用八、素数分布定理和算术函数A. 素数分布的基本规律和研究方法B. 算术函数的定义和性质C. 算术函数在数论中的应用九、数论应用举例A. 数论在密码学中的应用举例B. 数论在编码和解码中的应用举例C. 数论在数学竞赛中的应用举例D. 数论在实际问题中的应用举例十、总结与展望A. 数论教学内容的回顾和总结B. 数论研究领域的发展趋势和前景展望C. 数论在其他数学学科中的重要性和应用前景D. 对学生的建议和学习方法分享十一、参考文献以上是初等数论教学大纲的框架，旨在帮助学生全面理解数论的基本概念和应用，培养解决数论问题的能力。

教学过程中，可适当结合具体例题和实际问题进行讲解和讨论，提高学生的数学思维和分析问题的能力。

同时，鼓励学生参与数论领域的研究和应用，拓宽数学的视野和应用领域。

《初等数论》教学大纲课程名称：初等数论 Elementary Number Theory课程性质：专业必修课学分：3总学时：48 理论学时：48适用专业：数学与应用数学先修课程：中学数学、高等代数、数学分析、解析几何一、教学目的与要求：初等数论是数学与应用数学本科专业的专业基础课。

初等数论是研究整数的基本性质和方程(组)整数解的一个数学分支。

数学与应用数学专业开设本课程的目的在于使学生孰悉数论的初步理论、掌握数论的最基本方法，为今后学习相关课程打下必要的基础。

因此，在教学中要求：（1）对初等数论的基本内容作系统讲授；（2）注意数论与其它数学分支的联系与应用；（3）简要介绍一些数论的近代成就及我国数学家在数论方面的贡献。

二、教学内容与学时分配：三、各章节主要知识点与教学要求：第一章整除理论（15学时）第一节整除定义及其基本性质第二节最大公因数与最小公倍数第三节素数第四节算术基本定理本章重点：整除、公因子、素数的概念及性质，剩余定理，求最大公因子的方法，整数的素数分解定理。

最大公因数的性质及应用，算术基本定理的证明及应用。

本章难点：定理的证明处理方法，定理的灵活运用。

本章教学要求：理解整数整除、公因子、公倍数的概念及相关性质，理解剩余定理，熟练掌握用剩余定理求最大公因子、最小公倍数的方法。

理解素数与合数的概念、素数的性质，理解整数的素数分解定理，会用筛法求素数。

了解函数[x]与{x}的概念、性质，n!的素数分解、组合数为整数的性质。

第二章不定方程（9学时）1．一次不定方程2．勾股数3. 费尔马问题介绍本章重点：二元一次不定方程解的形式，二元一次不定方程有整数解的条件，利用剩余定理（辗转相除法）求二元一次不定方程的解。

本章难点：多元不定方程有整数解的判定及求解。

本章教学要求：了解二元一次不定方程解的形式、二元一次不定方程有整数解的条件，熟练掌握利用剩余定理（辗转相除法）求二元一次不定方程的方法。

知道多元一次不定方程有解的条件，会求解简单的多元一次不定方程。

初等数论教学大纲一、课程简介初等数论是数学的一门重要分支，主要研究整数的性质和结构。

通过对初等数论的学习，学生可以更深入地理解整数及其关系，培养数学逻辑思维和问题解决能力。

本教学大纲旨在提供一份全面的教学计划，帮助学生掌握初等数论的基本概念和方法。

二、教学目标1、理解整数的概念、性质和运算；2、掌握因数分解和质数判断的方法；3、理解最大公约数和最小公倍数的概念及其计算方法；4、掌握分数及其性质，了解分数分解的方法；5、理解代数方程及其解法，掌握二次方程的解法；6、培养学生对数学的兴趣和解决问题的能力。

三、教学内容1、整数的概念和性质a.整数的定义和分类b.整数的运算规则c.数的表示方法2、因数分解和质数判断a.因数分解的方法b.质数判断的方法3、最大公约数和最小公倍数a.最大公约数的定义和计算方法b.最小公倍数的定义和计算方法4、分数及其性质a.分数的定义和分类b.分数的运算规则c.分数的约分和通分5、二次方程及其解法a.二次方程的定义和分类b.二次方程的解法6、其他代数方程的解法介绍a.一元一次方程的解法b.一元二次方程的解法c.高次方程的解法简介7、数论在密码学中的应用介绍a. RSA算法简介b.其他密码学应用简介8、数论在其他领域的应用介绍a.数论在计算机科学中的应用b.数论在物理学中的应用等9、数论的历史和发展简介a.数论的起源和发展历程b.数论在现代数学中的应用及发展前景10、初等数论与中学数学的与区别分析。

在数学的学习中，数论是一个非常重要的分支，它研究的是数的性质和规律。

在大学数学中，初等数论是数论的基础课程，它主要包括了以下几个方面的内容：整除性理论：整除性理论是数论的基础，它主要研究的是整数之间的除法性质。

通过研究素数和分解定理，我们可以更好地理解整数的内部结构和性质。

同余理论：同余理论是数论的核心内容之一，它主要研究的是整数之间的同余关系。

通过研究同余方程和模逆元，我们可以解决许多与整数相关的问题。

初等数论教学大纲一、引言初等数论作为数学的一个分支，主要研究自然数的性质和整数运算的规律。

本教学大纲旨在帮助学生全面了解初等数论的基本概念，并培养他们解决数论问题的能力。

二、基础知识1. 自然数和整数的概念及性质：自然数和整数的集合，自然数的顺序关系，整数的正负性质等。

2. 素数和合数的概念：素数和合数的定义，素数的性质和判定方法。

3. 最大公约数和最小公倍数的概念：最大公约数和最小公倍数的定义，欧几里德算法等相关知识。

三、初等数论应用1. 同余关系：同余关系的定义和性质，同余关系在整数运算中的应用。

2. 费马小定理和欧拉定理：费马小定理和欧拉定理的表述和应用，与同余关系的关联。

3. 数论函数：数论函数的定义和性质，欧拉函数和莫比乌斯函数的应用。

四、数的表示与分解1. 奇数和偶数的性质：奇数和偶数的定义，奇数和偶数的性质和运算规律。

2. 因数分解：正整数的因数分解定理，质因数分解及其应用。

3. 有理数和不可约分数：有理数和不可约分数的定义和性质，分数的运算规律。

五、数论定理与证明1. 质数无穷性：证明质数有无穷多个的数论定理及其证明过程。

2. 正整数平方和定理：证明正整数可以表示为两个平方数之和的数论定理及其证明过程。

3. 费马大定理：费马大定理的表述和证明过程。

六、解决数论问题的方法和技巧1. 数论问题的特点：数论问题常见的特点和解题思路。

2. 数学归纳法：数论问题解决中常用的归纳法原理。

3. 递归思想：递归思想在数论问题中的应用。

七、实践与综合应用结合具体例子，综合运用前述的知识和技巧，解决实际数论问题。

八、教学评估和反馈通过课堂练习、小组讨论和个人作业等方式进行教学评估，并及时提供学生的学习反馈。

九、教学资源与参考书目推荐使用的教材和参考书目。

十、教学计划编排初等数论教学内容的时间安排和教学进度。

十一、教学方式采用多种教学方式，如讲授、讨论、实践等，激发学生的学习兴趣和参与度。

十二、总结通过初等数论的学习，学生将深入理解数学的本质和逻辑，增强数学思维和解决问题的能力。

《初等数论》教学大纲课程编号：10180126英文名称：Elementary Number Theory学分：2.5学时：总学时40学时，其中理论40学时先修课程：数学分析、高等代数课程类别：专业课程（选修1）授课对象：数学与应用数学(师范)专业学生教学单位：数理信息学院修读学期：第3学期一、课程描述和预期目标初等数论是数学专业的重要课程，是研究整数基本性质的数学学科；其基本理论被广泛应用于数学其他学科以及计算机等相关专业中，部分内容还出现在中小学数学竞赛中。

本课程的学习既对数学专业其他课程的学习有促进作用，也对中小学数学教学有指导意义。

本课程总学时共40学时，其中理论课40学时，教与学的教学活动中，本课程坚持理念“以学生发展为中心，学生学习结果（课程教学目标）为导向，并持续改进(教学反思)学生的学习效果”。

本课程的主要内容是整数性质的基础知识和基本方法，包括整数的整除理论和同余理论，某些特定的不定方程和同余方程的求解等几个部分。

本课程教学活动结束，预期学生将达到以下学习结果：【学生学习结果1】：了解初等数论的基本内容和发展历史，熟悉整数的整除性理论、同余理论，掌握一次不定方程和二次不定方程的基本解法，了解Fermat大定理的内容，熟悉同余方程的基本概念，会解一元一次同余方程，熟悉孙子定理并掌握求解一元一次同余方程组的基本方法，知道一元同余方程的一般解法。

【学生学习结果2】：通过了解数论的发展历史，特别是中国数学家在数论研究方面的卓越贡献，学生的学习热情和民族自豪感得到提高，能积极的思考并逐渐形成主动学习的习惯。

【学生学习结果3】：通过学习各类方程的具体解法，数学运算能力得到增强；通过探究理解理论体系中概念之间的内在逻辑联系，逻辑推理能力得到提升；通过理解主要方法和重要定理的来源背景和适用范围，特别是变化形式的应用情况，抽象思维能力和发散思维能力得到提高，最终适应中学数学教育的学科综合素养得到提高。