线路和绕组中的波过程
- 格式:doc
- 大小:686.50 KB
- 文档页数:21



⾼电压课件第七章线路和绕组中的波过程第线路和绕组中的波过程7-1 ⽆损耗单导线线路中的波过程先讨论单导线-地的等值电路,将线路看成是由⽆数个长度为dx 的⼩段所组成。
若每单位长度导线的电感及电阻为L 0和r 0;每单位长度导线对地的电容及电导为C 0及g 0,则长度为dx 线段的参数应为L 0dx 、r 0dx 、C 0dx 和g 0dx ,线路的等值电路见图7-1-1。
实际上,L 0、r 0、C 0、g 0这些参数都和频率有关,当线路导线发⽣电晕时尚与电压有关,但在分析波过程的基本规律时,可以假定它们都是常数。
这样就可以有下了⽅程:7-1-1将此⽅程式经过拉式变换可以得到:7-1-2其中)(u v x t q -是⼀个以速度v 向x 正⽅向⾏进的电压波,)(u vxt f +代表⼀个以速度v 向x 负⽅向⾏进的波。
由式7-1-2可得OOC L z =。
z 具有阻抗的性质,其单位应为欧姆,通常称z 为波阻抗,其值取决于单位长度线路的电感L 0和对地电容C 0,波阻抗z 与线路长度⽆关,即z并⽆单位长度的含义。
综上所述,可以得到如下结论,⽆损单导线线路波过程的基本规律由下⾯四个⽅程所决定:7-1-3它们的含义可以概括如下:导线上任何⼀点的电压或电路,等于通过该点的前⾏波与反⾏波之和,前⾏波电压与电流之⽐为+z,反省波电压与电流之⽐为-z。
有这四个基本⽅程出发加上便捷条件和骑⼠条件就可以解决各种具体问题了。
注意:从功率的观点来看,波阻抗z与⼀数值相等的集中参数电阻相当,但在物理含义上不相同,电阻要消耗能量,⽽波阻抗并不消耗能量,当⾏波幅值⼀定时,波阻抗决定了单位时间内导线获得电磁能量的⼤⼩。
7-2 ⾏波的折射与反射⼀、⾏波的折射反射规律若具有不同波阻抗的两条线路相连接,如图7-2-1所⽰,连接点为A。
现将线路z1合闸于直流电源U,合闸后沿线路z1有⼀与电源电压相同的前⾏电压波u 1q ⾃电源向节点A传播,达到结点A遇到波阻抗为z2的线路,根据前节所述,在结点A前后都必须保持单位长度导线的电场能与磁场能相等的规律,但是由于线路z1和z2的单位长度电感与对地电容都不相同,因此当u1q到达A点时必然要发⽣电压、电流的变化,也就是说,在结点A出要发⽣薪风波的折射与反射过程,通过分析可以得到u1f 与u2q的表达式。
吉大《高电压技术》(五)
第五章 线路和绕组中的波过程
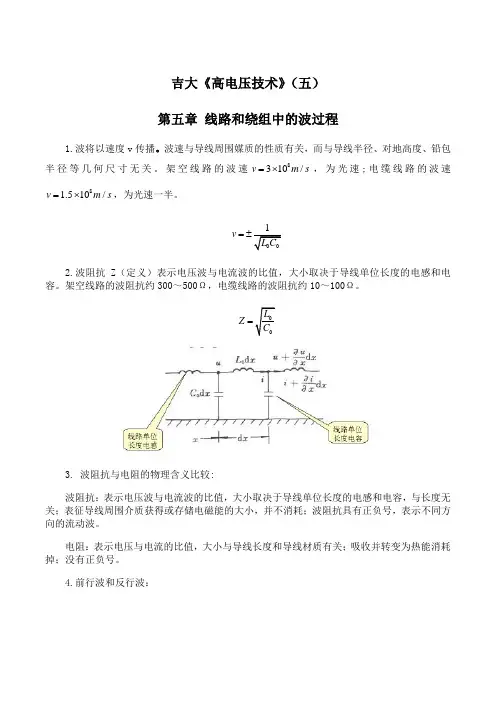
1.波将以速度v 传播。
波速与导线周围媒质的性质有关,而与导线半径、对地高度、铅包半径等几何尺寸无关。
架空线路的波速8310/v m s =⨯,为光速;电缆线路的波速81.510/v m s =⨯,为光速一半。
0
0v L C =± 2.波阻抗Z (定义)表示电压波与电流波的比值,大小取决于导线单位长度的电感和电容。
架空线路的波阻抗约300~500Ω,电缆线路的波阻抗约10~100Ω。
00
L Z C =
3. 波阻抗与电阻的物理含义比较:
波阻抗:表示电压波与电流波的比值,大小取决于导线单位长度的电感和电容,与长度无关;表征导线周围介质获得或存储电磁能的大小,并不消耗;波阻抗具有正负号,表示不同方向的流动波。
电阻:表示电压与电流的比值,大小与导线长度和导线材质有关;吸收并转变为热能消耗掉;没有正负号。
4.前行波和反行波:
5.行波在均匀无损单根导线上传播的基本规律的物理意义是:
导线上任一点的电压或电流等于通过该点的前行波与反行波之和;前行波电压与电流之比等于+Z ;反行波电压与电流之比等于‐Z 。
6.折射系数和反射系数: 其中:电压波折射系数:21
22z z z α=÷;电压波反射系数:1212
z z z z β+=÷。
1αβ+= 7.彼德逊法则:
集中参数的等值电路:将入射波看成内阻为1z ,电压为入射波两倍12f u 电源,与波阻抗2z 相连,则2z 两端的压降即为折射电压1f u —彼得逊等值电路。
使用条件:。






线路和绕组中的波过程
波是指一种能够传递能量的扰动或振动。
在线路和绕组中,波的传播
是电磁波或电磁场的传播过程。
在线路中,通常存在两种类型的波传播:行波和驻波。
行波是指波沿着线路传播的过程。
行波可以是平面波或波列,其中平
面波是指波的振动方向垂直于波的传播方向并且波前是平行的,而波列是
指波的波前是曲线的。
行波的传播速度取决于介质的特性,例如电磁波在
真空中的传播速度为光速。
驻波是指波在线路中的反射和干涉形成的波。
驻波形成时,波前和波
峰或波谷之间存在固定的空间间隔,这些区域被称为节点和腹部。
驻波的
形成与波的反射和干涉有关。
在驻波的波过程中,能量来回传播并在节点
处相互抵消,因此没有能量的传输。
驻波常见于终端开路或短路的线路中。
绕组是指由导线组成的线圈或线圈的一部分。
波在绕组中的传播也可
以是行波或驻波。
在绕组中,波的传播速度取决于绕组的各种参数,如线圈的自感和电容。
当频率较低时,波在绕组中的传播基本上是行波。
然而,当频率很高时,波在绕组中的传播会变得复杂,包括电磁波辐射和引入许多附加参数,如互感和电阻。
此时,驻波的形成也是可能的。
总结而言,线路和绕组中的波过程可以是行波或驻波。
行波是波沿着
线路传播的过程,而驻波是波的反射和干涉形成的波。
波的传播速度取决
于介质的特性和绕组的参数。
通过研究波的传播和行为,可以更好地理解
电磁波在线路和绕组中的特性和性能,从而应用于电路和电磁设备的设计
和分析中。
⾼电压第七章线路及绕组中的波过程第⼆篇电⼒系统过电压及其防护电⼒系统中各种电⽓设备的绝缘在运⾏过程中除了长期受到⼯作电压的作⽤(要求它能够长期耐受、不损坏、也不会迅速⽼化)外,由于种种原因还会受到⽐⼯作电压⾼的多的电压作⽤,会直接危害到绝缘的正常⼯作,造成事故。
我们称这种对绝缘有危险的电压升⾼和电位差升⾼为“过电压”。
⼀般来说,过电压都是由于系统中的电磁场能量发⽣了变化⽽引起的。
究其原因,这种变化可能是由于系统外部突然加⼊⼀定的能量(例如雷击导线、设备或导线附近的⼤地)⽽引起的,或者是由于电⼒系统内部,当系统参数发⽣变化时,电磁场能量发⽣了重新分配⽽引起。
因此可将过电压作如下分类。
电⼒系统过电压包括:雷电(⼤⽓)过电压、内部过电压雷电过电压:直击雷电过电压、感应雷电过电压内部过电压:操作过电压、暂时过电压【⼯频电压升⾼、谐振过电压】不论哪种过电压,它们作⽤时间虽然很短(谐振过电压,有时较长),但其数值较⾼,可能使电⼒系统的正常运⾏受到破坏,使设备的绝缘受到威胁。
因此为了保证系统安全、经济的运⾏,必须研究过电压产⽣的机理和物理过程、影响因素,从⽽提出限制过电压的措施,以保证电⽓设备能够正常运⾏和得到可靠地保护。
第七章线路及绕组中的波过程本章要求:过电压的定义和分类⽆损单导线中的波过程:波动⽅程,波阻抗和波速,波的折射与反射,彼德逊等值电路,⾏波通过串联电感和并联电容波的多次折反射。
冲击电晕对波过程的影响:变压器绕组中的波过程:等值电路的建⽴,电压的初始分布与稳态分布,最⼤电位包络线,⼊⼝电容,三相变压器绕组中的波过程。
波的传递及电机绕组波过程简介电⼒系统中各个元件都是通过导线连接成⼀个整体,⽽电⼒系统中的过电压绝⼤多数是发源于输电线路,在发⽣雷击或进⾏开关操作时,线路上都可能产⽣以流动波形式出现的过电压。
过电压在线路上的传播,就其本质⽽⾔是电磁场能量沿线路的传播过程,即在导线周围空间逐步建⽴起电场E 和磁场H 的过程,也是在导线周围空间储存或传递电磁能的过程。
第四章 线路和绕组中的波过程4.1 单导线波过程一、均匀无损长线R0=0dt di Lu L = dt du C i c =二、波过程的物理图景 1、行波建立电场在dt 时间内,行波前进了dx 距离,则长度为dx 的线路被充电,使其电位为u ,导线获得的电荷为dq=udc=uc 0dx充电电流 dtdxu dt dc u dt dq i c 0===2、行波建立磁场行波前进了dx 距离,磁通的增加量dx i d L 0=ϕ导线与地间电压dtdx i dt dL i dt d u L 0==ϕ 两式相乘dtdx i dt dx u L c u i ⋅⋅=00CL dtdx v 01±==(正负表示行波传播的两个可能方向)两式相除CL iu z 00±==波阻抗与阻抗的区别表征分布参数电路特点,是储能元件,表示导线周围介质获得电磁能的大小,具有阻抗的量纲。
例架空线L 0=1.6⨯10-6H/m C 0=7⨯10-12F/m ∴z=470Ω上式可改写为uc i L 20202121= 三、波动方程及其解 均匀无损线方程tix u L ∂∂⋅=∂∂-0(式4-1)电压沿x 方向的变化是由于电流在L c 上的电感压降。
tux i c ∂∂⋅=∂∂-0(式4-2)电流沿x 方向的变化是由于在c 0上分去了电容电流,“-”表示在x 的正方向上,电压电流都将减小。
波动方程tv tc L x u uu22222221∂=∂=∂∂∂∂(式4-3)tv tc L x i ii22222221∂=∂=∂∂∂∂(式4-4)其解 )()(21vt x vt x u u u ++-=(式4-5) )()(21vt x vt x i i i ++-=(式4-6)电压波的符号只取决于导线对地电容上所充电荷的符号,而与电荷的运动方向无关。
电流波的符号不仅与相应电荷符号有关,而且也与电荷运动方向有关,一般取正电荷沿着x 方向运动所形成的波为正电流波。
CL z iquq0==,z ifuf-=4.2 波的折射与反射∵能量守恒∴在不同波阻抗的导线的特点必然发生波的折反射。
导线1中电压波对电流波的比值与导线2中电压波对电流波的比值不同,前行电压波和点电流波在两导线的连接点处必然发生变化,从而造成波的折射。
另一方面,由于在两导线的连接点上的电压和电流只能有一个值,因此波在连接点除了有折射外一定还有反射。
一、折反射计算u u u u f A +==12(式4-14)ii i i fA+==12或 zu z u zu f 11122-=(式4-15) 解得 z z u i 21122+=(式4-16)u u z z z zi u 112122222α=+=⨯=(式4-17)u u zz z z u u uf11211212β=+-=-=(式4-18)βα+=1 (式4-19)α=1+β1、线路末端开路z 2=∞,则1,2==βα 即u u u u f 112,2-== 开路末端电流u zu i i ff 112,0-=-==电压波正的全反射 电流波负的全反射过电压波在开路末端的加倍升高对绝缘很危险,应充分注意。
装在线路开路终端的设备,有受到高幅值的雷电过电压作用的危险。
2、线路末端短路z 2=0,则1,0-==βα 即u u u f 12,0-==i zu zu iff==-=1111i ii i f1122=+=3、线路末端接有负载R 1=z 1,则0=α,1-=β 即u u 12=,0=u f01=-=zu iff说明入射波的电磁能量全部消耗在电阻R 上,没有反射。
注意:波只有沿着分布参数电路入射时,才有可能发生反射,即从分布参数电路到到分布参数电路,从分布电路参数到集中电路参数,在其连接点上满足β不为零时才会发生反射。
因此在高压测试中,常在电缆末端接匹配电阻的消除该处折反射所引起的测量误差。
二、计算折射波的等值电路u z z zu121222+=计算分布参数输电线路上节点A 的电压u 2,用集中采集等值电路来求——彼得逊法则。
z2是负载,也可以是电阻、电感、电容等集中参数。
例1 变电所有n 条出线,一条线路落雷,求母线上电压。
)(2t u nu A =4.3 行波通过并联电容和串联电感一、串联电感i i L2=dtd L iz z i u 22120)(2⋅++=设z z T LL 21+=)1(02e u uT L t-=α(式4-23) u 0为入射电压t=0时陡度最大,[dtd u 2]max =Lz u 202图6-11 电压波穿过电感和旁路电容时的折反射t=0时,U u f 0=,∵电感中电流不能突变,开始时L 相当于开路,反射电压=入射电压,使电压升高到两倍。
t →∞时,u zz zz u 021122+-=,这时电感已不起作用,相当于短路。
波通过串联电感二、并联电容方程u u c 2=dtd c iz z z z i u 2212120)(2⋅++=设C zz zz T c ⋅+=2112)1(21122e zz z z u u T c t-+==)1(0e u T ct-αt=0时陡度有最大值,[dtd u 2]max =Cz u 102电感使得折射波波头陡度降低可以理解为:i L 不能突变,所以当波作用到电感的初瞬,电感相当于开路,它江波完全反射回去。
即此时i=0,因而u 2=0以后u 2再随着i 2的增大而增大。
电容使得折射波波头陡度降低可以理解为:u c 不能突变,波旁边电容初瞬电容相当于短路。
串联电感时、并联电容折射波波头陡度都降低,但又它们个各自所产生的电压反射波却完全相反。
1、串L初瞬在电感前发生电压正的全反射使电感前的电压提高一倍。
2、并C初瞬在电容前发生电压负的全反射,使电容前的电压下降为零,由于反射波会使电感前电压抬高可能危及绝缘,∴常用并联电容降陡度。
几点结论:1、 行波通过并联电容或串联电感后降低波的陡度,C 或L 越大,陡度越低,∴u c 、i L 不能突变。
当波到达时,折射电压只能随着电容的逐渐充电或电感中电流的逐渐增大而增大。
2、 在无穷长直角波作用下,电容和电感对电压的最终稳态值无影响。
∵直流作用下,电容相当于短路,电感相当于开路。
3、 但在波刚投射到电容或电感时,它们上面出现的反射波却不一样,电容上出现的负反射波(电容相当于短路)电感则相当于开路出现正反射波。
例1 P294.4 行波的多次反射——网格法若在两无限长中间接入一有限长线段,那么,当行波到达这一阶段后,必将在两个节点间产生来回多次反射及折射。
无限长:当所研究的对象(线路集中电阻等)不考虑从另一端传来的反射波的影响时,就可以将其当无限长线处理。
而集中电阻由于其内部无波过程,及能量的反射,也相当(等值)于无限长线,其波阻抗等于电阻值。
z z 01→折射系数α1,z z 10→反射系数β1z z20→折射系数α2,z z 20→反射系数β2注意zz z z 01011+-=β 线路z2上的电压]21```````21[)()(1221212ββββββαα-++=n H U U=ββββαα212101211)(--nU (式4-27)∵|β|<1,|ββ21|<1,故当n →∞,(ββ21)n →0ββααα2121011-=U U U zz zU 0212022+==αU 2到达稳态值前的电压变化波形,有阻抗的关系。
(1)z z 01>,z z 02>阶梯形上升的波形可近似用一个按指数规律上升的平滑波形代替CL z 000=比z z 21,都小,若略去中间线段的电感,相当于并联电容L C C 0=,∴陡度↓(2)z z 01<,z z 02<=z大 电容 串联电感l L L 0=(3)z z 01<z <2 u 2为振荡的 (4)z z 01>z>2但 u 2的稳态值应小于入射波U 04.5 行波在平行多导线系统中的传播静电场中多导体系统的马克斯威方程组q qq u nn ααα12121111`````+++=(式4-29)自电位系数 nh kk r kk 2ln 210εεα∏=互电位系数dD kmkm r km ln 21εεα∏=上式乘)1(εμ=v vVv q ikk= ,自波阻抗vkkkk z α=,互波阻抗vkjkj z α=i z iz i z u n kn k k k +++=````2211在平面波的情况下,导线中的电流可以由单位长度上的电荷q 的运动求得,而各导线上的电荷相而言是相互静止的,∴可以qv i =出发,直接将静电场中麦克斯韦方程运用到波过程的计算中。
1、 电压源同时合闸于多根导线,求总的等值波阻抗。
三相 z i z i z i u 133122111++=z i z i z i u 233222211++= z i z i z i u 333322311++=z z z332211==,z z z 132312==, i i i i ===321z z ui 12112+=接到同一电源的三根导线可以用等值的单导线代替,其等值阻抗为3231211z z iu z +==n 根导线为nn z z z1211)1(-+=多根导线的电流的等值波阻抗由自波阻抗增大为z z 12112+(互相系统,三相同时进波)∵相邻导线的电流通过互波在本导线上产生感应电压,等值波阻↑ 2、三导线系统电源u 合闸于导线1,导线2对地绝缘,导线2处在导线1电磁波产生的电磁场内会出现耦合波,∵1上行波的传播,导线2上这种电荷分离也同步的向前推进。
∴有u 2但无电荷沿导线2作纵向运动,∴无i 2zi u u 1111==zi u 1212=u k zz u u 12111212== k12—耦合系数导线间的耦合系数对计算多导线系统的波过程有重要意义。
此时,u u u u k k u u <-=-=-)1(121221k12越大,则u 12越小,越有利于绝缘子串的安全运行。
∴ii z z i u u u 212211321,0,===== 单避r b k d D∏=2ln ln 1212,双避r b k dD d D d D ∏++=2lnln ln ln 121223231313 1、2 为避雷线,3为导线,以上D 、d 计算用“平均高度”4.6 线路上行波的衰减和变形(其决定因素为电晕)1、冲击电晕和交流电晕一样,由系列导电的流注所构成 ∵电流密度∝电压变化率,∴电流密度大得多。
大的冲击电流使流注通道温度升高,场强降低→电感不变对地电容导线有效半径↑↑}→自波阻↓20~30%,轴向电流不变,∴互波阻抗并不改变c v 43=,耦合系数↑波的损耗有五种: 1、 导线电阻(包括集肤效应和邻近效应的影响)的损失。