下载文档原格式
2-1 1[()]2E x t =，1212(,)3X t t R t t = 2-2 略。
2-3111[()]sin cos 333E x t t t=++12112212121111111(,)sin cos sin cos sin()cos()9999999X R t t t t t t t t t t =+++++++-2-4 [()]0E X t =，20(,)cos R t t w τστ+=2-5 [()]0E X t =，20(,)cos 2a R t t w ττ+= 2-6 略。
2-7 [()]0E X t =，10(,)200R t t τττ⎧=⎪+=⎨⎪≠⎩2-8 1210()()()2cos(10)(21)X X X R R R eτττττ-=+=++，2[()](0)5X E X t R ==，2(0)2X X R σ==2-9 11()()cos 22jw jw X X o G w R e d w e d τττττ∞∞---∞-∞==⎰⎰00()()()22X P w w w w w ππδδ=-++2-10 00()(()())2Y X X aG w G w w G w w =-++2-11 ())()X R u ττ=+-3-1 二元信号统计检测的贝叶斯平均代价C 为110000000100100110111111()()=()()()() ()()()()ij i i j j i C c P H P H H c P H P H H c P H P H H c P H P H H c P H P H H ===+++∑∑ 利用01()1()P H P H =-1101()1()P H H P H H =- 0010()1()P H H P H H =-得平均代价C 为[][]0011010110011011110100101110111000111011000101()1()1()() ()()()1() ()() ()()()()()()C c P H P H H c P H P H H c P H P H H c P H P H H c c c P H H P H c c c c P H H c c P H H =-⎡-⎤+-+⎣⎦+⎡-⎤⎣⎦=+-+⎡-+---⎤⎣⎦3-2 1）由于各假设j H 的先验概率()(0,1,2)j P H j =相等，所以采用最大似然准则。
时间：6月16日（星期一）晚上6：30－8：30 地点：六教104室（上课教室）试卷共8题，其中4题属于教材第一章内容，其余4题分别的其他章节。
请同学们对匹配滤波器，离散卡尔曼滤波，离散维纳滤波，高斯白噪声下确知信号的检测，K －L 展开，高斯白噪声信道中的单参量信号估计等内容重点关注。
1.1 （付柏成 20060150）在例1.2中，设噪声均方差电压值为σ＝2v ，代价为f c ＝2，m c ＝1。
信号存在的先验概率P ＝0.2。
试确定贝叶斯意义下最佳门限β，并计算出相应的平均风险。
解：根据式（1-15），可以算出00.8280.21f mQc Pc ⨯Λ===⨯ 而判决门限2201ln 0.52ln 88.822βσ=+Λ=+= 根据式（1-21）可知平均风险1010Pr 0.2r 0.8R Qr r =+=+01100.2(|)0.8(|)m f c P D H c P D H =+ 而011(|)(|)D P D H p x H dx =⎰1100(|)(|)D P D H p x Hdx =⎰而2121(1)(|)exp[]22x p x H σπσ-=- 2021(|)exp[]22x p x H σπσ=-所以201121(1)(|)(|)exp[]22D D x P D H p x H dx dx σπσ-==-⎰⎰221(1)e x p []22x dx βσπσ-∞-=-⎰＝17.82()()(3.91)22β-Φ=Φ=Φ 同理11210021(|)(|)exp[]22D D x P D H p x Hdx dx σπσ==-⎰⎰221e x p ()22x dx βσπσ∞=-⎰8.821()1()1(4.41)22β=-Φ=-Φ=-Φ 所以0.21(3.91)0.82[1(4.41)]R =⨯⨯Φ+⨯⨯-Φ 1．2 (关瑞东 20060155)假定加性噪声()n t 服从均值为零，方差为的正态分布。
信号检测与估值作业1.考虑下面观测样本为y 的简单二元假设检验问题：110011:()()22:(),0y y H f y rect H f y e y --⎧=⎪⎨⎪=>⎩ 其中，12121,()=0rect t if t -<<⎧⎨⎩，otherwise(a)求该假设检验的似然比检测器并确定判决域（即确定样本空间划分方法） (b)当00012,21P P P ===，时分别计算可能获得的最小错误概率解：（a ）11100011,02,02:()()220,0,:(),0(),0y yy y H f y p y otherwise otherwise H f y e y p y e y --⎧⎧⎧⎧<<<<⎪⎪⎪⎪==⎨⎨⎪⎪⇒⎨⎨⎪⎪⎩⎩⎪⎪⎪⎪=>=>⎩⎩11100110100 0y 222ln 11()y >2 ()112ln 1 H H y H H H H H H H H e y p y p y y y εεεεελλεεεεε⎧>>⎪⇒⎪<<-->⎪==⎨<-⎪>⎪∞<-⎪<≤⎩><-（）=化简得：0 0y 2>2H y ⎧⎪<≤⎪⎨⎪⎪⎩判为（b ）()001E F MP P P P P =+-,()10F y R P p y d =⎰,()01M yR P p y d=⎰2ln 220ln 2011111112ln 2=+ln 2222424y E P y P e dy dy e λ--=+=-⎰⎰当时，()=, 2ln 420ln 4021112123ln 4=ln 4332636y E P y P e dy dy e λ--=+=-+⎰⎰当时，()=,220011110=333y E P y P e dy e λ--==-⎰，()=,当时2.考虑下面观测样本为y 的简单二元假设检验问题：110011:()()221:()2y H f y rect H f y rect y -⎧=⎪⎪⎨⎛⎫⎪=- ⎪⎪⎝⎭⎩（a ） 求该假设检验的似然比检测器并确定判决域（即确定样本空间划分方法） （b ） 计算虚报概率F M P P 和漏报概率 解：（a ）11100011:()()1(),022221:()()1,02y H f y rect p y y H f y rect y p y y -⎧=⎧⎪=<<⎪⎪⇒⎨⎨⎛⎫⎪⎪=-=<<⎩ ⎪⎪⎝⎭⎩１ 111000()1y ()121H H H H p y p y εελλλεε>>=⇒=<<--（）=即：1010 1<y<21 0y 1 2H H H λ⎧⎪⎪>⎨<≤⎪<⎪⎩判为（b ）11000001100100100010()1111>=<0d 2()222()11=1d 102()2()11=,12()211,2F M F M F M p y P P y p y p y P y P p y p y H H p y P P λλλλλλεεεε===<>=====-=-=⎰⎰当时，，所以判为H ，，当时，，所以判为H ，，当时，，所以假设以的概率判为的概率判为则3.一个二元通信系统的表达式可以由下面的公式表示：y x n =+其中，y 是接收机观测到的样本，x 是发射的信号，n 是接收机端引入的高斯白噪声（均值为0，方差为2σ），x 取值可为-A 或+A ，分别对应假设01H H 和 （a ）要求确定最小错误概率检测器的形式（b ）给出先验概率分布满足1001103,,5P P P P P P ===情况下的最小错误概率检测器，并计算出相应的最小错误概率解：（a）2211022:()()())()):2 2 H y A n y A y A p y y H y A n p σσ=++⎧-+⇒=-=-⎨=-+⎩ 11122100()()=ln()1121H H H AyH H H p y y e y p y A σεεσελλεεε>>>=⇒⇒<<<---Ｔ （b ）0E F M P P P P P =+０（１－） 2010010131ln 33,3442P P P P P y P A σλ=⇒==⇒==⇒Ｔ当＝ 22ln3222ln30123133ln 31ln 3()()()()4444242A E A P p y dy p y dy A A A Aσσσσ+∞-∞=+=-Φ-+Φ+⎰⎰010010111,122P P P P P y P λ=⇒==⇒==⇒Ｔ当＝０ 001011111()()()()22222E P p y dy p y dy A A +∞-∞=+=-Φ-+Φ+⎰⎰ 201001013ln35355,8852P P P P P y P A σλ=⇒==⇒==⇒Ｔ当＝22322ln52301ln 5233lnln3533555()()(-)(+)8888282AE AP p y dy p y dy A A A Aσσσσ+∞-∞=+=-Φ+Φ⎰⎰ 4.接收机输出为信号电压S 和噪声电压N 之和，其二者的联合概率密度函数为：0(,), 0&0s SN f s n N N n e s αα-≤<∞≤≤=(a) 分别给出S 和N 的边缘概率密度函数()()S N f s f n 和； (b) 证明S 和N 统计独立；(c) 推导Y=S+N 的概率密度函数，并画出图形；(d) 推导()()S N f s f n 和对应假设10H H 和成立下的条件概率密度，即1()()S f y f y =0()()N f y f y =，现给定02=1N α=和，请写出最小错误概率检测器；(e) 分别计算在1001103,,23P P P P P P ===。
信号检测及估计试题-答案（不完整版）一、概念：1. 匹配滤波器。
概念：所谓匹配滤波器是指输出判决时刻信噪比最大的最佳线性滤波器。
应用：在数字信号检测和雷达信号的检测中具有特别重要的意义。
在输出信噪比最大准则下设计一个线性滤波器是具有实际意义的。
2. 卡尔曼滤波工作原理及其基本公式(百度百科)首先，我们先要引入一个离散控制过程的系统。
该系统可用一个线性随机微分方程（Linear Stochastic Difference equation）来描述：X(k)=A X(k-1)+B U(k)+W(k)再加上系统的测量值：Z(k)=H X(k)+V(k)上两式子中，X(k)是k时刻的系统状态，U(k)是k时刻对系统的控制量。
A和B是系统参数，对于多模型系统，他们为矩阵。
Z(k)是k时刻的测量值，H是测量系统的参数，对于多测量系统，H为矩阵。
W(k)和V(k)分别表示过程和测量的噪声。
他们被假设成高斯白噪声(White Gaussian Noise)，他们的covariance 分别是Q，R（这里我们假设他们不随系统状态变化而变化）。
对于满足上面的条件(线性随机微分系统，过程和测量都是高斯白噪声)，卡尔曼滤波器是最优的信息处理器。
下面我们来用他们结合他们的covariances 来估算系统的最优化输出（类似上一节那个温度的例子）。
首先我们要利用系统的过程模型，来预测下一状态的系统。
假设现在的系统状态是k，根据系统的模型，可以基于系统的上一状态而预测出现在状态：X(k|k-1)=A X(k-1|k-1)+B U(k) (1)式(1)中，X(k|k-1)是利用上一状态预测的结果，X(k-1|k-1)是上一状态最优的结果，U(k)为现在状态的控制量，如果没有控制量，它可以为0。
到现在为止，我们的系统结果已经更新了，可是，对应于X(k|k-1)的covariance还没更新。
我们用P表示covariance：P(k|k-1)=A P(k-1|k-1) A’+Q (2)式(2)中，P(k|k-1)是X(k|k-1)对应的covariance，P(k-1|k-1)是X(k-1|k-1)对应的covariance，A’表示A的转置矩阵，Q是系统过程的covariance。
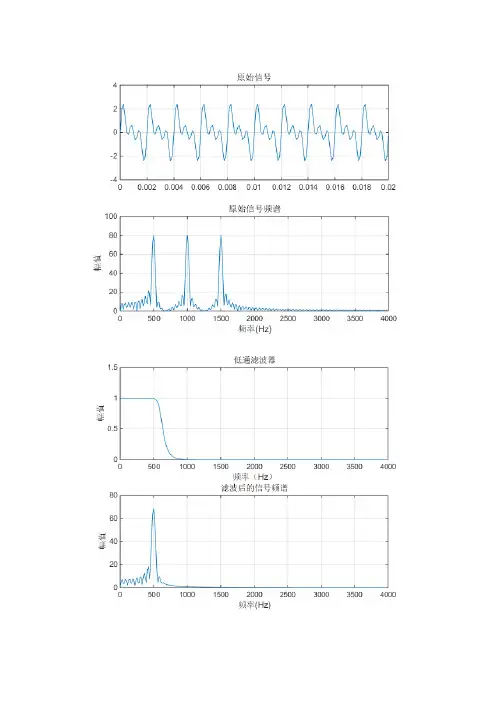
% 含有频率f ，2f 和3f 的正弦波叠加原始信号Fs=8000; %采样频率8KHzf=500; %信号基频A=1;t=0:1/Fs:0.02; %产生时间序列x=A*sin(2*pi*f*t)+A*sin(4*pi*f*t)+A*sin(6*pi*f*t); %产生目标信号figure(1);subplot(2,1,1);plot(t,x);grid;title('原始信号');%FFT分析信号频谱len=512;y=fft(x,len); %对信号做len点FFT变换f1=Fs*(0:len/2-1)/len;subplot(2,1,2);plot(f1,abs(y(1:len/2)));grid;title('原始信号频谱')xlabel('频率(Hz)');ylabel('幅值');%数字滤波器设计，均采用巴特沃斯滤波器Rp=3; %通带最大衰减率为3dBRc=40; %祖代最小衰减率为40dB%IIR数字低通滤波器设计Fp=1.2*f;Fc=1.8*f;Wp=2*Fp/Fs;Wc=2*Fc/Fs;[N,Wn]=buttord(Wp,Wc,Rp,Rc);[B,A]=butter(N,Wn,'low');[H,W]=freqz(B,A,len,Fs);figuresubplot(2,1,1);plot(W,abs(H));grid;title('低通滤波器');xlabel('频率（Hz）');ylabel('幅值');xx=filter(B,A,x);yy=fft(xx,len);subplot(2,1,2);plot(f1,abs(yy(1:len/2)));grid;title('滤波后的信号频谱');xlabel('频率(Hz)');ylabel('幅值');%IIR 数字高通滤波器的设计Fp=2.6*f;Fc=2.2*f;Wc=2*Fc/Fs;[N,Wn]=buttord(Wp,Wc,Rp,Rc);[B,A]=butter(N,Wn,'high');[H,W]=freqz(B,A,len,Fs);figuresubplot(2,1,1);plot(W,abs(H));grid;title('高通滤波器');xlabel('频率（Hz）');ylabel('幅值');xx=filter(B,A,x);yy=fft(xx,len);subplot(2,1,2);plot(f1,abs(yy(1:len/2)));grid;title('滤波后的信号频谱');xlabel('频率(Hz)');ylabel('幅值'); %3.IIR 数字带通滤波器设计Fp=[1.8*f 2.2*f];Fc=[1.6*f 2.8*f];Wp=2*Fp/Fs;Wc=2*Fc/Fs;[N,Wn]=buttord(Wp,Wc,Rp,Rc);[B,A]=butter(N,Wn,'bandpass');[H,W]=freqz(B,A,len,Fs);figuresubplot(2,1,1);plot(W,abs(H));grid;title('带通滤波器');xlabel('频率（Hz）');ylabel('幅值');xx=filter(B,A,x);yy=fft(xx,len);subplot(2,1,2);plot(f1,abs(yy(1:len/2)));grid;title('滤波后的信号频谱');xlabel('频率（Hz）');ylabel('幅值');%3.IIR数字带阻滤波器设计Fp=[1.6*f 2.8*f];Fc=[1.8*f 2.2*f];Wc=2*Fc/Fs;[N,Wn]=buttord(Wp,Wc,Rp,Rc); [B,A]=butter(N,Wn,'stop'); [H,W]=freqz(B,A,len,Fs); figuresubplot(2,1,1);plot(W,abs(H));grid;title('带阻滤波器');xlabel('频率（Hz）');ylabel('幅值');xx=filter(B,A,x);yy=fft(xx,len);subplot(2,1,2);plot(f1,abs(yy(1:len/2))); grid;title('滤波后的信号频谱'); xlabel('频率（Hz）');ylabel('幅值');。
