第九章10:向量的外积和外微分形式
- 格式:pdf
- 大小:6.61 MB
- 文档页数:7

向量内积及外积
向量的内积和外积在计算方式、几何意义以及各自的性质上都有区别。
具体如下:
1、计算方式不同
向量的内积(点乘/数量积),是对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作;向量的外积,又叫叉乘、叉积向量积,其运算结果是一个向量而不是一个标量。
并且两个向量的外积与这两个向量组成的坐标平面垂直。
2、几何意义不同
内积(点乘)的几何意义包括:表征或计算两个向量之间的夹角;向量在a向量方向上的投影;在三维几何中,向量a和向量b 的外积结果是一个向量,有个更通俗易懂的叫法是法向量,该向量垂直于a和b向量构成的平面。
3、性质不同
内积性质:a^2≥0;当a^2 = 0时,必有a = 0.(正定性);(λa +μb)×c =λa×c +μb×c,对任意实数λ,μ成立(线性);cos∠(a,b) =a×b/(|a|×|b|);|a×b|≤|a||b|,等号只在a 与b共线时成立。
向量外积的性质:a × b = -b × a(反称性);(λa +μb) × c =λ(a ×c) +μ(b ×c)(线性)。

向量场和微分形式的初步理解向量场和微分形式是微积分和微分几何中的重要概念,它们在数学和物理学等领域中有着广泛的应用。
本文将对向量场和微分形式进行初步理解和介绍。
一、向量场在数学中,向量场是指在空间中的每一点都与一个向量相对应的函数。
向量场可以用来描述物理现象中的力、速度、磁场等向量量。
在二维平面中,向量场可以表示为:F(x, y) = M(x, y)i + N(x, y)j,其中,(x, y)为平面上的点的坐标,M(x, y)和N(x, y)为与点(x, y)对应的向量的分量。
向量场可以通过矢量箭头的形式进行可视化。
向量场具有一些重要的性质,如散度、旋度和调和性等。
散度用于描述向量场的发散和聚集特性,可以表示为:div F = ∇·F = (∂M/∂x) + (∂N/∂y),其中,∇是偏导数算子。
散度为正值表示向量场从该点发散,为负值表示向量场在该点聚集。
旋度用于描述向量场的旋转特性,可以表示为:curl F = ∇ × F = (∂N/∂x - ∂M/∂y),旋度为0表示向量场是无旋的。
调和向量场则是指既具有零散度又具有零旋度的向量场,满足拉普拉斯方程。
二、微分形式微分形式是微分几何中的重要工具,用于描述流形上的几何特性。
在流形上,微分形式是切向量场的线性组合,并且具有反对称性质。
在一维流形中,微分形式可以表示为:ω(x) = f(x)dx,其中,f(x)为函数,dx为微分形式,并且满足dx∧dx = 0。
微分形式可以进行外积、外导数和星算子等运算。
外积用于将两个微分形式相乘得到新的微分形式,外导数用于计算微分形式的导数。
星算子用于将n维微分形式映射到(n-m)维微分形式,在微分几何中有重要的意义。
三、向量场与微分形式的关系向量场和微分形式之间存在着密切的联系。
在流形上,向量场可以通过微分形式的外导数来表示,微分形式也可以通过向量场的积分来求解。
斯托克斯定理则是向量场和微分形式之间联系的一个重要定理,它建立了向量场的曲面积分和微分形式的外导数之间的关系。
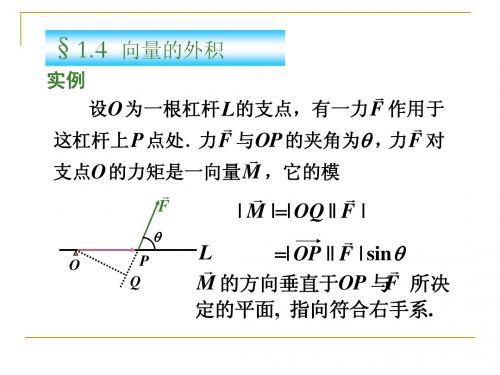
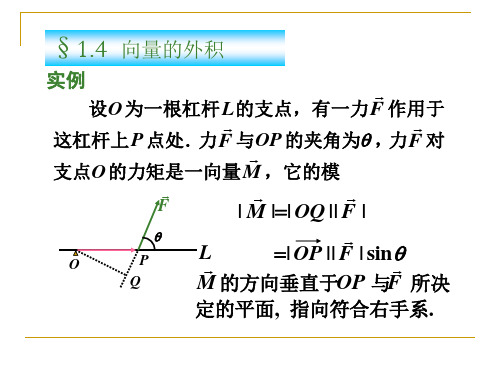

外微分形式的微积分外微分形式是微积分中的一个重要概念,广泛应用于微分几何、物理学和工程学等领域中。
它是描述多元函数和曲面的工具,帮助我们理解和计算复杂的曲线和曲面上的积分以及它们之间的关系。
为了更好地理解外微分形式,首先需要了解微分形式的概念。
微分形式是一种能够描述曲线或曲面上各点的性质的数学对象。
它在数学上是一种广义的概念,可以用来描述不同维度的对象。
例如,在曲线上,微分形式可以表示为f(x)dx,其中f(x)是一个函数,dx表示微小的位移。
在曲面上,微分形式可以表示为f(x,y)dxdy,其中f(x,y)是一个二元函数。
外微分形式则是微分形式的推广,它可以描述更高维度的对象,如三维空间中的曲面或四维空间中的流形。
外微分形式使用向量的外积来定义,具有更强的代数性质。
例如,在三维空间中,一个外微分形式可以表示为f(x,y,z)dxdydz,其中f(x,y,z)是一个三元函数。
这种表示方式非常直观,它将函数值与微小的位移相乘,得到一个描述各点性质的形式。
外微分形式的一个重要性质是它能够描述曲线或曲面上的微积分运算,如积分和微分。
通过外微分形式,我们可以定义曲线和曲面上的曲线积分、曲面积分以及通量等概念。
这些积分与微分形式之间存在紧密的联系,它们互为逆运算。
使用外微分形式,我们可以将复杂的积分问题转化为简单的运算,使得计算更为方便。
在物理学和工程学中,外微分形式被广泛应用于描述电磁场、流体力学以及广义相对论等领域中的物理现象。
例如,在电磁场中,我们可以用外微分形式来描述电场和磁场的分布情况,进而计算电场和磁场的通量、环路积分等物理量。
在流体力学中,外微分形式可以描述流体的速度场、压力场等性质,帮助我们分析流体的运动行为。
在广义相对论中,外微分形式能够描述时空的曲率和引力场的分布情况,帮助我们理解引力的本质和时空的弯曲性质。
总之,外微分形式是微积分中的重要工具,它能够描述曲线和曲面上的性质,并帮助我们计算复杂的积分和微分。
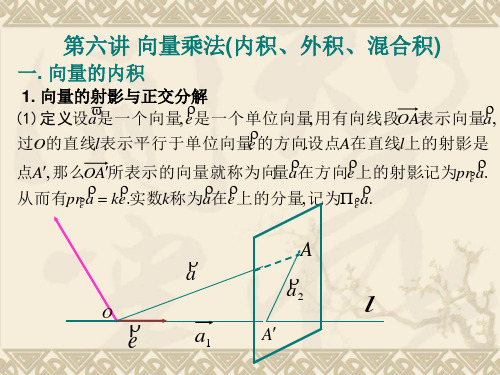
向量运算:外积与混合积在数学和物理学领域中,向量是一种重要的概念,它可以表示物理量的大小和方向。
向量的运算包括加法、数乘、内积、外积和混合积,其中外积和混合积是两种比较复杂的运算。
外积(叉乘)外积,又称叉乘或向量积,是两个向量之间的一种运算。
对于给定的两个三维向量$\\vec{a}$和$\\vec{b}$,它们的外积定义为一个新向量,记为$\\vec{a}\\times \\vec{b}$。
外积的计算公式如下:$$ \\vec{a} \\times \\vec{b} = \\begin{pmatrix} a_{1} \\\\ a_{2} \\\\ a_{3}\\end{pmatrix} \\times \\begin{pmatrix} b_{1} \\\\ b_{2} \\\\ b_{3}\\end{pmatrix} = \\begin{pmatrix} a_{2}b_{3} - a_{3}b_{2} \\\\ a_{3}b_{1} -a_{1}b_{3} \\\\ a_{1}b_{2} - a_{2}b_{1} \\end{pmatrix} $$在物理学中,外积经常用于描述两个向量之间的叉乘关系,并常用于计算力矩等物理量。
混合积(点乘)混合积,又称点乘或数量积,是三个向量之间的一种运算。
对于给定的三个向量$\\vec{a}$、$\\vec{b}$和$\\vec{c}$,它们的混合积定义为一个标量(纯数量),记为$\\vec{a} \\cdot (\\vec{b} \\times \\vec{c})$。
混合积的计算公式如下:$$ \\vec{a} \\cdot (\\vec{b} \\times \\vec{c}) = \\vec{a} \\cdot \\vec{d} =a_{1}d_{1} + a_{2}d_{2} + a_{3}d_{3} $$其中,$\\vec{d} = \\vec{b} \\times \\vec{c}$ 是$\\vec{b}$和$\\vec{c}$的叉积所得的向量。
概念向量是由n个实数组成的一个n行1列(n*1)或一个1行n列(1*n)的有序数组;向量的点乘,也叫向量的内积、数量积,对两个向量执行点乘运算,就是对这两个向量对应位一一相乘之后求和的操作,点乘的结果是一个标量。
点乘公式对于向量a和向量b:a和b的点积公式为:要求一维向量a和向量b的行列数相同。
点乘几何意义点乘的几何意义是可以用来表征或计算两个向量之间的夹角,以及在b向量在a 向量方向上的投影,有公式:推导过程如下,首先看一下向量组成:定义向量:根据三角形余弦定理有:根据关系c=a-b(a、b、c均为向量)有:即:向量a,b的长度都是可以计算的已知量,从而有a和b间的夹角θ:根据这个公式就可以计算向量a和向量b之间的夹角。
从而就可以进一步判断这两个向量是否是同一方向,是否正交(也就是垂直)等方向关系,具体对应关系为:a·b>0 方向基本相同,夹角在0°到90°之间a·b=0 正交,相互垂直a·b<0 方向基本相反,夹角在90°到180°之间叉乘公式两个向量的叉乘,又叫向量积、外积、叉积,叉乘的运算结果是一个向量而不是一个标量。
并且两个向量的叉积与这两个向量组成的坐标平面垂直。
对于向量a和向量b:a和b的叉乘公式为:其中:根据i、j、k间关系,有:叉乘几何意义在三维几何中,向量a和向量b的叉乘结果是一个向量,更为熟知的叫法是法向量,该向量垂直于a和b向量构成的平面。
在3D图像学中,叉乘的概念非常有用,可以通过两个向量的叉乘,生成第三个垂直于a,b的法向量,从而构建X、Y、Z坐标系。
如下图所示:成的平行四边形的面积。
外积的几何解释外积是向量运算中的一种重要操作。
在几何学中,外积也被称为向量积或叉积。
它的几何解释可以通过以下方式进行说明:1. 定义:给定三维空间中的两个向量 A 和 B,它们的外积可以表示为另一个向量 C = A × B,该向量垂直于 A 和 B 所在的平面。
外积的结果是一个新的向量,其模长等于面积,方向垂直于原始向量所在平面。
A和B,它们的外积可以表示为另一个向量C = A ×B,该向量垂直于A和B所在的平面。
外积的结果是一个新的向量,其模长等于面积,方向垂直于原始向量所在平面。
2. 几何意义:外积可以帮助我们理解向量之间的关系和相互作用。
当两个向量具有一个公共点,并且它们都不为零向量时,它们的外积结果会产生一个新的向量,指向由这两个向量所确定的平面的法向量。
这个法向量的长度等于这两个向量所确定的平面的面积。
3. 右手法则:外积的方向可以通过右手法则确定。
将右手的拇指放在 A 上,并使其指向 B,其他四个手指则会朝着外积结果的方向延伸。
这个右手定则可以帮助我们确定外积结果的方向。
A上,并使其指向B,其他四个手指则会朝着外积结果的方向延伸。
这个右手定则可以帮助我们确定外积结果的方向。
4. 应用:外积有多种应用,特别是在物理学和工程学领域。
它可以用于计算面积、体积、角度和力矩等。
外积也可以用于计算平面的法向量,这对于解决许多几何问题非常有用。
总结起来,外积的几何解释是通过求解两个向量的叉积来得到一个新的向量,它垂直于原始向量所在的平面,并且长度等于这两个向量所确定的平面的面积。
外积在几何学和物理学中有广泛的应用,它可以帮助我们理解向量之间的关系和相互作用。
参考资料:。