第三讲 二次函数与几何变换计算 (教师版)

二次函数与几何综合（讲义）➢ 课前预习1. 如图，直线112y x =+经过点A (1，m )，B (4，n )，点C 的坐标为(2，5)，则△ABC 的面积为__________．提示：利用点坐标求面积，需要将点坐标转化为横平竖直的线段长，常考虑作横平竖直的线来对图形进行割补． 具体操作：①过点C 作CD ∥y 轴，交AB 于点D ； ②借助C ，D 坐标求解CD 长；③以CD 为底，则A ，B 两点间的水平距离为高，即1()2ABC ADC DBC B A S S S CD x x =+=⋅⋅-△△△．2. 如图，在平面直角坐标系xOy 中，直线334y x =-+与x 轴，y 轴分别交于点A ，B ，点C 的坐标为(0，-2)．若点D 在直线AB 上运动，点E 在直线AC上运动，当以O，A，D，E为顶点的四边形是平行四边形时，点D的坐标为__________．提示：（1）分析定点（A，O），动点（D，E），属于两定两动的平行四边形存在性问题．（2）连接两定点得定线段，考虑：①若定线段作为平行四边形的边，则通过平移确定点的坐标；②若定线段作为平行四边形的对角线，则绕定线段中点旋转，利用中点坐标公式确定点的坐标．（3）利用函数特征和几何特征求解后，结合图形进行验证．➢知识点睛1.“函数与几何综合”问题的处理原则：_________________，_____________________．2.研究背景图形：①研究函数表达式．二次函数关注____________，一次函数关注__________．②___________________________．找特殊图形、特殊位置关系，寻求边长和角度信息．3. 二次函数之面积问题的常见模型①割补法——铅垂法求面积：1()2APB B A S PM x x =⋅⋅-△ 1()2APB B A S PM x x =⋅⋅-△②转化法——借助平行线转化：若S △ABP =S △ABQ ， 若S △ABP =S △ABQ ， 当P ，Q 在AB 同侧时，当P ，Q 在AB 异侧时， PQ ∥AB ．AB 平分PQ ．➢ 精讲精练1. 如图，抛物线y =-x 2+2x +3经过A ，B ，C 三点．点M 是直线BC 上方抛物线上的点（不与B ，C 重合），过点M 作MN ∥y 轴交线段BC 于点N ，连接MB ，MC ．（1）若设点M 的横坐标为m ，四边形OBMC 的面积为S ，则S 与m 的函数关系式为________________．（2）四边形OBMC 的最大面积为________，此时点M 的坐标为____________．2.如图，在平面直角坐标系中，抛物线y=-x2+2x+3经过A，B，C三点，点D的坐标为(0，1)，直线AD与抛物线交于另一点E．（1）若M是直线AD上方抛物线上的一个动点，则△AME面积的最大值为__________．（2）在直线AD下方的抛物线上有一动点G，当S=6时，点G的坐标△AEG为_______________．3.如图，已知抛物线y=ax2-2ax-b（a＞0）与x轴交于A，B两点，点A在点B的右侧，且点B的坐标为(-1，0)，与y轴的负半轴交于点C，顶点为D．连接AC，CD，∠ACD=90°．（1）直接写出抛物线的解析式；（2）若点M在抛物线上，且以点M，A，C以及另一点N为顶点的平行四边形ACNM的面积为12，设M的横坐标为m，求m的值．4. 如图，已知二次函数y =x 2-3x -4的图象与x 轴交于点A ，B ，且经过点C(2，标；若不能，请说明理由．5.如图，抛物线y=ax2-5ax+4（a＜0）经过△ABC的三个顶点，已知BC∥x轴，点A在x轴上，点C在y轴上，且AC=BC．（1）求抛物线的解析式；（2）已知点D在抛物线对称轴上，点E在抛物线上，且以A，B，D，E为顶点的四边形是平行四边形，求点E的坐标；（3）已知点F是抛物线上的动点，点G是直线y=-x上的动点，且以O，C，F，G为顶点的四边形是平行四边形，求点G的横坐标．【参考答案】➢课前预习1.9 22.1126 () 55D，，2286 () 55D-，➢知识点睛1.利用横平竖直的线段长，函数特征与几何特征互转2.①四点一线；k，b②坐标转线段长➢精讲精练。

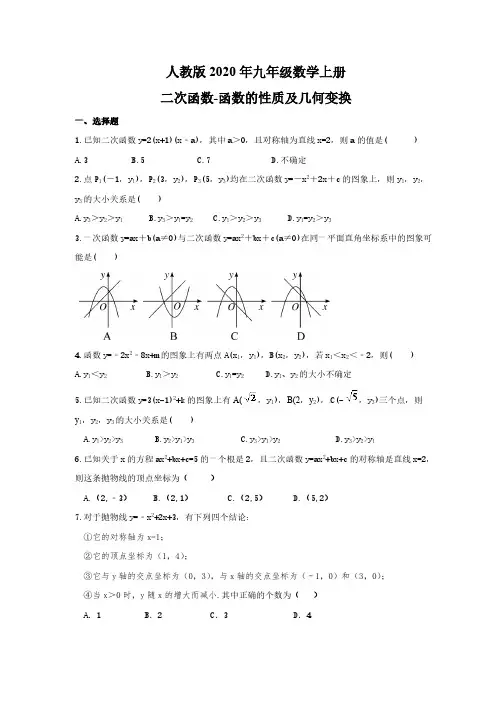
人教版2020年九年级数学上册二次函数-函数的性质及几何变换一、选择题1.已知二次函数y=2(x+1)(x﹣a)，其中a＞0，且对称轴为直线x=2，则a的值是( )A.3B.5C.7D.不确定2.点P1(－1，y1)，P2(3，y2)，P3(5，y3)均在二次函数y=－x2＋2x＋c的图象上，则y1，y2，y3的大小关系是( )A.y3＞y2＞y1B.y3＞y1=y2C.y1＞y2＞y3D.y1=y2＞y33.一次函数y=ax＋b(a≠0)与二次函数y=ax2＋bx＋c(a≠0)在同一平面直角坐标系中的图象可能是( )4.函数y=﹣2x2﹣8x+m的图象上有两点A(x1，y1)，B(x2，y2)，若x1＜x2＜﹣2，则( )A.y1＜y2B.y1＞y2C.y1=y2D.y1、y2的大小不确定5.已知二次函数y=3(x-1)2+k的图象上有A(，y1)，B(2，y2)，C(-，y3)三个点，则y1，y2，y3的大小关系是( )A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y3>y2>y16.已知关于x的方程ax2+bx+c=5的一个根是2，且二次函数y=ax2+bx+c的对称轴是直线x=2，则这条抛物线的顶点坐标为（）A.（2,﹣3）B.（2,1）C.（2,5）D.（5,2）7.对于抛物线y=﹣x2+2x+3，有下列四个结论：①它的对称轴为x=1；②它的顶点坐标为（1，4）；③它与y轴的交点坐标为（0，3），与x轴的交点坐标为（﹣1，0）和（3，0）；④当x＞0时，y随x的增大而减小.其中正确的个数为（）A．1 B．2 C．3 D．48.若将抛物线y=5x2先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为( )A.y =5(x-2)2+1B.y =5(x+2)2+1C.y =5(x-2)2-1D.y =5(x+2)2-19.在平面直角坐标系中，将抛物线y＝x2－4先向右平移2个单位，再向上平移2个单位，得到的抛物线解析式为( )A.y=(x＋2)2＋2B.y=(x-2)2-2C.y=(x-2)2＋2D.y=(x＋2)2-210.抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣2x﹣3，则b、c的值为（）A.b=2，c=2B.b=2，c=0C.b=﹣2，c=﹣1D.b=﹣3，c=2二、填空题11.已知A(0，3)，B(2，3)是抛物线y=－x2＋bx＋c上两点，该抛物线的顶点坐标是________.12.二次函数y=x2+6x+5图象的顶点坐标为 ．13.如图，点E是抛物线y=a(x﹣2)2+k的顶点，抛物线与y轴交于点C，过点C作CD∥x轴，与抛物线交于点B，与对称轴交于点D．点A是对称轴上一点，连结AC、AB．若△ABC是等边三角形，则图中阴影部分图形的面积之和是．14.抛物线y=﹣x2+bx+c的部分图象如图所示，若y=0，则x= ．15.如图，抛物线y=ax2＋bx＋c与x轴相交于点A、B(m＋2，0)，与y轴相交于点C，点D在该抛物线上，坐标为(m，c)，则点A的坐标是________.16.把抛物线y=x2-4x+5的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式是三、解答题17.已知抛物线y=﹣x2+bx+c经过点A（3，0），B（﹣1，0）．（1）求抛物线的解析式；（2）求抛物线的顶点坐标．18.如图，已知抛物线y=ax2＋bx＋c与x轴交于点A(1，0)，点B(3，0)，且过点C(0，－3).(1)求抛物线的函数表达式和顶点坐标；(2)请你写出一种平移的方法，使平移后抛物线的顶点落在直线y=－x上，并写出平移后抛物线的函数表达式.19.已知二次函数y=ax2＋bx-3的图象经过点A（2,-3）,B（-1,0）.（1）求二次函数的解析式；（2）若把图象沿y轴向下平移5个单位,求该二次函数的图象的顶点坐标.20.如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点．(1)求该抛物线的函数关系式；(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD,请求出P点的坐标．21.如图，二次函数的图象与x轴交于A（﹣3，0）和B（1，0）两点，交y轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D.（1）请直接写出D点的坐标.（2）求二次函数的解析式.（3）根据图象直接写出使一次函数值大于二次函数值的x的取值范围.22.已知二次函数y=ax2-4x+c的图象过点(-1, 0)和点(2,-9)．(1) 求该二次函数的解析式并写出其对称轴；(2) 已知点P(2 , -2),连结OP , 在x轴上找一点M,使△OPM是等腰三角形,请直接写出点M的坐标(不写求解过程).参考答案1.答案为：B.2.D　3.C4.A5.答案为：C6.C7.C.8.A9.B10.B11.答案为：(1，4)；12.答案为：(﹣3，﹣4)．13.答案为2．14.答案为:﹣3或115.答案为：(－2，0).16.答案为：y=x2-10x+2417.解：（1）∵抛物线y=﹣x2+bx+c经过点A（3，0），B（﹣1，0）．∴抛物线的解析式为；y=﹣（x﹣3）（x+1），即y=﹣x2+2x+3，（2）∵抛物线的解析式为y=﹣x2+2x+3=﹣（x﹣1）2+4，∴抛物线的顶点坐标为：（1，4）．18.解：(1)∵抛物线与x轴交于点A(1，0)，点B(3，0)，∴可设抛物线表达式为y=a(x－1)(x－3)，把C(0，－3)的坐标代入，得3a=－3，解得a=－1，故抛物线表达式为y=－(x－1)(x－3)，即y=－x2＋4x－3.∵y=－x2＋4x－3=－(x－2)2＋1，∴抛物线的顶点坐标为(2，1)；(2)答案不唯一，如：先向左平移2个单位，再向下平移1个单位，得到的抛物线的解析式为y=－x2，平移后抛物线的顶点为(0，0)，落在直线y=－x上.19.解：(1)由已知,有,即,解得∴所求的二次函数的解析式为.(2)（1,）20.解：(1)∵抛物线的顶点D的坐标为(1,﹣4),∴设抛物线的函数关系式为y=a(x﹣1)2﹣4,又∵抛物线过点C(0,﹣3),∴﹣3=a(0﹣1)2﹣4,解得a=1,∴抛物线的函数关系式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3；(2)∵S△PAB=S△ABD,且点P在抛物线上,∴点P到线段AB的距离一定等于顶点D到AB的距离,∴点P的纵坐标一定为4．令y=4,则x2﹣2x﹣3=4,解得x1=1+2,x2=1﹣2．∴点P的坐标为(1+2,4)或(1﹣2,4)．21.解：（1）∵如图，二次函数的图象与x轴交于A（﹣3，0）和B（1，0）两点，∴对称轴是x=﹣1.又点C（0，3），点C、D是二次函数图象上的一对对称点，∴D（﹣2，3）；（2）设二次函数的解析式为y=ax2+bx+c（a≠0，a、b、c常数），根据题意得，解得，所以二次函数的解析式为y=﹣x2﹣2x+3；（3）如图，一次函数值大于二次函数值的x的取值范围是x＜﹣2或x＞1.22.解：(1)对称轴是x=2(2)。

《二次函数》教案8篇(二次函数应用教案设计)下面是整理的《二次函数》教案8篇(二次函数应用教案设计)，欢迎参阅。

《二次函数》教案1教学目标掌握二次函数y=ax2+bx+c的图象与x轴的交点个数与一元二次方程ax2+bx+c=0的解的情况之间的关系。

重点、难点：二次函数y=ax2+bx+c的图象与一元二次方程ax2+bx+c=0的根之间关系的探索。

教学过程：一、情境创设一次函数y=x+2的图象与x轴的交点坐标问题1.任意一次函数的图象与x轴有几个交点？问题2.猜想二次函数图象与x轴可能会有几个交点？可以借助什么来研究？二、探索活动活动一观察在直角坐标系中任意取三点A、B、C，测出它们的纵坐标，分别记作a、b、c，以a、b、c为系数绘制二次函数y=ax2+bx+c的图象，观察它与x轴交点数量的情况；任意改变a、b、c值后，观察交点数量变化情况。

活动二观察与探索如图1，观察二次函数y=x2-x-6的图象，回答问题:(1)图象与x轴的交点的坐标为A(，),B(，)(2)当x=时，函数值y=0。

(3)求方程x2-x-6=0的解。

(4)方程x2-x-6=0的解和交点坐标有何关系？活动三猜想和归纳(1)你能说出函数y=ax2+bx+c的图象与x轴交点个数的其它情况吗？猜想交点个数和方程ax2+bx+c=0的根的个数有何关系。

（2）一元二次方程ax2+bx+c=0的根的个数由什么来判断？这样我们可以把二次函数y=ax2+bx+c的图象与x轴交点、一元二次方程ax2+bx+c=0的实数根和根的判别式三者联系起来。

三、例题分析例1.不画图象，判断下列函数与x轴交点情况。

(1)y=x2-10x+25(2)y=3x2-4x+2(3)y=-2x2+3x-1例2.已知二次函数y=mx2+x-1(1)当m为何值时，图象与x轴有两个交点(2)当m为何值时，图象与x轴有一个交点？(3)当m为何值时，图象与x轴无交点？四、拓展练习1.如图2，二次函数y=ax2+bx+c的图象与x轴交于A、B。

一、二次函数图象的平移变换（1）具体步骤：先利用配方式把二次函数化成2()y a x h k =-+的形式，确信其极点(,)h k ，然后做出二次函数2y ax =的图像，将抛物线2y ax =平移，使其极点平移到(,)h k .具体平移方式如下图：（2）平移规律：在原有函数的基础上“左加右减”.二、二次函数图象的对称变换二次函数图象的对称一样有五种情形，能够用一样式或极点式表达 1. 关于x 轴对称2y ax bx c =++关于x 轴对称后，取得的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，取得的解析式是()2y a x h k =---； 2. 关于y 轴对称2y ax bx c =++关于y 轴对称后，取得的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，取得的解析式是()2y a x h k =++； 3. 关于原点对称2y ax bx c =++关于原点对称后，取得的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，取得的解析式是()2y a x h k =-+-； 4. 关于极点对称2y ax bx c =++关于极点对称后，取得的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于极点对称后，取得的解析式是()2y a x h k =--+．5. 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，取得的解析式是()222y a x h m n k =-+-+- 依照对称的性质，显然不管作何种对称变换，抛物线的形状必然可不能发生转变，因此a 永久不变．求抛物线的对称抛物线的表达式时，能够依据题意或方便运算的原那么，选择适合的形式，适应上是先确信原抛物线（或表达式已知的抛物线）的极点坐标及开口方向，再确信其对称抛物线的极点坐标及开口方向，然后再写出其对称抛物线的表达式．知识点拨二次函数图象的几何变换一、二次函数图象的平移变换【例1】 函数23(2)1y x =+-的图象可由函数23y x =的图象平移取得，那么平移的步骤是：（ ）A. 右移两个单位，下移一个单位B. 右移两个单位，上移一个单位C. 左移两个单位，下移一个单位D. 左移两个单位，上移一个单位【例2】 函数22(1)1y x =---的图象可由函数22(2)3y x =-++的图象平移取得，那么平移的步骤是（ ）A. 右移三个单位，下移四个单位B. 右移三个单位，上移四个单位C. 左移三个单位，下移四个单位D. 左移四个单位，上移四个单位【例3】 二次函数2241y x x =-++的图象如何移动就取得22y x =-的图象（ ）A. 向左移动1个单位，向上移动3个单位.B. 向右移动1个单位，向上移动3个单位.C. 向左移动1个单位，向下移动3个单位.D. 向右移动1个单位，向下移动3个单位.【例4】 将函数2y x x =+的图象向右平移()0a a >个单位，取得函数232y x x =-+的图象，那么a 的值为（ ）A ．1B ．2C ．3D ．4【例5】 把抛物线2y ax bx c =++的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是235y x x =-+，那么a b c ++=________________．【例6】 关于每一个非零自然数n ，抛物线()()221111n y x x n n n n +=-+++与x 轴交于n n A B 、两点，以n n A B 表示这两点间的距离，那么112220092009A B A B A B +++…的值是（ ）A ． 20092008B ．20082009C ．20102009D ．20092010【例7】 把抛物线2y x =-向左平移1个单位，然后向上平移3个单位，那么平移后抛物线的解析式为A ．()213y x =--- B ．()213y x =-+- C ．()213y x =--+D ．()213y x =-++【例8】 将抛物线22y x =向下平移1个单位，取得的抛物线是（ ）A ．()221y x =+B ．()221y x =-C ．221y x =+D ．221y x =-【例9】 将抛物线23y x =向上平移2个单位，取得抛物线的解析式是（ ）A. 232y x =-B. 23y x =C. 23(2)y x =+D. 232y x =+【例10】 一抛物线向右平移3个单位，再向下平移2个单位后得抛物线224y x x =-+，那么平移前抛物线的解析式为________________．【例11】 已知二次函数5632+-=x x y ，求知足以下条件的二次函数的解析式：（1）图象关于x 轴对称；（2）图象关于y 轴对称；（3）图象关于通过其极点且平行于x 轴的直线对称例题精讲【例12】 如图，ABCD 中，4AB =，点D 的坐标是(0，8)，以点C 为极点的抛物线2y ax bx c =++通过x 轴上的点A ，B ．⑴ 求点A ，B ，C 的坐标．⑵ 假设抛物线向上平移后恰好通过点D ，求平移后抛物线的解析式．【例13】 抛物线254y ax x a =-+与x 轴相交于点A B 、，且过点()54C ，． ⑴ 求a 的值和该抛物线极点P 的坐标．⑵ 请你设计一种平移的方式，使平移后抛物线的极点落要第二象限，并写出平移后抛物线的解析式．二、二次函数图象的对称变换【例14】 函数2y x =与2y x =-的图象关于______________对称，也能够以为2y x =是函数2y x =-的图象绕__________旋转取得．【例15】 已知二次函数221y x x =--，求：⑴关于x 轴对称的二次函数解析式；⑵关于y 轴对称的二次函数解析式；⑶关于原点对称的二次函数解析式．【例16】 在平面直角坐标系中，先将抛物线22y x x =+-关于x 轴作轴对称变换，再将所得的抛物线关于y轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为 A ．22y x x =--+ B ．22y x x =-+- C ．22y x x =-++ D ．22y x x =++【例17】 已知二次函数2441y ax ax a =++-的图象是1c ．⑴ 求1c 关于()10R ，成中心对称的图象2c 的函数解析式； ⑵ 设曲线12c c 、与y 轴的交点别离为A B ，，当18AB =时，求a 的值．【例18】 已知抛物线265y x x =-+，求⑴ 关于y 轴对称的抛物线的表达式；⑵ 关于x 轴对称的抛物线的表达式； ⑶ 关于原点对称的抛物线的表达式．【例19】 设曲线C 为函数()20y ax bx c a =++≠的图象，C 关于y 轴对称的曲线为1C ，1C关于x 轴对称的曲线为2C ，那么曲线2C 的函数解析式为________________．【例20】 关于任意两个二次函数：()2211112222120y a x b x c y a x b x c a a =++=++≠，，当12a a =时，咱们称这两个二次函数的图象为全等抛物线，现有ABM ∆，()()1010A B -，，，，记过三点的二次函数抛物线为“C”（“□□□”中填写相应三个点的字母）．⑴ 假设已知()01M ，，ABM ABN ∆∆≌（图1），请通过计算判定ABM C 与ABN C 是不是为全等抛物线；⑵ 在图2中，以A B M 、、三点为极点，画出平行四边形． ① 假设已知()0M n ，，求抛物线ABM C 的解析式，并直接写出所有过平行四边形中三个极点且能与ABM C 全等的抛物线解析式．② 假设已知()M m n ，，当m n 、知足什么条件时，存在抛物线ABM C ？依照以上的探讨结果，判定是不是存在过平行四边形中三个极点且能与ABM C 全等的抛物线．假设存在，请写出所有知足条件的抛物线“C”；假设不存在，请说明理由．【例21】 已知：抛物线2:(2)5f y x =--+． 试写出把抛物线f 向左平行移动2个单位后，所得的新抛物线1f 的解析式；和f 关于x 轴对称的曲线2f 的解析式．画出1f 和2f 的略图， 并求：⑴ x 的值什么范围，抛物线1f 和2f 都是下降的；⑵ x 的值在什么范围，曲线1f 和2f 围成一个封锁图形；⑶ 求在1f 和2f 围成封锁图形上，平行于y 轴的线段的长度的最大值．。

2014年中考解决方案——二次函数解析式及几何变换能通过分析实际问题的情境确定二次函数的解析式；能从图象上认识二次函数的性质；会根据二次函数的解析式求其图象与坐标轴的交点坐标，会确定图象的顶点、开口方向和对称轴；会利用二次函数的图象求一元二次方程的近似解．知识点一 二次函数解析式的确定一、待定系数法（1）一般式：2(0)y ax bx c a =++≠．如果已知二次函数的图象上的三点坐标（或称函数的三对对应值）()11x y ，、()22x y ，、()33x y ，，那么方程组211122222333y ax bx cy ax bx c y ax bx c⎧=++⎪=++⎨⎪=++⎩就可以唯一确定a 、b 、c ，从而求得函数解析式2y ax bx c =++．总结：1．任何二次函数都可以整理成一般式2(0)y ax bx c a =++≠的形式； 2．已知任意3点坐标，可用一般式求解二次函数解析式． （2）顶点式：2()(0)y a x h k a =-+≠．由于222424b ac b y ax bx c a x a a -⎛⎫=++=++⎪⎝⎭，所以当已知二次函数图象的顶点坐标2424b ac b a a ⎛⎫-- ⎪⎝⎭， 时，就可以设二次函数形如22424b ac b y a x a a -⎛⎫=++⎪⎝⎭，从而利用其他条件，容易求得此函数的解析式．这里直线2bx a=-又称为二次函数图象的对称轴．总结：1．已知顶点坐标或对称轴时，可用顶点式求解二次函数解析式．2．已知二次函数的顶点和图象上的任意一点，都可以用顶点式来确定解析式． （3）交点式：12()()(0)y a x x x x a =--≠．我们知道，()()22212424b ac b y ax bx c a x a x x x x a a -⎛⎫=++=++=-- ⎪⎝⎭，这里12x x ，分别是方程20ax bx c ++=的两根．当已知二次函数的图象与x 轴有交点（或者说方程20ax bx c ++=有实根）时，就可以令函数解析式为()()12y a x x x x =--，从而求得此函数的解析式．总结：1．已知抛物线与x 的两个交点坐标，可用交点式求解二次函数解析式．2．已知二次函数与x 轴的交点坐标，和图象上任意一点时，可用交点式求解二次函数解析式． 3．已知二次函数与x 轴的交点坐标()()12,0,,0x x ，可知二次函数的对称轴为122x x x +=． 4．根据二次函数的对称性可知，对于函数图象上的两点()()12,,,x a x a ，如果它们有相同的纵坐标，自检自查必考点2014年中考怎么考则可知二次函数的对称轴为122x x x +=． 5．对于任意的二次函数2y ax bx c =++，当0x =时，利用求根公式可得2142b b acx a-+-=，2242b b acx a ---=，可知22212444||22b b ac b b ac b ac x x a a a -+------=-=．（4）对称式：12()()(0)y a x x x x k a =--+≠．总结：当抛物线经过点1(,)x k 、2(,)x k 时，可以用对称式来求二次函数的解析式．注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化．知识点二、二次函数的几何变换一、平移变换 （1）具体步骤：先利用配方法把二次函数化成2()y a x h k =-+的形式，确定其顶点(,)h k ，然后做出二次函数2y ax =的图象，将抛物线2y ax =平移，使其顶点平移到(,)h k ．具体平移方法如图所示：（2）平移规律：在原有函数的基础上“左加右减，上加下减”． 二、对称变换二次函数图象的对称一般有五种情况，可以用一般式或顶点式表达 1． 关于x 轴对称2y ax bx c =++关于x 轴对称后，得到的解析式是2y ax bx c =---；()2y a x h k =-+关于x 轴对称后，得到的解析式是()2y a x h k =---；2． 关于y 轴对称2y ax bx c =++关于y 轴对称后，得到的解析式是2y ax bx c =-+；()2y a x h k =-+关于y 轴对称后，得到的解析式是()2y a x h k =++；3． 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 4． 关于顶点对称2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．5． 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+- 根据对称的性质，显然无论作何种对称变换，抛物线的形状一定不会发生变化，因此a 永远不变．求抛物线的对称抛物线的表达式时，可以依据题意或方便运算的原则，选择合适的形式，习惯上是先确定原抛物线（或表达式已知的抛物线）的顶点坐标及开口方向，再确定其对称抛物线的顶点坐标及开口方向，然后再写出其对称抛物线的表达式． 三、旋转变换在二次函数的旋转变换中，将抛物线绕顶点旋转90︒或180︒，之后抛物线的开口大小不变，方向改变，但是顶点坐标不改变，这也是解题的关键，具体如下：1． 关于原点对称2y ax bx c =++关于原点对称后，得到的解析式是2y ax bx c =-+-； ()2y a x h k =-+关于原点对称后，得到的解析式是()2y a x h k =-+-； 2． 关于顶点对称2y ax bx c =++关于顶点对称后，得到的解析式是222b y ax bx c a=--+-；()2y a x h k =-+关于顶点对称后，得到的解析式是()2y a x h k =--+．3． 关于点()m n ，对称 ()2y a x h k =-+关于点()m n ，对称后，得到的解析式是()222y a x h m n k =-+-+-【例1】已知二次函数的图象经过(1,3)A -、(1,3)B 、(2,6)C ； 求它的解析式．【巩固】已知一个二次函数，当1x =时，2y =；当0x =时，2y =；当5x =时，3y =．求这个二次 函数的解析试．【巩固】已知一个二次函数过原点、()111-，、()19，三点，求二次函数的解析式．【例2】已知一个二次函数的图象过点(1,0)，它的顶点坐标是(8,9)，求这个二次函数的关系式．例题精讲【巩固】已知抛物线的顶点是(2,4)-，它与y 轴的一个交点的纵坐标为4，求函数的关系式．【巩固】已知抛物线的对称轴为3x =-，且抛物线经过(1,0)-，与y 轴的交点到原点的距离为52，求此抛物线的解析式．【例3】已知一抛物线与x 轴的交点是(2,0)A -、(1,0)B ，且经过点(2,8)C ，求这个二次函数的解析式．【巩固】已知二次函数的图象与x 轴有两个交点(3,0)A -，(1,0)B ，且顶点到x 轴的距离为4，求此二次函数解析式．【巩固】已知一抛物线的形状与21722y x =+的形状相同．它的对称轴为2x =-，它与x 轴的两交点之间的距离为2，求此抛物线的解析式．【例4】已知二次函数的图象经过(1,2)-、(3,2)、(2,4)，求它的解析式．【例5】函数25(1)2y x =+-的图象可由函数25y x =的图象平移得到，那么平移的步骤是（ ）A.右移一个单位，下移两个单位B.右移一个单位，上移两个单位C.左移一个单位，下移两个单位D.左移一个单位，上移两个单位【巩固】函数23(1)2y x =-+-的图象可由函数23(5)3y x =--+的图象平移得到，那么平移的步骤是（ ）A.右移六个单位，下移五个单位B.右移四个单位，上移五个单位C.左移六个单位，下移五个单位D.左移四个单位，上移五个单位【例6】把抛物线的图象先向右平移4个单位，再向下平移1个单位，所得的图象的解析 式是263y x x =-+，则a b c ++=________________．【例7】函数2y x =与2y x =-的图象关于______________对称，也可以认为2y x =是函数2y x =-的图象绕__________旋转得到．【例8】已知二次函数223y x x =--，求：⑴关于x 轴对称的二次函数解析式；⑵关于y 轴对称的二次函数解析式； ⑶关于原点对称的二次函数解析式．【巩固】 已知抛物线265y x x =-+，求⑴ 关于y 轴对称的抛物线的表达式；⑵ 关于x 轴对称的抛物线的表达式； ⑶ 关于原点对称的抛物线的表达式．【例9】已知抛物线246y x x =+-，求⑴关于1x =对称的抛物线的表达式；⑵关于1y =对称的抛物线的表达式； ⑶关于(2,1)旋转180︒的抛物线的表达式．【巩固】已知抛物线222y x x =+-，求⑴关于2x =-对称的抛物线的表达式；⑵关于1y =-对称的抛物线的表达式； ⑶关于(2,1)-旋转180︒的抛物线的表达式．【例10】已知二次函数2441y ax ax a =++-的图象是1C求⑴1C 关于点()10R ，中心对称的图象2C 的解析式； ⑵设曲线1C 、2C 与y 轴的交点分别为,A B ，当18AB =时，求a 的值．【例11】小聪用描点法画出了函数y x =的图象F ，如图所示．结合旋转的知识，他尝试着将图象F 绕原点逆时针旋转90︒得到图象1F ，他发现点(4,2)P --在1F 的图象上，求1F 的解析式．xO Fy【例12】点P 为抛物线222y x mx m =-+(m 为常数，0m >)上任一点，将抛物线绕顶点G 逆时针旋转90︒后得到的新图象与y 轴交于A 、B 两点（点A 在点B 的上方），点Q 为点P 旋转后的对应点． （1）当2m =，点P 横坐标为4时，求Q 点的坐标； （2）设点(,)Q a b ，用含m 、b 的代数式表示a ；y xD GC Q O BA【题1】如果二次函数的图象经过点(3,0)-，(1,0)，(0,3)-，求二次函数的解析式．【题2】如果二次函数的图象与x 轴交点的横坐标是3-，1，与y 轴交点的纵坐标是3-，求二次函数解析式．【题3】如果二次函数的图象经过点(3,0)-，(0,3)-，且对称轴是直线1x =-，求二次函数解析式．【题4】如果二次函数的图象的顶点坐标为(2,4)-，且经过原点，求二次函数解析式．【题5】如果二次函数的图象经过原点，当2x =-时，函数的最大值为4，求二次函数解析式．【题6】已知一条抛物线的形状和2y x =相同，它的对称轴为2x =-，它与x 轴的两交点之间的距离为2，求此抛物线的解析式．课后作业【题7】把抛物线2y ax bx c =++的图象先向右平移5个单位，再向下平移4个单位，所得的图象的解析式是23y x x =-+，则a b c ++=________________．【题8】已知抛物线247y x x =-+(1)写出与它关于y 轴对称的抛物线的解析式_____________； (2)写出与它关于x 轴对称的抛物线的解析式_____________； (3)写出与它关于原点中心对称的抛物线的解析式_____________； (4)写出它绕着顶点旋转180︒后得到的抛物线的解析式_____________； (5)向右平移__________个单位，图象经过点(5,4)； (6)向下平移__________个单位，图象也经过点(5,4)．【题9】如图，已知抛物线21:(2)5C y a x =+-的顶点为P ，与x 轴相交于A 、B 两点（点A 在点B 的左边），点B 的横坐标是1．（1）求P 点坐标及a 的值；（2）如图（1），抛物线2C 与抛物线1C 关于x 轴对称，将抛物线2C 向右平移，平移后的抛物线记为3C ，3C 的顶点为M ，当点P 、M 关于点B 成中心对称时，求3C 的解析式；PM C 2yxOC 1BA。

2015中考－提高篇－22－二次函数 － 教师版一、二次函数的定义、图象与性质图象1． （2014广西玉林防城港，12，3分）如图，边长分别为1和2的两个等边三角形，开始它们在左边重合，大三角形固定不动，然后把小三角形自左向右平移直至移出大三角形外停止，设小三角形移动的距离为x ，两个三角形重叠面积为y ，则y 关于x 的函数图象是（ ）【考点解剖】本题综合考查了函数图象的表示、三角形的面积等知识，解题的关键是建立重叠面积y 关于x 的函数关系式． 【解题思路】将图象分为二段[小三角形完全在大三角形里面（即0≤x ≤1）和小三角形开始穿出大三角形（即1＜x ≤2）]处理，当小三角形完全在大三角形里面时计算小三角形的面积即为重叠面积y ，当小三角形穿出大三角形的过程中则求出重叠面积y 关于x 的函数关系式．【解答过程】当小三角形完全在大三角形里面（即0≤x ≤1）时，两个三角形重叠面积为小三角形的面积，y＝11224⨯⨯=为定值；当小三角形开始穿出大三角形（即1＜x ≤2）时，重叠三角形的边长为2－x ，高为)2x -，y＝1(2)2x ⨯-=2)2(43-x ，为开口向上的二次函数，故选择B ．【易错点睛】此类问题容易出错的地方是忽视纵坐标y 的值导致选择D ．2． （2014山东临沂，14，3分）在平面直角坐标系中，函数22(y x x x =-≥0)的图象为1C ，1C 关于原点对称的图象为2C ，则直线y a =（a 为常数）与1C ，2C 的交点共有（ ） A ．1个． B ．1个，或2个．C ．1个，或2个，或3个．D ．1个，或2个，或3个，或4个．【考点解剖】本题考查了二次函数的图像及几何变换，解答本题的关键是熟练进行几何图形的变换．【解题思路】首先画出函数的图象1C ，根据关于原点对称的关系，可得C 2，根据直线y ＝a （a 为常数）与C 1、C 2的交点，可得答案．【解答过程】如图，画出，函数y ＝x 2－2x （x ≥0）的图象为C 1，C 1关于原点对称的图象为C 2，当－2<a ＜2时，直线y a =（a 为常数）与1C ，2C 的交点共有3个，当a ＝2或－2时，直线y a =（a 为常数）与1C ，2C 的交点共有2个，当a ＞2或a ＜－2时，直线y a =（a 为常数）与1C ，2C 的交点共有1个．故选C ．3． （2014江苏扬州，16，3分）如图，抛物线)0(2>++=a c bx ax y 的对称轴是过点(1，0)且平行于y 轴的直线，若点P （4，0）在该抛物线上，则c b a +-24的值为______．【考点解剖】本题考查了二次函数图象的对称性、整体求代数式值，解题的关键是理解代数式4a －2b ＋c 的意义．A ．B ．C ．D ．【解题思路】本题中，首先明确代数式4a －2b ＋c 的意义，然后根据抛物线的对称轴，结合抛物线的对称性求得抛物线与x 轴的另一个交点坐标为（－2，0），代入求值即可．【解答过程】因为抛物线的对称轴直线x ＝1，由对称性可知，P （4，0）和（－2，0）关于这条直线对称，因此点（－2，0）也在这个抛物线上，然后将x ＝－2代入c b a +-24计算，得c b a +-24＝0．另外，本题还可建立方程组⎪⎩⎪⎨⎧=++=-41612c b a a b，得⎩⎨⎧-=-=a c a b 82，代入c b a +-24的值为0．【归纳拓展】抛物线)0(2≠++=a c bx ax y 上有一对对称点坐标分别为),(1y x 和),(2y x ，则对称轴直线为2221x x a b x +=-=，这个公式可以根据纵坐标相同的两点确定对称轴，也可通过对称轴和其中一点的坐标确定另一个对称点的坐标．4． （2014山东菏泽，12，3分）如图，平行于x 轴的直线AC 分别交函数1y ＝2x （x ≥0）与2y ＝23x （x ≥0）的图象于B 、C 两点，过点C 作y 轴的平行线交1y 的图象于点D ，直线DE ∥AC ，交2y 的图象于点E ，则DEAB＝_________．【考点解剖】本题考查了二次函数的图象的代数应用、平行线的性质，解题的关键是掌握二次函数的图象的特征及平行线的性质．【解题思路】利用了二次函数图象上点的坐标特征，根据平行与x 轴的点的纵坐标相同，平行于y 轴的点的横坐标相同，求出用点A 的纵坐标表示出各点的坐标，进而求出DEAB的值．【解答过程】设A 点坐标为（0，k ），因为AB 平行x 轴，所以B 点的纵坐标与A 点相同，又因为点B 在函数1y ＝2x 上，所以Bk ），所以ABC 在函数2y ＝23x 上，且AC 平行x 轴，所以点C，k ），因为CD 平行y 轴，所以C 、D 两点的横坐标相同，即D，又因为D 点在函数1y ＝2x 上，所以D3k ）．因为DE 平行x 轴，所以E 点的纵坐标为3k ，又因为E 点在函数2y ＝23x 上，所以E 点的坐标为（3k ），所以DE ＝．所以DE AB3=．故答案为3【方法规律】与坐标轴平行的线上的点的坐标特征：（1）与x 轴平行，纵坐标相同；（2）与y 轴平行，横坐标相同． 5．（2014甘肃天水，18，4分）如图，一段抛物线(1)(01)y x x m =--≤≤记为m 1，它与x 轴交点为O ，A 1，顶点为P 1；将m 1绕点A 1旋转180°得m 2，交x 轴于点A 2，顶点为P 2；将m 2绕点A 2旋转180°得m 3，交x 轴于点A 3，顶点为P 3；…，如此进行下去，直至得m 10，顶点为P 10，则P 10的坐标为（________）【解题思路】求出抛物线m 1与x 轴的交点坐标，及顶点P 1的坐标，观察图形可知第奇数号抛物线都在x 轴上方，第偶数号抛物线都在x 轴下方，然后求出到抛物线m 10平移的距离，再根据向右平移横坐标加表示出抛物线m 10的2x顶点P 10的坐标即可．【解答过程】∵y ＝－x (x －1)＝21124x ⎛⎫--+ ⎪⎝⎭，∴P 111,24⎛⎫ ⎪⎝⎭，A 1 (1，0)，∵将m 1绕点A 1旋转180°得m 2，交x 轴于点A 2，顶点为P 2，∴A 2 (2，0)，P 231,24⎛⎫- ⎪⎝⎭，∴由图可得：抛物线m 10在x 轴下方，相当于抛物线m 2的顶点P 2向右平移8个单位得到，∴P 10（192，14-）．故答案为（192，14-） ．6． （2014安徽，22，12分）若两个二次函数图象的顶点、开口方向都相同，则称这两个二次函数为“同簇二次函数”．（1）请写出两个为“同簇二次函数”的函数；（2）已知关于x 的二次函数y 1＝2x 2－4mx ＋2m 2＋1和y 2＝ax 2＋bx ＋5，其中y 1的图象经过点A （1，1），若y 1＋y 2与y 1为“同簇二次函数”，求函数y 2的表达式，并求出当0≤x ≤3时，y 2的最大值． 【解题思路】（1）根据“同簇二次函数”的定义，先确定所写函数的顶点坐标，然后用同号两数作为二次项的系数（数值不同），用顶点式表示两个为“同簇二次函数”的函数表达式即可．（2）由y 1的图象经过点A （1，1）求出m ，然后根据y 1＋y 2与y 1为“同簇二次函数”，求出函数y 2的表达式，最后将函数y 2的表达式转化为顶点式，判断函数的最大值． 【解答过程】（1）本题是开放题，答案不唯一，符合题意即可，如y 1＝2x 2和y 2＝x 2． （2）∵函数y 1的图象经过点A （1，1），则2－4m ＋2m 2＋1＝1，解得m ＝1． ∴y 1＝2x 2－4x ＋3＝2（x －1）2＋1．解法一：∵y 1＋y 2与y 1为“同簇二次函数”，∴ y 1＋y 2＝k (x －1)2＋1(k ＞0)， 则y 2＝2（x －1）2＋1－y 1＝（k －2）（x －1）2． 由题可知函数y 2的图象经过（0，5），则（k －2）×12＝5，∴k －2＝5． ∴y 2＝5（x －1）2＝5 x 2－10x ＋5．∴函数y 2的图象的对称轴为x ＝1．∵5＞0，∴函数y 2的图象开口向上． ①当0≤x ≤1时，∵函数y 2的图象开口向上，∴y 2随x 的增大而减小． ∴当x ＝0时，y 2取最大值，最大值为5（0－1）2＝5．②当1＜x ≤3时， ∵函数y 2的图象开口向上，∴y 2随x 的增大而增大． ∴当x ＝3时，y 2取最大值，最大值为5（3－1）2＝20． 综上所述：当0≤x ≤3时，y 2的最大值为20．解法二：∵y 1＋y 2与y 1为“同簇二次函数”，则 y 1＋y 2＝（a ＋2）x 2＋(b －4)x ＋8 (a ＋2＞0)．∴－)2(24+-a b ＝1，化简得b ＝－2a ，又)2(4)4()2(322+--+a b a ＝1，将b ＝－2a 代入，解得a ＝5，b ＝－10，所以y 2＝5 x 2－10x ＋5．即y 2＝5（x －1）2，①当0≤x ≤1时，∵函数y 2的图象开口向上，∴y 2随x 的增大而减小．∴当x ＝0时，y 2取最大值，最大值为5×（0－1）2＝5．②当1＜x ≤3时，∵函数y 2的图象开口向上，∴y 2随x 的增大而增大．∴当x ＝3时，y 2取最大值，最大值为5×（3－1）2＝20．综上所述：当0≤x ≤3时，y 2的最大值为20． 7．（2014浙江绍兴，22，12分）如果二次函数的二次项系数为1，则此二次函数可表示为y ＝x 2＋px ＋q ，我们称[p ，q ]为此函数的特征数，如函数y ＝x 2＋2x ＋3的特征数是[2，3]． （1）若一个函数的特征数是[－2，1]，求此函数的顶点坐标． （2）探究下列问题：①若一个函数的特征数是[4，－1]，将此函数图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应函数的特征数．②若一个函数的特征数是[2，3]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[3，4]？【考点解剖】本题考查了二次函数的平移规律，解题的关键是掌握抛物线平移时其顶点坐标的变化规律． 【解题思路】（1）先根据新定义问题，写出二次函数表达式，再利用配方法将二次函数写成顶点式或直接应用二次函数的顶点公式求出其顶点坐标．（2）①先将特征数是[4，－1]的二次函数化成顶点式，再根据平移规律写出平移后的抛物线的解析式，即可得到平移后图象对应的函数特征数；②将特征数是[2，3]和[3，4]的两个二次函数化为顶点式，比较两函数的顶点坐标之间的变化，即可得到平移的步骤． 【解答过程】（1）∵一个函数的特征数是[－2，1]， ∴该函数的解析式为y ＝x 2－2x ＋1．∵y ＝x 2－2x ＋1＝(x －1)2，∴此函数的顶点坐标是（1，0）．（2）①∵一个函数的特征数是[4，－1]，∴该函数的解析式为y ＝x 2＋4x －1，配方成顶点式为y ＝(x ＋2)2－5． ∴将抛物线y ＝(x ＋2)2－5先向右平移1个单位，再向上平移1个单位得到抛物线的解析式为y ＝(x ＋2－1)2－5＋1，即y ＝(x ＋1)2－4，亦即y ＝x 2＋2x －3．∴得到的图象对应函数的特征数为[2，－3]． ②∵一个函数的特征数是[2，3]， ∴y ＝x 2＋2x ＋3＝(x ＋1)2＋2， ∵一个函数的特征数是[3，4]，∴y ＝x 2＋3x ＋4＝(x ＋32)2＋74＝(x ＋1＋12)2＋2－14， ∴将抛物线y ＝x 2＋2x ＋3先向左平移12个单位，再向下平移14个单位即可得到抛物线y ＝x 2＋3x ＋4，其特征数为[3，4]．性质8． （2014甘肃兰州，14，4分）二次函数y ＝ax 2＋bx ＋c (a ≠0)的图像如图所示，其对称轴为x ＝1，下列结论中错误的是（ ）A ．abc ＜0B ．2a ＋b ＝0C ．b 2－4ac ＞0D ．a －b ＋c ＞0【解题思路】依据题中给出的二次函数的图像结合二次函数的有关性质对各选项作出判断 【解答过程】由抛物线开口向下知a ＜0，抛物线与y 轴交点位于y 轴正半轴知c ＞0，由对称轴－ab2＝1＞0知b ＞0，所以abc ＜0，选项A 正确；由－ab2＝1，得2a ＋b ＝0，选项C 正确；由于抛物线与x 轴有两个不同的交点，即一元二次方程ax 2＋bx ＋c ＝0(a ≠0)，有两个不相等的实数根，b 2－4ac ＞0，选项C 正确；由图像知x ＝－1时y ＜0，即a －b ＋c ＜0，选项D 错误．故选D ．【方法规律】解答此类问题，需确定二次函数的图像与a ，b ，c 之间的关系．一般地，抛物线开口方向确定a 的大小，开口向上时a ＞0，开口向下时a ＜0；抛物线与x 轴交点的多少确定b 2－4ac 的值的大小，抛物线与x 轴有两个交点时b 2－4ac ＞0，抛物线与x 轴有唯一的交点，b 2－4ac ＝0，抛物线与x 轴没有交点，b 2－4ac ＜0；x ＝1时对应的函数值大小确定了a ＋b ＋c 的值的大小，x ＝－1时对应的函数值大小确定了a －b ＋c 的值的大小． 9．（2014四川资阳，10，3分）二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象如图所示，给出下列四个结论：①4ac －b 2＜0；②4a ＋c ＜2b ；③3b ＋2c ＜0；④m (am ＋b )＋b ＜a (m ≠－1)其中正确结论的个数是（ ） A ．4个 B ．3个 C ．2个 D ． 1个【解答过程】(1)由函数图象与x 轴有两个交点知b 2－4ac ＞0，即4ac －b 2＜0，结论①4ac －b 2＜0正确；(2)由函数图象的对称轴为x ＝－1，即12ba-=-，得2a ＝b ，即4a ＝2b ．又图象与y 轴交于正半轴，所以c ＞0，所以 4a ＋c ＞2b ，因此结论②4a ＋c ＜2b 错误；(3)当x ＝1，观察图象得a ＋b ＋c ＜0，将2a ＝b 代入得32b c +＜0，即3b ＋2c＜0，因此结论③3b ＋2c ＜0正确；(4) m (am ＋b )＋b －a ＝am 2＋bm ＋b －a ＝a (m 2－1)＋b (m ＋1)＝(m ＋1)〔a (m －1)＋b 〕，将2a ＝b 代入得：(m ＋1) 〔a (m －1)＋2a 〕＝ (m ＋1)a (m －1＋2)＝a (m ＋1)2，因为a ＜0，m ≠－1，所以a (m ＋1)2 ＜0，即m (am ＋b )＋b ＜a ，所以结论④m (am ＋b )＋b ＜a 正确．因此4个结论中有3个是正确，故选择 B ． 10． （2014山东莱芜，12，3分）已知二次函数2y ax bxc =++的图象如图所示，下列结论： ①abc ＞0 ② 2a －b ＜0 ③ 4a －2b ＋c ＜0 ④ (a ＋c )2＜b 2 其中正确的个数有（ ）A ． 1B ． 2C ． 3D ． 4【解答过程】抛物线开口向下，a <0； 对称轴在y 轴左侧，02<-ab，得0>b ，抛物线与y 轴交于x 轴上方，0>c ，所以abc <0，由对称轴12->-ab，得02>-a b ，从抛物线可知当x ＝－2时，函数值小于零，即024<+-c b a ，当x ＝1，函数值小于零，当x ＝－1时，抛物线的函数值大于零，所以0<++c b a ，0>+-c b a ，从而0))((<+-++c b a c b a ，得到22)(b c a <+，故答案为D ．【思维模式】由函数的图形判定对应的解析式的大小，重点体现了数形结合的思想： （1）看到抛物线开口方向向下，就可得出a ＜0． （2）看到对称轴在x 轴的负半轴上，就得到02<-ab， （3）看到抛物线与y 轴的交点在y 轴正半轴，则c ＞0 （4）看到22)(b c a <+就想到0))((<+-++c b a c b a（5）看到a ＋b ＋c ，就想到二次函数当x ＝1时的函数值，看到c b a +-就想到二次函数当x ＝－1时的函数值，看到c b a +-24就想到二次函数当－2时的函数值． 11．（2014天津，12，3分）已知二次函数()20y ax bx c a =++≠的图象如图所示，且关于x 的一元二次方程20ax bx c m ++-=没有实数根，有下列结论：①240b ac ->；②0abc <；③2m >．其中，正确结论的个数是（ ）A ． 0B ．1C ．2D ．3【解答过程】信息一：抛物线开口向下，则a ＜0；信息二：对称轴在y 轴的右侧，则02ba->，即a 与b 异号，因为a ＜0，所以b ＞0；信息三：抛物线与y 轴的交点在x 轴的上方，故c ＞0；信息四：抛物线与x 轴有两个交点，则一元二次方程20ax bx c ++=有两个不相等的实数根，即240b ac ->；信息五：关于x 的一元二次方程20ax bx c m ++-=没有实数根对应着将抛物线向下平移m 个单位长度以后与x 轴没有交点，因为原抛物线的顶点纵坐标为2，故m ＞2．综上，①②③均正确；故选择D ． 【方法规律】对于二次函数()20y ax bx c a =++≠（）【解答过程】∵二次函数y＝ax2＋bx＋c(a≠0)的图象与y轴的交点在点（0，－1）的下方，∴c＜－1，选项A错误．∵抛物线开口向上，∴a＞0．∵抛物线的对称轴在y轴的右侧，∴x＝－2ba＞0，∴b＜0，选项B错误．∵抛物线与x轴交点在点（－2，0）和点（4，0）之间，∴抛物线的对称轴可以为直线x＝－2ba＝1，∴2a＋b＝0，选项C错误．∵当x＝－3时，y＞0，∴9a－3b＋c＞0，即9a＋c＞3b．故选D．【方法规律】二次函数y＝ax2＋bx＋c（a≠0）①二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；|a|还可以决定开口大小，|a|越大开口就越小．②一次项系数b和二次项系数a共同决定对称轴的位置．由于抛物线y＝ax2＋bx＋c的对称轴是直线x＝－b2a，故b＝0时，对称轴为y轴；当a与b同号时（即ab＞0），对称轴在y轴左边；当a与b异号时（即ab＜0），对称轴在y轴右边．（简称：左同右异）③常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．c＝0，抛物线经过原点；c ＞0，抛物线与y轴交于正半轴；c＜0，抛物线与y交于负半轴．④抛物线与x轴交点个数．△＝b2－4ac＞0时，抛物线与x轴有2个交点；△＝b2－4ac＝0时，抛物线与x轴有1个交点；△＝b2－4ac＜0时，抛物线与x轴没有交点．13．（2014山东威海，11，3分）已知二次函数y＝2ax bx c++（a≠0）的图象如图所示，则下列说法：①c＝0；②该抛物线的对称轴是直线x＝－1；③当x＝1时，y＝2a；④2am bm a++＞0（m≠－1）．其中正确的个数是（）A．1 B．2 C．3 D．4【解答过程】图象过原点，故c＝0所以①正确；由抛物线是轴对称性知该抛物线的对称轴是直线＝－1，故②正确；由②知,12-=-ab所以b＝2a，把x＝1代入解析式得：,3abay=+=所以③不正确；由b＝2a知am2＋bm＋a＝22am am a++()2221(1),a m m a m=++=+又因为m≠－1，所以,0)1(2>+m从图象知,0>a故④am2＋bm＋a＞0（m≠－1）正确，故选择C．14．(2014四川达州，10，3分)右图是二次函数2y ax bx c=++的图象的一部分，对称轴是直线x＝1．①b2＞4ac；②4a－2b＋c＜0；③不等式ax2＋bx＋c＞0的解集是x≥3．5；④若(－2，y1)，(5，y2)是抛物线上的两点，则y1＜y2．上述4个判断中，正确的是( )A．①②B．①④C．①③④D．②③④【解题过程】∵二次函数y ＝ax 2＋bx ＋c 的图象与x 轴有两个交点，可知b 2－4ac ＞0，∴b 2＞4ac ，∴①正确；∵当x ＝－2时，y ＝ax 2＋bx ＋c ＞0，即4a －2b ＋c ＞0，∴②不正确；由图象可看出ax 2＋bx ＋c ＞0的解集有两种情况，所以③不正确；由抛物线的开口方向向上，可知a ＞0，∵抛物线对称轴方程x ＝－b2a＝1，∴b ＝－2a ．又∵y 1＝4a－2b ＋c ，y 2＝25a ＋5b ＋c ，∴y 2－y 1＝21a ＋7b ＝21a －14a ＝7a ＞0，即y 1＜y 2，所以④正确，故选B ．15． （2014贵州黔东南州，9，4分）如图，已知二次函数y ＝ax 2＋bx ＋c (a ≠0)的图象如图所示，下列4个结论：①abc <0；②b <a ＋c ；③4a ＋2b ＋c >0；④b 2－4ac >0．其中正确结论的有 ( ) A ．①②③ B ．①②④ C ．①③④ D ．②③④【解答过程】由抛物线开口向上知a ＞0，由二次函数的图象与y 轴交于正半轴知：c ＞0，由对称轴直线x ＝2，可得出b 与a 异号，即b ＜0，则abc ＜0，故①正确；把x ＝－1代入y ＝ax 2＋bx ＋c 得：y ＝a －b ＋c ，由函数图象可以看出当x ＝－1时，二次函数的值为正，即a －b ＋c ＞0，则b ＜a ＋c ，故②选项正确；把x ＝2代入y ＝ax 2＋bx ＋c 得：y ＝4a ＋2b ＋c ，由函数图象可以看出当x ＝2时，二次函数的值为负，即4a ＋2b ＋c ＜0，故③选项错误；由抛物线与x 轴有两个交点可以看出方程ax 2＋bx ＋c ＝0的根的判别式b 2－4ac ＞0，故④选项正确，故选择B ．16． （2014黑龙江绥化，17，3分）如图是二次函数y ＝ax 2＋bx ＋c 图象的一部分，且过点A(3，0)．二次函数图象的对称轴是x ＝1，下列结论正确的是 （ ）A ．b 2＞4ac B ．ac ＞0 C ．a －b ＋c ＞0 D ．4a ＋2b ＋c ＜0【解答过程】∵抛物线y ＝ax 2＋bx ＋c 关于直线x ＝1对称，∴点A(3，0)关于x ＝1的对称点'A 也在x 轴上，得'A (－1，0) ，抛物线与x 轴有两个交点，即ax 2＋bx ＋c ＝0有两个不等的实根，∴Δ＝b 2－4ac ＞0，即b 2＞4ac ，故选A ．17． （2014黑龙江齐齐哈尔，9，3分）如图，二次函数c bx ax y ++=2(a ≠0)图象的一部分，对称轴为直线x ＝12，且经过点（2，0）．下列说法：①abc <0；②a ＋b ＝0；③4a ＋2b ＋c <0；④若（－2，y 1），（52，y 2）是抛物线上的两点，则y 1＜y 2，其中说法正确的是 ( )A ．①②④B ．③④C ．①③④D ．①②【解答过程】由抛物线与y 轴的交点在正半轴，得到c ＞0；由抛物线开口方向得a <0，再由抛物线的对称轴在y 轴的右侧得a 、b 异号，即b >0，所以abc <0；由抛物线对称轴为直线x ＝12，可以得﹣2b a ＝12，所以a ＋b ＝0；因第17题图为抛物线经过点（2，0），所以4a ＋2b ＋c ＝0；根据抛物线的对称性得到抛物线与x 轴的另外一个交点坐标为(－1，0)，因为（－2，0）到(－1，0)的距离比（52，0）到（2，0）距离大，根据抛物线图象的对称性得y 1＜y 2，故选择A ．18． （2014山东烟台，11，3分）二次函数y ＝ax 2＋bx ＋c （a ≠0）的部分图象如图所示，图象过点（－1，0），对称轴为直线x ＝2． 下列结论：①4a ＋b ＝0；②9a ＋c ＞3b ；③8a ＋7b ＋2c ＞0；④当x ＞－1时，y 的值随x 值的增大而增大． 其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【解答过程】①，由图象知对称轴x ＝2ba-＝2，得4a ＋b ＝0，故①对． ②，由图象知当x ＝－3时，9a －3b ＋c <0，9a ＋c <3b ，故②错．③，由图象知当x ＝2时，4a ＋2b ＋c >0，8a ＋4b ＋2c >0． 因为图象开口向下，所以a <0，又x ＝2ba-＝2，所以b >0，所以3b >0． 所以8a ＋7b ＋2c >0． 故③对． ④由图象知当x >2时，y 随x 的增大而减少，故④错． 综上①③正确． 故选B ． 19．（2014山东聊城，12，3分）如图是二次函数y ＝ax 2＋bx ＋c (a ≠0)图象的一部分，x ＝－1是对称轴，有下列判断：①b －2a ＝0；②4a －2b ＋c <0；③a －b ＋c ＝ －9a ；④若（－3，y 1），（23，y 2）是抛物线上两点，则y 1>y 2．其中正确的是（ ）．A ．①②③B ．①③④C ．①②④D ．②③④【解答过程】∵－a2b＝－1，∴b ＝2a ，即b －2a ＝0，∴①正确； ∵当x ＝－2时点在x 轴的上方，即4a －2b ＋c >0，②不正确；∵4a ＋2b ＋c ＝0，∴c ＝－4a －2b ，∵b ＝2a ，∴a －b ＋c ＝a －b －4a －2b ＝－3a －3b ＝－9a ，∴③正确； ∵抛物线是轴对称图形，点（－3，y 1）到对称轴的距离小于点（23，y 2）到对称轴的距离，即y 1>y 2，∴④正确．综上所述，选B ．20． （2014山东日照，11，4分）如图，是抛物线y ＝ax 2＋bx ＋c （a ≠0）图象的一部分．已知抛物线的对称轴为x ＝2，与x 轴的一个交点是（－1，0）．有下列结论：①abc >0；②4a －2b ＋c <0；③4a ＋b ＝0；④抛物线与x 轴的另一个交点是（5，0）；⑤点（－3，y 1），（6，y 2）都在抛物线上，则有y 1<y 2．x其中正确的是（）A．①②③B．②④⑤C．①③④D．③④⑤a>0，∵图象交y轴于负半轴，∴c<0，∵对称轴在y轴的右侧，根据“左同右异”知，b<0，∴abc>0，∴①正确；∵图象过点（－1，0），开口向上，∴图象上横坐标x＝－2的点在x轴上方，则y>0，即4a－2b＋c>0，∴②错误；抛物线的对称轴为x＝2，即－2ba＝2，∴b＝－4a，即4a＋b＝0，∴③正确；∵抛物线是轴对称图形，∴与x轴的一个交点坐标为（－1，0），∴另一个交点坐标为（5，0），∴④正确；∵抛物线是以直线x＝2为对称轴的轴对称图形，∴点（－3，y1）关于对称轴的对称点坐标为（7，y1），点（7，y1）、（6，y2）同在对称轴的右侧，根据y随x的增大而增大可知y1>y2，∴⑤错误．综上所述，故选C．21．（2014湖北孝感，12，3分）抛物线2y ax bx c=++的顶点为(1,2)D-，与x轴的一个交点A在点(3,0)-和(2,0)-之间，其部分图象如图所示，则以下结论：①240b ac-<；②0a b c++<；③2c a-=；④方程220ax bx c++-=有两个相等的实数根，其中正确结论的个数为A．1个B．2个C．3个D．4个【解答过程】根据抛物线的轴对称性，容易补出函数的图象如下图所示．∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，所以①错误；∵顶点为D（﹣1，2），∴抛物线的对称轴为直线x＝﹣1，∵抛物线与x轴的一个交点A在点（﹣3，0）和（﹣2，0）之间，∴抛物线与x轴的另一个交点在点（0，0）和（1，0）之间，∴当x＝1时，y＝a＋b＋c＜0，∴以②正确；∵抛物线的顶点为D（﹣1，2），∴a﹣b＋c＝2，∵抛物线的对称轴为直线x＝﹣2ba＝—1，∴b＝2a，∴a﹣2a＋c＝2，∴c﹣a＝2，所以③正确；∵当x＝﹣1时，二次函数有最大值为2，即只有x＝﹣1时，ax2＋bx＋c＝2，∴方程ax2＋bx＋c﹣2＝0有两个相等的实数根，所以④正确．故选择C．22．（2014四川广元，9，3分）设b＞0，二次函数y＝ax2＋bx＋a2－1的图象为下列之一，则a的值为（）1A ．－1B ．1 CD【解答过程】∵b ＞0，对称轴x ＝2b a -，∴可排除第1和第2两个图象，又第3和第4的对称轴 x ＝2ba-＞0，∴a ＜0，∴抛物线的开口向下，∴第3个图象符合，∵抛物线过原点（0，0），∴a 2－1＝0，∴a ＝±1，∴a ＝－1，故选择A ． 23．（2014新疆乌鲁木齐，15，4分）对于二次函数()2211y ax a x a =--+-（0a ≠），有下列结论： ①其图象与x 轴一定相交；②若0a <，函数在1x >时，y 随x 的增大而减小； ③无论a 取何值，抛物线的顶点始终在同一条直线上； ④无论a 取何值，函数图象都经过同一个点． 其中所有正确的结论是___．（填写正确结论的序号）【解答过程】①根据△＝ac b 42-判断，△＝())1(4122---a a a ＝1442+-a a －a a 442+＝１＞０，所以图象与x 轴一定相交，所以①正确；②若0a <，则抛物线开口向下，对称轴直线2b x a =-(21)2a a --=-112a=-，因为0a <，所以1112a->，即对称轴直线1x >，所以函数在1x >时，函数应是先增后减的过程，故不能判断y 随x 就一定增大而减小，故②错误；③抛物线的顶点坐标可表示为24(,)24b ac b a a--，2b x a =-112a =-，24144ac b y a a -==-，所以有112,14x ay a ⎧=-⎪⎪⎨⎪=-⎪⎩得1122y x =-，故无论a 取何值，抛物线的顶点始终在同一条直线1122y x =-上，所以③正确；④观察解析式，发现当1x =时，函数值0y =，与a 的取值无关，所以④也正确．故正确是结论是①③④．增减性与最值24 （2014广西南宁，10，3分）如图3，已知二次函数x x y 22+-=，当－1＜x ＜a 时，y 随x 的增大而增大，则实数a 的取值范围是（ ）A ．a ＞1B ．－1＜a ≤1C ．a ＞0D ． －1＜a ＜2 【解答过程】易知函数图象的对称轴为1x =，因为函数开口向下，在对称轴左侧，y 随x 的增大而增大，所以a ≤1，∵－1＜x ＜a ，∴－1<a ，∴－1<a ≤1，故选择B ．25． （2014年福建三明，10，4分）已知二次函数y ＝－x 2＋2bx ＋c ，当x ＞1时，y 的值随x 值的增大而减小，则实数b 的取值范围是（ ） A ．b ≥－1 B ．b ≤－1 C ．b ≥1 D ．b ≤1【解答过程】∵二次项系数为－1＜0，∴抛物线开口向下，在对称轴右侧，y 的值随x 值的增大而减小，由题设可知，当x ＞1时，y 的值随x 值的增大而减小，∴抛物线y ＝－x 2＋2bx ＋c 的对称轴应在直线x ＝1的左侧而抛物线y ＝－x 2＋2bx ＋c 的对称轴为()221b x b =-=⨯-， 即b ≤1，故选择D ．26． （2014广西河池，9，3分）已知点（x 1，y 1），（x 2，y 2）均在抛物线y ＝x 2－1上，下列说法中正确的是（ ）A ．若y 1＝y 2，则x 1＝x 2B ．若x 1＝－x 2，则y 1＝－y 2C ．若0＜x 1＜x 2，则y 1＞y 2D ．若x 1＜x 2＜0，则y 1＞y 2【解题思路】依据抛物线y ＝x 2－1的图象对称轴、开口方向、增减性来分析二次函数图象性质．【解答过程】如图所示，选项A ：若y 1＝y 2，则x 1＝－x 2，所以选项A 是错误的；选项B ：若x 1＝－x 2，则y 1＝y 2，所以选项B 是错误的；选项C ：若0＜x 1＜x 2，则在对称轴的右侧，y 随x 的增大而增大，则y 1＜y 2，所以选项C 是错误的；选项D ：若x 1＜x 2＜0，则在对称轴的右侧，y 随x 的增大而增大，则y 1＞y 2，所以选项D 是正确的．【方法规律】对于二次函数2y ax bx c =++，若顶点坐标为(h ，k )，当自变量的取值范围为x 1≤x ≤x 2时，函数有最大值和最小值，但是要考虑h 是否在x 1与x 2之间．(1)若h 在x 1与x 2之间，a ＞0时，k 为最小值，y 2为最大值；a ＜0时，k 为最大值，y 2为最小值．(2)若h 不在x 1与x 2之间，a ＞0时，y 1为最小值，y 2为最大值；a ＜0时，y 2为最小值，y 1为最大值．27． （2014浙江嘉兴，10，4分）当－2≤x ≤1时，二次函数y ＝－（x －m ）2＋m 2＋1有最大值4，则实数m 的值为（ ）A ．7-4BC ．2D ．27-4【考点解剖】本题考查了二次函数最大值的确定方法，解题的关键是根据自变量的取值范围分类讨论．【解题思路】当﹣2≤m ≤1时，函数y 的最大值就是抛物线顶点的纵坐标；当m ＜﹣2时，函数y 的最大值就是当x ＝﹣2时y 的值；当m ＞1时，函数y 的最大值就是当x ＝1时y 的值，由此列出关于m 的方程求解．【解答过程】对于y ＝﹣（x －m ）2＋m 2＋1，∵a ＝﹣1＜0，∴抛物线的开口向下，对称轴为x ＝m ，顶点坐标（m ，m 2＋1）．当﹣2≤m ≤1时，最大值m 2＋1＝4，解得m 1＝，m 2m ＜﹣2时，可知x＝﹣2时有最大值，即﹣（﹣2－m ）2＋ m 2＋1＝4，解得m ＝﹣74（不合题意，舍去）．当m ＞1时，可知x ＝1时有最大值，即﹣（1－m ）2＋ m 2＋1＝4，解得m ＝2．综上可知，m 的值为2C ． 【易错点睛】此类问题容易出错的地方是忽略抛物线的对称轴不在自变量的取值范围内的情形．【方法规律】在求二次函数的最大值（或最小值）时，如果自变量的取值范围有限制，就需要根据抛物线的性质，确定端点的函数值是否为最大值（或最小值）．28． （2014四川德阳，7，3分）已知0≤x ≤12，那么函数2286y x x =-+-的最大值是（ ） A ．﹣10.5 B ．2 C ．﹣2.5 D ．﹣6【解答过程】222862(2)2y x x x =-+-=--+，∵自变量取值范围0≤x ≤12，∴图象都在对称轴的左侧，且y 随x 的增大而增大．∴当x ＝12时，y 有最大值，最大值为：22112862()86 2.522y x x =-+-=-⨯+⨯-=-，故选择C ． 29． （2014湖北咸宁，15，3分）科学家为了推测最适合某种珍奇植物生长的温度，将这种植物分别放在不同温度的环境中，经过一定时间后，测试出这种植物高度的增长情况，部分数据如下表：______℃． 【解答过程】设l 与t 之间的函数关系是为2l at bt c =++ ，把 （－2，49）、（0，49）、（1，46）分别代入得：42494946a b c c a b c -+=⎧⎪=⎨⎪++=⎩ ，解得1249a b c =-⎧⎪=-⎨⎪=⎩．∴2249l t t =--+，即()2150l t =-++，∴当t ＝ －1时，l 的最大值为50． 即当温度为－1℃时，最适合这种植物生长．故答案为 －1．【思维模式】求函数解析式一般采用待定系数法．用待定系数法解题，先要明确解析式中待定系数的个数，再从已知中得到相应个数的独立条件（一般来讲，最直接的条件是点的坐标），最后代入求解．当解析式中的待定系数只有一个时，代入已知条件后会得到一个一元一次方程；当解析式中的待定系数为两个或两个以上时，代入独立条件后会得到方程组．正因如此，正确求解方程（组）的能力成为运用待定系数法求解析式的前提和基础．二、二次函数的解析式1． （2014山东泰安，20，3分）二次函数2y ax bx c =++（,,a b c 为常数，且0a ≠）中的x 与y 的部分对应值如下表：下列结论：（1）0ac <；（2）当1x >时，y 的值随x 值的增大而减小；（3）3是方程()210ax b x c +-+=的一个根；（4）当13x -<<时，()210ax b x c +-+>．其中正确的个数为（ ）A ． 4个B ． 3个C ． 2个D ． 1个【考点解剖】本题考查了二次函数解析式的确定、图象与性质、二次函数与一元二次方程、不等式的关系等知识，解题的关键是用待定系数法确定函数解析式，掌握二次函数的图象及有关性质．【解题思路】任选三组点的坐标代入函数解析式可求得,,a b c 的值，从而可以确定函数解析式，结合二次函数的性质、二次函数与一元方程的关系及表格中反映出的变量间的大小关系等可分别对各选项进行判断． 【解答过程】把（－1，－1），（0，3），（1，5）代入2y ax bx c =++，得1,3,5,a b c c a b c -+=-⎧⎪=⎨⎪++=⎩解得1,3,3.a b c =-⎧⎪=⎨⎪=⎩∴233y x x =-++，其对称轴为直线()3 1.521x =-=⨯-． 由1330ac =-⨯=-<，可知（1）正确；抛物线233y x x =-++的开口向下，当 1.5x >时，y 的值随x 值的增大而减小，故（2）错误；由表可知（3，3）在抛物线2y ax bx c =++的图象上，则933a b c ++=． 当3x =时，()21933330ax b x c a b c +-+=+-+=-=，所以3是方程()210ax b x c +-+=的一个根，故（3）正确；不等式()210ax b x c +-+>可变形为2ax bx c x ++>，即y x >． 从表格中给出的数据可以看出，当1,3x =-时，y x =；当13x -<<时，y x >，故（4）正确． 故选B ．【方法规律】给出函数图象上几组点的坐标或几组对应的函数值，运用待定系数法可确定函数解析式． 本题除了根据求得的函数解析式结合相关性质判断外，还可以画出函数图象的草图，运用数形结合思想进行分析、判断．2．（2014山东淄博，12，4分）已知二次函数)0()(2>+-=a k h x a y ，其图象过点A （0，2），B （8，3），则h 的值可以是（ ）A ．6B ．5C ．4D ．3【解答过程】从此题的选项可以看出，二次函数的对称轴大于0，图象过点A （0，2），B （8，3），如下图所示，在对称轴的右侧，当函数值等于2时，所对应的自变量x 的值一定小于8，可知对称轴一定小于4．故选择D ．另解：把A （0，2），B （8，3）代入)0()(2>+-=a k h x a y ，得ah 2＋k ＝2，64a －16ah ＋ah 2＋k ＝3，∴64a －16ah ＝1，即16a (4－h )＝1．又∵a ＞0，∴4－h ＞0，h ＜4，因此，只有选项D 符合要求，故选择D ．三、二次函数与一元二次方程1． (2014山东济宁，8，3分)“如果二次函数y ＝ax 2＋bx ＋c 的图象与x 轴有两个公共点，那么一元二次方程ax 2＋bx ＋c ＝0有两个不相等的实数根．”请根据你对这句话的理解，解决下面问题：若m 、n (m <n )是关于x 的方程()()01=---b x a x 的两根，且a < b ， 则a 、b 、m 、n 的大小关系是( )A ． m ＜ a ＜b ＜nB ． a ＜m ＜n ＜bC ． a ＜m ＜b ＜nD ． m ＜a ＜n ＜b【考点解剖】本题考查了二次函数与一元二次方程，解题的关键是根据题意准确画出图形．【解题思路】依题意，画出函数y ＝(x －a )(x －b )的图象，如图所示．函数图象为抛物线，开口向上，与x 轴两个交点的横坐标分别为a ，b (a ＜b )．方程1－(x －a )(x －b )＝0转化为(x －a )(x －b )＝1，方程的两根是抛物线y ＝(x －a )(x －b )与直线y ＝1的两个交点．故可进行比较．【解答过程】依题意，画出函数y ＝(x －a )(x －b )的图象，如图所示．函数图象为抛物线，开口向上，与x 轴两个交点的横坐标分别为a ，b (a ＜b )．方程1－(x －a )(x －b )＝0转化为(x －a )(x －b )＝1，方程的两根是抛物线y ＝(x －a )(x －b )与直线y ＝1的两个交点．由m ＜n ，可知对称轴左侧交点横坐标为m ，右侧为n ．由抛物线开口向上，则在对称轴左侧，y 随x 增大而减少，则有m ＜a ；在对称轴右侧，y 随x 增大而增大，则有b ＜n ．综上所述，可知m ＜a ＜b ＜n ．故选A ．2． （2014四川巴中，10，3分）已知二次函数2y ax bx c =++的图象如图所示，则下列叙述正确的是（ ）A ．abc ＜0B ．－3a ＋c ＜0。