头歌赫夫曼树及其应用实践

实验报告课程名称：数据结构实验名称：赫夫曼编码及应用院（系）：计算机与通信工程学院专业班级：计算机科学与技术姓名：学号：指导教师：2020 年 5 月12 日一、实验目的掌握赫夫曼树和赫夫曼编码的基本思想和算法的程序实现。

二、实验内容及要求1、任务描述a.提取原始文件中的数据（包括中文、英文或其他字符），根据数据出现的频率为权重，b.构建Huffman编码表；c.根据Huffman编码表对原始文件进行加密，得到加密文件并保存到硬盘上；d.将加密文件进行解密，得到解码文件并保存点硬盘上；e.比对原始文件和解码文件的一致性，得出是否一致的结论。

2、主要数据类型与变量a.对Huffman树采用双亲孩子表示法，便于在加密与解密时的操作。

typedef struct Huffman* HuffmanTree;struct Huffman{unsigned int weight; //权值unsigned int p, l, r;//双亲，左右孩子};b．对文本中出现的所有字符用链表进行存储。

typedef struct statistics* List;struct statistics {char str; //存储此字符int Frequency; //出现的频率（次数）string FinalNum; //Huffman编码struct statistics* Next;};3、算法或程序模块对读取到的文本进行逐字符遍历，统计每个字符出现的次数，并记录在创建的链表中。

借助Huffman树结构，生成结构数组，先存储在文本中出现的所有字符以及它们出现的频率（即权值），当作树的叶子节点。

再根据叶子节点生成它们的双亲节点，同样存入Huffman树中。

在完成对Huffman树的创建与存储之后，根据树节点的双亲节点域以及孩子节点域，生成每个字符的Huffman编码，并存入该字符所在链表节点的FinalNum域。

/*哈夫曼树的应用和实现（1）根据输入的字符和相应的权值建立哈夫曼树，并输出已建的相应内容作为检查；（2）用哈夫曼树实现前缀编码，并输出各字符的编码串；（3）输入一组二进制报文，进行译码，并输出译文。

*/#include<stdio.h>#include<stdlib.h>#include<string.h>#include<math.h>#define N 1000 //定义结点数最大值#define M 2*N-1#define maxval 10000.0 //定义float的最大值typedef struct //定义哈夫曼树类型{char data;float weight;int lchild,rchild,parent;}hufmtree;hufmtree tree[M];typedef struct //定义哈夫曼树编码类型{char bits[N];int start;char data;}codetype;codetype code[N];void HUFFMAN(hufmtree t[]);void HUFFMANCODE(codetype code[],hufmtree t[]);void HUFFMANDECODE(codetype code[],hufmtree t[]);void OUTTREE(hufmtree t[]);static int n,m; //定义静态全局变量n储存需要的结点数//m为构建哈夫曼树后的总结点数//菜单的建立void main(){int x,flag1=0;printf("\t\t\t哈夫曼树的应用和实现\n");while(1){printf("——————————————————————————————————\n");printf("菜单：1 建立哈夫曼树 2 哈夫曼树编码 3 输入电文译码0 退出使用\n");printf("——————————————————————————————————\n");printf("请选择操作：\n");scanf("%d",&x);switch(x){case 1:HUFFMAN(tree);break;case 2:HUFFMANCODE(code,tree);break;case 3:HUFFMANDECODE(code,tree);break;case 0:flag1=1; //输入号为0时使flag1=1break;default:printf("输入的选择有误！请重新输入！\n");break;}if(flag1) break; //表明选择了退出操作故跳出循环}printf("Thank You!\n");}//哈夫曼树的构建void HUFFMAN(hufmtree t[]){int i,j,p1,p2;char ch;float small1,small2,f;printf("请输入叶子结点数：\n");scanf("%d",&n);m=2*n-1;for(i=0;i<m;i++) //初始化哈夫曼树{tree[i].parent=0;tree[i].lchild=0;tree[i].rchild=0;tree[i].data='0';tree[i].weight=0.0;}for(i=0;i<n;i++){getchar(); //getchar 吃掉回车printf("请输入第%d个结点的字符和权重（空格隔开）：\n",i);scanf("%c %f",&ch,&f); //输入结点字符和权重tree[i].data=ch;tree[i].weight=f;}for(i=n;i<m;i++) //进行n-1次合并产生n-1个新结点{p1=0;p2=0; //预置最小次小权值的下标为0small1=maxval; //预置最小次小权值为float型最大值small2=maxval;for(j=i-1;j>=0;j--) //循环找出最小、次小权值和下标if(tree[j].parent==0)if((tree[j].weight-small1)<0.0001) //float精度，当两者之差小于0.0001认为相等{small2=small1; //小于当前最小权值，更新最小权值和次小权值以及位置small1=tree[j].weight;p2=p1;p1=j;}elseif((tree[j].weight-small2)<0.0001) //小于当前次小权值，更新次小权值和位置{small2=tree[j].weight;p2=j;}tree[p1].parent=i; //修改最小、次小结点的双亲为新生成的结点tree[p2].parent=i;tree[i].lchild=p1; //新结点的左右孩子指向最小次小值的结点tree[i].rchild=p2;tree[i].weight=tree[p1].weight+tree[p2].weight; //新生成结点权值为两小之和}OUTTREE(tree);}//哈夫曼编码void HUFFMANCODE(codetype code[],hufmtree t[]){int i,j,c,p;codetype cd; //定义缓冲变量for(i=0;i<n;i++){cd.start=n;c=i; //从叶子节点出发线上回溯p=tree[c].parent; //p指向c的双亲结点cd.data=tree[c].data;while(p!=0){cd.start--;if(tree[p].lchild==c) //判断是否是左孩子，是编码为‘0’cd.bits[cd.start]='0';else //否则编码为‘1’cd.bits[cd.start]='1';c=p; //更新p的双亲结点，进行下一次循环p=tree[c].parent;}code[i]=cd; //把一个字符的编码赋给相应code[i]}printf("输出每个字符的哈夫曼编码:\n"); //输出每个字符的哈弗曼编码for(i=0;i<n;i++){printf("%c: ",code[i].data);for(j=code[i].start;j<n;j++)printf("%c ",code[i].bits[j]);printf("\n");}}//哈夫曼译码void HUFFMANDECODE(codetype code[],hufmtree t[]){int i,c=0;char b[100]; //定义字符数组储存输入的字符串int endflag='#'; //电文结束标志位#i=m-1; //从根结点开始向下搜索printf("请输入电文：\n");printf("注意：电文结束标志为#\n");getchar();gets(b);while(b[c]!=endflag) //遍历输入的字符串{if(b[c]=='0') //编码为0 走向左孩子i=tree[i].lchild;elsei=tree[i].rchild; //编码为1 走向右孩子if(tree[i].lchild==0) //结点为叶子结点{putchar(code[i].data); //输出译码值i=m-1; //回到根结点}c++ ;}printf("\n");if((tree[i].lchild!=0)&&(b[c]!='#')) //电文读完尚未到叶子结点printf("输入的电文有错误！\n");}//打印哈夫曼树void OUTTREE(hufmtree t[]){int i;printf("\n\n");printf("结点数据权重双亲左孩子右孩子\n");for(i=0;i<m;i++){printf("%d",i);printf(" %c",tree[i].data);printf(" %f",tree[i].weight);printf(" %d",tree[i].parent);printf(" %d",tree[i].lchild);printf(" %d\n",tree[i].rchild);}}。

哈夫曼编码树实现及应用场景讲解哈夫曼编码树（Huffman coding tree）是一种被广泛应用于数据压缩的算法，它通过利用输出频率不同的字符分配不同长度的编码，从而实现数据的高效压缩。

本文将介绍哈夫曼编码树的实现方法，并探讨其在实际应用中的场景。

一、哈夫曼编码树的实现方法1.1 字符频率统计在构建哈夫曼编码树之前，我们首先需要对目标数据中的字符进行频率统计。

可以通过遍历数据集，并利用哈希表或数组记录每个字符出现的次数。

例如，对于字符串"Hello World!"，我们可以统计出每个字符的频率为：H: 1, e: 1, l: 3, o: 2, W: 1, r: 1, d: 1, !: 1。

1.2 构建哈夫曼编码树构建哈夫曼编码树的过程分为两个步骤：创建叶节点集合和合并节点。

创建叶节点集合：根据字符频率统计结果，创建一个包含所有字符的叶节点集合。

每个叶节点包含字符、频率以及指向其左右子节点的指针（若存在子节点）。

合并节点：从叶节点集合中选取频率最低的两个节点，合并成一个新节点，该新节点的频率等于这两个节点的频率之和。

将合并后的节点插入叶节点集合中，并从集合中移除被合并的节点。

重复该操作，直到叶节点集合只剩下一个节点，即为哈夫曼编码树的根节点。

1.3 构建哈夫曼编码表遍历哈夫曼编码树，沿着根节点到叶节点的路径，给每个字符赋予对应的二进制编码。

例如，对于字符串"Hello World!"，哈夫曼编码表如下：H: 00e: 01l: 10o: 11W: 010r: 011d: 100!: 101二、哈夫曼编码树的应用场景2.1 数据压缩哈夫曼编码树最常见的应用场景之一是数据压缩。

通过使用较短的二进制编码表示频率较高的字符，以及使用较长的二进制编码表示频率较低的字符，可以大幅减小数据的存储空间。

这种压缩方法被广泛应用于文本、图像和音频等多媒体数据的传输和存储。

举个例子，在一个文件中，字符'E'出现频率最高，通过哈夫曼编码树，我们可以将其编码为一个比特（如0），而字符'Z'出现频率最低，可以将其编码为多个比特（如11001），从而实现数据的高效压缩。

目录第一章哈夫曼树的基本术语 (1)1．1路径和路径长度 (1)1.2树的带权路径长度 (1)1．3哈夫曼树的定义 (1)第二章哈夫曼树的构造 (2)2.1哈夫曼树的构造 (2)第三章哈夫曼树的存储结构及哈夫曼算法的实现 (3)3.1哈夫曼树的存储结构 (3)3.2 哈夫曼算法的简要描述 (3)第四章哈夫曼树的应用 (5)4.1哈夫曼编码 (5)4.2求哈夫曼编码的算法 (5)4.21思想方法 (5)4.22字符集编码的存储结构及其算法描述 (6)4.3哈夫曼树和编码程序实现： (6)4.4程序运行结果： (9)心得体会 (10)参考文献 (10)第一章哈夫曼树的基本术语1．1路径和路径长度在一棵树中，从一个结点往下可以达到的孩子或子孙结点之间的通路，称为路径。

通路中分支的数目称为路径长度。

若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

1.2结点的权及带权路径长度若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

1.2树的带权路径长度树的带权路径长度(Weighted Path Length of Tree)：也称为树的代价，定义为树中所有叶结点的带权路径长度之和，通常记为：其中：n表示叶子结点的数目wi和li分别表示叶结点ki的权值和根到结点ki之间的路径长度。

1．3哈夫曼树的定义在权为wl ，w2，…，wn的n个叶子所构成的所有二叉树中，带权路径长度最小(即代价最小)的二叉树称为最优二叉树或哈夫曼树。

[例]给定4个叶子结点a，b，c和d，分别带权7，5，2和4。

构造如下图所示的三棵二叉树(还有许多棵)，它们的带权路径长度分别为：(a)WPL=7*2+5*2+2*2+4*2=36(b)WPL=7*3+5*3+2*1+4*2=4(c)WPL=7*1+5*2+2*3+4*3=35其中(c)树的WPL最小，可以验证，它就是哈夫曼树。

哈夫曼树的实际应用
哈夫曼树（Huffman Tree）是一种重要的数据结构，它在信息编码和压缩、数据传输和存储、图像处理等领域有广泛应用。

1. 数据压缩：哈夫曼树是一种无损压缩的方法，能够有效地减小数据的存储空间。

在进行数据压缩时，可以使用哈夫曼树构建字符编码表，将出现频率较高的字符用较短的编码表示，而出现频率较低的字符用较长的编码表示，从而减小数据的存储空间。

2. 文件压缩：在文件压缩领域，哈夫曼树被广泛应用于压缩算法中。

通过构建哈夫曼树，可以根据字符出现的频率来生成不同长度的编码，从而减小文件的大小。

常见的文件压缩格式如ZIP、GZIP等都使用了哈夫曼树。

3. 图像压缩：在图像处理中，哈夫曼树被用于图像压缩算法中。

通过将图像中的像素值映射为不同长度的编码，可以减小图像的存储空间，提高图像传输和存储的效率。

常见的图像压缩格式如JPEG、PNG等都使用了哈夫曼树。

4. 文件传输：在数据传输中，哈夫曼树被用于数据压缩和传输。

通过对数据进行压缩，可以减小数据的传输时间和带宽占用。

在传输过程中，接收方可以通过哈夫曼树解码接收到的数据。

5. 数据加密：在数据加密中，哈夫曼树可以用于生成密钥，从而实现数据的加密和解密。

通过将字符映射为不同长度的编码，可以实
现对数据的加密和解密操作。

哈夫曼树在信息编码和压缩、数据传输和存储、图像处理等领域有广泛应用，能够有效地减小数据的存储空间、提高数据传输效率、实现数据加密等功能。

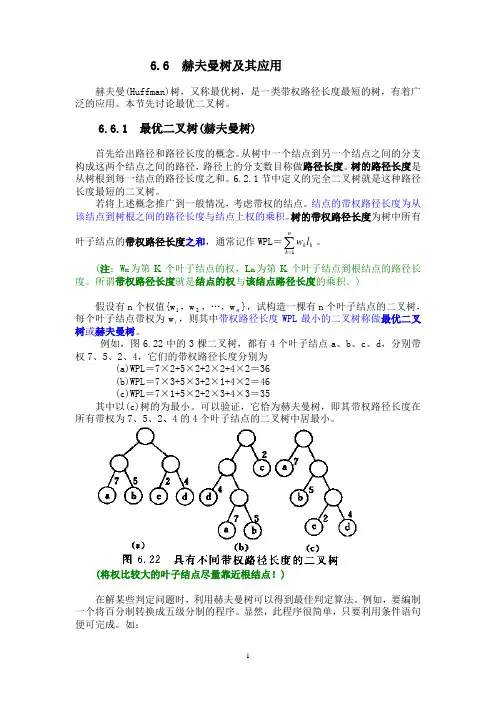
6.6 赫夫曼树及其应用赫夫曼(Huffman)树，又称最优树，是一类带权路径长度最短的树，有着广泛的应用。

本节先讨论最优二叉树。

6.6.1 最优二叉树(赫夫曼树)首先给出路径和路径长度的概念。

从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称做路径长度。

树的路径长度是从树根到每一结点的路径长度之和。

6.2.1节中定义的完全二叉树就是这种路径长度最短的二叉树。

若将上述概念推广到一般情况，考虑带权的结点。

结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。

树的带权路径长度为树中所有叶子结点的带权路径长度之和，通常记作WPL ＝∑=nk k k l w 1。

(注：W K 为第K 个叶子结点的权，L K 为第K 个叶子结点到根结点的路径长度。

所谓带权路径长度就是结点的权与该结点路径长度的乘积。

)假设有n 个权值{w 1，w 2，…，w n }，试构造一棵有n 个叶子结点的二叉树，每个叶子结点带权为w i ，则其中带权路径长度WPL 最小的二叉树称做最优二叉树或赫夫曼树。

例如，图6.22中的3棵二叉树，都有4个叶子结点a 、b 、c 、d ，分别带权7、5、2、4，它们的带权路径长度分别为(a)WPL ＝7×2+5×2+2×2+4×2＝36(b)WPL ＝7×3+5×3+2×1+4×2＝46(c)WPL ＝7×1+5×2+2×3+4×3＝35其中以(c)树的为最小。

可以验证，它恰为赫夫曼树，即其带权路径长度在所有带权为7、5、2、4的4个叶子结点的二叉树中居最小。

(将权比较大的叶子结点尽量靠近根结点！)在解某些判定问题时，利用赫夫曼树可以得到最佳判定算法。

例如，要编制一个将百分制转换成五级分制的程序。

显然，此程序很简单，只要利用条件语句便可完成。

赫夫曼树的作用及应用1.引言在计算机科学中，赫夫曼树是一种重要的数据结构，它被广泛应用于数据压缩、存储和解码等领域。

赫夫曼树以其高效的特点，成为了压缩算法中的重要组成部分。

本文将介绍赫夫曼树的作用以及它在不同应用领域中的具体应用。

2.赫夫曼树的基本概念赫夫曼树，也称为最优二叉树，是一种树形结构。

它的构建基于赫夫曼编码算法，该算法通过将频率较高的字符编码为较短的二进制码，从而实现数据的高效压缩。

3.赫夫曼树的构建赫夫曼树的构建过程包括以下几个步骤：1.统计字符频率：遍历待压缩的数据，统计各个字符出现的频率。

2.构建叶子节点：将每个字符及其频率作为叶子节点，构成初始的二叉树。

3.合并节点：选择两个频率最低的节点合并，并将合并后的节点作为新的节点插入二叉树中。

4.重复合并：重复执行合并节点的操作，直到只剩下一个节点，即赫夫曼树的根节点。

4.赫夫曼树的作用赫夫曼树在数据压缩和解压缩中发挥着重要作用，主要体现在以下几个方面：4.1数据压缩赫夫曼树通过赫夫曼编码将频率较高的字符编码为较短的二进制码，从而实现数据的高效压缩。

压缩后的数据体积大大减小，方便存储和传输。

4.2文件压缩赫夫曼树可用于对文件进行压缩，将文件中的字符编码为对应的二进制码，从而减小文件的大小。

在文件传输和存储中，减小文件的大小可以提高传输速度和节省存储空间。

4.3图像压缩赫夫曼树也可用于图像数据的压缩，通过对图像中的像素进行编码，减小图像的大小。

图像压缩在图像处理和存储中起到重要的作用，减小图像的大小可以提高图像的传输速度和存储效率。

4.4视频压缩赫夫曼树在视频编码中也有重要应用，通过对视频帧中的数据进行编码，实现对视频的压缩。

视频压缩可以降低视频的带宽占用率，提高视频传输的效率和稳定性。

5.赫夫曼树的应用举例除了数据压缩方面，赫夫曼树在其他领域也有广泛应用，以下列举几个常见的应用场景：5.1字符串匹配赫夫曼树可以用于字符串匹配算法中，通过构建赫夫曼树和相关数据结构，提高字符串匹配的效率和准确性。

哈夫曼树的应用-哈夫曼树代码实现一、简介哈夫曼树又称为最优树。

1、路径和路径长度在一棵树中，从一个结点往下可以达到的孩子或子孙结点之间的通路，称为路径。

通路中分支的数目称为路径长度。

若规定根结点的层数为1，则从根结点到第L层结点的路径长度为L-1。

2、结点的权及带权路径长度若将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

结点的带权路径长度为：从根结点到该结点之间的路径长度与该结点的权的乘积。

3、树的带权路径长度树的带权路径长度规定为所有叶子结点的带权路径长度之和，记为WPL二、哈夫曼树的应用1、哈夫曼编码在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。

例如，需传送的报文为“AFTER DATA EAR ARE ART AREA”，这里用到的字符集为“A，E，R，T，F，D”，各字母出现的次数为{8，4，5，3，1，1}。

现要求为这些字母设计编码。

要区别6个字母，最简单的二进制编码方式是等长编码，固定采用3位二进制，可分别用000、001、010、011、100、101对“A，E，R，T，F，D”进行编码发送，当对方接收报文时再按照三位一分进行译码。

显然编码的长度取决报文中不同字符的个数。

若报文中可能出现26个不同字符，则固定编码长度为5。

然而，传送报文时总是希望总长度尽可能短。

在实际应用中，各个字符的出现频度或使用次数是不相同的，如A、B、C的使用频率远远高于X、Y、Z，自然会想到设计编码时，让使用频率高的用短码，使用频率低的用长码，以优化整个报文编码。

为使不等长编码为前缀编码(即要求一个字符的编码不能是另一个字符编码的前缀)，可用字符集中的每个字符作为叶子结点生成一棵编码二叉树，为了获得传送报文的最短长度，可将每个字符的出现频率作为字符结点的权值赋予该结点上，求出此树的最小带权路径长度就等于求出了传送报文的最短长度。

因此，求传送报文的最短长度问题转化为求由字符集中的所有字符作为叶子结点，由字符出现频率作为其权值所产生的哈夫曼树的问题。

头歌赫夫曼树及其应用实践1. 什么是头歌赫夫曼树头歌赫夫曼树（Huffman Tree）是一种用于数据压缩和编码的树形结构。

它是由统计学家David A. Huffman于1952年提出的，被广泛应用于数据压缩、通信和存储等领域。

2. 头歌赫夫曼树的构建方法头歌赫夫曼树的构建方法与二叉树有关，它采用了一种贪心算法来生成最佳的编码方案。

构建头歌赫夫曼树的步骤如下：2.1 统计字符频率首先，需要统计待编码的文本中每个字符出现的频率，频率越高的字符在编码中占用的位数越少。

2.2 构建叶节点根据字符频率，构建对应频率的叶节点，并按照频率从小到大的顺序排列。

2.3 合并节点从频率最小的两个节点开始，将它们合并为一个新的节点，并设定新节点的频率为两个节点的频率之和。

重复这个过程，直到只剩下一个节点为止，这个节点就是头歌赫夫曼树的根节点。

2.4 构建编码表从根节点开始，对每个节点进行遍历，在遍历的过程中赋予左右子节点分别为0和1的编码。

最终得到一个字符与对应编码的映射表。

2.5 进行数据编码根据编码表，将原始数据每个字符对应的编码串联起来，得到编码后的数据。

3. 头歌赫夫曼树的应用实践头歌赫夫曼树在数据压缩和编码中有广泛的应用。

3.1 数据压缩头歌赫夫曼树可以将原始数据进行高效地压缩，减少数据的存储空间。

利用字符频率来构建编码表，出现频率高的字符用较短的编码表示，出现频率低的字符用较长的编码表示。

这样可以实现对数据的有损压缩，即在压缩过程中可能会丢失一些信息，但可以在一定程度上减小数据体积。

3.2 数据编码头歌赫夫曼树将每个字符映射为对应的编码，将文本或其他数据转化为一串由0和1组成的编码。

这种编码方式具有唯一性，即每个字符对应的编码没有前缀是其他字符编码的前缀。

这样可以在数据传输和储存过程中节约带宽和存储空间。

3.3 文件压缩头歌赫夫曼树的应用不仅局限于简单的文本压缩，也可以用于文件压缩。

文件压缩是在文件级别上进行压缩，将一个或多个文件进行合并和压缩存储。

哈夫曼树的实际应用
哈夫曼树在实际中有许多应用，以下是一些例子：
1. 数据压缩：哈夫曼树常用于数据压缩算法，如哈夫曼编码。

哈夫曼编码是一种前缀编码，它可以将数据中的字符编码为二进制字符串，使得平均编码长度最短，从而达到数据压缩的效果。

2. 文件存储：在文件存储中，哈夫曼树可以用于数据存储和检索。

例如，可以使用哈夫曼树来存储文件索引，以便快速找到文件。

3. 图像处理：在图像处理中，哈夫曼树可以用于图像压缩和编码。

例如，可以使用哈夫曼树来编码图像中的像素值，从而减小图像文件的大小。

4. 通信网络：在通信网络中，哈夫曼树可以用于数据传输和调度。

例如，可以使用哈夫曼树来优化数据的传输路径和顺序，以提高网络传输的效率和可靠性。

5. 数据库优化：在数据库优化中，哈夫曼树可以用于索引和查询处理。

例如，可以使用哈夫曼树来构建索引，以便快速检索数据库中的数据。

总的来说，哈夫曼树在许多领域中都有广泛的应用，特别是在需要数据压缩、文件存储、图像处理、通信网络和数据库优化的领域中。

摘要：哈夫曼树是带权路径长度（WPL）最小的二叉树，通过对哈夫曼算法的研究，提出一种求取哈夫曼树带权路径长度的计算方法和应用。

关键词：哈夫曼算法、二叉树、WPL、编码1 引言：哈夫曼树是一种特殊的二叉树，又称最优二叉树：假设有一组（无序）实数｛w1,w2,w3,w4,…,wm｝，现要构造一棵以wi（i=1，2，3，4…，m）为权的m个外部结点的扩充二叉树，使得带权的外部路径长度WPL最小。

满足这一要求的扩充二叉树就称为哈夫曼树或最优二叉树。

若l表示从根到第i个外部结点的路径长度，m为外部结点的个数，wi 为第i个外部结点的权值，则有WPL=∑wili（0<i<=m）。

2 正文：2.1 算法的基本思想：（1）由给定的m个权值｛w1,w2,…wm｝，构造一棵由空二叉树扩充得到的扩充二叉树｛T1,T2,…,Tm｝。

每个Ti（1<i<m）只有一个外部结点（也是根结点），它的权值置为w1。

（2）在已经构造的所有扩充二叉树中，选取根结点的权值最小和次最小的两棵，将它们作为左、右子树，构造成一棵新的扩充二叉树，它的根结点（新建立的内部结点）的权值为其左、右子树根结点权值之和。

（3）重复执行步骤（2），每次都使扩充二叉树的个数减少一，当只剩下一棵扩充二叉树时，它便是所要构造的哈夫曼树。

一棵二叉树要使其WPL最小，必须使权值的外部结点离根越近，权值越小的离根越远。

2.1.1 程序实现：/*哈夫曼树的构造方法*/#include<stdlib.h>#include<stdio.h>#define MAXINT 50#define MAXNUM 50 /* 数组w中最多容纳的元素个数，注意m<=MAXNUM */#define MAXNODE 100 /* 哈夫曼树中的最大结点数，注意2*m-1<MAXNODE */structHtNode { /* 哈夫曼树结点的结构*/intww;intparent,llink,rlink;};structHtTree {int root;/* 哈夫曼树根在数组中的下标*/structHtNodeht[MAXNODE];};typedefstructHtTree *PHtTree; /* 哈夫曼树类型的指针类型*//* 构造具有m个叶结点的哈夫曼树*/PHtTreehuffman(int m, int *w) {PHtTreepht;int i, j, x1, x2, m1, m2;pht = (PHtTree)malloc(sizeof(structHtTree)); /* 创建空哈夫曼树*/if (pht == NULL) {printf("Out of space!! \n");returnpht;}for (i = 0; i < 2*m-1; i++) {/* 置初态*/pht->ht[i].llink = -1;pht->ht[i].rlink = -1;pht->ht[i].parent = -1;if (i < m)pht->ht[i].ww = w[i];elsepht->ht[i].ww = -1;}for ( i = 0; i < m-1; i++) {/* 每循环一次构造一个内部结点*/m1 = MAXINT;m2 = MAXINT;/* 相关变量赋初值*/x1 = -1;x2 = -1;for (j = 0; j <m+i; j++) /* 找两个最小权的无父结点的结点*/ if (pht->ht[j].ww< m1 &&pht->ht[j].parent == -1) {m2 = m1;x2 = x1;m1 = pht->ht[j].ww;x1 = j;}else if (pht->ht[j].ww< m2 &&pht->ht[j].parent == -1) {m2 = pht->ht[j].ww;x2 = j;}pht->ht[x1].parent = m+i; /* 构造一个内部结点*/pht->ht[x2].parent = m+i;pht->ht[m+i].ww = m1+m2;pht->ht[m+i].llink = x1;pht->ht[m+i].rlink = x2;pht->root = m+i;}returnpht;}int main() {int m = 0, j = 0, i = 0, parent = 0;int* w;PHtTreepht;printf("please input m = ");/*输入外部结点个数*/scanf("%d", &m);if (m < 1) {printf("m is not reasonable!\n");return 1;}w = (int *)malloc(sizeof(int)*m);if (w == NULL) {printf("overflow!\n");return 1;}printf("please input the %d numbers：\n",m);/*输入权值*/for (j = 0; j < m; j++)scanf("%d", w+j);pht = huffman(m, w);for (j = 0; j < m; j++) {printf("the Reverse code of the %d node is:", j+1);/*得到的编码应倒过来*/i = j;while (pht->ht[i].parent != -1) {parent = pht->ht[i].parent;if (pht->ht[parent].llink == i)printf("0");elseprintf("1");i = parent;}printf("\n");}return 0;}2.1.2 例子：下面以w=｛2,3,5,7,11,13,17,17,19,23,29,31,37,41｝,按照上述方法构造出来的哈夫曼树如下图所示：用哈夫曼算法构造的哈夫曼树2.2 哈夫曼树的应用：2.2.1 哈夫曼编码：哈夫曼树可以直接应用于通信及数据传送中的二进制编码。

一、实验目的1. 理解赫夫曼树的概念和原理；2. 掌握赫夫曼树的构建方法；3. 学会使用赫夫曼树进行数据压缩和解压缩；4. 了解赫夫曼树在实际应用中的优势。

二、实验原理赫夫曼树是一种带权路径长度最短的二叉树，也称为最优二叉树。

在构建赫夫曼树的过程中，每次选择两个权值最小的节点作为左右子节点，然后合并成一个新的节点，权值为两个子节点权值之和。

重复此过程，直到只剩下一个节点，即为赫夫曼树的根节点。

赫夫曼树在数据压缩中的应用主要体现在编码和解码过程中。

通过对字符进行赫夫曼编码，可以将字符序列转换成二进制序列，从而减少数据存储空间。

在解码过程中，根据赫夫曼树的结构，可以将二进制序列还原成原始字符序列。

三、实验内容1. 构建赫夫曼树（1）输入字符及其权值，例如：A=5, B=9, C=12, D=13, E=16, F=45。

（2）将输入的字符和权值放入最小堆中，每次取出两个最小权值的节点，合并成一个新的节点，权值为两个子节点权值之和。

（3）重复步骤（2），直到只剩下一个节点，即为赫夫曼树的根节点。

2. 使用赫夫曼树进行数据压缩和解压缩（1）根据赫夫曼树生成字符的编码，例如：A=01, B=100, C=101, D=110, E=1110, F=1111。

（2）对输入的字符序列进行编码，例如：输入字符串"ABCDEF"，编码后为"01010010101111111111"。

（3）将编码后的二进制序列存储或传输。

（4）接收方根据赫夫曼树的结构，对二进制序列进行解码，还原成原始字符序列。

四、实验结果与分析1. 实验结果（1）构建赫夫曼树```F/ \B D/ \ / \A C E G```（2）字符编码```A=01, B=100, C=101, D=110, E=1110, F=1111```（3）输入字符串"ABCDEF"的编码结果为"01010010101111111111"。

哈夫曼树及其应⽤1、基本概念a、路径和路径长度若在⼀棵树中存在着⼀个结点序列 k1，k2，……，kj，使得 ki是ki+1 的双亲（1<=i<j），则称此结点序列是从 k1 到 kj 的路径。

从 k1 到 kj 所经过的分⽀数称为这两点之间的路径长度，它等于路径上的结点数减1.b、结点的权和带权路径长度在许多应⽤中，常常将树中的结点赋予⼀个有着某种意义的实数，我们称此实数为该结点的权，(如下⾯⼀个树中的蓝⾊数字表⽰结点的权)结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积。

c、树的带权路径长度树的带权路径长度定义为树中所有叶⼦结点的带权路径长度之和，公式为：其中，n表⽰叶⼦结点的数⽬，wi 和 li 分别表⽰叶⼦结点 ki 的权值和树根结点到 ki 之间的路径长度。

如下图中树的带权路径长度 WPL = 9 x 2 + 12 x 2 + 15 x 2 + 6 x 3 + 3 x 4 + 5 x 4 = 122d、哈夫曼树哈夫曼树⼜称最优⼆叉树。

它是 n 个带权叶⼦结点构成的所有⼆叉树中，带权路径长度 WPL 最⼩的⼆叉树。

如下图为⼀哈夫曼树⽰意图。

2、构造哈夫曼树假设有n个权值，则构造出的哈夫曼树有n个叶⼦结点。

n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为：(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有⼀个结点)；(2) 在森林中选出两个根结点的权值最⼩的树合并，作为⼀棵新树的左、右⼦树，且新树的根结点权值为其左、右⼦树根结点权值之和；(3)从森林中删除选取的两棵树，并将新树加⼊森林；(4)重复(2)、(3)步，直到森林中只剩⼀棵树为⽌，该树即为所求得的哈夫曼树。

如：对下图中的六个带权叶⼦结点来构造⼀棵哈夫曼树，步骤如下：注意：为了使得到的哈夫曼树的结构尽量唯⼀，通常规定⽣成的哈夫曼树中每个结点的左⼦树根结点的权⼩于等于右⼦树根结点的权。

数据结构实验赫夫曼树的建立和应用概述赫夫曼树（Huffman Tree），又称最优二叉树（Optimal Binary Tree），是一种特殊的二叉树，常用于数据压缩算法中。

赫夫曼树的主要特点是，树中距离根节点较近的叶子节点的权值较小，距离根节点较远的叶子节点的权值较大。

本文将介绍赫夫曼树的建立过程和一些应用场景。

赫夫曼树的建立赫夫曼树的建立过程主要包含以下几个步骤：1.统计待编码的字符出现的频率，得到频率表。

2.将频率表中的字符和频率作为叶子节点，构成一个森林。

3.每次从森林中选择两个权值最小的节点（可以是叶子节点也可以是非叶子节点），合并为一个新的节点，并将该节点重新插入森林中。

4.重复上述步骤，直到森林中只剩下一个根节点，即为赫夫曼树的根节点。

下面是一个示例：字符频率A6B3C4D2E5根据以上频率表，我们可以构建下面的赫夫曼树： 20/ \\10 10/ \\ / \\5 5 4 6/ \\2 3赫夫曼编码赫夫曼编码是一种前缀编码的方式，即没有任何编码是其他编码的前缀。

赫夫曼编码通过将赫夫曼树中经过的路径用0或1进行编码，实现对字符的压缩。

在上面的例子中，赫夫曼编码如下：字符编码A10B110C111D00E01可以看到，编码表中每个字符的编码都是其他字符的前缀，符合赫夫曼编码的要求。

赫夫曼树的应用赫夫曼树在数据压缩领域有广泛的应用，常用于压缩文本文件。

通过统计字符出现的频率，并建立赫夫曼树和编码表，可以将原始文本中的字符用更短的二进制位来表示，从而达到压缩数据的目的。

除了数据压缩，赫夫曼树还可以应用于其他领域，例如网络数据传输中的数据压缩、图像编码等。

总结赫夫曼树是一种特殊的二叉树，通过统计字符出现的频率，建立赫夫曼树，并生成对应的赫夫曼编码表，可以实现对数据的压缩。

赫夫曼树在数据压缩领域有广泛的应用，可以大幅度减小数据存储和传输的开销。

需要注意的是，在使用赫夫曼树进行数据压缩时，对于频率较低的字符可能会出现编码较长的情况，这可能会导致压缩效果不佳。

最新赫夫曼树实验报告实验原理：霍夫曼编码(Huffman Coding)是一种编码方式，是一种用于无损数据压缩的爛编码(权编码)算法。

1952年，David A. Huffman在麻省理工攻读博士时所发明的。

在计算机数据处理中，霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

例如，在英文中，e的出现机率最高，而z的出现概率则最低。

当利用霍夫曼编码对一篇英文进行压缩时，e极有可能用一个比特来表示，而z则可能花去25个比特(不是26)。

用普通的表示方法时，每个英文字母均占用一个字节(byte),即8个比特。

二者相比，e使用了一般编码的1/8的长度, z则使用了3倍多。

倘若我们能实现对于英文中各个字母出现概率的较准确的估算，就可以大幅度提高无损压缩的比例。

霍夫曼树乂称最优二义树，是一种带权路径长度最短的二叉树。

所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度 (若根结点为0层，叶结点到根结点的路径长度为叶结点的层数)。

树的路径长度是从树根到每一结点的路径长度之和，记为WPL=(Wl*Ll+W2*L2+W3*L3+...+Wn*Ln), N 个权值Wi (i=l,2,...n)构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li (i=l,2,...n)o 可以证明霍夫曼树的WPL是最小的。

实验目的：本实验通过编程实现赫夫曼编码算法，使学生掌握赫夫曼树的构造方法, 理解树这种数据结构的应用价值，并能熟练运用C语言的指针实现构建赫夫曼二义树，培养理论联系实际和自主学习的能力，加强对数据结构的原理理解，提高编程水平。

实验内容：(1)实现输入的英文字符串输入，并设计算法分别统计不同字符在该字符串中出现的次数，字符要区分大小写；（2）实现赫夫曼树的构建算法；（3）遍历赫夫曼生成每个字符的二进制编码;（4）显示输出每个字母的编码。

头歌哈夫曼树实验及提升训练在我们的日常生活中，数据传输和信息存储就像是空气和水，缺一不可。

今天，咱们来聊聊一种有趣的东西，叫做哈夫曼树。

这家伙听起来高大上，但其实就像一块儿披萨，简单又好玩。

想象一下，哈夫曼树就像是你家里的一棵大树，上面挂满了不同的水果，而这些水果代表着不同的数据。

说到这里，大家可能会想：“这树到底是怎么长的？”别急，让我慢慢道来。

哈夫曼树的故事其实是由一个聪明的家伙发明的，那个家伙可不是别人，正是大名鼎鼎的哈夫曼。

他用了一种特别的办法来给不同的数据赋予不同的权重。

打个比方吧，咱们每个人都有自己喜欢的食物，有的人爱吃披萨，有的人偏爱汉堡。

哈夫曼树就是把这些食物按受欢迎程度排排坐，越受欢迎的，越靠近树的根部，越不受欢迎的，远离根部，听起来是不是特别有趣？来吧，咱们再深入一层，看看这个哈夫曼树的实际应用。

假设你想把你最爱的音乐传给朋友，传输速度就像是在给你的小狗遛弯，越快越好。

哈夫曼树就能帮你实现这个目标。

它通过减少冗余的数据，给每个信息分配一个独特的“地址”，就像给每个小区的住户贴上门牌号。

这样一来，信息传输速度就像飞起来一样，迅速又高效！说到这里，可能有人会觉得哈夫曼树只是个冷冰冰的数学公式，其实它在生活中无处不在。

比如说你在网上购物，结账的时候那些折扣信息、商品名称其实都是经过哈夫曼编码处理过的。

是不是感觉生活变得更加便利了？这就是哈夫曼树给我们带来的美好体验，真是居家旅行必备的神器呀。

制作哈夫曼树也不是随随便便就能搞定的。

想象一下，你在厨房里做饭，要把所有食材都准备好，才能做出美味的菜肴。

建立哈夫曼树需要统计每个数据的频率，像是在调查谁家冰箱里的食物最多。

搞清楚这些信息后，才能搭建起这棵树。

树的结构就像搭积木，有高有低，有粗有细，最终形成一个完美的形状，嘿，这就像是艺术品一样，真让人心醉。

这棵树的成长过程还充满了趣味。

每次加入新的数据，就像是在为树上增加新的水果。

树越长越大，最终形成一个复杂的网络。

赫夫曼算法及其应用的研究与实现摘要本文主要给出了数据结构中的Huffman算法，并详细介绍了Huffman 算法，Huffman编码，按照这一思路，将其应用于通信编码、多分支结构程序设计中，提高了效率。

结合计算机文件存储方式，设计并用软件实现了对文件的数据压缩，其过程主要分为压缩和解压缩两部分。

在应用Huffman编码进行压缩时，其压缩效率与文件大小无关，只与文件中字符出现的频率有关。

根据字符出现的概率来构造平均长度最短的编码，它是一种变长的编码。

在编码中，若各编码长度严格按照编码所对应符号出现概率的大小排列，则编码的平均长度是最小的。

本文的主要目的是通过对Huffman算法的论述和演示，阐述了Huffman算法的原理及其特性，说明了这种压缩算法的优越性和它被广泛应用的原因。

且在数据压缩等领域中，Huffman算法是一种常用的数据压缩方法，应用结果表明，该算法具有很高的实用价值。

关键词Huffman算法；平均长度；数据压缩1 Huffman算法的概述所谓赫夫曼算法是由赫夫曼（D.A.Huffman）在1952年最早就构造带权路径长度WPL最小的二叉树（亦称最优二叉树或赫夫曼树）而给出的一个带有一般规律的算法，其算法描述如下。

1）根据给定的n 个权值{ω1，ω2，…，ωn}构成n棵二叉树的森林集合F={T1，T2，…，Tn}，其中每棵二叉树Ti中只有一个带权值为ωi的根结点，其左右子树为空。

2）在森林F中任意选取两棵根结点的权值最小的树作为左右子树，构造一棵新的二叉树，且设置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。

3）在F中删除这两棵树，同时将新得到的二叉树加入F中。

4）重复2）和3），直到森林F只含一棵树为止。

这棵树便是赫夫曼树。

在得到最优二叉树之后，从叶子出发走一条从叶子到根的路径即可得到该叶子结点字符对应的Huffman编码。

本文中的Huffman编码采用一维数组表示，其中每个元素是一个带有头结点的线性链表。