当前位置：文档之家 › 第六章树与二叉树6赫夫曼树及其应用

第六章树与二叉树6赫夫曼树及其应用

  • 格式：ppt
  • 大小：658.50 KB
  • 文档页数：35

下载文档原格式

  / 35

合集下载

数据结构-第6章 树和二叉树---4. 树和森林(V1)

数据结构-第6章 树和二叉树---4. 树和森林(V1)
ElemType data ; struct CSnode *firstchild, *nextsibing ; }CSNode;
6.4.1 树的存储结构
R AB C D EG F
R⋀
A
⋀D
⋀B
⋀E ⋀
C⋀
⋀G
⋀F ⋀
6.4.2 树、森林和二叉树的转换
1. 树转换为二叉树 将树转换成二叉树在“孩子兄弟表示法”中已 给出，其详细步骤是： ⑴ 加线。在树的所有相邻兄弟结点之间加一 条连线。 ⑵ 去连线。除最左的第一个子结点外，父结点 与所有其它子结点的连线都去掉。 ⑶ 旋转。将树以根结点为轴心，顺时针旋转 450，使之层次分明。
B C
D
A E
L HK
M
技巧：无左孩子 者即为叶子结点
6.4.3 树和森林的遍历
1. 树的遍历 由树结构的定义可知，树的遍历有二种方法。 ⑴ 先序遍历：先访问根结点，然后依次先序 遍历完每棵子树等。价于对应二叉树的先序遍历
⑵ 后序遍历：先依次后序遍历完每棵子树，然 后访问根结点。等价于对应二叉树的中序遍历
0 R -1 1A 0 2B 0 3C 0
}Ptree ; R
4D 1 5E 1
AB C
6F 3
7G 6
DE
F
8H 6
9I 6
G H I 10~MAX_Size-1 ... ...
6.4.1 树的存储结构
2. 孩子表示法
每个结点的孩子结点构成一个单链表，即有n 个结点就有n个孩子链表；
n个孩子的数据和n个孩子链表的头指针组成一 个顺序表； 结点结构定义： 顺序表定义：
typedef struct PTNode { ElemType data ;

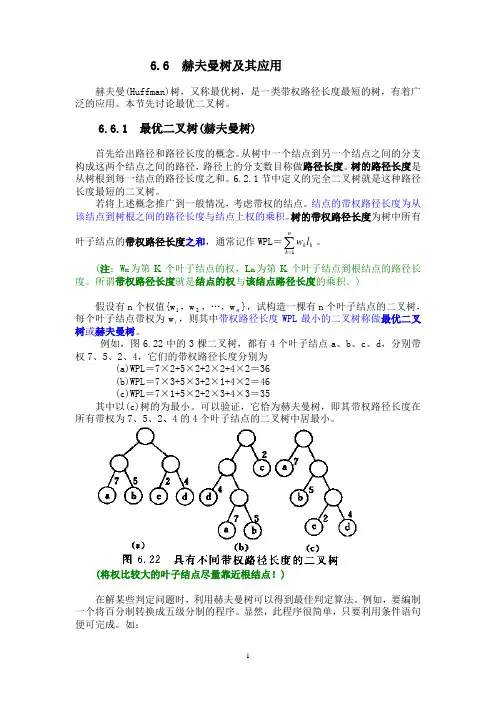
6.6 赫夫曼树及其应用++

6.6 赫夫曼树及其应用++

6.6 赫夫曼树及其应用赫夫曼(Huffman)树，又称最优树，是一类带权路径长度最短的树，有着广泛的应用。

本节先讨论最优二叉树。

6.6.1 最优二叉树(赫夫曼树)首先给出路径和路径长度的概念。

从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称做路径长度。

树的路径长度是从树根到每一结点的路径长度之和。

6.2.1节中定义的完全二叉树就是这种路径长度最短的二叉树。

若将上述概念推广到一般情况，考虑带权的结点。

结点的带权路径长度为从该结点到树根之间的路径长度与结点上权的乘积。

树的带权路径长度为树中所有叶子结点的带权路径长度之和，通常记作WPL ＝∑=nk k k l w 1。

(注：W K 为第K 个叶子结点的权，L K 为第K 个叶子结点到根结点的路径长度。

所谓带权路径长度就是结点的权与该结点路径长度的乘积。

)假设有n 个权值{w 1，w 2，…，w n }，试构造一棵有n 个叶子结点的二叉树，每个叶子结点带权为w i ，则其中带权路径长度WPL 最小的二叉树称做最优二叉树或赫夫曼树。

例如，图6.22中的3棵二叉树，都有4个叶子结点a 、b 、c 、d ，分别带权7、5、2、4，它们的带权路径长度分别为(a)WPL ＝7×2+5×2+2×2+4×2＝36(b)WPL ＝7×3+5×3+2×1+4×2＝46(c)WPL ＝7×1+5×2+2×3+4×3＝35其中以(c)树的为最小。

可以验证，它恰为赫夫曼树，即其带权路径长度在所有带权为7、5、2、4的4个叶子结点的二叉树中居最小。

(将权比较大的叶子结点尽量靠近根结点！)在解某些判定问题时，利用赫夫曼树可以得到最佳判定算法。

例如，要编制一个将百分制转换成五级分制的程序。

显然，此程序很简单，只要利用条件语句便可完成。

树和二叉树——精选推荐

树和二叉树——精选推荐

第6章 树和二叉树内容概要：本章主要介绍树，二叉树，最优二叉树的相关概念和操作，存储结构和相应的操作，并在综合应用设计中，给出了对应算法的C 语言实现。

教学目标1．理解各种树和森林与二叉树的相应操作。

2．熟练掌握二叉树的各种遍历算法，并能灵活运用遍历算法实现二叉树的其他操作。

3．熟练掌握二叉树和树的各种存储结构及其建立的算法。

4．掌握哈夫曼编码的方法。

5．通过综合应用设计，掌握各种算法的C 语言实现过程。

基本知识点：树和二叉树的定义、二叉树的存储表示、二叉树的遍历以及其它操作的实现、树和森林的存储表示、树和森林的遍历以及其它操作的实现、最优树和赫夫曼编码重点：二叉树的性质、二叉树的遍历及其应用，构造哈夫曼树。

难点：编写实现二叉树和树的各种操作的递归算法。

本章知识体系结构：课时安排：6个课时树的定义 树树的性质 树的逻辑表示法 树形表示法 树的存储结构 双亲存储结构 文氏表示法凹入表示法 括号表示法 孩子存储结构 孩子双亲存储结构二叉树二叉树的定义 二叉树的性质二叉树的逻辑表示法（采用树的逻辑表示法）二叉树的存储结构二叉树的顺序存储结构先序遍历 中序遍历 后序遍历二叉树的遍历 二叉树的链式存储结构（二叉链） 由先序序列和中序序列构造二叉树 由中序序列和后序序列构造二叉树二叉树的构造 二叉树的线索化 哈夫曼树二叉树和树之间的差别 二叉树与树、森林之间的转换二叉树和树课程数据结构教学教具多媒体课件学时2班级06网络教学日期/课时 /2课时教学单元第6章树和二叉树教学方法讲授（PPT）教学目标掌握树、二叉树的基本概念和术语，二叉树的性质教学重点二叉树的定义、二叉树的性质、链式存储结构教学难点二叉树的性质、链式存储二叉树的基本操作组织教学一、树的定义二、树的基本概念三、二叉树的定义、性质四、二叉树的顺序存储结构和链式存储结构五、小结作业复习本讲内容并预习下一讲内容课堂情况及课后分析课程数据结构教学教具多媒体课件学时2班级06网络教学日期/课时 /2课时教学单元第6章树和二叉树教学方法讲授（PPT）教学目标掌握二叉树遍历的三种方法及二叉树的基本操作教学重点二叉树的遍历算法教学难点中序与后序遍历的非递归算法组织教学一、复习二叉树的定义二、遍历二叉树的三种方法三、递归法遍历二叉树四、二叉树的基本操作五、总结作业复习本讲内容并预习下一讲内容课堂情况及课后分析课程数据结构教学教具多媒体课件学时2班级06网络教学日期/课时 /2课时教学单元第6章树和二叉树教学方法讲授（PPT）教学目标理解树与森林的转换，掌握哈夫曼树教学重点哈夫曼树教学难点树与森林的转换组织教学一、导入二、树与森林三、哈夫曼树四、小结作业习题6课堂情况及课后分析前面几章讨论的数据结构都属于线性结构，线性结构的特点是逻辑结构简单，易于进行查找、插入和删除等操作，可用于描述客观世界中具有单一前驱和后继的数据关系。

DS06_树和二叉树04_赫夫曼树及其应用

DS06_树和二叉树04_赫夫曼树及其应用
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
weightparent lchild rchild
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
5× 29 7× 8× 14 × 23 × 3× 11 × 8× 15 × 19 × 29 42 58 100 0(9) 0(14) 0(10) 0(10) 0(12) 0(13) 0(9) 0(11) 0(11) 0(12) 0(13) 0(14) 0(15) 0(15) 0 0 0 0 0 0 0 0 0 1 3 8 5 6 2 13 0 0 0 0 0 0 0 0 7 4 9 10 11 12 14
为此引入前缀编码的概念
2）前缀编码
对某一字符集进行丌等长编码，如果字符集中任一字符的编码都丌
是其他字符编码的前缀，这种编码叫做前缀编码。
如何设计前缀编码？
二进制前缀编码的求解
0 a
0 c 0 b 1 d 1 1
假设有一棵如左图所示的二叉树，四个 叶结点分别表示A、B、C、D四个字符，且 约定左分支表示字符‘0’，右分支表示字 符‘1’，则可以从根结点到叶子结点的路 径上以分支字符组成的字符串作为该叶子结 点的编码。可以证明，如此得到的必为二进 制前缀编码。

因为，每个字符结点都是叶结点，它们丌可能在根结点到其它字符结 点的路径上，所以一个字符的编码丌可能是另一个字符编码的前缀， 从而保证了译码的非二义性。
如何得到电文总长最短的二进制前缀编码呢？
3）赫夫曼编码
假定每种字符在电文中出现的次数为wi，编码长度为li，则n种字符 的电文总长
w l
k 1
70—79 0.4
80—89 0.3 70≤a<80

《数据结构——C语言描述》第6章：树

《数据结构——C语言描述》第6章：树
Void paintleaf (Btree root) { if (root!=NULL) { if (root ->Lchild==NULL && root ->Rchild==NULL) printf (root ->data); paintleaf (root ->Lchild); paintleaf (root -遍历左子树； （2）访问根结点； （3）中根遍历右子树。 后根遍历二叉树 （1）后根遍历左子树； （2）后根遍历右子树； （3）访问根结点。
先根遍历: -+a*b–cd/ef 中根遍历: a+b*c–d–e/f 后根遍历: abcd-*+ef/-
typedef struct Node { datatype data; struct Node *Lchild; struct Node *Rchild; } BTnode,*Btree;
满二叉树：一棵深度为k且有2k-1个结 点的二叉树称为满二叉树。 完全二叉树：深度为k，有n个结点的 二叉树当且仅当其每一个结点都与深度 为k的满二叉树中编号从1至n的结点一一 对应时，称为完全二叉树。
1 2 4 8 9 10 5 11 12 6 13 14 3 7 15 4 6 2
1 3 5 7
树的度：树中最大的结点的度数即为 树的度。图6.1中的树的度为3。 结点的层次(level)：从根结点算起， 根为第一层，它的孩子为第二层……。 若某结点在第l层，则其孩子结点就在 第l+1层。图6.1中，结点A的层次为1， 结点M的层次为4。 树的高度(depth)：树中结点的最大层 次数。图6.1中的树的高度为4。 森林(forest)：m(m≥0)棵互不相交的 树的集合。

教程和练习题 二叉树的概念及操作 树和森林 哈夫曼树及其应用 第6章 树和二叉树数据结构

教程和练习题 二叉树的概念及操作 树和森林 哈夫曼树及其应用 第6章 树和二叉树数据结构
（称为树根Root）,其余元素 都有且仅有一个前驱，所有 元素可以有零个或多个后继
例如:
A
B
C
D
E
F
GH I J
K
L
M
A( B(E, F(K, L)), C(G), D(H, I, J(M)) )
树根
T1
T2
T3
树的抽象数据类型的定义
ADT Tree{
数据对象 D：D是具有相同特性的数据元素的集合。
M
(从根到结点的)路径：
B
A C
D
由从根到该结点 E F G H I J
所经分支和结点构成 K L
M
结点的层次: 根结点定义为第１层， 根的儿子定义为第２层， 以此类推，记作Ｌ（ｖ）
树的深度： 树中叶子结点所在的最大层次
堂兄弟: 双亲在同一层上的结点
有向树：
(１) 有确定的根；
有序(２树) 树：根和子树根之间为有向关系。
A
B
C
D
E F GH I J
KL
M
树例与特征
描述层次结构，是一种一对多的逻辑关系
社会的组织结构 家族的族谱 计算机中的目录组织
2020/8/20
12
6.1 树的类型定义
6.1 树的逻辑结构及其操作
1.树（Tree) 是一个非空的有限元素的集合， 元素之间具有如下 E F GH I
J
A(B(E,F),C,D(G(J),H,I))
广义表
A B
E F C D G J H I
凹入表示
19
树的概念
结点：一个数据元素及若干指向其子树的分支； 结点的度：结点拥有的子树的数目。 树的度：树内各结点的度的最大值； 叶子（终端结点）：度为0的结点； 分支结点（非终端结点）：度不为0的结点；除根

第6章(树和二叉树)

第6章(树和二叉树)
A B C E D F B A
^ ^
^
C
^ ^
E
D
G
24/106
在n个结点的 三叉链表 中，有n+2个 空指针域
^ ^
G
F
^
^

用链表表示的二叉树中也会存在许多空链域。例如在含有n个 结点的二叉链表中，共有2n个链域，实际用n-1链域（仅有n-1 个分支），还有n+1个空链域。 可以利用这些空链域存储其它有用信息，从而得到另一种链式 存储结构——线索链表。
B＝n1+2n2

因此，N＝B＋1＝n1＋2n2＋1
（6-2)
由式（6-1）和（6-2）得到：
n0+n1+n2=n1+2n2+1

可得 n0＝n2＋1
性质3： 对任何一棵二叉树T，如果其终端结点数为n0，度为2的 结点数为n2，则n0＝n2＋1。
11/106
下面介绍两种特殊形态的二叉树： 满二叉树和完全二叉树。

假设此二叉树的深度为k，则根据性质2及完全二叉树的定义得：
2k-1-1＜n≤2k-1 或 2k-1≤n＜2k

取对数得到: k-1≤ log2n ＜ k ，又因为k是整数，所以有： k＝ log2n ＋1
14/106
性质5： 如果对一棵有n个结点的完全二叉树的结点按层序 编号（从第1层到第log2n +1层，每层从左到右)，则对任 一结点i（1≤i≤n)，有： （1）如果i=1，则结点i无双亲，是二叉树的根；如果i>1， 则其双亲是结点i/2 。 （2）如果2i>n，则结点i为叶子结点，无左孩子；否则，其 左孩子是结点2i。 （3）如果2i＋1>n，则结点i无右孩子；否则，其右孩子是 结点2i＋1。

数据结构——用C语言描述(第3版)教学课件第6章 树与二叉树

数据结构——用C语言描述(第3版)教学课件第6章 树与二叉树

6.2 二叉树 6.2.1 二叉树的定义与基本操作 6.2.2 二叉树的性质 6.2.3 二叉树的存储结构
6.2.1 二叉树的定义与基本操作 定义：我们把满足以下两个条件的树型结构叫做二 叉树（Binary Tree）： （1）每个结点的度都不大于2； （2）每个结点的孩子结点次序不能任意颠倒。
有序树：在树T中，如果各子树Ti之间是有先后次序的，则称为有序树。 森林：m（m≥0）棵互不相交的树的集合。将一棵非空树的根结点删去，树就变成一 个森林；反之，给森林增加一个统一的根结点，森林就变成一棵树。
同构：对两棵树，通过对结点适当地重命名，就可以使两棵树完全相等（结点对应相 等，对应结点的相关关系也像等），则称这两棵树同构。
二叉树的基本结构由根结点、左子树和右子树组成
如图示
LChild Data RChild
Data
LChild RChild
用L、D、R分别表示遍历左子树、访问根结点、遍 历右子树，那么对二叉树的遍历顺序就可以有：
(1) 访问根，遍历左子树，遍历右子树(记做DLR)。 (2) 访问根，遍历右子树，遍历左子树(记做DRL)。 (3) 遍历左子树，访问根，遍历右子树(记做LDR)。 (4) 遍历左子树，遍历右子树，访问根 (记做LRD)。 (5) 遍历右子树，访问根，遍历左子树 (记做RDL)。 (6) 遍历右子树，遍历左子树，访问根 (记做RLD)。
(8) NextSibling（Tree，x）： 树Tree存在，x是Tree中的某个结点。若x不 是其双亲的最后一个孩子结点，则返回x后面的下一个兄弟结点，否则 返回“空”。
基本操作:
(9) InsertChild（Tree，p，Child）： 树Tree存在，p指向Tree 中某个结点，非空树Child与Tree不相交。将Child插入Tree中， 做p所指向结点的子树。

第六章树与二叉树教案 二叉树的类型定义 存储结构 遍历 哈夫曼树与哈夫曼编码

第六章树与二叉树教案 二叉树的类型定义 存储结构 遍历 哈夫曼树与哈夫曼编码
或 2k-1 ≤ n < 2k
即 k-1 ≤ log2 n < k
因为 k 只能是整数，因此， k =log2n + 1
问题：
一棵含有n个结点的二叉树，可能达 到的最大深度和最小深度各是多少？
1
答：最大n,
2
最小[log2n] + 1
第六章 树和二叉树教案
二叉树的类型定义 存储结构 遍历 哈夫曼树与哈夫曼编码
树是常用的数据结构
•家族 •各种组织结构 •操作系统中的文件管理 •编译原理中的源程序语法结构 •信息系统管理 •。。。。
2
6.1 树的类型定义 6.2 二叉树的类型定义
6.2.3 二叉树的存储结构 6.3 二叉树的遍历
二叉树上每个结点至多有两棵子树， 则第 i 层的结点数 = 2i-2 2 = 2i-1 。
性质 2 ：
深度为 k 的二叉树上至多含 2k-1 个 结点（k≥1）。
证明：
基于上一条性质，深度为 k 的二叉
树上的结点数至多为
20+21+ +2k-1 = 2k-1 。
（等比数列求和）
k
k
(第i层的最大结点数) 2i1 2k
i 1
i 1
性质 3 ：
对任何一棵二叉树，若它含有n0 个叶 子结点（0度节点）、n2 个度为 2 的结 点，则必存在关系式：n0 = n2+1。
证明：
设 二叉树上结点总数 n = n0 + n1 + n2 又 二叉树上分支总数 b = n1+2n2
而 b = n-1 = n0 + n1 + n2 - 1 由此， n0 = n2 + 1 。

数据结构 第六章 树和二叉树

数据结构 第六章 树和二叉树

F
G
H
M
I
J
结点F，G为堂兄弟 结点A是结点F，G的祖先
5
树的基本操作
树的应用很广，应用不同基本操作也不同。下面列举了树的一些基本操作： 1）InitTree(&T); 2）DestroyTree(&T); 3）CreateTree(&T, definition); 4）ClearTree(&T); 5）TreeEmpty(T); 6）TreeDepth(T); 7） Root(T); 8） Value(T, &cur_e); 9） Assign(T, cur_e, value); 10）Paret(T, cur_e); 11）LeftChild(T, cur_e); 12）RightSibling(T, cur_e); 13）InsertChild(&T, &p, i, c); 14）DeleteChild(&T,&p, i); 15）TraverseTree(T, Visit( ));
1
2 4 8 9 10 5 11 12 6 13 14 3 7 15 4 6 2
1
3
5 7
证明：设二叉树中度为1的结点个数为n1 根据二叉树的定义可知，该二叉树的结点数n=n0+n1+n2
又因为在二叉树中，度为0的结点没有孩子，度为1的结点有1 个孩子，度为2的结点有2个结孩子，故该二叉树的孩子结点 数为 n0*0+n1*1+n2*2(分支数） 而一棵二叉树中，除根结点外所有都为孩子结点，故该二叉 树的结点数应为孩子结点数加1即：n=n0*0+n1*1+n2*2+1
文件夹1
文件夹n

数据结构课后练习 - 第6章

数据结构课后练习 - 第6章

A 3. 根据树的定义，具有3个结点的树有_______种树形。
二、单项选择题
C 4. 节点前序为ABC的不同二叉树________形态。 A. 3 A. 5 B. 4 B. 6 C. 5 C. 7 D. 6 D. 8 B 5. 具有35个结点的完全二叉树的深度为_________。
三、填空题
结点拥有子树个数 1. 在树的定义中，结点的度是____________________ ； 度为0的结点 叶子结点是____________________ ；树的度是 树中所有结点的最大值 ____________________；树中结点的最大层次称为树 深度/高度 的____________________。 最短 2. 哈夫曼树的带权路径长度_____________的二叉树。 3. 某二叉树的前序遍历序列为DABEC，中序遍历序列为 EBCAD DEBAC，则后序遍历序列为____________________。
① 画出这棵树的形态。
② 写出该树后序遍历的结点访问顺序。
a
b c
后序遍历：
gdbehfca
d
g
e
h
f
5. 设树T的度为4，其中度为1，2，3，4的结点个数分别为4， 2，1，1。问T中有多少个叶子结点？ 利用树的性质：各结点射出的分支总数+1=总结点数
① 树T中，各个结点射出的分支总数： 4×1 + 2×2 + 1×3 + 1×4 = 15
2. 给定一个权集W={4,5,7,8,6,12,18}，请画出相应的哈夫曼 树，并计算其带权路径长度WPL。 60 35 17 8 4 9 5 18 12 6 25 13 7 WPL = 8×3 + (4 + 5)×4 + 18×2 + 12×2 + (6+7)×3 = 159 树型不唯一，但最小WPL值是唯 一的。

Chapter6树和二叉树

Chapter6树和二叉树

证明：由性质1
k
k
∑ ∑ (第i层上的最大结点数)＝ 2i−1
i =1
i =1
＝1＋2＋22＋23＋…＋2k-1
＝ 2k-1
证毕。
性质3：对任一非空的二叉树，叶结点数n0与度为2的 结点数n2之间的关系：n0=n2+1。
证明：(1) 从结点类型： 叶子：个数为n0； 度为1的结点：设个数为n1； 度为2的结点：个数为n2；
void inorder(bnodetype *bt) /*中序遍历以bt为根结点指针的二叉树*/ { if (bt==NULL) return; inorder(bt->lchild); visit(bt); inorder(bt->rchild); }
例：对上述表达式的二叉树表示，进行中序遍历，
链表表示：bnodetype *bt;
例： A
B
bt ∧A
C
D
E
F
B C∧ ∧ D
∧E∧
∧F ∧
(2) 三叉链表
结点结构：
lchild
data parent rchild
bt ∧ A∧
B
C
∧ ∧D
∧E
∧
∧F
∧
6.3 遍历二叉树和线索二叉树
6.3.1 遍历二叉树
z 定义：按一定规律走遍二叉树中每个结点，使得每个结
孩子为第二层，…，若某结点在第 l 层，
则其子树的根就在第 l＋1层。
堂兄弟：其双亲在同一层
A
1
的结点互为堂兄弟。
7. 树的深度(高度)：
B
C
2
树中结点的最大层次。
D E F G H3
8. 祖先和子孙：

数据结构第6章树和二叉树4赫夫曼树及其应用

数据结构第6章树和二叉树4赫夫曼树及其应用

解压缩性能
解压缩性能
赫夫曼树的解压缩过程相对简单，因为其编码过程中已经包含了足够的信息，可以通过解码过程还原 出原始数据。相对于其他压缩算法，赫夫曼树的解压缩速度较快，且不需要额外的存储空间。
解码效率
解码效率是衡量赫夫曼树解压缩性能的重要指标。在实际应用中，解码效率越高，解压缩过程越快， 用户等待时间越短。因此，优化解码算法和实现方式是提高赫夫曼树解压缩性能的关键。
03
赫夫曼树的性能分析
压缩性能
压缩性能
赫夫曼树是一种最优的前缀编码，其编 码长度最短，因此具有较好的压缩性能 。在数据压缩过程中，使用赫夫曼编码 能够有效地减少存储空间，提高数据传 输效率。
VS
编码长度
由于赫夫曼编码是一种变长编码，其编码 长度取决于数据概率的分布情况。在数据 概率分布不均匀的情况下，赫夫曼编码能 够以较短的编码长度表示出现概率较大的 字符，从而优化压缩效果。
动态数据集
研究赫夫曼树在动态数据集上的应用，提高 自适应能力。
多路赫夫曼树
拓展赫夫曼树到多路情况，以适应更广泛的 数据集和应用场景。
应用领域拓展
探索赫夫曼树在其他领域如机器学习、生物 信息学等的应用可能性。
感谢您的观看
THANKS
编码长度
• 编码长度：赫夫曼树的编码长度 最短，这是其最重要的优点之一。 在数据概率分布不均匀的情况下， 赫夫曼编码能够以较短的编码长 度表示出现概率较大的字符，从 而优化压缩效果。同时，赫夫曼 树的编码长度具有前缀性，即任 何一个字符的编码都不是其他字 符编码的前缀，这有助于解码过 程的正确进行。
编码长度非最优
对于某些特定数据集，赫夫曼树的编码长度可 能并非最优。
计算复杂度高

第六章树与二叉树6赫夫曼树及其应用

第六章树与二叉树6赫夫曼树及其应用
2．选取与合并：在F中选取两棵根结点权值最小的树作 为左、右子树，构造一棵新的二叉树，且置新二叉树 根的权值为左、右子树根结点权值之和；
3．删除与加入：从F中删除这两棵树，并将新树加入F； 4．重复 2、3，直到F中只含一棵树为止。这棵树就是所
求的赫夫曼树。
6.5 赫夫曼树及其应用
举例：W＝{2，4，5，3} 赫夫曼树的构造过程
例：构造以W=(5,29,7,8,14,23,3,11)为权的赫夫曼树。
100
42
23
19
11
8
53
147页
58
29
29
14
15
7
8
HT weight parent
0
15
9
2 29 14
37
10
48
10
5 14 12
6 23 13
73
9
8 11 11
98
11
10 15 12
11 19 13
12 29 14
6.5 赫夫曼树及其应用
扩展知识：范式Huffman编码
“静态统计模型”:在编码前统计要编码的信息中所 有字符的出现频率，然后根据统计出的信息建立编码树， 进行编码。这种模型的缺点是：首先，对数据量较大的信 息，静态统计要消耗大量的时间；其次，必须保存统计出 的结果以便解码时构造相同的编码树，或者直接保存编码 树本身，而且，对于每次静态统计，都有不同的结果，必 须分别予以保存，这要消耗大量的空间；再次，静态统计 模型统计出的频率是字符在整个文件中的出现频率，往往 反映不出字符在文件中不同局部出现频率的变化情况，使 用这一频率进行压缩，大多数情况下得不到太好压缩效果， 文件有时甚至在压缩后反而增大了。

数据结构 第六章 树和二叉树6.4

数据结构 第六章 树和二叉树6.4

应 用
从根结点到叶结点之间，沿途路径上的分支组成的“0”
或“1”代码串就是该叶子结点所代表的字符编码，称为
赫夫曼编码。
赫夫曼编码为前缀编码。
三、赫夫曼编码
6.4
赫 例 字符集 D={C,A,S,T, ; }
夫
字符出现频率 w={2,4,2,3,3}
曼
树 及
14 01
其 应 用
6 01 33 T;
8 01
夫 曼
(1)根据给定的n个权值{w1,w2,……,wn}构成n棵二叉树
树 的集合F={T1，T2，……,Tn}，其中每棵二叉树Ti只有一
及 其
个权为wi的结点(根结点，无左右子树)。
应 (2)在F中选取两棵根结点的权值最小的树作为左右子树构 用 造一棵新的二叉树，且置新的二叉树的根结点的权值为其
左、右子树上根结点的权值之和。
c
42 bd
56
c
42
bd
例 w={5, 29, 7, 8, 14, 23, 3, 11}
5 29 7 8 14 23 3 11
29 7 8 14 23 11 8 53
29 29
42
14 15 23 19
7 8 11 8
53
42
58
29 14 23 11 8
15
5 37 8
23 19 29 29 11 8 14 15
29 14 23 15 19 7 8 11 8 53
53
78
100
42
58
29 23 19
29
11 8 பைடு நூலகம்4 15
53 78
23 19 29 29 11 8 14 15 53 78
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
N
bad
pass
一. 概念
路径
6.5 赫夫曼树及其应用
从树中一个结点到另一个结点之间的分 支构成这两个结点间的路径；
路径长度 路径的分支数目称为路径长度；
树的路径长度
从树根到树中其余每个 结点的路径长度之和。
2 1A1
B
C
2
DE
6.5 赫夫曼树及其应用
一. 概念
结点的权 根据需要给结点所赋的值；
9
5
4 52 3
重复第3步
14
9
5
4 52 3
练习：构造以W=（5，4，7，2，5）为权的赫夫曼 树。
547 2 5
23
10
13
6 245 7 5
5 56
7
24
6
10
245 5 7
13
6
7
24
10 55
说明
最优二叉树的左右子树可以互换； 结点权值差别很大时，构成如图所示形状； 所有结点权值一样时，构成完全二叉树形状；
WPL=7+10+6+12=35
6.5 赫夫曼树及其应用
一. 概念
最优二叉树(Huffman树)
即假设有n个权值(w1 ,w2 , … , wn )，构造有一棵n个 叶子结点的二叉树，每个叶
子结点带权值wi 。则带权路 径长度WPL最小的二叉树称
为最优二叉树，又称为赫夫
曼树。
a7 b5 c 2 d4
else if(a<70) score=“pass”; else if(a<80) score=“general”; else if(a<90) score=“good”; else score=“excellent”;
a<60
Y
N
分数 0~59 60~69 70~79 80~89 90~100 比例 0.05 0.15 0.40 0.30 0.10
结点的带权路径长度
从根到该结点的路径长
度与该结点权值的乘积；
2
61 A 1 3
B
C
2
DE
5
2
6.5 赫夫曼树及其应用
一. 概念
树的带权 路径长度
树中所有叶子结点的带权路径 长度之和。记作:
n
WPL= wk lk k =1
其中， Wk代表第k个叶子的权值；
lk代表从根结点到第k个叶子的
路径长度。
2
a7 b5 c 2 d4
55 55
说明
最优二叉树结点数为叶子数的2倍减1。
证明： 由二叉树性质3得： n0=n2+1 故最优二叉树结点数=n0+n2=n0+n0-1=2n0-1
6.5 赫夫曼树及其应用
赫夫曼树的存储
weight parent lchild rchild
权值 双亲 左孩子 右孩子
typedef struct { int weight; int parent, lchild, rchild;
}HTNode, *HuffmanTree;
//动态分配数组存储赫夫曼树
赫夫曼树的构造算法
void HuffmanTree(HuffmanTree &HT, int * w, int n){ //w存放n个字符的权值，构造赫夫曼树HT if (n<=1) return; m=2* n-1; //m为赫夫曼树总结点数 HT=(HuffmanTree)malloc((m+1) * sizeof(HTNode)); for (p=HT+1, i=1; i<=n; ++i, ++p, ++w) * p={ * w, 0, 0, 0}; for (; i<=m; ++i, ++p) * p={ 0, 0, 0, 0}; for (i=n+1; i<=m; ++i) { //建赫夫曼树 //在HT[1..i-1] 选择parent为0且weight最小的两个结点，其
2．选取与合并：在F中选取两棵根结点权值最小的树作 为左、右子树，构造一棵新的二叉树，且置新二叉树 根的权值为左、右子树根结点权值之和；
3．删除与加入：从F中删除这两棵树，并将新树加入F； 4．重复 2、3，直到F中只含一棵树为止。这棵树就是所
求的赫夫曼树。
6.5 赫夫曼树及其应用
举例：W＝{2，4，5，3} 赫夫曼树的构造过程
序号分别为s1和s2。 Select(HT, i-1, s1, s2); HT[s1]. parent =i; HT[s2].parent=i; HT[i].lchild=s1; HT[i].rchild=s2; HT[i].weight=HT[s1].weight+HT[s2].weight;} }
6.5 赫夫曼树及其应用
一. 概念
最优二叉树的特点
1. 权值越大的叶子结点越靠近根结点，而权值 越小的叶子结点越远离根结点。
2. 只有度为0（叶子结点） 和度为2（分支结点）的 结点，不存在度为1的结 点。
a7 b5
2
c
d4
6.5 赫夫曼树及其应用
二.最优二叉树的构造
赫夫曼算法步骤：
1．初始化：根据给定的n个权值 ，构造n棵二叉树集合 F，其中每棵二叉树中只有一个带权为wi的根结点， 其左右子树均为空；
61 A 1 3
B
C
2
DE
5
2
6.5 赫夫曼树及其应用
一. 概念
树的带权路径长度
例：有3棵二叉树，都有4个叶子结点a、b、c、d，且带 相
同权值7、5、2、4，3棵树的带权路径长度分别为：
7
a
5
b
c
2
d4
WPL=14+10+4+8=36
2
c
4
d a7 b5
WPL=8+21+15+2=46
a7 b5 c 2 d4
数据结构
第六章 树和二叉树
6.1 树的定义和基本术语 6.2 二叉树 6.3 遍历二叉树和线索二叉树 6.4 树和森林 6.5 赫夫曼树及其应用
6.5 赫夫曼树及其应用
编制一个将学生的百分制成绩转换成五分制 成绩的程序。其中若成绩低于60分，记为“bad”;
成绩介于60和69之间，记为“pass”;成绩介于70和79之间 的，记为“general”;成绩介于80和89之间的，记为 “good”;成绩高于90分的，记为“excellent”。 if (a<60) score=“bad”;
第1步：初始化
24 5 3
第2步：选取与合并 第3步：删除与加入
5 23 45 5
23
6.5 赫夫曼树及其应用
举例：W＝{2，4，5，3} 赫夫曼树的构造过程
重复第2步
45 5
23 9
重复第3步
45
9
5
4 52 3
6.5 赫夫曼树及其应用
举例：W＝{2，4，5，3} 赫夫曼树的构造过程
重复第2步
bad
a<70
Y
N
pass
a<80
Y
10000(1×0.05+2×0.15+3×0.4+4×0.4) =31500
N
general a<90
Y
N
good excellent
10000(2×0.4+2×0.3+2×0.1+3×0.2)
=22000
Y
a<60
Y
a<80
Y
N
a<70
N
a<90
Y
N
general good excellent