当前位置：文档之家 › 材料力学课件例题

材料力学课件例题

  • 格式：docx
  • 大小：1.64 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

材料力学例题

材料力学例题
C
0.75m 1m
A
D 1.5m
B
F
横梁BC为刚杆，自重Q＝2KN，力P＝10KN可在横 梁BC上自由移动。AB杆的许用应力为[σ]=100MP ａ，设计AB杆的横截面面积。如果AB杆采用直径 为10毫米的细丝，需要几根？
P C
30°
Ｂ
• [例] 长为 L=2m 的圆杆受均布力偶 m=20Nm/m 的作用，如图，若杆的内外径之比为 =0.8 ，
例题 空心圆杆AB和CD杆焊接成整体结构，受力如图.AB杆的外径 D=140mm，内外 径之比α= d/D=0.8，材料的许用应力[] = 160MPa。试用第三强度理论校核AB杆的 强度。 解:（1）外力分析 将力向AB杆的B截面形心简化得
10kN
0.8m A
B D
F 25kN
M e 15 1 . 4 10 0 . 6 15 kN m
G=80GPa ，许用剪应力 []=30MPa，试设计杆
的外径；若[]=2º /m ，试校核此杆的刚度，并
求右端面转角。
[例题] 某传动轴设计要求转速n = 500 r / min，输入功率P1 = 500 马力， 输出功率分别 P2 = 200马力及 P3 = 300马力，已 知：G=80GPa ，[ ]=70M Pa，[ ]=1º /m ，试确定： ①AB 段直径 d1和 BC 段直径 d2 ？ ②若全轴选同一直径，应为多少？ ③主动轮与从动轮如何安排,轴的受力合理？ P2 A 500 B 400 P3 C
y Me A x B l/2 F1
F2
D F2 D M e C ( F1 F 2 ) 2 2 20 F2 kN 3 F 20kN
轴产生扭转和垂直纵向对称面内的平 面弯曲

材料力学(资料例题)

材料力学(资料例题)

材料力学（一）轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。

为设计既安全可靠又经济合理的构件，提供有关强度、刚度与稳定性分析的基本理论与方法。

【重点、难点】重点考察基本概念，掌握截面法求轴力、作轴力图的方法，截面上应力的计算。

【内容讲解】一、基本概念强度——构件在外力作用下，抵抗破坏的能力，以保证在规定的使用条件下，不会发生意外的断裂或显著塑性变形。

刚度——构件在外力作用下，抵抗变形的能力，以保证在规定的使用条件下不会产生过分的变形。

稳定性——构件在外力作用下，保持原有平衡形式的能力，以保证在规定的使用条件下，不会产生失稳现象。

杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件，称为杆件或简称杆。

根据轴线与横截面的特征，杆件可分为直杆与曲杆，等截面杆与变截面杆。

二、材料力学的基本假设工程实际中的构件所用的材料多种多样，为便于理论分析，根据它们的主要性质对其作如下假设。

(一)连续性假设——假设在构件所占有的空间内均毫无空隙地充满了物质，即认为是密实的。

这样，构件内的一些几何量，力学量(如应力、位移)均可用坐标的连续函数表示，并可采用无限小的数学分析方法。

(二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。

按此假设通过试样所测得的材料性能，可用于构件内的任何部位(包括单元体)。

(三)各向同性假设——沿各个方向均具有相同力学性能。

具有该性质的材料，称为各向同性材料。

综上所述，在材料力学中，一般将实际材料构件，看作是连续、均匀和各向同性的可变形固体。

三、外力内力与截面法(一)外力对于所研究的对象来说，其它构件和物体作用于其上的力均为外力，例如载荷与约束力。

外力可分为：表面力与体积力；分布力与集中力；静载荷与动载荷等。

当构件(杆件)承受一般载荷作用时，可将载荷向三个坐标平面(三个平面均通过杆的轴线，其中两个平面为形心主惯性平面)内分解，使之变为两个平面载荷和一个扭转力偶作用情况。

材料力学课件复习习题

材料力学课件复习习题

例题 5.1
F A A
A
求图所示悬臂梁A端的挠度与转角。
x
B
x
l
y
例题 5.2
求图所示悬臂梁B端的挠度与转角。
B
A
x
l
x
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
q
A
B
EI z
C
x
k
l 2
（4）在弯扭组合变形圆截面杆的外边界上，各点的应力状 态都处于平面应力状态。（ ）
（5）在弯曲与扭转组合变形圆截面杆的外边界上，各点主 应力必然是σ1＞ σ2 ，σ2＝0，σ3＜0 。 （ ）
（6）在拉伸、弯曲和扭转组合变形圆截面杆的外边界上， 各点主应力必然是σ1 ＞0， σ2＝0， σ3＜0 。（ ）
Me
2
1
d
D
例题 4.6
20 kN
X1
图示外伸梁,,试作剪力图和弯矩图.
10kN m
X2
40 kN m
A
35kN
B
1m
4m
25kN
例题
4.9
作图示梁的内力图
3kN
D
4.5kN m
A
2kN m
B E
C
FA 10kN 1m 2m
2m
FB 2kN 1m
kN
kNm
例题
4.10
4kN m
A
B
96.4 C
l 2
l 2
200 50
z
例题 4.30
q
A
简支梁如图所示，试求梁的最底层纤维的总伸长。

材料力学习题(PPT)共17页文档

材料力学习题(PPT)共17页文档
2 Pa 3
3E I
3
1
2l 1
Pll ) Pll l
2
3 GIp
fc

2Pl3 3EI
Pl3 GIp
T图
施加的单位力和P同位置、同方向， 所以M0c图、T0c图和M图、T图形 状一样
例7：图示开口刚架，EI=const。求沿P力作用线方向的相对 线位移 ΔAB 。
解：
AB2E Pa I38 11 322 12 1
2F
压
画出AC的M图，DB 的轴力图。
F
FN
FN
2 2F
A
F C 2.加单位载荷m0=1，画内力图
B
FN a
1 2/2
2 a
压
45º
D
（M）
2 2
FN
FN
2 2 FN
m0=1
1
画出AC的 M 图，DB 的FN图。
FN
2
FN
a
3.图乘法
(M)
Fa
(FN)
M
2 2F
1
2 2F 2a 2
C
例3：图示梁的抗弯刚度为EI，试求D点的铅垂位移。
vC

3 EI
Pa2 2
2a
3
Pa 3 EI
例 题4
求C处的线位移。
解： 1.画内力图
BC段为弯曲（x 轴为 中性轴）
AB段为弯曲（z 轴为 中性轴）+扭转
y
x z
Al
ql 2 2
(MT)
ql 2
qC l
B
ql 2 2
2.求 cx ,应在C处沿x方向加单位力。
qa A 2

材料力学复习习题(可打印版)ppt课件

材料力学复习习题(可打印版)ppt课件
r 4 1 2 3
两者均小于 []=170MPa 。可见，无论采用第三或是 第四强度理论进行强度校核，该结构都是安全的。
qL 2
L=3m
qL 2
+
x
M
qL 8
2
qL 3600 3 F 540 N S max 2 2
x
2 2 qL 3600 3 M 405 N max 8 8
+
q=3.6kN/m
求最大应力并校核强度
M M 6 4050 max 6 max max 2 2 W bh 0 . 12 0 . 18 z
件，[]=40MPa,试用第一强度理论校核杆的强度。 T P A T A A P
解：危险点A的应力状态如图：
P 4 50 3 10 6 . 37 MP 2 A 0 . 1


2
2
T 16 7000 35 . 7 MPa 3 W 0 . 1 n
sin 2 cos 2 xy
2、求主应力、主平面
主应力： m ax
m in
x y
2
(
x y2
2
) xy
2
80 . 7 ( MPa ), 0 ,3 60 . 7 ( MPa ) 1 2
主平面位置：

80 . 7 ( MP ) 40 60 40 60 2 2 ( ) ( 50 ) 60 . 7 ( MP ) 2 2
F 2 F A N 1 1 1
3、根据水平杆的强度，求许可载荷 查表得水平杆AB的面积为A2=2×12.74cm2
F F cos 3 F N 2 N 1

工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解

工程力学---材料力学(第七章- 梁弯曲时位移计算与刚度设计)经典例题及详解

得： D 0
Pl 2 得： C 16
AC段梁的转角方程和挠曲线方程分别为：
P 2 2 (4 x l ) 16 EI Px y (4 x 2 3 l 2 ) 48 EI
y
P
B
A
x
l 2
C
l 2
x
最大转角和最大挠度分别为：
max A B
ymax y
q 7qa 8k 384 EI
3
q/2
B C
q/2
A B C
顺时针
q/2
例16：图示梁Ｂ处为弹性支座，弹簧刚 度
EI k 求C端挠度fC。 2a 3
q
A
EI k
B
C
2a
a
解：(1)梁不变形，仅弹簧变形引起的C点挠度为 4 3 qa 3qa B处反力=qa fC 1 2 k EI
q
B
x
l
由边界条件： x 0时，y 0
x l时，y 0
得：
ql 3 C , D0 24
梁的转角方程和挠曲线方程分别为：
y
q 2 3 3 (6lx 4 x l ) 24 EI
q
x
A qx y (2lx 2 x 3 l 3 ) 24 EI
ql 3 24 EI
A a a
q
B C
a
qa 12 EI
顺时针
3 3
P=qa
A B
P=qa
m=qɑ²/2
qa qa C B 6 EI 4 EI
4
顺时针
B
q
C
qa 5qa fC B a 8EI 24 EI

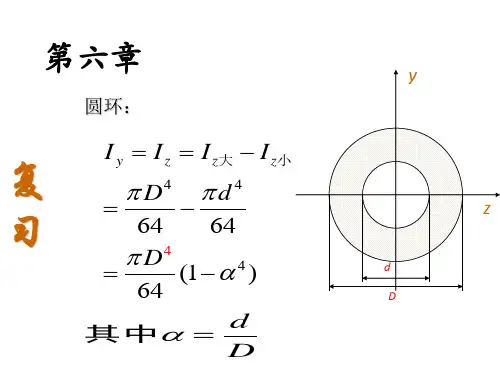
工程力学--材料力学(第五、六章)经典例题及讲解

工程力学--材料力学(第五、六章)经典例题及讲解

P
A
0.5 m
C D
0.4 m 1m
B
20
40
解：C点的应力 σ C = E ε = 200 × 10 3 × 6 × 10 − 4
= 120M Pa
C截面的弯矩
M C = σ C W z = 640 N ⋅ m
由 M C = 0.5 R A = 0.5 × 0.4 P = 0.2 P = 640 N ⋅ m 得 P = 3.2kN
度减小一半时，从正应力强度条件考虑， 该梁的承载能力将是原来的多少倍？ 解： 由公式
σ max
M max M max = = 2 Wz bh 6
可以看出：该梁的承载能力将是原来的2 可以看出：该梁的承载能力将是原来的2倍。
例4：主梁AB，跨度为l，采用加副梁CD AB，跨度为l 采用加副梁CD
的方法提高承载能力， 的方法提高承载能力，若主梁和副梁材料 相同，截面尺寸相同， 相同，截面尺寸相同，则副梁的最佳长度 a为多少？ 为多少？
2 2
2
bh b( d − b ) Wz = = 6 6
2 2 2
∂ Wz d 2 b 2 = − =0 ∂b 6 2
d 由此得 b = 3
d
2 2
h
h = d −b =
h = 2 ≈3:2 b
2 d 3
b
例12:跨长l =2m的铸铁梁受力如图示,已知材料许用拉、 12:跨长l =2m的铸铁梁受力如图示 已知材料许用拉、 的铸铁梁受力如图示,
10 kN / m
200 2m 4m 100
10 kN / m
200
2m
Fs( kN ) 25 Fs(
45 kN
4m
100

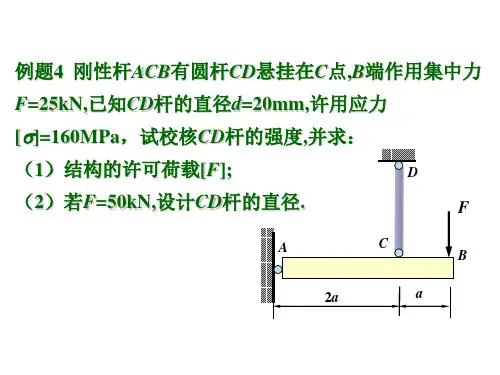
材料力学例题

材料力学例题

B
DC
1
3
2
A
B
DC
1
3
2
A
1 32
A
Δl1
Δl3
F
A'
A'
变形几何方程为 Δl1 Δl3 cos
物理方程为
Δl1
FN1l1 EA1
Δl3
FN3l cos
E3 A3
（3）补充方程
FN1
FN 3
EA E3 A3
cos2
（4）联立平衡方程与补充方程求解 B
DC
FN1 FN2
FN1 cos FN2 cos FN3 F 0
d
[] = 60MPa ,许用挤压应力为 [bs]= 200MPa .试校核销钉的
强度.
F
B
A
d1
d d1
F
解: （1）销钉受力如图b所示
F
剪切面
F
d
F
F
2
2
挤压面
d
B
A
d1
d d1
F
（2）校核剪切强度
剪切面
F
由截面法得两个面上的剪力
FS
F 2
d
剪切面积为 A d 2
4
FS 51MPa
3
2
1
l
a
a
B
C
A
F
解：（1） 平衡方程
Fx 0 Fx 0 l
3 a
2 a
1
Fy 0
B
C
A
FN1 FN2 FN3 F 0
MB 0
F FN3
FN2
FN1
3 a
2 a
1

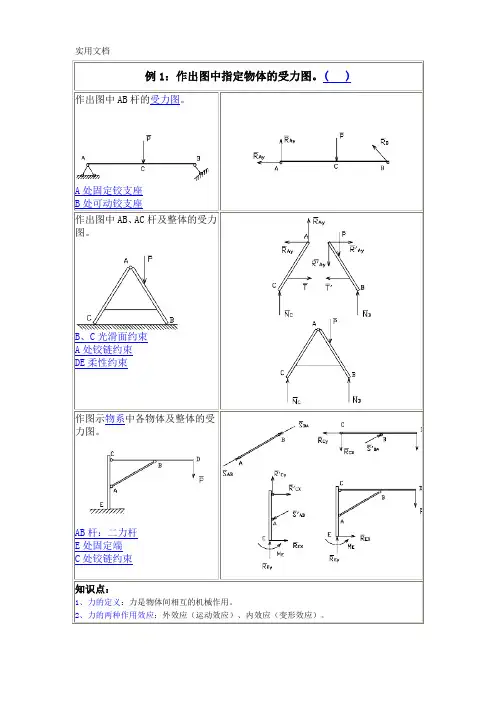
工程力学材料力学-知识点-及典型例题

工程力学材料力学-知识点-及典型例题

作出图中AB杆的受力图。

A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。

B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。

AB杆：二力杆E处固定端C处铰链约束（1）运动效应：力使物体的机械运动状态发生变化的效应。

（2）变形效应：力使物体的形状发生和尺寸改变的效应。

3、力的三要素：力的大小、方向、作用点。

4、力的表示方法：（1）力是矢量，在图示力时，常用一带箭头的线段来表示力；（注意表明力的方向和力的作用点！）（2）在书写力时，力矢量用加黑的字母或大写字母上打一横线表示，如F、G、F1等等。

5、约束的概念：对物体的运动起限制作用的装置。

6、约束力（约束反力）：约束作用于被约束物体上的力。

约束力的方向总是与约束所能限制的运动方向相反。

约束力的作用点，在约束与被约束物体的接处7、主动力：使物体产生运动或运动趋势的力。

作用于被约束物体上的除约束力以外的其它力。

8、柔性约束：如绳索、链条、胶带等。

(1)约束的特点：只能限制物体原柔索伸长方向的运动。

(2)约束反力的特点：约束反力沿柔索的中心线作用，离开被约束物体。

（）9、光滑接触面：物体放置在光滑的地面或搁置在光滑的槽体内。

（1）约束的特点：两物体的接触表面上的摩擦力忽略不计，视为光滑接触面约束。

被约束的物体可以沿接触面滑动，但不能沿接触面的公法线方向压入接触面。

（2）约束反力的特点：光滑接触面的约束反力沿接触面的公法线，通过接触点，指向被约束物体。

（）10、铰链约束：两个带有圆孔的物体，用光滑的圆柱型销钉相连接。

约束反力的特点:是方向未定的一个力；一般用一对正交的力来表示，指向假定。

（）11、固定铰支座（1）约束的构造特点：把中间铰约束中的某一个构件换成支座，并与基础固定在一起，则构成了固定铰支座约束。

（2）约束反力的特点：固定铰支座的约束反力同中间铰的一样，也是方向未定的一个力；用一对正交的力来表示，指向假定。

()12、可动铰支座（1）约束的构造特点把固定铰支座的底部安放若干滚子，并与支撑连接则构成活动铰链支座约束，又称锟轴支座。

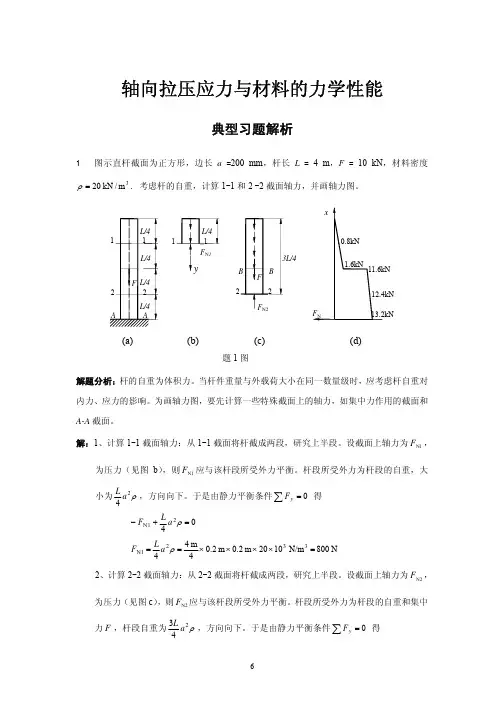
材料力学典型例题与详解(经典题目)

材料力学典型例题与详解(经典题目)
G = [σ ]A(l) − F
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18，或 1.33∶1.09∶1。 讨论：计算结果表明，采用等强度石柱时最节省材料，这是因为这种设计使得各截面的正应 力均达到许用应力，使材料得到充分利用。 3 滑轮结构如图，AB 杆为钢材，截面为圆形，直径 d = 20 mm ，许用应力 [σ ] = 160 MPa ，BC 杆为木材，截面为方形，边长 a = 60 mm ，许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解：1、计算 1-1 截面轴力：从 1-1 截面将杆截成两段，研究上半段。设截面上轴力为 FN1 ，
为压力（见图 b），则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重，大

材料力学讲课例题

材料力学讲课例题
则扭矩图如右下图所示， 由此可知，合理布置荷载 可以降低内力的最大值。
例4.2 在图示受扭圆轴横截面上的切应力 分布图中，正确的结果是( )。
答案 D
3、扭转变形（扭转角）
MT
MTl
GI p
GI p
例4.3 已知扭转刚度GIP，扭转求轴两端面的
相对扭转角（写结果）
例4.4 实心圆轴受扭，若将轴的直径减小一半时，则圆 轴的扭转角是原来的( ) (A) 2倍 (B) 4倍 (C) 8倍 (D) 16倍
解：（a）、(c) 、(f)是平面弯曲。 (b)、(d) 是斜弯曲。 (e) 是斜弯曲与扭转组合变形。
例8.3 斜支梁AB如图示，确定梁的变形，有( ) (A) AB (B) AC段弯曲变形，CB (C) AC段压缩与弯曲，BC (D) AC段压缩与弯曲，BC
答案 D
例8.4 图示结构中，杆的AC部分将发生的变形为( )
例2.2 已知图示杆的轴力 图， 请选择该杆相应的载荷图。
答案 D
例2.3 杆长l、截面积A及弹性模量E已知。求悬 挂直杆由纵向均匀分布荷载q引起的应力和纵向 变形。
解：距下端为x的横截面 m-m，轴力为N(x)＝qx， 轴力图如图（b)
最大轴力 Nmax＝ql
最大正应力 max ql / A
N
2
M
2
3
MT
2
A W 2W
N
2
M
2
3
MT
Pa 2
2a a2 6
2Pa2
答：增加7倍， 选答案B
例8.6 圆杆横截面积为A，截面惯性矩为W，受到 轴力N、扭矩MT和弯矩M的共同作用（拉、弯、 扭组合变形），第四强度理论的相当应力为( )。

材料力学复习 PPT课件

材料力学复习 PPT课件

M c y1 Iz
[sc ]
y1 y2
[st ] [s c ]
20 y
20
F
q＝F/b
A
CB
D
b
b
b
Fb/2
C截面的强度条件由最大的拉应
力控制。
Fb/4
s t max

MC y1 Iz

( F 2) 0.134 4 5493108

30 106
F 24.6 kN
B截面
s t max

T 0.2d 3
T
1930
d 3 0.2tmax 3 0.2 66.7 106 0.053 m 5.3 cm
A空 8.5 0.303 A实 28.2
可见, 采用钢管时, 其重量只有实心圆 轴的30％, 耗费的材料要少得多。
例: 作内力图。已知F1＝F2＝2 kN, Me＝10 kN·m, q＝1 kN/m。
s t max

My1 Iz
s cmax

My2 Iz
60 280
sc max
Oz
st max
s t max y1 [s t ] 1 s c max y2 [s c ] 3
y1 1 y2 3
d
60 280
y
y2
y1 y2 280 mm
由上两式确定出
Oz
y1
y
y y2 210 mm
80
120 20
y1
B截面
st

M B y1 Iz

4000 0.052 763108
27.2106 Pa 27.2 MPa [s t]

材料力学力法典型例题解

材料力学力法典型例题解

l
q
RB
B
l q
X1
B Δ1F
B δ11
1
Example 2 .画图示钢架旳弯矩图，EI=const .
P
a
B
A
CP B
A
a
CP
a
B
C
B
C
X1
M
1
M
A
A
Pa
a
解 : 1）选图示相当系统（：一次超静定）
2）力法方程：
X 0
11 1
1P
3）利用图乘法求系数:
a
P
a
B
A
a
C
P
a
B
C
B
C
M
1
M
A
A
PPal
X1
2）力法方程
F
X 0
11 1
1P
3）图乘法求系数
11
2 EI
(1 2
aa
2 3
a)
2a3 3EI
1P
2 EI
(1 2
a
Fa
2 3
a)
a a
2Fa3
M
3EI
4）解得:
1
C
X1
1P
11
F
1
C
Fa
X1=1 Fa
F
1
M
F
F1 C
F
Example 1 . 求RB (EI=const.).
解: 1）选图示相当系统 （一次超静定）
B
CP
P
P
a
a
X1
a a
X1 1
A
Pa
解：1）选图示静定基及相当系统

材料力学--外力偶矩的计算 扭矩和扭矩图 ppt课件

材料力学--外力偶矩的计算 扭矩和扭矩图 ppt课件
可见在载荷相同的条件下，空心轴的重量仅为实心轴的31% 。
ppt课件 22
§3.4 圆轴扭转时的应力
例题3.4 已知：P＝7.5kW, n=100r/min,最大切应力不 得超过40MPa,空心圆轴的内外直径之比 = 0.5。二轴长度相同。
求: 实心轴的直径d1和空心轴的外直径D2；确 定二轴的重量之比。 解： 首先由轴所传递的功率计算作用在轴上的扭矩
d1
A
M e1
C
M e2
d2
B M e3
解：1.外力偶矩
P 400 1 T1 M e1 9549 9549 7640 N m n 500 240 T2 M e 3 T1 4580N m 400
ppt课件 31
§3.5
2.扭矩图
圆轴扭转时的变形
d1
A
M e1
d 0.945 D Wt 0.2 D3 (1 4 ) 0.2 8.93 (1 0.9454 ) 29 cm3

（2） 强度校核
max
T 1930 6 66.7 10 Pa 6 Wt 29 10 66.7MPa [ ]ppt 课件 70MPa
3 2
d2＝23 mm
长度相同的情形下，二轴的重量之比即为横截面面积之比：
A1 d 1 45 10 2 ＝ 1.28 2 3 2 A2 D2 1 46 10 1 0.5
ppt课件 24
§3.4 圆轴扭转时的应力
例题3.5 已知：输入功率P1＝14kW,P2= P3=P1/2， n1=n2=120r/min, z1=36,z3=12;d1=70mm, d 2=50mm, d3=35mm.[]=30MPa。.

材料力学课件例题

材料力学课件例题

例：重力坝受水的压力如图。

设水深为h ，水的密度为ρ ，试求水压力简化的结果。

解: 坐标系如图所示，以O 点为简化中心将平面平行力系向点简化 力系的主矢力系对O 点的主矩 力系进一步简化为一合力 合力作用线距点的距离为 例：悬臂式简易起重机简化为图示结构。

AB 是吊车梁，BC 是钢索，A 端支承可简化为铰链支座。

设已知电动葫芦和重物其重P = 10 kN ，梁自重W = 5 kN ，θ= 30o 。

试求钢索BC 和铰链A 的约束力，及钢索受力的最大值。

解：以吊车梁AB 为研究对象，受力图和坐标系如图所示。

电动葫芦距A 处距离为x ，建立平衡方程d d F gy y=ρ2R1d 2hx F gy y gh '∴=-=-⎰ρρR0y F '=2R R R 12x F F F gh ''===-ρO R 23M OO h F '=='3O 01d 3h M y gy y gh =-⋅=-⎰ρρA ()0:M F =∑B sin 02lW P x F l -⋅-⋅+⋅=θB ()0:M F =∑A ()02y lP l x W F l ⋅-+⋅+⋅=0:xF=∑A B cos 0x F F -=θ解得：例：试求图示悬臂固定端 A 处的约束力。

其中q 为均布载荷集度，单位为kN/m ，设集中力F = ql ，集中力偶矩M = ql 2。

解：以梁AB 为研究对象，受力图和坐标系如图所示。

建立平衡方程解得：例：边长为a 的等边三角形平板 ABC 在铅垂平面内，用三根沿边长方向的直杆铰接如图所示。

BC 边水平，三角形平板上作用一已知力偶，其力偶矩为M 。

三角形平板重为P ， 杆不计自重。

试求三杆多三角形平板的约束力。

解：以三角形平板ABC 为研究对象，受力图和坐标系如图所示。

建立平衡方程A 3()2xP W F x l =+A ()2y l x WF P l -=-+B 2P F x Wl =+Bmax 225kNF P W ∴=+=0:x F =∑0Ax F =0:y F =∑20Ay F q l F -⋅+=A()0:M F =∑A 220M q l l M F l -⋅⋅++⋅=A 0x F =A y F ql=2A M ql =A ()0:M F =∑C 0F M -=B ()0:M F =∑A 022aF P M ⋅-⋅-=C ()0:M F =∑B 022a F a P M ⋅+⋅-=解得： 例：塔式起重机简图如图所示。

材料力学经典例题

材料力学经典例题

Ip R
称为抗扭截面 系数(模量 模量)， 系数 模量 ， 单位： 单位：mm3。
Nm mm
3
MT = W p
=10 MPa
3
五、Ip和Wp公式
π D4
32
工程上采用空心截面构件：提高强度， 工程上采用空心截面构件：提高强度，节约 材料， 材料，重量轻 结构轻便，应用广泛。 结构轻便，应用广泛。
Ip =
例题2.4 例题2.4 油缸盖与缸体采用6个螺栓连接。已知油缸内径 油缸盖与缸体采用6个螺栓连接。 D=350mm，油压p=1MPa 螺栓许用应力[σ]=40MPa p=1MPa。 [σ]=40MPa， D=350mm，油压p=1MPa。螺栓许用应力[σ]=40MPa， 求螺栓的内径。 求螺栓的内径。 解： 油缸盖受到的力 F = D 2 p
目录
FN 1 = 2 F1 ≤ [σ ] A1
失效、 §2.7 失效、安全因数和强度计算
3、根据水平杆的强度，求许可载荷 根据水平杆的强度， 查表得水平杆AB的面积为A2=2×12.74cm2 =2×
FN 2 = − FN 1 cos α = − 3F
FN 2 = 3F2 ≤ [σ ] A2
FN 1
（kN·m） ）
MT
2. 校核强度
MT1 10×103 ×16 ×103 = 50.9MPa＜ [τ] (τmax )1 = W = π×1003 p1
MT2 3×103 ×16 τmax ) 2 = = ×103 = 70.7 MPa ＞ [τ] ( Wp2 π×603
MT1 180 10×103 ×32 180 ⋅ = ⋅ = 0.7 o m ＜[θ] θ1 = GIp1 π 80×109 ×π×1004 ×10−12 π MT2 180 3×103 ×32 3 180 ⋅ = ×10 ⋅ = 1.7 o m ＞[θ] θ2 = GIp2 π 80×π×604 π
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例：重力坝受水的压力如图。

设水深为h ，水的密度为ρ ，试求水压力简化的结果。

解: 坐标系如图所示，以O 点为简化中心将平面平行力系向点简化 力系的主矢力系对O 点的主矩 力系进一步简化为一合力 合力作用线距点的距离为 例：悬臂式简易起重机简化为图示结构。

AB 是吊车梁，BC 是钢索，A 端支承可简化为铰链支座。

设已知电动葫芦和重物其重P = 10 kN ，梁自重W = 5 kN ，θ= 30o 。

试求钢索BC 和铰链A 的约束力，及钢索受力的最大值。

解：以吊车梁AB 为研究对象，受力图和坐标系如图所示。

电动葫芦距A 处距离为x ，建立平衡方程d d F gy y=ρ2R1d 2hx F gy y gh '∴=-=-⎰ρρR0y F '=2R R R 12x F F F gh ''===-ρO R 23M OO h F '=='3O 01d 3h M y gy y gh =-⋅=-⎰ρρA ()0:M F =∑B sin 02lW P x F l -⋅-⋅+⋅=θB ()0:M F =∑A ()02y lP l x W F l ⋅-+⋅+⋅=0:xF=∑A B cos 0x F F -=θ解得：例：试求图示悬臂固定端 A 处的约束力。

其中q 为均布载荷集度，单位为kN/m ，设集中力F = ql ，集中力偶矩M = ql 2。

解：以梁AB 为研究对象，受力图和坐标系如图所示。

建立平衡方程解得：例：边长为a 的等边三角形平板 ABC 在铅垂平面内，用三根沿边长方向的直杆铰接如图所示。

BC 边水平，三角形平板上作用一已知力偶，其力偶矩为M 。

三角形平板重为P ， 杆不计自重。

试求三杆多三角形平板的约束力。

解：以三角形平板ABC 为研究对象，受力图和坐标系如图所示。

建立平衡方程A 3()2xP W F x l =+A ()2y l x WF P l -=-+B 2P F x Wl =+Bmax 225kNF P W ∴=+=0:x F =∑0Ax F =0:y F =∑20Ay F q l F -⋅+=A()0:M F =∑A 220M q l l M F l -⋅⋅++⋅=A 0x F =A y F ql=2A M ql =A ()0:M F =∑C 0F M -=B ()0:M F =∑A 022aF P M ⋅-⋅-=C ()0:M F =∑B 022a F a P M ⋅+⋅-=解得： 例：塔式起重机简图如图所示。

已知机架重量W ，作用线距右轨 B 的距离 e ，载重W 1 离右轨 B 的最远距离 l ，平衡物重为W 2 ，离左轨 A 的距离 a ，轨距 b 。

要使起重机在空载和满载且载重W 1 在最远处时均不致翻倒，试确定平衡物重W 2 。

解：空载时起重机绕 A 点向左翻倒，F B = 0 。

所以空载时起重机不翻倒的条件是F B ≥ 0。

解得： 满载时起重机绕 B 点向右翻倒，此时F A = 0 。

所以满载时起重机不翻倒的条件是F A ≥0。

解得例：图所示三角形平板 A 点为铰链支座，销钉 C 固定在杆DE 上，并与滑道光滑接触。

不计各构件重量，试求铰链支座 A 和 D 约束力。

解：以三角形平板 ABC 为研究对象，受力图和坐标系如图所示。

建立平衡方程A F =B F =-C F =A()0:MF =∑B 2()0F b W e b W a ⋅-⋅++⋅=2B ()W e b W a F b +-=2()W e b W a+∴≤B()0:MF =∑A 21()0F b W a b W e W l -⋅+⋅+-⋅-⋅=21A ()W a b We W lF b+--=12We W l W a b+∴≥+A ()0:M F =∑C 0.21000.140F ⨯-⨯=0:x F =∑A C 100sin 0x F F +-=α0:yF =∑A C cos 0y F F +=α由几何关系可得 解得以杆 DE 为研究对象，受力图和坐标系如图所示。

建立平衡方程 解得例：承重框架如图所示，A 、D 、E 均为铰链，各杆件和滑轮的重量不计。

试求A 、D 、E 点的约束力。

解：以整个刚体系统为研究对象，受力图和坐标系如图所示。

建立平衡方程解得： 以杆DE 为研究对象，受力图和坐标系如图所示。

建立平衡方程解得： sin 0.6=αcos 0.8=αA 58Nx F =-A 56Ny F =-C 70NF =E()0:M F =∑D C0.2sin 0.080x F F '⨯+⨯=α0:yF =∑D Ccos 0y F F α'-=D 16.8Nx F =-D 56Ny F =A ()0:M F =∑E 2000.250.20x F -⨯-⨯=0:x F =∑A E 0x x F F +=0:yF =∑A E 2000y y F F +-=A 250Nx F =E 250Nx F =-D ()0:M F =∑0:x F =∑0:yF =∑E E 0.20.30.150x y F F F -⨯-⨯+⨯=D E 0x x F F F +-=D E 0y y F F +=E 266.7Ny F =D 450Nx F =D 266.7Ny F =-A 66.7Ny F ∴=-例：结构如图所示。

已知AB = BC = 1m ，DK = KE ，F = 1732kN ，W = 1000kN ，各杆重量不计，试求结构的外约束力。

以杆DE 为研究对象，受力图和坐标系如图所示。

建立平衡方程解得： 以杆AC 为研究对象，受力图和坐标系如图所示。

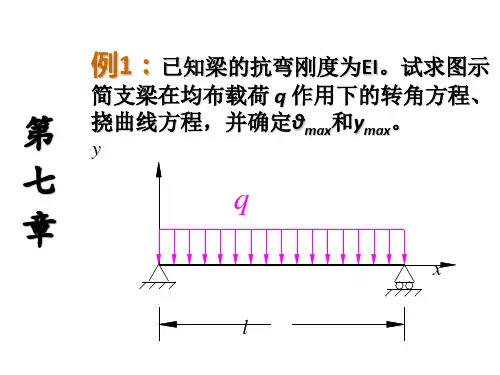
建立平衡方程解得： 例：图所示构架由杆AC 、CE 及 BH 铰接而成。

杆CE 和 E 端用滚子搁置在光滑面上，杆BH 水平，在H 点作用一铅垂力F 1 = 1kN 。

销钉C 上作用一水平力F 2 = 600N 和一铅垂力F 3 = 600N ，不计各杆重量。

试求A 、B 、D 处的约束力。

E ()0:MF =∑o D cos 300F ED F EK ⋅-⋅=0:x F =∑o E sin 300x F F -=0:yF =∑o E D cos300y F F F +-=D 1000kNF =E 866kNx F =E 500kNy F =C D 1000kNF F ==A()0:M F =∑0:x F =∑0:yF =∑A C 0M W AB F AC -⋅-⋅=A 0x F =A C 0y F W F --=A 0x F =A 2000kNy F =A 3000kN mM =⋅解：以整个刚体系统为研究对象，受力图和坐标系如图所示。

建立平衡方程解得：以杆BH 为研究对象，受力图和坐标系如图所示。

建立平衡方程解得 以杆AC 为研究对象，受力图和坐标系如图所示。

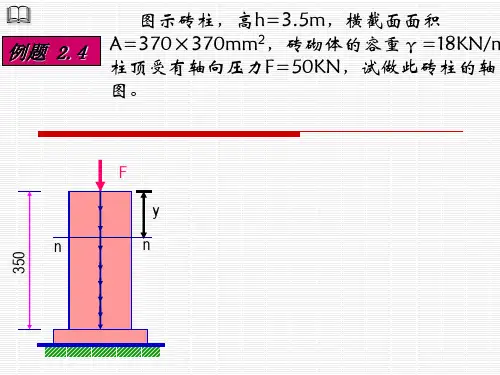
建立平衡方程解得： 例：一等直杆受力情况如图所示。

试作杆的轴力图。

解：⑴ 求约束力⑵ 截面法计算各段轴力AB 段：BC 段CD 段： DE 段：⑶ 绘制轴力图A ()0:M F =∑0:x F =∑0:yF =∑o E 123sin 452 2.25210F F F F ⨯-⨯-⨯-⨯=o A 2E cos 450x F F F +-=o A 3E 1sin450y F F F F -+-=E 2864NF =A 1425Nx F =A 42Ny F =-B()0:M F =∑0:xF =∑D()0:M F =∑D 11 1.750y F F ⨯-⨯=B 110.750y F F -⨯-⨯=B D 0x x F F +=B 750Ny F =-D 1750Ny F =A 1425N x F =A 42N y F =-B B750N y y F F '==-C()0:MF =∑A A BB 2110.50x y x y F F F F ''⨯-⨯-⨯+⨯=B2900N x F '=B B 2900N x x F F '∴==D B 2900Nx x F F =-=-0:xF=∑RA 405525200F +-+-=RA 10kNF =0:xF=∑N1RA 0F F -=N110kNF =0:xF=∑N2RA 400F F --=N250kNF =0:xF=∑N325200F +-=N35kNF =-N4200F -=N420kNF =0:xF=∑例：图所示轴向受压等截面杆件，横截面面积 A = 400mm 2 ，载荷F = 50kN ，试求横截面及斜截面m -m 上的应力。

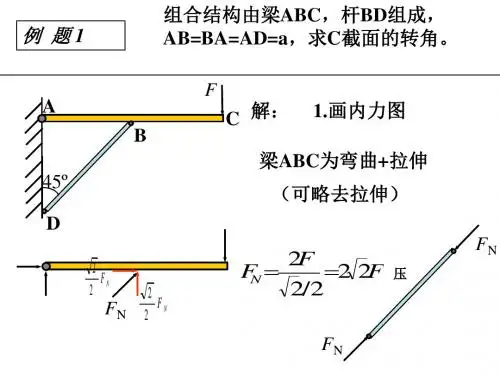
解：由题可得横截面上的正应力 斜截面上的正应力 斜截面上的切应力例：图所示变截面由两种材料制成，AE 段为铜质，EC 段为钢质。

钢的许用应力[σ]1 = 160MPa ，铜的许用应力[σ]2 = 120MPa ，AB 段横截面面积1000mm 2,BC 段的横截面面积是AB 段的一半。

外力F = 60kN ，作用线沿杆方向，试对此杆进行强度校核。

解：⑴ 求杆的轴力，作轴力图AD 段： DB 段 BC 段：⑵ 确定危险截面经分析危险截面在AD 段⑶ 强度校核所以杆件强度满足要求o50α=N 50kNF =-38N 065010 1.2510Pa 125MPa 40010F A σ--⨯===-⨯=-⨯o22o 050cos 125cos 5051.6MPaσσα==-⨯=-oo 050125sin 2sin(250)61.6MPa 22στα-==⨯⨯=-0:x F =∑N120F F +=N12120kNF F =-=-0:xF =∑N220F F F +-=N260kNF F =-=-0:xF=∑N30F F -=N360kNF F ==[]3AD max262AD 12010120MPa 101010F A σσ--⨯===-≤⨯⨯例：图所示吊环由斜杆AB 、AC 与横梁BC 组成，已知 α=20o ，吊环承受的最大吊重为F = 500kN ，许用应力[σ] = 120MPa 。

试求斜杆的直径。

解：以节点 A 为研究对象，受力图及坐标系如图所示。

建立平衡方程例：图所示桁架，已知两杆的横截面面积均为A = 100mm 2 ，许用拉应力[σt ]=200MPa ，许用压应力[σc ]=150MPa 。

试求载荷的最大许用值。

解：求1 、2杆的轴力以节点B 为研究对象，受力图和坐标系如图。

建立平衡方程确定载荷的最大许用值 1杆强度条件 2杆强度条件所以载荷F 的最大许用值为14.14kN0:yF=∑N 2cos 0F F α-=N 0500266kN2cos 2cos 20F F α===⨯[]N N24F F A dσσπ==≤25.3110m 53.1mm d -∴≥==⨯=0:x F =∑o N2N1cos450F F --=0:y F =∑o N1sin 450F F -=N1F =N2F F=-N1tF A σ=≤⎡⎤⎣⎦6614.14kNA F σ-⎡⎤∴≤==N2c F F A σ=≤⎡⎤⎣⎦66c 100101501015.0kN F A σ-∴≤=⨯⨯⨯=⎡⎤⎣⎦例：图所示钢螺栓，内径d 1 = 15.3mm ，被连接部分的总长度l = 54mm ，拧紧时螺栓AB 段的伸长△l = 0.04mm ，钢的弹性模量E = 200GPa ，泊松比μ = 0.3。