2018届新疆呼图壁县一中高三上学期9月月考 数学文

学年度期初分班测试数学(文科卷)考试时间：120分钟；总分：120分；命题人：王伟一、选择题（3*15=45）1．已知集合{}1 2 3 4A =，，，，{}0 2 4 6B =，，，，则A B 等于（ ）A ．{}0 1 2 3 4 6，，，，，B ．{}1 3，C ．{}2 4，D ．{}0 6， 2．函数1-=x y 的定义域是（ ）A.}1|{-≥x xB.1}{x/x >C.{}|13x x x ≠-≠且D.{}|13x x x ≥-≠且3．复数z 满足i z +=1，则z 对应的点位于复平面的（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限4．设函数21,1()2,1x x f x x x⎧+≤⎪=⎨>⎪⎩则((3))f f =A 、15 B 、3 C 、23 D 、1395．函数()f x 是R 上的偶函数，且在[0,)+∞上单调递增，则下列各式成立的是（ ） A ．)1()0()2(f f f >>-B ．)0()1()2(f f f >->- C ．)2()0()1(->>f f f D ．)0()2()1(f f f >-> 6．函数()39xf x =-的零点是（ ）A ．(2,0)B ．(3,0)C ．2D ．3 7．根据下边的框图，当输入x 为2017时，输出的y =（ ） （倒数第三方框为13y x+=-）A. 910B. 2C. 4D. 108．某三棱锥的三视图如图所示，该三棱锥的体积是（ ） A ．43 B ．83C ．4D ．623+ 9．设m ，n 是两条不同的直线， 是两个不同的平面，下列命题中正确的是( ) A ．若，，，则B ．若，，，则 C ．若，，，则D ．若，，，则10．甲乙两人有三个不同的学习小组A ，B ，C 可以参加，若每人必须参加并且仅能参加一个学习小组，则两人参加同一个小组的概率为（ ） A ．13 B ．14 C ．15 D ．1611．下列命题：①至少有一个x 使x 2＋2x ＋1＝0成立； ②对任意的x 都有x 2＋2x ＋1＝0成立； ③对任意的x 都有x 2＋2x ＋1＝0不成立； ④存在x 使x 2＋2x ＋1＝0成立． 其中是全称命题的有( ) A ．1个 B ．2个 C ．3个 D ．0个12．已知双曲线22x a-25y =1的右焦点为(3,0),则该双曲线的离心率等于( )(A)31414(B)324(C)32 (D)4313．O 为坐标原点，F 为抛物线2:2C y x =的焦点，P 为C 上一点，若||2PF =则POF ∆的面积为（ ） （A ）2（B ）2（C ）23（D ）414310x y +-=的倾斜角为 A. 6π B. 3πC. 23π D. 56π15．下表是某工厂6～9月份电量(单位：万度)的一组数据：月份x 6 7 8 9 用电量y 6532由散点图可知，用电量y 与月份x 间有较好的线性相关关系，其线性回归直线方程是，则等于( )A. B. C. D.二、填空题（4*4=16）16．设x ，y 满足约束条件：；则z=x ﹣2y 的最大值为.17．设函数()sin()(0,0,,)22f x A x A x R ππωϕωϕ=+>>-<<∈的部分图象如图所示.则A ωϕ++=18．12lg 4lg 254(4-0++--π)．19．直线0323=-+y x 截圆422=+y x 所得的弦长是．三、解答题（10*6=60）20．某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<2π)在某一个周期内的图象时,列表并填入了部分数据,如表:(1)请将上表数据补充完整,并直接写出函数f(x)的解析式. (2)判断函数单调增区间21．在等差数列{}n a 中，已知242,4a a == （1）求数列{}n a 的通项公式；（2）设2n a n b =，（此处右上角为n a ）求数列{n b }前5项的和5S .22．在AB C ∆中，c b a ,,分别是角，，C B,A 的对边，且c a bC B -=2cos cos ．（Ⅰ）求角B 的大小；（Ⅱ）若7=b ，且AB C ∆的面积为233，求a c +的值．23．如图，在三棱柱111ABC A B C -中，已知1B A A A C ⊥底面，AC BC ⊥.四边形11BB C C 为正方形，设1AB 的中点为D ，11.B C BC E = 求证：（Ⅰ）11//DE AAC C 平面； （Ⅱ）11BC AB C ⊥平面.24．已知在平面直角坐标系中的一个椭圆，它的中心在原点，左焦点为）（03,F -,且过点）（02,D . （1）求该椭圆的标准方程；（2）设点），（211A ，若P 是椭圆上的动点，求线段PA 的中点M 的轨迹方程.25．已知函数()33f x x x =-.（1）求函数()f x 的极值；（2）过点()2,6P -作曲线()y f x =的切线，求此切线的方程.16：317：18：19：220：略21：（1）；（2）.【解析】试题分析：（1）因为数列是等差数列，所以设数列的首项为，公差为，带入公式后求得首项和公差，；（2）根据（1）可得，所以是等比数列，代入等比数列的求和公式.试题解析：（1）解；（2）由（1）得是等比数列，；考点：1.等差数列；2.等比数列.22：（Ⅰ）（Ⅱ）【解析】试题分析：（Ⅰ）由正弦定理将已知条件转化为三内角表示，通过三角函数公式将其化简可求得B的大小；（Ⅱ）由三角形面积可求得的值，由三角形余弦定理可求得的值，从而得到的值试题解析：（Ⅰ）由正弦定理可得，，可得，∵，∴2，∴，∵为三角形的内角，∴（Ⅱ），由面积公式可得：，即，①由余弦定理，可得：，即②，由②变形可得：，③将①代入③可得，故解得：考点：正余弦定理解三角形23：【解析】试题分析：（1）由正方形性质得E为的中点，从而DE∥AC，由此能证明DE∥平面;（2）由线面垂直得AC⊥，由AC⊥BC，得AC⊥平面，由此能证明BC1⊥平面试题解析：（Ⅰ）∵、分别是、的中点∴又平面,平面∴…………………………………5分（Ⅱ）∵四边形为正方形∴∵三棱柱是直三棱柱，由知，∴∴…………………………………………………10分24：(1) . (2).【解析】试题分析：(1)由已知得椭圆的半长轴，半焦距，则半短轴. 3分又椭圆的焦点在轴上, ∴椭圆的标准方程为. 5分(2)设线段的中点为 ,点的坐标是，由，得， 9分由点在椭圆上,得,11分∴线段中点的轨迹方程是. 12分考点：本题考查了椭圆的标准方程及轨迹方程的求法，y0)的变动而变动，且x0、y0可用x、y表点评：若动点P(x，y)随已知曲线上的点Q(x示，则将Q点坐标表达式代入已知曲线方程，即得点P的轨迹方程．这种方法称为相关点法(或代换法)．25：（1）极大值，极小值；（2）或．【解析】试题分析：（1）由得到，求解的根，列表，即可求解函数的极值；（2）设切点得，即切线方程由切线过点，代入求解的值，即可求解切线方程.试题解析：（1）,令，解得或，列表如下当时，有极大值；当时，有极小值.（2）设切点，切线方程切线过点或，切线方程为或.。

新疆呼图壁县2017-2018学年高一数学上学期期中试题一、 选择题（每题4分，共40分） 1、下列哪组对象不能构成集合 （ ） A 、所有的平行四边形B 、高一年级所有高于170厘米的同学C 、数学必修一中的所有难题D 、240x -=方程在实数范围内的解 2、下列关系式中正确的是1,,03R Q N ∈∈（ ）A 、1B 、2C 、3D 、4{}233,,210103103x x x x x B x C x x x D x x x -≠-≠≠-≠≠≠-≠≠、集合中，应满足的条件是（ ）A 、、、且且、或或4、下列图形(横轴表示x 轴，纵轴表示y 轴)中，表示y 是x 的函数的是( )5、已知集合M ＝{－1,0,1}，N ＝{0,1,2}，则M ∪N ＝( )A ．{－1,0,1}B ．{－1,0,1,2}C ．{－1,0,2}D ．{0,1}6、函数f(x)=xa a 2)2(-是指数函数,则( ) A 、a=1或a=3B 、a=1C 、a=3D 、a>0且a ≠17、若log a 34<1(a >0，且a ≠1)，则实数a 的取值范围是()A.⎝ ⎛⎭⎪⎫0，34B.⎝ ⎛⎭⎪⎫0，34∪(1，＋∞) C ．(1，＋∞) D ．(0,1)()2f x x =+8、函数的零点是（ ）A 、2B 、（2,0）C 、-2D 、（-2,0）9、二次函数2不求a ，b ，c A ．(－3，－1)和(2,4) B ．(－3，－1)和(－1,1) C ．(－1,1)和(1,2) D ．(－∞，－3)和(4，＋∞)10、函数y ＝log a x ，y ＝log b x ，y ＝log c x ，y ＝log d x 的图象如下图所示，则a ，b ，c ，d 的大小顺序是( )A 、1<d <c <a <bB 、c <d <1<a <bC 、c <d <1<b <aD 、d <c <1<a <b二、填空题（每题4分，共16分）1、幂函数的图像过点（4,2），则18f ⎛⎫= ⎪⎝⎭()22log f x x =、函数的定义域[]3()0,13x f x a a ==、函数在区间上的最大值与最小值的和为，则12(31)4,14()-+log ,1a x a x f x a x x -+⎧⎪=∞∞⎨≥⎪⎩＜、已知函数是（，）上的减函数，那么的取值范围三、解答题（共44分）{}{}=37=210()(2),()R R R R A x x B x x C A C A B≤ 1、(10分)设全集为，＜，＜＜，求（1）A B ，C A B22()-f x x =-∞、(10分)判断函数在（，0）的单调性，并证明结论.3、（12分）已知函数f (x )＝x 21＋x2.(1)求f (2)＋f ⎝ ⎛⎭⎪⎫12，f (3)＋f ⎝ ⎛⎭⎪⎫13的值； (2)求证：f (x )＋f ⎝ ⎛⎭⎪⎫1x 是定值；(3)求f (2)＋f ⎝ ⎛⎭⎪⎫12＋f (3)＋f ⎝ ⎛⎭⎪⎫13＋…＋f (2 017)＋f ⎝ ⎛⎭⎪⎫12 017的值．{}{}25,121,(1),A x x B x a x a B A a a =-≤≤=+≤≤-⊆4、(12分)已知集合求实数的取值范围；（2）若A 是B 的真子集，求的范围高一数学答案 一、 选择题1 2、{}0x x ＞ 3、 2 4、11,73⎡⎫⎪⎢⎣⎭三、解答题{}{}{}1,()21037()2710R R R A B B C A B x x x C A x x x C A B x x x ==≤≥=≥=≤ 、或＜或＜＜3或＜2212112222221212212121122121121220(),(),()()()()()0,0()()()()x x f x x f x x f x f x x x x x x x x x x x x x x x f x f x f x f x =-=--=---=-=-+∴+-∴- 、函数在给定区间为单调增函数。

呼图壁县一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 设S n 为等比数列{a n }的前n 项和，若a 1=1，公比q=2，S k+2﹣S k =48，则k 等于（ ）A ．7B ．6C ．5D ．42． 设x ，y ∈R ，且x+y=4，则5x +5y 的最小值是（）A ．9B ．25C ．162D ．503． 已知i 为虚数单位，则复数所对应的点在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4． 记,那么AB C D5． 复数是虚数单位）的虚部为（ ）i iiz (21+=A ．B ．C ．D ．1-i -i 22【命题意图】本题考查复数的运算和概念等基础知识，意在考查基本运算能力．6． 函数f （x ）=，则f （﹣1）的值为（）A ．1B ．2C ．3D ．47． 设函数y=的定义域为M ，集合N={y|y=x 2，x ∈R}，则M ∩N=（ ）A ．∅B ．NC ．[1，+∞）D ．M8． 已知角θ的终边经过点P （4，m ），且sin θ=，则m 等于（ ）A ．﹣3B ．3C ．D ．±39． 若实数x ，y 满足不等式组则2x+4y 的最小值是（ ）A ．6B ．﹣6C ．4D ．2班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________10．已知F 1、F 2分别是双曲线﹣=1（a ＞0，b ＞0）的左、右焦点，过点F 2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ，若点M 在以线段F 1F 2为直径的圆外，则双曲线离心率的取值范围是（ ）A ．（1，）B ．（，+∞）C ．（，2）D ．（2，+∞）11．A={x|x ＜1}，B={x|x ＜﹣2或x ＞0}，则A ∩B=（ ）A ．（0，1）B ．（﹣∞，﹣2）C ．（﹣2，0）D ．（﹣∞，﹣2）∪（0，1）12．sin （﹣510°）=（ ）A ．B ．C ．﹣D ．﹣二、填空题13．如图，正方形的边长为1，它是水平放置的一个平面图形的直观图，则原图的''''O A B C cm 周长为．1111]14．在中，已知，则此三角形的最大内角的度数等ABC ∆sin :sin :sin 3:5:7A B C =于__________.15．若全集，集合，则16．函数y=sin 2x ﹣2sinx 的值域是y ∈ ．17．一组数据2，x ，4，6，10的平均值是5，则此组数据的标准差是 ．　18．函数f （x ）=2a x+1﹣3（a ＞0，且a ≠1）的图象经过的定点坐标是 ．三、解答题19．已知平面直角坐标系xoy 中的一个椭圆，它的中心在原点，左焦点为，右顶点为D （2，0），设点A （1，）．（1）求该椭圆的标准方程；（2）若P 是椭圆上的动点，求线段PA 的中点M 的轨迹方程；（3）过原点O 的直线交椭圆于B ，C 两点，求△ABC 面积的最大值，并求此时直线BC 的方程．20．命题p：关于x的不等式x2+2ax+4＞0对一切x∈R恒成立，q：函数f（x）=（3﹣2a）x是增函数．若p∨q 为真，p∧q为假．求实数a的取值范围．21．已知函数f（x）=e﹣x（x2+ax）在点（0，f（0））处的切线斜率为2．（Ⅰ）求实数a的值；（Ⅱ）设g（x）=﹣x（x﹣t﹣）（t∈R），若g（x）≥f（x）对x∈[0，1]恒成立，求t的取值范围；（Ⅲ）已知数列{a n}满足a1=1，a n+1=（1+）a n，求证：当n≥2，n∈N时f（）+f（）+L+f（）＜n•（）（e为自然对数的底数，e≈2.71828）．22．如图，四边形ABCD内接于⊙O，过点A作⊙O的切钱EP交CB 的延长线于P，己知∠PAB=25°．（1）若BC是⊙O的直径，求∠D的大小；（2）若∠DAE=25°，求证：DA2=DC•BP．23．（本小题满分12分）某媒体对“男女延迟退休”这一公众关注的问题进行名意调查，下表是在某单位得到的数据：赞同反对合计男50 150200女30 170 200合计80320400（Ⅰ）能否有能否有的把握认为对这一问题的看法与性别有关？97.5%（Ⅱ）从赞同“男女延迟退休”的80人中，利用分层抽样的方法抽出8人，然后从中选出2人进行陈述发言，求事件“选出的2人中，至少有一名女士”的概率．参考公式：，22()K ()()()()n ad bc a b c d a c b d -=++++()n a b c d =+++【命题意图】本题考查统计案例、抽样方法、古典概型等基础知识，意在考查统计的思想和基本运算能力24．在数列{a n }中，a 1=1，a n+1=1﹣，b n =，其中n ∈N *．（1）求证：数列{b n }为等差数列；（2）设c n =b n+1•（），数列{c n }的前n 项和为T n ，求T n ；（3）证明：1+++…+≤2﹣1（n ∈N *）呼图壁县一中2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题题号12345678910答案D D A B A A B B B D题号1112答案D C二、填空题13．8cm14．120o15．{|0＜＜1｝16．　[﹣1，3]　．17．　2　．18．　（﹣1，﹣1）　．三、解答题19．20．21．22．23．24．。

[X 2 + y 2 < 1 < x + y > — 111. 已知乂,丫满足1 yvO ，贝ijz = x-y 的取值范围是() A.[-返叮 B.[・ 1,1] C.[-返返] D. [ - 1,返] 12.已知定义在R 上的函数f (x)在(-8, -2)上是减函数，若g (x) =f (x - 2)是奇函数，且g (2)=0,则不等式xf (x) W0的解集是(A. ( - °°, - 2] U [2, +°°) C. ( - 8, - 4]U[ - 2, +8)二、填空题(20分)13. 已知f (x )= log 3(x 2-2x)?则函数f(x)的单调递减区间是 _____________ .14. 已知函数f(x) = x 3 + ax 2 + bx + a 2(a,b 6 R)且函数f(x)在x = 1处有极值10,则实数b 的值为15. _________ 已知f (x) = |e x -l|,又g(x) =f 2(x)-tf(x)(tG R),若满足g(x) = 一1的x 有三个，贝吐的取值范 围是 ____________ •16. 设f(x)是定义在R 上的偶函数，且当x > 0时，f(x) = 2X ,若对任意的xG [a,a + 2],不等式 f(x + a) >『(x)恒成立，则实数a 的取值范围是 _____________ .=、解答题：木题共6道题，共70分.17. 锐角AABC 的内角A, B, C 的对边分别为a, b, c,己知AABC 的外接圆半径为R,旦满足R = t asinA (1) 求角A 的大小；(2)若a = 2,求AABC 周长的最大值.A. ( -- 3] B. [ - 3, +°°) C. ( - °°, VS] D. [V3, +8))B. [-4, -2]U[0, +°o) D. ( - °°, - 4] U [0, +8)2018届高三数学9月考题（含答案）2017-9-28一、选择题(60分)1. 若集合A={x|x> - 1},则( )A. OCAB. {0}cAC. {0}£AD. 0£A2. 设集合A = (X|X2-2X-3 < 0},B = {x|y = ln(2-x)},则A n B =()A. {x|-l < x < 3}B. {x|-l < x < 2}C. {x|-3 < x < 2}D. {x|l < x < 2}2 _3. 若复&z =屮i为虚数单位，^z=()A. 1 + iB. 1-iC. -1-iD. -1-i4. 已知命题p:Vx > 0,总有(x + l)e x > 1,则「p为()A. 3x o 三°，使得do + l)e X°三1B. 3x o > 0,使得do + l)e X°三1C. 3x o > °，使得(X。

一、选择题(本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中, 只有一项是符合题目要求的.)1. 设函数y = yl4-x 2的定义域A,函数y=ln(l-x)的定义域为B,则AnB= A. (1,2) B. (1,2] C. (-2, 1) D. [~2, 1)2. 在等差数列｛%｝中，a x =2,a 3+a 5 =10，则如=( )A. 5B. 8C. 10D. 144.在AABC 中，已知J = 30°,C = 45°,a = 2,则AABC 的面积等于(A. V2B. 2A /2C. V3+1D. |(V3+1)5.已知两条直线加，〃和两个不同平面a.p ,满足a 丄0, a c 卩=1, ml la, 〃丄0,则 A. ml InB. mlnC. ml HD. nil6. 函数f (x) =(a 2 -l)x 在R 上是减函数，则a 的取值范围是() A. \a\>lB. |«| <2C. a<V2D. l<|tz|< A /27. 设a = log 3 7^ = 2L 1?C = 0.831,则 ()A.c<a<bB.b<a<cC. c<b<aD. a<c<b&已知直线l:kx-y + 2k-l = 0与圆x 2+y 2=6 交于两点，若\AB\ = 2^2，贝( )3 34 4 A.——B. —C.——D.—4 43 3x+y>l9.若变量x, y 满足约束条件<y —x<l ,则z = 2x-y + 3的最小值为() x<l A. -1 B. 0 C. 1 一D. 210.设M 是AABC 内一点，且S&BC 的面积为2，定义/(J W) =,其中m,n,p 分别是 i 4AMBC, NMCA, \MAB 的面积，若AABC 内一动点户满足/（尸）=（1，兀丿），则一+ —的最 小值是（）A. 1B. 4C. 9D. 123. A. B.c.D. 已知aw二、填空题（本大题共7小题，多空题每题6分，单空题每题4分，共36分・）11.设向量° = （1,2）,& = （2-2，一1）,若a 丨,则2 = ______ , ° •&= ___________2 212.双曲线--二=1的离心率为，焦点到渐近线的距离为16 9" I—13.已知函数/（x）= 贝!］/（/⑷）= _______ ；/（x）的最大值是 _________ .2蔦兀vO14.若抛物线C:y2=2px（p>0）的焦点F（l,0）,则戶= ______________ ；设M是抛物线C上的动点，/（4,3）,则+ 的最小值为__________ •15.已知空间几何体的三视图如图所示，则该几何体的表面积是______________ ;几何体的体积是2 216.已知椭圆G ：l + L = l（a>b>0）与双曲线C2:x2-y2= 4有相同的右焦点耳，点P是椭a b圆C］与双曲线C2在第一象限的公共点，若,|P^| = 2,则椭圆C］的离心率等于_________ .17.已知点A,B,C在圆x2+y2 = 1好运动，且45丄BC ,若点P的坐标为（3,0）,则|P2+F5+P C|的最力、值为__________ .三、解答题：本大题共5小题，共74分.解答应写出文字说明，证明过程或演算步骤.18.已知函数地/（x） = A/3 sin2x + cos2x + a（tz为常数）（1）求/（x）的单调递增区间；（2）若/（对-在［0,彳］上有最小值1,求Q的值.19、已知等差数列｛%｝的前"项和为S”一，ne N*,a3 =5,510 =100 .20、如图，在几何体以BCD 中，平面P48丄平面48CD,四边形/BCD 是正方形,PA = PB,且平面丄平面PAC.（I ）求证：4P 丄平面PBC ； （II ）求直线PD 与平面E4C 所成角的正弦值.21、如图，已知中心在原点，焦点在x 轴上的椭圆的一个焦点为（的,0）,个点.（1）求椭圆的标准方程;（2）设椭圆的上、下顶点分别为A,B , P （x 0, j 0） （%工0）是椭圆上异于的任意一点， P0丄，轴，0为垂足，为线段P0中点，直线交直线l:y = -l 于点C, N 为线段BC 3 的中点，如果AMON 的面积为寸，求几的值.（1）求数列仏”｝的通项公式；（2）设b”"(a”+5)求数列｛b”｝的前"项和7；.是椭圆上的一22、已知定义在R上的函数/(x) = (x-2)2.(I )若不等式/(x + 2-Z)</(2x + 3)对一切"[0,2]恒成立，求实数/的取值范围; (II)设g(x) = xj/(x),求函数g(x)在> 0) _h的最大值0伽)的表达式.参考答案1. D【解析】由4 — / >0得一2WXW2,由1 — x〉0得x<l,故A c B={x | -2 < x < 2} n {x | x < 1} = {x | -2 < x < 1},选D.2. B【解析】试题分析：因为a,+<i i = 7=10...2a l=ia 0» = 5又因为5=2.所以a- =di4-6rf = 2+6=8 故答案 &3. A3 (Jr A —4 sine/ 3••• sina 十又 x (亍可••• cosa = y,'. tana =—=-sin (龙 + a) = -sina =-—4. C .2少/ + B + C = 180°nB = 105。

呼图壁县一中2018-2019学年上学期高三数学10月月考试题班级__________ 座号_____ 姓名__________ 分数__________一、选择题1． 设函数在上单调递增，则与的大小关系是（ ）()log |1|a f x x =-(,1)-∞(2)f a +(3)f A ．B ．C.D ．不能确定(2)(3)f a f +>(2)(3)f a f +<(2)(3)f a f +=2． 二项式的展开式中项的系数为10，则（ ）(1)(N )nx n *+Î3x n =A ．5B ．6C ．8D ．10【命题意图】本题考查二项式定理等基础知识，意在考查基本运算能力．3． 函数f （x ）=1﹣xlnx 的零点所在区间是（）A ．（0，）B ．（，1）C ．（1，2）D ．（2，3）4． 已知{}n a 是等比数列，25124a a ==，，则公比q =（ ）A ．12-B ．-2C ．2D ．125． 已知集合A ，B ，C 中，A ⊆B ，A ⊆C ，若B={0，1，2，3}，C={0，2，4}，则A 的子集最多有（）A ．2个B ．4个C ．6个D ．8个6． 在中，，等于（ ）ABC ∆60A =1b =sin sin sin a b cA B C++++A ．BCD 7． 已知函数的定义域为，函数的图象如图甲所示，则函数的图象是()f x [],a b ()y f x =(||)f x 图乙中的（ ）8． 点A 是椭圆上一点，F 1、F 2分别是椭圆的左、右焦点，I 是△AF 1F 2的内心．若，则该椭圆的离心率为（）A ．B ．C ．D ．9． 下列四组函数中表示同一函数的是（ ）A ．，B ．，()f x x =2()g x =2()f x x =2()(1)g x x =+C ．，D ．，1111]()f x =()||g x x =()0f x =()g x =10．在△ABC 中，角A ，B ，C 所对的边分别是a ，b ，c ，若﹣+1=0，则角B 的度数是（）A ．60°B ．120°C ．150°D ．60°或120°11．已知的终边过点，则等于（ ）()2,37tan 4πθ⎛⎫+ ⎪⎝⎭A ． B ．C ．-5D ．515-1512．以椭圆+=1的顶点为焦点，焦点为顶点的双曲线C ，其左、右焦点分别是F 1，F 2，已知点M 坐标为（2，1），双曲线C 上点P （x 0，y 0）（x 0＞0，y 0＞0）满足=，则﹣S（）A ．2B ．4C ．1D ．﹣1二、填空题13．图中的三个直角三角形是一个体积为20的几何体的三视图，则__________.h =14．某公司租赁甲、乙两种设备生产A B ，两类产品，甲种设备每天能生产A 类产品5件和B 类产品10件，乙种设备每天能生产A 类产品6件和B 类产品20件.已知设备甲每天的租赁费为200元，设备乙每天的租赁费用为300元，现该公司至少要生产A 类产品50件，B 类产品140件，所需租赁费最少为__________元.15．已知f （x ）＝x （e x ＋a e －x ）为偶函数，则a ＝________．16．已知函数的一条对称轴方程为，则函数的最大值为21()sin cos sin 2f x a x x x =-+6x π=()f x （）A ．1B ．±1CD ．【命题意图】本题考查三角变换、三角函数的对称性与最值，意在考查逻辑思维能力、运算求解能力、转化思想与方程思想．三、解答题17．（本小题12分）在多面体中，四边形与是边长均为正方形，平面ABCDEFG ABCD CDEF a CF ⊥，平面，且．ABCD BG ⊥ABCD 24AB BG BH ==（1）求证：平面平面；AGH ⊥EFG （2）若，求三棱锥的体积．4a =G ADE -【命题意图】本题主要考查空间直线与平面间的垂直关系、空间向量、二面角等基础知识，间在考查空间想象能力、逻辑推理能力，以及转化的思想、方程思想．18．（本小题满分10分）选修4-5：不等式选讲已知函数．()|21|f x x =-（1）若不等式的解集为，求实数的值；1(21(0)2f x m m +≤+>(][),22,-∞-+∞ m （2）若不等式，对任意的实数恒成立，求实数的最小值．()2|23|2yyaf x x ≤+++,x y R ∈a 19．（本小题满分13分）在四棱锥中，底面是梯形，，，，P ABCD -ABCD //AB DC 2ABD π∠=AD =22AB DC ==为的中点．F PA （Ⅰ）在棱上确定一点，使得平面；PB E //CE PAD （Ⅱ）若的体积．PA PB PD ===P BDF -ABCDPF20．设集合A={x|0＜x ﹣m ＜3}，B={x|x ≤0或x ≥3}，分别求满足下列条件的实数m 的取值范围．（1）A ∩B=∅；（2）A ∪B=B ．21．（本小题满分12分）△ABC 的三内角A ，B ，C 的对边分别为a ，b ，c ，已知k sin B ＝sin A ＋sin C （k 为正常数），a ＝4c .（1）当k ＝时，求cos B ；54（2）若△ABC 面积为，B ＝60°，求k 的值．322．已知二次函数的最小值为1，且．()f x (0)(2)3f f ==（1）求的解析式；()f x （2）若在区间上不单调，求实数的取值范围；()f x []2,1a a +（3）在区间上，的图象恒在的图象上方，试确定实数的取值范围．[]1,1-()y f x =221y x m =++m 23．（本小题满分12分）如图，多面体中，四边形ABCD 为菱形，且，，，ABCDEF 60DAB∠= //EF AC 2AD =.EA ED EF ===（1）求证：；AD BE ⊥（2）若，求三棱锥的体积.BE =-F BCD呼图壁县一中2018-2019学年上学期高三数学10月月考试题（参考答案）一、选择题1． 【答案】A 【解析】试题分析：由且在上单调递增，易得()()()()()log 1,,1log 1,1,a a x x f x x x -∈-∞⎧⎪=⎨-∈+∞⎪⎩()f x (),1-∞.在上单调递减,，故选A.01,112a a <<∴<+<()f x ∴()1,+∞()()23f a f ∴+>考点：1、分段函数的解析式；2、对数函数的单调性.2． 【答案】B【解析】因为的展开式中项系数是，所以，解得，故选A ．(1)(N )n x n *+Î3x 3C n 3C 10n =5n =3． 【答案】C【解析】解：∵f （1）=1＞0，f （2）=1﹣2ln2=ln ＜0，∴函数f （x ）=1﹣xlnx 的零点所在区间是（1，2）．故选：C ．【点评】本题主要考查函数零点区间的判断，判断的主要方法是利用根的存在性定理，判断函数在给定区间端点处的符号是否相反．　4． 【答案】D 【解析】试题分析：∵在等比数列}{a n 中，41,2a 52==a ,21,81q 253=∴==∴q a a .考点：等比数列的性质.5． 【答案】B【解析】解：因为B={0，1，2，3}，C={0，2，4}，且A ⊆B ，A ⊆C ；∴A ⊆B ∩C={0，2}∴集合A 可能为{0，2}，即最多有2个元素，故最多有4个子集．故选：B ．　6． 【答案】B 【解析】试题分析：由题意得，三角形的面积，所以，又，所011sin sin 6022S bc A bc ====4bc =1b =以，又由余弦定理，可得，所以4c =222222cos 14214cos 6013a b c bc A =+-=+-⨯⨯=a =，故选B ．sin sin sin sin a b c a A B C A ++===++考点：解三角形．【方法点晴】本题主要考查了解三角形问题，其中解答中涉及到三角形的正弦定理和余弦定理、三角形的面积公式等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，以及推理与运算能力，本题的解答中利用比例式的性质，得到是解答的关键，属于中档试题．sin sin sin sin a b c aA B C A++=++7． 【答案】B 【解析】试题分析：的图象是由这样操作而来：保留轴右边的图象，左边不要.然后将右边的图象关于(||)f x ()f x y y 轴对称翻折过来，故选B ．考点：函数图象与性质．【思路点晴】本题主要考查函数的奇偶性、数形结合的数学思想方法.由加绝对值所得的图象有如下几种，()f x 一个是——将函数在轴下方的图象翻折上来，就得到的图象，实际的意义就是将函数值()f x ()f x ()f x 为负数转化为正的；一个是，这是偶函数，所以保留轴右边的图象，左边不要.然后将右边的图象关()f x y 于轴对称翻折过来.y8． 【答案】B【解析】解：设△AF 1F 2的内切圆半径为r ，则S △IAF1=|AF 1|r ，S △IAF2=|AF 2|r ，S △IF1F2=|F 1F 2|r ，∵，∴|AF 1|r=2×|F 1F 2|r ﹣|AF 2|r ，整理，得|AF 1|+|AF 2|=2|F 1F 2|．∴a=2，∴椭圆的离心率e===．故选：B ．　9． 【答案】C 【解析】试题分析：A 定义域值域均不相同，B 对应法则不相同，D 定义域不相同，故选C. 考点：定义域与值域．10．【答案】A【解析】解：根据正弦定理有：=，代入已知等式得：﹣+1=0，即﹣1=，整理得：2sinAcosB﹣cosBsinC=sinBcosC，即2sinAcosB=sinBcosC+cosBsinC=sin（B+C），又∵A+B+C=180°，∴sin（B+C）=sinA，可得2sinAcosB=sinA，∵sinA≠0，∴2cosB=1，即cosB=，则B=60°．故选：A．【点评】此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．11．【答案】B【解析】考点：三角恒等变换．12．【答案】A【解析】解：∵椭圆方程为+=1，∴其顶点坐标为（3，0）、（﹣3，0），焦点坐标为（2，0）、（﹣2，0），∴双曲线方程为，设点P（x，y），记F1（﹣3，0），F2（3，0），∵=，∴=，整理得：=5，化简得：5x=12y ﹣15，又∵，∴5﹣4y 2=20，解得：y=或y=（舍），∴P （3，），∴直线PF 1方程为：5x ﹣12y+15=0，∴点M 到直线PF 1的距离d==1，易知点M 到x 轴、直线PF 2的距离都为1，结合平面几何知识可知点M （2，1）就是△F 1PF 2的内心．故﹣===2，故选：A ．【点评】本题考查椭圆方程，双曲线方程，三角形面积计算公式，注意解题方法的积累，属于中档题．　二、填空题13．【答案】【解析】试题分析：由三视图可知该几何体为三棱锥，其中侧棱底面，且为直角三角形，且VA ⊥ABC ABC ∆，所以三棱锥的体积为，解得.5,,6AB VA h AC ===115652032V h h =⨯⨯⨯==4h=考点：几何体的三视图与体积.14．【答案】2300【解析】111]试题分析：根据题意设租赁甲设备，乙设备，则⎪⎪⎩⎪⎪⎨⎧≥+≥+≥≥14020y 10x 506y 5x 0y 0x ，求目标函数300y 200x Z +=的最小值.作出可行域如图所示，从图中可以看出，直线在可行域上移动时，当直线的截距最小时，取最小值2300.1111]考点：简单线性规划.【方法点晴】本题是一道关于求实际问题中的最值的题目，可以采用线性规划的知识进行求解；细查题意，设甲种设备需要生产天，乙种设备需要生产y 天，该公司所需租赁费为Z 元，则y x Z 300200+=，接下来列出满足条件的约束条件，结合目标函数，然后利用线性规划的应用，求出最优解，即可得出租赁费的最小值.15．【答案】【解析】解析：∵f （x ）是偶函数，∴f （－x ）＝f （x ）恒成立，即（－x ）（e －x ＋a e x ）＝x （e x ＋a e －x ），∴a （e x ＋e －x ）＝－（e x ＋e －x ），∴a ＝－1.答案：－116．【答案】A【解析】三、解答题17．【答案】【解析】（1）连接，由题意，知，，∴平面．FH CD BC ⊥CD CF ⊥CD ⊥BCFG 又∵平面，∴．GH ⊂BCFG CD ⊥GH 又∵，∴……………………………2分EF CD A EF GH ⊥由题意，得，，，∴，14BH a =34CH a =12BG a =2222516GH BG BH a =+=，，22225()4FG CF BG BC a =-+=22222516FH CF CH a =+=则，∴．……………………………4分222FH FG GH =+GH FG ⊥又∵，平面．……………………………5分EF FG F = GH ⊥EFG ∵平面，∴平面平面．……………………………6分GH ⊂AGH AGH ⊥EFG18．【答案】【解析】【命题意图】本题主要考查绝对值不等式的解法、三角不等式、基本不等式等基础知识，以及考查等价转化的能力、逻辑思维能力、运算能力．19．【答案】（本小题满分13分）解：（Ⅰ）当为的中点时，平面． （1分）E PB //CE PAD连结、，那么，． EF EC //EF AB 12EF AB =∵，，∴，，∴． （3分）//DC AB 12DC AB =//EF DC EF DC =//EC FD 又∵平面， 平面，∴平面． （5分）CE ⊄PAD FD ⊂PAD //CE PAD （Ⅱ）设为的中点，连结、，∵，∴，O AD OP OB PA PD =OP AD ⊥在直角三角形中，, 又∵，∴，∴,∴ABD 12OB AD OA ==PA PB =PAO PBO ∆≅∆POA POB ∠=∠，OP OB ⊥∴平面． （10分）OP ⊥ABD，2PO ===2BD ==∴三棱锥的体积． （13分）P BDF -1112222233P BDF P ABD V V --==⨯⨯⨯=A BCD POEF 20．【答案】【解析】解：∵A={x|0＜x ﹣m ＜3}，∴A={x|m ＜x ＜m+3}，（1）当A ∩B=∅时；如图：则，解得m=0，（2）当A ∪B=B 时，则A ⊆B ，由上图可得，m ≥3或m+3≤0，解得m ≥3或m ≤﹣3．21．【答案】【解析】解：（1）∵sin B ＝sin A ＋sin C ，由正弦定理得b ＝a ＋c ，5454又a ＝4c ，∴b ＝5c ，即b ＝4c ，54由余弦定理得cos B ＝＝＝.a 2＋c 2－b 22ac （4c ）2＋c 2－（4c ）22×4c ·c 18（2）∵S △ABC ＝，B ＝60°.3∴ac sin B ＝.即ac ＝4.123又a ＝4c ，∴a ＝4，c ＝1.由余弦定理得b 2＝a 2＋c 2－2ac cos B ＝42＋12－2×4×1×＝13.12∴b ＝，13∵k sin B ＝sin A ＋sin C ，由正弦定理得k ＝＝＝，a ＋c b 51351313即k 的值为.5131322．【答案】（1）；（2）；（3）.2()243f x x x =-+102a <<1m <-试题解析：（1）由已知，设，2()(1)1f x a x =-+由，得，故．(0)3f =2a =2()243f x x x =-+（2）要使函数不单调，则，则．211a a <<+102a <<（3）由已知，即，化简得，2243221x x x m -+>++2310x x m -+->设，则只要，2()31g x x x m =-+-min ()0g x >而，得．min ()(1)1g x g m ==--1m <-考点：二次函数图象与性质．【方法点晴】利用待定系数法求二次函数解析式的过程中注意选择合适的表达式，这是解题的关键所在；另外要注意在做题过程中体会：数形结合思想，方程思想，函数思想的应用．二次函数的解析式（1）一般式：；（2）顶点式：若二次函数的顶点坐标为，则其解析式为()()20f x ax bx c a =++≠(),h k ；（3）两根式：若相应一元二次方程的两根为，则其解析式为()()()20f x a x h k a =-+≠()12,x x .()()()()120f x a x x x x a =--≠23．【答案】【解析】【命题意图】本小题主要考查空间直线与直线、直线与平面的位置关系及几何体的体积等基础知识，考查空间想象能力、推理论证能力、运算求解能力，考查化归与转化思想等．（2）在中，，，EAD △EA ED ==2AD =。

新疆呼图壁县一中2018届高三10月月考数学（文）试题一、选择题（每小题5分，共60分）1、已知集合, ,则( )A. B. C. D.的关系无法确定2、已知i 是虚数单位，则=（ ）A. B. C. D.3、对抛物线,下列描述正确的是( )A.开口向下，焦点为B.开口向下,焦点为(0,-1)C.开口向左，焦点为D.开口向左,焦点为(-1,0)4、已知平面向量与平行,则的值是 ( )A.-2B.2C.D.5、“”是的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6、如图所示,程序框图(算法流程图)的输出结果是( )A. B. C. D.7、已知曲线,则曲线在点处的切线方程为（ ）A. B. C. D.8、函数y=log 2|x|的图象大致是( )A B C D9、函数的零点所在的一个区间是( )A.(-2,-1)B.(-1,0)C.(0,1)D.(1,2)10、设2.022.02,2.0,2log ===c b a ，则（ ）A.a<b<cB.c<b<aC.c<a<bD.b<a<c11、已知函数)2,0,0,)(sin()(πϕωϕω<>>∈+=A R x x A x f 的图象(部分)如图所示,则的解析式是( )A. B.)62sin(2)(ππ+=x x fC. D.)32sin(2)(ππ+=x x f12、设函数⎪⎩⎪⎨⎧≥<-⎪⎭⎫ ⎝⎛=0,0,721)(x x x x f x,若,则实数的取值范围是() A. B. C.(-3,1) D.二、填空题（每小题5分，共20分）13、已知实数对满足⎪⎩⎪⎨⎧≥-≥≤012y x y x ,则的最小值是 .14、已知函数,则= .15、函数的极小值为 .16、 观察下列等式;;;;…照此规律,第n 个等式为 .三、解答题17、（12分）已知数列是等差数列,其中,。

新疆呼图壁县一中2018届高三期初考试数学（理）试题一、选择题12*5=601．已知集合，，则（）A. B. C. D.2．复数（）A．B．-1 C．D．13．在等比数列中，若，则=（）A．B．C．D．94．函数的零点所在的区间是( )A. B. C. D.5．下列选项中，说法正确的是（）A. 命题“”的否定是“”B. 命题“为真”是命题“为真”的充分不必要条件C. 命题“若，则”是假命题D. 命题“在中，若,则”的逆否命题为真命题6．元朝著名数学家朱世杰在《四元玉鉴》中有一首诗：“我有一壶酒，携着游春走，遇店添一倍，逢友饮一斗，店友经三处，没了壶中酒，借问此壶中，当原多少酒？”用程序框图表达如图所示，即最终输出的，则一开始输入的X值为（）A. B. C. D. 47.某几何体的三视图如图所示，则该几何体的体积是（ ）A. B.B. C. D.8．在中，内角的对边分别是，，，，则的值是( )A. B. C. D.9．已知4,,cos ,25παπα⎛⎫∈=- ⎪⎝⎭则（ ）A. B. C. D.10．若直线与圆至多有一个公共点，则（ ）A. B. C. D.11．若变量满足约束条件，则的最大值是（ ）A. B. 0 C. D.12．函数()24sin ,,22f x x x x ππ⎡⎤=-∈-⎢⎥⎣⎦的图象大致是（ ）A BC D二、填空题4*5=2013．已知平面向量,，且，则__________．14．在的二项展开式中，常数项为__________．15．曲线():sin 2x C f x x e =++在处的切线方程为__________．注意16、17两题任选一题，若两题都做，则只改16题16．某同学通过计算机测试的概率为，他连续测试3次，且三次测试相互独立，其中恰有1次通过的概率为__________．17．点在椭圆上，求点到直线的最大距离是__________________．三、解答题18．选修4-4：坐标系与参数方程已知直线：52{ 12x y t =+=（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.（1）将曲线的极坐标方程化为直角坐标方程；（2）设点的直角坐标为，直线与曲线的交点为，求的值.19．从5名男生和3名女生中任选3人参加奥数训练，设随机变量X 表示所选3人中女生的人数（1）求“所选3人中女生人数X>1”的概率.（2）求X 的分布列及数学期望.20．设等差数列{a n }满足a 3=5,a 10=-9.(1)求{a n }的通项公式;(2)求{a n }的前n 项和S n 的最大值.21．在△中，角所对的边分别为、、.若＝，＝，且.（Ⅰ）求角A 的大小；（Ⅱ）若＝，三角形面积＝，求的值.22． 已知椭圆)0(1:2222>>=+b a by a x C 的焦距为，椭圆上任意一点到椭圆两个焦点的距离之和为6．（Ⅰ）求椭圆的方程；（Ⅱ）设直线与椭圆交于两点，点（0，1），且=，求直线的方程．23．如图，在直三棱柱中，已知，分别为的中点，求证：（1）平面平面；（2）平面.24．已知函数32()3,f x x ax x a R =-+∈（I ）若是的极值点，求的极值；（Ⅱ）若函数是上的单调递增函数，求实数的取值范围.2017-2018学年第一学期期初理科数学试题参考答案一、选择题1．B 2．C. 3．B 4．B 5．C 6．B7．A 8．C 9．A 10．D 11．C 12．D18．试题解析：（1）等价于①将222=,cos x y x ρρθ+=代入①既得曲线C 的直角坐标方程为，② 4分（2）将5{12x y t =+=代入②得， 设这个方程的两个实根分别为则由参数t 的几何意义既知，. 10分19．试题解析：(1)4分(2)X 的所有可能取值为0,1,2,39分E(x)=0*+1*+2*+3*= 10分20．试题解析：(1)由及,得,，解得，数列{a n }的通项公式为.6分 (2)由(1)知()211102n n n S na d n n -=+=-.因为，所以时,取得最大值25. 12分21．【解析】（Ⅰ）∵＝，＝，且,∴ 21s i n s i n c o s c o s =⋅-⋅C B C B , ∴,即 , 即－，又，∴. 6分 （Ⅱ）332sin 21sin 21=⋅=⋅=∆πbc A bc S ABC ，∴又由余弦定理得：bc c b bc c b a ++=-+=220222120cos 2∴16＝，故.12分22． 【解析】（Ⅰ）由已知，,解得，,所以，所以椭圆C 的方程为。

高三10月月考数学（文）试卷一、选择题（每小题5分，共60分）1、已知集合{}21<<-=x x A ,{}11<<-=x x B ,则( ) A.B.C.D.的关系无法确定2、已知i 是虚数单位，则ii++121=（ ） A.23i - B.23i+ C.i -3 D.i +3 3、对抛物线y x 42-=,下列描述正确的是( ) A.开口向下，焦点为⎪⎭⎫⎝⎛161-0， B.开口向下,焦点为(0,-1) C.开口向左，焦点为⎪⎭⎫⎝⎛0161-， D.开口向左,焦点为(-1,0) 4、已知平面向量)3,(-=λa 与)2,3(-=b 平行,则λ的值是 ( ) A.-2 B.2 C.29- D.29 5、“”是”“02>+x x 的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6、如图所示,程序框图(算法流程图)的输出结果是( )A.61 B.2425 C.43 D.1211 7、已知曲线34313+=x y ,则曲线在点)4,2(P 处的切线方程为（ ）A.0124=-+y xB.0124=++y xC.044=--y xD.044=+-y x8、函数y=log 2|x|的图象大致是( )A B C D9、函数2213)(-+=x x f x 的零点所在的一个区间是( )A.(-2,-1)B.(-1,0)C.(0,1)D.(1,2)10、设2.022.02,2.0,2log ===c b a ，则（ ） A.a<b<c B.c<b<a C.c<a<b D.b<a<c11、已知函数)2,0,0,)(sin()(πϕωϕω<>>∈+=A R x x A x f 的图象(部分)如图所示,则)(x f 的解析式是( )A. )6sin(2)(ππ+=x x f B.)62sin(2)(ππ+=x x f C.)3sin(2)(ππ+=x x f D.)32sin(2)(ππ+=x x f12、设函数⎪⎩⎪⎨⎧≥<-⎪⎭⎫ ⎝⎛=0,0,721)(x x x x f x,若1)(<a f ,则实数a 的取值范围是( )A.)3,-∞-（B.），（∞+1C.(-3,1)D.),1()3,+∞⋃-∞-（二、填空题（每小题5分，共20分）13、已知实数对),y x （满足⎪⎩⎪⎨⎧≥-≥≤012y x y x ,则y x +2的最小值是 .14、已知函数x f x x f )1(2)(3'+=,则)1(f '= . 15、函数x xx f ln 1)(+=的极小值为 .16、 观察下列等式;;;;…照此规律,第n 个等式为 .三、解答题17、（12分）已知数列{}n a 是等差数列,其中251=a ,175=a 。

月考试题（文科卷）一、选择题（每题5分，共60分）1. 已知集合A={x│x-1>0}，B={y│y2－2y－3≤0}，则A∩B= （）A. （1，3）B. [1，3）C. [1，3]D. （1，3]【答案】D所以A∩B= [1，3].故选D.2. 命题“x∈R，都有ln(x2+1)>0”的否定为（）A. x∈R，都有ln(x2+1)≤0B. x0∈R，都有ln(x02+1)>0C. x∈R，都有ln(x2+1)<0D. x0∈R，都有ln(x02+1)≤0【答案】D【解析】全称命题的否定为特称，所以“x∈R，都有ln(x2+1)>0”的否定为x0∈R，都有ln(x02+1)≤0.故选D.3. 判断下列函数是同一函数的是（）A. B.C. D. y=x0与y=1【答案】B【解析】的定义域为，的定义域为R，不是同一函数；，俩函数定义域也相同，是同一函数；定义域为，而的定义域为，不是同一函数；D.y=x0定义域为，y=1的定义域为R，不是同一函数.故选B.4. 若i是虚数单位，则复数z=的虚部为（）A. B. C. D.【解析】复数z=.虚部为.故选D.5. 要得到函数y=sinx的图像，只需将函数的图像（）A. 向右平移个单位B. 向右平移个单位C. 向左平移个单位D. 向左平移个单位【答案】C故选C.6. 如图，当输入的x值为5时，则输出的结果（）A. 5B. 4C. 3D. 2【答案】D【解析】输入，不满足条件，有；不满足条件有，，满足条件，所以.故选D.7. 设，求f(－2)的值（）A. 4B. －4C.D.【解析】故选C.8. 函数的零点所在的区间是（）A. B. （1，2） C. （2，e） D. （e，3）【答案】C【解析】试题分析：函数的定义域是，显然与在上单调递增，∴在上单调递增，当时，，当时，，根据零点存在定理可知函数的零点在内，故选C.考点：1.函数的性质；2.函数的零点．9. 已知（）A. B. C. － D.【答案】B【解析】.由与垂直，可得.解得.故选B.10. 已知m为一条直线，α，β为两个不同的平面，则下列说法正确的是（）A. 若m∥α，α∥β，则m∥βB. 若m⊥α，α⊥β，则m⊥βC. 若m∥α，α⊥β，则m⊥βD. 若m⊥α，α∥β，则m⊥β【答案】D【解析】对于A,若m∥α,α∥β,则m∥β或m⊂β，不正确；对于B,∵α⊥β,∴设α∩β=a,在平面β内作直线b⊥a,则b⊥α,∵m⊥α,∴m∥b，若m⊄β,则m∥β,若m⊂β,也成立.∴m∥β或m⊂β，不正确；对于C,若m∥α,α⊥β,则则m∥β或m，β相交，不正确；对于D,若m⊥α,α∥β，利用平面与平面平行的性质，可得m⊥β，正确。

呼图壁县第一中学高三年级10月月考语文试卷第Ⅰ卷阅读题一、现代文阅读（35分）(一）论述类文本阅读（本题共3小题，共9分)阅读下面的文字，完成1-3题。

格调胡海“格调”作为诗论术语，是要求诗歌既具有美的形式，又具有大格局、高境界，前者是“调”的审美含义决定的，后者是“格”的人格、道德含义决定的。

这两个字起初是并举而非连用的,连用之后，有时也还分而论之。

皎然《诗式》中说谢灵运的诗“其格高，其调逸”，这里的“格”是就内容整体而言的,是谢灵运特立独行的人格转化成的精神境界;“调"不单指音调，是就形式整体而言的,指其音调和谐而自由,遣词造句纵心任情。

欧阳修的《六一诗话》论“格"而不论“调"，如说郑谷诗“极有意思,亦多佳句,但其格不甚高”。

此“格”指的是诗的境界。

又说晚唐诗人“无复李、杜豪放之格，然亦务以精意相高”。

此“格”是诗人胸怀、境界赋予作品的总体风格。

严羽《沧浪诗话·诗辨》中说：诗之法有五,体制、格力、气象、兴趣、音节。

前三者大体对应于“格",后二者则是对应“调"。

严羽系统地探讨诗法，后世诗法及文法的基本问题大多不出此范围.宽泛意义上的格调论,包括思想要求和艺术要求、内容与形式关系以及整体上效法古典还是重视新变的古今之争问题，而这些问题在《沧浪诗话》中都有所涉及，故而严羽被视为开后世格调论先河之人。

“格”“调”在诗文评中的连用标志着格调论正式出现，但其含意不固定，有时偏于“格”的含义,是就内容而言的思想境界；有时偏于“调”的含义，是就形式而言的审美性。

因为“格”指诗歌体制，是观作品整体,所以就有了格局、境界的意思.概括明代的格调论，“格”是诗歌体制、整体格局，是知觉层面的诗歌内容,指代作品的境界和思想价值；“调”则是听觉层面的音节声调，与视觉层面的诗体——四言、五言、七言、长短句等相应，关乎情绪和感觉，不一定涉及意义。

二者的结合，是形式美与或高远或深沉境界的一体,只是在具体的诗文评论中可能偏于某一方面的意义.格调论除讨论诗歌的形式与境界外，还展开了两个具有一般性的文论问题，一是崇古还是创新；二是重内容还是重形式，主情还是主理。

2017-2018学年第一学期期初理科数学一、选择题12*5=60 1．已知集合，，则（ ）A. B.C.D.2．复数=-+ii11（ ） A ．i - B ．-1 C ．i D ．13．在等比数列{}n a 中，若3357(a a a ⋅⋅=，则28a a ⋅=（ ） A ．3-B ．3C ．9-D ．94．函数()2ln f x x x=-的零点所在的区间是 ( ) A. ()1,2 B. ()2,e C. (),3e D. ()3,+∞ 5．下列选项中，说法正确的是（ ）A. 命题“2,0x R x x ∃∈-≤”的否定是“2,0x R x x ∃∈->”B. 命题“p q ∨为真”是命题“p q ∧为真”的充分不必要条件C. 命题“若22am bm ≤，则a b ≤”是假命题D. 命题“在ABC ∆中，若1sin 2A <,则6A π<”的逆否命题为真命题6．元朝著名数学家朱世杰在《四元玉鉴》中有一首诗：“我有一壶酒，携着游春走，遇店添一倍，逢友饮一斗，店友经三处，没了壶中酒，借问此壶中，当原多少酒？”用程序框图表达如图所示，即最终输出的，则一开始输入的X 值为（ ）A. B. C.D. 47.某几何体的三视图如图所示，则该几何体的体积是（ ）A.12π+ B. 32π+ B. C. 312π+ D. 332π+ 8．在ABC 中，内角,,A B C 的对边分别是,,a b c ，5b =，4B π∠=，tan 2A =，则a 的值是( )A. C. 9．已知4,,cos ,25παπα⎛⎫∈=- ⎪⎝⎭则tan 4πα⎛⎫+= ⎪⎝⎭（ ）A.17 B. 7 C. 17- D. 7- 10．若直线2x y +=与圆22x y a +=至多有一个公共点，则（ ） A. 2a < B. 2a ≤ C. 02a << D. 02a <≤11．若变量满足约束条件，则的最大值是（ ）A. B. 0 C. D. 12．函数()24sin ,,22f x x x x ππ⎡⎤=-∈-⎢⎥⎣⎦的图象大致是（ ）ABC D 二、填空题4*5=2013．已知平面向量(),1a m m =-,()1,2b =，且a b ⊥，则m =__________．14．在6x ⎛⎝的二项展开式中，常数项为__________．15．曲线():sin 2xC f x x e =++在0x =处的切线方程为__________．注意16、17两题任选一题，若两题都做，则只改16题 16．某同学通过计算机测试的概率为13，他连续测试3次，且三次测试相互独立，其中恰有1次通过的概率为__________．17．点P 在椭圆221169x y +=上，求点P 到直线3424x y -=的最大距离是__________________． 三、解答题18．选修4-4：坐标系与参数方程已知直线l：5{12x y t=+=（t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为2cos ρθ=. （1）将曲线C 的极坐标方程化为直角坐标方程；（2）设点M的直角坐标为(，直线l 与曲线C 的交点为,A B ，求MA MB ⋅的值.19．从5名男生和3名女生中任选3人参加奥数训练，设随机变量X 表示所选3人中女生的人数（1）求“所选3人中女生人数X>1”的概率. （2）求X 的分布列及数学期望.20．设等差数列{a n }满足a 3=5,a 10=-9. (1)求{a n }的通项公式;(2)求{a n }的前n 项和S n 的最大值.21．在△ABC 中，角,,A B C 所对的边分别为a 、b 、c .若m ＝()C B sin ,cos ，n ＝()B C sin ,cos -，且21=⋅. （Ⅰ）求角A 的大小；（Ⅱ）若a ＝32，三角形面积S ＝3，求c b +的值.22． 已知椭圆)0(1:2222>>=+b a by a x C 的焦距为62，椭圆C 上任意一点到椭圆两个焦点的距离之和为6． （Ⅰ）求椭圆C 的方程；（Ⅱ）设直线l 2:-=kx y 与椭圆C 交于B A ,两点，点P （0，1），且PA =PB ，求直线l 的方程．23．如图，在直三棱柱111ABC A B C -中，已知AB AC =，,,M N P 分别为11,,BC CC BB 的中点，求证：（1）平面AMP ⊥平面11BB C C ； （2）1//A N 平面AMP .24．已知函数32()3,f x x ax x a R =-+∈ （I ）若3x =是()f x 的极值点，求()f x 的极值；f x是R上的单调递增函数，求实数a的取值范围. （Ⅱ）若函数()2017-2018学年第一学期期初理科数学试题参考答案一、选择题1．B 2．C. 3．B 4．B 5．C 6．B 7．A 8．C 9．A 10．D 11．C 12．D18．试题解析：（1）=2cos ρθ等价于2=2cos ρρθ①将222=,cos x y x ρρθ+=代入①既得曲线C 的直角坐标方程为2220x y x +-=，②4分（2）将5{12x y t==代入②得2180t +=，设这个方程的两个实根分别为12,,t t则由参数t 的几何意义既知， 1218MA MB t t ⋅==. 10分19．试题解析：(1)4分(2)X 的所有可能取值为0,1,2,39分E(x)=0*错误！未找到引用源。

高三上学期第二次月考试卷（150分钟，满分150分）一、现代文阅读（35分）（一）论述类文本阅读（本题共3小题，9分）阅读下面文字，完成1-3题。

过去总说我们的阅读量小，其实那要看阅读什么，我们读书的数量确实不多，可读微信的时间和数量，恐怕在世界上都数一数二。

不妨看看四周，无时无刻不在那里看微信，可以说是任何地方的风景。

开会、上课、听讲，凡是低着头的，十有八九是在读微信；上班时间看微信，已经成了常态行为，更何况微信与工作有关的也不在少数；坐公交、乘火车，等在候车室、候机室、候诊室里，盯着微信的恐怕占大多数，幸亏飞机上不许开手机，否则，读微信的比例大概接近百分之百。

从前纸质媒体独占天下时，蹲厕所看报是一景，今天，上厕所不看微信的还剩下多少？微信的诞生，当然是好事，让阅读大大提速，看什么都变得无比便捷，可这种如潮水一般涌来的微信量也很容易令人沉迷。

须臾离不开微信，一刻不盯着微信就有如失魂落魄，这已经是很多人的生活常态；一家几口各看各的微信，还互转互动，这已经是当今家庭生活的普遍景致。

姑且不说在看微信中度过的生活究竟是好是赖，仅是把阅读都耗费在微信里，就会让原本已经少得可怜的读书时间更无一席之地。

书痴，古往今来向来都是少数，但微信痴如今正与日俱增。

阅读微信一旦成瘾，茶饭无心、睡眠不足、耽误了正事，恐怕就是病态了，不仅无益于身心健康，而且还会带来诸多副作用。

因为这种病态阅读常常是排他的、痴迷的、偏听偏信的，即便谬误就在眼前，也浑然不觉。

尽管读微信也是阅读，好微信就是好文章，好的微信公众号就是一张好报纸、一本好刊物，甚至是一部便携式的好书，可是，阅读那些转来发去的微信时你也会发现，这毕竟有别于书籍、报刊。

个人间转发的微信大多是单向的，很少能看到相左的意见，即使有，往往也难得再次转发到同一个人的手里。

这还不如阅读报刊，起码不同的说法、争论的意见都可以相继呈现；更不如网页，不但有不同的声音，而且还有纠错的跟帖及时出现。

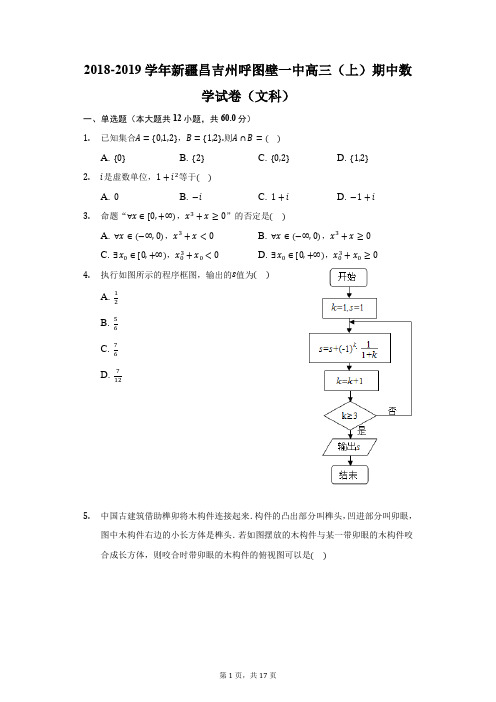
2018-2019学年新疆昌吉州呼图壁一中高三（上）期中数学试卷（文科）一、单选题（本大题共12小题，共60.0分）1.已知集合A={0,1,2}，B={1,2}.则A∩B=()A. {0}B. {2}C. {0,2}D. {1,2}2.i是虚数单位，1+i2等于()A. 0B. −iC. 1+iD. −1+i3.命题“∀x∈[0,+∞)，x3+x≥0”的否定是()A. ∀x∈(−∞,0)，x3+x<0B. ∀x∈(−∞,0)，x3+x≥0C. ∃x0∈[0,+∞)，x03+x0<0D. ∃x0∈[0,+∞)，x03+x0≥04.执行如图所示的程序框图，输出的s值为()A. 12B. 56C. 76D. 7125.中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是()A.B.C.D.6. 已知a ⃗ =(4,2)，b ⃗ =(6,y)，若a ⃗ //b ⃗ ，则y 等于( )A. −12B. −3C. 3D. 127. 等差数列{a n }中，a 1，a 2，a 3分别是下表第一、二、三行中的某一个数，且a 1，a 2，a 3中的任何两个数不在下表的同一列．第一列第二列第三列第一行 2 3 5 第二行 8 6 14 第三行11913则a 4的值为( )A. 18B. 15C. 12D. 208. 若实数x ，y 满足{y ≥2x −2y ≥−x +1y ≤x +1，则z =3x −y 的最大值是( )A. −2B. −1C. 5D. 39. 在△ABC 中，三个内角A ，B ，C 所对的边分别为a ，b ，c ，若sin 2B −sin 2C −sin 2A =√3sinAsinC ，则角B 的大小为( )A. 30°B. 60°C. 120°D. 150°10. 函数y =2|x|sin2x 的图象可能是( )A. B.C. D.11.设P是椭圆x25+y23=1上的动点，则P到该椭圆的两个焦点的距离之和为()A. 2√2B. 2√3C. 2√5D. 4√212.曲线f(x)=x2+2x−e x在点(0,f(0))处的切线的方程为()A. y=x−1B. y=x+1C. y=2x−1D. y=2x+1二、单空题（本大题共4小题，共20.0分）13.若某群体中的成员只用现金支付的概率为0.45，既用现金支付也用非现金支付的概率为0.15，则不用现金支付的概率为______．14.某公司有大量客户，且不同年龄段客户对其服务的评价有较大差异．为了解客户的评价，该公司准备进行抽样调查，可供选择的抽样方法有简单随机抽样、分层抽样和系统抽样，则最合适的抽样方法是______．15.直线y=x+1与圆x2+y2+2y−3=0交于A，B两点，则|AB|=．16.函数y=tan(2x+π3)的最小正周期是______ ．三、解答题（本大题共7小题，共82.0分）17.已知函数f(x)=A(sinωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示．(1)求函数的解析式；(2)求函数的单调递增区间；(3)当x∈[0, π2]时，求f(x)的取值范围．18.如图，正方形ABCD的边长为1，正方形ADEF所在平面与平面ABCD互相垂直，G，H是DF，FC的中点．(1)求证：GH//平面CDE；(2)求证：BC⊥平面CDE；(3)求三棱锥G−ABC的体积．19. 央视记者柴静的《穹顶之下》的播出，让大家对雾霾天气的危害有了更进一步的认识，对于雾霾天气的研究也渐渐活跃起来，某研究机构对春节燃放烟花爆竹的天数x 与雾霾天数y 进行统计分析，得出表中数据．(1)请画出表中数据的散点图；(画在答题卷上的坐标纸上)(2)请根据上表提供的数据，用最小二乘法求出y 关于x 的线性回归直线方程y ̂=b ̂x +a ̂；(3)试根据(2)求出线性回归方程，预测燃放烟花爆竹的天数为9的雾霾天数． (相关公式：b =∑x i n i=1y i −nx −y−∑x i 2n i=1−nx−2，a ̂=y −−b ̂x −)20. 求椭圆x 2+9y 2=81的长轴长、短轴长、离心率、焦点和顶点坐标．21. 已知函数f(x)=xlnx(Ⅰ)求函数f(x)的极值点；(Ⅱ)若直线l 过点(0,−1)，并且与曲线y =f(x)相切，求直线l 的方程．22. 以直角坐标系的原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，已知曲线C 的极坐标方程为ρsin 2θ=4cosθ． (1)求曲线C 的直角坐标方程；(2)若直线l 的参数方程为{x =1+2√55ty =1+√55t(t 为参数)，设点P(1,1)，直线l 与曲线C 相交于A ，B 两点，求|PA|+|PB|的值．23. 已知定义在R 上的函数f(x)=|x +1|+|x −2|的最小值为a ．(Ⅰ)求a 的值；(Ⅱ)若p ，q ，r 为正实数，且p +q +r =a ，求证：p 2+q 2+r 2≥3．答案和解析1.【答案】D【解析】【分析】本题主要考查了交集及其运算，考查学生的计算能力，属于基础题．进行交集的运算即可．【解答】解：∵A={0,1,2}，B={1,2}；∴A∩B={1,2}．故选D．2.【答案】A【解析】解：由题意知，1+i2=1−1=0故选：A．由题意知，本题直接根据i的运算性质进行计算即可得出答案，选出正确选项本题考查复数的虚数单位i的计算性质，属于简单计算题3.【答案】C【解析】【分析】本题考查全称量词命题的否定，掌握此类命题的否定的规则是解答的关键，属于基础题．全称量词命题的否定是一个存在量词命题，按此规则写出其否定即可得出正确选项．【解答】解：∵命题“∀x∈[0,+∞)，x3+x≥0”是一个全称量词命题．∴其否定命题为：∃x0∈[0,+∞)，x03+x0<0，故选C．4.【答案】B【解析】解：执行循环前：k=1，s=1，在执行第一次循环时，s=1−12=12，由于k=2<3，所以执行下一次循环，s=12+13=56，k=3，直接输出s=56，故选：B．根据题意，即可得解．本题考查程序框图和循环结构，属于基础题．5.【答案】A【解析】【分析】本题看出简单几何体的三视图的画法，是基本知识的考查．直接利用空间几何体的三视图的画法，判断选项的正误即可．【解答】解：由题意可知，如图摆放的木构件与某一带卯眼的木构件咬合成长方体，小的长方体，是榫头，从图形看出，轮廓是长方形，内含一个长方形，并且一条边重合，另外3边是虚线，所以木构件的俯视图是A．故选：A．6.【答案】C【解析】解：a⃗=(4,2)，b⃗ =(6,y)，若a⃗//b⃗ ，可得4y=12，解得y=3，故选：C．利用向量共线的充要条件列出方程求解即可．本题考查向量共线的充要条件的应用，是基础题．7.【答案】A【解析】 【分析】本题主要考查等差数列的定义，等差数列的通项公式，属于基础题．由题意可得a 1 =3，a 2 =8，a 3=13，可得此等差数列的公差d =5，即得a 4=a 3+d 的值． 【解答】解：由题意可得a 1=3，a 2=8，a 3=13， 故此等差数列的公差为5， 故a 4=a 3+d =18， 故选A ．8.【答案】C【解析】解：由约束条件{y ≥2x −2y ≥−x +1y ≤x +1作出可行域如图，联立{y =x +1y =2x −2，解得A(3,4)，化目标函数z =3x −y 为y =3x −z ，由图可知，当直线y =3x −z 过A 时，直线在y 轴上的截距最小，z 有最大值为5． 故选：C ．由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数得答案．本题考查简单的线性规划，考查数形结合的解题思想方法，是中档题．9.【答案】D【解析】解：在△ABC中，根据sin2B−sin2C−sin2A=√3sinAsinC，利用正弦定理可得b2−c2−a2=√3ac，即c2+a2−b2=−√3ac，∴cosB=c2+a2−b22ac =−√32，∴B=150°，故选：D．由题意利用正弦定理可得b2−c2−a2=√3ac，再利用余弦定理求出cosB=c2+a2−b22ac的值，可得B的值．本题主要考查正弦定理、余弦定理的应用，属于基础题．10.【答案】D【解析】【分析】本题考查函数的性质和赋值法的应用，属于基础题．直接利用函数的奇偶性和特殊值求出结果．【解答】解：根据函数的解析式y=2|x|sin2x，，得到函数为奇函数，其图象关于原点对称，故排除A和B．当x=π2时，函数的值为0，故排除C．故选D．11.【答案】C【解析】【分析】本题考查椭圆的定义，属于基础题．直接利用椭圆方程求出a，再利用椭圆定义求解即可．解：椭圆x25+y23=1的焦点坐标在x轴，a=√5，P是椭圆x25+y23=1上的动点，由椭圆的定义可知，P到该椭圆的两个焦点的距离之和为2a=2√5．故选C．12.【答案】A【解析】【分析】本题考查导数的运用：求切线的方程，考查直线方程的运用，正确求导是解题的关键，属于基础题．求出导数，求得切线的斜率，由斜截式方程，即可得到切线的方程．【解答】解：f(x)=x2+2x−e x的导数为f′(x)=2x+2−e x，∴f′(0)=1，∵f(0)=−1，∴曲线f(x)=x2+2x−e x在点(0,f(0))处的切线的方程为y=x−1．故选A．13.【答案】0.4【解析】解：某群体中的成员只用现金支付的概率为0.45，既用现金支付也用非现金支付的概率为0.15，则不用现金支付的概率为P=1−0.45−0.15=0.4．故答案为：0.4．利用对立事件概率计算公式能求出不用现金支付的概率．本题考查概率的求法，考查对立事件概率计算公式等基础知识，考查运算求解能力，是基础题．14.【答案】分层抽样【分析】本题考查抽样方法的判断，考查简单随机抽样、分层抽样和系统抽样的性质等基础知识，是基础题．利用简单随机抽样、分层抽样和系统抽样的定义、特点直接求解．【解答】解：某公司有大量客户，因为不同年龄段客户对其服务的评价有较大差异，所以最合适的抽样方法是分层抽样．故答案为：分层抽样．15.【答案】2√2【解析】【分析】求出圆的圆心与半径，通过点到直线的距离以及半径、半弦长的关系，求解即可．本题考查直线与圆的位置关系的应用，弦长的求法，考查计算能力．属于基础题．【解答】解：圆x2+y2+2y−3=0的标准方程为x2+(y+1)2=4，则圆心(0,−1)，半径为：2，=√2，圆心到直线的距离为：√2所以|AB|=2√22−(√2)2=2√2．故答案为：2√2．16.【答案】π2)，【解析】解：∵y=tan(2x+π3∴函数的周期T=π，2故答案为：π．2根据正切函数的周期公式即可得到结论．本题主要考查三角函数的周期的计算，利用三角函数的周期公式是解决本题的关键，比17.【答案】解：(1)由图象知A=2，T=2×(11π12−5π12)=π，∴2πω=π，∴ω=2由图象过点(5π12,0)，得到：2sin(5π6+φ)=0，观察图象取5π6+φ=π，得φ=π6∴f(x)=2sin(2x+π6) (2)利用整体思想：令：−π2+2kπ≤2x+π6≤π2+2kπ，k∈Z解得−π3+kπ≤x≤π6+kπ，k∈Z故函数的单调递增区间为[−π3+kπ,π6+kπ]，k∈Z(3)0≤x≤π2，∴π6≤2x+π6≤5π6∴f(x)的取值范围为[−1,2]．【解析】(1)根据函数的图象确定A，ω，φ的值，从而求出函数的解析式．(2)利用整体思想求出函数的单调区间．(3)根据函数的图象，利用函数的定义域求函数的值域．本题考查的知识要点：利用正弦型函数的图象求解析式，正弦型函数单调区间的确定，利用定义域求函数的值域．属于基础题型．18.【答案】(1)证明：∵G，H分别是DF，FC的中点，∴△FCD中，GH//CD，∵CD⊂平面CDE，GH⊄平面CDE，∴GH//平面CDE ．(2)证明：平面ADEF ⊥平面ABCD ，交线为AD ，∵ED ⊥AD ，ED ⊂平面ADEF ，AD ⊂平面ABCD ，∴DE ⊥平面ABCD ，∴BC ⊂平面ABCD ，∴ED ⊥BC ，又∵BC ⊥CD ，CD ∩DE =D ，∴BC ⊥平面CDE ．(3)解：依题意：点G 到平面ABCD 的距离ℎ等于点F 到平面ABCD 的一半，…(11分) 即：ℎ=12.…(12分)∴V G−ABC =13⋅12⋅1⋅1⋅12=112.…(14分)(求底面积对的有1分)【解析】(1)通过G ，H 分别是DF ，FC 的中点，说明GH//CD ，然后证明GH//平面CDE ．(2)平面ADEF ⊥平面ABCD ，交线为AD ，证明DE ⊥平面ABCD ，ED ⊥BC ，然后证明BC ⊥平面CDE ；(3)点G 到平面ABCD 的距离ℎ等于点F 到平面ABCD 的一半，求出底面面积，即可求三棱锥G −ABC 的体积．本题考查直线与平面平行与垂直的证明，考查几何体的体积的求法，考查计算能力、空间想象能力．19.【答案】解：(1)根据表中数据，画出散点图如图所示：(2)根据公式，计算∑x i 4i=1y i =4×2+5×3+7×5+8×6=106，x −=14(4+5+7+8)=6，y −=14(2+3+5+6)=4，∑x i 24i=1=42+52+72+82=154，则b ̂=∑x i n i=1y i −nx −y −∑x i 2n i=1−4x −2=106−4×6×4154−4×62=1； a ̂=y −−b ̂x −=4−6=−2， 所以线性回归方程为y ̂=b ̂x +a ̂=x −2，(3)由线性回归方程可以预测，燃烧烟花爆竹的天数为x =9时，雾霾天数为y ̂=9−2=7天．【解析】(1)根据表中数据，画出散点图即可；(2)根据公式，计算线性回归方程的系数即可；(3)由线性回归方程预测x =9时，y ̂=7．本题考查了统计知识中的画散点图与求线性回归方程的应用问题，解题的关键是求出线性归回方程中的系数，是基础题目．20.【答案】解：由x 2+9y 2=81，得x 281+y 29=1， 则a =9，b =3，c =√81−9=6√2．∴椭圆x 2+9y 2=81的长轴长为18，短轴长为6，离心率e =6√29=2√23， 焦点坐标为F 1(−6√2,0)、F 2(6√2,0)，顶点坐标为A 1(−9,0)、A 2(9,0)、B 1(0,−3)、B 2(0,3)．【解析】化椭圆方程为标准方程，分别求出a 、b 、c 的值，则答案可求．本题考查椭圆的标准方程与几何性质，是基础题．21.【答案】解：(Ⅰ)f′(x)=lnx +1，x ∈(0,+∞)又∵当f′(x)=lnx +1=0，得x =1e ，如下表∴f(x)在(0,1e )上单调递减，在(1e ,+∞)上单调递增，在x =1e 处取得极小值， 且极小值为f(1e )=−1e ．(Ⅱ)∵f′(x)=lnx +1，∴f(x)=xlnx 在(x 0,x 0lnx 0)处的切线方程为y −x 0lnx 0=(lnx 0+1)(x −x 0)， ∵切线l 过点(0,−1)，∴−1−x 0lnx 0=(lnx 0+1)(−x 0)，解得x 0=1，∴直线l 的方程为：y =x −1．【解析】(Ⅰ)由原函数的解析式，我们易求出函数的导函数，进而根据导函数的零点对函数的定义域进行分段讨论后，即可得到答案．(Ⅱ)由f′(x)=lnx +1，知f(x)=xlnx 在(x 0,x 0lnx 0)处的切线方程为y −x 0lnx 0=(lnx 0+1)(x −x 0)，由切线l 过点(0,−1)，解得x 0=1，由此能求出直线l 的方程． 本题考查曲线的切线方程的求法，解题时要认真审题，仔细解答，注意导数性质的合理运用．22.【答案】解：(1)∵曲线C 的极坐标方程为ρsin 2θ=4cosθ，即ρ2sin 2θ=4ρcosθ， ∴曲线C 的直角坐标方程为y 2=4x ．(2)直线l 的参数方程为{x =1+2√55t y =1+√55t (t 为参数)， 代入曲线C 方程y 2=4x.可得(1+√52=4(1+√5，整理得t 2−6√5t −15=0，∵t 1⋅t 2=−15<0，∴点P 在AB 之间，∴|PA|+|PB|=|t 1−t 2|=√(t 1+t 2)2−4t 1t 2=4√15．【解析】(1)曲线C 的极坐标方程转化为ρ2sin 2θ=4ρcosθ，由此能求出曲线C 的直角坐标方程．(2)直线l 的参数方程代入曲线C 方程y 2=4x.可得t 2−6√5t −15=0，由此能求出|PA|+|PB|．本题考查曲线的直角坐标方程的求法，考查两条线段和的求法，考查参数方程、极坐标方程、直角坐标方程的互化等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．23.【答案】(Ⅰ)解：∵f(x)=|x +1|+|x −2|≥|(x +1)−(x −2)|=3， ∴f(x)min =3，即a =3．(Ⅱ)证明：由(Ⅰ)知，a=3，因为p2+q2≥2pq，p2+r2≥2pr，q2+r2≥2qr，∴2(p2+q2+r2)≥2pq+2pr+2qr，∴3(p2+q2+r2)≥p2+q2+r2+2pq+2pr+2qr=(p+q+r)2=32=9，∴p2+q2+r2≥3．【解析】(Ⅰ)利用绝对值不等式的几何意义可得f(x)=|x+1|+|x−2|≥|(x+1)−(x−2)|=3，从而可得a的值；(Ⅱ)利用重要不等式p2+q2≥2pq，p2+r2≥2pr，q2+r2≥2qr，可得3(p2+q2+ r2)≥p2+q2+r2+2pq+2pr+2qr=(p+q+r)2=32=9，于是可证的结论．本题考查绝对值不等式的性质及应用，着重考查重要不等式的应用，考查推理证明的能力，考查转化思想．。

高三10月月考理科数学试卷一、选择题（每小题5分，共计60分）1．集合A={x|x 2+2x ＞0｝，B={x ｜x 2+2x ﹣3＜0｝，则A∩B=（ ) A. （﹣3,1) B 。

(﹣3，﹣2） C 。

R D 。

（﹣3，﹣2）∪(0，1) 2．( )A. B 。

C.D 。

3．已知{}n a 是等差数列，且23101148a a a a +++=，则67a a +=（ ）A 。

12 B. 24 C 。

20 D 。

164．直线被圆截得的弦长为 （ )A.B 。

C. D 。

5．已知平面向量()1,a m =，()3,1b =-且()2//a b b +，则实数m 的值为（ ） A 。

13B.13-C. 23D.23-6．执行如图所示的程序框图，则输出的S =（ ）A. 7B. 11C.26 D.307．在区间[]2,3-上随机选取一个数X ，则1X ≤的概率为（ ） A 。

45B 。

35C 。

25D 。

158如图是某几何体的三视图，则该几何体的外接球表面积为( )A ．200πB ．150πC ．100πD ．50π 9．函数()21log f x x x =-的一个零点落在下列哪个区间（)A. ()0,1 B 。

()1,2 C. ()2,3 D 。

()3,410．若实数,x y 满足不等式组330{23010x y x y x y +-≥--≤-+≥，则x y +的最大值为( ）A 。

1 B.157C. 9 D 。

71511．已知抛物线24y x =的焦点为,F A B 、，为抛物线上两点，若3AF FB =，O 为坐标原点，则AOB ∆的面积为（ ）A．3B．3C．3D．312．已知定义在R 上的奇函数()f x 在[)0,+∞上递减，若()()321f xx a f x -+<+对[]1,2x ∈-恒成立，则a 的取值范围为（ ）A 。

()3,-+∞B 。

(),3-∞- C. ()3,+∞ D. (),3-∞ 二、填空题（每小题5分共计20分） 13．在ABC ∆中,75,45AB A B ∠=︒∠=︒,则AC = ．14、12(1)xdx -+⎰=___________.15．已知1x >,则()11f x x x =+-的最小值是__________．16．设函数f （x ）是定义在R 上的偶函数，且对任意的x ∈R 恒有f (x ＋1）＝f （x －1)，已知当x ∈[0，1］时,f (x )＝2x ，则有：①2是函数f （x )的周期;②函数f (x )在（1，2）上是减函数,在(2，3)上是增函数； ③函数f (x ）的最大值是1，最小值是0. 其中所有正确命题的序号是________．三、解答题（共计70分） 17．已知函数()f x 3sin 23x π⎛⎫=+ ⎪⎝⎭.（1)求函数()f x 的单调递增区间； （2）在ABC 中,内角A ， B ， C 的对边为a ， b ， c ，已知()32f A =，2a =，3B π=，求ABC 的面积. (本小题满分12分）18在直三棱柱ADE －BCF 中，平面ABFE 和平面ABCD 都是正方形且互相垂直,M 为AB 的中点,O 为DF 的中点．求证 (1）OM ∥平面BCF ;（2)平面MDF ⊥平面EFCD .（本小题满分12分)19。

呼图壁县一中2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 设S n 为等比数列{a n }的前n 项和，若a 1=1，公比q=2，S k+2﹣S k =48，则k 等于（ ）A ．7B ．6C ．5D ．4 2． 设x ，y ∈R ，且x+y=4，则5x +5y 的最小值是（ ）A ．9B ．25C ．162D ．503． 已知i为虚数单位，则复数所对应的点在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 4． 记,那么ABCD5． 复数i iiz (21+=是虚数单位）的虚部为（ ）A ．1-B ．i -C ．i 2D ．2【命题意图】本题考查复数的运算和概念等基础知识，意在考查基本运算能力． 6． 函数f （x ）=，则f （﹣1）的值为（ ）A ．1B ．2C ．3D ．47． 设函数y=的定义域为M ，集合N={y|y=x 2，x ∈R}，则M ∩N=（ ） A ．∅B ．NC ．[1，+∞）D ．M8． 已知角θ的终边经过点P （4，m ），且sin θ=，则m 等于（ ） A ．﹣3 B ．3 C．D ．±39． 若实数x ，y 满足不等式组则2x+4y 的最小值是（ ）A ．6B ．﹣6C ．4D ．2班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________10．已知F 1、F 2分别是双曲线﹣=1（a ＞0，b ＞0）的左、右焦点，过点F 2与双曲线的一条渐近线平行的直线交双曲线另一条渐近线于点M ，若点M 在以线段F 1F 2为直径的圆外，则双曲线离心率的取值范围是（ ）A ．（1，）B ．（，+∞） C ．（，2）D ．（2，+∞）11．A={x|x ＜1}，B={x|x ＜﹣2或x ＞0}，则A ∩B=（ ）A ．（0，1）B ．（﹣∞，﹣2）C ．（﹣2，0）D ．（﹣∞，﹣2）∪（0，1）12．sin （﹣510°）=（ ）A ．B ．C ．﹣D ．﹣二、填空题13．如图，正方形''''O A B C 的边长为1cm ，它是水平放置的一个平面图形的直观图，则原图的 周长为 ．1111]14．在ABC ∆中，已知sin :sin :sin 3:5:7A B C =，则此三角形的最大内角的度数等 于__________.15．若全集，集合，则16．函数y=sin 2x ﹣2sinx 的值域是y ∈ ．17．一组数据2，x ，4，6，10的平均值是5，则此组数据的标准差是 ．18．函数f （x ）=2a x+1﹣3（a ＞0，且a ≠1）的图象经过的定点坐标是 ．三、解答题19．已知平面直角坐标系xoy 中的一个椭圆，它的中心在原点，左焦点为，右顶点为D （2，0），设点A （1，）． （1）求该椭圆的标准方程；（2）若P 是椭圆上的动点，求线段PA 的中点M 的轨迹方程；（3）过原点O 的直线交椭圆于B ，C 两点，求△ABC 面积的最大值，并求此时直线BC 的方程．20．命题p：关于x的不等式x2+2ax+4＞0对一切x∈R恒成立，q：函数f（x）=（3﹣2a）x是增函数．若p ∨q为真，p∧q为假．求实数a的取值范围．21．已知函数f（x）=e﹣x（x2+ax）在点（0，f（0））处的切线斜率为2．（Ⅰ）求实数a的值；（Ⅱ）设g（x）=﹣x（x﹣t﹣）（t∈R），若g（x）≥f（x）对x∈[0，1]恒成立，求t的取值范围；（Ⅲ）已知数列{a n}满足a1=1，a n+1=（1+）a n，求证：当n≥2，n∈N时f（）+f（）+L+f（）＜n•（）（e为自然对数的底数，e≈2.71828）．22．如图，四边形ABCD内接于⊙O，过点A作⊙O的切钱EP交CB 的延长线于P，己知∠PAB=25°．（1）若BC是⊙O的直径，求∠D的大小；（2）若∠DAE=25°，求证：DA2=DC•BP．23．（本小题满分12分）某媒体对“男女延迟退休”这一公众关注的问题进行名意调查，下表是在某单位（Ⅱ）从赞同“男女延迟退休”的80人中，利用分层抽样的方法抽出8人，然后从中选出2人进行陈述 发言，求事件“选出的2人中，至少有一名女士”的概率． 参考公式：22()K ()()()()n ad bc a b c d a c b d -=++++，()n a b c d =+++【命题意图】本题考查统计案例、抽样方法、古典概型等基础知识，意在考查统计的思想和基本运算能力24．在数列{a n }中，a 1=1，a n+1=1﹣，b n =，其中n ∈N *．（1）求证：数列{b n }为等差数列；（2）设c n =b n+1•（），数列{c n }的前n 项和为T n ，求T n ；（3）证明：1+++…+≤2﹣1（n ∈N *）呼图壁县一中2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题13．8cm14．12015．{|0＜＜1｝16．[﹣1，3]．17．2．18．（﹣1，﹣1）．三、解答题19．20．21．22．23．24．。