四川省绵阳南山中学2016-2017学年高一上学期10月月考试题 数学word 版含答案

四川省绵阳南山中学2016届高三数学上学期10月月考试题 理一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的1. 已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |－5＜x ＜5}，则( ) A ．A ∩B ＝φ B ．A ∪B ＝R C ．B ⊆A D ．A ⊆B2.下列有关命题的说法正确的是( )．A ．“x ＝－1”是“x 2－5x －6＝0”的必要不充分条件B ．命题“若x ＝y ，则sin x ＝sin y ”的逆否命题为真命题C ．命题“若x 2＝1，则x ＝1”的否命题为：“若x 2＝1，则x ≠1”D ．命题“∃x ∈R ，使得：x 2＋x ＋1<0”的否定是：“∀x ∈R ，均有x 2＋x ＋1<0”3.若2a b a b a +=-=r r r r r，则a b +r r 与a r 的夹角为（ ）A .6π B . 3π C. 23π D . 56π 4. 已知01a b <<<，则（ ） A .11b a > B . 11()()22a b < C .22(lg )(lg )a b < D . 11lg lg a b>5． 函数sin ()xy ex ππ=-≤≤的大致图像为()6.设2z x y =+，其中变量,x y 满足条件433525x y x y x m -≤-⎧⎪+≤⎨⎪≥⎩，若z 的最小值为3，则m 的值为（ ）A ．1 B ． 2C ． 3D ． 47.在△ABC中，222sin a b c C ++=，则△ABC 的形状是( ) A ．直角三角形 B ．锐角三角形 C ．钝角三角形 D ．正三角形8.已知函数()f x =[]()11,2,02(2),0,x x f x x ⎧-+∈-⎪⎨-∈+∞⎪⎩若方程f (x )＝x ＋a 在区间[－2，4]内有3个不等的实根，则实数a 的取值范围是( )A ．{a |－2<a <0}B ．{a |－2<a ≤0}C ．{a |－2<a <0或1<a <2}D ．{a |－2<a <0或a ＝1}9. 已知定义在R 上的可导函数()f x 的导函数为()f x '，满足()()f x f x '<，且(2)f x +为偶函数，(4)1f =，则不等式()xf x e <的解集为( )A ．(－2，＋∞)B ．(0，＋∞)C ．(1，＋∞)D ．(4，＋∞) 10.在实数集R 中定义一种运算“*”,对任意b a R b a *,,∈为唯一确定的实数,且具有性质: (1)对任意;**,,a b b a R b a =∈ (2)对任意;0*,a a R a =∈(3)对任意.2)*()*()(**)*(,,c b c c a ab c c b a R b a -++=∈ 关于函数xx x f 21*)2()(=的性质,有如下说法: ①函数f (x )的最小值为3; ②函数f (x )为奇函数;③函数f (x )的单调递增区间为),21(),21,(+∞--∞. 其中所有正确说法的个数为 ( )A .0B .1C .2D .3二、填空题：本大题共5小题，每小题5分，共25分．把答案填在答题卡的相应位置． 11.计算22log 3321272log lg 42lg58-⋅++得的值为 . 12. 已知正项等比数列{}n a 的前n 项和n S ，若352651,20,64,q a a a a S >+===则 ．13.已知函数()3sin 2cos f x x x x =+-的图像在点A (0x ，0()f x )处的切线斜率为3，则0tan x 的值是________．14.设0,a b >>1，若4121a b a b +=+-，则的最小值为 . 15.有下列4个命题：①若函数()f x 定义域为R ,则()()()g x f x f x =--是奇函数;②若函数()f x 是定义在R 上的奇函数,R x ∈∀,()(2)0f x f x +-=,则()f x 图像关于x =1对称;③已知x 1和x 2是函数定义域内的两个值(x 1<x 2),若12()()f x f x >,则()f x 在定义域内单调递减;④若()f x 是定义在R 上的奇函数, (2)f x +也是奇函数,则()f x 是以4为周期的周期函数. 其中,正确命题是 （把所有正确结论的序号都填上）.三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．解答写在答题卡上的指定区域内．16.(本小题满分12分)已知p :函数2()24()f x x mx m R =-+∈在[2,)+∞上单调递增,q :关于的不等式244(2)10x m x +-+>(m ∈R )的解为R .若“p 或q ”为真命题,“p 且q ”为假命题,求实数m 的取值范围.17.（本小题满分12分）已知向量,3(sin ,1),(cos ,),()()2m x n x f x m n m =-==+u r r u r r u r g(1)当x ∈[0,2π]时，求函数y ＝f (x )的值域；(2)锐角三角形ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，若5,a b ==(),.2B f a c =求边18. （本小题满分12分）已知等差数列}{n a 各项均为正数，11=a ，且34115,,2a a a +成等比数列．(1)求数列}{n a 的通项公式；(2)设 ,11=b 且当2≥n 时，11-=n n n a a b ，n T 为数列}{n b 的前n 项和，证明：35<n T .19.(本小题满分12分)某厂生产某种产品的年固定成本为250万元,每生产x 千件,需另投入成本C (x )万元.当年产量不足80千件时,21()103C x x x =+(万元),当年产量不小于80千件时,10000()511450C x x x=+-(万元),每件商品售价为05.0万元,通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L (x ) (万元)关于年产量x (千件)的函数解析式;(2)当年产量为多少千件时,该厂在这一商品的生产中所获利润最大？并求出最大利润.20.(本小题满分13分)已知二次函数2()1f x ax bx =++.(1)若1b a =+,且对任意[1,1]a ∈-时都有()0f x ≥成立,求实数x 的取值范围; (2)若对1212,,<x x R x x ∈,12()()f x f x ≠,方程121()[()()]2f x f x f x =+有两个不等实根,证明必有一根属于12(,)x x .21. （本小题满分14分）已知函数()f x 12ln ,m emx x m R x-+=--∈函数1()ln cos g x x x θ=+在[1，＋∞)上为增函数，且(,)22ππθ∈-.(1)求θ得值(2)当m ＝0时，求函数()f x 的单调区间和极值；(3)若在[1，e]上至少存在一个x 0，使得00()()f x g x >成立，求m 的取值范围． 南山中学2016级高三一诊模拟考试数学(理科)答案一.选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项二.11. 20. 12. 31. 13.12-14. 9. 15. ①④. 三.解答题(本大题共6小题,共75分,解答应写出文字说明证明过程或推演步骤.) 16.函数2()24()f x x mx m R =-+∈的对称轴为m x =,故p 为真时,2≤m .…………………3 q 为真时,310144)]2(4[2<<⇒<⨯⨯--=∆m m .……………………………………………6 ∵“p 或q ”为真命题, “p 且q ”为假命题,∴p 与q 一真一假. 若p 真q 假,则,2≤m 且1≤m 或3≥m ,∴1≤m ; (8)若p假q 真,则,2>m 且31<<m ,∴32<<m (10)综上,实数m 的取值范围是1≤m 或32<<m (12)17.（1）1(sin cos ,)2m n x x +=+u r r ，所以21111()(sin cos )sin sin sin cos sin 2cos 22222f x x x x x x x x x =+-=+-=-，…3分即()f x )4x π=-，………………………………………………………………4分当[0,]2x π∈时，32[,]444x πππ-∈-，sin(2)[42x π-∈-，所以当[0,]2x π∈时，函数()y f x =的值域是1[2-；……………………………6分 （2）由()25B f =，得3sin()45B π-=，又(,)444B πππ-∈-，所以4cos()45B π-=，………………………………………………………………………8分因此”cos cos[()]cos()cos sin()sin 444444B B B B ππππππ=-+=---=, ……9分由余弦定理2222cos b a c ac B =+-，得2223298225510c c c =+-⨯⨯， ……11分所以：8c a ==。

川省彭州中学高16级高一上期10月月考数学试题命题人审题人本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，考试时间120分钟。

第I卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1、已知全集U={1, 2, 3, 4, 5, 6, 7, 8}，集合A={2, 3, 5, 6}，集合B={1, 3, 4, 6, 7}，则集合A C U B=（）A．{2, 5} B．{3, 6} C．{2, 5, 6} D．{2, 3, 5, 6, 8}2、设集合M={0, 1, 2}，N={x|x23x+20}，则M N=（）A．{1} B．{2} C．{0, 1} D．{1, 2}3、已知集合A={2, 0, 1}，集合B={x||x|<a，且x Z}，则满足A B的实数a可以取的一个值是（）A．0 B．1 C．2 D．34、50名同学参加跳远和铅球测验，跳远和铅球测验成绩分别为及格40人和31人，两项测验成绩均不及格的有4人，两项测验成绩都及格的人数是（）A．35 B．25 C．28 D．155、下列各图中，可表示函数y=f(x)的图象的只可能是图中的（）6、函数y=1x 1--+1的图象是下列图象中的（ ）7、设函数f(x)=⎩⎨⎧≥<-.1x ,x 2,1x ,b x 3若f(f(65))=4，则b=（ ）A ．1B ．87 C ．43 D ．218、函数y=x22x+3 (1x2)的值域是（ ）A ．RB ．C ．D ．上是增函数，在上是增函数，且最大值是6 B ．在上是减函数，且最大值是6 C ．在上是增函数，且最小值是6 D ．在上是减函数，且最小值是612、若奇函数f(x)在(0, +)上是增函数，又f(3)=0，则不等式)x (f x<0的解集为（ ）A ．(3, 0)(3, +)B ．(3, 0)(0, 3)C ．(,3)(3, +) D ．(, 3)(0, 3)第II 卷 （非选择题，共90分）二、填空题（本大题共4小题，每小题5分，共20分）13、已知集合A={x|0<x<5}，B={x|x>3}，则A (C R B)= 。

四川省绵阳南山中学2016届高三数学上学期10月月考试题 文1.本试卷分第Ⅰ卷(客观题)和第Ⅱ卷(主观题)两部分,全卷共150分,考试时间120分钟.2.所有试题均答在答题卡上,答在题卷上无效．第Ⅰ卷(客观题,共50分)一.选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.全集U=R ,集合{}220A x x x =-?{}cos ,B y y x x R ==?,则A B ?( )A .{}1,2x x x <->或 B .{}12x x-＃C .{}1x x ? D.{}01x x ＃.2.已知向量,a b r r 满足1a b ==r r , 12a b ?-r r ,则2a b +=r r( )A B C D3.下列四种说法:①{}0,1A =的子集有3个；②“若22am bm <，则a b <”的逆命题为真；③“命题p q Ú为真”是“命题p q Ù为真”的必要不充分条件；④命题“2,320x R xx "?-?均有” 的否定是：“2000,320x R x x $?-?均有”.其中错误．．命题的个数有 （ ）A .0个B .1个C . 2个D . 3个4.函数3y x = 与212x y -⎛⎫= ⎪⎝⎭图象的交点坐标为(),a b ，则a 所在区间为 ( )A .()0,1B .()1,2C .()2,3D .()3,4 5.设变量x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋y ≤3，x －y ≥－1，y ≥1，则目标函数z ＝4x ＋2y 的最大值为( )A ．12B ．10C ．8D ．26.已知f (x )＝a x －2，g (x )＝log a |x |(a >0且a ≠1)，若f (4)·g (－4)<0，则y ＝f (x )，y ＝g (x )在同一坐标系内的大致图象是 ( )A. B. C. D.7.函数f (x )＝sin(2x ＋φ)⎝ ⎛⎭⎪⎫|φ|＜π2向左平移π6个单位后是奇函数，则函数f (x )在⎣⎢⎡⎦⎥⎤0，π2上的最小值为A. -B ．12-C ．12D 8.下列三个数：33ln,ln ,ln 3322a b c p p =-=-=-，大小顺序正确的是 ( ) A . a c b >> B . a b c >> C . b c a >> D . b a c >>9.在边长为1的正三角形AOB 中，P 为边AB 上一个动点，则OP BP ×u u u r u u u r的最小值是 ( )A . 316-B . 316C . 116-D . 11610.设函数()f x 是定义在R 上的奇函数，且当0x <时，()2f x x =.若对任意[],2x k k ?，不等式()()9f x k f x +?恒成立，则()2log g k k=的最小值是( )A . 2B .12C .12- D .2-第Ⅱ卷(主观题,共100分)二.填空题(本大题共5小题,每小题5分,共25分)11. tan ⎝ ⎛⎭⎪⎫－43π=________. 12.已知等差数列{a n }的首项a 1＝11，公差d ＝－2，则{a n }的前n 项和S n 的最大值为________. 13.若直线()100,0ax by a b +-=>>过曲线()1sin 02y x x p =+<<的对称中心，则12a b+的最小值为________.14.已知函数()3223f x x ax bx a =+++在1x =-处取得极值0，则a b -＝______.15.已知函数(),0,ln ,0,x ae x f x x x ì£ï=í->ïî(其中e 为自然对数的底数)，若关于x 的方程()()0f f x =有且只有一个实数解，则实数a 的取值范围为______________.三.解答题(本大题共6小题,共75分,解答应写出文字说明证明过程或推演步骤.) 16.(本小题满分12分)已知函数2()2cos .2xf x x =(Ⅰ)求函数()f x 的最小正周期和值域; (Ⅱ)若1,(),33f 为第二象限角且παα-=求cos 21cos 2sin 2a a a+-的值.17.(本小题满分12分) 已知等比数列{a n }(*n N Î)满足2a 1＋a 3＝3a 2，且a 3＋2是a 2，a 4的等差中项．(Ⅰ)求数列{a n }的通项公式； (Ⅱ)若2121log ,n n n n nb a S b b b a =+=+++L ，求使S n －2n ＋1＋47<0成立的n 的最小值．18.(本小题满分12分)设函数()()2210g x ax ax b a =-++>在区间[]2,3上有最小值1和最大值4，设函数()()g x f x x=. (Ⅰ)求函数()g x 的解析式；(Ⅱ)若不等式()220x x f k -壮在区间[]1,1-上有解，求实数k 的取值范围.19.(本小题满分12分)已知A,B 分别在射线CM,CN （不含端点C ）上运动，23MCN p ?.在三角形ABC 中，角A,B,C 所对的边分别为,,a b c . (Ⅰ)若,,a b c 成等差数列，且公差为2，求c 的值；(Ⅱ)当cθ∠ABX =,试用q 表示三角形的周长，并求周长的最大值.AB MCN20.(本小题满分13分)已知函数()ln xf x a x bx =+的图象过点11,,e e ⎛⎫- ⎪⎝⎭且在点()()1,1f 处的切线与直线0x y e +-=垂直(e 为自然对数的底数，且 2.71828e L =).(Ⅰ) 求,a b 的值;(Ⅱ)若存在 01,x e e 轾Î犏犏臌，使得不等式2000113()222f x x tx +-≥-成立，求实数t 的取值范围.21.(本小题满分14分)已知函数()2(),g 2,.xf x e x x x a a R ==-++∈(Ⅰ)讨论函数()()()h x f x g x =?的单调性; (Ⅱ) 记函数()()(),0,,0,f x x x g x x jì<ï=í>ïî，设()()()()1122,,,A x x B x x ϕϕ为函数()x j 图象上的两点，且12x x <. ① 当0x >时，若()x j在A ，B 处的切线相互垂直，求证：211xx -?；② 若在点A ，B 处的切线重合，求实数a 的取值范围. 2015年10月绵阳南山中学2015年秋季2016届 一诊模拟考试数学(文科)试题答案一. 选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是二.填空题(本大题共5小题,每小题5分,共25分)11. - 12.36 13. 3+ 14. -7 15.()(),00,1-∞⋃三.解答题(本大题共6小题,共75分,解答应写出文字说明证明过程或推演步骤.) 16.(Ⅰ)5()12sin 6f x x ⎛⎫=++ ⎪⎝⎭π （或()12sin 6f x x ⎛⎫=+-⎪⎝⎭π或()12cos 3f x x ⎛⎫=++ ⎪⎝⎭π） .................................... (3)故最小正周期为π，值域为[]1,3- (6)(Ⅱ)由1()33f -=πα,得1cos 3=-α. 又因为,为第二象限角α则sin 3=α. (9)222cos 2cos sin cos sin 11cos 2sin 22cos 2sin cos 2cos 2a a a a a a a a a a a -+-===+-- (12)17.(Ⅰ) 设等比数列{a n }的公比为q ，依题意，有⎩⎪⎨⎪⎧2a 1＋a 3＝3a 2，a 2＋a 4＝2(a 3＋2)，即⎩⎪⎨⎪⎧a 1(2＋q 2)＝3a 1q ，a 1(q ＋q 3)＝2a 1q 2＋4，①②由①得q 2－3q ＋2＝0，解得q ＝1或q ＝2.当q ＝1时，不合题意，舍去；当q ＝2时，代入②得a 1＝2，所以a n ＝2·2n －1＝2n.故所求数列{a n }的通项公式a n ＝2n(n ∈N *)． .………………………………………6 (Ⅱ)b n ＝a n ＋log 21a n ＝2n ＋log 212n ＝2n－n .所以S n ＝2－1＋22－2＋23－3＋ (2)－n ＝(2＋22＋23＋ (2))－(1＋2＋3＋…＋n )＝2(1－2n)1－2－n (1＋n )2＝2n ＋1－2－12n －12n 2. (9)因为S n －2n ＋1＋47<0，所以2n ＋1－2－12n －12n 2－2n ＋1＋47<0，即n 2＋n －90>0，解得n >9或n <－10. 因为n ∈N *，故使S n －2n ＋1＋47<0成立的正整数n 的最小值为10. (12)18.(Ⅰ) ()()()211.0,g x a x b a a g x =-++->\Q 在区间[]2,3上是增函数，\()()21,34,g g ì=ïí=ïî解得： 1,0a b == \函数()g x 的解析式为()221g x x x =-+. (6)(Ⅱ)由(Ⅰ)知()221g x x x =-+()12f x x x∴=+-，()220x x f k \-壮可化为2111222x xk 骣琪+-壮琪桫………………………………………………9 令12x t =，则221k t t ?+，[]11,1,,22x t 轾?\?犏犏臌Q记()221h t t t =-+，1,22t 轾Î犏犏臌Q ，()min 1h t \=故所求实数k的取值范围是：(],1-?. (12)19.(Ⅰ) Q ,,a b c 成等差数列，且公差为2，4,2a c b c ∴=-=-.又Q 23MCN p ?，1cosC 2∴=-.∴在三角形ABC 中，有222122a b c ab +-=-, 即()()()()2224212422c c c c c -+--=---，化简得：29140c c -+=， 解得：7,c =或2c =.又4,7.c c Q >∴= (6)(Ⅱ)在三角形ABC 中，sin sin sin AC BC ABABC BAC ACB==∠∠∠22sin sin sin 33AC BC ∴===ππθ⎛⎫-θ ⎪⎝⎭，即2sin ,2sin 3AC BC π⎛⎫=θ=-θ ⎪⎝⎭. (8)∴三角形ABC 的周长()2sin 2sin 3f AC BC AB π⎛⎫θ=++=θ+-θ+ ⎪⎝⎭2sin 3π⎛⎫=+θ+ ⎪⎝⎭ (10)又20,3333Q ππππ<θ<∴<θ+<，当32ππθ+=，即6πθ=时，()f θ有最大值2. (12)20.(Ⅰ)()()ln ln ,ln xf x a x bx ax x bx f x a x a b Q '=+=+∴=++.又点()()1,1f 处的切线与直线0x y e +-=垂直，()11f a b '∴=+=. (2)又()ln xf x a x bx Q =+的图象过点11,,e e ⎛⎫- ⎪⎝⎭11a b f e e e e⎛⎫∴=-+=- ⎪⎝⎭，即1,a b -= (4)1,0a b ∴== ………………………………………………………… (6)(Ⅱ)由(Ⅰ)知()ln f x x x =，由题意()2113222f x x tx +-≥-，即2113ln 222x x x tx +-≥-， 则32ln t x x x≤++. (8)若存在 01,x e e 轾Î犏犏臌，使得不等式2000113()222f x x tx +-≥-成立， 只需t 小于或等于312ln ,,x x x e x e ⎡⎤++∈⎢⎥⎣⎦的最大值.设()312ln ,,h x x x x e x e ⎡⎤=++∈⎢⎥⎣⎦则()()()231x x h x x +-'=，当1,1x e ⎡⎤∈⎢⎥⎣⎦时，()0h x '<；当[]1,x e ∈时，()0h x '>. 故()h x 在1,1e ⎡⎤⎢⎥⎣⎦上单调递减，在[]1,e 上单调递增.()332ln 2,h e e e e e e Q =++=++11112ln 323,h e e e e e e ⎛⎫=++=-++ ⎪⎝⎭ (1)()()121240,h h e e h h e e e e ⎛⎫⎛⎫∴-=-->∴> ⎪ ⎪⎝⎭⎝⎭，故当1,,x e e ⎡⎤∈⎢⎥⎣⎦时，()h x 的最大值为1123,h e e e ⎛⎫=-++ ⎪⎝⎭故123,t e e ≤-++即实数t的取值范围是：1,23e e ⎛⎤-∞-++ ⎥⎝⎦. (13)21. (Ⅰ) ()()()()22x h x f x g xe x x a =?-++,()()22x h x e x a ¢\=-++.①当20a +?，即2a ?时，220x a -++? ，()()0,0,xe h x h x ¢Q 在R 上单调递减.②当20a +>，即2a >-时，()(xh x ex x ¢\=--当(x ?时，()0h x ¢>；当(),x ???+?时，()0h x ¢<.综上所述，当2a ?时，()h x 在R 上单调递增；当2a >-时，()h x在(-单调递增，在(),,-?+?上单调递减. (6)(Ⅱ)证明：①()()20,2,x x g x x x a Q >∴ϕ==-++()22,x x '∴ϕ=-+ 由题意可知，()()121,x x ''∴ϕ⋅ϕ=-即()()1222221,x x -+-+=- 当1x =时，()0;x 'ϕ=当01x <<时，()0;x 'ϕ>当1x >时，()0.x 'ϕ<()()121210,x x x x Q ''ϕ⋅ϕ=-<<，()()12120,0,01.x x x x 且''∴ϕ>ϕ<<<<()()()()1212122221,11,4x x x x Q -+-+=-∴--=-()121141x x =--， ()21221141x x x x ∴-=-+-.221,10,x x Q >∴->()212211141x x x x ∴-=-+≥=-,当且仅当()2211,41x x -=- 即232x ∴=时，等号成立. (10)②当()()20,2,x x g x x x a >∴ϕ==-++()()22,2x x '∴ϕ=-+∈-∞且()x 'ϕ单调递减. 当()()0,,xx x f x e <∴ϕ==()()0,1xx e '∴ϕ=∈且()x 'ϕ单调递增.由题意可得， 120.x x <<()11,xx e '∴ϕ=()2222x x 'ϕ=-+令()12122,0,0,1xe x k x k Q ∴=-+=<∴∈，12ln ,1,2k x k x ∴==-()2ln ,,1,1,24k k A k k B a ⎛⎫∴--++ ⎪⎝⎭切线重合，则A ，B 均在切线上.214,1ln 2k a k k k k -++-∴=--化简得()212ln ,0,14k a k k k k =--+-∈令()()212ln ,0,14k h k k k k k =--+-∈，()1ln ,2kh k k '=-+- ()0,1,k Q ∈易知()h k '为单调递减，()()1102h k h ''∴>=> ，()h k ∴单调递增，()31,,4h k ⎛⎫∴∈- ⎪⎝⎭即31,.4a ⎛⎫∈- ⎪⎝⎭ (14)。

联系电话：4000-916-716四川省绵阳南山中学2017届高三上学期10月月考试题（文）一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一项是符合题目要求的．1．集合}}{{2|10,|4,M x g x N x x M N =>=≤=I 则（ ）A ．（0，2）B ．（1，2]C ．（1，2）D ．[1，2）2．i 为虚数单位，若i3)i 3(-=+z ,则=||z （ ）A ．1B ．2C ．3D ．23．1-=m 是直线()0112=+-+y m mx 和直线093=++my x 垂直的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件4．已知抛物线:C 28y x =，过点(2,0)P 的直线与抛物线交于A ，B 两点，O 为坐标原点，则O A O B ⋅uur uuu r的值为（ ）A ．16-B ．12-C ．4D ．0 5．等差数列{}n a 中564a a +=，则310122lo g (2222)a a a a ⋅⋅⋅⋅=…（ ）A ．10B ．20C ．40D ．22lo g 5+ 6．若某空间几何体的三视图如图所示，则该几何体的体积是（ ）A ．32B ．16C ．24D ．48 7．下列结论中正确的是（ ）A.若)(q p ⌝∧为真命题，则q 为真命题联系电话：4000-916-716B.回归直线方程b x a y ˆˆˆ+=一定经过(),x y C.将一组数据中的每个数据都减去同一个数后，平均数与方差均没有变化D.某单位有职工750人，其中青年职工350人，中年职工250人，老年职工150人．为了解该单位职工的健康情况，应采用系统抽样的方法从中抽取样本.若样本青年职工为7人，刚样本容量为15．8．若变量x ，y 满足约束条件则的取值范围是（ ）A ．(，7)B ．(，3)C ．(，7]D ．[，7]9．执行如下图所示的程序框图，若输出k 的值为6，则判断框内可填入的条件是（ ）A ．s >45B ．s >710C ．s >35D ．s >1210．过抛物线y 2=4x 的焦点的一条直线交抛物线于A 、B 两点，正三角形ABC 的顶点C 在该抛物线的准线上，则△ABC 的边长是（ ）A.8 B ．10 C ．12 D ．14 11．定义在R 上的函数()x f y =，满足()()2f x fx -=，()1x f-'()x <，若()()313f a f +<，则实数a的取值范围是（ ）联系电话：4000-916-716A ．2,3⎛⎫-∞-⎪⎝⎭B ．2,3⎛⎫+∞⎪⎝⎭C ．22,33⎛⎫-⎪⎝⎭D ．22,,33⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭12．若函数)(x f 的零点与224)(-+=x x g x的零点之差的绝对值不超过0.25， 则)(x f 可以是（ ） A.1()4f x x =-B.2()2(1)f x x =- C ．31()lo g 2f x x ⎛⎫=-⎪⎝⎭D ．()21x f x =-二、填空题：本大题共4个小题，每小题5分，共20分．请将答案填在答题卡对应题号．．．．．．．的位置上．13．从标有1,2,3,4,5,6的6张纸片中任取2张，那么这2张纸片数字之积为6的概率是 14．已知函数，若函数图象上的一个对称中心到对称轴的距离的最小值为，则的值为 ．15．设()f x 是定义在R 上的奇函数且(4)(3)2f f +-=，则(3)(4)f f -= 16．设△ABC 的三个内角A 、B 、C 所对的三边分别为a , b , c ，若△ABC 的面积为 S = a 2－（b －c ）2，则AA cos 1sin -= ．三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．(本题满分12分)已知在等比数列}{n a 中，11=a ，且2a 是1a 和13-a 的等差中项. （1）求数列}{n a 的通项公式；（2）若数列}{n b 满足)(12*N n a n b n n ∈+-=，求}{n b 的前n 项和n S .联系电话：4000-916-71618．(本题满分12分)如图，在直三棱柱ABC-A 1B 1C 1中，∠BAC ＝90°，AB ＝AC ＝2，AA 1＝3，D 是BC 的中点，点E 在棱BB 1上运动． （1）证明：AD ⊥C 1E ；（2）当异面直线AC ，C 1E 所成的角为60°时，求三棱锥C 1-A 1B 1E 的体积．19．(本题满分12分)某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组，第二组，…，第五组，下图是按上述分组方法得到的频率分布直方图．(1) 根据频率分布直方图，估计这50名学生百米测试成绩的平均值；(2) 若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1的概率.[13,14)[14,15)[]17,18联系电话：4000-916-71620．(本题满分12分) 已知椭圆C ：22221x y ab+=（a>b>0），过点(0，1)，且离心率为2．(1)求椭圆C 的方程；(2)A ，B 为椭圆C 的左右顶点，直线l ：xx 轴交于点D ，点P 是椭圆C 上异于A ，B 的动点，直线AP ，BP 分别交直线l 于E ， F 两点．证明：当点P 在椭圆C 上运动时，|DE |·|DF |恒为定值．21．(本题满分12分) 已知函数()(1) 若在点处的切线方程为，求的解析式及单调递减区间；(2) 若在上存在极值点，求实数的取值范围．b x a xaxx f ++-+=)22(2131)(23R a ∈)(x f y =))1(,1(f P 21=y )(x f y =)(x f y =]0,2[-a联系电话：4000-916-716选做题：22—23任选一题，如果多选，仅以所选第一题计分。

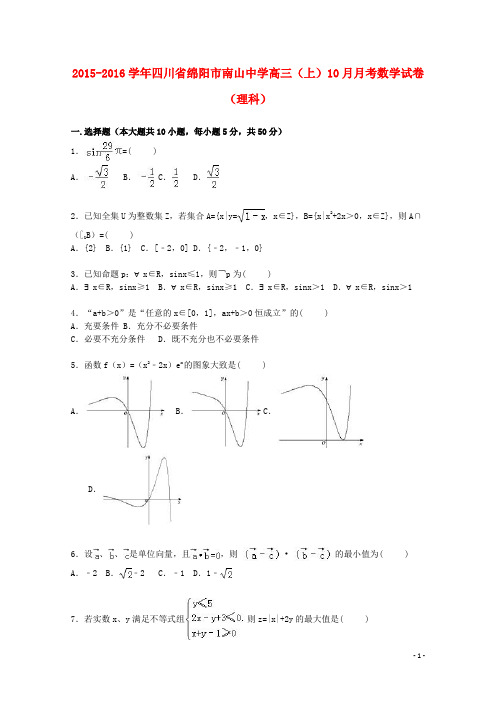
2015-2016学年四川省绵阳市南山中学高三（上）10月月考数学试卷（理科）一.选择题（本大题共10小题，每小题5分，共50分）1．=( )A．B． C．D．2．已知全集U为整数集Z，若集合A={x|y=，x∈Z}，B={x|x2+2x＞0，x∈Z}，则A∩（∁U B）=( )A．{2} B．{1} C．[﹣2，0] D．{﹣2，﹣1，0}3．已知命题p：∀x∈R，sinx≤1，则￢p为( )A．∃x∈R，sinx≥1B．∀x∈R，sinx≥1C．∃x∈R，sinx＞1 D．∀x∈R，sinx＞14．“a+b＞0”是“任意的x∈[0，1]，ax+b＞0恒成立”的( )A．充要条件 B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件5．函数f（x）=（x2﹣2x）e x的图象大致是( )A．B．C．D．6．设、、是单位向量，且，则•的最小值为( )A．﹣2 B．﹣2 C．﹣1 D．1﹣7．若实数x、y满足不等式组则z=|x|+2y的最大值是( )A．10 B．11 C．13 D．148．已知函数f（x）=ln，若f（）+f（）+…f（）=（a+b），则a2+b2的最小值为( )A．8 B．9 C．12 D．189．函数g（x）=log2x（x＞）关于x的方程|g（x）|2+m|g（x）|+2m+3=0恰有三个不同的实数解，则实数m的取值范围为( )A．（﹣∞，4﹣2）∪（4+2，+∞）B．（4﹣2，4+2）C．（﹣，﹣） D．（﹣，﹣]10．对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为M函数：（i）对任意的x∈[0，1]，恒有f（x）≥0；（ii）当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．则下列四个函数中不是M函数的个数是( )①f（x）=x2②f（x）=x2+1③f（x）=ln（x2+1）④f（x）=2x﹣1．A．1 B．2 C．3 D．4二.填空题（本大题共5小题，每小题5分，共25分）11．函数的定义域是__________．12．若log4（3a+4b）=log2，则a+b的最小值是__________．13．对定义域内的任意实数x都有（其中△x表示自变量的改变量），则a的取值范围是__________．14．已知钝角α满足，则=__________．15．给出下列四个命题：①函数y=为奇函数；②若非零向量=（1，m+3）和=（m，4）夹角为锐角，则实数m的取值范围是；③函数的值域是（0，+∞）；④若函数f（2x）的定义域为[1，2]，则函数f（2x）的定义域为[1，2]；⑤函数y=lg（﹣x2+2x）的单调递增区间是（0，1]．其中正确命题的序号是__________．（填上所有正确命题的序号）三.解答题（本大题共6小题，共75分，解答应写出文字说明证明过程或推演步骤.）16．已知等差数列{a n}满足a3=2，前3项和S3=．（Ⅰ）求{a n}的通项公式；（Ⅱ）设等比数列{b n}满足b1=a1，b4=a15，求{b n}前n项和T n．17．已知p：x2﹣12x+20＜0，q：x2﹣2x+1﹣a2＞0（a＞0），若¬p的充分不必要条件是¬q，求a的取值范围．18．如图，为对某失事客轮AB进行有效援助，现分别在河岸MN选择两处C、D用强光柱进行辅助照明，其中A、B、C、D在同一平面内．现测得CD长为100米，∠ADN=105°，∠BDM=30°，∠ACN=45°，∠BCM=60°．（1）求△BCD的面积；（2）求船AB的长．19．函数f（x）=Asin（ωx+ϕ）的部分图象如图所示．（Ⅰ）求函数f（x）的解析式；（Ⅱ）已知函数，，求g（x）的最值及其对应的x 值．20．（13分）已知函数，且f′（﹣1）=0（Ⅰ）试用含a的代数式表示b；（Ⅱ）求f（x）的单调区间；（Ⅲ）令a=﹣1，设函数f（x）在x1，x2（x1＜x2）处取得极值，记点M（x1，f（x1）），N（x2，f（x2）），证明：线段MN与曲线f（x）存在异于M、N的公共点．21．（14分）已知函数和g（x）=m（x﹣1），m∈R．（Ⅰ）m=1时，求方程f（x）=g（x）的实根；（Ⅱ）若对于任意的x∈[1，+∞），f（x）≤g（x）恒成立，求m的取值范围；（Ⅲ）求证：．2015-2016学年四川省绵阳市南山中学高三（上）10月月考数学试卷（理科）一.选择题（本大题共10小题，每小题5分，共50分）1．=( )A．B． C．D．【考点】运用诱导公式化简求值．【专题】三角函数的求值．【分析】原式中的角度变形后，利用诱导公式化简，再利用特殊角的三角函数值计算即可得到结果．【解答】解：sinπ=sin（4π+π﹣）=sin（π﹣）=sin=．故选C【点评】此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．2．已知全集U为整数集Z，若集合A={x|y=，x∈Z}，B={x|x2+2x＞0，x∈Z}，则A∩（∁U B）=( )A．{2} B．{1} C．[﹣2，0] D．{﹣2，﹣1，0}【考点】交、并、补集的混合运算．【专题】集合．【分析】求出集合的等价条件，根据集合的基本运算进行求解即可．【解答】解：由集合A={x|y=，x∈Z}={x|x≤1且x∈Z}，由集合B={x|x2+2x＞0，x∈Z}={x|x＞0或x＜﹣2，x∈Z}，则∁U B={x|﹣2≤x≤0，x∈Z}，∴A∩（∁U B）={﹣2，﹣1，0}．故选：D．【点评】本题主要考查集合的基本运算，求出集合的等价条件，是解决本题的关键..3．已知命题p：∀x∈R，sinx≤1，则￢p为( )A．∃x∈R，sinx≥1B．∀x∈R，sinx≥1C．∃x∈R，sinx＞1 D．∀x∈R，sinx＞1 【考点】命题的否定．【专题】简易逻辑．【分析】根据全称命题的否定是特称命题可得命题的否定为∃x∈R，使得sinx＞1【解答】解：根据全称命题的否定是特称命题可得，命题p：∀x∈R，sinx≤1，的否定是∃x∈R，使得sinx＞1故选：C【点评】本题主要考查了全称命题与特称命题的之间的关系的应用，属于基础试题4．“a+b＞0”是“任意的x∈[0，1]，ax+b＞0恒成立”的( )A．充要条件 B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【专题】简易逻辑．【分析】根据充分条件和必要条件的定义进行判断即可．【解答】解：若任意的x∈[0，1]，ax+b＞0恒成立”，则设f（x）=ax+b，则满足，即a+b＞0，b＞0，则“a+b＞0”是“任意的x∈[0，1]，ax+b＞0恒成立”的必要不充分条件，故选：C【点评】本题主要考查充分条件和必要条件的判断，根据函数关系是解决本题的关键．5．函数f（x）=（x2﹣2x）e x的图象大致是( )A．B．C．D．【考点】函数的图象与图象变化．【专题】数形结合．【分析】本题是选择题，可采用排除法进行逐一排除，根据f（0）=0可知图象经过原点，以及根据导函数大于0时原函数单调递增，求出单调增区间，从而可以进行判定．【解答】解：因为f（0）=（02﹣2×0）e0=0，排除C；因为f'（x）=（x2﹣2）e x，解f'（x）＞0，所以或时f（x）单调递增，排除B，D．故选A．【点评】本题主要考查了利用导数研究函数的单调性，以及函数的图象等基础知识，考查了排除法，属于基础题．6．设、、是单位向量，且，则•的最小值为( )A．﹣2 B．﹣2 C．﹣1 D．1﹣【考点】平面向量数量积的运算．【专题】压轴题．【分析】由题意可得=，故要求的式子即﹣（）•+=1﹣cos=1﹣cos，再由余弦函数的值域求出它的最小值．【解答】解：∵、、是单位向量，，∴，=．∴•=﹣（）•+=0﹣（）•+1=1﹣cos=1﹣cos≥．故选项为D【点评】考查向量的运算法则；交换律、分配律但注意不满足结合律．7．若实数x、y满足不等式组则z=|x|+2y的最大值是( )A．10 B．11 C．13 D．14【考点】简单线性规划．【专题】不等式的解法及应用．【分析】由约束条件作出可行域，分类化目标函数为直线方程的斜截式，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．【解答】解：由约束条件作出可行域如图，当x≥0时，z=|x|+2y化为y=﹣x+z，表示的是斜率为﹣，截距为的平行直线系，当过点（1，5）时，直线在y轴上的截距最大，z最大，z max=1+2×5=11；当x＜0时，z=|x|+2y化为，表示斜率为，截距为，的平行直线系，当直线过点（﹣4，5）时直线在y轴上的截距最大，z最大，z max=4+2×5=14．∴z=|x|+2y的最大值是14．故选：D．【点评】本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．8．已知函数f（x）=ln，若f（）+f（）+…f（）=（a+b），则a2+b2的最小值为( )A．8 B．9 C．12 D．18【考点】对数的运算性质．【专题】函数的性质及应用．【分析】由已知函数解析式可得f（）=ln=ln，则由f（）+f（）+…f（）=（a+b）求得a+b=6，然后利用基本不等式求得a2+b2的最小值．【解答】解：∵f（x）=ln，∴f（）=ln=ln；∴f（）+f（）+…f（）=ln+ln+…+ln=ln（）=lne2014=2014=（a+b），∴a+b=6．则a2+b2=．上式当且仅当a=b时“=”成立．∴a2+b2的最小值为18．故选：D．【点评】本题考查对数的运算性质，考查了数学转化思想方法，训练了利用基本不等式求最值，是中档题．9．函数g（x）=log2x（x＞）关于x的方程|g（x）|2+m|g（x）|+2m+3=0恰有三个不同的实数解，则实数m的取值范围为( )A．（﹣∞，4﹣2）∪（4+2，+∞）B．（4﹣2，4+2）C．（﹣，﹣） D．（﹣，﹣]【考点】根的存在性及根的个数判断．【专题】计算题；函数的性质及应用．【分析】由题意|g（x）|2+m|g（x）|+2m+3=0在x＞内有三个不同实数解可化为t2+mt+2m+3=0有两个根，分别在（0，1），[1，+∞）上或在（0，1），{0}上；从而分别讨论即可．【解答】∵g（x）=log2x在x＞上单调递增，∴g（x）＞﹣1，令t=|g（x）|故|g（x）|2+m|g（x）|+2m+3=0在x＞内有三个不同实数解可化为t2+mt+2m+3=0有两个根，分别在（0，1），[1，+∞）上或在（0，1），{0}上；当若在（0，1），{0}上，则2m+3=0，则m=﹣；故t=0或t=＞1，不成立；若在（0，1），{1}上，则1+m+2m+3=0，故m=﹣；故t2+mt+2m+3=0的解为t=或t=1，成立；若在（0，1），（1，+∞）上，则△=m2﹣4（2m+3）＞0，f（1）=2m+3+m+1＜0；f（0）=2m+3＞0，解得﹣＜m＜﹣；故答案为：（﹣，﹣]；故答案为D【点评】本题考查了函数的零点与方程的根的关系应用，属于基础题．10．对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为M函数：（i）对任意的x∈[0，1]，恒有f（x）≥0；（ii）当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．则下列四个函数中不是M函数的个数是( )①f（x）=x2②f（x）=x2+1③f（x）=ln（x2+1）④f（x）=2x﹣1．A．1 B．2 C．3 D．4【考点】函数与方程的综合运用．【专题】函数的性质及应用．【分析】利用已知条件函数的新定义，对四个选项逐一验证两个条件，判断即可．【解答】解：（i）在[0，1]上，四个函数都满足；（ii）x1≥0，x2≥0，x1+x2≤1；对于①，，∴①满足；对于②，=2x1x2﹣1＜0，∴②不满足．对于③，=而x1≥0，x2≥0，∴，∴，∴，∴，∴，∴③满足；对于④，=，∴④满足；故选：A．【点评】本题通过函数的运算与不等式的比较，另外也可以利用函数在定义域内的变化率、函数图象的基本形式来获得答案，本题对学生的运算求解能力和数形结合思想提出一定要求．二.填空题（本大题共5小题，每小题5分，共25分）11．函数的定义域是（﹣2，1]．【考点】函数的定义域及其求法．【专题】方程思想；定义法；函数的性质及应用．【分析】根据函数成立的条件即可求函数的定义域．【解答】解：要使函数有意义，则≥0，即﹣2＜x≤1，即函数的定义域为（﹣2，1]，故答案为：（﹣2，1]．【点评】本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．12．若log4（3a+4b）=log2，则a+b的最小值是7+4．【考点】基本不等式．【专题】不等式的解法及应用．【分析】log4（3a+4b）=log2，可得3a+4b=ab，a，b＞0.＞0，解得a＞4．于是a+b=a+=+7，再利用基本不等式的性质即可得出．【解答】解：∵log4（3a+4b）=log2，∴=，∴，∴3a+4b=ab，a，b＞0．∴＞0，解得a＞4．a+b=a+=+7≥7+=，当且仅当a=4+2时取等号．∴a+b的最小值是7+4．故答案为：7+4．【点评】本题考查了对数的运算性质、基本不等式的性质，考查了计算能力，属于基础题．13．对定义域内的任意实数x都有（其中△x表示自变量的改变量），则a的取值范围是．【考点】极限及其运算；导数的概念．【专题】计算题；分类讨论；函数的性质及应用．【分析】根据导数定义得出函数在定义域上单调递增，再由分段函数单调的条件列式计算．【解答】解：根据导数定义，f'（x）=，所以，f（x）在定义域为单调递增，则f（x）在各分段都为增函数，①当x≥0时，f（x）=ax2+1，要使函数递增，则a＞0，②当x＜0时，f（x）=（a2﹣1）e ax，要使函数递增，则或（舍），综合①②得，a＞1，又f（x）≥f（x），即1≥a2﹣1，解得a≤，所以，实数a的取值范围为（1，]，故答案为：（1，]．【点评】本题主要考查了导数的定义，以及运用导数与单调性间的关系，分段函数单调性的求解，属于中档题．14．已知钝角α满足，则=﹣．【考点】两角和与差的正切函数．【专题】三角函数的求值．【分析】由两角差的正弦函数公式化简已知等式可得sin（α﹣）=，结合角的范围可求cos（α﹣），由同角三角函数关系式即可求得tan（α﹣）的值．【解答】解：∵钝角α满足，∴sinα﹣cosα=，即sin（α﹣）=，∴α﹣≈53°或是127°，∵α为钝角，前面一种假设显然不成立，∴α﹣≈127°，∴cos（α﹣）=﹣，∴则==﹣．故答案为：﹣．【点评】本题主要考查了两角差的正弦函数公式，同角三角函数关系式的应用，属于基本知识的考查．15．给出下列四个命题：①函数y=为奇函数；②若非零向量=（1，m+3）和=（m，4）夹角为锐角，则实数m的取值范围是；③函数的值域是（0，+∞）；④若函数f（2x）的定义域为[1，2]，则函数f（2x）的定义域为[1，2]；⑤函数y=lg（﹣x2+2x）的单调递增区间是（0，1]．其中正确命题的序号是①④⑤．（填上所有正确命题的序号）【考点】命题的真假判断与应用．【专题】转化思想；数学模型法；简易逻辑．【分析】①由，解得﹣1≤x≤1，且x≠0，其定义域关于原点对称，函数y==，又f（﹣x）=﹣f（x），即可判断出奇偶性；②若非零向量=（1，m+3）和=（m，4）夹角为锐角，则=m+4（m+3）＞0，且m（m+3）≠4，解得m范围，即可判断出正误；③由≠0，可得≠1，即可得出函数的值域；④由函数f（2x）的定义域为[1，2]，可得1≤x≤2，2≤2x≤4，可得2≤2x≤4，解得x范围即可得出函数f（2x）的定义域；⑤由﹣x2+2x＞0，解得0＜x＜2．利用对数函数、二次函数的单调性、复合函数的单调性的判定方法即可得出即可得出函数y=lg（﹣x2+2x）=lg[﹣（x﹣1）2+3]的单调递增区间．【解答】解：①由，解得﹣1≤x≤1，且x≠0，其定义域{x|﹣1≤x≤1，且x≠0}关于原点对称，∴函数y==，又f（﹣x）==﹣f（x）∴函数y=为奇函数，正确；②若非零向量=（1，m+3）和=（m，4）夹角为锐角，则=m+4（m+3）＞0，且m（m+3）≠4，解得，且m≠1．因此不正确；③∵≠0，∴≠1，函数的值域是（0，1）∪（1，+∞），因此不正确；④若函数f（2x）的定义域为[1，2]，∴1≤x≤2，2≤2x≤4，∴2≤2x≤4，解得1≤x≤2，则函数f（2x）的定义域为[1，2]，正确；⑤由﹣x2+2x＞0，解得0＜x＜2．函数y=lg（﹣x2+2x）=lg[﹣（x﹣1）2+3]的单调递增区间是（0，1]，正确．其中正确命题的序号是①④⑤．故答案为：①④⑤．【点评】本题考查了简易逻辑的判定方法、函数的单调性与奇偶性、向量夹角公式与数量积运算性质，考查了推理能力与计算能力，属于中档题．三.解答题（本大题共6小题，共75分，解答应写出文字说明证明过程或推演步骤.）16．已知等差数列{a n}满足a3=2，前3项和S3=．（Ⅰ）求{a n}的通项公式；（Ⅱ）设等比数列{b n}满足b1=a1，b4=a15，求{b n}前n项和T n．【考点】等差数列与等比数列的综合．【专题】等差数列与等比数列．【分析】（Ⅰ）设等差数列{a n}的公差为d，则由已知条件列式求得首项和公差，代入等差数列的通项公式得答案；（Ⅱ）求出，再求出等比数列的公比，由等比数列的前n项和公式求得{b n}前n项和T n．【解答】解：（Ⅰ）设等差数列{a n}的公差为d，则由已知条件得：，解得．代入等差数列的通项公式得：；（Ⅱ）由（Ⅰ）得，．设{b n}的公比为q，则，从而q=2，故{b n}的前n项和．【点评】本题考查了等差数列和等比数列的通项公式，考查了等差数列和等比数列的前n项和，是中档题．17．已知p：x2﹣12x+20＜0，q：x2﹣2x+1﹣a2＞0（a＞0），若¬p的充分不必要条件是¬q，求a的取值范围．【考点】必要条件、充分条件与充要条件的判断．【专题】转化思想；数学模型法；简易逻辑．【分析】利用一元二次不等式的解法可得：p与q，由于¬q是¬p的充分不必要条件，可得p是q的充分不必要条件即，p⇒q，即可得出．【解答】解：由x2﹣12x+20＜0，解得2＜x＜10，∴p：{x|2＜x＜10}，由x2﹣2x+1﹣a2＞0，解得x＜1﹣a或x＞1+a，∴q：{x|x＜1﹣a，或x＞1+a}，∵¬q是¬p的充分不必要条件，∴p是q的充分不必要条件即，p⇒q，∴1+a≤2，∴0＜a≤1．【点评】本题考查了充要条件的判定、不等式的解法，考查了推理能力与计算能力，属于中档题．18．如图，为对某失事客轮AB进行有效援助，现分别在河岸MN选择两处C、D用强光柱进行辅助照明，其中A、B、C、D在同一平面内．现测得CD长为100米，∠ADN=105°，∠BDM=30°，∠ACN=45°，∠BCM=60°．（1）求△BCD的面积；（2）求船AB的长．【考点】解三角形的实际应用．【专题】解三角形．【分析】（1）根据题意求得∠CBD，进而求得BC，BD，进而根据三角形面积公式求得答案．（2）利用正弦定理求得AD，进而利用余弦定理分别求得BD，AB．【解答】解：（1）由题，∠BDM=30°，∠ACN=45°，∠BCM=60°，得∠CBD=30°，所以BC=BD=100，所以=平方米．（2）由题，∠ADC=75°，∠ACD=45°，∠BDA=45°，在△ACD中，，即，所以，在△BCD中，，在△ABD中，==，即船长为米．【点评】本题主要考查了正弦定理和余弦定理的运用．解题的重要步骤就是建立数学模型．19．函数f（x）=Asin（ωx+ϕ）的部分图象如图所示．（Ⅰ）求函数f（x）的解析式；（Ⅱ）已知函数，，求g（x）的最值及其对应的x 值．【考点】正弦函数的图象．【专题】数形结合；转化思想；综合法；三角函数的图像与性质．【分析】（Ⅰ）由周期求出ω，由五点法作图求出φ的值，根据特殊点的坐标求出A，可得函数的解析式．（Ⅱ）由条件利用三角恒等变换化简g（x）的解析式，再利用正弦函数的定义域和值域，求得g（x）的最值及其对应的x值．【解答】解：（Ⅰ）由函数f（x）=Asin（ωx+ϕ）的部分图象，可得T=2（﹣）=，∴ω=2．由五点法作图可得2•+φ=π，求得ϕ=．再根据Asin=1，求得A=2，故f（x）=2sin（2x+）．（Ⅱ）====•+sin2x+=．∵，∴，∴．∴当x=0时；当时．【点评】本题主要考查函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值．还考查了三角恒等变换，正弦函数的定义域和值域，属于中档题．20．（13分）已知函数，且f′（﹣1）=0（Ⅰ）试用含a的代数式表示b；（Ⅱ）求f（x）的单调区间；（Ⅲ）令a=﹣1，设函数f（x）在x1，x2（x1＜x2）处取得极值，记点M（x1，f（x1）），N（x2，f（x2）），证明：线段MN与曲线f（x）存在异于M、N的公共点．【考点】利用导数研究函数的单调性；导数的运算；利用导数研究函数的极值．【专题】计算题；压轴题；分类讨论；反证法．【分析】（Ⅰ）：已知f′（﹣1）=0，根据求导数的方法先求出f′（x），把x=﹣1代入得到关于a和b的等式解出b即可；（Ⅱ）：令f′（x）=0求出稳定点时x的值1﹣2a和﹣1，根据1﹣2a和﹣1的大、小、相等分三种情况讨论函数的增减性即可；（Ⅲ）：利用反证法，假设线段MN与曲线f（x）不存在异于M、N的公共点．推出函数不单调矛盾．原结论正确．【解答】解：（Ⅰ）f′（x）=x2+2ax+b依题意，得f′（﹣1）=1﹣2a+b=0故b=2a﹣1．（Ⅱ）由（a）得故f′（x）=x2+2ax+2a﹣1=（x+1）（x+2a﹣1）令f′（x）=0，则x=﹣1或x=1﹣2a分情况讨论得：当x变化时，f′（x）与f（x）的变化如下表：1﹣2a）和（﹣1，+∞），单调减区间为（1﹣2a，﹣1）．（2）当a=1时，1﹣2a=﹣1．此时f′（x）≥0恒成立，且仅在x=﹣1处f′（x）=0故函数f（x）的单调增区间为R．（3）当a＜1时，1﹣2a＞﹣1同理可得函数f（x）的单调增区间为（﹣∞，﹣1）和（1﹣2a，+∞）单调减区间为（﹣1，1﹣2a）．（Ⅲ）假设线段MN与曲线f（x）不存在异于M、N的公共点．当a=﹣1时，由（a）的b=2a﹣1=﹣3．f（x）=﹣x2﹣3x就不在区间内单调与a＜﹣1单调减矛盾．所以假设错误．故线段MN与曲线f（x）存在异于M、N的公共点．【点评】此题考查学生利用导数研究函数单调的方法，以及反证法的运用．21．（14分）已知函数和g（x）=m（x﹣1），m∈R．（Ⅰ）m=1时，求方程f（x）=g（x）的实根；（Ⅱ）若对于任意的x∈[1，+∞），f（x）≤g（x）恒成立，求m的取值范围；（Ⅲ）求证：．【考点】函数恒成立问题；函数的值．【专题】分类讨论；数学模型法；函数的性质及应用．【分析】（Ⅰ）代入m=1时，f（x）=g（x）即=（x﹣1），整理方程得，利用导函数判断函数的单调性为递减函数，故最多有一个零点，而h（1）=0，故方程f（x）=g （x）有惟一的实根x=1；（Ⅱ）对于任意的x∈[1，+∞），f（x）≤g（x）恒成立，通过构造函数设，利用导函数判断函数的单调性，，通过讨论m，判断是否符合题意；由（Ⅱ）知，当x＞1时，时，成立．结合题型，构造不妨令，得出，利用累加可得结论；【解答】（Ⅰ）m=1时，f（x）=g（x）即=（x﹣1），∵x＞0，所以方程即为，令，则，∴h（x）单调递减，而h（1）=0，故方程f（x）=g（x）有惟一的实根x=1…4'（Ⅱ）对于任意的x∈[1，+∞），f（x）≤g（x）恒成立，∴lnx≤m（x﹣），设，即∀x∈[1，+∞），F（x）≤0，①若m≤0，则F'（x）＞0，F（x）≥F（1）=0，这与题设F（x）≤0矛盾②若m＞0，方程﹣mx2+x﹣m=0的判别式△=1﹣4m2，当△≤0，即时，F'（x）≤0，∴F（x）在（1，+∞）上单调递减，∴F（x）≤F（1）=0，即不等式成立当时，方程﹣mx2+x﹣m=0有两正实根，设两根为x1，x2，当x∈（1，x2），F'（x）＞0，F（x）单调递增，F（x）＞F（1）=0与题设矛盾，综上所述，．所以，实数m的取值范围是…9'（Ⅲ）由（Ⅱ）知，当x＞1时，时，成立．不妨令，所以，累加可得（n∈N*）．取n=1007，即得．【点评】考查了零点与单调性，利用导数判断恒成立问题，利用已证结论，构造函数解决实际问题．属于难题．。

2016年10月绵阳南山中学高2019届2016年秋10月月考数 学 试 题命题人：文媛 审题人：王怀修1.本试卷分第Ⅰ卷(客观题)和第Ⅱ卷(主观题)两部分,全卷共100分,考试时间100分钟.2.所有试题均答在答题卡上,答在题卷上无效．第Ⅰ卷(客观题,共48分)一. 选择题(本大题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.集合},{b a 的子集有( ). A.2个B.3个C.4个D.5个2.设集合{}|43A x x =-<<，{}|2B x x =≤，则AB =( ).A.(4,3)-B.(4,2]-C.(,2]-∞D.(,3)-∞ 3.已知函数1,0,(),0,x x f x ax x -≤⎧=⎨>⎩，若(1)(1)f f =-，则实数a 的值等于( ).A.1B.2C.3D.44.已知集合{04}P x x =≤≤，{02}Q y y =≤≤，下列从P 到Q 的各个对应关系f 不是．．映射的是( ).A.1:2f x y x →=B.1:3f x y x →= C.21:8f x y x →= D.2:3f x y x →=5.已知偶函数()f x 的定义域是R ，且()f x 在(0,)+∞是增函数，则(2),a f =-(),b f π=c (3)f =-的大小关系是( ).A.a c b <<B.b a c <<C.b c a <<D.c a b <<6.若函数2()2(1)2f x x a x =+-+在区间[4,)+∞上是增函数，则实数a 的取值范围是( ). A.3a ≤ B.3a ≤- C.3a ≥- D.5a ≤ 7.函数()f x 的图象如图所示，则()f xA.()1f x x =--B.()1f x x =-C.()1f x x =-+D. ()1f x x =+8.已知函数(21)32f x x +=+，且()2f a =A.8 B.1 C.5 D.1-9.若函数()f x =的定义域为R ，则实数m 的取值范围是( ). A.04m <<B.04m ≤≤C.4m ≥D.04m <≤10.已知二次函数()f x 图象的对称轴是直线2x =，且(0)3,(2)1,f f ==若在[0,]m 有最大值3，最小值1，则实数m 的取值范围是( ).A.(0,)+∞B.[2,)+∞C.(0,2]D.[2,4]11.若一系列函数的解析式相同，值域相同，但定义域不同，则称这些函数为“同族函数”.那么函数解析式为2y x =-，值域为{1,9}--的“同族函数”共有( ).A.9种B.8种C.5种D.4种12.设函数()f x 是定义在R 上的奇函数，当0x ≥时，()2f x x =，若对任意[,2]x t t ∈+，不等式()2()f x t f x +≥恒成立，则实数t 的取值范围是( ).A.)+∞B.[2,)+∞C.(0,2]D.[1]-⋃第Ⅱ卷(主观题,共52分) 二. 填空题(本大题共4小题,每小题3分,共12分.)13.设集合{}1,2,3A =，{}2,4B =，全集{}0,1,2,3,4U =则()U C A B ⋃= . 14.若函数 f (x )= (k -2)x 2+(k -1)x +3是偶函数,则f (x )的递减区间是 .15.函数()f x 是定义在R 上的奇函数，当0x ≥时，()22f x x x =-，则当0x <时，()f x = .16.对任意实数a ，b 定义运算“⊗”：a ⊗b ＝⎩⎪⎨⎪⎧b ，a －b ≥1，a ，a －b ＜1.设f (x )＝(x 2－1)⊗(4＋x )，若函数y ＝f (x )＋k的图象与x 轴恰有三个不同交点，则k 的取值范围是 .三.解答题(本大题共4小题,每小题10分，共40分,解答应写出文字说明证明过程或推演步骤.)17.已知集合U R =,函数xx x f ---=713)(的定义域为集合A ，集合{}=210B x x ≤<，集合{}=C x x a >.(1)求A ，()U C A B ⋂；(2)若(C )U B C R ⋃=，求实数a 的取值范围.18.已知集合{}2=230A x x x -+=，{}=10B x ax -=. (1)若{1}A B ⋂=-，求实数a 的值；(2)若A B B ⋂=，求实数a 的值.19.一个工厂生产某种产品每年需要固定投资100万元，此外每生产1件该产品还需要增加投资1万元，年产量为x (x ∈N *)件．当x ≤ 20时，年销售总收入为(33x －x 2)万元；当x ＞20时，年销售总收入为260万元．记该工厂生产并销售这种产品所得的年利润为y 万元. (年利润＝年销售总收入－年总投资) (1)求y (万元)与x (件)的函数关系式；(2)当该工厂的年产量为多少件时，所得年利润最大?最大年利润是多少？20.已知函数()f x 是定义在[1,1]-上的奇函数，且(1)1f =，若对任意的,[1,1]x y ∈-，且0x y +≠，都有()[()()]0x y f x f y +⋅+>. (1)判断()f x 的单调性，并加以证明； (2)解不等式()12102f x f x ⎛⎫++-< ⎪⎝⎭；(3)若2()22f x m am ≤-+对任意的[1,1],[1,2]x m ∈-∈恒成立，求实数a 的取值范围.2016年10月绵阳南山中学高2019届2016年秋10月月考数 学 试 题 答 案三. 选择题(本大题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的.) 题号12345678 9 10 11 12 答案 C B B D A C C BBDAA四. 填空题(本大题共4小题,每小题3分,共12分.) 13. {}0,2,4；14. (0,)+∞15. 22x x +16. －2≤k ＜1解析 当x 2－1≥4＋x ＋1，即x ≤－2或x ≥3时，f (x )＝4＋x ，当x 2－1＜4＋x ＋1，即－2＜x ＜3时，f (x )＝x 2－1，如图所示，作出f (x )的图象，由图象可知，要使－k ＝f (x )有三个根，需满足－1＜－k ≤2，即－2≤k ＜1.三.解答题(本大题共4小题,每小题10分，共40分,解答应写出文字说明证明过程或推演步骤.)17.解:(1)由30,70,x x -≥⎧⎨->⎩得：37x ≤<，{}=37A x x ∴≤<.{}=3,7U C A x x x <≥或，{}(C )=23,710U A B x x x ∴⋂≤<≤<或.(2)C {2,10}U B x x x =<≥或，∴由(C )U B C R ⋃=，得2a ≥.18.解: {}{}2=2301,3A x x x -+==-，(1) {1}A B ⋂=-，1B ∴-∈，10a ∴--=即1a ∴=- (2),A B B B A ⋂=∴⊆当B =∅时，方程10ax -=无解，故0a =； 当B ≠∅时，则1=B a ⎧⎫⎨⎬⎩⎭.若11a =-，即1a =-；若13a =，则13a =. 综上所述，a 的值为0，1-或13. 19. 解: (1)当0＜x ≤20时，y ＝(33x －x 2)－x －100＝－x 2＋32x －100；当x ＞20时，y ＝260－100－x ＝160－x .故y ＝⎩⎪⎨⎪⎧－x 2＋32x －100，0＜x ≤20，160－x ，x ＞20(x ∈N *)．(2)当0＜x ≤20时，y ＝－x 2＋32x －100＝－(x －16)2＋156，x ＝16时，y max ＝156.而当x ＞20时，160－x ＜140，故x ＝16时取得最大年利润，最大年利润为156万元. 答：当该工厂年产量为16件时，取得最大年利润为156万元. 20.解：(1)()f x 在[1,1]-上为增函数.证明：任取12,[1,1]x x ∈-，且12x x <，则210x x ->， 由题意知2121()[()()]0x x f x f x -⋅+->，又()f x 为奇函数，2121()[()()]0x x f x f x ∴-⋅->，21()()0f x f x ∴->，即21()()f x f x >()f x ∴在[1,1]-上为增函数.(2)由题意及(1)知，111,21121,112,2x x x x ⎧-≤+≤⎪⎪-≤-≤⎨⎪⎪+<-⎩解得：106x ≤<.故所求不等式的解集为：1{|0}6x x ≤<.(3)由()f x 在[1,1]-上为增函数，知max ()(1)1f x f ==.由题意，得2122m am ≤-+，即2210m am -+≥对任意[1,2]m ∈恒成立， 法一： 即12m a m +≥对任意[1,2]m ∈恒成立，则只需min 12m a m ⎛⎫+≥ ⎪⎝⎭，[1,2]m ∈即可.令1()g m m m=+，[1,2]m ∈，易证()g m 在[1,2]上是增函数，所以min ()g(1)2g m ==. 故22a ≥，即1a ≤.法二：则只需()2min210m am -+≥，[1,2]m ∈即可.令2()21h m m am =-+，[1,2]m ∈，其函数图象的对称轴为m a = ① 当1a ≤时，()h m 在[1,2]上是增函数，则min ()(1)22h m h a ==-.∴由220a -≥得：1a ≤，从而1a ≤；② 当12a <<时，2min ()()1h m h a a ==-+∴由210a -+≥得：11a -<<，从而a 无解；③ 当2a ≥时，()h m 在[1,2]上是减函数，则min ()(2)54h m h a ==-.∴由540a -≥得：54a ≤，从而a 无解. 综上所述，a 的取值范围为1a ≤.。

2015-2016学年四川省绵阳市南山中学高三（上）10月月考数学试卷（理科）一.选择题（本大题共10小题，每小题5分，共50分）1．=( )A．B． C．D．2．已知全集U为整数集Z，若集合A={x|y=，x∈Z}，B={x|x2+2x＞0，x∈Z}，则A∩（∁U B）=( )A．{2} B．{1} C．[﹣2，0]D．{﹣2，﹣1，0}3．已知命题p：∀x∈R，sinx≤1，则￢p为( )A．∃x∈R，sinx≥1 B．∀x∈R，sinx≥1 C．∃x∈R，sinx＞1 D．∀x∈R，sinx＞14．“a+b＞0”是“任意的x∈[0，1]，ax+b＞0恒成立”的( )A．充要条件 B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件5．函数f（x）=（x2﹣2x）e x的图象大致是( )A．B．C．D．6．设、、是单位向量，且，则•的最小值为( ) A．﹣2 B．﹣2 C．﹣1 D．1﹣7．若实数x、y满足不等式组则z=|x|+2y的最大值是( )A．10 B．11 C．13 D．148．已知函数f（x）=ln，若f（）+f（）+…f（）=（a+b），则a2+b2的最小值为( )A．8 B．9 C．12 D．189．函数g（x）=log2x（x＞）关于x的方程|g（x）|2+m|g（x）|+2m+3=0恰有三个不同的实数解，则实数m的取值范围为( )A．（﹣∞，4﹣2）∪（4+2，+∞）B．（4﹣2，4+2）C．（﹣，﹣）D．（﹣，﹣]10．对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为M函数：（i）对任意的x∈[0，1]，恒有f（x）≥0；（ii）当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．则下列四个函数中不是M函数的个数是( )①f（x）=x2②f（x）=x2+1③f（x）=ln（x2+1）④f（x）=2x﹣1．A．1 B．2 C．3 D．4二.填空题（本大题共5小题，每小题5分，共25分）11．函数的定义域是__________．12．若log4（3a+4b）=log2，则a+b的最小值是__________．13．对定义域内的任意实数x都有（其中△x表示自变量的改变量），则a的取值范围是__________．14．已知钝角α满足，则=__________．15．给出下列四个命题：①函数y=为奇函数；②若非零向量=（1，m+3）和=（m，4）夹角为锐角，则实数m的取值范围是；③函数的值域是（0，+∞）；④若函数f（2x）的定义域为[1，2]，则函数f（2x）的定义域为[1，2]；⑤函数y=lg（﹣x2+2x）的单调递增区间是（0，1]．其中正确命题的序号是__________．（填上所有正确命题的序号）三.解答题（本大题共6小题，共75分，解答应写出文字说明证明过程或推演步骤.）16．已知等差数列{a n}满足a3=2，前3项和S3=．（Ⅰ）求{a n}的通项公式；（Ⅱ）设等比数列{b n}满足b1=a1，b4=a15，求{b n}前n项和T n．17．已知p：x2﹣12x+20＜0，q：x2﹣2x+1﹣a2＞0（a＞0），若¬p的充分不必要条件是¬q，求a的取值范围．18．如图，为对某失事客轮AB进行有效援助，现分别在河岸MN选择两处C、D用强光柱进行辅助照明，其中A、B、C、D在同一平面内．现测得CD长为100米，∠ADN=105°，∠BDM=30°，∠ACN=45°，∠BCM=60°．（1）求△BCD的面积；（2）求船AB的长．19．函数f（x）=Asin（ωx+ϕ）的部分图象如图所示．（Ⅰ）求函数f（x）的解析式；（Ⅱ）已知函数，，求g（x）的最值及其对应的x 值．20．（13分）已知函数，且f′（﹣1）=0（Ⅰ）试用含a的代数式表示b；（Ⅱ）求f（x）的单调区间；（Ⅲ）令a=﹣1，设函数f（x）在x1，x2（x1＜x2）处取得极值，记点M（x1，f（x1）），N（x2，f（x2）），证明：线段MN与曲线f（x）存在异于M、N的公共点．21．（14分）已知函数和g（x）=m（x﹣1），m∈R．（Ⅰ）m=1时，求方程f（x）=g（x）的实根；（Ⅱ）若对于任意的x∈[1，+∞），f（x）≤g（x）恒成立，求m的取值范围；（Ⅲ）求证：．2015-2016学年四川省绵阳市南山中学高三（上）10月月考数学试卷（理科）一.选择题（本大题共10小题，每小题5分，共50分）1．=( )A．B． C．D．【考点】运用诱导公式化简求值．【专题】三角函数的求值．【分析】原式中的角度变形后，利用诱导公式化简，再利用特殊角的三角函数值计算即可得到结果．【解答】解：sinπ=sin（4π+π﹣）=sin（π﹣）=sin=．故选C【点评】此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．2．已知全集U为整数集Z，若集合A={x|y=，x∈Z}，B={x|x2+2x＞0，x∈Z}，则A∩（∁U B）=( )A．{2} B．{1} C．[﹣2，0]D．{﹣2，﹣1，0}【考点】交、并、补集的混合运算．【专题】集合．【分析】求出集合的等价条件，根据集合的基本运算进行求解即可．【解答】解：由集合A={x|y=，x∈Z}={x|x≤1且x∈Z}，由集合B={x|x2+2x＞0，x∈Z}={x|x＞0或x＜﹣2，x∈Z}，则∁U B={x|﹣2≤x≤0，x∈Z}，∴A∩（∁U B）={﹣2，﹣1，0}．故选：D．【点评】本题主要考查集合的基本运算，求出集合的等价条件，是解决本题的关键..3．已知命题p：∀x∈R，sinx≤1，则￢p为( )A．∃x∈R，sinx≥1 B．∀x∈R，sinx≥1 C．∃x∈R，sinx＞1 D．∀x∈R，sinx＞1【考点】命题的否定．【专题】简易逻辑．【分析】根据全称命题的否定是特称命题可得命题的否定为∃x∈R，使得sinx＞1【解答】解：根据全称命题的否定是特称命题可得，命题p：∀x∈R，sinx≤1，的否定是∃x∈R，使得sinx＞1故选：C【点评】本题主要考查了全称命题与特称命题的之间的关系的应用，属于基础试题4．“a+b＞0”是“任意的x∈[0，1]，ax+b＞0恒成立”的( )A．充要条件 B．充分不必要条件C．必要不充分条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【专题】简易逻辑．【分析】根据充分条件和必要条件的定义进行判断即可．【解答】解：若任意的x∈[0，1]，ax+b＞0恒成立”，则设f（x）=ax+b，则满足，即a+b＞0，b＞0，则“a+b＞0”是“任意的x∈[0，1]，ax+b＞0恒成立”的必要不充分条件，故选：C【点评】本题主要考查充分条件和必要条件的判断，根据函数关系是解决本题的关键．5．函数f（x）=（x2﹣2x）e x的图象大致是( )A．B．C．D．【考点】函数的图象与图象变化．【专题】数形结合．【分析】本题是选择题，可采用排除法进行逐一排除，根据f（0）=0可知图象经过原点，以及根据导函数大于0时原函数单调递增，求出单调增区间，从而可以进行判定．【解答】解：因为f（0）=（02﹣2×0）e0=0，排除C；因为f'（x）=（x2﹣2）e x，解f'（x）＞0，所以或时f（x）单调递增，排除B，D．故选A．【点评】本题主要考查了利用导数研究函数的单调性，以及函数的图象等基础知识，考查了排除法，属于基础题．6．设、、是单位向量，且，则•的最小值为( ) A．﹣2 B．﹣2 C．﹣1 D．1﹣【考点】平面向量数量积的运算．【专题】压轴题．【分析】由题意可得=，故要求的式子即﹣（）•+=1﹣cos=1﹣cos，再由余弦函数的值域求出它的最小值．【解答】解：∵、、是单位向量，，∴，=．∴•=﹣（）•+=0﹣（）•+1=1﹣cos=1﹣cos≥．故选项为D【点评】考查向量的运算法则；交换律、分配律但注意不满足结合律．7．若实数x、y满足不等式组则z=|x|+2y的最大值是( )A．10 B．11 C．13 D．14【考点】简单线性规划．【专题】不等式的解法及应用．【分析】由约束条件作出可行域，分类化目标函数为直线方程的斜截式，数形结合得到最优解，求出最优解的坐标，代入目标函数得答案．【解答】解：由约束条件作出可行域如图，当x≥0时，z=|x|+2y化为y=﹣x+z，表示的是斜率为﹣，截距为的平行直线系，当过点（1，5）时，直线在y轴上的截距最大，z最大，z max=1+2×5=11；当x＜0时，z=|x|+2y化为，表示斜率为，截距为，的平行直线系，当直线过点（﹣4，5）时直线在y轴上的截距最大，z最大，z max=4+2×5=14．∴z=|x|+2y的最大值是14．故选：D．【点评】本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．8．已知函数f（x）=ln，若f（）+f（）+…f（）=（a+b），则a2+b2的最小值为( )A．8 B．9 C．12 D．18【考点】对数的运算性质．【专题】函数的性质及应用．【分析】由已知函数解析式可得f（）=ln=ln，则由f（）+f（）+…f（）=（a+b）求得a+b=6，然后利用基本不等式求得a2+b2的最小值．【解答】解：∵f（x）=ln，∴f（）=ln=ln；∴f（）+f（）+…f（）=ln+ln+…+ln=ln（）=lne2014=2014=（a+b），∴a+b=6．则a2+b2=．上式当且仅当a=b时“=”成立．∴a2+b2的最小值为18．故选：D．【点评】本题考查对数的运算性质，考查了数学转化思想方法，训练了利用基本不等式求最值，是中档题．9．函数g（x）=log2x（x＞）关于x的方程|g（x）|2+m|g（x）|+2m+3=0恰有三个不同的实数解，则实数m的取值范围为( )A．（﹣∞，4﹣2）∪（4+2，+∞）B．（4﹣2，4+2）C．（﹣，﹣）D．（﹣，﹣]【考点】根的存在性及根的个数判断．【专题】计算题；函数的性质及应用．【分析】由题意|g（x）|2+m|g（x）|+2m+3=0在x＞内有三个不同实数解可化为t2+mt+2m+3=0有两个根，分别在（0，1），[1，+∞）上或在（0，1），{0}上；从而分别讨论即可．【解答】∵g（x）=log2x在x＞上单调递增，∴g（x）＞﹣1，令t=|g（x）|故|g（x）|2+m|g（x）|+2m+3=0在x＞内有三个不同实数解可化为t2+mt+2m+3=0有两个根，分别在（0，1），[1，+∞）上或在（0，1），{0}上；当若在（0，1），{0}上，则2m+3=0，则m=﹣；故t=0或t=＞1，不成立；若在（0，1），{1}上，则1+m+2m+3=0，故m=﹣；故t2+mt+2m+3=0的解为t=或t=1，成立；若在（0，1），（1，+∞）上，则△=m2﹣4（2m+3）＞0，f（1）=2m+3+m+1＜0；f（0）=2m+3＞0，解得﹣＜m＜﹣；故答案为：（﹣，﹣]；故答案为D【点评】本题考查了函数的零点与方程的根的关系应用，属于基础题．10．对定义在[0，1]上，并且同时满足以下两个条件的函数f（x）称为M函数：（i）对任意的x∈[0，1]，恒有f（x）≥0；（ii）当x1≥0，x2≥0，x1+x2≤1时，总有f（x1+x2）≥f（x1）+f（x2）成立．则下列四个函数中不是M函数的个数是( )①f（x）=x2②f（x）=x2+1③f（x）=ln（x2+1）④f（x）=2x﹣1．A．1 B．2 C．3 D．4【考点】函数与方程的综合运用．【专题】函数的性质及应用．【分析】利用已知条件函数的新定义，对四个选项逐一验证两个条件，判断即可．【解答】解：（i）在[0，1]上，四个函数都满足；（ii）x1≥0，x2≥0，x1+x2≤1；对于①，，∴①满足；对于②，=2x1x2﹣1＜0，∴②不满足．对于③，=而x1≥0，x2≥0，∴，∴，∴，∴，∴，∴③满足；对于④，=，∴④满足；故选：A．【点评】本题通过函数的运算与不等式的比较，另外也可以利用函数在定义域内的变化率、函数图象的基本形式来获得答案，本题对学生的运算求解能力和数形结合思想提出一定要求．二.填空题（本大题共5小题，每小题5分，共25分）11．函数的定义域是（﹣2，1]．【考点】函数的定义域及其求法．【专题】方程思想；定义法；函数的性质及应用．【分析】根据函数成立的条件即可求函数的定义域．【解答】解：要使函数有意义，则≥0，即﹣2＜x≤1，即函数的定义域为（﹣2，1]，故答案为：（﹣2，1]．【点评】本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．12．若log4（3a+4b）=log2，则a+b的最小值是7+4．【考点】基本不等式．【专题】不等式的解法及应用．【分析】log4（3a+4b）=log2，可得3a+4b=ab，a，b＞0.＞0，解得a＞4．于是a+b=a+=+7，再利用基本不等式的性质即可得出．【解答】解：∵log4（3a+4b）=log2，∴=，∴，∴3a+4b=ab，a，b＞0．∴＞0，解得a＞4．a+b=a+=+7≥7+=，当且仅当a=4+2时取等号．∴a+b的最小值是7+4．故答案为：7+4．【点评】本题考查了对数的运算性质、基本不等式的性质，考查了计算能力，属于基础题．13．对定义域内的任意实数x都有（其中△x表示自变量的改变量），则a的取值范围是．【考点】极限及其运算；导数的概念．【专题】计算题；分类讨论；函数的性质及应用．【分析】根据导数定义得出函数在定义域上单调递增，再由分段函数单调的条件列式计算．【解答】解：根据导数定义，f'（x）=，所以，f（x）在定义域为单调递增，则f（x）在各分段都为增函数，①当x≥0时，f（x）=ax2+1，要使函数递增，则a＞0，②当x＜0时，f（x）=（a2﹣1）e ax，要使函数递增，则或（舍），综合①②得，a＞1，又f（x）≥f（x），即1≥a2﹣1，解得a≤，所以，实数a的取值范围为（1，]，故答案为：（1，]．【点评】本题主要考查了导数的定义，以及运用导数与单调性间的关系，分段函数单调性的求解，属于中档题．14．已知钝角α满足，则=﹣．【考点】两角和与差的正切函数．【专题】三角函数的求值．【分析】由两角差的正弦函数公式化简已知等式可得sin（α﹣）=，结合角的范围可求cos（α﹣），由同角三角函数关系式即可求得tan（α﹣）的值．【解答】解：∵钝角α满足，∴sinα﹣cosα=，即sin（α﹣）=，∴α﹣≈53°或是127°，∵α为钝角，前面一种假设显然不成立，∴α﹣≈127°，∴cos（α﹣）=﹣，∴则==﹣．故答案为：﹣．【点评】本题主要考查了两角差的正弦函数公式，同角三角函数关系式的应用，属于基本知识的考查．15．给出下列四个命题：①函数y=为奇函数；②若非零向量=（1，m+3）和=（m，4）夹角为锐角，则实数m的取值范围是；③函数的值域是（0，+∞）；④若函数f（2x）的定义域为[1，2]，则函数f（2x）的定义域为[1，2]；⑤函数y=lg（﹣x2+2x）的单调递增区间是（0，1]．其中正确命题的序号是①④⑤．（填上所有正确命题的序号）【考点】命题的真假判断与应用．【专题】转化思想；数学模型法；简易逻辑．【分析】①由，解得﹣1≤x≤1，且x≠0，其定义域关于原点对称，函数y==，又f（﹣x）=﹣f（x），即可判断出奇偶性；②若非零向量=（1，m+3）和=（m，4）夹角为锐角，则=m+4（m+3）＞0，且m（m+3）≠4，解得m范围，即可判断出正误；③由≠0，可得≠1，即可得出函数的值域；④由函数f（2x）的定义域为[1，2]，可得1≤x≤2，2≤2x≤4，可得2≤2x≤4，解得x范围即可得出函数f（2x）的定义域；⑤由﹣x2+2x＞0，解得0＜x＜2．利用对数函数、二次函数的单调性、复合函数的单调性的判定方法即可得出即可得出函数y=lg（﹣x2+2x）=lg[﹣（x﹣1）2+3]的单调递增区间．【解答】解：①由，解得﹣1≤x≤1，且x≠0，其定义域{x|﹣1≤x≤1，且x≠0}关于原点对称，∴函数y==，又f（﹣x）==﹣f（x）∴函数y=为奇函数，正确；②若非零向量=（1，m+3）和=（m，4）夹角为锐角，则=m+4（m+3）＞0，且m（m+3）≠4，解得，且m≠1．因此不正确；③∵≠0，∴≠1，函数的值域是（0，1）∪（1，+∞），因此不正确；④若函数f（2x）的定义域为[1，2]，∴1≤x≤2，2≤2x≤4，∴2≤2x≤4，解得1≤x≤2，则函数f（2x）的定义域为[1，2]，正确；⑤由﹣x2+2x＞0，解得0＜x＜2．函数y=lg（﹣x2+2x）=lg[﹣（x﹣1）2+3]的单调递增区间是（0，1]，正确．其中正确命题的序号是①④⑤．故答案为：①④⑤．【点评】本题考查了简易逻辑的判定方法、函数的单调性与奇偶性、向量夹角公式与数量积运算性质，考查了推理能力与计算能力，属于中档题．三.解答题（本大题共6小题，共75分，解答应写出文字说明证明过程或推演步骤.）16．已知等差数列{a n}满足a3=2，前3项和S3=．（Ⅰ）求{a n}的通项公式；（Ⅱ）设等比数列{b n}满足b1=a1，b4=a15，求{b n}前n项和T n．【考点】等差数列与等比数列的综合．【专题】等差数列与等比数列．【分析】（Ⅰ）设等差数列{a n}的公差为d，则由已知条件列式求得首项和公差，代入等差数列的通项公式得答案；（Ⅱ）求出，再求出等比数列的公比，由等比数列的前n项和公式求得{b n}前n项和T n．【解答】解：（Ⅰ）设等差数列{a n}的公差为d，则由已知条件得：，解得．代入等差数列的通项公式得：；（Ⅱ）由（Ⅰ）得，．设{b n}的公比为q，则，从而q=2，故{b n}的前n项和．【点评】本题考查了等差数列和等比数列的通项公式，考查了等差数列和等比数列的前n项和，是中档题．17．已知p：x2﹣12x+20＜0，q：x2﹣2x+1﹣a2＞0（a＞0），若¬p的充分不必要条件是¬q，求a的取值范围．【考点】必要条件、充分条件与充要条件的判断．【专题】转化思想；数学模型法；简易逻辑．【分析】利用一元二次不等式的解法可得：p与q，由于¬q是¬p的充分不必要条件，可得p是q的充分不必要条件即，p⇒q，即可得出．【解答】解：由x2﹣12x+20＜0，解得2＜x＜10，∴p：{x|2＜x＜10}，由x2﹣2x+1﹣a2＞0，解得x＜1﹣a或x＞1+a，∴q：{x|x＜1﹣a，或x＞1+a}，∵¬q是¬p的充分不必要条件，∴p是q的充分不必要条件即，p⇒q，∴1+a≤2，∴0＜a≤1．【点评】本题考查了充要条件的判定、不等式的解法，考查了推理能力与计算能力，属于中档题．18．如图，为对某失事客轮AB进行有效援助，现分别在河岸MN选择两处C、D用强光柱进行辅助照明，其中A、B、C、D在同一平面内．现测得CD长为100米，∠ADN=105°，∠BDM=30°，∠ACN=45°，∠BCM=60°．（1）求△BCD的面积；（2）求船AB的长．【考点】解三角形的实际应用．【专题】解三角形．【分析】（1）根据题意求得∠CBD，进而求得BC，BD，进而根据三角形面积公式求得答案．（2）利用正弦定理求得AD，进而利用余弦定理分别求得BD，AB．【解答】解：（1）由题，∠BDM=30°，∠ACN=45°，∠BCM=60°，得∠CBD=30°，所以BC=BD=100，所以=平方米．（2）由题，∠ADC=75°，∠ACD=45°，∠BDA=45°，在△ACD中，，即，所以，在△BCD中，，在△ABD中，==，即船长为米．【点评】本题主要考查了正弦定理和余弦定理的运用．解题的重要步骤就是建立数学模型．19．函数f（x）=Asin（ωx+ϕ）的部分图象如图所示．（Ⅰ）求函数f（x）的解析式；（Ⅱ）已知函数，，求g（x）的最值及其对应的x 值．【考点】正弦函数的图象．【专题】数形结合；转化思想；综合法；三角函数的图像与性质．【分析】（Ⅰ）由周期求出ω，由五点法作图求出φ的值，根据特殊点的坐标求出A，可得函数的解析式．（Ⅱ）由条件利用三角恒等变换化简g（x）的解析式，再利用正弦函数的定义域和值域，求得g（x）的最值及其对应的x值．【解答】解：（Ⅰ）由函数f（x）=Asin（ωx+ϕ）的部分图象，可得T=2（﹣）=，∴ω=2．由五点法作图可得2•+φ=π，求得ϕ=．再根据Asin=1，求得A=2，故f（x）=2sin（2x+）．（Ⅱ）====•+sin2x+=．∵，∴，∴．∴当x=0时；当时．【点评】本题主要考查函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值．还考查了三角恒等变换，正弦函数的定义域和值域，属于中档题．20．（13分）已知函数，且f′（﹣1）=0（Ⅰ）试用含a的代数式表示b；（Ⅱ）求f（x）的单调区间；（Ⅲ）令a=﹣1，设函数f（x）在x1，x2（x1＜x2）处取得极值，记点M（x1，f（x1）），N（x2，f（x2）），证明：线段MN与曲线f（x）存在异于M、N的公共点．【考点】利用导数研究函数的单调性；导数的运算；利用导数研究函数的极值．【专题】计算题；压轴题；分类讨论；反证法．【分析】（Ⅰ）：已知f′（﹣1）=0，根据求导数的方法先求出f′（x），把x=﹣1代入得到关于a 和b的等式解出b即可；（Ⅱ）：令f′（x）=0求出稳定点时x的值1﹣2a和﹣1，根据1﹣2a和﹣1的大、小、相等分三种情况讨论函数的增减性即可；（Ⅲ）：利用反证法，假设线段MN与曲线f（x）不存在异于M、N的公共点．推出函数不单调矛盾．原结论正确．【解答】解：（Ⅰ）f′（x）=x2+2ax+b依题意，得f′（﹣1）=1﹣2a+b=0故b=2a﹣1．（Ⅱ）由（a）得故f′（x）=x2+2ax+2a﹣1=（x+1）（x+2a﹣1）令f′（x）=0，则x=﹣1或x=1﹣2a分情况讨论得：当x变化时，f′（x）与f（x）的变化如下表：x （﹣∞，1﹣（1﹣2a，﹣1）（﹣1，+∞）2a）f′（x）+ ﹣+f（x）单调递增单调递减单调递增（1）当a＞1时，1﹣2a＜﹣1由此得，函数f（x）的单调增区间为（﹣∞，1﹣2a）和（﹣1，+∞），单调减区间为（1﹣2a，﹣1）．（2）当a=1时，1﹣2a=﹣1．此时f′（x）≥0恒成立，且仅在x=﹣1处f′（x）=0故函数f（x）的单调增区间为R．（3）当a＜1时，1﹣2a＞﹣1同理可得函数f（x）的单调增区间为（﹣∞，﹣1）和（1﹣2a，+∞）单调减区间为（﹣1，1﹣2a）．（Ⅲ）假设线段MN与曲线f（x）不存在异于M、N的公共点．当a=﹣1时，由（a）的b=2a﹣1=﹣3．f（x）=﹣x2﹣3x就不在区间内单调与a＜﹣1单调减矛盾．所以假设错误．故线段MN与曲线f（x）存在异于M、N的公共点．【点评】此题考查学生利用导数研究函数单调的方法，以及反证法的运用．21．（14分）已知函数和g（x）=m（x﹣1），m∈R．（Ⅰ）m=1时，求方程f（x）=g（x）的实根；（Ⅱ）若对于任意的x∈[1，+∞），f（x）≤g（x）恒成立，求m的取值范围；（Ⅲ）求证：．【考点】函数恒成立问题；函数的值．【专题】分类讨论；数学模型法；函数的性质及应用．【分析】（Ⅰ）代入m=1时，f（x）=g（x）即=（x﹣1），整理方程得，利用导函数判断函数的单调性为递减函数，故最多有一个零点，而h（1）=0，故方程f（x）=g （x）有惟一的实根x=1；（Ⅱ）对于任意的x∈[1，+∞），f（x）≤g（x）恒成立，通过构造函数设，利用导函数判断函数的单调性，，通过讨论m，判断是否符合题意；由（Ⅱ）知，当x＞1时，时，成立．结合题型，构造不妨令，得出，利用累加可得结论；【解答】（Ⅰ）m=1时，f（x）=g（x）即=（x﹣1），∵x＞0，所以方程即为，令，则，∴h（x）单调递减，而h（1）=0，故方程f（x）=g（x）有惟一的实根x=1…4'（Ⅱ）对于任意的x∈[1，+∞），f（x）≤g（x）恒成立，∴lnx≤m（x﹣），设，即∀x∈[1，+∞），F（x）≤0，①若m≤0，则F'（x）＞0，F（x）≥F（1）=0，这与题设F（x）≤0矛盾②若m＞0，方程﹣mx2+x﹣m=0的判别式△=1﹣4m2，当△≤0，即时，F'（x）≤0，∴F（x）在（1，+∞）上单调递减，∴F（x）≤F（1）=0，即不等式成立当时，方程﹣mx2+x﹣m=0有两正实根，设两根为x1，x2，当x∈（1，x2），F'（x）＞0，F（x）单调递增，F（x）＞F（1）=0与题设矛盾，综上所述，．所以，实数m的取值范围是…9'（Ⅲ）由（Ⅱ）知，当x＞1时，时，成立．不妨令，所以，累加可得（n∈N*）．取n=1007，即得．【点评】考查了零点与单调性，利用导数判断恒成立问题，利用已证结论，构造函数解决实际问题．属于难题．。

四川省绵阳市高一上学期数学10月月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分） (2018高一下·衡阳期末) 已知集合，，若，则实数的取值范围（）A .B .C .D .2. （2分） (2016高三上·太原期中) 函数的定义域是（）A . A（﹣1，+∞）B . （﹣1，2）∪（2，+∞）C . （﹣1，2）D . （2，+∞）3. （2分） (2016高三上·虎林期中) 已知集合A={x|x（x+1）=0}，那么（）A . ﹣1∉AB . 0∈AC . 1∈AD . 0∉A4. （2分） (2020高三上·海淀期末) 已知集合，，，则集合是（）B .C .D .5. （2分） (2017高一上·定远期中) 下列各组函数表示同一函数的是（）A .B . f（x）=1，g（x）=x0C .D .6. （2分） (2019高一上·台州期中) 己知函数，那么的值为（）A . 9B .C .D .7. （2分）下列计算正确的是（）A .B .C .8. （2分）下列各式成立的是（）A . =B . （）2=C . =D . =9. （2分）已知f（x）为二次函数，对任意的二次函数f（x）和实数t，关于x的方程f（|x﹣t|）=0的解集都不可能的是（）A . {1，2}B . {1，3}C . {1，2，3}D . {1，2，4}10. （2分）已知集合，，则满足条件的集合C的个数为（）A . 5B . 4C . 3D . 211. （2分）若两个函数的图象经过若干次平移后能够重合，则称这两个函数为“同形”函数，给出下列四个函数：f1(x)=2log2x,f2(x)=log2(x+2),f3(x)=log22x,f4(x)=log2(2x),则“同形”函数是（）A . f1(x)与f2(x)B . f2(x)与f3(x)C . f2(x)与f4(x)D . f1(x)与f4(x)12. （2分） (2017高三上·定州开学考) 已知a为实数，函数f（x）=x2﹣|x2﹣ax﹣2|在区间（﹣∞，﹣1）和（2，+∞）上单调递增，则a的取值范围为（）A . [1，8]B . [3，8]C . [1，3]D . [﹣1，8]二、填空题 (共4题；共4分)13. （1分） (2019高一上·赣榆期中) 若幂函数的图像经过点，则 ________．14. （1分） (2017高一上·西城期中) 已知函数，分别由下表给出：则当时， ________．15. （1分） (2019高一上·大庆月考) 函数的值域为________.16. （1分）(2017·南京模拟) 以知f（x）是定义在区间[﹣1，1]上的奇函数，当x＜0时，f（x）=x（x﹣1），则关于m的不等式f（1﹣m）+f（1﹣m2）＜0的解集为________．三、解答题 (共6题；共50分)17. （10分） (2019高一上·兰州期中) ，（1）若，求 ;（2）若，求实数的取值范围.18. （10分） (2018高一上·江津月考) 已知二次函数对都有成立，且．（1）求函数的解析式；（2）若函数在上的最小值为，求实数的值。

四川省绵阳南山中学高一上学期第一次月考（数学）考试时间:10月14日下午4:00—5:40本套试卷分为第Ⅰ卷与第Ⅱ卷,其中第Ⅰ卷为选择题,第Ⅱ卷为填空题与解答题,共6页,满分100分,时间100分钟.只收第Ⅱ卷.第Ⅰ卷(主观题,共48分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上.2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试题卷上.一.选择题(本大题共12个小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{1,2,3,4,5,6}I =,{1,2,6}M =,{2,3,4}N =,则{1,6}=( )A .M NB .M NC .()I M N ðD .以上都不对2.下列五个写法:①{0}∈{1,2,3};②∅⊆{0};③{0,1,2}⊆{1,2,0};④0∈∅;⑤0∩∅=∅.其中,正确写法的个数为( )A .1B .2C .3D .43.设全集U ={2,4,6,8},集合A ={2,|a-2|},ðU A ={6,8},则实数a 的值为( )A .-6或-2B .-2或6C .-6或2D .2或64.命题p :a 2+b 2<0(a ,b ∈R ),命题q :a 2+b 2≥0(a ,b ∈R ),下列结论正确的是( )A .“p 或q ”为真B .“p 且q ”为真C .“非p ”为假D .“非q ”为真5.方程x 2- px +6=0的解集为M ,方程x 2+6x- q =0的解集为N ,且M ∩N ={2},那么p +q 等于( )A .21B .8C .6D .76.某食品的广告词为:“幸福的人们都拥有”,初听起来,这似乎只是普通的赞美说词,然而他的实际效果大呢,原来这句话的等价命题是( )A .不拥有的人们不一定幸福B .不拥有的人们可能幸福C .拥有的人们不一定幸福D .不拥有的人们不幸福7.若U 是全集,下列表述中错误．．的是( ) A .若A ⊆B ,则A ∩B =A B .若A ∪B =B ,则A ⊆BC .(A ∩B )A (A ∪B )D .ðU (A ∩B )=(ðU A )∪(ðU B )8.设集合21{|2},{|1}2A x xB x x =-<<=≤,则A B =( ) A .{12}x x -≤< B .1{|1}2x x -<≤ C .{|2}x x < D .{|12}x x ≤<9.如果集合S ={x |x =2n -1,n ∈Z },集合T ={y |y =4k ±1,k ∈Z },则( )A .S ∩T =∅B .S =TC .S TD .T S10.已知不等式ax 2+bx +2>0的解集为{x |13-<x <2},则不等式2x 2+bx +a <0的解集( ) A .}312|{<<-x x B .}213|{>-<x x x 或C .}213|{<<-x xD .}312|{>-<x x x 或 11.若集合21{||21|3},{|0}3x A x x B x x+=-<=<-,则A ∩B 是( ) A .1{|123}2x x x -<<-<<或 B .{|23}x x <<C .1{|2}2x x -<<D .1{|1}2x x -<<- 12.已知x ,y 是正实数,若x 2+2xy =y 2,则x y x y+=-( ) A.1.1- C.1.1-二.填空题(本大题共4小题,每小题3分,共12分)13.已知集合A={x|3≤x<7},B={x|5<x<10},则ðR(A∪B) .14.已知集合A,B 满足运算A*B={x|x∈A 且x ∉B},若集合A={1,2,3},B={2,4},则A*B=____________.15.不等式组2430x x a >⎧⎨+>⎩的解集是{x|x ＞2},则实数a 的取值范围是___________. 16.下列命题:①∅{0};②“若x2+y2=0,则x,y 全为0”的否命题;③命题“全等三角形是相似三角形”的逆命题;④“圆内接四边形对角互补”的逆否命题.其中,真命题的序号是________________(把你认为真命题的序号都填上).三.解答题(本大题共4小题,每题10分,共40分,解答应写出文字说明证明过程或推演步骤.)17.(本小题满分10分)已知集合A={1,3,2m －1},集合B ＝{3,m2}.若B ⊆A,求实数m 的值.18.(本小题满分10分)解关于x 的不等式: x2-(a+1)x+a≤0.19.(本小题满分10分)给定两个命题,p:对任意实数x 都有ax2+ax+1>0恒成立;q:关于x 的方程x2-x+a=0有实数根.如果命题“p 或q”为真,命题“p 且q”为假,求实数a 的取值范围.本小题满分10分)已知关于x 的不等式50ax x a -<-的解集为M . (Ⅰ)当a =4时,求集合M ;(Ⅱ)若3∈M ,且5∉M ,求实数a 的取值范围.。