测定钨丝的逸出功

钨逸出功的测定实验目的（1）学会用查逊(Richardson)直线法测定钨的逸出功。

（2）学习图表法数据处理的方法。

（3）熟悉WF-6逸出功测定仪的使用，并理解其工作原理。

实验原理电子从金属中逸出，需要能量．增加电子能量有多种方法，如用光照、利用光电效应使电子逸出，或用加热的方法使金属中的电子热运动加剧，也能使电子逸出．本实验用加热金属，使热电子发射的方法来测量金属的逸出功．如图1所示，若真空二极管的阴极(用被测金属钨丝做成)通以电流加热，并在阳极上加以正电压，在连接这二个电极的外电路中将有电流通过．这种电子从加热金属线发射出来的现象，称为热电子发射．研究热电子发射的目的之一，是选择合适的阴极材料．诚然，可以在相同加热温度下测量不同阳极材料的二极管的饱和电流，然后相互比较，加以选择．但通过对阴极材料物理性质的研究来掌握其热电子发射的性能，是带有根本性的工作，因而更为重要．在通常温度下由于金属表面与外界(真空)之间存在一个势垒W a ，所以电子要从金属中逸出必须至少具有能量W a ，在绝对零度时电子逸出金属至少需要从外界得到的能量为W 0=W a -W f =e ΦW 0称为金属电子的逸出功，其常用单位为电子伏特(eV)，它表征要使处于绝对零度下的金属中具有最大能量的电子逸出金属表面所需要给予的能量．Φ称为逸出电位，其数值等于以电子伏特表示的电子逸出功．热电子发射就是用提高阴极温度的办法以改变电子的能量分布，使其中一部分电子的能量大于W a ，使电子能够从金属中发射出来．因此，逸出功的大小对热电子发射的强弱具有决定性作用．１ 热电子发射公式根据费米–狄拉克能量分布公式，可以导出热电子发射的里查逊—杜什曼(Richar-dson-Dushman)公式：kTe AST I Φ-=e 2． (1)式中I 为热电子发射的电流强度，单位为A ；A 为和阴极表面化学纯度有关的系数，单位为Ａ/cm 2·C 2；S 为阴极的有效发射面积，单位为cm 2；k 为玻尔兹曼常数(k ＝1.38×10-23J/K)．原则上我们只要测定I ，A ，S 和T ，就可以根据式(1)计算出阴极材料的逸图1出功，但困难在于A 和S 这两个量是难以直接测定的，所以在实际测量中常用下述的里查逊直线法，以设法避开A 和S 的测量．２ 里查逊直线法将式(1)两边除以T 2，再取对数得到T ΦAS KT e ΦAS T I 1105.04log 2.30log log 32⨯-=-=． (2) 从式(2)可以看出,2log T I与1/T 成线性关系．如果以2log T I作纵坐标，以1/T为横坐标作图，从所得直线的斜率即可求出电子的逸出电位Φ，从而求出电子的逸出功e Φ．这个方法叫做里查逊直线法，它的好处是可以不必求出A 和S 的具体数值，直接从I 和T 就可以得出Φ的值，A 和S 的影响只是使2log T I―1/T 直线平行移动．这种实验方法在实验、科研和生产上都有广泛应用．３ 从加速场外延求零场电流为了维持阴极发射的热电子能连续不断地飞向阳极，必须在阴极和阳极间外加一个加速电场E a ．然而由于E a 的存在使阴极表面的势垒E b 降低，因而逸出功减小，发射电流增大．这一现象称为肖脱基(Scholtky)效应．可以证明，在加速电场E a 的作用下，阴极发射电流I a 与E a 有如下的关系：T E a aI I 0.439e = ． (3)式中，I a 和I 分别是加速电场为E a 和零时的发射电流．对式(3)取对数得a a E T I I 2.300.439log log += ．(4)如果把阴极和阳极做成共轴圆柱形，并忽略接触电位差和其它影响，则加速电场可表示为121ln r r r U E aa = ．(5)式中，r 1和r 2分别为阴极和阳极的半径，U a 为加速电压．将式(5)代入式(4)得a a U r r r T I I 121ln 12.300.439log log +=． (6)由式(6)可见，在一定的温度T 和管子结构下，logI a 和a U 成线性关系．如果以logIa为纵坐标，以a U为横坐标作图，此直线的延长线与纵坐标的交点为logI．由此即可求出在一定温度下，加速电场为零时的发射电流I(如图2所示).综上所述，要测定金属材料的逸出功，首先应该把被测材料做成二级管的阴极．当测定了阴极温度T，阳极电压Ua 和发射电流Ia后，通过数据处理，得到零场电流I，然后即可求出逸出功eΦ(或逸出电位Φ) 来了．实验仪器根据上述实验原理，本实验全套仪器采用WF-6型逸出功测定仪．本仪器具有以下特点：1．本仪器将所有的电源和测量电表集成在一起，免去了外部连线，缩小了实验场地。

钨逸出功实验报告
实验报告：钨逸出功
实验目的：
1.了解钨的物理性质。

2.通过实验测量钨的逸出功。

3.加深对钨的认识，为进一步研究打下基础。

实验器材：
光电效应测量仪、钨阴极、金属样品台。

实验原理：
金属与光子相互作用时，如果光子的能量足够大，则可将金属内的电子抛出，这一现象称之为光电效应。

逸出功就是光子与金属相互作用时，最小需要的光子能量。

通过光电效应测量仪可以测量出金属的逸出功。

实验步骤：
1.将钨阴极放置于样品台上，保证阴极与台面平行；
2.打开光电效应测量仪，调节电子倍增管的工作电压和放大倍数；
3.打开氦氖激光器，调节光子能量，使得光子束垂直射向钨阴极；
4.观察并记录下电压与电流随时间的变化，确定光子能量正好等于钨的逸出功时，电压和电流的值；
5.更改光子能量，重复上述步骤，记录多组数据；
6.关闭氦氖激光器和测量仪，整理实验数据。

实验结果：
按照上述步骤进行多次实验，记录各组数据如下：
光子能量/eV 逸出功/ eV
4.25 4.55
4.55 4.80
4.85 4.82
5.10 4.98
5.30 5.10
实验分析：
通过对不同光子能量下对钨的逸出功测量，得到了钨的逸出功在不同光子能量下的数值，证明了光子能量越大，需要的光子能量就越少。

在本次实验中，多组数据结果一致，误差在5%以内。

实验结论：
通过本次实验，得到了钨的逸出功数值。

实验结果与理论值相近，证明了实验方法和数据准确可靠。

该实验结果对于进一步研究钨等金属的物理性质具有重要的参考意义。

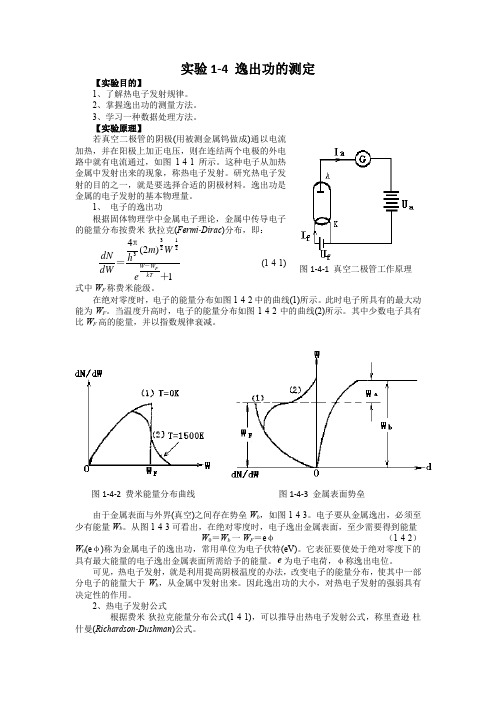
实验1-4 逸出功的测定【实验目的】1、了解热电子发射规律。

2、掌握逸出功的测量方法。

3、学习一种数据处理方法。

【实验原理】若真空二极管的阴极(用被测金属钨做成)通以电流加热，并在阳极上加正电压，则在连结两个电极的外电路中就有电流通过，如图1-4-1所示。

这种电子从加热金属中发射出来的现象，称热电子发射。

研究热电子发射的目的之一，就是要选择合适的阴极材料。

逸出功是金属的电子发射的基本物理量。

1、 电子的逸出功根据固体物理学中金属电子理论，金属中传导电子的能量分布按费米-狄拉克(Fermi -Dirac )分布，即：1)2(421233＋π＝－kTW W FeW m hdWdN (1-4-1)式中W F 称费米能级。

在绝对零度时，电子的能量分布如图1-4-2中的曲线(1)所示。

此时电子所具有的最大动能为W F 。

当温度升高时，电子的能量分布如图1-4-2中的曲线(2)所示。

其中少数电子具有比W F 高的能量，并以指数规律衰减。

由于金属表面与外界(真空)之间存在势垒W b ，如图1-4-3。

电子要从金属逸出，必须至少有能量W b 。

从图1-4-3可看出，在绝对零度时，电子逸出金属表面，至少需要得到能量W 0＝W b 一W F ＝e φ （1-4-2）W 0(e φ)称为金属电子的逸出功，常用单位为电子伏特(eV)。

它表征要使处于绝对零度下的具有最大能量的电子逸出金属表面所需给予的能量。

e 为电子电荷，φ称逸出电位。

可见，热电子发射，就是利用提高阴极温度的办法，改变电子的能量分布，使其中一部分电子的能量大于W b ，从金属中发射出来。

因此逸出功的大小，对热电子发射的强弱具有决定性的作用。

2、热电子发射公式根据费米-狄拉克能量分布公式(1-4-1)，可以推导出热电子发射公式，称里查逊-杜什曼(Richardson -Dushman )公式。

图1-4-1 真空二极管工作原理图1-4-2 费米能量分布曲线 图1-4-3 金属表面势垒kTe eAST I Φ－＝20 (1-4-3)式中：I 0-热电子发射的电流强度(A)S -阴极金属的有效发射面积(cm 2) k -玻尔兹曼常数 T -绝对温度e φ-金属的逸出功A -与阴极化学纯度有关的系数原则上，只要测出I 0，A ，S ，T ，便可由(1-4-3)式计算出逸出功e φ，但困难的是A 和S 是难以直接测量的，所以，在实际测量中，常用下述的里查逊直线法确定e φ，以设法避开A 和S 的测量。

钨 逸 出 功 的 测 定一、实验目的1．用里查逊（Richardson ）直线法测定钨的逸出功。

2．学习数据处理方法。

二、实验原理若真空二极管的阴极（用被测金属钨丝做成）通以电流加热，并在阳极上加以正电压时，在连接这二个电极的外电路中将有电流通过，如右图所示。

这种电子从加热金属丝发射出来的现象，称为热电子发射，研究热电子发射的目的之一可以选择合适的阴极材料。

1．电子的逸出功在通常温度下由于金属表面与外界（真空）之间存在一个势垒E b ，所以电子要从金属中逸出必须至少具有能量E b ，在绝对零度时电子逸出金属至少需要从外界得到的能量为E 0=E b －EF =ϕe （1）E 0(ϕe )称为金属电子的逸出功，其常用单位为电子伏特（ev ），它表征要使处于绝对零度下的金属中具有最大能量的电子逸出金属表面所需要给予的能量。

ϕ称为逸出电位，其数值等于以电子伏特表示的电子逸出功。

可见，热电子发射就是用提高阴极温度的办法以改变电子的能量分布，使其中一部分电子的能量大于E b ，这样能量大于E b 的电子就可以从金属中发射出来。

因此，逸出功ϕe 的大小，对热电子发射的强弱，具有决定性作用。

2．热电子发射公式根据固体物理理论热电子发射应满足里查逊—杜什曼公式I=2AST KT e e −ϕ（2）式中 I ——热电子发射的电流强度，单位为安培。

A ——和阴极表面化学纯度有关的系数，单位为安培/厘米2·度2。

S ——阴极的有效发射面积，单位为平方厘米。

K ——玻尔兹曼常数（K=1.38×10-23焦耳/开）原则上我们只要测定I 、A 、S 和T ，就可以根据（2）式计算出阴极的逸出功ϕe 。

但困难在于A 和S 这两个量是难以直接测定的，所以在实际测量中常用下述的里查逊直线法，以设法避开A 和S 的测量。

3．里查逊直线法将（2）式两边除以T 2，再取对数得到T AS KT e AS T I 11004.5log 30.2log log32ϕϕ×−=−= （3） 从（3）式可以看出，2log T I 与T 1成线性关系。

【精品】钨的逸出功测定(大学近代物理实验)钨是一种高熔点、高密度的金属，在实际应用中有着广泛的用途。

其中一项重要的性质是它的逸出功，即钨表面上的电子需要具有多大的能量才能够从钨表面逸出。

逸出功的测定对于研究钨在各种条件下的电子物理性质有着重要的意义。

本实验利用极限电流法测定钨的逸出功。

1. 实验原理在金属表面上，电子受到来自金属原子核和其他电子的吸引作用。

如果一个外部电子具有大于金属表面电势的能量，则可以逸出到真空中。

逸出能量的大小与表面电势差有关系，而表面电势差则决定了逸出功的大小。

如果在金属表面上施加外电场，可以降低钨表面电势，使得电子更容易逸出。

因为钨对外电场的响应更强，所以当正向电势差可控制时，逸出电子的电流随电势差变化的关系是很敏感的。

逸出电流可以通过使用极限电流法来测定。

在应用足够大的正向电势差时，在电子的逸出电流和肯定能量之间建立了一个平衡。

在这个平衡点处，逸出电流等于到达钨表面上的能流，此时钨表面上的逸出电并不随电势差的增加而增加，这个状态叫做饱和状态。

2. 实验步骤实验中需要用到的主要仪器设备为三角板、钨丝、电源、电压表、电流表和电荷计。

1）将钨丝固定在三角板上。

2）将三角板架上恒压电源，将正负极之间连线。

3）选择合适的电压，向钨丝加电。

4）调节电压、电流仪器读数范围及方向使电压逐步加大，同时用一个集电极测量逸出电流。

5）记录电压、电流和逸出电流随电压的变化。

6）统计数据以确定饱和电流。

7）根据实验数据计算钨的逸出功。

3. 实验注意事项1）实验过程中应注意安全。

2）实验时应选择合适的电压范围，以避免过大的电压对仪器设备造成损坏。

3）实验数据要进行多次测量，以得到更准确的结果。

4. 实验结果及分析在本实验中，实验数据如下表：| 电压（V） | 电流（mA） | 饱和电流（mA） ||----------|-------------|------------------|| 2.00 | 0.050 | 0.017 || 2.10 | 0.100 | 0.022 || 2.20 | 0.150 | 0.026 || 2.30 | 0.200 | 0.031 || 2.40 | 0.250 | 0.035 || 2.50 | 0.300 | 0.039 |其中，电压是钨丝和集电极之间的电势差，电流是钨丝上的电流，饱和电流是逸出电流随电压的变化而平稳到达的极限电流。

课程名称：大学物理实验（二）实验名称：金属电子逸出功的测定二、实验原理2.1金属电子逸出功逸出功：指要使电子从固体表面逸出，所必须提供的最小能量，用∆∅表示。

费米-狄拉克分布规律：在金属内部，电子按由低能态到高能态的次序占据，服从f(E,T)=1(1)1+exp⁡[(E−E F)/kT]如图1所示，在绝对零度时电子的最大动能是EF。

当温度升高时，有少部分电子的能量大于EF，能量的变化在~0.1eV 量级图1 费米-狄拉克分布规律测量时，逸出功等于费米能与真空能级之间的能量差。

∆∅=E Vacuum−E Fermi=eU(2)图2 金属钨表面电子的势能曲线2.2电子逸出功的测量方法1、里查逊—杜西曼公式（Richardson-Dushman formulaI=AST2exp(−eUkT)(3)式中：I是热电子发射的电流强度（单位：A）S是阴极金属的有效发射面积（单位：cm2）T是热阴极的绝对温度（单位：K）A是与阴极化学纯度有关的系数（单位：A⋅cm2⋅K−2）k是玻尔兹曼常数（k=1.38×10−23J⋅K−1）2、里查逊直线法I=AST2exp(−eUkT)(4)转化为I T2=ASexp(−eUkT)(5)取对数得：lg IT2=lg(AS)−eUklg⁡(e)1T(6)其中e和k是常数，U是逸出电势带入常数得：lg IT2=lg(AS)−5.04×103U1T(7)得：lg IT2和1T的线性关系，其斜率为5.04×103U里查逊直线法优点：可以不必测出A、S 的具体数值，只要测出I，T 的关系，由斜率可以得到逸出电势U。

温度T 可由通过灯丝的电流对照给出：表1 灯丝电流与温度的对应关系I f(A)0.580.600.620.640.660.680.70T(103K) 2.06 2.10 2.14 2.18 2.22 2.26 2.303、用外延法求零场电流测金属丝做成的阴极K，通过电流加热，在阳极加正向电压，则在连接这两个电极的外围电路中将有电流Ia通过。

钨的逸出功实验报告数据处理一、实验目的本实验旨在通过测量不同温度下钨的热电子发射电流，确定钨的逸出功，并加深对热电子发射现象和相关物理概念的理解。

二、实验原理根据热电子发射定律，金属中的自由电子在温度升高时，动能增大，部分电子具有足够的能量克服表面势垒而逸出金属表面，形成热电子发射电流。

热电子发射电流密度＄j$ 与温度＄T$ 之间的关系遵循理查森杜什曼（RichardsonDushman）方程：＼j ＝ A_0T^2e^｛＼frac{＼varphi}｛kT}｝＼其中，＄A_0$ 是与金属材料有关的常数，＄＼varphi$ 为金属的逸出功，＄k$ 为玻尔兹曼常数。

对上述方程两边取对数，可得：＼＼ln j ＝＼ln A_0 ＋ 2\ln T ＼frac{＼varphi}｛kT}＼若以＄＼ln j$ 为纵坐标，＄＼frac{1}｛T}＄为横坐标作图，可得一条直线。

直线的斜率为＄＼frac{＼varphi}｛k}＄，截距为＄＼lnA_0 ＋ 2\ln T$。

通过测量不同温度下的热电子发射电流，进行数据处理和直线拟合，即可求得钨的逸出功＄＼varphi$。

三、实验仪器1、热电子发射实验仪：包括钨丝阴极、阳极、加热电源、测量电路等。

2、温控仪：用于精确控制钨丝的温度。

3、数字电流表：测量热电子发射电流。

四、实验步骤1、连接实验仪器，确保电路连接正确无误。

2、开启温控仪，设置升温程序，使钨丝温度逐渐升高。

3、在不同温度下，记录数字电流表的读数，即热电子发射电流值。

4、测量足够多的数据点，以保证数据的准确性和可靠性。

五、实验数据记录｜温度＄T$ （K)｜热电子发射电流＄j$ （＄＼mu A$）｜｜｜｜｜1800|12|｜1900|28|｜2000|56|｜2100|98|｜2200|165|｜2300|257|｜2400|382|六、数据处理1、计算＄＼ln j$ 和＄＼frac{1}｛T}＄的值：｜温度＄T$ （K)｜热电子发射电流＄j$ （＄＼mu A$）｜＄＼ln j$ ｜＄＼frac{1}｛T}＄（＄＼times 10^｛－3} K^｛－1}＄）｜｜｜｜｜｜｜1800|12|01823|5556|｜1900|28|10296|5263|｜2000|56|17228|5000|｜2100|98|22833|4762|｜2200|165|28074|4545|｜2300|257|32472|4348|｜2400|382|36428|4167|2、以＄＼ln j$ 为纵坐标，＄＼frac{1}｛T}＄为横坐标，绘制散点图。

金属钨电子逸出功的测量金属电子逸出功的测量是近代物理学一个重要实验，它不仅可以证明电子的存在，而且为无线电电子学发展起到过不可磨灭的作用。

1884年。

当美国著名发明家爱迪生对白炽灯进行研究时，他发现灯泡里的白炽碳丝会逸出带负电的电荷。

1897年J．J.汤姆孙用磁场截止法测量了这个电荷的荷质比，证明从白炽碳丝逸出的电荷就是电子，后来被称为热电子。

由此科学家确定了“有比原子小得多的微观粒子”，J．J.汤姆孙也被誉为“一位最先打开通向基本粒子物理学大门的伟人”。

随后，通过对热电子发射现象的进一步研究，导致了真空电子管的出现。

电子管曾在无线电电子学的发展史中起过重要的作用，虽然目前在电子线路中它已绝大部分被晶体管和集成电路所取代，但在一些特殊场合，如显像、示波等，仍必须使用真空电子管。

因此研究真空电子管的工作物质——阴极灯丝的电子发射特性(用逸出功大小表征)，仍具有实际意义。

选择熔点高、逸出功小的金属作阴极材料对提高真空电子管的性能是很重要的。

金属钨由于具有熔点高、制成的管子寿命长等优点而被当作常用的阴极灯丝材料。

影响钨的逸出功的主要因素有：金属的纯净度、表面沾附层及结构处理工艺等，分别研究它们对逸出功的影响有利于对制造工艺的改进，提高电子管的性能．在这个实验里我们将测量具有洁净表面的纯金属钨的逸出功，在该实验中，采用的里查逊直线法处理数据、利用光测高温计测量温度等均是甚为巧妙的实验方法。

因此它对学生的基本实验技能是一个很好的训练。

一、实验目的1. 学习金属电子理论，了解金属热电子发射的基本规律；2. 学习里查森直线法的数据处理技术；3. 测量钨的逸出功eφ(或逸出电位φ)。

二、实验仪器介绍．本实验采用东南大学物理系根据上述实验原理研制生产的 WF-5型逸出功测定仪．仪器主要部分包括理想二极管、二极管供电电源、温度测量系统和测量阳极电压、电流的电表等。

仪器具有以下特点：①将所有的电源和测量电表集成在一起，并将理想二极管、测温系统收缩到仪器内部，形成黑匣子式实验仪器。

逸出功的测量一、实验目的:用里查孙直线法测定阴极材料（钨）的电子逸出功；通过实验, 了解热电子发射的规律和掌握逸出功的测量方法。

二、实验原理:热电子发射的里查孙-德希曼公式:()()2121a i W W kTe e J R AT e --=- （*）其中 为单位面积的发射电流, 为该金属的逸出功, 单位是电子伏特, 是普适常数, , k 是波尔兹曼常数, m 为电子质量, h 为普朗克常数, 为金属表面对发射电子的反射系数, T 为热力学温度。

若令 , 则上式可改写成:02e kTe J AT e φ-=于是可得发射电流 的公式为: , S 为阴极金属的有效发射面积。

三、测量及数据处理:1.A 与S 两个量的处理将（*）式除以 再取以10为底的常用对数, 得()021lglg 2.303e I e AS T kTφ=- 采用国际单位制并将 和k 的数值代入, 得()32lglg 5.30910e I AS T Tφ=-⨯ 2、 可看出 和 呈线性关系, 若以 和 作为纵横坐标, 直线的斜率可定出 。

3、 发射电流e I 的测量通常, 在加速场 的作用下, 阴极发射电流 和 有如下关系:Tee I I e '=与 分别为在加速场 及 =0时的发射电流。

取以10为底的对数, 得:lg lg ee I I '=+把阳极作成圆柱形, 并与阴极共轴, 忽略小量, 得:lg lg ee I I '=4、 其中 和 为阴极和阳极的半径, 为阳极电压。

可见, 在阴极温度一定的情况下, 与呈线性关系。

画出其关系曲线, 并将其外推至0处, 由此可定出 值。

5、 温度T 的测量本实验通过测量阴极加热电流来确定温度。

通过查表或从曲线上可查出与电流对应的温度。

四、仪器装置:1、直热式二极管, 阴极为纯钨丝。

2.实验所用仪器及规格 灯丝电源 约为0V~5V 电流表 量程1A, 测灯丝电流 数字电压表 0mV~200mV , 四位半读数实验板[甲] 安装有标准二极管, KH 已经并联上有两个相同电阻 串联而成的电阻。