逸出功的测定

逸出功的测量逸出功的测量粗略地讲，电子在金属内部所具有的能量低于在外部所具有的能量，因而逸出金属表面时需要给电子提供一定的能量，这份能量称为电子的逸出功。

在一高度真空的玻璃管中装上两个电极（如普通的二极管），其中一个用金属丝作成（一般称为阴极），并通以电流使之加热；在另一电极（即阳极）上加一高于金属丝的正电位，则在连接这两个电极的外电路中就有电流通过。

反之，若被加热金属丝的电位高于阳极，则外电路中就没有电流。

有电子从加热了的金属丝中射出，这现象称为热电子发射。

研究各种材料在不同温度下的热电子发射，对于以热阴极为基础的各种电子管的研制是极为重要的，电子的逸出功正是热电子发射的一个基本物理参量。

一、实验目的（1）用里查孙直线法测定阴极材料（钨）的电子逸出功；（2）通过实验，了解热电子发射的规律和掌握逸出功的测量方法。

二、实验原理根据量子论，原子内电子的能级是量子化的。

当某一能级被一个电子所占有，其他的电子就不能再占有这个能级。

在金属内部运动着的自由电子遵循类似的规律：①金属中自由电子的能量是量子化的；②电子具有全同性（即各电子是不可区分的）；③能级的填充状况要符合泡利不相容原理。

根据现代的量子论观点，金属中电子的能量分布服从费密—狄喇克分布。

在热力学温度零度时，电子数按能量的分布曲线如左图中的曲线①所示，此时电子所电子能量分布图具有的最大动能为Wi。

当温度升高时，电子能量分布曲线如上图中的曲线②所示，其中少数电子能量上升到比Wi高，并且电子数以接近于指数的规律减少。

由于金属与真空之间有位能壁垒Wa，如右图（d为电子距金属外表面的距离）。

因此电子要从金属中逸出，必须具有大于Wa的动能。

W0=Wa-Wi即为逸出功。

热电子发射是用提高阴极温度的办法以改变电子的能量分布，使动能大于Wi的电子增多，从而使动能大于Wa的电子数达到一可观测的大小，这位能势垒图时动能大于Wa的电子就有可能从金属发射出来。

可见，逸出功的大小对热电子发射的强弱有决定性的作用。

逸出功测量实验报告逸出功测量实验报告引言逸出功是指物质表面上的电子从固体内部逸出到外部所需的能量。

逸出功的大小与物质的性质有关，通过测量逸出功可以了解物质的电子结构和表面性质。

本实验旨在通过测量逸出功来研究不同材料的表面性质，并分析实验结果。

实验装置与步骤实验装置主要包括逸出功测量装置、光源、电子能量分析器和样品台。

实验步骤如下：首先，将待测材料放置在样品台上，并将光源照射在样品上；然后，通过电子能量分析器测量逸出电子的能量和角度分布；最后，根据测量结果计算逸出功。

实验结果与分析通过实验测量得到了不同材料的逸出功数据，并进行了分析。

结果显示，逸出功与材料的表面性质密切相关。

例如，金属材料的逸出功通常较低，这是因为金属表面存在大量自由电子，容易逸出；而半导体材料的逸出功较高，这是因为半导体表面的电子结构复杂，逸出电子需要克服更高的势垒。

此外，逸出功还与材料的化学成分和结构有关。

实验结果表明，不同合金材料的逸出功存在差异，这是由于合金中不同元素的化学性质不同。

同时，通过对不同晶面的逸出功测量，发现晶面的结构对逸出功也有影响。

例如，某些晶面上的原子排列更紧密，逸出功较低；而其他晶面上的原子排列较松散，逸出功较高。

实验结果的意义与应用逸出功测量在材料科学和表面物理研究中具有重要意义。

首先，逸出功是评价材料电子结构和表面性质的重要参数，可以为材料设计和表面改性提供依据。

其次，逸出功测量还可用于研究材料的光电子发射特性，包括光电效应和光电子能谱分析。

此外，逸出功测量还可应用于半导体器件的制备和表征，以及光电子器件的研究。

结论通过逸出功测量实验，我们可以了解不同材料的表面性质和电子结构。

逸出功的大小与材料的性质、化学成分和结构密切相关。

逸出功测量在材料科学和表面物理研究中具有重要意义，并可应用于材料设计、表面改性和光电子器件等领域。

本实验为进一步研究材料的电子结构和表面性质提供了基础。

致谢在此，感谢实验中提供的仪器设备和技术支持，以及实验中的指导和帮助。

逸出功的测量实验报告
《逸出功的测量实验报告》
在物理学中，逸出功是指从金属表面逸出的最小能量。

测量逸出功对于理解金
属的电子结构和性质具有重要意义。

本实验旨在通过实验方法测量金属的逸出功，并对实验结果进行分析。

实验过程中，我们选择了几种常见金属作为实验样品，包括铜、铝、铁等。

首先，我们将金属样品放置在真空室中，并通过加热或光照的方式激发金属表面
的电子。

随后，我们使用逸出功仪器测量金属表面逸出的电子能量，并记录实
验数据。

通过实验数据的分析，我们发现不同金属的逸出功存在一定的差异。

这一结果
与理论预期相符，因为不同金属的电子结构和束缚能会影响逸出功的大小。

此外，我们还发现逸出功与金属的表面特性和处理方式有关，例如金属的晶格结构、表面粗糙度等因素也会对逸出功产生影响。

通过本次实验，我们不仅成功测量了几种常见金属的逸出功，还深入了解了逸
出功与金属性质之间的关系。

这些实验结果对于深入理解金属的电子结构和应
用于光电器件等领域具有重要意义。

总的来说，本次实验为我们提供了一种简单而有效的方法来测量金属的逸出功，并为我们提供了更深入的认识金属性质的机会。

我们相信通过不断的实验探索
和理论分析，我们将能够更好地理解金属的电子结构和性质，为相关领域的研
究和应用提供更多的参考和支持。

实验3.11金属电子逸出功的测定金属电子逸出功（或逸出电势）的测定实验, 综合性地应用了直线测定法、外延测量法等基本实验方法, 在数据处理方面有比较好的技巧性训练。

从实际意义来看, 很多电子器件都与电子发射有关, 如电视机的电子枪, 它的发射效果会影响电视机的质量, 因此研究这种材料的物理性质, 对提高材料的性能是十分重要的。

【实验目的】1. 了解热电子发射的基本规律2. 用理查孙直线法测定金属钨电子的逸出功（或逸出电位）。

3. 学习直线测量法、外延测量法等基本实验方法。

【实验仪器】1. 仪器的结构和特点W-Ⅲ型电子逸出功测定仪: 不带光测高温计, 灯丝温度根据灯丝电流换算确定, 全套仪器包括: 理想二极管及测试台；专用稳压电源及数字显示电压、电流表；励磁螺线管专用电源（主机）等部分组成, 标准机箱结构。

2. 使用说明（1）将仪器面板上的3个电位器逆时针旋到底。

（2）将主机背板的插孔和理想二极管测试台的插孔用红黑连接线按编号一一对应接好（请勿接错）。

（3）接通主机电源开关, 开关指示灯和数字表亮。

（4）调节相应的灯丝电流和电压。

（5）从数字表上读出灯丝电流、阳极电压、阳极电流和励磁电流, 进行数据处理。

（6）仪器面板如图3-49所示。

图3-49 仪器面板3. 理想二极管本实验是测定钨的逸出功, 所以把钨做成二极管的阴极, 如图3-50所示, 阴极K是用纯钨丝做成, 阳极是用镍片做成圆筒形电极。

在圆筒上有一个小孔, 以便用光测高温计测定灯丝温度, 为了避免阳极两端因灯丝温度较低而引起的冷端效应和电场的边缘效应, 故在阳极上下端各装一个栅环电极B（或称保护电极）与阳极加相同电压, 但其电流不计入阳极电流中, 这样使其成为理想二极管。

理想二极管是一种进行了严格设计的理想器件, 这种真空管采用直热式结构。

为了便于进行分析, 电极的几何形状一般设计成同轴圆柱形系统。

【实验原理】1. 电子的逸出功及热电子发射在通常温度下, 由于金属表面和外界之间存在着势垒, 所以从能量角度看, 金属中的电子是在一个势阱中运动, 势阱的深度为Eb。

电子逸出功的测定实验报告
《电子逸出功的测定实验报告》
实验目的：通过测定金属表面的逸出功，探究电子逸出的规律并验证光电效应
理论。

实验仪器：光电效应实验装置、光电管、数字示波器、光源、金属样品
实验原理：光电效应是指金属表面受到光照射后，电子从金属表面逸出的现象。

逸出功是指光照射金属表面，使得电子逸出所需的最小能量。

根据光电效应理论，逸出功与光的频率成正比，与光的强度无关。

实验步骤：
1. 将金属样品放置在光电管的阳极上，并连接光电管和数字示波器。

2. 调节光源的频率和强度，使得光照射到金属样品上。

3. 观察数字示波器上的波形变化，记录光照射金属样品后的电压值。

4. 根据实验数据，计算出金属样品的逸出功。

实验结果：通过实验测定，得到金属样品的逸出功为X电子伏特。

实验结论：实验结果验证了光电效应理论，即逸出功与光的频率成正比。

通过
测定金属样品的逸出功，可以进一步了解光电效应的规律，并为相关理论研究
提供实验数据支持。

总结：本实验通过测定金属样品的逸出功，验证了光电效应理论，并为进一步
研究光电效应提供了实验数据支持。

同时，实验结果也可以应用于光电器件的
设计和制造中，具有一定的实际意义。

通过本次实验，我们对电子逸出功的测定有了更深入的理解，同时也对光电效
应的原理有了更加清晰的认识。

希望通过不断的实验和研究，我们能够更好地
探索光电效应的规律，为相关领域的发展做出更大的贡献。

逸出功的测量实验报告逸出功的测量实验报告引言逸出功是表征材料表面电子逸出能力的重要参数，对于理解材料的电子结构和表面性质具有重要意义。

本实验旨在通过测量逸出功的方法，探究不同材料的电子逸出特性。

实验方法1. 实验装置本实验使用的装置为逸出功测量系统，包括光源、光电倍增管、电压源和数据采集系统等。

光源用于照射样品，光电倍增管用于检测逸出电子，电压源用于施加电场，数据采集系统用于记录实验数据。

2. 实验步骤（1）准备样品：选择不同材料的样品，如金属、半导体等，并将其清洗干净，以保证表面光洁度。

（2）安装样品：将样品固定在实验装置的样品台上，并调整样品的位置，使其与光源和光电倍增管之间保持合适的距离。

（3）调整电压：根据样品的特性和预期的实验结果，调整电压源的电压，以施加合适的电场强度。

（4）测量数据：打开数据采集系统，开始测量逸出电子的光电流信号，并记录实验数据。

（5）重复实验：对于每个样品，重复以上步骤多次，以获得更加准确的实验结果。

实验结果与分析通过以上实验步骤，我们得到了不同材料的逸出电流信号，并根据实验数据计算得到了逸出功的数值。

以下是我们得到的一些实验结果和分析。

1. 金属材料我们选择了几种常见的金属材料进行实验，如铜、铝等。

通过测量逸出电流信号，我们得到了它们的逸出功数值。

实验结果显示，不同金属的逸出功存在一定的差异。

这是因为金属的电子结构和表面性质不同，导致其电子逸出能力也不同。

2. 半导体材料我们还选择了一些半导体材料进行实验，如硅、锗等。

与金属材料相比，半导体材料的逸出功通常较高。

这是因为半导体材料具有较宽的能带隙，需要更大的能量才能使电子逸出。

3. 表面处理对逸出功的影响我们还对一些样品进行了不同的表面处理实验，如氧化、薄膜涂覆等。

实验结果显示，表面处理对逸出功有一定的影响。

例如，经过氧化处理的金属样品逸出功较原始样品更高，这是因为氧化层增加了电子逸出的能量阻隔。

结论通过本实验的测量与分析，我们得到了不同材料的逸出功数值，并对其原因进行了一定的探讨。

金属逸出功的测定实验报告实验报告：金属逸出功的测定
实验目的：
测量金属样品逸出功，了解电子在固体中的行为。

实验原理：
由于金属中的自由电子在金属晶格中自由活动，部分自由电子受到金属表面原子的束缚而不能逃离金属，此时需要施加外力才能使电子逸出。

逸出功就是从固体表面逸出一个电子所需要的最小输入能量。

实验器材：
安全电源、万用表、电磁锁、样品台、吸附剂、金属样品
实验步骤：
1. 将金属薄板用吸附剂粘附在样品台上，确保金属样品表面平整。

2. 将电磁锁接上安全电源，连接万用表。

3. 将电磁锁固定在金属样品表面，开始施加外力。

4. 当万用表显示电压达到一定数值时，电磁锁会因为施加的外力而松开，此时电磁锁消耗的电能就是金属的逸出功。

5. 重复以上步骤3-4多次，取平均值做为测量结果。

实验数据记录：
1. 金属样品：铜板
2. 测量数据：
次数电磁锁瞬间消耗电能/mJ
1 2.7
2 2.8
3 2.6
4 2.7
5 2.9
平均值 2.74
实验结果分析：
根据以上实验数据，可以得到铜的逸出功约为2.74mJ。

由于金属逸出功与温度和样品表面的杂质有关，因此在实验中应保证样品的温度和表面的洁净度。

实验结论：
本实验通过施加外力，测量电磁锁消耗的电能，得到了铜的逸出功约为2.74mJ。

参考文献：
1. 高等物理实验教学指导委员会.《高等物理实验·第二册》.北京:高等教育出版社,2008.。

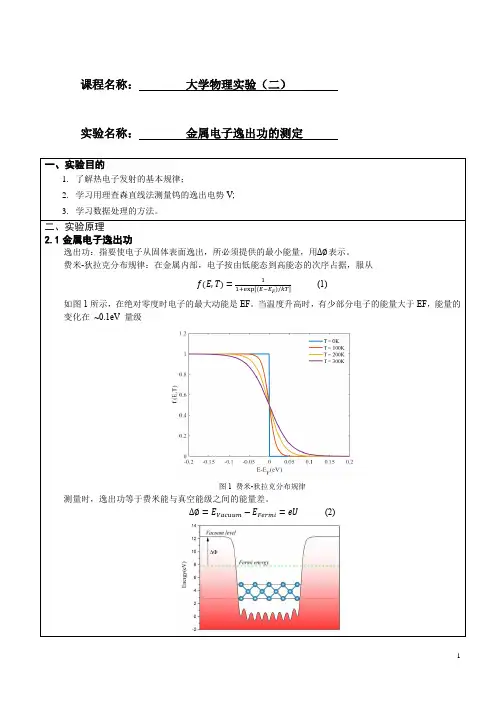
课程名称：大学物理实验（二）实验名称：金属电子逸出功的测定二、实验原理2.1金属电子逸出功逸出功：指要使电子从固体表面逸出，所必须提供的最小能量，用∆∅表示。

费米-狄拉克分布规律：在金属内部，电子按由低能态到高能态的次序占据，服从f(E,T)=1(1)1+exp⁡[(E−E F)/kT]如图1所示，在绝对零度时电子的最大动能是EF。

当温度升高时，有少部分电子的能量大于EF，能量的变化在~0.1eV 量级图1 费米-狄拉克分布规律测量时，逸出功等于费米能与真空能级之间的能量差。

∆∅=E Vacuum−E Fermi=eU(2)图2 金属钨表面电子的势能曲线2.2电子逸出功的测量方法1、里查逊—杜西曼公式（Richardson-Dushman formulaI=AST2exp(−eUkT)(3)式中：I是热电子发射的电流强度（单位：A）S是阴极金属的有效发射面积（单位：cm2）T是热阴极的绝对温度（单位：K）A是与阴极化学纯度有关的系数（单位：A⋅cm2⋅K−2）k是玻尔兹曼常数（k=1.38×10−23J⋅K−1）2、里查逊直线法I=AST2exp(−eUkT)(4)转化为I T2=ASexp(−eUkT)(5)取对数得：lg IT2=lg(AS)−eUklg⁡(e)1T(6)其中e和k是常数，U是逸出电势带入常数得：lg IT2=lg(AS)−5.04×103U1T(7)得：lg IT2和1T的线性关系，其斜率为5.04×103U里查逊直线法优点：可以不必测出A、S 的具体数值，只要测出I，T 的关系，由斜率可以得到逸出电势U。

温度T 可由通过灯丝的电流对照给出：表1 灯丝电流与温度的对应关系I f(A)0.580.600.620.640.660.680.70T(103K) 2.06 2.10 2.14 2.18 2.22 2.26 2.303、用外延法求零场电流测金属丝做成的阴极K，通过电流加热，在阳极加正向电压，则在连接这两个电极的外围电路中将有电流Ia通过。

逸出功的测量一、实验目的:用里查孙直线法测定阴极材料（钨）的电子逸出功；通过实验, 了解热电子发射的规律和掌握逸出功的测量方法。

二、实验原理:热电子发射的里查孙-德希曼公式:()()2121a i W W kTe e J R AT e --=- （*）其中 为单位面积的发射电流, 为该金属的逸出功, 单位是电子伏特, 是普适常数, , k 是波尔兹曼常数, m 为电子质量, h 为普朗克常数, 为金属表面对发射电子的反射系数, T 为热力学温度。

若令 , 则上式可改写成:02e kTe J AT e φ-=于是可得发射电流 的公式为: , S 为阴极金属的有效发射面积。

三、测量及数据处理:1.A 与S 两个量的处理将（*）式除以 再取以10为底的常用对数, 得()021lglg 2.303e I e AS T kTφ=- 采用国际单位制并将 和k 的数值代入, 得()32lglg 5.30910e I AS T Tφ=-⨯ 2、 可看出 和 呈线性关系, 若以 和 作为纵横坐标, 直线的斜率可定出 。

3、 发射电流e I 的测量通常, 在加速场 的作用下, 阴极发射电流 和 有如下关系:Tee I I e '=与 分别为在加速场 及 =0时的发射电流。

取以10为底的对数, 得:lg lg ee I I '=+把阳极作成圆柱形, 并与阴极共轴, 忽略小量, 得:lg lg ee I I '=4、 其中 和 为阴极和阳极的半径, 为阳极电压。

可见, 在阴极温度一定的情况下, 与呈线性关系。

画出其关系曲线, 并将其外推至0处, 由此可定出 值。

5、 温度T 的测量本实验通过测量阴极加热电流来确定温度。

通过查表或从曲线上可查出与电流对应的温度。

四、仪器装置:1、直热式二极管, 阴极为纯钨丝。

2.实验所用仪器及规格 灯丝电源 约为0V~5V 电流表 量程1A, 测灯丝电流 数字电压表 0mV~200mV , 四位半读数实验板[甲] 安装有标准二极管, KH 已经并联上有两个相同电阻 串联而成的电阻。

逸出功的测量实验报告逸出功的测量实验报告引言：逸出功是指在光照射下，材料中电子从固体表面逸出所需的最小能量。

它是材料表面电子状态和光电效应的重要参数，对于研究材料的光电性质以及应用于光电器件的设计具有重要意义。

本实验旨在通过测量材料的光电流和光强之间的关系，来确定材料的逸出功。

实验方法：1. 实验仪器和材料准备：本实验使用的仪器包括光电效应实验装置、光电效应测量系统、光源等。

材料准备包括金属样品或半导体样品，以及适当的清洁溶液等。

2. 实验步骤：（1）将实验装置搭建好，确保光源能够均匀照射到样品表面。

（2）选取不同波长的光源，如紫外光、可见光等，逐步照射样品表面，并记录下光电流的数值。

（3）根据测得的光电流数据和光源光强的关系，绘制出光电流与光强的曲线。

（4）通过拟合曲线，确定光电流为零时的光强值，即为逸出功。

实验结果：根据实验数据，我们得到了光电流与光强的曲线，如图1所示。

通过对曲线的拟合，我们可以得到光电流为零时的光强值，即为逸出功。

根据实验所用的不同材料，逸出功的数值也有所差异，这与材料的电子结构以及表面状态有关。

讨论与分析：逸出功的测量对于研究材料的光电性质具有重要意义。

逸出功的大小直接影响着材料的光电转换效率，因此在光电器件的设计中需要充分考虑逸出功的数值。

逸出功的测量方法可以通过光电流与光强的关系来确定，但是在实际操作中需要注意一些因素的影响。

首先，材料的表面状态对逸出功的测量结果有较大的影响。

如果材料表面存在氧化层或污染物，会使逸出功的测量结果产生偏差。

因此，在实验前需要对样品进行适当的清洁处理，以保证测量结果的准确性。

其次，光源的选择也会对逸出功的测量结果产生影响。

不同波长的光源对材料的逸出功有不同的激发效果，因此在实验中需要选择适当的光源来进行测量。

同时，光源的光强也需要适当调整，以保证测量结果的可靠性。

此外，实验中还需要注意测量条件的稳定性。

光电流的测量需要保持一定的稳定性，避免因测量误差导致逸出功的测量结果不准确。

金属逸出功的测定实验报告一、实验目的1、了解热电子发射的基本规律。

2、用理查逊直线法测定金属钨的逸出功。

二、实验原理1、热电子发射金属中的自由电子在一定的温度下会具有一定的动能，当电子的动能大于金属表面的逸出功时，电子就会从金属表面逸出，这种现象称为热电子发射。

2、理查逊杜什曼定律热电子发射的电流密度＄j$ 与金属表面的温度＄T$ 和逸出功＄W$ 之间有如下关系：＼j ＝ A T^2 e^｛＼frac{W}｛kT}｝＼其中，＄A$ 是与金属材料有关的常数，＄k$ 为玻尔兹曼常数。

对上式两边取对数可得：＼＼ln j ＝＼ln A ＋ 2\ln T ＼frac{W}｛kT}＼若以＄＼ln j$ 为纵坐标，＄＼frac{1}｛T}＄为横坐标作图，可得一直线。

直线的斜率为＄＼frac{W}｛k}＄，由此可求出金属的逸出功＄W$ 。

三、实验仪器WF-1 型金属电子逸出功测定仪、理想二极管、检流计、标准电阻、稳压电源、温度计等。

四、实验步骤1、按实验电路图连接好电路。

2、接通电源，预热仪器约 20 分钟，使灯丝达到热稳定状态。

3、调节灯丝电流，测量不同灯丝电流下的阳极电压和对应的阳极电流。

4、同时记录灯丝温度，灯丝温度可通过灯丝电流和仪器所给的灯丝电流与温度关系曲线查出。

五、实验数据记录与处理1、实验数据记录｜灯丝电流＄I_f$ （A) ｜阳极电压＄U_a$ （V) ｜阳极电流＄I_a$ （＄＼times 10^｛－6}＄ A) ｜灯丝温度＄T$ （K) ｜｜｜｜｜｜｜050 ｜25 ｜03 ｜1800 ｜｜055 ｜30 ｜05 ｜1850 ｜｜060 ｜35 ｜08 ｜1900 ｜｜065 ｜40 ｜12 ｜1950 ｜｜070 ｜45 ｜18 ｜2000 ｜｜075 ｜50 ｜25 ｜2050 ｜2、数据处理（1）计算不同温度下的电流密度＄j$ ，电流密度＄j ＝＼frac{I_a}｛S}＄，其中＄S$ 为阳极的有效面积。

逸出功的测量::实验内容::一、实验内容:1.学习了解热电子发射的基本规律;2.用里查孙直线法测定金属钨的电子逸出功;3.学习避开某些不易测常数而直接得到结果的实验数据处理方法。

二、实验原理:从固体物理学的金属电子理论知道，金属中电子的能量是量子化的，且服从泡利不相容原理，其传导电子的能量分布遵循费密??狄拉克分布。

在通常温度下，由于金属表面与外界之间存在着势垒，所以从能量的角度来看，金属中的电子是在一个势阱中运动，势阱的深度为E。

在热力学温b度零度时，电子所具有的最大能量为E，E称为费密能级，这时电子逸出金属表面至少需要从外界得到的能量为E,E,E,，E称为金 FF0bF0属电子的逸出功，常用电子伏特(V)作单位。

逸出功表征要使处于绝对零度的金属中具有最大能量的电子逸出金属表面所需要给予的最小能量。

是电子电荷，称为逸出电位。

电子从被加热金属中逸出的现象称为热电子发射。

热电子发射是通过提高金属温度的方法，改变电子的能量分布，使其中一部分电子的能量大于E，这些电子就可以从金属中发射出来。

不同的金属具有不同的逸出功，因此，逸出功的大小对热电子发0射的强弱有重要的影响。

实验常用里查孙直线法测定金属电子的逸出功。

1(热电子发射如图1所示，用钨丝作阴极的理想二极管，通以电流加热，并在阳极和阴极间加上正向电压(阳极为高电势)时，在外电路中就有电流通过。

电流的大小主要与灯丝温度及金属逸出功的大小有关，灯丝温度越高或者金属逸出功越小，电流就越大。

根据费密??狄拉克分布可以导出热电子发射遵守的里查孙??杜西曼公式2I , ASTexp(,) (1)-23式中I为热电子发射的电流强度，A为与阴极材料有关的系数，S为阴极的有效发射面积，为玻耳兹曼常数，,1.3807×10J/K，T为热阴-19极灯丝的热力学绝对温度(k为度数)，为逸出功，= 1.6022×10C。

从式(1)得, ASexp(,)两边取常用对数ln= lnAS, (2)从式(2)可以看出，ln与成线性关系。

金 属 电 子 逸 出 功 的 测 定Metal Work Function Measurement原理1．金属电子逸出功：电子在金属内部所具有的能量低于在外部所具有的能量，因而逸出金属表面需要给电子提供一定的能量。

电子逸出金属表面所需要的最小能量称为金属电子逸出功。

2．热电子发射的里查逊-热西曼公式单位面积的发射电流j ：()()kTWi W e a e T A R j /2112---=； 常数()22021/09.602K cm A hme k A ⋅==π； 00a i W W W e φ=-= —金属逸出功；0e —电子电量，190 1.60210e C -=⨯；φ—逸出电位，单位为V ；e R —金属表面对发射电子的反射系数；T —阴极金属的热力学温度；m —电子质量0.9109×10-30㎏； k —玻尔兹曼常数1.381×10-231/J K -； h —普朗克常数6.626×10-34J S ⋅发射电流公式： 0/2e kT I AST e φ-= S —阴极金属有效发射面积。

()112A R A e -=：A 与金属表面对发射电子的反射系数e R 有关，e R 与金属表面化学纯度有关，其数值决定于位能壁垒。

金属表面是否洁净，电子管内真空度情况直接影响e R 的测量。

金属表面是粗糙的，计算出的阴极发射面积与实际的有效面积S 也可能有差异。

因此，A 与S 无法准确测量。

注意事项1． 严防真空二极管磕碰或跌落。

2． 测量中每次改变灯丝电流f I 时要先预热几分钟再测量。

3． 不得将电源正负极短接。

测量表格 表1．在不同灯丝电流下测量阳极电压与阳极电流之间的关系：表2表1数据的转换值：表3在不同灯丝温度时的零场发射电流及其换算值：测量。

逸出功的测定【实验目的】1、了解热电子发射规律。

2、掌握逸出功的测量方法。

3、学习一种数据处理方法 【实验原理】若真空二极管的阴极(用被测金属钨做成)通以电流加热，并在阳极上加正电压，则在连结两个电极的外电路中就有电流通过，如图1-4-1所示。

这种电子从加热金属中发射出来的现象，称热电子发射。

研究热电子发射的目的之一，就是要选择合适的阴极材料。

逸出功是金属的电子发射的基本物理量。

1、 电子的逸出功由于金属表面与外界(真空)之间存在势垒W b ，如图1-4-3。

电子要从金属逸出，必须至少有能量W b 。

在绝对零度时，电子逸出金属表面，至少需要得到能量W 0＝W b 一W F ＝e φ （1-4-2）W 0(e φ)称为金属电子的逸出功，常用单位为电子伏特(eV)。

它表征要使处于绝对零度下的具有最大能量的电子逸出金属表面所需给予的能量。

e 为电子电荷，φ称逸出电位。

可见，热电子发射，就是利用提高阴极温度的办法，改变电子的能量分布，使其中一部分电子的能量大于W b ，从金属中发射出来。

因此逸出功的大小，对热电子发射的强弱具有决定性的作用。

2、热电子发射公式根据费米-狄拉克能量分布公式(1-4-1)，可以推导出热电子发射公式，称里查逊-杜什曼(Richardson-Dushman )公式。

kTe eAST I Φ－＝20 (1-4-3)式中：I 0-热电子发射的电流强度(A)S-阴极金属的有效发射面积(cm 2) k -玻尔兹曼常数 T -绝对温度e φ-金属的逸出功A-与阴极化学纯度有关的系数 3、里查逊直线法将(1-4-3)式两边除以T 2，再取对数，得到T 1004.5AS lg kT 30.2e AS lg T I lg320Φ－＝Φ－＝ (1-4-4)从(1-4-4)式可以看出，20lg T I 与T 1成线性关系。

如果以20lg TI 为纵坐标轴，T 1为横坐标轴作图1-4-1 真空二极管工作原理图，从得到的直线斜率即可求出电子的逸出功e φ值。

#### 一、实验目的1. 理解热电子发射的基本规律。

2. 掌握理查逊直线法测量金属逸出功的方法。

3. 学习数据处理和图表分析方法。

#### 二、实验原理金属中存在大量的自由电子，但电子在金属内部所具有的能量低于在外部所具有的能量。

因此，电子逸出金属时需要提供一定的能量，这个能量称为电子逸出功。

本实验通过加热金属，使其发生热电子发射，从而测量金属的逸出功。

实验中，利用理查逊直线法测量金属的逸出功。

该法基于以下原理：当金属阴极温度升高时，电子从金属表面逸出的概率增加，逸出电子的能量分布也随之改变。

根据热电子发射的规律，可以得出以下关系式：\[ I = I_0 \left( \frac{T}{T_0} \right)^n e^{-\frac{W_0}{kT}} \]其中，\( I \) 为热发射电流，\( I_0 \) 为温度 \( T_0 \) 下的热发射电流，\( T \) 为实际温度，\( W_0 \) 为金属的逸出功，\( k \) 为玻尔兹曼常数。

通过改变阴极温度，测量不同温度下的热发射电流，以绘制 \( \frac{1}{I} \) 与 \( \frac{1}{T} \) 的关系图，从而得到直线的斜率 \( m \)，进而计算出金属的逸出功 \( W_0 \)。

#### 三、实验仪器1. 金属电子逸出功测定仪（包括二极管灯丝温度测量系统、专用电源、显示测量电压电流的数字电表）。

2. 理想标准二极管。

3. 温度计。

4. 恒温水浴。

#### 四、实验步骤1. 将金属阴极（钨丝）放入恒温水浴中，调整温度至 \( T_0 \)。

2. 在金属阴极和阳极之间施加电压，使二极管导通。

3. 记录此时阴极的温度 \( T_0 \) 和对应的电流 \( I_0 \)。

4. 改变恒温水浴的温度，分别记录 \( T_1, T_2, \ldots, T_n \) 和对应的电流\( I_1, I_2, \ldots, I_n \)。

金属电子逸出功的测定实验报告一、实验目的1、了解热电子发射的基本规律。

2、用理查逊直线法测定金属钨的电子逸出功。

二、实验原理1、热电子发射金属中的自由电子在一定温度下会具有足够的能量，克服表面势垒而逸出金属表面，这种现象称为热电子发射。

2、理查逊杜什曼定律热电子发射电流密度＄j$ 与金属表面温度＄T$ 之间的关系遵循理查逊杜什曼定律：＼j ＝ A T^2 e^｛＼frac{e\varphi}｛kT}｝＼其中，＄A$ 是与金属材料性质有关的常数，＄e$ 是电子电荷量，＄k$ 是玻尔兹曼常数，＄＼varphi$ 是金属的逸出功。

3、逸出功的测定对上述公式两边取对数，得到：＼＼ln\frac{j}｛T^2} ＝＼ln A ＼frac{e\varphi}｛kT}＼若以＄＼ln\frac{j}｛T^2}＄为纵坐标，＄＼frac{1}｛T}＄为横坐标作图，得到一条直线。

根据直线的斜率，可以计算出电子逸出功＄＼varphi$ 。

三、实验仪器1、理想二极管（理查逊热电子发射管）2、加热电源3、电流表4、电压表5、温控仪四、实验步骤1、按实验电路图连接好仪器，检查线路无误后接通电源。

2、开启温控仪，逐步升高加热电流，使灯丝温度缓慢升高。

同时观察电流表和电压表的读数，记录不同温度下的电流和电压值。

3、当温度达到一定值后，停止加热，待温度稍降后再继续测量。

4、测量完毕后，关闭电源，整理仪器。

五、实验数据处理1、根据测量数据，计算出不同温度下的发射电流密度＄j$ ，公式为：＼j ＝＼frac{I}｛S}＼其中，＄I$ 是发射电流，＄S$ 是阴极发射面积。

2、计算出＄＼ln\frac{j}｛T^2}＄和＄＼frac{1}｛T}＄的值。

3、以＄＼ln\frac{j}｛T^2}＄为纵坐标，＄＼frac{1}｛T}＄为横坐标作图，得到一条直线。

4、通过直线的斜率＄K$ ，计算电子逸出功＄＼varphi$ ，公式为：＼＼varphi ＝＼frac{k}｛e}K\六、实验结果与分析1、实验数据记录表格｜温度 T （K)｜发射电流 I （A)｜发射电流密度 j （A/m²)｜＄＼ln\frac{j}｛T^2}＄｜＄＼frac{1}｛T}＄（1/K)｜｜｜｜｜｜｜｜＿____|＿____|＿____|＿____|＿____|｜＿____|＿____|＿____|＿____|＿____|｜＿____|＿____|＿____|＿____|＿____|｜｜｜｜｜｜2、绘制＄＼ln\frac{j}｛T^2}＄＄＼frac{1}｛T}＄图像根据实验数据，在坐标纸上绘制出＄＼ln\frac{j}｛T^2}＄与＄＼frac{1}｛T}＄的关系曲线。

逸出功的测量实验报告
《逸出功的测量实验报告》
在物理学中，逸出功是指光电效应中，光子能量大于金属表面的电子逸出所需
的最小能量。

逸出功的测量对于理解光电效应和金属表面电子特性具有重要意义。

在本次实验中，我们将通过实验方法测量金属表面的逸出功，并撰写实验
报告。

实验步骤如下：
1. 准备工作：首先，我们准备了一块金属样品，用来进行逸出功的测量。

同时，我们还准备了一台光电效应实验装置，用来照射光子，并测量光电子的动能。

2. 实验操作：我们将金属样品放置在光电效应实验装置中，然后通过调节光源
的光强和波长，照射金属样品。

随后，我们使用电子能谱仪测量光电子的动能，并记录下相应的数据。

3. 数据处理：通过实验测量得到的光电子动能数据，我们可以利用光电效应的
基本公式来计算逸出功。

逸出功的计算公式为：逸出功 = 光子能量 - 光电子动能。

4. 结果分析：通过实验数据的处理和计算，我们得到了金属样品的逸出功数值。

通过对比不同金属样品的逸出功数值，我们可以了解不同金属的电子特性和光
电效应的规律。

通过以上实验步骤和数据处理，我们成功测量了金属表面的逸出功，并得到了
相应的实验结果。

逸出功的测量实验为我们深入理解光电效应和金属电子特性
提供了重要的实验数据和理论支持。

希望本次实验报告能够对相关领域的研究
和教学提供一定的参考价值。