五年级长方体与正方体必会的题型汇编

完整版)长方体正方体经典题型汇总1.这个长方体的棱长总和是64分米。

2.这个长方体框架的高是15分米。

3.需要42厘米长的塑料带。

4.这个正方体的棱长是4厘米。

5.这个长方体的棱长总和是30分米。

6.这个长方体框架的高是20厘米。

7.这个正方体的棱长是28米÷4=7米。

8.这个长方体的棱长总和是21厘米。

9.每个正方体木块的棱长总和是40厘米。

1.至少需要36平方分米铁皮。

2.这张商标纸的面积是320平方厘米。

3.原来正方形铁皮的面积是625平方厘米。

4.这个长方体的表面积是162平方厘米。

5.粉刷水泥的面积是63平方米，需要252千克水泥。

6.至少需要480平方厘米铁皮，12节需要5760平方厘米铁皮。

7.20个这样的长方体需要400平方厘米的硬纸。

1.商标纸面积问题：一盒饼干长20厘米，宽15厘米，高30厘米。

要在它的四周贴上高6厘米的商标纸，求商标纸的面积。

解：首先计算长方体的表面积，即2(长×宽+长×高+宽×高)，得到2(20×15+20×30+15×30)=2700平方厘米。

然后计算加上商标纸后的长方体的表面积，即2[(20+2×6)×(15+2×6)+(20+2×6)×(30+2×6)+(15+2×6)×(30+2×6)] =2×(32×27+32×42+27×42)=2×3024=6048平方厘米。

商标纸的面积即为加上商标纸后的表面积减去原表面积，即6048-2700=3348平方厘米。

2.侧面积问题：一个长方体侧面积是360平方厘米，高是9厘米，长是宽的3倍。

求它的表面积。

解：由题可得，长方体的宽为120/9=40厘米，长为3×40=120厘米。

因此，长方体的表面积为2(40×9+120×9+40×120)=2×(360+1080+4800)=2×6240=平方厘米。

长方体正方体专项训练应用题一、长方体正方体的基本概念1. 长方体- 长方体有6个面，每个面都是长方形（可能有两个相对的面是正方形），相对的面完全相同。

- 长方体有12条棱，相对的棱长度相等，可以分为三组，每组有4条棱。

- 长方体有8个顶点。

2. 正方体- 正方体是特殊的长方体，它的6个面都是正方形，且6个面完全相同。

- 正方体有12条棱，12条棱的长度都相等。

- 正方体有8个顶点。

二、长方体正方体的表面积相关应用题1. 题目- 一个长方体的长是5厘米，宽是4厘米，高是3厘米，求这个长方体的表面积。

- 解析：- 长方体表面积公式为S=(ab + ah+bh)×2（其中a为长，b为宽，h为高）。

- 把a = 5厘米，b = 4厘米，h = 3厘米代入公式。

- 首先计算ab=5×4 = 20平方厘米，ah = 5×3=15平方厘米，bh=4×3 = 12平方厘米。

- 然后(ab + ah+bh)×2=(20 + 15+12)×2=(35 + 12)×2 = 47×2=94平方厘米。

2. 题目- 一个正方体的棱长为6分米，求它的表面积。

- 解析：- 正方体表面积公式为S = 6a^2（其中a为棱长）。

- 把a = 6分米代入公式，S=6×6^2=6×36 = 216平方分米。

三、长方体正方体的体积相关应用题1. 题目- 一个长方体的长是8米，宽是5米，高是4米，求这个长方体的体积。

- 解析：- 长方体体积公式为V=abh（其中a为长，b为宽，h为高）。

- 把a = 8米，b = 5米，h = 4米代入公式，V = 8×5×4=40×4 = 160立方米。

2. 题目- 一个正方体的棱长为7厘米，求它的体积。

- 解析：- 正方体体积公式为V=a^3（其中a为棱长）。

- 把a = 7厘米代入公式，V=7^3=7×7×7 = 343立方厘米。

北师大五下第二单元长方体和正方体题型汇总1、长方体和正方体都有（）个面，（）条棱，（）个顶点。

长方体的六个面最多有（）个是正方形。

2、长方体和正方体的（）之和叫它们的表面积。

3、单位换算5平方米=（）平方分米500平方厘米=（）平方米0.5公顷=（）平方米30分=（）时4、一个长方体和一个正方体的棱长和相等，已知长方体的长、宽、高分别为10㎝、5㎝、3㎝，那么正方体的棱长为（）㎝,表面积为（）5、至少用（）个相同的小正方体才可以拼成一个较大的正方体。

6、用三个棱长为2㎝的正方体拼成一个长方体，长方体的表面积是（）。

7、一个长方体的鱼缸，长8分米，宽5分米，高6分米，左面的玻璃不小心被打坏了，修理时配上的玻璃面积是（）。

8、如右图是一个正方体的展开图，和2号面相对的面是（）9、计算下面图形的表面积。

10、一个长方体纸箱，长8分米，宽10分米，高5分米，放在地上时占地面积最小是（），最大是（）12、长方体是特殊的正方体。

（）13、棱长为2厘米的正方体的表面积和棱长和相等。

（）14、正方体的每条棱扩大2倍，那么它的表面积扩大（）倍。

15、一种长方体的广告灯箱，框架是由铝合金条制成，各个面由灯箱布围成。

（长120厘米，宽100厘米，高80厘米）（1）制作这样一个广告灯箱框架，至少需要铝合金条多少分米？（2）做这样一个灯箱需要灯箱布多少平方米？16、五年级教室长9米，宽6米，高3.6米。

现在要给教室的四壁和天花板粉刷乳胶漆，除去门窗面积20平方米。

如果每平方米用乳胶漆0.8千克，一共需要乳胶漆多少千克？17、一个长方体的通风管长3米，横截面为宽2分米的正方形，做30节这样的通风管至少需要多少铁皮？18、淘气用厚纸做一个长方体的插笔筒，已知这个这个笔筒长8厘米，宽6厘米，高是12厘米，他做这个笔筒要用多少厚纸板？（接头处不计）19、把一个长方体的长减少3厘米，它就变为表面积是150平方厘米的正方体，求长方体的棱长和是多少厘米？长方体的表面积是多少？20、3个棱长都是10厘米的正方体堆放在墙角处（如下图）。

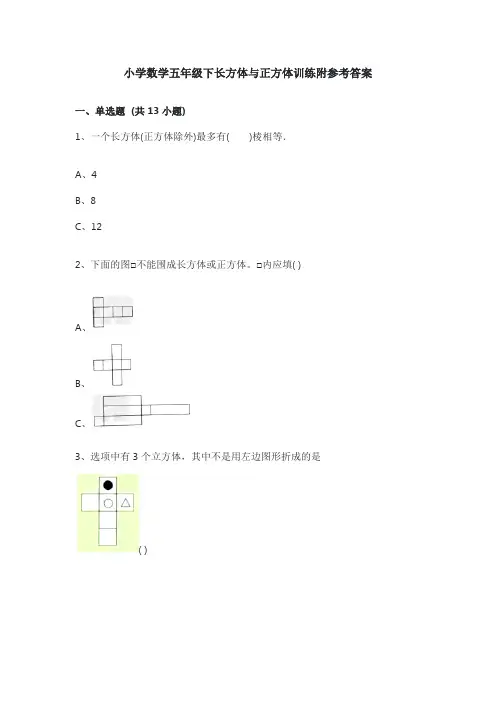
小学数学五年级下长方体与正方体训练附参考答案一、单选题(共 13 小题)1、一个长方体(正方体除外)最多有()棱相等．A、4B、8C、122、下面的图□不能围成长方体或正方体。

□内应填( )A、B、C、3、选项中有3个立方体，其中不是用左边图形折成的是( )A、B、C、4、把下边的正方体的表面展开，可能得到的展开图是( )A、B、C、D、C、4条D、5条6、图中有()个面中露在外面。

A、14B、15C、167、下面哪个不是正方体的展开图( )A、B、C、8、用一根长铁丝正好可以做一个长7厘米、宽4厘米、高5厘米的长方体框架，则这根铁丝长( )A、16厘米B、126平方厘米C、64厘米9、选项中哪个正方体展开后可以得到下面的展开图( )A、B、C、D、10、如图，有一个无盖的正方体纸盒，下底标有字母“M”，沿图中粗线将其剪开展成平面图形想想会是( )A、B、C、11、下面第哪个图形不能折成正方体？( )A、B、C、12、下列图形中，是正方体的表面展开图的是( )A、B、C、13、一个立方体木块，6个面都涂上红色，然后把它切成大小相等的27个小立方体，其中有三个面是红色的小立方体有( )A、4B、12C、6D、8二、多选题(共 1 小题)1、把下边图中的五个小方格折起来，可以是一个无盖的纸盒的是( )A、B、C、三、判断题(共 1 小题)1、一个长方体，如果有两个相邻的面是正方形，这个长方体就是正方体．______．四、填空题(共 16 小题)1、如图中，棱AE与平面DCGH的关系是______．2、如图中，与平面BCGF垂直的平面有______个．3、长方体和正方体都有______个面，______条棱，______个顶点．4、长方体有8个顶点，______条棱，______个面．5、用一根144厘米长的铁丝，围成一个正方体框架，它的棱长是______厘米；如果用它围成一个长方体的框架，长20厘米、宽10厘米、高______厘米．6、小丽为奶奶选了一份生日礼物．(如图)用彩带捆扎，至少需要______cm彩带．(打结处用了30cm)7、在长方体ABCD-EFGH中，与棱EF和棱EH都异面的棱是______．8、如图在长方体ABCD-EFGH中，与棱EF垂直的棱是______．(写出符合题意的所有棱)9、右面的正方体，按图中所示切去一角，剩下的图形有______个面，______条棱，______个顶点．10、如图，长方体ABCD-A1B1C1D1中，与平面ADD1A1平行的棱是______．11、如图是长方体的展开图，与1号面相对的面是( )号面。

长方体和正方体重点题型总结这单元的题型种类颇多，但是都脱离不了公式。

对公式必须熟烂于心。

综合题型的强度比较大，要求我们在做题时必须灵活，随机应变。

综合题型一、等体问题：1. 有一块棱长是20厘米的正方体的铁块，现在要把它溶铸成一个横截面积是20平方厘米的长方体，这个长方体的长是多少厘米？2. 一个棱长4分米的正方体容器，盛满水后倒入一个长8分米，宽2分米，高5分米的长方体水槽中，水深多少分米？3.把12立方米的黄沙铺在一个长8米，宽3米的长方体沙坑里，可以铺多厚？4.一个封闭的长方体容器，长是10厘米，宽是10厘米，高15厘米，里面水的高度是9厘米。

如果把这个容器由竖放改成横放，现在水面的高度是多少厘米？综合题型二、切、拼求表面积和体积问题：1.一个长方体正好可以切成5个同样大小的正方体，切成的5个正方体的表面积比原来长方表面积多了200平方厘米，求原来长方体的表面积和体积分别是多少？2.把三个棱长都是4厘米的正方体拼成一个长方体，拼成的长方体表面积和体积分别是多少？3.把4个棱长2厘米的正方体拼成一个长文体一，拼成的长方体体积是多少，表面积是多少？综合题型三、挖小正方体求剩下图形的表面积和体积：2.王师傅在一个棱长为6厘米的正方体木块上挖下一个棱长2厘米的小正方体，剩下部分表面积可能是多少平方厘米？3.有一个长方体形状的零件，中间挖去一个正方体的孔（如图），你能算出它的体积和表面积吗？（单位：厘米）4.一个零件形状大小如下图：算一算，它的体积是多少立方厘米？表面积是多少平方厘米？（单位：厘米）综合题型四、长方体切最大正方体问题：1.在一个长23分米，宽5分米，高5分米的长方体木上切一个最大的正方体，切成的正方体的表面积和体积分别是多少？最多能切多少个？2.在一个长20分米，宽6分米，高5分米的长方体木上切一个最大的正方体，切成的正方体的表面积和体积分别是多少？综合题型五、长方体切成小正方体，求个数问题：1. 把一个长6分米，宽4分米，高5分米的长方体木块切成，棱长为1分米的小正方体木块，最多能切多少个？2.在一个长23分米，宽5分米，高5分米的长方体木上切棱长为2分米的正方体能切多少个？综合题型六、长方体高增加或减少后成正方体，求表面积、体积问题：1.一个长方体，如果高增加3厘米，就成为一个正方体。

长、正方体必会题型1、至少用（）米的铁丝才能焊成一个长7米，宽6米，高2米的长方体框架，若改焊成正方体，表面糊纸，则用纸的面积是（）平方米，正方体的体积是（）。

2、往长8米，宽和高都是5米的长方体水池中注入96立方米的水，水深（）米。

3、从一个长10分米，宽6分米，高5分米的长方体木块切下一个最大的正方体，剩余的体积是（）立方分米。

4、搭建一个长6米、宽5米、高4米的长方体框架，需要准备（）种不同长度的铁丝，每种各（）根，共需要（）米。

5、3个棱长是2分米的正方体拼成一个大长方体，这个长方体的表面积是（）平方分米，体积是（）立方分米。

6、棱长是a米的一个正方体，截成3段后，表面积比原来增加（）平方米。

7、正方体棱长扩大3倍，表面积扩大（）倍，体积扩大（）倍。

8、长方体长扩大3倍，宽扩大2倍，高缩小4倍，则体积（）倍。

9、4200立方厘米=（）升（）毫升2.8立方分米＝（）升＝（）毫升6立方分米30立方厘米＝（）升7.03升＝（）升（）毫升3060毫升=（）立方分米（）立方厘米10、用长36厘米的铁丝围成一个正方体的框架，这个正方体的表面积是（），体积是（）。

11、把一根1米长的木料，平均截成3段，表面积增加了12平方分米，原来这根木料的体积是（）立方分米。

12、判断：①体积相等的两个箱子容积也相等。

（）②长方体橡皮泥捏成正方体后，表面积和体积都不变。

（）③棱长6厘米的正方体表面积和体积相等。

（）④表面积相等的两个正方体，体积也相等。

（）⑤棱长之和相等的两个长方体，体积也一定相等。

（）13、至少用（）个同样大小的小正方体才能拼成一个大正方体。

一个小正方体的棱长是4厘米，一个大正方体的棱长是8厘米，大正方体的表面积是小正方体表面积的（）倍。

14、爸爸准备用一种地板来装修房间，每块地板的长50厘米，宽8厘米，厚2厘米，刚好用了300块这样的地板，房间的面积有多少平方米？15、将一块长30厘米，宽15厘米的长方形铁板焊接成一个无盖、高1厘米的长方体盒子，要使铁盒的容积最大，该怎样焊接？容积是多少？16、一种下水管每根长2米，横截面是边长5分米的正方形，做10根这样的下水管至少要用多少平方米的铁皮？17、体育馆有4个长方体混凝土核心筒作支撑，每个核心筒的横截面是边长15米的正方形，高60米，每个核心筒占地面积是多少平方米？每个核心筒中能浇灌多少混凝土？每个核心筒的侧面贴瓷砖，求贴瓷砖的面积？18、从一个长方体上截下一个体积是32立方厘米的小长方体后，剩下部分正好是一个棱长4厘米的正方体，原来长方体的体积是多少？19、一个长方体高去掉2厘米后正好是一个正方体，表面积减少24平方厘米，原来长方体的体积是多少？20、一个棱长15厘米的正方体容器内装满水，然后把水倒入一个长20厘米，宽15厘米的长方体空水箱内，这时水深多少厘米？21、一个长方体交于一个顶点的三条棱分别是4厘米、3厘米、5厘米，这个长方体占地面积最少是（）平方厘米。

（完整版）五年级下册长⽅体与正⽅体分类题型练习（2）长⽅体与正⽅体重点题型⼀、⾼的变化引起表⾯积的变化。

1、⼀个长⽅体，如果⾼增加2厘⽶就成了正⽅体，⽽且表⾯积要增加56平⽅厘⽶，原来这个长⽅体的体积是多少⽴⽅厘⽶？2、⼀个长⽅体，如果⾼减少2厘⽶就成了正⽅体，⽽且表⾯积要减少56平⽅厘⽶，原来这个长⽅体的体积是多少⽴⽅厘⽶？3、⼀个长⽅体，如果长减少2厘⽶就成了⼀个正⽅体，⽽且表⾯积要减少56平⽅厘⽶。

原来这个长⽅体的体积是多少⽴⽅厘⽶？4、⼀个长⽅体，长a分⽶，宽b分⽶，⾼h分⽶，如果⾼减少3分⽶，这个长⽅体表⾯积⽐原来减少（）平⽅分⽶？体积⽐原来减少（）⽴⽅分⽶？⼆、段的变化1、⼀个长⽅体长2⽶，截⾯是边长3厘⽶的正⽅形，将这个长⽅体⽊料锯成五段后，表⾯积⼀共增加了多少平⽅厘⽶？2、将⼀个长3⽶的长⽅体⽊料平均截成3段，表⾯积⼀共增加了0.36平⽅分⽶，这根⽊料的体积是多少⽴⽅分⽶？六、挖1、⽤8个⼩正⽅体⽊块拼成⼀个⼤的正⽅体，如果拿⾛1个⼩⽅块，它的表⾯积和原来⽐( )。

2、在棱长1分⽶的正⽅体的顶点处挖去⼀个棱长1厘⽶的⼩正⽅体，剩下物体的表⾯积和体积分别是多少？3、在⼀个棱长4厘⽶的正⽅体六个⾯的中⼼都挖去⼀个棱长1厘⽶的⼩正⽅体，剩下物体的表⾯积是多少平⽅厘⽶？七、扩⼤和增加倍数。

1、⼀个正⽅体棱长扩⼤2倍，表⾯积扩⼤（）倍，体积扩⼤（）倍，表⾯积增加（）倍，体积增加（）倍。

2、⼀个正⽅体的棱长增加2倍，表⾯积增加（）倍，体积增加（）倍。

3、⼀个⼤正⽅体的棱长是⼩正⽅体棱长的2倍，已知⼤正⽅体的体积⽐⼩正⽅体多21⽴⽅厘⽶，⼤⼩正⽅体的体积分别是多少？⼗、⽯块沉浮（物体浸⼊⽔中的体积=排开⽔的体积）1、在⼀只长25厘⽶，宽20厘⽶的玻璃缸中，有⼀块棱长10厘⽶的正⽅体铁块，这时⽔深15厘⽶，如果把这块铁块从缸中取出来，缸中的⽔深多少厘⽶？2、把⼀个体积为80⽴⽅厘⽶的铁块浸在底⾯积为20平⽅厘⽶的长⽅体容器中，⽔⾯⾼度为10厘⽶，如果把铁块捞出后，⽔⾯⾼多少？3、⼀个长⽅体玻璃缸，从⾥⾯量长40厘⽶，宽25厘⽶，缸内⽔深12厘⽶。

14、体积相等的两个正方体，它们的表面积一定相等。 （ √ ）
15、正方体的棱长扩大2倍，它的表面积就扩大8倍。（ × ） 16、体积单位比面积单位大，面积单位比长度单位大．（ ×
）
17、一个冰箱的容积就是它的体积。（ × ）
18、把一块正方体形状的橡皮泥压制成长方体的形状，与原来的 正方体相比，体积不变。（ √ ）
8、一个魔方的表面积是54平方厘米，它的一个面的面积 是（ 9 ）平方厘米。
9、一个长方体不同方向三个面的面积分别是6平方厘米， 12平方厘米，18平方厘米，则这个长方体的表面积是（ 72 ）平方厘米。
10、一个长4分米，宽3分米，高2分米的长方体，它的占 地面积最大是（ 12 ）平方分米，它的表面积是（ 52 ） 平方分米。
开图正好也是一个正方形，这个长方体的侧面积是（ B ）
平方米． A．16 B．64 C．48
7．用两个棱长为1分米的小正方体拼成一个长方体，发生了什么变
化？（D ）
A．体积变大，表面积变小 B．体积变小，表面积变大 C．体积不变，表面积变大 D．体积不变，表面积变小
8．把一个长方体分成几个小长方体后，体积（ A ）.
18、把一根长80厘米，宽5厘米，高3厘米的长方体木料锯 成长都是40厘米的两段，表面积比原来增加了（ 30 ）平 方厘米。
19、物体（ 所占空间的大小 ）的大小叫做物体的体积。
20、棱长为（ 1米 ）的正方体的体积是1立方米，棱长为1 分米的正方体的体积是（ 1立方分米 ），棱长为1厘米 的正方体的体积是（ 1立方厘米 ）。
4．一个正方体的棱长总和是60厘米，它的表面积是（ B ）
. A．21600平方厘米 B．150平方厘米C．125立方厘米
5．一个长2米、宽2米、高3米木箱平放在地面上，占地面积至

长方体正方体体积经典题型分类
1. 满满都是陷阱型！比如给你一个看似简单的长方体，告诉你一些乱七八糟的条件，然后问你体积到底是多少呀，哎呀，那可得好好动动脑筋，稍不注意就掉坑里啦！
2. 复杂关系纠结型！就像有两个正方体和一个长方体搅和在一起，它们之间还有各种关联，这得捋清楚它们的关系才能算出体积啊，是不是很刺激呀！
3. 藏头露尾神秘型！只给你一部分关于长方体或正方体的信息，其他的要靠你自己去挖掘推理，就好像侦探破案一样，你能找出隐藏的体积秘密吗？
4. 超级变变变型！一开始是个正方体，变着变着就成了个长方体，或者反过来，然后让你算变化后的体积，这可太好玩啦！
5. 实际应用烦恼型！比如要你算一个盒子能装多少东西之类的实际问题，哎呀，这可得联系实际来思考，能解决这种题超有成就感的呢！
6. 创意无限想象型！会让你想象一些奇奇怪怪的长方体或正方体组合，然后计算体积，让你的思维尽情飞翔吧！
我的观点结论是：这些不同类型的长方体正方体体积经典题型，真的是各有各的趣味和挑战，能让我们在解题的过程中不断提升自己的思考能力和对空间的理解呀！。

长方体和正方体基本题型归纳1.鱼缸表面积问题：一个长90厘米、宽30厘米、高60厘米的长方体无盖玻璃鱼缸，制作这个鱼缸至少需要多大面积的玻璃？2.排气管道问题：一节横截面为正方形，边长为2厘米的排气管道长1米，制作这样一节排气管道至少需要多少平方米的铁皮？3.粉刷房间问题：一间长5米、宽4米、高3米的房间，门窗面积为8平方米，这间房的粉刷面积是多少？4.加工机套问题：制作1000个洗衣机机套（没有低面），每台洗衣机的长、宽、高分别为59.5厘米、42.5厘米、80厘米，至少需要多少平方米的布料？5.游泳池贴瓷砖问题：一个长50米、宽25米、深2.5米的游泳池，四周和低面都需要贴瓷砖，共需要多少平方米的瓷砖？6.长方体体积问题：一个底面积为20平方厘米、高为8厘米的长方体，体积是多少？7.截长方体成正方体问题：将一个长12厘米、宽10厘米、高5厘米的长方体截成一个体积最大的正方体，这个正方体的体积是多少？8.长方体表面积问题：一根2米长的长方体木块，平均截成两段后表面积增加了0.6平方米，原来长方体木块的体积是多少？9.游泳池注水问题：往一个长50米、宽30米的游泳池中注水，如果每小时能注水200平方米，多少时间才能使水深达2.4米？10.蓄水池问题：挖一个长10米、宽8米、深5米的长方体蓄水池，其占地面积、蓄水量、贴瓷砖面积和水位线长度分别是多少？11.长方体体积问题：一个长3米、宽0.5米、厚0.12米的长方体木料，其体积是多少？合多少立方分米？12.土坑问题：建筑工地要挖一个长50米、宽30米、深0.5米的长方体土坑，挖出多少方的土？13.方木体积问题：家具厂订购500根横截面面积为24平方分米、长为3米的方木，这些木料共多少方？14.围墙问题：一道长15厘米、厚24厘米、高3米的围墙需要多少块砖？15.木地板问题：一间长5米、宽3米的房间地面铺设了2厘米厚的木地板，至少需要多少立方米的木材。

五下数学长方体与正方体应用题汇总60题长方体与正方体应用题训练60题1、现有一根长150厘米的铁丝，用这根铁丝焊接成一个正方体框架，还剩6厘米铁丝，这个正方体框架的棱长是多少厘米？（接头处忽略不计）2、一根铁丝，可以做成长8厘米，宽6厘米，高4厘米的长方体框架，如果用它来做一个正方体框架，做成的正方体框架棱长是多少厘米？3、一个长方体的12条棱的总长度是104厘米，已知它的长是13厘米，宽是10厘米，高是多少厘米？4、用两个相同的正方体木块拼成一个长方体，棱长之和减少了24厘米，这两个正方体木块原来的棱长总和是多少？5、一个长方体木块被截成了两个完全相同的正方体，两个正方体的棱长之和比原来长方体的棱长之和增加了16厘米，求原来长方体的长是多少厘米？6、用三个完全相同的正方体拼成一个长方体，这个长方体的棱长和是180厘米，原来一个正方体的棱长和是多少厘米？7、一个棱长为8厘米的正方体罐头盒，在盒子的四周贴上商标纸，这张商标纸的面积最少是多少平方厘米？8、一个游泳池，长50米，宽20米，深2米，目前要给游泳池的四壁和底面抹水泥，抹水泥的面积是多少平方米？9、五（1）班教室在二楼（共四层）长10米,宽6米,高4米,门窗面积19.6平方米,如果每平方米用涂料0.25千克来粉刷,共需要涂料多少千克?10、把一个长6厘米，宽5厘米，高4厘米的长方体木块锯成两个小长方体，表面积最多增加多少平方厘米？最少增加多少？11、在棱长为10cm的正方体上放一个棱长为5cm的正方体（如图），这个图形的体积和表面积分别是多少？12、一个长方体它的底面是一个边长为15厘米的正方形，高为20厘米，如果把它的高增加5厘米，它的表面积会增加多少？13、一个长25厘米，宽20厘米的长方形铁皮，从四个角上各减去一个边长为5厘米的正方形，形成一个无盖的铁盒，这个无盖的铁盒五个面的面积和是多少？（铁皮的厚度不计）14、一个长方体能够切成两个完全一样的正方体（如右图），已知正方体的棱长为2厘米，原来的长方体的表面积是多少平方厘米？15、一个棱长为9厘米的正方体木块，在它的前后两个面的中央挖去一个相通的长方体，截口是边长为2厘米的正方形，剩余木块的外表积是多少平方厘米？16、一个正方体木块，把它分成3个大小不异的长方体后，外表积增长了36平方厘米，这个木块原来的外表积是多少平方厘米？17、用三个完全不异的正方体摆成一个长方体，这个长方体的外表积是350平方厘米，则每个正方体的外表积是多少平方厘米？18、用五个完全相同的正方体摆成一个长方体，这个长方体的表面积是770平方厘米，则每个正方体的表面积是多少平方厘米？19、将一根长52厘米的铁丝焊接成一个长6厘米、宽4厘米的长方体框架，这个长方体框架的表面积是多少平方厘米？20、XXX老师要做一个长1.2米、宽45厘米、高1.5米的陈列箱，陈列箱除了正面用玻璃，其余各面都用木板。

五年级数学压轴题下册一、长方体和正方体相关（8题）1. 一个正方体的棱长总和是72分米，这个正方体的表面积是多少平方分米？体积是多少立方分米？- 解析：正方体有12条棱，且每条棱长度相等。

已知棱长总和是72分米，那么每条棱的长度为72÷12 = 6分米。

- 正方体的表面积公式为6a^2（a为棱长），所以表面积为6×6^2=6×36 = 216平方分米。

- 正方体的体积公式为a^3，所以体积为6^3=216立方分米。

2. 一个长方体，长8厘米，宽6厘米，高4厘米。

如果从这个长方体上切下一个最大的正方体，这个正方体的体积是多少？- 解析：在这个长方体中切下最大的正方体，正方体的棱长取决于长方体最短的边，也就是高4厘米。

- 根据正方体体积公式V = a^3（a = 4厘米），体积为4^3=64立方厘米。

3. 有一个无盖的长方体鱼缸，长1.2米，宽0.5米，高0.8米。

制作这个鱼缸至少需要多少平方米的玻璃？- 解析：因为鱼缸无盖，所以求需要的玻璃面积就是求这个长方体5个面的面积之和。

- 这5个面的面积为S=1.2×0.5+(1.2×0.8 + 0.5×0.8)×2- 先计算1.2×0.5 = 0.6平方米，1.2×0.8 = 0.96平方米，0.5×0.8=0.4平方米。

- 则(0.96 + 0.4)×2=1.36×2 = 2.72平方米，再加上0.6平方米，得到0.6+2.72 = 3.32平方米。

4. 一个长方体水箱，从里面量长6分米，宽5分米，先倒入82升水，再浸入一块棱长2分米的正方体铁块，这时水面离水箱口1分米。

求这个水箱的容积。

- 解析：正方体铁块的体积为2^3=8立方分米，因为1升 = 1立方分米，82升=82立方分米。

- 倒入水和放入铁块后水和铁块的总体积为82 + 8=90立方分米。

长方体和正方体【知识点梳理】一、长方体和正方体1.我们周围许多物体的形状都是长方体或正方体（正方体也叫立方体）。

※举例：长方体：砖块、箱子……/正方体：魔方、骰子……2. （1）长方体是由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形。

在一个长方体中，相对的2个面完全相同，相对的4条棱长度相等。

长方体有12条棱，8个顶点。

（2）相交于一个顶点的三条棱分别叫做长方体的长、宽、高。

3.正方体是由6个完全相同的正方形围成的立体图形。

正方体有6个面，12条棱，8个顶点，6个面都是正方形，面积都相等，12条棱长度都相等。

4. 正方体可以看成是长、宽、高都相等的长方体。

我们可以用上图来表示长方体和正方体的关系。

当长方体有两个相对的面是正方形时，其他的4个面是相等的长方形。

（在长方体中最多可以有4个相同的面）5）正方体的6个面都是相等的正方形，12条棱的长度都相等。

6）正方体是特殊的长方体。

二、表面积1.长方体或正方体6个面的总面积，叫做它的表面积。

※举例：表面积即为长、正方体展开图总面积。

2.日常生活和生产中，经常需要计算一些长方体或正方体的表面积。

※举例：粉刷房间、贴瓷砖、包装礼盒、油漆水管、制作玻璃鱼缸（求面的大小）……3.求长方体、正方体表面积的公式：S长方体=（长×宽+长×高+宽×高）×2 =2（a·b+a·h+b·h）S正方体=棱长×棱长×6 =6a24.注意：求几个面。

当计算长方体的表面积时，有时候需要计算的不需要是6个面，因此需要仔细理解题意，求出需要的面的面积和。

求5个面的面积是：无盖的盒子、箱子等；游泳池的四壁和底面、一个抽屉、一个火柴盒的内盒、一本影集的封套；求4个面的面积是：一根方柱的涂漆表面、一个盒子四周的商标纸、一个烟囱或通风管或排水管、一个火柴盒的外盒；三、体积1.物体所占空间的大小叫做物体的体积。

习题讲解（相应题型的练习）
棱长加深拓展：
如图，有一个长5分米、宽和高都是3分米的长方体硬纸箱，如果用绳子将箱子横着捆两道，长着捆一道，打结处共用2分米。

一共要用绳子多长？
、
表面积：
4、如图，把一个长方体木料沿着虚线正好锯成3个完全一样的小正方体后，表面积增加了48平方分米。

这根木料的表面积是多少平方分米？
容积体积转化：
5、一个正方体水箱容积是343立方分米，把这一满水箱的水全部注入到一个长方体水箱内，已知长方体水箱长10分米，宽7分米，这个水箱内的水深多少分米？
7、有一只长150厘米，宽50厘米，高40厘米的水盒，里面装满水，这时放入一块高和长都是20厘米的长方体石块，水溢出4升，这块石头的宽是多少厘米？
8、一个玻璃鱼缸,长10分米,宽6分米,高8分米,鱼缸中原有水深7分米,现在一块假山石放入水中并浸没,水溢出48升.这块假石的体积有多少立方米?
9、把10升水倒入一个长2.5分米，宽2分米，高6分米的长方体水缸中。

⑴这时水面的高度离容器口有多少分米？
⑵此时，将一个正方体铁块全部浸入水中，水面离容器口还有2.4分米，你能求出正方体铁块的棱长吗？
(单位：cm)
３０。

一、长方体和正方体的棱长总和（长度单位）长方体棱长和=（长+宽+高）×4. 公式：4bL（a=c+)⨯+长变形：长=棱长和÷4-宽-高L正方体棱长和=棱长×12 公式：a=L12正棱长=棱长和÷12常见关键词：做一个长方体或正方体的框架、围成等。

典型题型：①用一根长84厘米的铁丝焊接成一个正方体的框架，这个正方体的棱长是多少？②用一根长72厘米的铁丝做一个宽5厘米，高5厘米的长方体灯笼框架，长是多少厘米？③一根铁丝可以扎成一个长9厘米，宽5厘米，高1厘米的长方体，如果用这根铁丝扎成一个正方体，这个正方体的棱长是多少？④一个长方体的棱长总和是160厘米，它的长是12厘米，宽是5厘米，这个长方体的高是多少厘米？⑤一个长方体的棱长总和是240厘米，相交于一个顶点的三条棱的长度和是多少？⑥一个长方体的棱长和是72厘米，它的长是9厘米，宽6厘米，它的表面积是多少平方厘米？⑦．用一根彩带困扎一种礼盒，如果接头处的彩带长30cm，求这条彩带的长度。

二、长方体和正方体的表面积（面积单位）前面=长×高右面=宽×高上面=长×宽长方体表面积=（前面+右面+上面）×2 正方体表面积=棱长×棱长×61.公式：2)⨯++=abbhahS（长26a S=正2.根据实际情况求表面积有时求5个面（如无盖鱼缸，粉刷墙面，铺瓷砖等），4个面（如烟囱（无上下），通风管（无左右），抽水管（无左右）等）。

典型题型：注意单位换算①一个装饼干的方形铁盒，底面是正方形，边长是20厘米，高是30厘米，这个铁盒的四周印满商标，商标的面积是多少平方厘米？②在校园里建一个长方体形状的游泳池，长50米，宽25米，深2.5米，在这个游泳池的四周和池底铺瓷砖，铺瓷砖的面积是多少平方米？③用60厘米长的铁丝焊接成一个正方体的框架，这个正方体的表面积是多少立方分米？④一个通风管的横截面是边长为5分米的正方形，长25米，如果用铁皮做这样的通风管50个，需要多少平方米的铁皮？⑤一张办公桌有3个抽屉，每个抽屉长50厘米，宽30厘米，高10厘米。

如果长方体的长、宽、高分别扩大到原来的2倍， 3倍，4倍，那么体积扩大 到 原来 的 倍
一根长方体的木料的体积是20立方分米，横截面 积是4平方分米，木料长是〔 〕
一根2米长的长方体钢材，沿横截面平均截成两段
后，外表积增加0.6平方分米，这段长方体钢材原
来的体积是
立方分米。
一个正方形的铁皮，边长8分米，在它的四角各 剪去一个边长为2分米的正方形后，再把剩下的
倍.
一根长方体木料，它的横截面积是9平方厘米，把它
截成2段，外表积增加
cm2
一个无盖的长方体金鱼缸，长8分米，宽6分米， 高7分米。制作这个鱼缸共需玻璃多少平方分米？ 这个鱼缸能装水多少升？〔玻璃厚度忽略不计〕
第6页，共20页。
正方体的外表积=棱长×棱长×6
把一个棱长为a的正方体，切成两个长方体，
几个物体锻造成一个物体，体积不变 把8块边长是1分米的正方体铁块熔成一个大正
方体，这个大正方体的体积和外表积各是多少?
体积：1×1×1×8=8〔dm3〕 大正方体的棱长为：2分米 大正方体的外表积：2×2×6=24〔dm2〕
第16页，共20页。
物体浸入水中的体积=排开水的体积
有一个底面积是300平方厘米、高10厘米的长方 体，里面盛有5厘米深的水。现在把一块石头浸 没到水里，水面上升2厘米。这块石头的体积是 多少立方厘米？
大正方体的棱长是小正方体的棱长的2倍，那么大
正方体的外表积是小正方体外表积的〔
〕
倍,大正方体的体积是小正方体体积的〔 〕倍。
第9页，共20页。
长方体的体积=长×宽×高
一个长方体的长、宽、高都扩大2倍，它的外表积扩大 倍，体积扩大 倍。
一个长方体的长、宽、高分别是a米、b米、h米。如果高

（必考题）小学数学五年级下册第三单元长方体和正方体测试题（包含答案解析）一、选择题1．一根正方体的木料，它的底面积是10cm2，把它截成3段，表面积增加了（）cm2。

A. 20B. 40C. 60D. 802．从8个小正方体拼成的大正方体中拿走一个小正方体，表面积（）A. 不变B. 变大了C. 变小了D. 无法确定3．用两个长为5cm，宽为4cm，高为3cm的长方体拼成一个表面积最小的大长方体，应把（）的两个面拼在一起。

A. 5×4B. 4×3C. 5×34．两个体积相等的正方体，它们棱的总长是24cm，每个正方体的体积是（）。

A. 16cm3B. 2cm3C. 1cm35．一根长方体木料，长1.5m，宽和高都是2dm，把它锯成4段，表面积最少增加（）dm²。

A. 8B. 16C. 24D. 326．如图，把这张硬纸片沿虚线折叠起来拼成一正方体，和3号相对的面是（）号。

A. 2B. 4C. 5D. 67．把一个棱长是2分米的正方体木块放入一个长12分米、宽9分米、高8分米的长方体盒子里面，最多能放（）个正方体木块．A. 90B. 96C. 1088．一个棱长和是172dm的长方体，它的长和宽之和为23dm，它的高是（）dm．A. 15B. 20C. 309．要用（）个棱长是1cm的小正方体才可以拼成一个棱长是3cm的大正方体．A. 9B. 18C. 27D. 54 10．一个长方体的长为20cm，宽为10cm，高为15cm，沿竖直或水平方向切一刀，将长方体切成两个相同的小长方体，表面积最多增加（）。

A. 200cm2B. 300cm2C. 400cm2D. 600cm2 11．下图中，（）是正方体的展开图.A. B. C.12．棱长是6厘米的正方体，它的表面积和体积（）A. 相等B. 不相等C. 不能相比二、填空题13．一个长方体的长是8厘米，宽和高一样长，都是长的，这个长方体有________个面是正方形，这个长方体的表面面积是________平方厘米，体积是________立方厘米。