下载文档原格式
《数值计算方法》复习试题一、填空题：1、⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=410141014A ，则A 的LU 分解为A ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦。
答案：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=15561415014115401411A 3、1)3(,2)2(,1)1(==-=f f f ，则过这三点的二次插值多项式中2x 的系数为 ，拉格朗日插值多项式为 。
答案：-1，)2)(1(21)3)(1(2)3)(2(21)(2--------=x x x x x x x L4、近似值*0.231x =关于真值229.0=x 有( 2 )位有效数字；5、设)(x f 可微,求方程)(x f x =的牛顿迭代格式是( )；答案)(1)(1n n n n n x f x f x x x '---=+6、对1)(3++=x x x f ,差商=]3,2,1,0[f ( 1 ),=]4,3,2,1,0[f ( 0 )；7、计算方法主要研究( 截断 )误差和( 舍入 )误差；8、用二分法求非线性方程 f (x )=0在区间(a ,b )内的根时，二分n 次后的误差限为( 12+-n a b )；10、已知f (1)＝2，f (2)＝3，f (4)＝5.9，则二次Newton 插值多项式中x 2系数为( 0.15 )； 11、 解线性方程组A x =b 的高斯顺序消元法满足的充要条件为(A 的各阶顺序主子式均不为零)。
12、 为了使计算32)1(6)1(41310---+-+=x x x y 的乘除法次数尽量地少，应将该表达式改写为11,))64(3(10-=-++=x t t t t y ，为了减少舍入误差，应将表达式19992001-改写为199920012+ 。
13、 用二分法求方程01)(3=-+=x x x f 在区间[0,1]内的根,进行一步后根的所在区间为 0.5，1 ,进行两步后根的所在区间为 0.5，0.75 。
第二章非线性方程求根习题2-11. 试寻找f(x)= x 3+6.6 x2-29.05 x +22.64=0的实根上下界,及正根所在的区间，区间长度取1。
解:由笛卡儿符号规则知，f(x)=0可能有二个正根或无正根f(-x)= -x 3+6.6 x2+29.05 x +22.64=0即x 3 -6.6 x2-29.05 x -22.64=0f(-x)=0有一个正根，因此，f(x)=0有一个负根。
由定理2-3，f(x)=0的正根上界f(x)=0的负根下界x0123456 6.39f(x)++-+++++正根所在区间为(1, 2),(2, 3)。
2．你能不利用多项式的求导公式，而借鉴于余数定理的思想，构造出P n(x)=a0x n+a1x n-1+...+a n-1x+a n在x0这点上的导数值的算法吗？习题2-21.用二分法求方程x2-x-1=0的正根，要求准确到小数点后第一位a F(a)b F(b)x F(x)0-1211-11-121 1.5-0.251.5-0.2521 1.750.31251.5-0.25 1.750.3125 1.6250.3015625 1.5-0.25 1.6250.015625 1.5625-0.12109375 1.5625-0.12104375 1.6250.015625 1.59375-0.053710937 1.59375-0.053710937 1.6250.015625 1.609375-0.019287109 1.609375-0.019287109 1.6250.015625 1.6171875-0.001892089 1.6171875-0.001892089 1.6250.015625 1.621093750.006851196 1.6171875-0.001892089 1.621093750.006851196 1.6191406250.002175738 1.6171875-0.001892089 1.619140620.002475738 1.6181640630.000290904X*=1.618K=5X*=1.593752．试证明用试位法（比例求根法），求在区间[0, 1]内的一个根必然收敛。
第一章 绪论（12）1、设0>x ，x 的相对误差为δ，求x ln 的误差。
[解]设0*>x 为x 的近似值，则有相对误差为δε=)(*x r ，绝对误差为**)(x x δε=，从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x ， 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%，求n x 的相对误差。
[解]设*x 为x 的近似值，则有相对误差为%2)(*=x r ε，绝对误差为**%2)(x x =ε，从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε，相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数，即误差不超过最后一位的半个单位，试指出它们是几位有效数字：1021.1*1=x ，031.0*2=x ，6.385*3=x ，430.56*4=x ，0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字；0031.0*2=x 有2位有效数字；6.385*3=x 有4位有效数字；430.56*4=x 有5位有效数字；0.17*5⨯=x 有2位有效数字。
4、利用公式（3.3）求下列各近似值的误差限，其中*4*3*2*1,,,x x x x 均为第3题所给的数。
（1）*4*2*1x x x ++； [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε；（2）*3*2*1x x x ；[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε；（3）*4*2/x x 。
数值分析（p11页）4 试证：对任给初值x 0,0)a >的牛顿迭代公式112(),0,1,2,......k ak k x x x k +=+= 恒成立下列关系式：2112(1)(,0,1,2,....(2)1,2,......kk k x k x x k x k +-=-=≥=证明：（1）(21122k k k k k kx a x x x x +-⎫⎛-=+==⎪ ⎝⎭（2） 取初值00>x ，显然有0>k x ，对任意0≥k ，a a x a x x a x x k k k k k ≥+⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛+=+2121216 证明：若k x 有n 位有效数字，则n k x -⨯≤-110218， 而()k k k k k x x x x x 288821821-=-⎪⎪⎭⎫⎝⎛+=-+ nnk k x x 2122110215.22104185.28--+⨯=⨯⨯<-∴>≥ 1k x +∴必有2n 位有效数字。
8 解：此题的相对误差限通常有两种解法. ①根据本章中所给出的定理：（设x 的近似数*x 可表示为m n a a a x 10......021*⨯±=，如果*x 具有l 位有效数字，则其相对误差限为()11**1021--⨯≤-l a x x x ，其中1a 为*x 中第一个非零数）则7.21=x ，有两位有效数字，相对误差限为025.010221111=⨯⨯≤--x x e 71.22=x ，有两位有效数字，相对误差限为025.010221122=⨯⨯≤--x x e 3 2.718x =，有两位有效数字，其相对误差限为：00025.010221333=⨯⨯≤--x e x ②第二种方法直接根据相对误差限的定义式求解 对于7.21=x ，0183.01<-e x∴其相对误差限为00678.07.20183.011≈<-x e x 同理对于71.22=x ，有003063.071.20083.022≈<-x e x 对于718.23=x ，有00012.0718.20003.033≈<-x e x备注：（1）两种方法均可得出相对误差限，但第一种是对于所有具有n 位有效数字的近似数都成立的正确结论，故他对误差限的估计偏大，但计算略简单些；而第二种方法给出较好的误差限估计，但计算稍复杂。
习 题 一 解 答1．取3.14，3.15，227，355113作为π的近似值，求各自的绝对误差，相对误差和有效数字的位数。
分析：求绝对误差的方法是按定义直接计算。
求相对误差的一般方法是先求出绝对误差再按定义式计算。
注意，不应先求相对误差再求绝对误差。
有效数字位数可以根据定义来求，即先由绝对误差确定近似数的绝对误差不超过那一位的半个单位，再确定有效数的末位是哪一位，进一步确定有效数字和有效数位。
有了定理2后，可以根据定理2更规范地解答。
根据定理2，首先要将数值转化为科学记数形式，然后解答。
解：（1）绝对误差:e(x)=π－3.14＝3.14159265…－3.14＝0.00159…≈0.0016。
相对误差：3()0.0016()0.51103.14r e x e x x-==≈⨯有效数字：因为π＝3.14159265…=0.314159265…×10，3.14＝0.314×10，m=1。
而π－3.14＝3.14159265…－3.14＝0.00159…所以│π－3.14│＝0.00159…≤0.005=0.5×10－2＝21311101022--⨯=⨯所以，3.14作为π的近似值有3个有效数字。
（2）绝对误差:e(x)=π－3.15＝3.14159265…－3.14＝－0.008407…≈－0.0085。
相对误差：2()0.0085()0.27103.15r e x e x x--==≈-⨯有效数字：因为π＝3.14159265…=0.314159265…×10，3.15＝0.315×10，m=1。
而π－3.15＝3.14159265…－3.15＝－0.008407…所以│π－3.15│＝0.008407……≤0.05=0.5×10－1＝11211101022--⨯=⨯所以，3.15作为π的近似值有2个有效数字。
（3）绝对误差:22() 3.14159265 3.1428571430.0012644930.00137e x π=-=-=-≈-相对误差：3()0.0013()0.4110227r e x e x x--==≈-⨯有效数字：因为π＝3.14159265...=0.314159265 (10)22 3.1428571430.3142857143107==⨯，m=1。
《数值计算与最优化》期末考试复习2一、填空（每题3分×12题）1．经过四舍五入得出1 6.1025x =，280.115x =，试问它们分别具有 5 ， 5 位有效数字。
1x +2x 的绝对误差限是 0.5ⅹ101-5+0.5ⅹ102-5 。
2．设()1(0)n n n f x a x a =+≠，则011[,,...,]n f x x x += 0 。
3．n 个节点的高斯求积公式具有 2n+1 次代数精度。
4．将区间[a,b]分为n 等份，复化梯形公式为 (b-a)/(2n)(f1+2f2+2f3+..+2fn+f n+1) 。
5．已知矩阵4316A -⎛⎫= ⎪-⎝⎭，则1||||A = 9 ，||||A ∞= 7 。
6．矩阵369282271218A ⎛⎫ ⎪= ⎪ ⎪⎝⎭的Crout 分解为A ⎛⎫⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭。
527042003- 1004103217．用迭代法解线性方程组(1)()k k x Bx f +=+,若0230B ⎛⎫= ⎪⎝⎭，55f ⎛⎫= ⎪⎝⎭，则此方法 不收敛 （填“收敛”或者“不收敛”）。
8．设Ax=b ，用SOR 迭代法解线性方程组，收敛的条件是（1）A 为 可逆 矩阵；（2）ω的取值范围是 0<ω<2 。
910．求方程23xx e -12ln ln 3k k x x +=+则 发散 。
（填“收敛”或者“发散”） 11．线性规划问题的基可行解X 对应于可行域D 的 基变量 。
12．将下列数学模型123123123123123max 23..72325,0,z x x x s t x x x x x x x x x x x x =-+-⎧++≤⎪-+≥⎪⎨-++=⎪⎪≥⎩为无约束化为标准型 。
解：min -z=x 1-2x 2+3x 3s.t. x 1+x 2+x 3+x 4=7x 1-x 2+x 3-x 5=2-3x 1+x 2+2x 3=5二、判断（每题1分×4题）1． 将3.141作为π的近似值，则它具有4位有效数字。
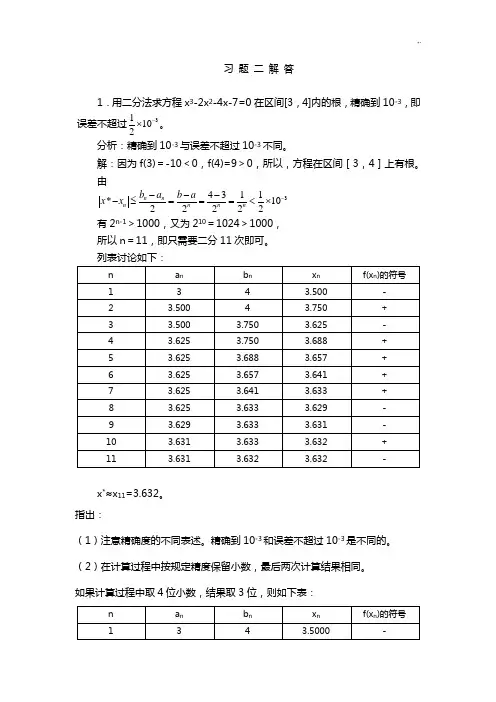
习 题 二 解 答1．用二分法求方程x 3-2x 2-4x-7=0在区间[3，4]内的根，精确到10-3，即误差不超过31102-⨯。
分析：精确到10-3与误差不超过10-3不同。
解：因为f(3)＝-10＜0，f(4)=9＞0，所以，方程在区间［3，4］上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1＞1000，又为210＝1024＞1000， 所以n ＝11，即只需要二分11次即可。
x *≈x 11=3.632。
指出：（1）注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
（2）在计算过程中按规定精度保留小数，最后两次计算结果相同。
如果计算过程中取4位小数，结果取3位，则如下表：（3）用秦九韶算法计算f(x n )比较简单。
1*．求方程x 3-2x 2-4x-7=0的隔根区间。
解：令32247y x x x =---， 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时，有12223,x x =-=。
函数单调区间列表分析如下：因为214902150327(),()y y -=-<=-<，所以方程在区间223(,)-上无根； 因为21490327()y -=-<，而函数在23(,)-∞-上单调增，函数值不可能变号，所以方程在该区间上无根；因为2150()y =-<，函数在(2,+∞)上单调增，所以方程在该区间上最多有一个根，而(3)=-10<0,y(4)=9>0，所以方程在区间(3,4)有一个根。
所以，该方程有一个根，隔根区间是(3.4)。
2．证明1sin 0x x --=在[0,1]内有一个根，使用二分法求误差不大于41102-⨯的根，需要迭代多少次？分析：证明方程在指定区间内有一个根，就是证明相应的函数在指定区间有至少一个零点。
1. 已知ln(
2.0)=0.6931;
ln(2.2)=0.7885, ln(2.3)=0.8329,
试用线性插值和抛物插值计算.ln2.1的值并估计误差（牛顿插值和拉格朗日插值）
3. 已知
求
的二次拟合曲线
，并求
的近似值。
4. 数值积分公式形如
试确定参数使公式代数精度尽量
高；（2）设
，推导余项公式
，并估计误差。
5. 已知数值积分公式为：
，试确定积分公式中的参数，使其代数精确度尽量高，并指出其代数精确度的次数。
6. 用复化Simpson 公式计算积分的近似值，要求误差限为。
7. 已知012113
,,424
x x x =
==，给出以这3个点为求积节点在[]0.1上的插值型求积公式。
8. 给出
900
,cos ≤≤x x 的函数表，步长 )60/1(1='=h ，若函数具有5位有效数字，研究用线性插值
求x cos 近似值时的总误差界。
9. 求一个次数不高于4次的多项式
)(x P ，使它满足0)0()0(='=P P ，1)1()1(='=P P ，1)2(
=P 。
10.单原子波函数的形式为bx
ae y -=，试按照最小二乘法决定参数a 和b ，已知数据如下：
11. 分别用梯形公式和辛普森公式计算下列积分：
⎰+1
024dx x x。
并估算误差。
12. 用矩阵的克劳特和克利特尔三角分解法求解方程组：⎪⎪⎪
⎪
⎪⎭
⎫
⎝⎛=
⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝
⎛71735301034211010
02014321x x x x )(x f )(2x p )0(f '⎰'+'++=≈1
)1()0()1()0()()(f D f C Bf Af x S dx x xf D C B A ,,,]1,0[)(4
C x f ∈⎰-=1
)
()()(x S dx x xf x R )]
()0([)]()0([2)(''20
h f f h h f f h
dx x f h
-++≈⎰
λλ()⎰
=1
0sin dx x x I 5105.0-⨯。
