例7 一射手的命中率为0.6, 连续向一目标射击 三次, 则命中的次数X ~B( 3, 0.6). ΩX ={ 0, 1, 2, 3 }.
若以 Ai 表示第 i 次命中, i =1, 2, 3, 则
P( X 0) P A1 A2 A3 (0.4)3 C30 (0.6)0 (0.4)3 P( X 1) P A1 A2 A3 P A1A2 A3 P A1 A2 A3
我们可以把可能的身高看作 随机变量X,
然后我们可以提出关于X的各种问题. 如 P(X>1.7) =? P(X≤1.5) =?
P(1.5<X<1.7) =?
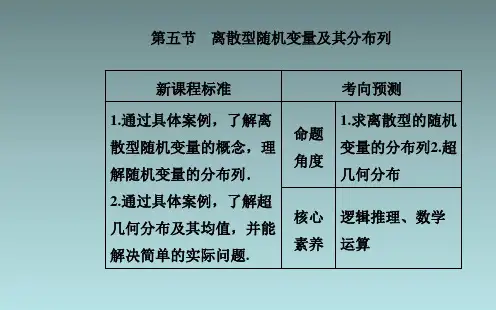
第二章 第一讲 随机变量及其分布律(离散型)
可见,随机事件这个概念实际上是包容在随机变 量这个更广的概念内. 也可以说,随机事件是从静态 的观点来研究随机现象,而随机变量则是一种动态的 观点,就象高等数学中常量与变量的区别那样.
3 (0.6)(0.4)2 C31(0.6)1(0.4)2
P( X 2) P A1A2 A3 P A1 A2 A3 P A1A2 A3
3 (0.6)2 (0.4) C32 (0.6)2 (0.4)1 P( X 3) P( A1A2 A3 ) (0.6)3 C33 (0.6)3(0.4)0
(1) X 0,1, 2,3,...... 问:P( X 10) ? (2) T t,t [0, ) P(100 X 1000) ?
(3) X 0,1,2,3,..., n 问:每日平均售多少朵?
第二章 第一讲 随机变量及其分布律(离散型)
例1 将一枚硬币抛掷两次, X 表示正面向上的次数, 则有如下对应关系:
P( X k) Cnk pk (1 p)nk , k 0,1, 2,...n