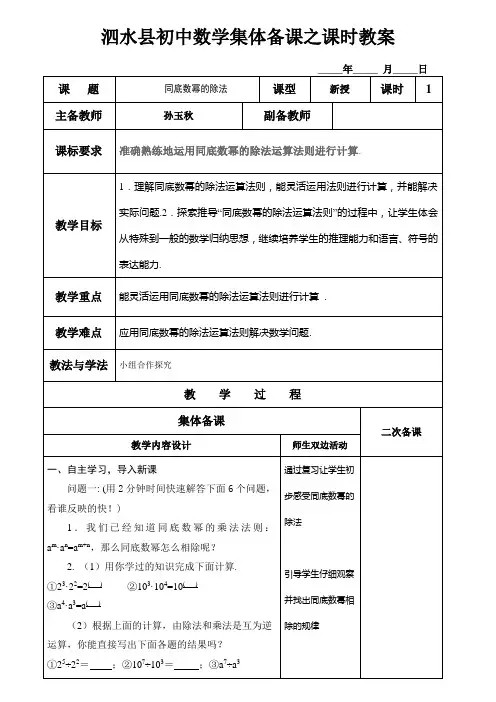
3.6.1 同底数幂的除法(1)

同底数幂的除法教案教案：同底数幂的除法一、教学目标：1.理解同底数幂的除法的概念和规则；2.掌握同底数幂的除法的计算方法；3.能够解决一些实际问题，运用同底数幂的除法进行计算。

二、教学内容：1.同底数幂的概念；2.同底数幂的除法的规则；3.同底数幂的除法的计算方法。

三、教学过程：1.导入新课：通过展示一道题目，激发学生对同底数幂的除法的兴趣，并进行讨论。

题目：计算2的4次方除以2的2次方。

解答：2的4次方除以2的2次方等于2的(4-2)次方，即2的2次方，所以答案是4、这是因为当分子和分母的底数相同时，我们可以把它们的指数相减，得到新的指数。

2.引入同底数幂的概念：通过简单的例子和图示，向学生介绍同底数幂的概念，并强调同底数幂的指数运算规律。

例子：计算3的5次方除以3的3次方。

解答：3的5次方除以3的3次方等于3的(5-3)次方，即3的2次方，所以答案是93.引入同底数幂的除法的规则：向学生介绍同底数幂的除法的规则，并通过举例进行解释。

规则：当同底数幂相除时，我们可以将它们的指数相减，得到新的指数。

例子：计算5的6次方除以5的4次方。

解答：5的6次方除以5的4次方等于5的(6-4)次方，即5的2次方，所以答案是254.练习与讨论：让学生自主完成下面的练习，并进行讨论和答案的讲解。

练习1：计算2的7次方除以2的5次方。

练习2：计算4的8次方除以4的6次方。

练习3：计算7的11次方除以7的8次方。

5.进一步拓展：让学生解决一些与同底数幂的除法相关的实际问题，加深对同底数幂的除法的理解和运用能力。

问题1：假设你每天走路步数都是3的5次方步，一周走了3的7次方步，你能计算出你每天走了几步吗？问题2：一个装有5的4次方毫升水的瓶子里，每天用水3的2次方毫升，这个瓶子里的水能用多少天？问题3：公司每年盈利6的5次方万元，用于分红的部分是6的3次方万元，每人分得的分红是多少万元？四、教学总结：通过本节课的学习，学生应该对同底数幂的除法有了较好的理解。

七年级同底数幂的知识点在学习数学的过程中，同底数幂是一个非常重要的知识点。

七年级是初中阶段的开始，学生们需要打好基础，扎实掌握同底数幂的知识。

本文将对同底数幂的概念、性质以及运算法则等方面进行详细讲解。

一、同底数幂的概念同底数幂是指底数相同但指数不同的幂，例如2的3次方和2的4次方都是同底数幂。

通常情况下，同一底数的不同幂形成一个数列，这个数列就叫做幂数列。

二、同底数幂的性质（1）同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加。

例如：2的3次方乘以2的4次方等于2的7次方。

（2）同底数幂的除法法则：同底数幂相除，底数不变，指数相减。

例如：2的5次方除以2的3次方等于2的2次方。

（3）同底数幂的幂法法则：同底数幂的指数相乘，底数不变。

例如：(2的3次方)的4次方等于2的12次方。

（4）同底数幂的负指数法则：一个数的负指数是指这个数的倒数的指数，即a的-b次方等于1/a的b次方。

例如：2的-3次方等于1/2的3次方。

（5）同底数幂相等的情况: 如果两个同底数幂的指数相等，那么这两个数就是相等的。

例如：2的4次方等于16，而4的2次方等于16，所以2的4次方和4的2次方相等。

三、同底数幂的运算法则同底数幂的运算法则主要包括加减、乘除和幂法运算。

（1）同底数幂的加减法：首先要将同底数幂中的底数分清楚，如果底数相同，则将指数相加或相减得到结果。

例如：2的3次方加上2的5次方等于2的8次方，2的5次方减去2的3次方等于2的2次方。

（2）同底数幂的乘法法则和除法法则前面已经讲解过，请读者自行回顾。

（3）同底数幂的幂法运算：同底数幂的幂法运算包括平方，立方，乘方和开方四种运算。

四、常见问题解答（1）什么是同底数幂？同底数幂是指底数相同但指数不同的幂，例如：2的3次方和2的4次方都是同底数幂。

（2）同底数幂的运算法则有哪些？同底数幂的运算法则包括加减、乘除和幂法运算。

（3）同底数幂的幂法运算有哪些？同底数幂的幂法运算包括平方，立方，乘方和开方四种运算。

同底数幂的除法同底数幂除法法则：同底数幂相除，底数不变，指数相减。

即a m ÷a n ==a m －n （a ≠0，m ，n 都是正整数，且m ＞n ）正确理解法则的含义应注意的问题：1. 在运算公式n m n m aa a -=÷中，0≠a ，因为当a=0时，a 的非零次幂都为0，而0不能作除数，所以0≠a2. 底数相同，如23)5(6-÷-是除法运算，但不是同底数幂相除，不能运用这个法则3. 相除运算，如23a a +是同底数幂，但不是相除运算，不能运用这个法则4. 运算结果是底数不变，指数相减，而不是指数相除例1 计算 （1）22243647)4();())(3(;)())(2(;b bxy xy x x a a m ÷÷-÷-÷+ 解：（1）（2）（3）（4）知能点6 同底数幂的除法应用例2 计算：（1）8322158213)())(2(;a a a x x x ÷-÷-÷÷提示：对于两个或三个以上的同底数幂相除，仍然适用运算性质。

解：（1）（2）知能点7 零指数与负整数指数的意义（1）零指数 )0(10≠=a a 即任何不等于0的数的0次幂都等于1（2）负整数指数 =-p a （p 是正整数）即任何不等于零的数的-p(p 是正整数)次幂，等于这个数的p 次幂的倒数。

规律点拔：（1） 零指数幂和负整数指数幂中，底数都不能为0，即0≠a（2） 规定了零指数和负整数指数的意义后，正整数指数幂的运算性质就可以推广到整数指数幂知能点8用小数或分数表示绝对值较小的数例3 （1）4203106.1)3(;87)2(;10---⨯+解：（1）（2）（3）【知能整合提升】一、选择题1、如果mn n m a A a =÷)(，那么A 的值为（ ）A 、m a ；B 、n a ；C 、1；D 、mn a 。

3.6同底数幂的除法班级 姓名一、复习引入1、填空：（1）∵ ⨯22（ ）＝52∴ 根据除法是乘法的逆运算可得=÷2522（ ）（2）实际上，根据乘方的意义可知：)() () () () () () (2225⨯⨯⨯⨯⨯=÷＝) () () (22-= 类似地，=÷23a a )() () () () (⨯⨯⨯ ＝) () () (-=a a （0≠a ）2、归纳同底数幂相除的法则：同底数幂相除，底数 ，指数 。

用字母可表示为：=÷n m a a 。

（0≠a n m,都是正整数，且n m >）二、知识梳理：1．同底数幂相除，底数不变，指数相 。

a m ÷a n = (a ≠0，m,n 都是正整数且m>n)2．小结幂的运算法则：Ⅰ同底数的幂相乘，底数_ ____，指数__ ___。

如a 2·a 3=___ _。

Ⅱ幂的乘方，底数_ ____，指数____ _。

如(a 2)3=__ __。

Ⅲ积的乘方，等于把积的每一个因式分别__ __，再把所得的幂 ____。

如32⨯__ _=__ _。

Ⅳ≠0，m,n 都是正整数且m>n)同底数的幂相除，底数__ ___，指数__ ___。

如a 20÷a 12=_ ___。

3、出示例1，计算：（1）39a a ÷ （2）71222÷（3）)()(4x x -÷- （4）811)3()3(-- 4、出示例2，计算：（1）8855÷ （2）245a a a ∙÷（3）34)(y y -÷ （4）26)()(ab ab ÷（6）35)()(b a b a +÷+三、课堂反馈：计算：（1）()()25xy xy -÷- （2）)(2410y y y÷÷ （3）x 4·x 6÷x 5(4) 37)21()21(-÷（5）m m a a )()(3-÷- （6）a 15÷a 7－2a 4·a 4（7）4263)()(x x -÷- （8）()5q p -÷()2p q -（9）43+n x÷（-1+n x ）÷n x 2 （n 是正整数）。

幂的运算法则公式
幂运算法则公式：同底数幂相乘，底数不变，指数相加，即a m×a n=a（m+n）；同底数幂相除，底数不变，指数相减，即a m÷a n=a（m-n）。

（1）同底数幂的乘法：同底数幂相乘，底数不变，指数相加。

a m×a n=a（m+n）(a≠0,m,n均为正整数，并且m>n)
（2）同底数幂的除法：同底数幂相除，底数不变，指数相减。

a m÷a n=a（m-n）(a≠0,m,n均为正整数，并且m>n)
（3）幂的乘方：幂的乘方，底数不变，指数相乘。

(a m)n=a(mn)，(m,n都为正整数)
（4）积的乘方：等于将积的每个因式分别乘方，再把所得的幂相乘。

(ab)n=a n b n，（n为正整数）
（5）分式的乘方：把分式的分子、分母分别乘方即为乘方结果
(a/b)n=(a n)/(b n)，（n为正整数）
（6）零指数：
a0=1 (a≠0)
（7）负整数指数幂
a-p=1/a p(a≠0, p是正整数）
（8）负实数指数幂
a(-p)=1/(a)p或（1/a）p(a≠0，p为正实数）（9）正整数指数幂
①a m a n=a m+n
②（a m）n=a mn
③a m/a n=a m-n(m大于n,a≠0)
④(ab)n=a n b n。

幂的运算法则公式
幂的运算法则公式如下：同底数幂相乘，底数不变，指数相加，即a^m×a^n=a^(m+n)；同底数幂相除，底数不变，指数相减，即a^m÷a^n=a^(m-n)（m>n）。

同底数幂的乘法是将同一底数的幂相乘，底数不变，指数相加。

例如，a^2×a^3=a^(2+3)=a^5.
同底数幂的除法是将同一底数的幂相除，底数不变，指数相减。

例如，a^5÷a^2=a^(5-2)=a^3.
幂的乘方是将幂的指数相乘，底数不变。

例如，
(a^m)^n=a^(m×n)。

积的乘方是将积的每个因式分别乘方，再把所得的幂相乘。

例如，(ab)^n=a^n×b^n。

分式的乘方是将分式的分子、分母分别乘方。

例如，
(a/b)^n=a^n/b^n。

零指数的幂为1，即a^0=1（a≠0）。

负整数指数幂为a的倒数，即a^(-p)=1/a^p（a≠0，p是正
整数）。

负实数指数幂为a的倒数或者1/a，即a^(-p)=1/a^p（a≠0，p为正实数）。

正整数指数幂有以下几种情况：①a^1=a；②a^0=1
（a≠0）；③a^m/a^n=a^(m-n)（m>n，a≠0）；
④(ab)^n=a^n×b^n。

需注意的是，原文中有大量的格式错误和无用的数字，已经在修改时进行了删除和改写。

同底数幂的除法四注意同底数幂的除法法则是：同底数的幂相除，底数不变，指数相减.用公式表示为：m a ÷n a =m n a -（0a ≠，m 、n 都是正整数，且m n >），这个公式看似简单，但如果理解不深，却很容易出错.因此在学习时，要特别注意以下几个方面：一、注意条件在所给的条件中，强调了0a ≠，这是因为：若0a =，则0m n a a ==，由于0不能作除数，所以0a ≠；从m 、n 都是正整数，且m n >的情况可以概括出同底数幂的除法法则，没有涉及零指数幂、负整数指数幂和分数指数幂等情况.二、注意底数公式中的底数是用一个字母a 表示的，但我们在理解的时候，不能简单地把它理解为一个数、一个字母，而应全面理解，其底数主要有以下几种情况：1.底数为常数这种情况比较容易处理，底数不变，指数相减就可以了.如1310÷610=13610-=710. 2.底数是单项式底数为单项式，特别是多个字母乘积的单项式，在运算中，要把多个字母乘积的项看作是公式中的“a ”，也就是说要把它看成一个整体，就容易计算了.如7()ab ÷4()ab =74()ab -=3()ab =33a b .3.底数为多项式若底数为多项式，也要把它看成是公式中的“a ”，即也要把它看成一个整体.如5()x y +÷3()x y +=532()()x y x y -+=+.三、注意指数当指数为常数、单项式、多项式时，按照法则运算即可，但当两个数的指数具有倍数关系时，我们就很容易把两个指数相除，导致出错.例如：（1）49÷29=29=81；（2）69÷39=29=81.在计算（1）时，指数相除和指数相减的结果是一样的，这只是一种特殊情况；在计算（2）时，这样相除就错了，可以和（1）对照一下，用相减和相除这两种方法计算所得的结果是不一样的，要特别注意.四、注意符号和括号底数带有负号、括号时，可分为同底和不同底两种情况.同底带括号的，在运算时，应把括号带上，运算结果的符号由指数的奇偶性决定.如4()a -÷2()a -=42()a --=2()a -=2a . 当底数不同时应先变为同底的，然后再按照法则计算，如7a ÷4()a -=7a ÷4a =3a .综上所述，在学习同底数幂除法的过程中，只要注意了上述几个方面的问题，就能正确运算了.。

浙教版数学七年级下册3.6《同底数幂的除法》教学设计一. 教材分析同底数幂的除法是初中数学中的一个重要概念，也是幂的运算法则之一。

浙教版数学七年级下册3.6节主要介绍同底数幂的除法法则，内容包括同底数幂的除法运算、指数的变化规律以及应用。

通过本节课的学习，学生能够掌握同底数幂的除法运算规则，并能够运用这些规则解决实际问题。

二. 学情分析学生在学习同底数幂的除法之前，已经学习了同底数幂的乘法、幂的乘方等知识。

因此，学生对于幂的概念和幂的运算规则已经有一定的了解。

但学生在运用同底数幂的除法规则解决实际问题时，可能会遇到一些困难。

因此，在教学过程中，教师需要引导学生通过实际例子来理解同底数幂的除法规则，并能够灵活运用。

三. 教学目标1.理解同底数幂的除法规则，掌握同底数幂的除法运算方法。

2.能够运用同底数幂的除法规则解决实际问题。

3.培养学生的逻辑思维能力和解决问题的能力。

四. 教学重难点1.同底数幂的除法规则的理解和运用。

2.指数变化规律的把握。

五. 教学方法1.情境教学法：通过实际例子引导学生理解同底数幂的除法规则。

2.归纳教学法：引导学生通过实际例子总结同底数幂的除法规则。

3.练习法：通过大量的练习题，让学生巩固同底数幂的除法运算。

六. 教学准备1.教学PPT：制作同底数幂的除法相关内容的PPT。

2.练习题：准备一些同底数幂的除法运算题目，用于课堂练习和课后作业。

七. 教学过程1.导入（5分钟）教师通过一个实际例子，如“计算34÷32”，引导学生思考同底数幂的除法规则。

让学生回顾已学的同底数幂的乘法规则，激发学生的学习兴趣。

2.呈现（15分钟）教师通过PPT展示同底数幂的除法规则，并用简洁的语言进行解释。

同时，教师可以通过一些具体的例子来说明同底数幂的除法规则，让学生更好地理解。

3.操练（15分钟）教师让学生进行同底数幂的除法运算练习。

教师可以设置一些不同难度的题目，让学生逐步掌握同底数幂的除法规则。

底数幂的运算法则
底数幂的运算法则是数学中常见的运算规律之一，它指导我们在进行幂运算时如何处理不同底数的幂的乘除、幂的乘方等操作。

具体来说，底数幂的运算法则包括以下几个方面：
1.同底数幂的乘除法则：当两个底数相同时，它们的幂可以通过将指数相加或相减得到。

即a的m次方乘以a的n次方等于a的m+n 次方，a的m次方除以a的n次方等于a的m-n次方。

2.幂的乘方法则：对于同一底数的幂，它们的幂次可以通过将指数相乘得到。

即(a的m次方)的n次方等于a的m×n次方。

3.幂的倒数和负指数法则：一个数的倒数是这个数的幂次为-1的值，即a的-1次方等于1/a。

同时，一个数的负指数是这个数的幂次为负数的值，即a的-n次方等于1/a的n次方。

这些底数幂的运算法则在数学中应用广泛，可以帮助我们简化计算、化简式子、推导公式等。

因此，熟练掌握这些运算法则对于学好数学至关重要。

- 1 -。

汇报人：日期:•定义和公式•运算性质•计算方法•实例解析•练习与解答定义和公式如果两个幂的底数相同，且第一个幂的指数大于第二个幂的指数，那么就称第一个幂能被第二个幂整除。

同底数幂的除法$10^{2}$ 能被 $10^{1}$ 整除，因为 $10^{2} \div 10^{1} = 10$。

例如同底数幂的除法公式$a^{m} \div a^{n} = a^{m - n}$ （其中 a 不为 0，m，n 均为正整数）。

解释根据指数的性质，$a^{m}$ 表示 a 的 m 次方，同理，$a^{n}$ 表示 a 的 n 次方。

当 m>n 时，$a^{m} \div a^{n}$ 就是 a 的 (m-n) 次方。

因此，$a^{m} \div a^{n} = a^{m - n}$。

例子$2^{4} \div 2^{2} = 2^{4 - 2} = 2^{2} = 4$。

运算性质$a^m/a^n=a^(m-n)$公式同底数幂相除，指数相减，底数不变。

解释在解决涉及同底数幂除法的问题时，可以直接使用该公式进行计算。

应用运算性质0102运算性质的适用范围当底数不同时，需要先转化为同底数幂才能进行除法运算。

该公式只适用于底数相同的幂相除的情况。

计算方法整数指数幂的除法是基本的幂运算，它可以表示为底数除以指数。

对于两个底数相同的幂相除，可以将底数不变，指数相减。

例如，$a^m \div a^n = a^{m-n}$。

当m>n时，结果为a^(m-n)；当m<n时，结果为1。

整数指数幂的除法详细描述总结词总结词负整数指数幂的除法是基于负整数指数幂的性质，它可以表示为底数的倒数乘以指数的相反数。

详细描述对于底数为a，指数为n的幂，它的负整数指数幂为a^(-n)，等于a的倒数的n次方。

因此，$a^m \div a^{-n} = a^{m+n}$。

当m>0，n>0时，结果为a^(m+n)；当m<0，n<0时，结果为1。