有效值 平均值和平均功率
- 格式:ppt
- 大小:457.54 KB
- 文档页数:17


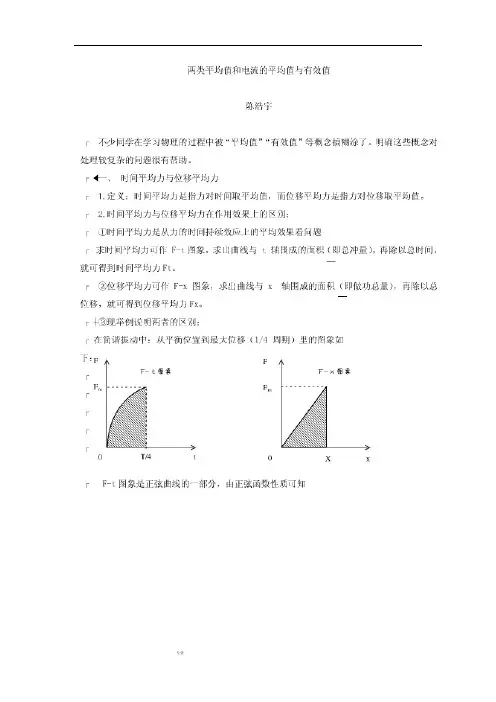
交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期的平均值为零,而技术上应用的交流电的平均值是指在一个周期交流电的绝对值的平均值.也等于交流电在正半个周期的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。



电流有效值和平均值电流是电荷在电路中流动时所带电荷的量度。
在电路中,我们常常会提到电流的有效值和平均值,这两个概念对于理解电流的性质和应用非常重要。
电流的有效值是指交流电流中等效于相同功率的直流电流值。
在交流电路中,电流的大小是随时间变化的,通过对电流的波形进行采样和计算,可以得到电流的有效值。
有效值的计算方法是将电流的每个采样点的平方值求平均后再开平方根。
这是因为交流电流的波形是正弦波形,它的平方和的平均值等于平方根的平方。
在电路设计和分析中,有效值常常用来计算电流通过电阻、电容或者电感时的功率损耗。
例如,在家庭用电中,我们常常使用交流电,而电器的功率通常是以有效值来标识的。
通过使用有效值,我们可以更准确地计算电器的功耗,并且可以更好地设计电路以满足功率要求。
另一方面,电流的平均值是指电流波形在一个周期内的平均值。
对于直流电流来说,平均值等于电流的值。
但对于交流电流来说,由于其波形的周期性变化,平均值并不等于电流的值。
交流电流的平均值计算方法是将电流波形在一个周期内的面积除以周期的长度。
平均值在某些特定情况下非常有用。
例如,在交流电路中,平均值可以用于计算电压和电流的相位差。
此外,平均值也可以用来计算电路中的功率因数,即有用功与视在功的比值。
功率因数对于电路的效率和运行稳定性非常重要。
总结起来,电流的有效值和平均值是电流波形的两个重要的量度。
有效值用于计算功率损耗和电器功耗,平均值用于计算相位差和功率因数。
通过准确理解和应用这两个概念,我们可以更好地设计和分析电路,提高电路的效率和稳定性。
对于电流的研究和应用,这两个概念是不可或缺的。


交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间内,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期内的平均值为零,而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值.也等于交流电在正半个周期内的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。


交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间内,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期内的平均值为零,而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值.也等于交流电在正半个周期内的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。

交流电的有效值和平均值交流电流的有效值按电流的热效应来规定,定义为:因此,有效值也叫均方根值.有效值的意义是:在一个周期的时间内,交流电流通过电阻R产生的热量与稳恒电流通过同一个电阻产生的热量相等.或者说,就电流通过电阻产生的热量说,(变化)与(稳定)等效.类似地,交流电压、交流电动势的有效值定义为:不同波形的交流电,有效值与最大值的关系不同.对正弦交流电,,由定义得:=即正弦交流电的有效值等于最大值被除.对下图所示的方波说,由定义显然可得有效值与最大值相等.对下图所示的三角波和锯齿波说,由定义可得有效值等于最大值被除..交流电在一个周期内的平均值为零,而技术上应用的交流电的平均值是指在一个周期内交流电的绝对值的平均值.也等于交流电在正半个周期内的平均值.即:= ,= ,=不同波形的交流电,平均值与最大值的关系不同.对正弦交流电,由定义得:= = = 0×637Im正弦交流电的有效值与平均值之比为:.对于方波:对于三角波、锯齿波,由定义得:=交流电的有效值与平均值是两个不同的概念,一般说,有效值比平均值大.实用上用得最多的交流电是正弦交流电.交流电的最大值、有效值、平均值中,有效值用得最多.这是因为我们在讨论交流电的平均功率时很自然地要引用有效值的概念.对正弦交流电,设:,则:= ==所以:==由此可见,从计算交流电的平均功率上看,交流电的有效值与稳恒电流的值相当.我们常用磁电式电表指针偏转的角度正比于通过偏转线框的电流强度.对单向脉动电流说,指针偏转角度正比于电流的平均值.在磁电式电表上加接整流二极管用来测量交流电流时,电表真正测量的是交流电流的平均值.因为有效值用得最多,几乎所有的交流电表的表盘都是按“有效值”来刻度的,这一点我们应该特别注意.电磁式电表指针偏转的角度正比于电流的平方,这是与磁电式电表不同的地方.。
第13章非正弦周期电流电路和信号的频谱13.1 复习笔记一、非正弦周期函数的傅里叶分解1.周期函数分解为傅里叶级数设周期函数f(t)=f(t+kT)(k=0,1,2…),T为周期。
若给定的f(t)满足狄里赫利条件,那么它就能展开成一个收敛的傅里叶级数,其数学表达式为其中,各个参数的表达式如下A0=a0φk=arctan(-b k/a k)2.周期函数的谐波定性分析定性判断周期函数存在哪些谐波成分,然后具体计算各次谐波的幅值与相位。
(1)f(t)为奇函数,即f(t)=-f(-t),f(t)的展开式中只能含有奇函数,即(2)f(t)为偶函数,即f(t)=f(-t),f(t)的展开式中只含有偶函数,即(3)f(t)为奇谐波函数,即f(t)=-f(t±T/2),f(t)的展开式中只含奇次谐波,即(4)f(t)为偶谐波函数,即f(t)=f(t±T/2),f(t)的展开式中只含直流分量和偶次谐波,即二、有效值、平均值和平均功率1.非正弦周期电流电路的有效值和平均值设非正弦周期电流其有效值、平均值的计算方法如表13-1-1所示。
表13-1-1注:①非正弦周期电流平均值等于此电流绝对值的平均值;②正弦量平均值I av=0.898I。
2.非正弦周期电流电路的功率计算(1)非正弦周期电流电路的瞬时功率为(2)非正弦周期电流电路的平均功率为其中,φk=φuk-φik,k=1,2…。
即平均功率等于恒定分量构成的功率和各次谐波平均功率的代数和。
(3)非正弦周期电流电路的视在功率:S=UI。
三、非正弦周期电流电路的计算在非正弦周期激励电压、电流或外施信号作用下,分析和计算线性电路的方法,主要利用傅里叶级数展开法——谐波分析法。
计算步骤:(1)把已知的非正弦周期电压u(t)或电流i(t)展开成傅里叶级数,高次谐波取到哪一项,要根据所需准确度的高低而定;(2)应用叠加定理对直流分量和各次谐波分量单独作用计算;(3)将第二步所得结果在时域中进行叠加,即得最后所需要的结果。
直流脉冲电流的平均值与有效值的关系-概述说明以及解释1.引言1.1 概述直流脉冲电流是一种特殊的电流波形,它由直流电流和脉冲电流组合而成。
直流电流是指电流在一段时间内保持不变的电流,而脉冲电流则是指电流在一段时间内以瞬时高电流或低电流的形式出现。
直流脉冲电流的平均值与有效值的关系在电力工程、电子技术和通信领域中具有重要的意义。
平均值是指在一个周期内电流的总和除以周期的长度,而有效值则是指一个周期内电流的平方和再取平均值后开平方根得到的值。
平均值和有效值是描述电流大小的两个重要指标。
本文将深入探讨直流脉冲电流平均值与有效值之间的关系,包括其定义、概念和计算方法。
通过对这些内容的研究,我们将能够更好地理解和应用直流脉冲电流的特性。
在正文部分,我们将首先对直流脉冲电流进行定义,并介绍平均值和有效值的概念。
随后,我们将详细讨论平均值和有效值的计算方法,并解释它们之间的数学关系。
结论部分将总结我们的研究结果,并探讨平均值和有效值的关系对于实际应用的意义。
我们还将介绍一些应用场景,说明在不同领域中如何利用平均值和有效值来解决实际问题。
通过本文的阅读,读者将能够全面了解直流脉冲电流的平均值与有效值的关系,并在实际应用中灵活运用这些知识。
无论是从事电力工程、电子技术还是通信领域的专业人士,都将受益于本文所提供的理论和实践指导。
1.2文章结构文章结构部分主要介绍了整篇文章的组织结构,包括引言、正文和结论三个部分。
通过明确文章的结构,读者可以更好地理解和阅读文章的内容。
在引言部分,我们将对该主题进行概述,介绍直流脉冲电流的基本定义和特点。
接着,我们会对文章的结构进行说明,包括正文部分的各个小节内容和目的。
正文部分是文章的核心内容,将详细探讨直流脉冲电流的平均值与有效值之间的关系。
我们首先会给出直流脉冲电流的定义,包括其产生原理和应用领域。
然后,我们会介绍平均值和有效值的概念,同时解释它们之间的区别和联系。
最后,我们会详细讲解平均值和有效值的计算方法,包括数学公式和实际操作步骤。